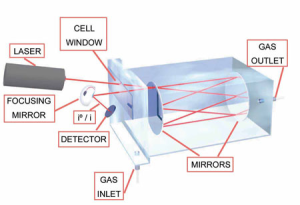
Định luật Beer-Lambert trong quang học là một mối quan hệ thực nghiệm liên hệ sự hấp thụ ánh sáng của một vật liệu với các đặc tính của vật liệu mà ánh sáng truyền qua. Đây là cơ sở của phương pháp quang phổ hấp thụ, cho phép đo nồng độ của các loại khí khác nhau trong một buồng chứa.

	Nguyên lý của một máy quang phổ hấp thụ, được minh họa ở bên trái, như sau. Hãy xem xét hai thí nghiệm sau đây. Đầu tiên, chúng ta thực hiện một thí nghiệm đối chứng, trong đó chúng ta chiếu ánh sáng ở một tần số nhất định từ một phía vào một bình chứa một loại khí tham chiếu nào đó. Ta đo cường độ ánh sáng (giả sử là [latex]I_0[/latex]) ở phía bên kia của bình chứa. Sau đó, chúng ta thêm một loại khí khác vào bình chứa, lặp lại thí nghiệm và đo lại cường độ ánh sáng (giả sử là [latex]I[/latex]). Tùy thuộc vào các đặc tính hấp thụ, cũng như nồng độ [latex]x[/latex] của khí được thêm vào, ánh sáng sẽ bị hấp thụ nhiều hay ít hơn so với trường hợp tham chiếu.
	Định luật Beer-Lambert giả định rằng log-tỷ số [latex]\log(I/I_0)[/latex] là tuyến tính với nồng độ [latex]x[/latex]. Nói cách khác, [latex]y = \log(I/I_0) = ax[/latex], trong đó hằng số [latex]a[/latex] phụ thuộc vào tần số ánh sáng và vào loại khí.

Nếu bình chứa có một hỗn hợp gồm [latex]n[/latex] khí ‘‘tinh khiết’’, định luật này giả định rằng logarit của tỷ số cường độ ánh sáng là một hàm tuyến tính của nồng độ của mỗi khí trong hỗn hợp. Do đó, log-tỷ số của các cường độ có dạng [latex]y=a^Tx[/latex] với một véctơ nào đó [latex]a \in \mathbb{R}^n[/latex], trong đó [latex]x[/latex] là véctơ nồng độ. Các hệ số [latex]a_j[/latex], [latex]j= 1, \cdots, n[/latex] tương ứng với log-tỷ số của cường độ ánh sáng khi [latex]x= e_j[/latex] (véctơ thứ [latex]j[/latex] của cơ sở chính tắc, tương ứng với khí tinh khiết thứ [latex]j[/latex]). Đại lượng [latex]a_j[/latex] được gọi là hệ số hấp thụ của khí thứ [latex]j[/latex] và có thể được đo trong phòng thí nghiệm.

Xem thêm: Quang phổ hấp thụ: sử dụng các phép đo ở các tần số ánh sáng khác nhau.