14. Universal derivation

[latexpage]

14.1  An example:  the Meno

In one of Plato’s dialogues, the Meno, Socrates uses questions and prompts to direct a young slave boy in the process of making a square that has twice the area of a given square, by using the diagonal of the given square as a side in the new square.  Socrates draws a square 1 foot on a side in the dirt.  The young boy at first just suggests that to double its area, the two sides of the square should be doubled, but Socrates shows him that this would result in a square that is four times the area of the given square; that is, a square of the size four square feet.  Next, Socrates takes this 2×2 square, which has four square feet, and shows the boy how to make a square double its size.

Socrates: Tell me, boy, is not this a square of four feet that I have drawn?
Boy: Yes.
Socrates: And now I add another square equal to the former one?
Boy: Yes.
Socrates: And a third, which is equal to either of them?
Boy: Yes.
Socrates: Suppose that we fill up the vacant corner?
Boy: Very good.
Socrates: Here, then, there are four equal spaces?
Boy: Yes.^[12]

So what Socrates has drawn at this point looks like:

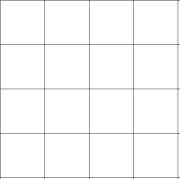
Suppose each square is a foot on a side.  Socrates will now ask the boy how to make a square that is of eight square feet, or twice the size of their initial 2×2 square.  Socrates has a goal and method in drawing the square four times the size of the original.

Socrates: And how many times larger is this space than the other?
Boy: Four times.
Socrates: But it ought to have been twice only, as you will remember.
Boy: True.
Socrates: And does not this line, reaching from corner to corner, bisect each of these spaces?

By “spaces”, Socrates means each of the 2×2 squares.  Socrates has now drawn the following:

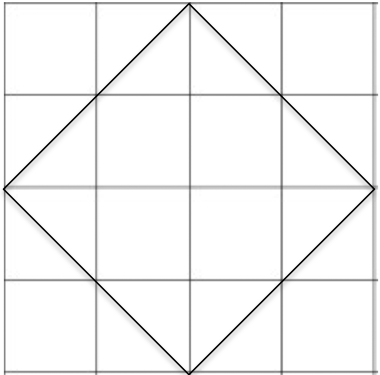
Boy: Yes.
Socrates: And are there not here four equal lines that contain this new square?
Boy: There are.
Socrates: Look and see how much this new square is.
Boy: I do not understand.

After some discussion, Socrates gets the boy to see that where the new line cuts a small square, it cuts it in half.  So, adding the whole small squares inside this new square, and adding the half small squares inside this new square, the boy is able to answer.

Socrates: The new square is of how many feet?
Boy: Of eight feet.
Socrates: And from what line do you get this new square?
Boy: From this.  [The boy presumably points at the dark line in our diagram.]
Socrates: That is, from the line which extends from corner to corner of the each of the spaces of four feet?
Boy: Yes.
Socrates: And that is the line that the educated call the “diagonal”. And if this is the proper name, then you, Meno’s slave, are prepared to affirm that the double space is the square of the diagonal?
Boy: Certainly, Socrates.

For the original square that was 2×2 feet, by drawing a diagonal of the square we were able to draw one side of a square that is twice the area.  Socrates has demonstrated how to make a square twice the area of any given square:  make the new square’s sides each as large as the diagonal of the given square.

It is curious that merely by questioning the slave (who would have been a child of a Greek family defeated in battle, and would have been deprived of any education), Socrates is able to get him to complete a proof.  Plato takes this as a demonstration of a strange metaphysical doctrine that each of us once knew everything and have forgotten it, and now we just need to be helped to remember the truth.  But we should note a different and interesting fact.  Neither Socrates nor the slave boy ever doubts that Socrates’s demonstration is true of all squares.  That is, while Socrates draws squares in the dirt, the slave boy never says, “Well, Socrates, you’ve proved that to make a square twice as big as this square that you have drawn, I need to take the diagonal of this square as a side of my new square.  But what about a square that’s much smaller or larger than the one you drew here?”

That is in fact a very perplexing question.  Why is Socrates’s demonstration good for all, for any, squares?

14.2  A familiar strangeness

We have saved for last the most subtle issue about reasoning with quantifiers:  how shall we prove something is universally true?

Consider the following argument.  We will assume a first order logical language that talks about numbers, since it is sometimes easier to imagine something true of everything in our domain of discourse if we are talking about numbers.

All numbers evenly divisible by eight are evenly divisible by four.

All numbers evenly divisible by four are evenly divisible by two.

_____

All numbers evenly divisible by eight are evenly divisible by two.

Let us assume an implicit translation key, and then we can say that the following is a translation of this argument.

∀x(Fx→Gx)

∀x(Gx→Hx)

_____

∀x(Fx→Hx)

This looks like a valid argument.  Indeed, it may seem obvious that it is valid.  But to prove it, we need some way to be able to prove a universal statement.

But how could we do such a thing?  There are infinitely many numbers, so surely we cannot check them all.  How do we prove that something is true of all numbers, without taking an infinite amount of time and creating an infinitely long proof?

The odds are that you already know how to do this, although you have never reflected on your ability. You most likely saw a proof of a universal claim far back in grade school, and without reflection concluded it was good and proper.  For example, when you were first taught that the sum of the interior angles of a triangle is equivalent to two right angles, you might have seen a proof that used a single triangle as an illustration.  It might have gone something like this:  assume lines AB and CD are parallel, and that two other line segments EF and EG cross those parallel lines, and meet on AB at E.  Assume also that the alternate angles for any line crossing parallel lines are equal.  Assume that a line is equivalent to two right angles, or 180 degrees.  Then, in the following picture, b’=b, c’=c, and b’+c’+a=180 degrees.  Thus, a+b+c=180 degrees.

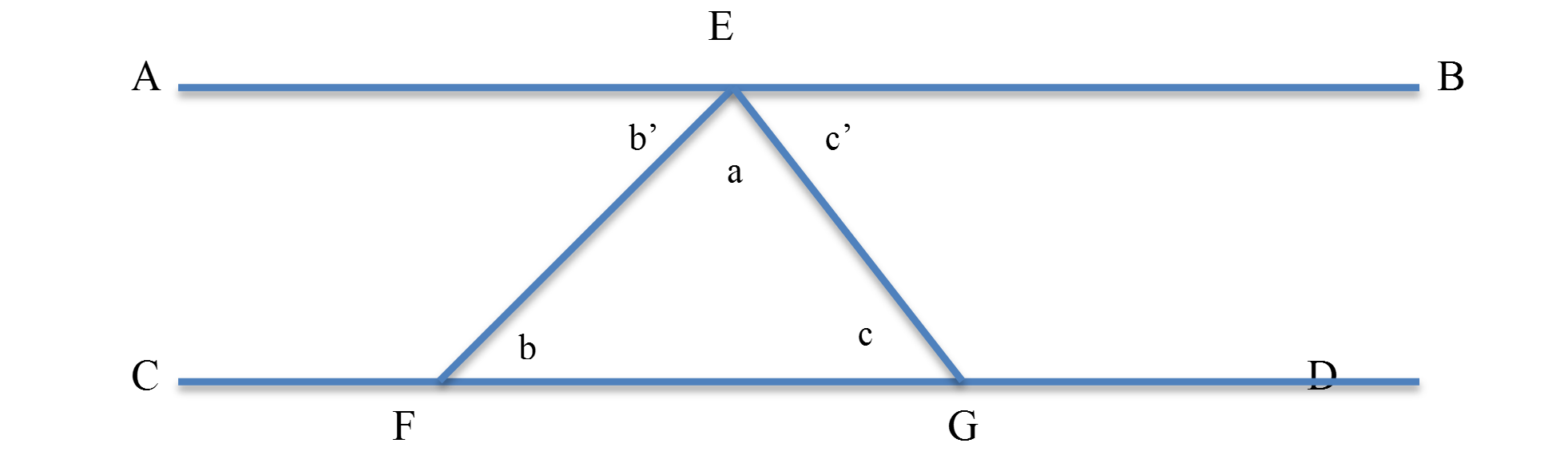
Most of us think about such a proof, see the reasoning, and agree with it.  But if we reflect for a moment, we should see that it is quite mysterious why such a proof works.  That’s because, it aims to show us that the sum of the interior angles of any triangle is the same as two right angles.  But there are infinitely many triangles (in fact, logicians have proved that there are more triangles than there are natural numbers!).  So how can it be that this argument proves something about all of the triangles?  Furthermore, in the diagram above, there are infinitely many different sets of two parallel lines we could have used.  And so on.

This also touches on the case that we saw in the Meno.  Socrates proves that the area of a square A twice as big as square B does not simply have sides twice as long as the sides of B; rather, each side of A must be the length of the diagonal of B.  But he and the boy drew just one square in the dirt.  And it won’t even be properly square.  How can they conclude something about every square based on their reasoning and a crude drawing?

In all such cases, there is an important feature of the relevant proof.  Squares come in many sizes, triangles come in many sizes and shapes.  But what interests us in such proofs is all and only the properties that all triangles have, or all and only properties that all squares have.  We refer to a triangle, or a square, that is abstract in a strange way:  we draw inferences about, and only refer to, its properties that are shared with all the things of its kind.  We are really considering a special, generalized instance.

We can call this special instance the “arbitrary instance”.  If we prove something is true of the arbitrary triangle, then we conclude it is true of all triangles.  If we prove something is true of the arbitrary square, then we conclude it is true of all squares.  If we prove something is true of an arbitrary natural number, then we conclude it is true of all natural numbers.  And so on.

14.3  Universal derivation

To use this insight, we will introduce not an inference rule, but rather a new proof method.  We will call this proof method “universal derivation” or, synonymously, “universal proof”.  We need something to stand for the arbitrary instance.  For a number of reasons, it is traditional to use unbound variables for this.  However, to make it clear that the variable is being used in this special way, and that the well-formed formula so formed is a sentence, we will use a prime—that is, the small mark “′”—to mark the variable.  Let α be any variable.  Our proof method thus looks like this.

\[
\fitchctx{

\boxedsubproof []{\alpha ‘}{}{
\ellipsesline \\
\pline{\phi (\alpha ‘)}
}
\pline{\lall \alpha \phi (\alpha)}
}
\]

Where α′ does not appear in any open proof above the beginning of the universal derivation.

Remember that an open proof is a subproof that is not completed.

We will call any symbolic term of this form (x′, y′, z′…) an “arbitrary term”, and it is often convenient to describe it as referring to the arbitrary object or arbitrary instance.  But there is not any one object in our domain of discourse that such a term refers to.  Rather, it stands in for an abstraction:  what all the things in the domain of discourse have in common.

The semantics of an arbitrary instance is perhaps less mysterious when we consider the actual syntactic constraints on a universal derivation.  One should not be able to say anything about an arbitrary instance α′ unless one has done universal instantiation of a universal claim.  No other sentence should allow claims about α′.  For example, you cannot perform existential instantiation to an arbitrary instance, since we required that existential instantiation be done to special indefinite names that have not appeared yet in the proof.  But if we can only makes claims about α′ using universal instantiation, then we will be asserting something about α′ that we could have asserted about anything in our domain of discourse.  Seen in this way, from the perspective of the syntax of our proof, the universal derivation hopefully seems very intuitive.

This schematic proof has a line where we indicate that we are going to use α′ as the arbitrary object, by putting α′ in a box.  This is not necessary, and is not part of our proof.  Rather, like the explanations we write on the side, it is there to help someone understand our proof.  It says, this is the beginning of a universal derivation, and α′ stands for the arbitrary object.  Since this is not actually a line in the proof, we need not number it.

We can now prove our example above is valid.

\[

\fitchprf{\pline[1.]{ \lall \textit{x} (F\textit{x} \lif G\textit{x})} [premise]\\
\pline[2.]{ \lall \textit{x} (G\textit{x} \lif H\textit{x})} [premise]\\
}
{
\boxedsubproof []{\textit{x}’}{}{
\subproof{\pline[3.]{F\textit{x}’}[assumption for conditional derivation]}{
\pline[4.]{(F\textit{x}’ \lif G\textit{x}’)}[universal instantiation, 1]\\
\pline[5.]{G\textit{x}’}[modus ponens, 4, 3]\\
\pline[6.]{(G\textit{x}’ \lif H\textit{x}’)}[universal instantiation, 2]\\
\pline[7.]{H\textit{x}’}[modus ponens, 6, 5]
}
\pline[8.]{(F\textit{x}’ \lif H\textit{x}’)}[conditional derivation, 3-7]
}
\pline[9.]{\lall \textit{x}(F\textit{x} \lif H\textit{x})}[universal derivation, 3-8]
}

\]

Remember that our specification of the proof method has a special condition, that α′ must not appear earlier in an open proof (a proof that is still being completed).  This helps us avoid confusing two or more arbitrary instances.  Here, there is no x′ appearing above our universal derivation in an open proof (in fact, there is no other arbitrary instance appearing in the proof above x′), so we have followed the rule.

14.4  Two useful theorems:  quantifier equivalence

Our definition of “theorem” remains the same for the first order logic and for the propositional logic:  a sentence that can be proved without premises.  However, we now have a distinction when it comes to the semantics of sentences that must be true.  Generally, we think of a tautology as a sentence that must be true as a function of the truth-functional connectives that constitute that sentence.  That is, we identified that a tautology must be true by making a truth table for the tautology.  There are, however, sentences of the first order logic that must be true, but we cannot demonstrate this with a truth table.  Here is an example:

∀x(Fx v ¬Fx)

This sentence must be true.  But we cannot show this with a truth table.  Instead, we need the concept of a model (introduced briefly in section 17.6) to describe this property precisely.  But even with our intuitive semantics, we can see that this sentence must be true.  For, we require (in our restriction on predicates) that everything in our domain of discourse either is, or is not, an F.

We call a sentence of the first order logic that must be true, “logically true”.  Just as it was a virtue of the propositional logic that all the theorems are tautologies, and all the tautologies are theorems; it is a virtue of our first order logic that all the theorems are logically true, and all the logically true sentences are theorems.  Proving this is beyond the scope of this book, but is something done in most advanced logic courses and texts.

Here is a proof that ∀x(Fx v ¬Fx).

\[

\fitchprf{
}
{
\boxedsubproof []{\textit{x}’}{}{
\subproof{\pline[1.]{\lnot (F\textit{x}’ \lor \lnot F\textit{x}’)}[assumption for indirect derivation]}{
\subproof{\pline[2.]{\lnot F\textit{x}’}[assumption for indirect derivation]}{
\pline[3.]{(F\textit{x}’ \lor \lnot F\textit{x}’)} [addition, 2]\\
\pline[4.]{\lnot (F\textit{x}’ \lor \lnot F\textit{x}’)}[repeat, 1]\\
}
\pline[5.]{F\textit{x}’}[indirect derivation, 2-4]\\
\pline[6.]{(F\textit{x}’ \lor \lnot F\textit{x}’)}[addition, 5]\\
\pline[7.]{\lnot (F\textit{x}’ \lor \lnot F\textit{x}’)}[repeat, 1]\\
}
\pline[8.]{(F\textit{x}’ \lor \lnot F\textit{x}’)}[indirect derivation, 1-7]
}
\pline[9.]{\lall \textit{x}(F\textit{x} \lor \lnot F\textit{x})}[universal derivation, 1-8]
}

\]

Let us consider another example of a logically true sentence that we can prove, and thus, practice universal derivation.  The following sentence is logically true.

((∀x (Fx → Gx) ^ ∀x (Fx → Hx))→ ∀x (Fx → (Gx ^Hx))

Here is a proof.  The formula is a conditional, so we will use conditional derivation.  However, the consequence is a universal sentence, so we will need a universal derivation as a subproof.

\[

\fitchprf{}{
\subproof{\pline[1.]{ (\lall \textit{x} (F\textit{x} \lif G\textit{x}) \land \lall \textit{x} (F\textit{x} \lif H\textit{x}))}[assumption for conditional derivation]}{
\boxedsubproof []{\textit{x}’}{}{
\subproof{\pline[2.]{F\textit{x}’}[assumption for conditional derivation]}{
\pline[3.]{\lall \textit{x} (F\textit{x} \lif G\textit{x}) }[simplification, 1]\\
\pline[4.]{(F\textit{x}’ \lif G\textit{x}’)}[universal instantiation, 3]\\
\pline[5.]{G\textit{x}’}[modus ponens, 4, 2]\\
\pline[6.]{\lall \textit{x} (F\textit{x} \lif H\textit{x}) }[simplification, 1]\\
\pline[7.]{(F\textit{x}’ \lif H\textit{x}’)}[universal instantiation, 6]\\
\pline[8.]{H\textit{x}’}[modus ponens, 7, 2]\\
\pline[9.]{(G\textit{x}’ \land H\textit{x}’)}[adjunction, 5, 8]\\
}
\pline[10.]{(F\textit{x}’ \lif (G\textit{x}’ \land H\textit{x}’)) }[conditional derivation, 2-9]\\
}
\pline[11.]{\lall \textit{x}(F\textit{x} \lif (G\textit{x} \land H\textit{x}))}[universal derivation, 2-10]\\
}
\pline[12.]{\brokenform{((\lall \textit{x} (F\textit{x} \lif G\textit{x}) \land \lall \textit{x} (F\textit{x} \lif H\textit{x})) \lif}{\lall \textit{x}(F\textit{x} \lif (G\textit{x} \land H\textit{x}))}}
[conditional derivation, 1-11]

}

\]

Just as there were useful theorems of the propositional logic, there are many useful theorems of the first order logic.  Two very useful theorems concern the relation between existential and universal claims.

(∃xFx ↔ ¬∀x¬Fx)

(∀xFx ↔ ¬∃x¬Fx)

Something is F just in case not everything is not F.  And, everything is F if and only if not even one thing is not F.

We can prove the second of these, and leave the first as an exercise.

\[

\fitchprf{}{
\subproof{\pline[1.]{\lall \textit{x} F\textit{x}}[assumption for conditional derivation]}{
\subproof{\pline[2.]{\lis \textit{x} \lnot F\textit{x}}[assumption for indirect derivation]}{
\pline[3.]{\lnot F\textit{p}}[existential instantiation, 2]\\
\pline[4.]{F\textit{p}}[universal instantiation, 1]
}
\pline[5.]{\lnot \lis \textit{x} \lnot F\textit{x}}[indirect derivation, 2-4]\\
}
\pline[6.]{(\lall \textit{x} F\textit{x} \lif \lnot \lis \textit{x} \lnot F\textit{x})}[conditional derivation 1-5]\\

\subproof{\pline[7.]{\lnot \lis \textit{x} \lnot F\textit{x}}[assumption for conditional derivation]}{
\boxedsubproof []{\textit{x’}}{}{
\subproof{\pline[8.]{\lnot F\textit{x’}}[assumption for indirect derivation]}{
\pline[9.]{\lis \textit{x} \lnot F\textit{x}}[existential generalization, 8]\\
\pline[10.]{\lnot \lis \textit{x} \lnot F\textit{x}}[repeat, 7]
}
\pline[11.]{F\textit{x’}}[indirect derivation, 8-10]
}
\pline[12.]{\lall \textit{x}F\textit{x}}[universal derivation, 8-11]
}

\pline[13.]{(\lnot \lis \textit{x} \lnot F\textit{x} \lif \lall x F\textit{x} )}[conditional derivation 7-12]\\
\pline[14.]{(\lall \textit{x} F\textit{x} \liff \lnot \lis \textit{x} \lnot F\textit{x}))}[bicondition, 6, 13]

}

\]

14.5  Illustrating invalidity

Consider the following argument:

∀x(Hx→Gx)

¬Hd

_____

¬Gd

This is an invalid argument.  It is possible that the conclusion is false but the premises are true.

Because we cannot use truth tables to describe the semantics of quantifiers, we have kept the semantics of the quantifiers intuitive.  A complete semantics for first order logic is called a “model”, and requires some set theory.  This presents a difficulty:  we cannot demonstrate that an argument using quantifiers is invalid without a semantics.

Fortunately, there is a heuristic method that we can use that does not require developing a full model.  We will develop an intuitive and partial model.  The idea is that we will come up with an interpretation of the argument, where we ascribe a meaning to each predicate, and a referent for each term, and where this interpretation makes the premises obviously true and the conclusion obviously false.  This is not a perfect method, since it will depend upon our understanding of our interpretation, and because it requires us to demonstrate some creativity.  But this method does illustrate important features of the semantics of the first order logic, and used carefully it can help us see why a particular argument is invalid.

It is often best to create an interpretation using numbers, since there is less vagueness of the meaning of the predicates.  So suppose our domain of discourse is the natural numbers.  Then, we need to find an interpretation of the predicates that makes the first two lines true and the conclusion false.  Here is one:

Hx:  x is evenly divisible by 2

Gx:  x is evenly divisible by 1

d:  3

The argument would then have as premises:  All numbers evenly divisible by 2 are evenly divisible by 1; and, 3 is not evenly divisible by 2.  These are both true.  But the conclusion would be:  3 is not evenly divisible by 1.  This is false.  This illustrates that the argument form is invalid.

Let us consider another example.  Here is an invalid argument:

∀x(Fx→Gx)

Fa

_____

Gb

We can illustrate that it is invalid by finding an interpretation that shows the premises true and the conclusion false.  Our domain of discourse will be the natural numbers.  We interpret the predicates and names in the following way:

Fx:  x is greater than 10

Gx:  x is greater than 5

a:  15

b:  2

Given this interpretation, the argument translates to:  Any number greater than 10 is greater than 5; 15 is greater than 10; therefore, 2 is greater than 5.  The conclusion is obviously false, whereas the premises are obviously true.

In this exercise, it may seem strange that we would just make up meanings for our predicates and names.  However, as long as our interpretations of the predicates and names follow our rules, our interpretation will be acceptable.  Recall the rules for predicates are that they have an arity, and that each predicate of arity n is true or false (never both, never neither) of each n things in the domain of discourse.  The rule for names is that they refer to only one object.

This illustrates an important point.  Consider a valid argument, and try to come up with some interpretation that makes it invalid.  You will find that you cannot do it, if you respect the constraints on predicates and names.  Make sure that you understand this.  It will clarify much about the generality of the first order logic.  Take a valid argument like:

∀x(Fx→Gx)

Fa

_____

Ga

Come up with various interpretations for a and for F and G.  You will find that you cannot make an invalid argument.

In summary, an informal model used to illustrate invalidity must have three things:

1. a domain of discourse;
2. an interpretation of the predicates; and
3. an interpretation of the names.

If you can find such an informal model that makes the premises obviously true and the conclusion obviously false, you have illustrated that the argument is invalid.  This may take several tries:  you can also sometimes come up with interpretations for invalid arguments that make all the premises and the conclusion true; this is not surprising, when you remember the definition of valid (that necessarily, if the premises are true then the conclusion is true—in other words, it is not enough that the conclusion just happens to be true).

14.6  Problems

1. Prove the following.  These will require universal derivation.  (For the third, remember that the variables used in quantifiers are merely used to indicate the place in the following expression that is being bound.  So, if we change the variable nothing else changes in our proof or use of inference rules.)  The last three are challenging.  For these last three problems, do not use the quantifier negation rules.

1. Premises:  ∀xFx, ∀x (Fx ↔ Gx).  Conclusion:  ∀xGx.
2. Premises: ∀x(Fx → Gx). Conclusion: ∀x(¬Gx → ¬Fx).
3. Premises: ∀x(Fx ↔ Hx), ∀y(Hy ↔ Gy). Conclusion: ∀z(Fz ↔ Gz).
4. Conclusion:  (∀x(¬Fx v Gx) → ∀x(Fx → Gx)).
5. Conclusion:  (∀x(Fx ↔Gx) → (∀xFx ↔ ∀xGx)).
6. Conclusion:  (¬∃xFx ↔ ∀x¬Fx).
7. Conclusion:  (¬∀xFx ↔ ∃x¬Fx).
8. Conclusion:  (∃xFx ↔ ¬∀x¬Fx).

2. Create a different informal model for each of the following arguments to illustrate that it is invalid.

1. Premises: ∀x(Fx → Gx), ¬Ga. Conclusion: ¬Fb.
2. Premises: ∀x(Fx v Gx), ¬Fa. Conclusion: Gb.
3. Premises: ∀x(Fx → Gx), ∃xFx. Conclusion: Gc.

3. In normal colloquial English, write your own valid argument with at least two premises and with a conclusion that is a universal statement.  Your argument should just be a paragraph (not an ordered list of sentences or anything else that looks like formal logic).  Translate it into first order logic and prove it is valid.

4. Do we have free will?  Much of the work that philosophers have done to answer this question focuses on trying to define or understand what free will would be, and understand the consequences if we do not have free will.  Doubts about free will have often been raised by those who believe that physics will ultimately explain all events using deterministic laws, so that everything had to happen one way.  Here is a simplified version of such an argument.

Every event is caused by prior events by way of natural physical laws.  Any event caused by prior events by way of natural physical laws could not have happened otherwise. But, if all events could not have happened otherwise, then there is no freely willed event. We conclude, therefore, that there are no freely willed events.

Symbolize this argument and prove it is valid.  You might consider using the following predicates:

Fx:  x is an event.

Gx:  x is caused by prior events by way of natural physical laws.

Hx:  x could have happened otherwise.

Ix:  x is a freely willed event.

(Hint:  this argument will require universal derivation.  The conclusion can be had using modus ponens, if you can prove: all events could not have happened otherwise.)  Do you believe that this argument is sound?