Supplementary Information: The 20-year Rule
A perpetuity is an annuity whose periodic payments (PMT) continue forever, based on an original endowment (PV) and a constant compound interest rate.
Solving Perpetuities with Formulas
The present value of a simple ordinary perpetuity is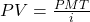 
Calculating the present value of a general perpetuity requires two additional formulas:
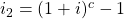
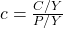, where C/Y = # compoundings per year, P/Y= # of payments per year
A perpetuity due requires a fourth formula.
- Can it be done using the financial calculator?
- How do you enter an infinite number of payments?
N must be large enough to reflect a perpetuity, but not too large for the calculator to handle (in some cases)!
We use the following rule:
The present value of any perpetuity is identical to
the present value of an equivalent annuity, whose
term is 20 years divided by the perpetuity’s nominal interest rate (as a decimal fraction)
the present value of an equivalent annuity, whose
term is 20 years divided by the perpetuity’s nominal interest rate (as a decimal fraction)
i.e.
- Number of years=
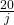
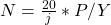
NOTE:
- N Should be rounded up if not an integer
- This is the minimum number of payments required to represent a perpetuity
- Larger values are fine, but sometimes only up to a certain point
See the attached Excel Template on using the 20 year rule: Perpetuities using 20 year rule
