Present Value of Simple Ordinary Annuity

We now consider the Present Value of a Simple Ordinary Annuity. This would be useful if we know how much money we want to make in payments but want to know how much it would be worth today.

Example 1

What is the present value of $800 payments, paid semi-annually over two years, if the discount rate is 6.3% compounded semi-annually?

To solve this problem, we can use the following EXCEL function:

where:

• Rate is the interest rate per period.
• Nper is the total number of payment periods in an annuity.
• Pmt is the payment made each period
• FV is the future value. If FV is omitted, it is assumed to be 0 (zero)
• Type is the number 0 or 1 and indicates when payments are due.  This argument is optional and if omitted is assumed to be 0.
  • 0 means payments are due at the end of the period
  • 1 means payments are due at the beginning of the period

For this example we are given:

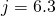• compounded semi-annually (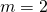). Hence the rate (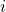) is

     

• Nper is 2 years x 2 times per year = 4 payment periods
• Pmt is $800
• FV is 0
• Type is 0 (an ordinary annuity)

PV Function

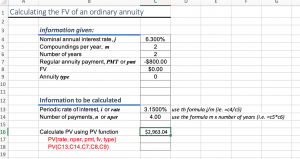
The present value of $800 payments, paid semi-annually over two years, if the discount rate is 6.3% compounded semi-annually is $2,963.04

Try recreating the spreadsheet above on your own. 

Click this link to see the completed spreadsheet: PV of ordinary annuity – Template

For more information about the PV function see Microsoft Support

Example 2 – Cash for life

You win the top prize in Cash for Life. You have two options:

1. Accept annuity payout of $1,000 a week for life.
2. Accept a lump sum payout of $675,000.

Note:

• A term of 20 years is used to calculate the lump sum.
• Assume an interest rate of 4.68% compounded weekly.

Which option do you choose and why?

Before considering the decision, you need to first determine the present value of option (1) and compare it to the lump sum payout from option (2).

We can use the PV function in Excel to determine the PV of the payments from option (1).

For this example we are given:

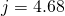• compounded weekly (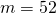). Hence the rate (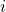) is

     

** note – 20 years is used for the lump sum calculation, but you are young and expect to live for for at least 50  more years.

• Nper is 50 years x 52 times per year = 2600 payment periods
• Pmt is $1,000
• FV is 0
• Type is 0 (an ordinary annuity)

Try recreating the spreadsheet from the previous question on your own and solve for PV. 

The PV of the payments given an expected 50 year life span is: $1,003,967.71

Click this link to see the completed spreadsheet: PV of ordinary annuity – cash for life – Template

Which option do you choose?

Some points to consider when making the decision:

• What is the higher present value?
• Is the lump sum more useful to you now even though the present value of the $1000 annuity is higher?
• Can you invest the lump sum at a higher rate than 4.68% compounded weekly?  Check current interest rates available on different financial institution web sites.