Future Value of Ordinary Simple Annuities

Example 1

You are saving for school and are able to save $1,000 every six months for two years. You are able to invest at 8% compounded semi-annually. How much will you have in your account at the end of the two-year period?

To solve this problem, we can use the following EXCEL function:

where:

• Rate is the interest rate per period.
• Nper is the total number of payment periods in an annuity.
• Pmt is the payment made each period
• Pv is the present value. If pv is omitted, it is assumed to be 0 (zero), and you must include pmt.
• Type is the number 0 or 1 and indicates when payments are due.  This argument is optional and if omitted is assumed to be 0.
  • 0 means payments are due at the end of the period
  • 1 means payments are due at the beginning of the period

For this example we are given:

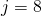• compounded semi-annually (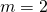). Hence the rate (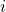) is

     

• Nper is 2 years x 2 times per year = 4 payment periods
• Pmt is $1,000
• PV is 0
• Type is 0 (an ordinary annuity)

FV Function

=FV(rate, nper, pmt, pv, type)

=FV(4,4,1000,0,0)

To be more efficient, we can set up our spreadsheet so we can use cell references instead of numbers. This will allow us to change the numbers in the cells and automatically calculate a new future value.

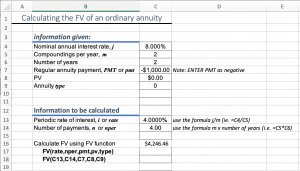
Try recreating the spreadsheet above on your own. 

Click this link to see the completed spreadsheet: FV of ordinary annuity – Template

Example 2

Suppose that you typically spend about $8 a day on lunch while at work. Today you have instead decided to save $8 a day for a period of 10 years.

Assume the following:

• you can earn 3% compounded daily.
• a simple ordinary annuity problem, where even on holidays and weekends you still spend this amount per day on food, that is, 365 days.

What amount of money will you have in 10 years?

For this example we are given:

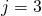• compounded daily (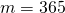). Hence the rate (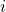) is

     

• Nper is 10 years x 365 times per year = 3650 payment periods
• Pmt is $8
• PV is 0
• Type is 0 (an ordinary annuity)

Try recreating the spreadsheet from the previous question on your own and solve for FV. 

You will have saved $34,051.30

Click this link to see the completed spreadsheet: FV of ordinary annuity – Template 2

For more information on the FV function, see Microsoft Support