Ordinary General Annuities
Example 1
Find the future value of an annuity of $80 paid at the end of each semi-annual period that earns interest of 8% compounded quarterly if the annuity is held for six years.
We can use the same function as we did for an ordinary simply annuity only we need to calculate the proper rate to use in the formula.
We are given the following information:
- Nominal Interest rate (
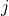 ) = 8%
) = 8% - Compounding per year (
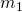 ) = 4
) = 4 - Payments per year (
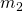 ) = 2
) = 2 - Number of years = 6
- PMT = $80
- Calculate
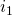 by dividing
by dividing 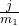
In order to use the formula we need to calculate ![]() :
:
![]()
and use ![]() as the rate in the formula.
as the rate in the formula.
In cell C14, we calculate ![]() by using the formula =C5/C6
by using the formula =C5/C6
In cell C15, we calculate ![]() using the formula above and using C14 in the place of
using the formula above and using C14 in the place of ![]()
The Future Value of the annuity is $1,204.83.
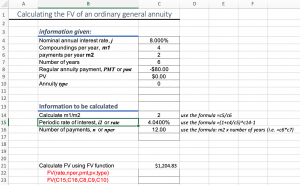
For the complete solution, see the Excel spreadsheet: FV of general annuity – Template 1
Example 2
Since the first year of Annabell’s birth, her parents have contributed to her Registered Saving Plan (RESP). They have been contributing $600 at the end of every calendar quarter. The plan is expected to continue to earn an average of 6% compounded monthly. How much can Annabell expect to have once she is 18 years old and ready to pursue a post-secondary education?
Work through the problem yourself then open the file FV of general annuity – Template 2 to check your answer.

