25 Outils d’analyses de simulation

Scénario : Votre responsable vous demande de travailler sur la stratégie de la région avec lui, afin d’atteindre 150 000 € de ventes en Bulgarie en 2021. Pour travailler sur cette question, vous allez utiliser des outils d’analyse.

Répondez à un objectif précis grâce aux valeurs cibles 

Vous vous rappelez vos cours de mathématiques quand vous étiez petit ? Ces fameux problèmes qui vous causaient (peut-être) des soucis ? 

Eh bien rassurez-vous ! Ici, Excel va vous aider à les résoudre !  

Dans un premier temps, nous allons donc poser le problème. 

Sachant que : 

  • le prix de vente moyen d’un vêtement est de 8,20 € ;
  • les charges de conditionnement sont fixes, 623 €. 

Combien de vêtements faut-il vendre pour atteindre 150 000 € de ventes ? 

Si vous entrez ces données dans un tableau Excel, le calcul du résultat revient à ceci : résultat = nombre de ventes x prix moyen d’un vêtement – charges fixes. 

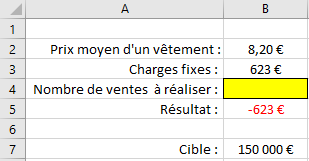Partie d’un classeur Excel. La colonne A contient le texte et la colonne B contient le nombre correspondant. Le prix moyen d’un vêtement est 8,20 euros. Les charges fixes sont de 623 euros. La cellule adjacente au texte « Nombre de ventes à réaliser : » est vide avec une couleur de remplissage jaune. Le résultat est -632 euros. La cible est 150000 euros. Le problème : trouver en B4 le nombre de vêtements à vendre pour atteindre 150 000 € en fonction du prix de vente. 

Pour qu’Excel trouve la valeur de la cellule jaune qui répondra à la cible à obtenir, vous allez utiliser la fonctionnalité de la valeur cible. 

Grâce à cet outil, Excel va tester toutes les valeurs possibles d’une cellule, afin qu’une autre cellule atteigne une valeur précise. 

La fonctionnalité valeur cible d’Excel est idéale quand vous n’avez qu’une seule inconnue dans votre problème. 

Dans notre exemple : 

  • Dans l’onglet Données, cliquez sur le bouton « Analyse scénario”, puis sur la ligne “Valeur cible… ».
  • Dans la zone “Cellule à définir”, sélectionnez la cellule contenant la formule du résultat, B5.
  • Renseignez la valeur à atteindre, ici 150000.
  • Renseignez la cellule à modifier, ici le nombre de ventes à réaliser, la cellule B4. 

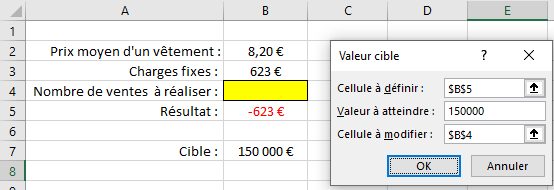
Partie d’un classeur Excel. La colonne A contient le texte et la colonne B contient le nombre correspondant. Le prix moyen d’un vêtement est 8,20 euros. Les charges fixes sont de 623 euros. La cellule adjacente au texte « Nombre de ventes à réaliser : » est vide avec une couleur de remplissage jaune. Le résultat est -632 euros. La cible est 150000 euros. Il y a également une fenêtre intitulée « Valeur cible ». Le champ « Cellule à définir : » contient la référence à la cellule $B$5. Le champ « Valeur à atteindre : » contient la valeur 150000. Le champ « Cellule à modifier : » contient la référence à la cellule $B$4.

Renseignez la cellule à modifier, ici $B$4 

Quand vous cliquez sur OK, Excel va chercher la valeur idéale de B4, afin que B5 atteigne la valeur cible. 

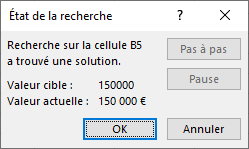Fenêtre intitulée État de la recherche. Le texte suivant apparaît dans la fenêtre : « Recherche sur la cellule B5 a trouvé une solution. Valeur cible : 150000 Valeur actuelle : 150000 euros ». Résultat de la recherche 

Si vous souhaitez conserver la valeur trouvée par Excel, cliquez sur “OK”, et Excel remplit la cellule B4. Sinon cliquez sur Annuler. 

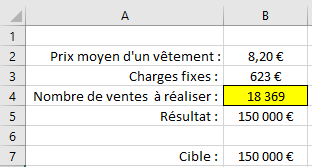Partie d’un classeur Excel. La colonne A contient le texte et la colonne B contient le nombre correspondant. Le prix moyen d’un vêtement est 8,20 euros. Les charges fixes sont de 623 euros. Le nombre de ventes à réaliser est de 18369 (la couleur de remplissage de cette cellule est jaune). Le résultat est 150000 euros. La cible est 150000 euros. Le résultat du nombre de ventes à réaliser est trouvé ! 

Dans ce problème à une inconnue, Excel a trouvé la solution en quelques secondes !  

Résolvez vos problèmes complexes grâce au solveur 

Si vous avez plusieurs inconnues dans votre problème, c’est alors le Solveur qui va vous aider. 

Le solveur ? Qu’est-ce que c’est ? 

Le solveur est un outil d’analyse comme la valeur cible, sauf qu’il va plus loin. L’objectif à atteindre peut être : 

  • une valeur exacte (ex. : objectif de 50 000 € de ventes) ;
  • une valeur minimum (ex. : au moins 50 000 € de ventes) ;
  • une valeur maximum (ex. : Quel montant maximum de ventes je peux atteindre avec ces critères ?). 

De plus, le solveur inclut la possibilité d’ajouter des limites (appelées “contraintes” dans Excel) au problème, comme par exemple : 

  • L’usine de production de vêtements ne peut pas produire plus de 1 000 vêtements par mois.
  • La matière première d’un vêtement coûte entre 5 € et 10 € selon le fournisseur. 

Excel peut gérer jusqu’à 200 contraintes cumulées !  

Installez le complément solveur 

Le solveur n’est pas installé par défaut dans Excel, il s’agit d’un complément gratuit, qu’il faut simplement activer. 

Pour l’activer : 

  • Dans l’onglet “Fichier”, cliquez sur le bouton “Options” tout en bas de l’écran.
  • Cliquez sur le menu” Compléments” puis sur le bouton “Atteindre…” en bas de la fenêtre.
  • La liste des compléments activables apparaît. 

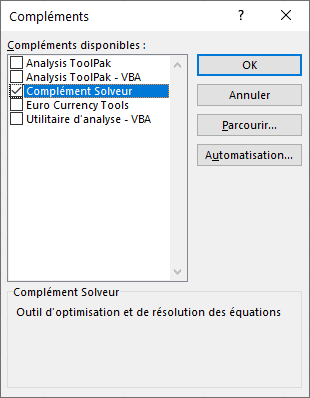Fenêtre intitulée Compléments. Parmi les options de la liste de compléments disponibles, la case à côté du Complément Solveur est cochée. La description du complément solveur est affichée au bas de la fenêtre, soit « Outil d’optimisation et de résolution des équations ». Ouvrez la liste des compléments et sélectionnez Complément Solveur 

  • Cochez la case Complément Solveur, et cliquez sur OK. 
  • Et voilà ! le solveur est installé.  

Utilisez le solveur 

Revenons à notre problématique : atteindre 150 000 € de ventes en Bulgarie en 2021. 

Le prix des différents types de vêtements n’étant pas le même, vous devez en tenir compte dans votre projection de ventes. De plus, vous ne pouvez pas produire plus d’une certaine quantité de vêtements par an, c’est la limite de votre usine de production. 

Ainsi, 

  • un vêtement de la catégorie “Haut” rapporte 10 € en moyenne, et sa production maximale est de 6 000 unités ;
  • un vêtement de la catégorie “Bas” rapporte 7 € en moyenne, et sa production maximale est de 6 000 unités ;
  • un vêtement de la catégorie “Haut et bas” rapporte 15 € en moyenne, et sa production maximale est de 4 500 unités ;
  • les charges fixes de conditionnement pour chaque catégorie de vêtement sont de 623 €. 

Intégrez ces données dans un tableau Excel, sans oublier la cible à atteindre : 

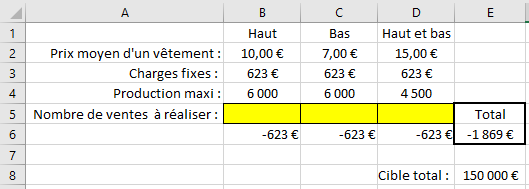Partie d’un classeur Excel. La ligne 1 contient les 3 titres Haut, Bas puis Haut et bas. La colonne A contient d’autres titres. Pour le prix moyen d’un vêtement, les données sont 10, 7 et 15 euros pour les colonnes haut, bas puis haut et bas respectivement. Pour les charges fixes, les données sont 623, 623 et 623 euros. Pour la production maxi, les données sont 6000, 6000 et 4500. Pour le nombre de ventes à réaliser, il n’y a pas de données ; les cellules ont une couleur de remplissage jaune et un encadré noir. En dessous de la ligne « Nombre de ventes à réaliser », il y a une ligne de données : -623, -623 et -623 euros, puis un total de -1869 euros. La cellule E8 contient la cible totale, soit 150000 euros. Le problème intégré dans un tableau 

Vous pouvez trouver ce tableau en téléchargeant ce fichier. 

Pour vous aider à résoudre ce problème ayant de multiples conditions, utilisez le solveur : 

  • Dans l’onglet “Données”, groupe “Analyse”, cliquez sur le bouton image.
  • La fenêtre du solveur comporte 3 zones : 

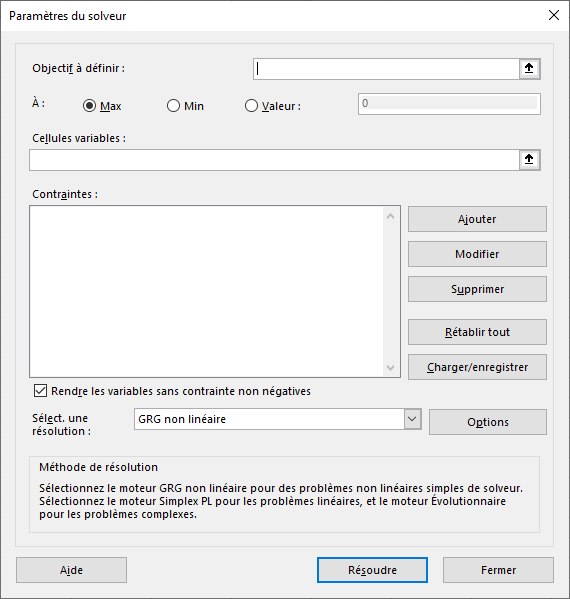Fenêtre intitulée Paramètres du solveur. Les champs à remplir sont : objectif à définir, à (avec les options max, min ou valeur), cellules variables et contraintes. La case « Rendre les variables sans contrainte non négatives » est cochée. Le champ Sélect. une résolution est rempli avec le texte GRG non linéaire. Ouvrez la fenêtre du solveur 

  • L’objectif à définir, ici la cellule E6, et en dessous, sa valeur à atteindre : 150 000.
  • Les cellules variables : ce sont les cellules jaunes (B5:D5), sur lesquelles le solveur va tester différentes combinaisons jusqu’à atteindre l’objectif voulu.
  • Les contraintes, qui sont les limites de notre problème :
    • les ventes de Hauts doivent être inférieures ou égales à 6 000 unités ;
    • les ventes de Bas doivent être inférieures ou égales à 6 000 unités ;
    • les ventes de Haut et bas doivent être inférieures ou égales à 4 500 unités ;
    • de plus, vous devez indiquer au solveur que les valeurs des cellules jaunes doivent être des chiffres entiers : vous ne pouvez pas produire 0,3 haut. 
  • Dans l’objectif à définir, sélectionnez la cellule contenant le calcul du total, soit $E$6.
  • Cochez l’option “Valeur”, avec l’objectif à atteindre, 150000.
  • Cliquez sur le bouton “Ajouter” afin de créer la première contrainte, celle disant que les ventes de Hauts (cellule B5) ne doivent pas dépasser 6 000 unités (cellule B4) : 

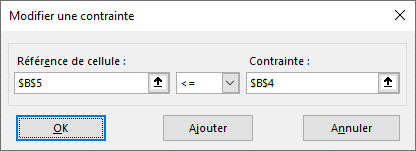Fenêtre intitulée Modifier une contrainte. À la gauche de la fenêtre, le champ référence de cellule contient la référence à la cellule $B$5. Au centre se retrouve le comparateur <=. À la droite de la fenêtre, le champ contrainte contient la référence à la cellule $B$4. Ajoutez la première contrainte 

  • Cliquez sur “Ajouter”, et créez les deux autres contraintes des ventes des vêtements “Bas” et “Haut et bas”.
  • Cliquez sur Ajouter, afin de créer la contrainte d’utiliser un nombre entier de ventes. Remplissez la fenêtre comme ceci : 

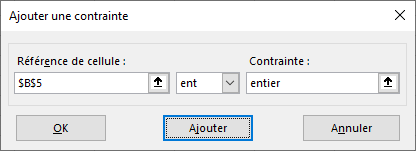Fenêtre intitulée Ajouter une contrainte. À la gauche de la fenêtre, le champ référence de cellule contient la référence à la cellule $B$5. Au centre se retrouve le texte ent. À la droite de la fenêtre, le champ contrainte contient le texte entier. Ajoutez une contrainte qui impose que B5 soit un entier 

  • Cliquez sur “Ajouter” et créez deux contraintes similaires pour les ventes des vêtements “Bas” et “Haut et bas”.
  • Enfin cliquez sur OK, la fenêtre du solveur doit être celle-ci : 

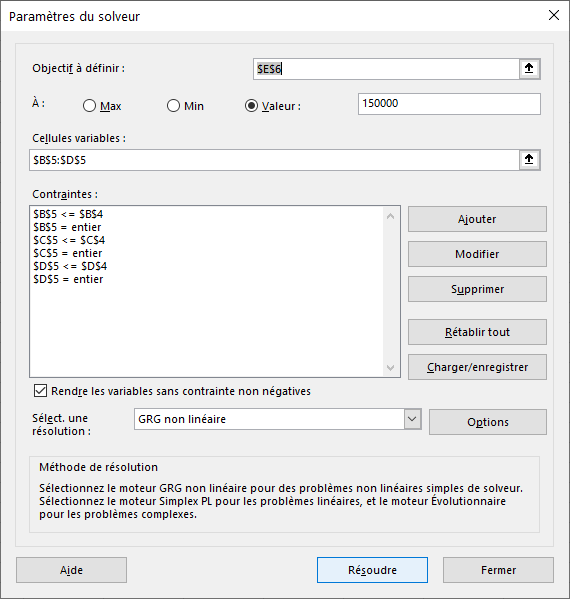Fenêtre intitulée Paramètres du solveur. L’objectif à définir est $E$6. Le bouton radio Valeur est choisi et le champ adjacent contient le nombre 150000. Le champ Cellules variables contient une référence à la plage $B$5:$D$5. Le champ contraintes contient les contraintes suivantes : $B$5 <= $B$4, $B$5 = entier, $C$5 <= $C$4, $C$5 = entier, $D$5 <= $D$4 et $D$5 = entier. La case « Rendre les variables sans contrainte non négatives » est cochée. Le champ Sélect. une résolution est rempli avec le texte GRG non linéaire. Le bouton Résoudre au bas de la fenêtre est en bleu pâle. Le solveur contient l’objectif, les cellules variables et les contraintes 

  • Cliquez sur “Résoudre” 
  • Le solveur vous indique qu’il a trouvé une solution : vous cliquez sur OK pour conserver la solution du solveur. 

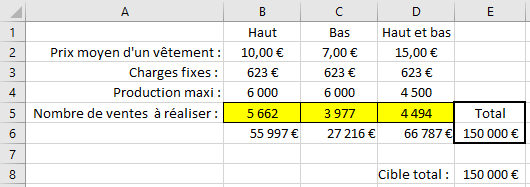Partie d’un classeur Excel. La ligne 1 contient les 3 titres Haut, Bas puis Haut et bas. La colonne A contient d’autres titres. Pour le prix moyen d’un vêtement, les données sont 10, 7 et 15 euros pour les colonnes haut, bas puis haut et bas respectivement. Pour les charges fixes, les données sont 623, 623 et 623 euros. Pour la production maxi, les données sont 6000, 6000 et 4500. Pour le nombre de ventes à réaliser, les cellules ont une couleur de remplissage jaune et un encadré noir puis les données sont 5662, 3977 et 4494. En dessous de la ligne « Nombre de ventes à réaliser », il y a une ligne de données : 55997, 27216 et 66787 euros, puis un total de 150000 euros. La cellule E8 contient la cible totale, soit 150000 euros. Les cellules variables sont maintenant remplies 

Vous constatez que les cellules jaunes sont maintenant remplies, et le total fait bien 150 000€ !  

Pour atteindre ce chiffre en prenant en compte les contraintes, le solveur conseille de vendre 5 662 vêtements « Haut », 3 977 vêtements « Bas », et 4 494 vêtements « Haut et bas ». 

Testez différents scénarios de données 

Votre responsable et ses collègues hésitent concernant les prix des vêtements à appliquer. Chacun a son idée de prix moyen concernant chaque catégorie de vêtement, et votre responsable vous demande quelle combinaison de prix serait la plus rentable pour l’entreprise. 

Voici les différentes propositions de prix : 

  • Proposition de votre responsable : 9 € pour les hauts, 8 € pour les bas, 14 € pour les hauts et bas.
  • Proposition de son collègue Tim : 10 € pour les hauts, 7 € pour les bas, 15 € pour les hauts et bas.
  • Proposition de son collègue Rob : 11 € pour les hauts, 8 € pour les bas, 13 € pour les hauts et bas. 

Grâce à Excel, vous pouvez comparer ces propositions en créant des scénarios !  

À cette étape, je vous conseille de télécharger le fichier avec les différents scénarios pour suivre la démonstration ci-dessous. 

Préparez l’analyse de vos scénarios 

Commencez par préparer le tableau de formules qui calcule le montant des ventes total : 

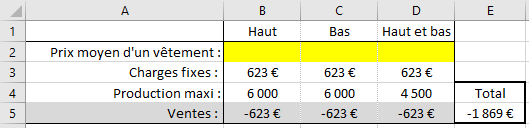Partie d’un classeur Excel. La ligne 1 contient les 3 titres Haut, Bas puis Haut et bas. La colonne A contient d’autres titres. Pour le prix moyen d’un vêtement, il n’y a pas de données, mais les cellules ont une couleur de remplissage jaune. Pour les charges fixes, les données sont 623, 623 et 623 euros. Pour la production maxi, les données sont 6000, 6000 et 4500. Pour les ventes, les données sont -623, -623 et -623 euros, puis un total de -1869 euros. Tableau qui calcule le montant total 

Pour faciliter la comparaison des scénarios, pensez à nommer les cellules importantes: 

  • Les 3 cellules variables jaunes :
    • Nommez B2 “PrixCategHaut”.
    • Nommez C2 “PrixCategBas”.
    • Nommez D2 “PrixCategHautEtBas”.
  • La cellule Total, E5, est nommée “TotalVentes”. 

Créez vos scénarios 

Créez le scénario de votre responsable 

  • Dans l’onglet “Données”, cliquez sur le bouton “Analyse scénarios”, puis sur la ligne “gestionnaire de scénarios…” 

Fenêtre intitulée Gestionnaire de scénarios. Aucun scénario n’est défini, il y a la possibilité d’en ajouter. La fenêtre des scénarios s’ouvre : à partir de là, vous allez créer autant de scénarios que de propositions de prix 

  • Cliquez sur le bouton “Ajouter…”.
  • Nommez le premier scénario, ici “Avis du responsable”.
  • Sélectionnez les cellules variables, ici les cellules en jaune (B2:D2).
  • Cliquez sur OK.
  • La fenêtre des variables apparaît, saisissez la première proposition. 

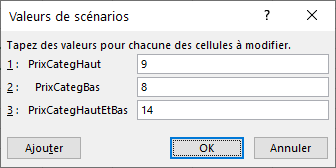Fenêtre intitulée Valeurs de scénarios qui contient la consigne « Tapez des valeurs pour chacune des cellules à modifier. » Le premier champ « PrixCategHaut » contient la valeur 9. Le deuxième champ « PrixCategBas » contient la valeur 8. Le troisième champ « PrixCategHautEtBas » contient la valeur 14. Le bouton « OK » est encadré en bleu. Entrez les valeurs du scénario de votre responsable pour chacune des cellules à modifier 

  • Cliquez sur OK. 

Créez le scénario de Tim 

  • Répétez les étapes ci-dessus pour le deuxième scénario, avec comme prix moyens : 10 € pour les hauts, 7 € pour les bas, 15 € pour les hauts et bas. 

Créez le scénario de Rob 

  • Répétez les étapes ci-dessus pour le troisième scénario, avec comme prix moyens : 11 € pour les hauts, 8 € pour les bas, 13 € pour les hauts et bas. 

Comparez les différents scénarios 

  • Cliquez sur le bouton “Synthèse…” 

Fenêtre intitulée Synthèse de scénarios. Deux boutons radio sont disponibles pour choisir le type de rapport, soit synthèse de scénarios ou scénario du rapport de tableau croisé dynamique (la première option est sélectionnée). Dans le champ Cellules résultantes, on retrouve la référence à la cellule E5. Dernière fenêtre avant la synthèse des scénarios 

  • Sélectionnez la cellule contenant la formule du résultat, soit la cellule E5, puis cliquez sur OK.
  • Et voilà ! Excel vient de créer un nouvel onglet, et fait tout seul la comparaison des 3 propositions : 

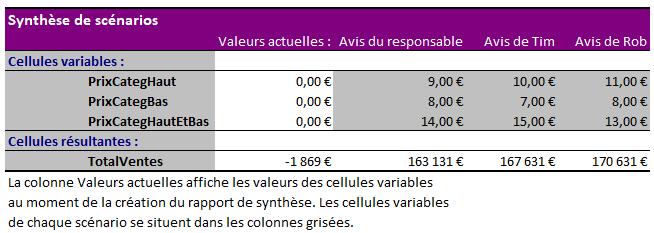Tableau dans Excel intitulé Synthèse de scénarios. Les titres à l’horizontale sont valeurs actuelles :, avis du responsable, avis de Tim et avis de Rob. Les titres à la verticale sont Cellules variables : avec les sous-titres PrixCategHaut, PrixCategBas et PrixCategHautEtBas ainsi que Cellules résultantes : avec le sous-titre TotalVentes. Tableau de comparaison des 3 scénarios 

Vous pouvez constater que c’est la proposition de Rob qui maximise le total des ventes. Bien vu, Rob !  

À vous de jouer ! 

Téléchargez ce fichier et réalisez les opérations suivantes : 

  • Utilisez la valeur cible afin de trouver la réponse du problème 1 (cellule verte). L’objectif est d‘arriver à 75 000 €.
  • Dans le problème 2, utilisez le solveur afin d’atteindre l’objectif de 70 000 € de ventes, en jouant sur le prix d’achat, le prix de vente et le nombre de ventes (les cellules orange).  

Vos contraintes sont : 

  • le prix d’achat se situe entre 4 € et 6 € ;
  • le prix de vente se situe entre 22 € et 26 € ;
  • la marge minimale doit être de 20 € ou plus. 

Corrigé 

Vous pouvez consulter ce fichier. 

Éléments clés à retenir

  • Excel propose différents outils d’analyse pour répondre à des problèmes complexes.
  • Vous pouvez résoudre des problèmes à une inconnue, grâce à la valeur cible.
  • Vous pouvez résoudre des problèmes complexes, avec de multiples limites, grâce au solveur.
  • Vous pouvez comparer des jeux de données différents en utilisant les scénarios.

Référence

Coulbault, D. (2021). Perfectionnez-vous sur Excel. OpenClassrooms. https://openclassrooms.com/fr/courses/7139456-perfectionnez-vous-sur-excel

Licence

Symbole de License Creative Commons Attribution - Pas d’utilisation commerciale - Partage dans les mêmes conditions 4.0 International

Manuel ADM1770 - Application des technologies de l'information en gestion (version 2) Droit d'auteur © 2023 par Muriel Mignerat est sous licence License Creative Commons Attribution - Pas d’utilisation commerciale - Partage dans les mêmes conditions 4.0 International, sauf indication contraire.

Partagez ce livre