4.1 – Advanced Routing

Overview

So far, we have learned about the gyroscope to keep track of which direction we are facing, but what about keeping track of our coordinates? In this lesson, we will learn how to use the “`move_to_coordinate()“` function to navigate and complete challenges using the catesian coordinate system.

Coordinates

When you think of a coordinate system, what do you think of? You might think of the Cartesian plane taught in math class.

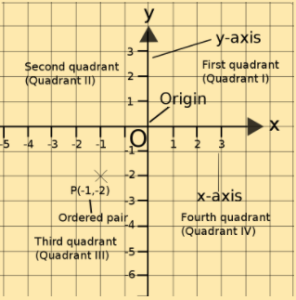
Recall that:
– The “origin” is your starting point, located at x=0 and y=0, or where the two lines intersect.
– X-Values to the right of the origin (greater than 0) are positive
– X-values to the left of the origin (less than 0) are negative.
– Y-values above the origin are positive
– Y-values below the origin are negative.

We can define any point on the plane with an ordered pair. In the picture above, (-1,-2) means that from the origin, we are one unit to the left and 2 units down.

Moving to a specific coordinate

Let’s say we wanted Zumi to move to a specific coordinate. To do this, we would have to use the “`move_to_coordinate()“` function. The line seen in the image below tells Zumi to move to the (x, y) cartesian coordinate (4, 4) from the origin (0,0).

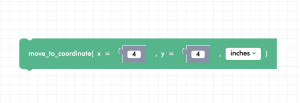
Example: Zumi coordinate square

Using the “`move_to_coordinate()“` command, let’s try to make the Zumi drive in a square formation!

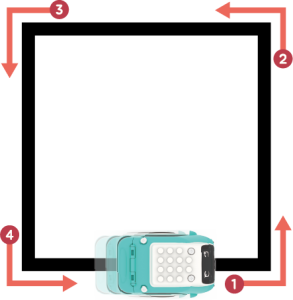
Provided below is a sample solution to what this may look like:

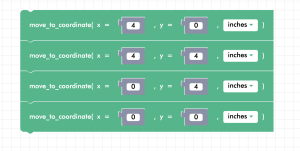
Activity: Zumi Tetris Block

Now it’s your turn! Try making the outline of the T-shaped block from the game Tetris! You can use this picture as a reference or pick any of the Tetris blocks.

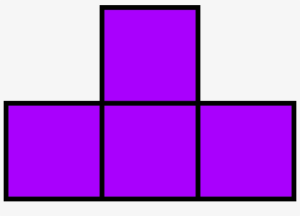
Hint: Get some graph paper and map out some possible coordinates first!

Demo Video

Questions