3.5 Methods and Examples

There are many techniques to create adversarial examples. The methods in this section focus on image classifiers with deep neural networks, as a lot of research is done in this area, and the visualization of adversarial images is very educational. Adversarial examples for images are images with intentionally perturbed pixels to deceive the model during application time. The examples impressively demonstrate how easily deep neural networks for object recognition can be deceived by images that appear harmless to humans. If you have not yet seen these examples, you might be surprised because the changes in predictions are incomprehensible for a human observer. Adversarial examples are like optical illusions but for machines.

Attacks based on Adversaries Knowledge

L-BFGS

Szegedy et al. (2013) proposed that vulnerability of pairs to specific perturbations would lead to serious deviation of model recognition results in their exploration of the explainable work of deep learning. They proposed the first anti-attack algorithm for deep learning, L-BFGS:

[latex]\text{min} c\norm{\delta}+J_𝜃 (x',l')[/latex]

[latex]\text{s.t. }x'\in[0,1][/latex]

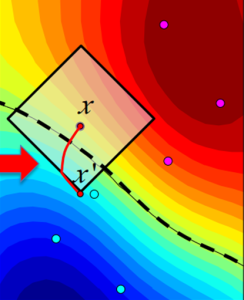
Where [latex]c[/latex] denotes a constant greater than [latex]0, x'[/latex] denotes the adversarial example formed by adding perturbation [latex]\delta[/latex] to the example, and [latex]J_\theta[/latex] denotes the loss function. The algorithm is limited by the selection of parameter [latex]c[/latex], so it is necessary to select the appropriate [latex]c[/latex] to solve the constrained optimization problem. L-BFGS can be used in models trained on different datasets by virtue of its transferability. The proposal of this method has set off a research upsurge of scholars on adversarial examples.

FGSM

Goodfellow et al. (2014) proposed the Fast Gradient Sign Method (FGSM) algorithm to prove that the high-dimensional linearity of deep neural networks causes the existence of adversarial examples. The algorithm principle generates adversarial perturbations according to the maximum direction of the gradient change of the deep learning model and adds the perturbations to the image to generate adversarial examples. The formula for FGSM to generate perturbation is as follows:

[latex]\delta=\varepsilon\cdot\text{sign}(\nabla_x J_\theta(\theta,x,y))[/latex]

where [latex]\delta[/latex] represents the generated perturbation; [latex]\theta[/latex] and [latex]x[/latex] are the parameters of the model and the input to the model, respectively; [latex]y[/latex] denotes the target associated with [latex]x[/latex]; [latex]J_\theta[/latex] is the loss function during model training. [latex]\varepsilon[/latex] denotes a constant.

PGD & BIM

Projected Gradient Descent is an iterative attack (multi-step attack) that is influenced by IFGSM/FGSM. The advantage of the FGSM algorithm is that the attack speed is fast, because the algorithm belongs to a single-step attack, sometimes the attack success rate of the adversarial examples generated by the single-step attack is low. Therefore, Kurakin et al. (2016) proposed an iteration-based FGSM (I-FGSM).

The main innovation of I-FGSM, also known as BIM, is to generate perturbations by increasing the loss function in multiple small steps, so that more adversarial examples can be obtained, and this has been further advanced by Madry et. al’s (2018) attack [A. Madry, A. Makelov, L. Schmidt, D. Tsipras, and A. Vladu. Towards deep learning models resistant to adversarial attacks. 2017] showed that the BIM can be significantly improved by starting from a random point within the [latex]\varepsilon[/latex] norm ball. Madry et al.’s work established PGD as the “gold standard” attack for adversarial robustness, which makes PGD a cornerstone of adversarial ML, both for attacking models and evaluating defenses. Defenses like adversarial training often rely on PGD-generated examples to build robust models. In other words, if a model is robust to PGD, it is robust to most first-order attacks.

Carlini & Wagner

In response to the attack methods proposed by scholars, Papernot et al. (2016) proposed defensive distillation, which uses the distillation algorithm (Hinton et al., 2015) to transfer the knowledge of the complex network to the simple network, so that the attacker cannot directly contact the original model to attack, Defensive distillation effectively defends against some adversarial examples. For defensive distillation, Carlini et al. (2017) proposed a C&W attack by constraining[latex]L_0,\:L_2[/latex] and[latex]L_\infty[/latex]. Experiments show that defensive distillation cannot defend against C&W attacks, and the general perturbation constraints of C&W attacks are as follows:

minimize [latex]D(x,x+\delta)+c\cdot f(x+\delta)[/latex]

such that[latex] x+\delta\in[0,1]^n[/latex]

where [latex]D[/latex] represents constraint paradigms such as [latex]L_0,L_2[/latex] and [latex]L_\infty[/latex], [latex]L_0[/latex] constraint the number of clean example points changed in the generation process, [latex]L_2[/latex] constraint the overall degree of perturbation, [latex]L_\infty[/latex]constraint the maximum allow perturbed per pixel, [latex]c[/latex] denotes the hyperparameter, and [latex][/latex] adopts a variety of objective functions. By conducting experiments on the MINIST and CIFAR datasets, C&W achieves an attack on the distillation network with a 100% success rate, and C&W can generate high-confidence adversarial examples by adjusting the parameters.

The Blindfolded Adversary

Black-box evasion attacks operate under a realistic adversarial model where the attacker has no prior knowledge of the model’s architecture or training data. Instead, the attacker interacts with a trained model by submitting queries and analyzing the predictions. This setup is like Machine Learning as a Service (MLaaS) platform, where users can access model outputs without insight into the training process. In the literature, black-box evasion attacks are generally categorized into two main types:

• Score-Based Attacks: In cases where attackers can access the model’s confidence scores or logits, they use optimization techniques to generate adversarial examples. Zeroth-order optimization (ZOO) is an example.
• Decision-Based Attacks: When only the model’s predicted labels are available, attackers must infer decision boundaries using techniques like Boundary Attack (Liao, 2018), which relies on random walks and rejection sampling.

ZOO

Different from some existing black-box attack methods based on surrogate models, Chen et al. (2017) proposed the zeroth order optimization (ZOO), which does not exploit the attack transferability of surrogate models, but It is to estimate the value of the first-order gradient and the second-order gradient, and then use Adma or Newton’s method to iterate to obtain the optimal adversarial example, and add a perturbation to a given input [latex]x:x=x+he_i[/latex], where [latex]h[/latex] is a small constant, [latex]e_i[/latex] represents a vector where [latex]i^{\text{th}}[/latex] is 1 and the rest are 0. The first-order estimated gradient value is calculated as follows:

[latex]\hat{g}_i: =\frac{\partial f(x)}{\partial x_𝑖}\approx \frac{f(x+he_𝑖)−f(x−he_𝑖)}{2h}[/latex],

The second-order estimated gradient is calculated as follows:

[latex]\hat{h}_i:=\frac{\partial^2f(x)}{\partial^2x_{𝑖𝑖}}\approx \frac{f(x+he_𝑖)−2f(x)+f(x−he_𝑖)}{h^2}[/latex],

Chen et al. (2017) verified by experiments on the MNIST and CIFAR10 datasets that the ZOO attack can achieve a high attack success rate, but compared with the white-box attack C&W, the ZOO attack takes more time.

Transferability

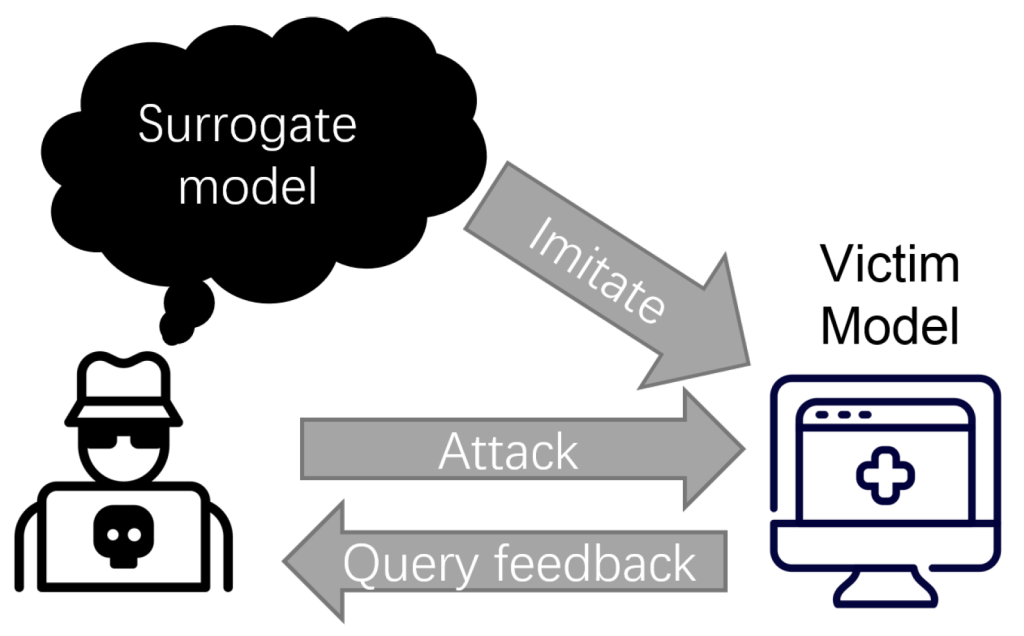
Another approach to generating adversarial attacks under restricted threat models is through attack transferability. Research has shown that adversarial examples can be generalized across different models (Liu et al., 2018).  In other words, many adversarial examples that successfully deceive one model can also deceive another, even if they are trained on different datasets or with different architectures. This phenomenon, known as transferability, is commonly leveraged to generate adversarial examples in black-box attack scenarios. In this method, an attacker trains a substitute machine-learning model, crafts white-box adversarial examples on the substitute, and then applies these attacks to the target model.

Imagine the following scenario: I give you access to my great image classifier via Web API. You can get predictions from the model, but you do not have access to the model parameters. From the convenience of your couch, you can send data and my service answers with the corresponding classifications. Papernot et al. (2017) showed that it is possible to create adversarial examples without internal model information and without access to the training data.

Content in “Attacks Based on Adversarial Knowledge” is from “Adversarial Attack and Defense: A Survey” by Hongshuo Liang, Erlu He, Yangyang Zhao, Zhe Jia, and Hao Li, licensed under a Creative Commons Attribution 4.0 International License, unless otherwise noted.

“The Blindfolded Adversary” from “Adversarial Machine Learning A Taxonomy and Terminology of Attacks and Mitigations” by Apostol Vassilev, Alina Oprea, Alie Fordyce, & Hyrum Anderson, National Institute of Standards and Technology – U.S. Department of Commerce. Republished courtesy of the National Institute of Standards and Technology.

Parts of “Transferability” from “Adversarial Examples” in Interpretable Machine Learning by Christopher Molnar, licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International Licence.