4.2 Solve Systems of Equations by Substitution
Learning Objectives
By the end of this section, you will be able to:
- Solve a system of equations by substitution
- Solve applications of systems of equations by substitution
Try It
Before you get started, take this readiness quiz:
1) Simplify [latex]-5(3-x)[/latex].
2) Simplify [latex]4-2(n+5)[/latex].
3) Solve for [latex]y[/latex]: [latex]8y-8=32-2y[/latex].
4) Solve for [latex]x[/latex]: [latex]3x-9y=-3[/latex].
Solving systems of linear equations by graphing is a good way to visualize the types of solutions that may result. However, there are many cases where solving a system by graphing is inconvenient or imprecise. If the graphs extend beyond the small grid with [latex]x[/latex] and [latex]y[/latex] both between [latex]−10[/latex] and [latex]10[/latex], graphing the lines may be cumbersome. And if the solutions to the system are not integers, it can be hard to read their values precisely from a graph.
In this section, we will solve systems of linear equations by the substitution method.
Solve a System of Equations by Substitution
We will use the same system we used first for graphing.
We will first solve one of the equations for either [latex]x[/latex] or [latex]y[/latex]. We can choose either equation and solve for either variable—but we’ll try to make a choice that will keep the work easy.
Then we substitute that expression into the other equation. The result is an equation with just one variable—and we know how to solve those!
After we find the value of one variable, we will substitute that value into one of the original equations and solve for the other variable. Finally, we check our solution and make sure it makes both equations true.
We’ll fill in all these steps now in Example 1
Example 1
Try It
5) Solve the system by substitution.
[latex]{\left\{\begin{array}{l}-2x+y=-11\\x+3y=9\end{array}\right.}[/latex]
Solution
[latex](6,1)[/latex]
6) Solve the system by substitution.
[latex]{\left\{\begin{array}{l}x+3y=10\\4x+y=18\end{array}\right.}[/latex]
Solution
[latex](4,2)[/latex]
How to
Solve a system of equations by substitution.
- Solve one of the equations for either variable.
- Substitute the expression from Step 1 into the other equation.
- Solve the resulting equation.
- Substitute the solution in Step 3 into one of the original equations to find the other variable.
- Write the solution as an ordered pair.
- Check that the ordered pair is a solution to both original equations.
If one of the equations in the system is given in slope–intercept form, Step 1 is already done! We’ll see this in Example 2
Example 2
Solve the system by substitution.
[latex]{\left\{\begin{array}{l}x+y=-1\\y=x+5\end{array}\right.}[/latex]
Solution
The second equation is already solved for [latex]y[/latex]. We will substitute the expression in place of [latex]y[/latex] in the first equation.
The second equation is already solved for [latex]y[/latex]. We will substitute it into the first equation.
[latex]\begin{eqnarray*}\left\{\begin{array}{l}x\;+\;y\;=\;-1\\y\;=\;x\;+\;5\end{array}\right.\\\end{eqnarray*}[/latex]
Step 1: Replace the [latex]y[/latex] with [latex]x + 5[/latex]
[latex]\begin{eqnarray*}y\;&=&\;{\color{red}{\boxed{x\;+\;5}}}\\x\;+\;{\color{red}{y}}\;&=&\;-1\\x\;+{\color{red}{\;}}{\color{red}{x}}{\color{red}{\;}}{\color{red}{+}}{\color{red}{\;}}{\color{red}{5}}&=&-1\end{eqnarray*}[/latex]
Step 2: Solve the resulting equation for [latex]x[/latex]
[latex]\begin{eqnarray*}x\;+{\color{red}{\;}}{\color{red}{x}}{\color{red}{\;}}{\color{red}{+}}{\color{red}{\;}}{\color{red}{5}}\;&=&\;-1\\2x\;+\;5\;&=&\;-1\\2x\;&=&\;-6\end{eqnarray*}[/latex]
Step 3: Substitute [latex]x = −3[/latex] into [latex]y = x + 5[/latex] to find [latex]y[/latex]
[latex]\begin{align*}{\color{red}{x}}&={\color{red}{\;}}{\color{red}{-}}{\color{red}{3}}\\ y\;&=\;{\color{red}{x}}\;+\;5\\y\;&=\;{\color{red}{-}}{\color{red}{3}}\;+\;5\\y&=\;2\end{align*}[/latex]
The ordered pair is [latex](−3, 2)[/latex].
Step 4: Check the ordered pair in both equations:
|
[latex]\begin{align*}x+y&=-1\\-3+2&\overset?=-1\\-1&=-1\checkmark\end{align*}[/latex] |
[latex]\begin{align*}y&=x+5\\2&\overset?=-3+5\\2&=2\checkmark\end{align*}[/latex] |
The solution is [latex](−3, 2)[/latex].
Try It
7) Solve the system by substitution.
[latex]{\left\{\begin{array}{l}x+y=6\\y=3x-2\end{array}\right.}[/latex]
Solution
[latex](2,4)[/latex]
8) Solve the system by substitution.
[latex]{\left\{\begin{array}{l}2x-y=1\\y=-3x-6\end{array}\right.}[/latex]
Solution
[latex](-1,-3)[/latex]
If the equations are given in standard form, we’ll need to start by solving for one of the variables. In this next example, we’ll solve the first equation for [latex]y[/latex].
Example 3
Solve the system by substitution.
[latex]{\left\{\begin{array}{l}3x+y=5\\2x+4y=-10\end{array}\right.}[/latex]
Solution
We need to solve one equation for one variable. Then we will substitute that expression into the other equation.
Solve for [latex]y[/latex]
[latex]3x\;+\;y\;=\;5[/latex]
Step 1: Substitute into the other equation.
Step 2: Replace the [latex]y[/latex] with [latex]−3x + 5[/latex].
[latex]\begin{align*}3x+y&=5\\ y&=-3+5\\ 2x+4y&=-10\\ 2x+4(-3+5)&=-10\end{align*}[/latex]
Step 3: Solve the resulting equation for [latex]x[/latex].
[latex]\begin{eqnarray*}2x\;-\;12x\;+\;20\;&=&\;-10\\-10x\;+\;20\;&=&\;-10\\-10x\;&=&\;-30\\x\;&=&\;3\end{eqnarray*}[/latex]
Step 4: Substitute [latex]x = 3[/latex] into [latex]3x + y = 5[/latex] to find [latex]y[/latex].
[latex]\begin{eqnarray*}{\color{red}{x}}{\color{red}{\;}}&=&{\color{red}{\;}}{\color{red}{3}}\\3{\color{red}{x}}\;+\;y\;&=&\;5\\3({\color{red}{3}})\;+\;y\;&=&\;5\\9\;+\;y\;&=&\;5\\y\;&=&\;-4\end{eqnarray*}[/latex]
The ordered pair is [latex](3, −4)[/latex].
Step 5: Check the ordered pair in both equations:
|
[latex]\begin{align*}3x+y&=5\\-3\times3+(-4)&\overset?=5\\9-4&\overset?=5\\5&=5\checkmark\end{align*}[/latex] |
[latex]\begin{align*}2x+4y&=-10\\2\times3+4(-4)&=-10\\6-16&\overset?=-10\\-10&=-10\checkmark\end{align*}[/latex] |
The solution is [latex](3, −4)[/latex].
Try It
9) Solve the system by substitution.
[latex]{\left\{\begin{array}{l}4x+y=2\\3x+2y=-1\end{array}\right.}[/latex]
Solution
[latex](1,-2)[/latex]
10) Solve the system by substitution.
[latex]{\left\{\begin{array}{l}-x+y=4\\4x-y=2\end{array}\right.}[/latex]
Solution
[latex](2,6)[/latex]
In Example 3 it was easiest to solve for [latex]y[/latex] in the first equation because it had a coefficient of [latex]1[/latex]. In Example 4 it will be easier to solve for [latex]x[/latex].
Example 4
Solve the system by substitution.
[latex]{\left\{\begin{array}{l}x-2y=-2\\3x+2y=34\end{array}\right.}[/latex]
Solution
We will solve the first equation for [latex]x[/latex] and then substitute the expression into the second equation.
[latex]x\;-\;2y\;=\;-2[/latex]
Step 1: Solve for [latex]x[/latex].
Step 2: Substitute into the other equation.
Step 3: Replace the [latex]x[/latex] with [latex]2y − 2[/latex].
[latex]\begin{eqnarray*}3{\color{red}{x}}\;+\;2y\;&=&\;34\\3({\color{red}{2}}{\color{red}{y}}{\color{red}{\;}}{\color{red}{-}}{\color{red}{\;}}{\color{red}{2}})\;+\;2y\;&=&\;34\end{eqnarray*}[/latex]
Step 4: Solve the resulting equation for [latex]y[/latex].
[latex]\begin{eqnarray*}6y\;-\;6\;+\;2y\;&=&\;34\\8y\;-\;6\;&=&\;34\\8y\;&=&\;40\\y\;&=&\;5\end{eqnarray*}[/latex]
Step 5: Substitute [latex]y = 5[/latex] into [latex]x − 2y = −2[/latex] to find [latex]x[/latex].
[latex]\begin{eqnarray*}x\;-\;2{\color{red}{y}}\;&=&\;-2\\x\;-\;2\;\times\;{\color{red}{5}}\;&=&\;-2\\x\;-\;10\;&=&\;-2\\x\;&=&\;8\\\end{eqnarray*}[/latex]
The ordered pair is [latex](8, 5)[/latex].
Step 6: Check the ordered pair in both equations:
|
[latex]\begin{align*}x-2y&=-2\\8-2\times 5&\overset?=-2\\8-10&\overset?=-2\\-2&=-2\checkmark\end{align*}[/latex] |
[latex]\begin{align*}3x+2y&=34\\3\times8+2\times 5&\overset?=34\\24+10&\overset?=34\\34&=34\checkmark\end{align*}[/latex] |
The solution is [latex](8, 5)[/latex].
Try It
11) Solve the system by substitution.
[latex]\left\{\begin{array}{l}x-5y=13\\4x-3y=1\end{array}\right.[/latex]
Solution
[latex](-2,-3)[/latex]
12) Solve the system by substitution.
[latex]\left\{\begin{array}{l}x-6y=-6\\2x-4y=4\end{array}\right.[/latex]
Solution
[latex](6,2)[/latex]
When both equations are already solved for the same variable, it is easy to substitute!
Example 5
Solve the system by substitution.
[latex]\left\{\begin{array}{l}y=-2x+5\\y=\frac12x\end{array}\right.[/latex]
Solution
Since both equations are solved for [latex]y[/latex], we can substitute one into the other.
Step 1: Substitute [latex]\frac{1}{2}x[/latex] for [latex]y[/latex] in the first equation.
[latex]\begin{eqnarray*}{\color{red}{y}}\;&=&\;{\color{red}{\frac12}}{\color{red}{x}}\\{\color{red}{y}}\;&=&\;-2x\;+\;5\end{eqnarray*}[/latex]
Step 2: Replace the [latex]y[/latex] with [latex]\frac{1}{2}x[/latex]
[latex]\begin{eqnarray*}{\color{red}{\frac12}}{\color{red}{x}}\;=\;-2x\;+\;5\\\end{eqnarray*}[/latex]
Step 3: Solve the resulting equation. Start by clearing the fraction.
[latex]2\left(\frac12x\right)\;=\;2\left(-2x\;+\;5\right)[/latex]
Step 4: Solve for [latex]x[/latex].
[latex]\begin{eqnarray*}x\;&=&\;-4x\;+\;10\\5x\;&=&\;10\\x\;&=&\;2\\\end{eqnarray*}[/latex]
Step 5: Substitute [latex]x = 2[/latex] into [latex]y=\frac{1}{2}x[/latex] to find [latex]y[/latex].
[latex]\begin{eqnarray*}{\color{red}{x}}\;&=&\;{\color{red}{2}}\\y\;&=&\;\frac12{\color{red}{x}}\\y\;&=&\;\frac12\;\times\;{\color{red}{2}}\\y\;&=&\;1\end{eqnarray*}[/latex]
The ordered pair is [latex](2,1)[/latex].
Step 6: Check the ordered pair in both equations
|
[latex]\begin{eqnarray*}y\;&=&\;\frac12x\\1\;&\overset?=&\;\frac12\times2\\1\;&=&\;1\;\checkmark\\\end{eqnarray*}[/latex] |
[latex]\begin{eqnarray*}y\;&=&\;-2x\;+\;5\\1\;&\overset?=&\;-2\;\times\;2\;+\;5\\1\;&=&\;1\;\checkmark\\\end{eqnarray*}[/latex] |
The solution is [latex](2,1)[/latex].
Try It
13) Solve the system by substitution.
[latex]\left\{\begin{array}{l}x+y=6\\y=3x-2\end{array}\right.[/latex]
Solution
[latex](2,4)[/latex]
14) Solve the system by substitution.
[latex]\left\{\begin{array}{l}4x-y=0\\2x-3y=5\end{array}\right.[/latex]
Solution
[latex](-\frac{1}{2},-2)[/latex]
Be very careful with the signs in the next example.
Example 6
Solve the system by substitution.
[latex]\left\{\begin{array}{l}4x+2y=4\\6x-y=8\end{array}\right.[/latex]
Solution
We need to solve one equation for one variable. We will solve the first equation for [latex]y[/latex].
[latex]4x\;+\;2y\;=\;4[/latex]
Step 1: Solve the first equation for [latex]y[/latex].
[latex]2y\;=\;-4x\;+\;4[/latex]
Step 2: Substitute [latex]−2x + 2[/latex] for [latex]y[/latex] in the second equation.
[latex]\begin{eqnarray*}{\color{red}{y}}\;&=&\;{\color{red}{-}}{\color{red}{2}}{\color{red}{x}}{\color{red}{\;}}{\color{red}{+}}{\color{red}{\;}}{\color{red}{2}}\\6x\;-\;{\color{red}{y}}\;&=&\;8\end{eqnarray*}[/latex]
Step 3: Replace the [latex]y[/latex] with [latex]−2x + 2[/latex].
[latex]{6x\;-\;(}{\color{red}{-}}{{\color{red}{2}}{\color{red}{x}}{\color{red}{\;}}{\color{red}{+}}{\color{red}{\;}}}{\color{red}{2}}{)\;=\;8}[/latex]
Step 4: Solve the equation for [latex]x[/latex].
[latex]\begin{eqnarray*}6x\;+\;2x\;-\;2\;&=&\;8\\8x\;-\;2\;&=&\;8\\8x\;&=&\;10\\x\;&=&\;\frac54\end{eqnarray*}[/latex]
Step 5: Substitute [latex]x=\frac{5}{4}[/latex] into [latex]4x + 2y = 4[/latex] to find [latex]y[/latex].
[latex]\begin{eqnarray*}x\;&=&\;\frac52\\4{\color{red}{x}}\;+\;2y\;&=&\;4\\4({\color{red}{\frac52}})\;+\;2y\;&=&\;4\\5\;+\;2y\;&=&\;4\\2y\;&=&\;-1\\y\;&=&-\frac12\end{eqnarray*}[/latex]
The ordered pair is [latex](\frac{5}{4},-\frac{1}{2})[/latex]
Step 6: Check the ordered pair in both equations.
|
[latex]\begin{eqnarray*}4x+2y&= 4\\4(\frac{5}{4}) + 2(-\frac{1}{2})&\overset?=4\\5 - 1&\overset?=4\\4&=4\checkmark\end{eqnarray*}[/latex] |
[latex]\begin{eqnarray*}6x\;-\;y\;&=&\;8\\6\left(\frac54\right)-\left(-\frac12\right)&\overset?=&8\\\frac{15}4-\left(-\frac12\right)\;&\overset?=&8\\\frac{16}2&\overset?=&8\\8&=&8\;\checkmark\end{eqnarray*}[/latex] |
The solution is [latex](\frac{5}{4},-\frac{1}{2})[/latex]
Try It
15) Solve the system by substitution.
[latex]{\left\{\begin{array}{l}3x+y=5\\2x+4y=10\end{array}\right.}[/latex]
Solution
[latex](-1,8)[/latex]
16) Solve the system by substitution.
[latex]{\left\{\begin{array}{l}4x-y=0\\2x-3y=5\end{array}\right.}[/latex]
Solution
[latex](-\frac{1}{2},-2)[/latex]
In Example 7, it will take a little more work to solve one equation for [latex]x[/latex] or [latex]y[/latex].
Example 7
Solve the system by substitution.
[latex]\left\{\begin{array}{l}4x-3y=6\\15y-20x=-30\end{array}\right.[/latex]
Solution
We need to solve one equation for one variable. We will solve the first equation for [latex]x[/latex].
[latex]\begin{eqnarray*}x\;&=&\;\frac52\\4x\;-\;3y\;&=&\;6\end{eqnarray*}[/latex]
Step 1: Solve the first equation for [latex]x[/latex].
[latex]4x\;=\;3y\;+\;6[/latex]
Step 2: Substitute [latex]\frac{3}{4}y+\frac{3}{2}[/latex] for [latex]x[/latex] in the second equation.
[latex]\begin{eqnarray*}{\color{red}{x}}\;&=&{\color{red}{\frac34}}{\color{red}{y}}+{\color{red}{\frac32}}\\15y\;-\;20{\color{red}{x}}&=&-30\end{eqnarray*}[/latex]
Step 3: Replace the [latex]x[/latex] with [latex]\frac{3}{4}y+\frac{3}{2}[/latex]
[latex]{15y\;-\;20}{\color{red}{\left(\frac34y\;+\;\frac32\right)}}{\;=\;-30}[/latex]
Step 4: Solve for [latex]y[/latex].
[latex]\begin{eqnarray*}15y\;-\;15y\;-\;30\;&=&\;-30\\0\;-\;30\;&=&\;-30\\0\;&=&\;0\end{eqnarray*}[/latex]
Since [latex]0 = 0[/latex] is a true statement, the system is consistent. The equations are dependent. The graphs of these two equations would give the same line. The system has infinitely many solutions.
Try It
17) Solve the system by substitution.
[latex]\left\{\begin{array}{l}2x-3y=12\\-12y+8x=48\end{array}\right.[/latex]
Solution
Infinitely many solutions.
18) Solve the system by substitution.
[latex]\left\{\begin{array}{l}5x+2y=12\\-4y-10x=-24\end{array}\right.[/latex]
Solution
Infinitely many solutions.
Look back at the equations in Example 7. Is there any way to recognize that they are the same line?
Let’s see what happens in the next example.
Example 8
Solve the system by substitution.
[latex]\left\{\begin{array}{l}5x-2y=-10\\y=\frac52x\end{array}\right.[/latex]
Solution
The second equation is already solved for [latex]y[/latex], so we can substitute for [latex]y[/latex] in the first equation.
Step 1: Substitute [latex]x[/latex] for [latex]y[/latex] in the first equation.
[latex]\begin{eqnarray*}{\color{red}{y}}\;&=&{\color{red}{\frac52}}{\color{red}{x}}\\5x-2{\color{red}{y}}&=&-10\end{eqnarray*}[/latex]
Step 2: Replace the [latex]y[/latex] with [latex]\frac{5}{2}x[/latex].
[latex]{5x\;-\;2}{\color{red}{\left(\frac52x\right)}}{\;=\;-10}[/latex]
Step 3: Solve for [latex]x[/latex].
[latex]\begin{eqnarray*}5x\;-\;5x\;&=&\;-10\\0\;&\neq&\;-10\end{eqnarray*}[/latex]
Since [latex]0 = −10[/latex] is a false statement the equations are inconsistent. The graphs of the two equation would be parallel lines. The system has no solutions.
Try It
19) Solve the system by substitution.
[latex]\left\{\begin{array}{l}3x+2y=9\\y=-\frac32x+1\end{array}\right.[/latex]
Solution
No solution.
20) Solve the system by substitution.
[latex]\left\{\begin{array}{l}5x-3y=2\\y=\frac53x-4\end{array}\right.[/latex]
Solution
No solution.
Solve Applications of Systems of Equations by Substitution
We’ll copy here the problem-solving strategy we used in the Solving Systems of Equations by Graphing section for solving systems of equations. Now that we know how to solve systems by substitution, that’s what we’ll do in Step 5:
How to
How to use a problem-solving strategy for systems of linear equations.
- Read the problem. Make sure all the words and ideas are understood.
- Identify what we are looking for.
- Name what we are looking for. Choose variables to represent those quantities.
- Translate into a system of equations.
- Solve the system of equations using good algebra techniques.
- Check the answer to the problem and make sure it makes sense.
- Answer the question with a complete sentence.
Some people find setting up word problems with two variables easier than setting them up with just one variable. Choosing the variable names is easier when all you need to do is write down two letters. Think about this in the next example—how would you have done it with just one variable?
Example 9
The sum of two numbers is zero. One number is nine less than the other. Find the numbers.
Solution
Step 1: Read the problem.
Step 2: Identify what we are looking for.
We are looking for two numbers.
Step 3: Name what we are looking for.
Let [latex]n=[/latex] the first number
Let [latex]m=[/latex] the second number
Step 4: Translate into a system of equations.
The sum of two numbers is zero.
[latex]n\;+\;m\;=\;0[/latex]
One number is nine less than the other.
[latex]n\;=\;m\;-\;9[/latex]
The system is:
[latex]\left\{\begin{array}{l}n+m=0\\n=m-9\end{array}\right.[/latex]
Step 5: Solve the system of equations.
We will use substitution since the second equation is solved for [latex]n[/latex].
Substitute [latex]m − 9[/latex] for [latex]n[/latex] in the first equation.
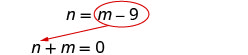
Solve for [latex]m[/latex].
[latex]\begin{eqnarray*}{\color{red}{m}}{\color{red}{-}}{\color{red}{9}}+m&=&0\\2m-9&=&0\\2m&=&9\end{eqnarray*}[/latex]
Substitute [latex]m=\frac{9}{2}[/latex] into the second equation and then solve for [latex]n[/latex].
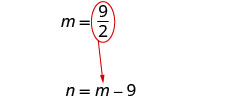
[latex]\begin{eqnarray*}m&=&{\color{red}{\frac92}}-9\\m&=&\frac92-\frac{18}2\\n&=&-\frac92\end{eqnarray*}[/latex]
Step 6: Check the answer to the problem.
Do these numbers make sense in the problem? We will leave this to you!
Step 7: Answer the question.
The numbers are [latex]\frac{9}{2}[/latex] and [latex]-\frac{9}{2}[/latex]
Try It
21) The sum of two numbers is [latex]10[/latex]. One number is [latex]4[/latex] less than the other. Find the numbers.
Solution
The numbers are [latex]3[/latex] and [latex]7[/latex].
22) The sum of two numbers is [latex]−6[/latex]. One number is [latex]10[/latex] less than the other. Find the numbers.
Solution
The numbers are [latex]2[/latex] and [latex]−8[/latex].
In Example 10, we’ll use the formula for the perimeter of a rectangle, [latex]P=2L+2W[/latex].
Example 10
The perimeter of a rectangle is [latex]88[/latex]. The length is five more than twice the width. Find the length and the width.
Solution
Step 1: Read the problem.

Step 2: Identify what you are looking for.
We are looking for the length and width.
Step 3: Name what we are looking for.
Let [latex]L[/latex] = the length
Let [latex]W[/latex] = the width
Step 4: Translate into a system of equations.
The perimeter of a rectangle is [latex]88[/latex].
[latex]2L+2W=P[/latex]
[latex]2L+2W=88[/latex]
The length is five more than twice the width.
[latex]L=2W+5[/latex]
The system is:
[latex]\left\{\begin{array}{l}2L+2W=88\\L=2W+5\end{array}\right.[/latex]
Step 5: Solve the system of equations.
We will use substitution since the second equation is solved for [latex]L[/latex].
Substitute [latex]2W + 5[/latex] for [latex]L[/latex] in the first equation.
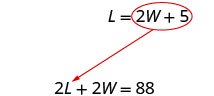
Solve for [latex]W[/latex].
[latex]\begin{align*}2({\color{red}{2}}{\color{red}{W}}{\color{red}{+}}{\color{red}{5}})+2W&=88\\4W+10+2W&=88\\6W+10&=88\\6W&=78\end{align*}[/latex]
Substitute [latex]W = 13[/latex] into the second equation and then solve for [latex]L[/latex].
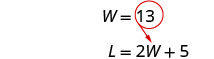
[latex]\begin{align*}L&=2\times13+5\\L&=31\end{align*}[/latex]
Step 6: Check the answer in the problem.
Does a rectangle with length [latex]31[/latex] and width [latex]13[/latex] have perimeter [latex]88[/latex]? Yes.
Step 7: Answer the equation.
The length is [latex]31[/latex] and the width is [latex]13[/latex].
Try It
23) The perimeter of a rectangle is [latex]40[/latex]. The length is [latex]4[/latex] more than the width. Find the length and width of the rectangle.
Solution
The length is [latex]12[/latex] and the width is [latex]8[/latex].
24) The perimeter of a rectangle is [latex]58[/latex]. The length is [latex]5[/latex] more than three times the width. Find the length and width of the rectangle.
Solution
The length is [latex]23[/latex] and the width is [latex]6[/latex].
For Example 11, we need to remember that the sum of the measures of the angles of a triangle is [latex]180[/latex] degrees and that a right triangle has one [latex]90[/latex] degree angle.
Example 11
The measure of one of the small angles of a right triangle is ten more than three times the measure of the other small angle. Find the measures of both angles.
Solution
We will draw and label a figure.
Step 1: Read the problem.

Step 2: Identify what you are looking for.
We are looking for the measures of the angles.
Step 3: Name what we are looking for.
Let [latex]a=[/latex] the measure of the 1st angle.
Let [latex]b=[/latex] the measure of the 2nd angle.
Step 4: Translate into a system of equations.
The measure of one of the small angles of a right triangle is ten more than three times the measure of the other small angle.
[latex]a=3b+10[/latex]
The sum of the measures of the angles of a triangle is [latex]180[/latex].
[latex]a+b+90=180[/latex]
The system is:
[latex]\left\{\begin{array}{l}a=3b+10\\a+b+90=180\end{array}\right.[/latex]
Step 5: Solve the system of equations.
We will use substitution since the first equation is solved for [latex]a[/latex].
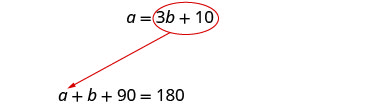
Substitute [latex]3b + 10[/latex] for [latex]a[/latex] in the second equation.
[latex]{(}{\color{red}{3}}{{\color{red}{b}}{\color{red}{+}}}{\color{red}{10}}{)+b+90=180}[/latex]
Solve for [latex]b[/latex].
[latex]\begin{align*}4b+100&=180\\4b&=80\end{align*}[/latex]

Substitute [latex]b = 20[/latex] into the first equation and then solve for [latex]a[/latex].
[latex]\begin{align*}a&=3\times{\color{red}{20}}+10\\a&=70\end{align*}[/latex]
Step 6: Check the answer in the problem.
We will leave this to you!
Step 7: Answer the question.
The measures of the small angles are [latex]20[/latex] and [latex]70[/latex].
Try It
25) The measure of one of the small angles of a right triangle is [latex]2[/latex] more than [latex]3[/latex] times the measure of the other small angle. Find the measure of both angles.
Solution
The measure of the angles are [latex]22[/latex] degrees and [latex]68[/latex] degrees.
26) The measure of one of the small angles of a right triangle is [latex]18[/latex] less than twice the measure of the other small angle. Find the measure of both angles.
Solution
The measure of the angles are [latex]36[/latex] degrees and [latex]54[/latex] degrees.
Example 12
Heather has been offered two options for her salary as a trainer at the gym. Option A would pay her [latex]$25,000[/latex] plus [latex]$15[/latex] for each training session. Option B would pay her [latex]$10,000 + $40[/latex] for each training session. How many training sessions would make the salary options equal?
Solution
Step 1: Read the problem.
Step 2: Identify what you are looking for.
We are looking for the number of training sessions that would make the pay equal.
Step 3: Name what we are looking for.
Let [latex]s=[/latex] Heather’s salary.
Let [latex]n=[/latex] be the number of training sessions
Step 4: Translate into a system of equations.
Option A would pay her [latex]$25,000[/latex] plus [latex]15[/latex] for each training session.
[latex]s=25,000+15n[/latex]
Option B would pay her [latex]$10,000 + $40[/latex] for each training session
[latex]s=10,000+40n[/latex]
The system is:
[latex]\left\{\begin{array}{l}s&=25,000+15n\\s&=10,000+40n\end{array}\right.[/latex]
Step 5: Solve the system of equations.
We will use substitution.
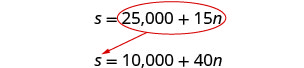
Substitute [latex]25,000 + 15n[/latex] for [latex]s[/latex] in the second equation.
[latex]{\color{red}{25,000}}{{\color{red}{+}}{\color{red}{15}}}{\color{red}{n}}{=10,000+40n}[/latex]
Solve for [latex]n[/latex].
[latex]\begin{align*}25,000&=10,000+25n\\15,000&=25n\\600&=n\end{align*}[/latex]
Step 6: Check the answer.
Are [latex]600[/latex] training sessions a year reasonable?
Are the two options equal when [latex]n = 600[/latex]?
Step 7: Answer the question.
The salary options would be equal for [latex]600[/latex] training sessions.
Try It
27) Geraldine has been offered positions by two insurance companies. The first company pays a salary of [latex]$12,000[/latex] plus a commission of [latex]$100[/latex] for each policy sold. The second pays a salary of [latex]$20,000[/latex] plus a commission of [latex]$50[/latex] for each policy sold. How many policies would need to be sold to make the total pay the same?
Solution
There would need to be [latex]160[/latex] policies sold to make the total pay the same.
28) Kenneth currently sells suits for company A at a salary of [latex]$22,000[/latex] plus a [latex]$10[/latex] commission for each suit sold. Company B offers him a position with a salary of [latex]$28,000[/latex] plus a [latex]$4[/latex] commission for each suit sold. How many suits would Kenneth need to sell for the options to be equal?
Solution
Kenneth would need to sell [latex]1,000[/latex] suits.
Access these online resources for additional instruction and practice with solving systems of equations by substitution.
Key Concepts
- Solve a system of equations by substitution
- Solve one of the equations for either variable.
- Substitute the expression from Step 1 into the other equation.
- Solve the resulting equation.
- Substitute the solution in Step 3 into one of the original equations to find the other variable.
- Write the solution as an ordered pair.
- Check that the ordered pair is a solution to both original equations.
Exercises: Solve a System of Equations by Substitution
Instructions: For questions 1-36, solve the systems of equations by substitution.
Solution
[latex]\left(-2,0\right)[/latex]
Solution
[latex]\left(7,6\right)[/latex]
Solution
[latex]\left(0,3\right)[/latex]
Solution
[latex]\left(6,-3\right)[/latex]
Solution
[latex]\left(3,-1\right)[/latex]
Solution
[latex]\left(6,6\right)[/latex]
Solution
[latex]\left(5,0\right)[/latex]
Solution
[latex]\left(-2,7\right)[/latex]
Solution
[latex]\left(-5,2\right)[/latex]
Solution
[latex]\left(-1,7\right)[/latex]
Solution
[latex]\left(-3,5\right)[/latex]
Solution
(10, 12)
Solution
[latex]\left(\frac{1}{2},3\right)[/latex]
Solution
[latex]\left(\frac{1}{2},-\frac{3}{4}\right)[/latex]
Solution
Infinitely many solutions
Solution
Infinitely many solutions
Solution
No solution
Solution
No solution
Exercises: Solve Applications of Systems of Equations by Substitution
Instructions: For questions 37-51, translate to a system of equations and solve.
Solution
The numbers are [latex]6[/latex] and [latex]9[/latex].
Solution
The numbers are [latex]-7[/latex] and [latex]-19[/latex].
Solution
The length is [latex]20[/latex] and the width is [latex]10[/latex].
Solution
The length is [latex]34[/latex] and the width is [latex]8[/latex].
Solution
The measures are [latex]16^\circ[/latex] and [latex]74^\circ[/latex].
Solution
The measures are [latex]45^\circ[/latex] and [latex]45^\circ[/latex].
Solution
[latex]80[/latex] cable packages would need to be sold.
Solution
Mitchell would need to sell [latex]120[/latex] stoves.
Exercises: Everyday Math
Instructions: For questions 52-53, answer the given everyday math word problems.
53. Stephanie left Riverside, California, driving her motorhome north on Interstate 15 towards Salt Lake City at a speed of [latex]56[/latex] miles per hour. Half an hour later, Tina left Riverside in her car on the same route as Stephanie, driving [latex]70[/latex] miles per hour. Solve the system [latex]\left\{\begin{array}{c}56s=70t\\ s=t+\frac{1}{2}\end{array}\right.[/latex].
a. for [latex]t[/latex] to find out how long it will take Tina to catch up to Stephanie.
b. what is the value of [latex]s[/latex], the number of hours Stephanie will have driven before Tina catches up to her?
Solution
a.[latex]t=2[/latex] hours
b. [latex]s=2\frac{1}{2}[/latex] hours
Exercises: Writing Exercises
Instructions: For questions 54-55, answer the given writing exercises.
54. Solve the system of equations [latex]\left\{\begin{array}{c}x+y=10\\ x-y=6\end{array}\right.[/latex]
a. by graphing
b. by substitution
c. Which method do you prefer? Why?
Solution
Answers will vary.







