3.2 Solve Equations using the Division and Multiplication Properties of Equality
Learning Objectives
By the end of this section, you will be able to:
- Solve equations using the Division and Multiplication Properties of Equality
- Solve equations that require simplification
- Translate to an equation and solve
- Translate and solve applications
Try It
Before you get started, take this readiness quiz:
1) Simplify: [latex]-7\cdot \frac{1}{-7}[/latex].
2) Evaluate [latex]9x+2[/latex] when [latex]x=-3[/latex].
Solve Equations Using the Division and Multiplication Properties of Equality
You may have noticed that all of the equations we have solved so far have been of the form [latex]x+a=b[/latex] or [latex]x-a=b[/latex]. We were able to isolate the variable by adding or subtracting the constant term on the side of the equation with the variable. Now we will see how to solve equations that have a variable multiplied by a constant and so will require the division to isolate the variable.
Let’s look at our puzzle again with the envelopes and counters in Figure 3.2.1.
The illustration shows a model of an equation with one variable multiplied by a constant. On the left side of the workspace are two instances of the unknown (envelope), while on the right side of the workspace are six counters.
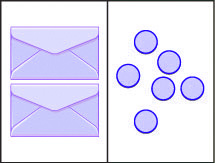
In the illustration, two identical envelopes contain the same number of counters. Remember, the left side of the workspace must equal the right side, but the counters on the left side are “hidden” in the envelopes. So how many counters are in each envelope?
How do we determine the number? We have to separate the counters on the right side into two groups of the same size to correspond with the two envelopes on the left side. The 6 counters divided into 2 equal groups gives 3 counters in each group (since [latex]6\div2=3[/latex]).
What equation models the situation shown in Figure 3.2.2? There are two envelopes, and each contains [latex]x[/latex] counters. Together, the two envelopes must contain a total of 6 counters.
The illustration shows a model of the equation [latex]2x=6[/latex].
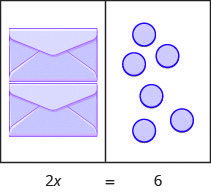
| [latex]2x=6[/latex] | |
| If we divide both sides of the equation by 2, as we did with the envelopes and counters, | [latex]\frac{2x}2=\frac62[/latex] |
| we get: | [latex]x=3[/latex] |
We found that each envelope contains 3 counters. Does this check? We know [latex]2\cdot 3=6[/latex], so it works! Three counters in each of two envelopes do equal six!
This example leads to the Division Property of Equality.
The Division Property of Equality
For any numbers [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex], if [latex]a=b[/latex], and [latex]c\neq 0[/latex],
When you divide both sides of an equation by any non-zero number, you still have equality.
The goal in solving an equation is to ‘undo’ the operation on the variable. In the next example, the variable is multiplied by 5, so we will divide both sides by 5 to ‘undo’ the multiplication.
Example 1
Solve: [latex]5x=-27[/latex].
Solution
Step 1: To isolate [latex]x[/latex], “undo” the multiplication by 5.
[latex]5x=-27[/latex]
Step 2: Divide to ‘undo’ the multiplication.
[latex]\begin{align*}&\;&\frac{5x}{\color{red}{5}}&=-\frac{27}{\color{red}{5}}\\ &\text{Simplify.}\;&x&=-\frac{27}{5}\\ \end{align*}[/latex]
Step 3: Check:
[latex]5x=-27[/latex]
Step 5: Substitute [latex]-\frac{27}{5}[/latex] for [latex]x[/latex].
[latex]\begin{eqnarray*}5\left({\color{red}{-}}{\color{red}{\frac{27}{5}}}\right)&\overset?=-27\\-27&=-27\checkmark\end{eqnarray*}[/latex]
Since this is a true statement, [latex]x=-\frac{27}{5}[/latex] is the solution to [latex]5x=-27[/latex].
Try It
3) Solve: [latex]3y=-41[/latex].
Solution
[latex]y=\frac{-41}{3}[/latex]
4) Solve: [latex]4z=-55[/latex].
Solution
[latex]z=-\frac{55}{4}[/latex]
Consider the equation [latex]\frac{x}{4}=3[/latex]. We want to know what number divided by 4 gives 3. So to “undo” the division, we will need to multiply by 4. The Multiplication Property of Equality will allow us to do this. This property says that if we start with two equal quantities and multiply both by the same number, the results are equal.
The Multiplication Property of Equality
For any numbers [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex],
If you multiply both sides of an equation by the same number, you still have equality.
Example 2
Solve: [latex]\frac{y}{-7}=-14[/latex].
Solution
Here [latex]y[/latex] is divided by [latex]-7[/latex]. We must multiply by [latex]-7[/latex] to isolate [latex]y[/latex].
Step 1: Multiply both sides by [latex]-7[/latex].
[latex]\begin{align*}\frac{y}{-7} \times \color{red}{-7} &=-14 \times \color{red}{-7}\\&\text{Simplify.}\;&y&=98\end{align*}[/latex]
Step 2: Check: [latex]\frac{y}{-7}=-14[/latex]
Step 3: Substitute [latex]y=98[/latex].
[latex]\begin{align*}\frac{\color{red}{98}}{-7}&\overset?=-14\\-14&=-14\checkmark\end{align*}[/latex]
Try It
5) Solve: [latex]\frac{a}{-7}=-42[/latex].
Solution
[latex]a=294[/latex]
6) Solve: [latex]\frac{b}{-6}=-24[/latex].
Solution
[latex]b=144[/latex]
Example 3
Solve: [latex]−n=9[/latex].
Solution
Step 1: Remember [latex]-n[/latex] is equivalent to [latex]-1n[/latex].
[latex]-1n=9[/latex]
Step 2: Divide both sides by [latex]-1[/latex].
[latex]\begin{align*}&\;&\frac{-1n}{{\color{red}{-}}{\color{red}{1}}}&=\frac9{{\color{red}{-}}{\color{red}{1}}}\\&\text{Divide}\;&n&=-9 \end{align*}[/latex]
Notice that there are two other ways to solve [latex]-n=9[/latex]. We can also solve this equation by multiplying both sides by [latex]-1[/latex] and also by taking the opposite of both sides.
Step 3: Check:
[latex]-n=9[/latex]
Step 4: Substitute [latex]n=-9[/latex].
[latex]\begin{align*}&\;&-\left(-{\color{red}{9}}\right)&\overset?=9\\&\text{Simplify}\;&9&=9\checkmark\end{align*}[/latex]
Try It
7) Solve: [latex]−k=8[/latex].
Solution
[latex]k=-8[/latex]
8) Solve: [latex]-g=3[/latex].
Solution
[latex]g=-3[/latex]
Example 4
Solve: [latex]\frac{3}{4}x=12[/latex].
Solution
Since the product of a number and its reciprocal is [latex]1[/latex], our strategy will be to isolate [latex]x[/latex] by multiplying by the reciprocal of [latex]\frac{3}{4}[/latex].
Step 1: Multiply by the reciprocal of [latex]\frac{3}{4}[/latex].
[latex]\begin{align*}&\;&{\color{red}{\frac43}}\cdot\frac34x&={\color{red}{\frac43}}\cdot12\\ &\text{Reciprocals multiply to 1}\;&1x&=\frac{4}{3}\cdot\frac{12}{1}\\ &\text{Mulitply.}\;&x&=16 \end{align*}[/latex]
Notice that we could have divided both sides of the equation [latex]\frac{3}{4}x=12[/latex] by [latex]\frac{3}{4}[/latex] to isolate [latex]x[/latex]. While this would work, most people would find multiplying by the reciprocal easier.
Step 2: Check:
Step 5: Substitute [latex]x=16[/latex].
[latex]\begin{align*}\frac{3}{4}x&=12\\\frac34\cdot{\color{red}{16}}&\overset?=12\\12&=12\checkmark\end{align*}[/latex]
Try It
9) Solve: [latex]\frac{2}{5}n=14[/latex].
Solution
[latex]n=35[/latex]
10) Solve: [latex]\frac{5}{6}y=15[/latex].
Solution
[latex]y=18[/latex]
In the next example, all the variable terms are on the right side of the equation. As always, our goal in solving the equation is to isolate the variable.
Example 5
Solve: [latex]\frac{8}{15}=-\frac{4}{5}x[/latex].
Solution
Step 1: Multiply by the reciprocal of [latex]-\frac{4}{5}[/latex].
[latex]\begin{align*}&\;&\left({\color{red}{-}}{\color{red}{\frac{5}{4}}}\right)\left(\frac8{15}\right)&=\left({\color{red}{-}}{\color{red}{\frac{5}{4}}}\right)\left(-\frac45x\right)\\ &\text{Reciprocals multiply to 1}\;&-\frac{\cancel5\cdot\cancel4\cdot2}{\cancel4\cdot3\cdot\cancel5}&=1x\\ &\text{Mulitply.}\;&-\frac{2}{3}&=x \end{align*}[/latex]
Step 2: Let [latex]x=-\frac{2}{3}[/latex].
[latex]\begin{align*}\frac{8}{15}&=-\frac{4}{5}x\\\frac8{15}&=-\frac45\left({\color{red}{-}}{\color{red}{\frac23}}\right)\\\frac{8}{15}&=\frac{8}{15}\checkmark\end{align*}[/latex]
Try It
11) Solve: [latex]\frac{9}{25}=-\frac{4}{5}z[/latex].
Solution
[latex]z=-\frac{9}{20}[/latex]
12) Solve: [latex]\frac{5}{6}=-\frac{8}{3}r[/latex]
Solution
[latex]r=-\frac{5}{16}[/latex]
Solve Equations That Require Simplification
Many equations start out more complicated than the ones we have been working with.
With these more complicated equations, the first step is to simplify both sides of the equation as much as possible. This usually involves combining like terms or using the distributive property.
Example 6
Solve: [latex]14-23=12y-4y-5y[/latex].
Solution
Begin by simplifying each side of the equation.
Step 1: Simplify each side.
[latex]-9=3y[/latex]
Step 2: Divide both sides by [latex]3[/latex] to isolate [latex]y[/latex].
[latex]\begin{align*}&\;&\frac{-9}{3}&=\frac{3y}{3}\\ &\text{Divide.}\;&-3&=y\end{align*}[/latex]
Step 3: Check:
[latex]14-23\overset?=12y-4y-5y[/latex]
Step 4: Substitute [latex]y=-3[/latex].
[latex]\begin{align*}14-23&\overset?=12\left({\color{red}{-}}{\color{red}{3}}\right)-4\left({\color{red}{-}}{\color{red}{3}}\right)-5\left({\color{red}{-}}{\color{red}{3}}\right)\\14-23&\overset?=-36+12+15\\-9&=-9\checkmark \end{align*}[/latex]
Try It
13) Solve: [latex]18-27=15c-9c-3c[/latex].
Solution
[latex]c=-3[/latex]
14) Solve: [latex]18-22=12x-x-4x[/latex].
Solution
[latex]x=-\frac{4}{7}[/latex]
Example 7
Solve: [latex]-4(a-3)-7=25[/latex].
Solution
Here we will simplify each side of the equation by using the distributive property first.
Step 1: Distribute.
[latex]\begin{align*}&\;&-4a+12-7&=25\\ &\text{Simplify.}\;&-4a+5&=25\\ &\text{Simplify.}\;&-4a&=20 \end{align*}[/latex]
Step 2: Divide both sides by [latex]-4[/latex] to isolate [latex]a[/latex].
[latex]\begin{align*}&\;&\left(\frac{-4a}{{\color{red}{-}}{\color{red}{4}}}\right)&=\left(\frac{20}{{\color{red}{-}}{\color{red}{4}}}\right)\\ &\text{Divide.}\;&a&=-5\end{align*}[/latex]
Step 3: Check:
[latex]-4(a-3)-7=25[/latex]
Step 4: Substitute [latex]a=-5[/latex].
[latex]\begin{align*}-4\left({\color{red}{-}}{\color{red}{5}}-3\right)-7&\overset?=25\\-4\left(-8\right)-7&\overset?=25\\32-7&\overset?=25\\25&=25\checkmark\end{align*}[/latex]
Try It
15) Solve: [latex]-4(q-2)-8=24[/latex].
Solution
[latex]q=-6[/latex]
16) Solve: [latex]-6(r-2)-12=30[/latex].
Solution
[latex]r=-5[/latex]
Now we have covered all four properties of equality—subtraction, addition, division, and multiplication. We’ll list them all together here for easy reference.
Properties of Equality
|
Subtraction Property of Equality for any real numbers [latex]a[/latex], [latex]b[/latex] and [latex]c[/latex], If [latex]a=b[/latex], then [latex]a-c=b-c[/latex]. |
Addition Property of Equality for any real numbers [latex]a[/latex], [latex]b[/latex] and [latex]c[/latex], If [latex]a=b[/latex], then [latex]a+c = b+c[/latex]. |
|
Division Property of Equality for any real numbers [latex]a[/latex], [latex]b[/latex] and [latex]c[/latex], and [latex]c\neq0[/latex] If [latex]a=b[/latex], then [latex]\frac{a}{c}=\frac{b}{c}[/latex]. |
Multiplication Property of Equality for any real numbers [latex]a[/latex], [latex]b[/latex] and [latex]c[/latex], If [latex]a=b[/latex], then [latex]a\times c = b\times c[/latex].
|
When you add, subtract, multiply, or divide the same quantity from both sides of an equation, you still have equality.
Translate to an Equation and Solve
In the next few examples, we will translate sentences into equations and then solve the equations. You might want to review the translation table in the previous chapter.
Example 8
Translate and solve: The number [latex]143[/latex] is the product of [latex]-11[/latex] and [latex]y[/latex].
Solution
Begin by translating the sentence into an equation.
Step 1: Translate.
[latex]\underbrace{The\;number\;143}_{143}\;\underbrace{is}_=\;\underbrace{the\;product\;of\;-11\;and\;y.}_{-11y}[/latex]
Step 2: Divide by [latex]-11[/latex].
[latex]\frac{143}{{\color{red}{-}}{\color{red}{11}}}=\frac{-11y}{{\color{red}{-}}{\color{red}{11}}}[/latex]
Step 3: Simplify.
[latex]-13=y[/latex]
Step 4: Check:
[latex]\begin{align*}143&=-11y\\143&\overset?=-11(-13)\\143&=143\checkmark\end{align*}[/latex]
Try It
17) Translate and solve: The number [latex]132[/latex] is the product of [latex]−12[/latex] and [latex]y[/latex].
Solution
[latex]132=-12y[/latex]; [latex]y=-11[/latex]
18) Translate and solve: The number [latex]117[/latex] is the product of [latex]−13[/latex] and [latex]z[/latex].
Solution
[latex]117=-13z[/latex]; [latex]z=-9[/latex]
Example 9
Translate and solve: [latex]n[/latex] divided by [latex]8[/latex] is [latex]-32[/latex].
Solution
Step 1: Begin by translating the sentence into an equation.
[latex]\underbrace{n\;divided\;by\;8}_\frac n8\;\underbrace{is}_=\;\underbrace{-32}_{-32}.[/latex]
Step 2: Multiple both sides by [latex]8[/latex].
[latex]\begin{align*}&\;&{\color{red}{8}}\cdot\frac n8&={\color{red}{8}}\left(-32\right)\\ &\text{Simplify.}\;&n&=-256\\ \end{align*}[/latex]
Step 3: Check:
Is [latex]n[/latex] divided by [latex]8[/latex] equal to [latex]−32[/latex]?
Step 4: Let [latex]n=-256[/latex].
[latex]\begin{align*}\frac{-256}{8}&\overset?=-32\\-32&=-32\checkmark\end{align*}[/latex]
Try It
19) Translate and solve: [latex]n[/latex] divided by [latex]7[/latex] is equal to [latex]-21[/latex].
Solution
[latex]\frac{n}{7}=-21[/latex]; [latex]n=-147[/latex]
20) Translate and solve: [latex]n[/latex] divided by [latex]8[/latex] is equal to [latex]-56[/latex].
Solution
[latex]\frac{n}{8}=-56[/latex]; [latex]n=-448[/latex]
Example 10
Translate and solve: The quotient of [latex]y[/latex] and [latex]-4[/latex] is [latex]68[/latex].
Solution
Begin by translating the sentence into an equation.
Step 1: Translate.
[latex]\underbrace{The\;quotient\;of\;y\;and\;-4}_\frac y{-4}\;\underbrace{is}_=\;\underbrace{68.}_{68}[/latex]
Step 2: Multiply both sides by [latex]-4[/latex].
[latex]\begin{align*} &\;&{\color{red}{-}}{\color{red}{4}}\left(\frac y{-4}\right)&={\color{red}{-}}{\color{red}{4}}\left(68\right)\\ &\text{Simplify.}\;&y&=-272\\ \end{align*}[/latex]
Step 3: Check:
Is the quotient of [latex]y[/latex] and [latex]-4[/latex] equal to [latex]68[/latex]?
Step 4: Let [latex]y=-272[/latex].
[latex]\begin{align*}\frac{-272}{-4}&\overset?=68\\68&=68\checkmark\end{align*}[/latex]
Try It
21) Translate and solve: The quotient of [latex]q[/latex] and [latex]-8[/latex] is [latex]72[/latex].
Solution
[latex]\frac{q}{-8}=72[/latex]; [latex]q=-576[/latex]
22) Translate and solve: The quotient of [latex]p[/latex] and [latex]-9[/latex] is [latex]81[/latex].
Solution
[latex]\frac{p}{-9}=81[/latex]; [latex]p=-729[/latex]
Example 11
Translate and solve: Three-fourths of [latex]p[/latex] is [latex]18[/latex].
Solution
Begin by translating the sentence into an equation. Remember, “of” translates into multiplication.
Step 1: Translate.
[latex]\underbrace{Three-fourths\;of\;p}_{\frac34p}\;\underbrace{is}_=\;\underbrace{18.}_{18}[/latex]
Step 2: Multiply both sides by [latex]\frac{4}{3}[/latex].
[latex]\begin{align*} &\;&{\color{red}{\frac43}}\cdot\frac34p&={\color{red}{\frac43}}\cdot18\\ &\text{Simplify.}\;&p&=24\\ \end{align*}[/latex]
Step 3: Check:
Is three-fourths of [latex]p[/latex] equal to [latex]18[/latex]?
Step 5: Let [latex]p=24[/latex].
Is three-fourths of [latex]24[/latex] equal to [latex]18[/latex]?
[latex]\begin{align*}\frac{3}{4}\times24&\overset?=18\\18&=18\checkmark\end{align*}[/latex]
Try It
23) Translate and solve: Two-fifths of [latex]f[/latex] is [latex]16[/latex].
Solution
[latex]\frac{2}{5}f=16[/latex]; [latex]f=40[/latex]
24) Translate and solve: Three-fourths of [latex]f[/latex] is [latex]21[/latex].
Solution
[latex]\frac{3}{4}f=21[/latex]; [latex]f=28[/latex]
Example 12
Translate and solve: The sum of three-eighths and [latex]x[/latex] is one-half.
Solution
Begin by translating the sentence into an equation.
Step 1: Translate.
[latex]\underbrace{The\;sum\;of\;three-eighths\;and\;x}_{\frac38+x}\;\underbrace{is}_=\;\underbrace{\frac12}_\frac12[/latex]
Step 2: Subtract [latex]\frac{3}{8}[/latex] from each side.
[latex]\begin{align*}&\;&\frac38-{\color{red}{\frac38}}+x&=\frac12-{\color{red}{\frac38}}\\ &\text{Simplify and rewrite} \\ &\text{fractions with common denominators.}\;&x&=\frac{4}{8}-\frac{3}{8}\\ &\text{Simplify.}\;&x&=\frac18 \end{align*}[/latex]
Step 3: Check:
Is the sum of three-eighths and [latex]x[/latex] equal to one-half?
Step 4: Let [latex]x=\frac{1}{8}[/latex]
Is the sum of three-eighths and one-eighth equal to one-half?
[latex]\begin{align*}&\;&\frac{3}{8}+\frac{1}{8}&\overset?=\frac{1}{2}\\ &\text{Simplify.}\;&\frac{4}{8}&\overset?=\frac{1}{2}\\ &\text{Simplify.}\;&\frac{1}{2}&=\frac{1}{2}\checkmark \end{align*}[/latex]
Try It
25) Translate and solve: The sum of five-eighths and [latex]x[/latex] is one-fourth.
Solution
[latex]\frac{5}{8}+x=\frac{1}{4}[/latex]; [latex]x=-\frac{3}{8}[/latex]
26) Translate and solve: The sum of three-fourths and [latex]x[/latex] is five-sixths.
Solution
[latex]\frac{3}{4}+x=\frac{5}{6}[/latex]; [latex]x=\frac1{12}[/latex]
Translate and Solve Applications
To solve applications using the Division and Multiplication Properties of Equality, we will follow the same steps we used in the last section. We will restate the problem in just one sentence, assign a variable, and then translate the sentence into an equation to solve.
Example 13
Denae bought [latex]6[/latex] pounds of grapes for [latex]\$10.74[/latex]. What was the cost of one pound of grapes?
Solution
Step 1: What are you asked to find?
The cost of 1 pound of grapes
Step 2: Assign a variable.
Let [latex]c[/latex] = the cost of one pound.
Step 3: Write a sentence that gives the information to find it.
The cost of [latex]6[/latex] pounds is [latex]\$10.74[/latex].
Step 4: Translate into an equation.
[latex]6c=10.74[/latex]
Step 5: Solve.
[latex]\begin{align*} \frac43(12,000) &= \frac43 \times \frac34p \\ 16,000 &= p \end{align*}[/latex]
The grapes cost [latex]\$1.79[/latex] per pound.
Step 6: Check:
If one pound costs [latex]\$1.79[/latex], do [latex]6[/latex] pounds cost [latex]\$10.74[/latex]?
[latex]\begin{align*} 6\left(1.79\right)&\overset?=10.74 \\ 10.74 &= 10.74\checkmark \end{align*}[/latex]
Try It
27) Translate and solve:
Arianna bought a 24-pack of water bottles for [latex]\$9.36[/latex]. What was the cost of one water bottle?
Solution
[latex]\$0.39[/latex]
28) Translate and solve:
At JB’s Bowling Alley, 6 people can play on one lane for [latex]\$34.98[/latex]. What is the cost for each person?
Solution
[latex]\$5.83[/latex]
Example 14
Andreas bought a used car for [latex]\$12,000[/latex]. Because the car was 4-years old, its price was [latex]\frac{3}{4}[/latex] of the original price, when the car was new. What was the original price of the car?
Solution
Step 1: What are you asked to find?
The original price of the car
Step 2: Assign a variable.
[latex]p[/latex] = the original price.
Step 3: Write a sentence that gives the information to find it.
[latex]\$12,000[/latex] is [latex]\frac{3}{4}[/latex] of the original price.
Step 4: Translate into an equation.
[latex]12,000=\frac{3}{4}p[/latex]
Step 5: Solve.
[latex]\begin{align*} \frac43\times \left(12,000\right)&=\frac43\times\frac34p \\ 16,000 &= p \end{align*}[/latex]
The original cost of the car was [latex]\$16,000[/latex].
Step 6: Check:
Is [latex]\frac{3}{4}[/latex] of [latex]\$16,000[/latex] equal to [latex]\$12,000[/latex]?
[latex]\begin{align*} \frac34\times \left(16,000\right)&\overset?=12,000 \\ 12,000 &= 12,000\checkmark \end{align*}[/latex]
Try It
29) Translate and solve:
The annual property tax on the Mehta’s house is [latex]\$1,800[/latex], calculated as [latex]\frac{15}{1,000}[/latex] of the assessed value of the house. What is the assessed value of the Mehta’s house?
Solution
[latex]\$120,000[/latex]
30) Translate and solve:
Stella planted 14 flats of flowers in [latex]\frac{2}{3}[/latex] of her garden. How many flats of flowers would she need to fill the whole garden?
Solution
21 flats
Key Concepts
- The Division Property of Equality—For any numbers [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex], and [latex]c\neq 0[/latex], if [latex]a=b[/latex], then [latex]\frac{a}{c}=\frac{b}{c}[/latex].
When you divide both sides of an equation by any non-zero number, you still have equality. - The Multiplication Property of Equality—For any numbers [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex], if [latex]a=b[/latex], then [latex]ac=bc[/latex].
If you multiply both sides of an equation by the same number, you still have equality.
Exercises: Solve Equations Using the Division and Multiplication Properties of Equality
Instructions: For questions 1-36, solve each equation using the Division and Multiplication Properties of Equality and check the solution.
1. [latex]8x=56[/latex]
Solution
[latex]x=7[/latex]
2. [latex]7p=63[/latex]
3. [latex]-5c=55[/latex]
Solution
[latex]c=-11[/latex]
4. [latex]-9x=-27[/latex]
5. [latex]-809=15y[/latex]
Solution
[latex]y=-\frac{809}{15}[/latex]
6. [latex]-731=19y[/latex]
7. [latex]-37p=-541[/latex]
Solution
[latex]p=-\frac{541}{37}[/latex]
8. [latex]-19m=-586[/latex]
9. [latex]0.25z=3.25[/latex]
Solution
[latex]z=13[/latex]
10. [latex]0.75a=11.25[/latex]
11. [latex]-13x=0[/latex]
Solution
[latex]x=0[/latex]
12. [latex]24x=0[/latex]
13. [latex]\frac{x}{4}=35[/latex]
Solution
[latex]x=140[/latex]
14. [latex]\frac{z}{2}=54[/latex]
15. [latex]-20=\frac{q}{-5}[/latex]
Solution
[latex]q=100[/latex]
16. [latex]\frac{c}{-3}=-12[/latex]
17. [latex]\frac{y}{9}=-16[/latex]
Solution
[latex]y=-144[/latex]
18. [latex]\frac{q}{6}=-38[/latex]
19. [latex]\frac{m}{-12}=45[/latex]
Solution
[latex]m=-540[/latex]
20. [latex]-24=\frac{p}{-20}[/latex]
21. [latex]-y=6[/latex]
Solution
[latex]y=-6[/latex]
22. [latex]-u=15[/latex]
23. [latex]-v=-72[/latex]
Solution
[latex]v=72[/latex]
24. [latex]-x=-39[/latex]
25. [latex]\frac{2}{3}y=48[/latex]
Solution
[latex]y=72[/latex]
26. [latex]\frac{3}{5}r=75[/latex]
27. [latex]-\frac{5}{8}w=40[/latex]
Solution
[latex]w=-64[/latex]
28. [latex]24=-\frac{3}{4}x[/latex]
29. [latex]-\frac{2}{5}=\frac{1}{10}a[/latex]
Solution
[latex]a=-4[/latex]
30. [latex]-\frac{1}{3}q=-\frac{5}{6}[/latex]
31. [latex]-\frac{7}{10}x=-\frac{14}{3}[/latex]
Solution
[latex]x=\frac{20}{3}[/latex]
32. [latex]\frac{3}{8}y=-\frac{1}{4}[/latex]
33. [latex]\frac{7}{12}=-\frac{3}{4}p[/latex]
Solution
[latex]p=-\frac{7}{9}[/latex]
34. [latex]\frac{11}{18}=-\frac{5}{6}q[/latex]
35. [latex]-\frac{5}{18}=-\frac{10}{9}u[/latex]
Solution
[latex]u=\frac{1}{4}[/latex]
36. [latex]-\frac{7}{20}=-\frac{7}{4}v[/latex]
Exercises: Solve Equations that Require Simplification
Instructions: For questions 37-46, solve each equation requiring simplification
37. [latex]100-16=4p-10p-p[/latex]
Solution
[latex]p=-12[/latex]
38. [latex]-18-7=5t-9t-6t[/latex]
39. [latex]\frac{7}{8}n-\frac{3}{4}n=9+2[/latex]
Solution
[latex]n=88[/latex]
40. [latex]\frac{5}{12}q+\frac{1}{2}q=25-3[/latex]
41. [latex]0.25d+0.10d=6-0.75[/latex]
Solution
[latex]d=15[/latex]
42. [latex]0.05p-0.01p=2+0.24[/latex]
43. [latex]-10(q-4)-57=93[/latex]
Solution
[latex]q=-11[/latex]
44. [latex]-12(d-5)-29=43[/latex]
45. [latex]-10(x+4)-19=85[/latex]
Solution
[latex]x=-\frac{72}{5}[/latex]
46. [latex]-15(z+9)-11=75[/latex]
Exercises: Mixed Practice
Instructions: For questions 47-65, solve each equation.
47. [latex]\frac{9}{10}x=90[/latex]
Solution
[latex]x=100[/latex]
48. [latex]\frac{5}{12}y=60[/latex]
49. [latex]y+46=55[/latex]
Solution
[latex]y=9[/latex]
50. [latex]x+33=41[/latex]
51. [latex]\frac{w}{-2}=99[/latex]
Solution
[latex]w=-198[/latex]
52. [latex]\frac{s}{-3}=-60[/latex]
53. [latex]27=6a[/latex]
Solution
[latex]a=\frac{9}{2}[/latex]
54. [latex]-a=7[/latex]
55. [latex]-x=2[/latex]
Solution
[latex]x=-2[/latex]
56. [latex]z-16=-59[/latex]
57. [latex]m-41=-14[/latex]
Solution
[latex]m=27[/latex]
58. [latex]0.04r=52.60[/latex]
59. [latex]63.90=0.03p[/latex]
Solution
[latex]p=2130[/latex]
60. [latex]-15x=-120[/latex]
61. [latex]84=-12z[/latex]
Solution
[latex]y=-7[/latex]
62. [latex]19.36=x-0.2x[/latex]
63. [latex]c-0.3c=35.70[/latex]
Solution
[latex]c=51[/latex]
64. [latex]-y=-9[/latex]
65. [latex]-x=-8[/latex]
Solution
[latex]x=8[/latex]
Exercises: Translate to an Equation and Solve
Instructions: For questions 66-85, translate to an equation and then solve
66. [latex]187[/latex] is the product of [latex]-17[/latex] and [latex]m[/latex].
67. [latex]133[/latex] is the product of [latex]-19[/latex] and [latex]n[/latex].
Solution
[latex]\begin{array}{rcl}133&=&-19n\\n&=&-7\end{array}[/latex]
68. [latex]-184[/latex] is the product of [latex]23[/latex] and [latex]p[/latex].
69. [latex]-152[/latex] is the product of [latex]8[/latex] and [latex]q[/latex].
Solution
[latex]\begin{array}{rcl}-152&=&8q\\q&=&-19\end{array}[/latex]
70. [latex]u[/latex] divided by [latex]7[/latex] is equal to [latex]-49[/latex].
71. [latex]r[/latex] divided by 12 is equal to [latex]-48[/latex].
Solution
[latex]\begin{array}{rcl}\frac{r}{12}&=&-48\\r&=&-576\end{array}[/latex]
72. [latex]h[/latex] divided by [latex]-13[/latex] is equal to [latex]-65[/latex].
73. [latex]j[/latex] divided by [latex]-20[/latex] is equal to [latex]-80[/latex].
Solution
[latex]\begin{array}{rcl}\frac{j}{-20}&=&-80\\j&=&1,600\end{array}[/latex]
74. The quotient [latex]c[/latex] and [latex]-19[/latex] is [latex]38[/latex].
75. The quotient of [latex]b[/latex] and [latex]-6[/latex] is [latex]18[/latex].
Solution
[latex]\begin{array}{rcl}\frac{b}{-6}&=&18\\b&=&-108\end{array}[/latex]
76. The quotient of [latex]h[/latex] and [latex]26[/latex] is [latex]-52[/latex].
77. The quotient [latex]k[/latex] and [latex]22[/latex] is [latex]-66[/latex].
Solution
[latex]\frac{k}{22}=-66;k=-1,452[/latex]
78. Five-sixths of [latex]y[/latex] is [latex]15[/latex].
79. Three-tenths of [latex]x[/latex] is [latex]15[/latex].
Solution
[latex]\begin{array}{rcl}\frac{3}{10}x&=&15\\x&=&50\end{array}[/latex]
80. Four-thirds of [latex]w[/latex] is [latex]36[/latex].
81. Five-halves of [latex]v[/latex] is [latex]50[/latex].
Solution
[latex]\begin{array}{rcl}\frac{5}{2}v&=&50\\v&=&20\end{array}[/latex]
82. The sum of nine-tenths and [latex]g[/latex] is two-thirds.
83. The sum of two-fifths and [latex]f[/latex] is one-half.
Solution
[latex]\begin{array}{rcl}\frac{2}{5}+f&=&\frac{1}{2}\\f&=&\frac{1}{10}\end{array}[/latex]
84. The difference of [latex]p[/latex] and one-sixth is two-thirds.
85. The difference of [latex]q[/latex] and one-eighth is three-fourths.
Solution
[latex]\begin{array}{rcl}q-\frac{1}{8}&=&\frac{3}{4}\\q&=&\frac{7}{8}\end{array}[/latex]
Exercises: Translate and Solve Applications
Instructions: For questions 86-93, translate into an equation and solve.
86. Kindergarten. Connie’s kindergarten class has [latex]24[/latex] children. She wants them to get into [latex]4[/latex] equal groups. How many children will she put in each group?
87. Balloons. Ramona bought [latex]18[/latex] balloons for a party. She wants to make [latex]3[/latex] equal bunches. How many balloons did she use in each bunch?
Solution
[latex]6[/latex] balloons
88. Tickets. Mollie paid [latex]$36.25[/latex] for [latex]5[/latex] movie tickets. What was the price of each ticket?
89. Shopping. Serena paid [latex]$12.96[/latex] for a pack of [latex]12[/latex] pairs of sport socks. What was the price of pair of sport socks?
Solution
[latex]$1.08[/latex]
90. Sewing. Nancy used [latex]14[/latex] yards of fabric to make flags for one-third of the drill team. How much fabric, would Nancy need to make flags for the whole team?
91. MPG. John’s SUV gets [latex]18[/latex] miles per gallon (mpg). This is half as many mpg as his wife’s hybrid car. How many miles per gallon does the hybrid car get?
Solution
[latex]36[/latex] mpg
92. Height. Aiden is [latex]27[/latex] inches tall. He is [latex]\frac{3}{8}[/latex] as tall as his father. How tall is his father?
93. Real estate. Bea earned [latex]$11,700[/latex] commission for selling a house, calculated as [latex]\frac{6}{100}[/latex] of the selling price. What was the selling price of the house?
Solution
[latex]$195,000[/latex]
Exercises: Everyday Math
Instructions: For questions 94-95, solve the given everyday math word problems.
94. Commission. Every week Perry gets paid [latex]$150[/latex] plus [latex]12\%[/latex] of his total sales amount. Solve the equation [latex]840=150+0.12(a-1250)[/latex] for [latex]a[/latex], to find the total amount Perry must sell in order to be paid [latex]$840[/latex] one week.
95. Stamps. Travis bought [latex]$9.45[/latex] worth of [latex]49[/latex]-cent stamps and [latex]21[/latex]-cent stamps. The number of [latex]21[/latex]-cent stamps was [latex]5[/latex] less than the number of [latex]49[/latex]-cent stamps. Solve the equation [latex]0.49s+0.21(s-5)=9.45[/latex] for [latex]s[/latex], to find the number of [latex]49[/latex]-cent stamps Travis bought.
Solution
[latex]15[/latex] [latex]49[/latex]-cent stamps
Exercises: Writing Exercises
Instructions: For questions 96-97, answer the given writing exercises.
96. Frida started to solve the equation [latex]-3x=36[/latex] by adding [latex]3[/latex] to both sides. Explain why Frida’s method will not solve the equation.
97. Emiliano thinks [latex]x=40[/latex] is the solution to the equation [latex]\frac{1}{2}x=80[/latex]. Explain why he is wrong.
Solution
Answers will vary.

