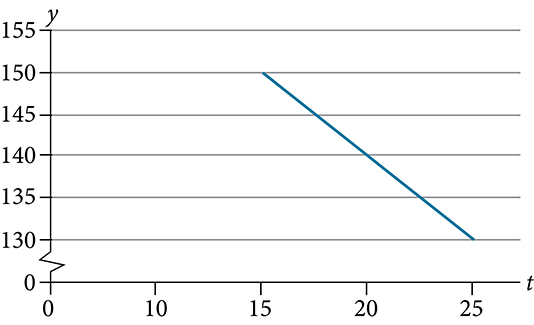3.12 Linear Functions and Applications of Linear Functions
Learning Objectives
In this section, you will:
- Represent a linear function.
- Write and interpret an equation for a linear function.
- Model real-world problems with linear functions.
- Build linear models from verbal descriptions.

Just as with the growth of a bamboo plant, many situations involve constant change over time. Consider, for example, the first commercial maglev train in the world, the Shanghai MagLev Train Figure 3.12.1. It carries passengers comfortably for a 30-kilometer trip from the airport to the subway station in only eight minutes[1] .
Suppose a maglev train travels a long distance and maintains a constant speed of 83 meters per second for some time once it is 250 meters from the station. How can we analyze the train’s distance from the station as a function of time? In this section, we will investigate a kind of function that is useful for this purpose, and use it to investigate real-world situations such as the train’s distance from the station at a given point in time.
Representing a Linear Function
The function describing the train’s motion is a linear function, which is defined as a function with a constant rate of change. This is a polynomial of degree [latex]1[/latex]. There are several ways to represent a linear function, including word form, function notation, tabular form, and graphical form. We will describe the train’s motion as a function using each method.
Representing a Linear Function in Word Form
Let’s begin by describing the linear function in words. For the train problem, we just considered, the following word sentence may be used to describe the function relationship.
- The train’s distance from the station is a function of the time during which the train moves at a constant speed plus its original distance from the station when it began moving at a constant speed.
The speed is the rate of change. Recall that a rate of change is a measure of how quickly the dependent variable changes with respect to the independent variable. The rate of change for this example is constant, which means that it is the same for each input value. As the time (input) increases by 1 second, the corresponding distance (output) increases by [latex]83[/latex] meters. The train began moving at this constant speed at a distance of [latex]250[/latex] meters from the station.
Representing a Linear Function in Function Notation
Another approach to representing linear functions is by using function notation. One example of function notation is an equation written in the slope-intercept form of a line, where [latex]x[/latex] is the input value, [latex]m[/latex] is the rate of change, and [latex]b[/latex] is the initial value of the dependent variable.
In the example of the train, we might use the notation [latex]D[/latex] where the total distance [latex]D[/latex] is a function of the time [latex]t[/latex]. The rate, [latex]m[/latex], is [latex]83[/latex] meters per second. The initial value of the dependent variable [latex]b[/latex] is the original distance from the station, [latex]250[/latex] meters. We can write a generalized equation to represent the motion of the train.
Can the input in the previous example be any real number?
No. The input represents time so while nonnegative rational and irrational numbers are possible, negative real numbers are not possible for this example. The input consists of non-negative real numbers.
Ask yourself what numbers can be input to the function. In other words, what is the domain of the function? The domain is comprised of all real numbers because any number may be doubled, and then have one added to the product.
Linear Function
A linear function is a function whose graph is a line. Linear functions can be written in the slope-intercept form of a line
where [latex]b[/latex] is the initial or starting value of the function (when input, [latex]x=0[/latex]), and [latex]m[/latex], is the constant rate of change, or slope of the function. The [latex]y[/latex]-intercept is at [latex](0,b)[/latex].
Example 1
Using a Linear Function to Find the Pressure on a Diver
The pressure, [latex]P[/latex] in pounds per square inch (PSI) on the diver in Figure 3.12.4 depends upon her depth below the water surface, [latex]d[/latex] in feet. This relationship may be modeled by the equation, [latex]P(d)=0.434d+14.696[/latex]. Restate this function in words.

Solution
To restate the function in words, we need to describe each part of the equation. The pressure as a function of depth equals four hundred thirty-four thousandths times depth plus fourteen and six hundred ninety-six thousandths.
Analysis
The initial value, [latex]14.696[/latex], is the pressure in PSI on the diver at a depth of [latex]0[/latex] feet, which is the surface of the water. The rate of change, or slope, is [latex]0.434[/latex] PSI per foot. This tells us that the pressure on the diver increases [latex]0.434[/latex] PSI for each foot her depth increases.
Model Real-World Problems with Linear Functions
In the real world, problems are not always explicitly stated in terms of a function or represented with a graph. Fortunately, we can analyze the problem by first representing it as a linear function and then interpreting the components of the function. As long as we know, or can figure out, the initial value and the rate of change of a linear function, we can solve many different kinds of real-world problems.
How to
Given a linear function [latex]f[/latex] and the initial value and rate of change, evaluate [latex]f[/latex] .
- Determine the initial value and the rate of change (slope).
- Substitute the values into [latex]f(x)=mx+b[/latex].
- Evaluate the function at [latex]x=c[/latex].
Example 2
Using a Linear Function to Calculate Salary Based on Commission
Working as an insurance salesperson, Ilya earns a base salary plus a commission on each new policy. Therefore, Ilya’s weekly income depends on the number of new policies, [latex]n[/latex] he sells during the week. Last week he sold [latex]3[/latex] new policies, and earned [latex]\$760[/latex] for the week. The week before, he sold [latex]5[/latex] new policies and earned [latex]\$920[/latex]. Find an equation for [latex]I[/latex] and interpret the meaning of the components of the equation.
Solution
The given information gives us two input-output pairs: [latex](3,\$760)[/latex] and [latex](5,\$920)[/latex] We start by finding the rate of change.
[latex]\begin{eqnarray*} \mbox{m} &=& \frac{\$920-\$760}{5-3} \\ \\ \ & = & \frac{\$160}{2\;policies} \\ \\ \ &=&$80 {\;per\;policy} \end{eqnarray*}[/latex]
Keeping track of units can help us interpret this quantity. Income increased by [latex]\$160[/latex] when the number of policies increased by [latex]2[/latex], so the rate of change is [latex]\$80[/latex] per policy. Therefore, Ilya earns a commission of [latex]\$80[/latex] for each policy sold during the week.
We can then solve for the initial value.
[latex]\begin{align*}\text{I(n)}&=80n+b\\\\760&=80(3)+b\;\text{when n=3, I(3)=760}\\\\760-80(3)&=b\\\\520&=b\end{align*}[/latex]
The value of [latex]b[/latex] is the starting value for the function and represents Ilya’s income when [latex]n=0[/latex] or when no new policies are sold. We can interpret this as Ilya’s base salary for the week, which does not depend upon the number of policies sold.
We can now write the final equation.
[latex]I =80n+520[/latex]
Our final interpretation is that Ilya’s base salary is [latex]\$520[/latex] per week and he earns an additional [latex]\$80[/latex] commission for each policy sold.
Example 3
Using Tabular Form to Write an Equation for a Linear Function
The below table relates the number of rats in a population to time, in weeks. Use the table to write a linear equation.
| number of weeks, [latex]w[/latex] | [latex]0[/latex] | [latex]2[/latex] | [latex]4[/latex] | [latex]6[/latex] |
|---|---|---|---|---|
| number of rats, [latex]P(w)[/latex] | [latex]1000[/latex] | [latex]1080[/latex] | [latex]1160[/latex] | [latex]1240[/latex] |
Solution
We can see from the table that the initial value for the number of rats is [latex]1000[/latex], so [latex]b=1000[/latex].
Rather than solving for [latex]m[/latex] we can tell from looking at the table that the population increases by [latex]80[/latex] for every [latex]2[/latex] weeks that pass. This means that the rate of change is [latex]80[/latex] rats per [latex]2[/latex] weeks, which can be simplified to [latex]40[/latex] rats per week.
If we did not notice the rate of change from the table we could still solve for the slope using any two points from the table. For example, using [latex](2, 1080)[/latex] and [latex](6, 1240)[/latex]
[latex]\begin{eqnarray*} \mbox{m} & = & \frac{1240-1080}{6-2} \\ \\ \ & = & \frac{160}{4} \\ \\ \ & = & 40 \end{eqnarray*}[/latex]
Is the initial value always provided in a table of values like Example 3.12.4?
No. Sometimes the initial value is provided in a table of values, but sometimes it is not. If you see an input of [latex]0[/latex], then the initial value would be the corresponding output. If the initial value is not provided because there is no value of input on the table equal to [latex]0[/latex], find the slope, substitute one coordinate pair, and the slope into [latex]f(x)=mx+b[/latex] and solve for [latex]b[/latex].
Try It
1) A new plant food was introduced to a young tree to test its effect on the height of the tree. The table shows the height of the tree, in feet, [latex]x[/latex] months since the measurements began. Write a linear function, [latex]H(x)[/latex], where [latex]x[/latex] is the number of months since the start of the experiment.
| [latex]x[/latex] | [latex]0[/latex] | [latex]2[/latex] | [latex]4[/latex] | [latex]8[/latex] | [latex]12[/latex] |
|---|---|---|---|---|---|
| [latex]H(x)[/latex] | [latex]12.5[/latex] | [latex]13.5[/latex] | [latex]14.5[/latex] | [latex]16.5[/latex] | [latex]18.5[/latex] |
Solution
[latex]H(x)=0.5x+12.5[/latex]
Building Linear Models from Verbal Descriptions
When building linear models to solve problems involving quantities with a constant rate of change, we typically follow the same problem strategies that we would use for any type of function. Let’s briefly review them:
How to
Building Linear Models from Verbal Descriptions
- Identify changing quantities, and then define descriptive variables to represent those quantities. When appropriate, sketch a picture or define a coordinate system.
- Carefully read the problem to identify important information. Look for information that provides values for the variables or values for parts of the functional model, such as slope and initial value.
- Carefully read the problem to determine what we are trying to find, identify, solve, or interpret.
- Identify a solution pathway from the provided information to what we are trying to find. Often this will involve checking and tracking units, building a table, or even finding a formula for the function being used to model the problem.
- When needed, write a formula for the function.
- Solve or evaluate the function using the formula.
- Reflect on whether your answer is reasonable for the given situation and whether it makes sense mathematically.
- Clearly convey your result using appropriate units, and answer in full sentences when necessary.
Using a Given Intercept to Build a Model
Some real-world problems provide the [latex]y[/latex]-intercept, which is the constant or initial value. Once the [latex]y[/latex]-intercept is known, the [latex]x[/latex]-intercept can be calculated. Suppose, for example, that Hannah plans to pay off a no-interest loan from her parents. Her loan balance is [latex]\$1,000[/latex]. She plans to pay [latex]\$250[/latex] per month until her balance is [latex]\$0[/latex]. The [latex]y[/latex]-intercept is the initial amount of her debt, or [latex]\$1,000[/latex]. The rate of change, or slope, is [latex]-\$250[/latex] per month. We can then use the slope-intercept form and the given information to develop a linear model.
[latex]\begin{eqnarray*} \mbox{f(x)} & = & {mx + b} \\ \\ \ & = & -250x+1000 \end{eqnarray*}[/latex]
The [latex]x[/latex]-intercept is the number of months it takes her to reach a balance of [latex]\$0[/latex]. The [latex]x[/latex]-intercept is [latex]4[/latex] months, so it will take Hannah four months to pay off her loan.
Using a Given Input and Output to Build a Model
Many real-world applications are not as direct as the ones we just considered. Instead, they require us to identify some aspect of a linear function. We might sometimes instead be asked to evaluate the linear model at a given input or set the equation of the linear model equal to a specified output.
How to
Given a word problem that includes two pairs of input and output values, use the linear function to solve a problem.
- Identify the input and output values.
- Convert the data to two coordinate pairs.
- Find the slope.
- Write the linear model.
- Use the model to make a prediction by evaluating the function at a given [latex]x[/latex]-value.
- Use the model to identify an [latex]x[/latex]-value that results in a given [latex]y[/latex]-value.
- Answer the question posed.
Example 4
Using a Linear Model to Investigate a Town’s Population
A town’s population has been growing linearly. In 2004, the population was 6,200. By 2009, the population had grown to 8,100. Assume this trend continues.
-
- Predict the population in 2013.
- Identify the year in which the population will reach 15,000.
Solution
The two changing quantities are the population size and time. While we could use the actual year value as the input quantity, doing so tends to lead to very cumbersome equations because the [latex]y[/latex]-intercept would correspond to the year 0, more than 2000 years ago!
To make computation a little nicer, we will define our input as the number of years since 2004.
Input: [latex]t[/latex], years since 2004
To determine the rate of change, we will use the change in output per change in input.
[latex]m=\frac{change\hspace{0.15cm}in\hspace{0.15cm}output}{change\hspace{0.15cm}in\hspace{0.15cm}input}[/latex]
The problem gives us two input-output pairs. Converting them to match our defined variables, the year 2004 would correspond to [latex]t=0[/latex] giving the point [latex](0,6200)[/latex]. Notice that through our clever choice of variable definition, we have “given” ourselves the [latex]y[/latex]-intercept of the function. The year 2009 would correspond to, [latex]t=5[/latex] giving the point [latex](5,8100)[/latex].
The two coordinate pairs are [latex](0,6200)[/latex] and [latex](5,8100)[/latex]. Recall that we encountered examples in which we were provided two points earlier in the chapter. We can use these values to calculate the slope.
[latex]\begin{eqnarray*}\mbox{m}&=&\frac{8100-6200}{5-0}\\\\&=&\frac{1900}{5}\\\\&=&380\end{eqnarray*}[/latex]
We already know the [latex]y[/latex]-intercept of the line, so we can immediately write the equation:
[latex]P(t)=380t+6200[/latex]
[latex]\begin{eqnarray*}\mbox{P(9)}&=&380(9)+6,200\\\\&=& 9,620\end{eqnarray*}[/latex]
if the trend continues, our model predicts a population of 9,620 in 2013.
To find when the population will reach 15,000, we can set
[latex]\begin{eqnarray*}\text{P(t)}&=&15000\\\\150000&=&380t+6200\\\\8800&=&380t\\\\&\approx&23.158\end{eqnarray*}[/latex]
Our model predicts the population will reach 15,000 in a little more than 23 years after 2004, or somewhere around the year 2027.
Try It
2) A company sells doughnuts. They incur a fixed cost of $25,000 for rent, insurance, and other expenses. It costs $0.25 to produce each doughnut.
a. Write a linear model to represent the cost [latex]C[/latex] of the company as a function of [latex]x[/latex], the number of doughnuts produced.
b. Find and interpret the [latex]y[/latex]-intercept.
Solution
a. [latex]C(x)=0.25x+25,000[/latex]
b. The [latex]y[/latex]-intercept is [latex](0,25,000)[/latex]. If the company does not produce a single doughnut, they still incur a cost of 25,000.
3) A city’s population has been growing linearly. In 2008, the population was 28,200. By 2012, the population was 36,800. Assume this trend continues.
a. Predict the population in 2014.
b. Identify the year in which the population will reach 54,000.
Solution
a. 41,100
b. 2020
Key Concepts
- Linear functions can be represented in words, function notation, tabular form, and graphical form.
- The equation for a linear function can be written if the slope [latex]m[/latex] and initial value [latex]b[/latex] are known.
- A linear function can be used to solve real-world problems given information in different forms.
- We can use the same problem strategies that we would use for any type of function.
- When modeling and solving a problem, identify the variables and look for key values, including the slope and [latex]y[/latex]-intercept.
- Draw a diagram, where appropriate.
- Check for the reasonableness of the answer.
- Linear models may be built by identifying or calculating the slope and using the [latex]y[/latex]-intercept.
- The [latex]x[/latex]-intercept may be found by setting, [latex]y=0[/latex], which is setting the expression [latex]mx+b[/latex] equal to [latex]0[/latex].
- The point of intersection of a system of linear equations is the point where the [latex]x[/latex]- and [latex]y[/latex]-values are the same.
- A graph of the system may be used to identify the points where one line falls below (or above) the other line.
Glossary
- decreasing linear function
- a function with a negative slope: If [latex]f(x)=mx+b[/latex], [latex]m<0[/latex].
- a function with a positive slope: If [latex]f(x)=mx+b[/latex], [latex]m>0[/latex].
- linear function
- a function with a constant rate of change that is a polynomial of degree 1, and whose graph is a straight line
Exercises: Verbal Problems
Instructions: For questions 1-7, answer the given verbal word problems.
Solution
Terry starts at an elevation of [latex]3000[/latex] feet and descends [latex]70[/latex] feet per second.
Solution
[latex]d(t)=100-10t[/latex]
Solution
Determine the independent variable. This is the variable upon which the output depends.
Solution
To determine the initial value, find the output when the input is equal to zero.
Exercises: Algebraic Problems
Instructions: For questions 8-9, consider this scenario: A town’s population has been decreasing at a constant rate. In 2010 the population was [latex]5\text{,}900[/latex]. By 2012 the population had dropped to [latex]4\text{,}700[/latex]. Assume this trend continues.
8. Identify the year in which the population will reach [latex]0[/latex].
9. Predict the population in 2016.
Solution
[latex]2\text{,}300[/latex]
Exercises: Algebraic Problems
Instructions: For questions 10-11, consider this scenario: A town’s population has been increasing at a constant rate. In 2010 the population was [latex]46\text{,}020[/latex]. By 2012 the population had increased to [latex]52\text{,}070[/latex]. Assume this trend continues.
Solution
[latex]64\text{,}170[/latex]
Exercises: Algebraic Problems
Instructions: For questions 12-17, consider this scenario: A town has an initial population of [latex]75\text{,}000[/latex]. It grows at a constant rate of [latex]2\text{,}500[/latex] per year for [latex]5[/latex] years.
12. Find a reasonable domain and range for the function [latex]P[/latex].
13. Find the linear function that models the town’s population [latex]P[/latex]as a function of the year, [latex]t[/latex], where[latex]t[/latex]is the number of years since the model began.
Solution
[latex]P(t)=75,000+2500t[/latex]
14. If the function [latex]P[/latex] is graphed, find and interpret the slope of the function.
Solution
[latex](–30,0)[/latex] Thirty years before the start of this model, the town had no citizens.
[latex](0,75\text{,}000)[/latex] Initially, the town had a population of [latex]75\text{,}000[/latex].
16. What is the population in the year [latex]12[/latex] years from the onset of the model?
Solution
Ten years after the model began
Exercises: Algebraic Problems
Instructions: For questions 18-23, consider this scenario: The weight of a newborn is [latex]7.5[/latex] pounds. The baby gained one-half pound a month for its first year.
18. Find a reasonable domain and range for the function [latex]W[/latex].
Solution
[latex]W(t)=0.5t+7.5[/latex]
20. If the function [latex]W[/latex] is graphed, find and interpret the slope of the function.
Solution
[latex](-15,0)[/latex]: The [latex]x[/latex]-intercept is not a plausible set of data for this model because it means the baby weighed [latex]0[/latex] pounds 15 months prior to birth. [latex](0,7.5)[/latex]: The baby weighed [latex]7.5[/latex] pounds at birth.
22. What is the output when the input is [latex]6.2[/latex]?
Solution
At age [latex]5.8[/latex] months
Exercises: Algebraic Problems
Instructions: For questions 24-29, consider this scenario: The number of people afflicted with the common cold in the winter months steadily decreased by [latex]205[/latex] each year from 2005 until 2010. In 2005, [latex]12\text{,}025[/latex] people were inflicted.
24. Find a reasonable domain and range for the function [latex]C[/latex].
25. Find the linear function that models the number of people inflicted with the common cold [latex]C[/latex] as a function of the year, [latex]t[/latex].
Solution
[latex]C(t)=12\text{,}025-205t[/latex]
26. If the function [latex]C[/latex] is graphed, find and interpret the slope of the function.
Solution
[latex](58.7,0)[/latex]: In roughly [latex]59[/latex] years, the number of people inflicted with the common cold would be [latex]0[/latex].
[latex](0,12\text{,}025)[/latex]: Initially there were [latex]12\text{,}025[/latex] people afflicted by the common cold.
28. In what year will the number of people be [latex]9\text{,}700[/latex]?
Solution
2063
Exercises: Graphical Problems
31. Find the linear function[latex]y[/latex], where[latex]y[/latex] depends on [latex]t[/latex], the number of years since 1980.
Solution
[latex]y=-2t+180[/latex]
Solution
In 2070, the company’s profit will be zero.
Exercises: Graphical Problems
Instructions: For questions 34-37, use the graph in Figure 3P.12.2, which shows the profit, [latex]y[/latex],in thousands of dollars, of a company in a given year, [latex]t[/latex],where[latex]t[/latex]represents the number of years since 1980.
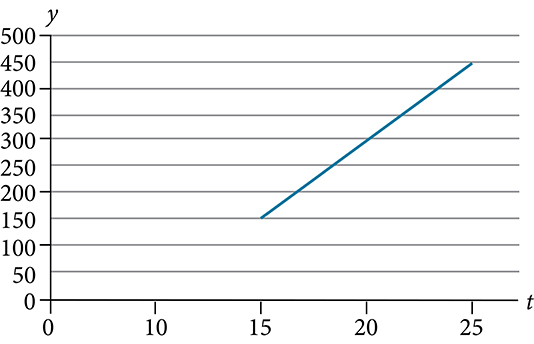
Solution
[latex]y=30t-300[/latex]
Solution
[latex](0,-300)[/latex] In 1980, the company lost [latex]$300\text{,}000[/latex].
Solution
[latex]y=30t-300[/latex] of form [latex]y=mx+b,m=30[/latex]. For each year after 1980, the company's profits increased [latex]$30\text{,}000[/latex] per year
Exercises: Numeric Problems
Instructions: For questions 38-40, use the median home values in Mississippi and Hawaii (adjusted for inflation) shown in Table 3P.12.1. Assume that the house values are changing linearly.
| Year | Mississippi | Hawaii |
|---|---|---|
| 1950 | [latex]$25\text{,}200[/latex] | [latex]$74\text{,}400[/latex] |
| 2000 | [latex]$71\text{,}400[/latex] | [latex]$272\text{,}700[/latex] |
Solution
[latex]$80\text{,}640[/latex]
Exercises: Numeric
Instructions: For questions 41-43, use the median home values in Indiana and Alabama (adjusted for inflation) shown in (Figure). Assume that the house values are changing linearly.
| Year | Indiana | Alabama |
|---|---|---|
| 1950 | $37,700 | $27,100 |
| 2000 | $94,300 | $85,100 |
Solution
Alabama
Solution
2328
Exercises: Real-World Applications
Instructions: For questions 44-66, solve the given real-world application problems.
44. A gym membership with two personal training sessions costs [latex]$125[/latex], while gym membership with five personal training sessions costs [latex]$260[/latex]. What is cost per session?
Solution
[latex]20+0.5n[/latex]
Solution
[latex]p(n)=-0.004n+34[/latex]
Solution
[latex]y=-0.5n+45[/latex]
50. Suppose that average annual income (in dollars) for the years 1990 through 1999 is given by the linear function: [latex]I(x)=1054x+23\text{,}286[/latex], where [latex]x[/latex] is the number of years after 1990. Which of the following interprets the slope in the context of the problem?
b. In the ten-year period from 1990–1999, average annual income increased by a total of [latex]$1\text{,}054[/latex].
c. Each year in the decade of the 1990s, average annual income increased by [latex]$1\text{,}054[/latex].
Solution
[latex]P(t)=1700t+45,000[/latex]
a. How much did the population grow between the year 2004 and 2008?
b. How long did it take the population to grow from [latex]1001[/latex] students to [latex]1697[/latex] students?
c. What is the average population growth per year?
d. What was the population in the year 2000?
e. Find an equation for the population, [latex]P[/latex], of the school [latex]t[/latex] years after 2000.
f. Using your equation, predict the population of the school in 2011.
a. Find the rate of change of Fahrenheit temperature for each unit change temperature of Celsius.
b. Find and interpret [latex]F(28)[/latex].
c. Find and interpret [latex]F(–40)[/latex].
Solution
a. [latex]\text{Rate of change =}\frac{\Delta F}{\Delta C}=\frac{212-32}{100-0}=1.8\text{ degrees F for one degree change in C}[/latex]
b. [latex]F(28)=1.8(28)+32=82.4\text{ degrees F is 28 degrees C}[/latex]
c. [latex]F(-40)=1.8(-40)+32=-40\text{ degrees F is -40 degrees C}[/latex]
a. Find a linear equation for the monthly cost of the cell plan as a function of [latex]x[/latex], the number of monthly minutes used.
b. Interpret the slope and [latex]y[/latex]-intercept of the equation.
c. Use your equation to find the total monthly cost if [latex]687[/latex] minutes are used.
a. How much did the population grow between the years 2003 and 2007?
b. How long did it take the population to grow from [latex]1431[/latex] people to [latex]2134[/latex] people?
c. What is the average population growth per year?
d. What was the population in the year 2000?
e. Find an equation for the population, [latex]P[/latex], of the town [latex]t[/latex] years after 2000.
f. Using your equation, predict the population of the town in 2014.
Solution
a. [latex]2134-1431=703[/latex] people
b. [latex]2007-2003=4[/latex] years
c. Average rate of growth [latex]=\frac{703}{4}=175.75[/latex] people per year. So, using [latex]y=mx+b[/latex], we have [latex]y=175.75x+1431[/latex].
d. The year 2000 corresponds to [latex]t=-3[/latex].
So, [latex]y=175.75(-3)+1431=903.75[/latex] or roughly [latex]904[/latex] people in year 2000
e. If the year 2000 corresponds to [latex]t=0[/latex], then we have ordered pair [latex](0,903.75)[/latex].
[latex]y=175.75x+903.75[/latex] corresponds to [latex]P(t)=175.75t+903.75[/latex].
f. The year 2014 corresponds to [latex]t=14[/latex]. Therefore, [latex]P(14)=175.75(14)+903.75=3364.25[/latex].
So, a population of 3364.
a. Find a formula for the moose population, [latex]P[/latex] since 1990.
b. What does your model predict the moose population to be in 2003?
a. Find a linear equation for the monthly cost of the data plan as a function of [latex]x[/latex], the number of MB used.
b. Interpret the slope and [latex]y[/latex]-intercept of the equation.
c. Use your equation to find the total monthly cost if [latex]250[/latex] MB are used.
Solution
a.
[latex]\begin{array}{l}\text{Ordered pairs are }(20,11.20)\text{ and }(130,17.80)\\\begin{array}{rcl}m&=&\frac{17.80-11.20}{130-20}=0.06\text{ and }b\text{ is at the point }(0,10)\\y&=&mx+b\\y&=& 0.06x+10\\\text{or }C(x)&=&0.06x+10 \end{array}\end{array}[/latex]
b.
[latex]0.06[/latex] - For every MB, the client is charged [latex]6[/latex] cents.
[latex](0,10)[/latex] - If no usage occurs, the client is charged [latex]$10[/latex].
c.
[latex]\begin{array}{rcl}C(250)&=& 0.06(250)+10\\&=&$25\end{array}[/latex]
a. Give a linear equation for the remaining federal helium reserves, [latex]R[/latex], in terms of [latex]t[/latex], the number of years since 2010.
b. In 2015, what will the helium reserves be?
c. If the rate of depletion doesn’t change, in what year will the Federal Helium Reserve be depleted?
a. Find a formula for the owl population, [latex]P[/latex]. Let the input be years since 2003.
b. What does your model predict the owl population to be in 2012?
Solution
a.
[latex]\begin{array}{l}\text{Ordered pairs are }(0,340)\text{ and }(4,285)\\\begin{array}{rcl}m&=&\frac{285-340}{4-0}=-13.75\text{ and }b\text{ is at the point }(0,340)\\y&=&mx+b\\y&=&-13.75x+340 \\ \text{or }P(t)&=&-13.75t+340\hfill \end{array}\end{array}[/latex]
b.
[latex]\begin{array}{l}\text{The year 2012 corresponds to }t=9\\\begin{array}{rcl}P(9)&=&-13.75(9)+340\\&=&216.25\text{ or }216\text{ owls}\end{array}\end{array}[/latex]
60. You are choosing between two different prepaid cell phone plans. The first plan charges a rate of [latex]26[/latex] cents per minute. The second plan charges a monthly fee of [latex]$19.95[/latex] plus [latex]11[/latex] cents per minute. How many minutes would you have to use in a month in order for the second plan to be preferable?
a. Give a linear equation for the remaining oil reserves, [latex]R[/latex], in terms of [latex]t[/latex], the number of years since now.
b. Seven years from now, what will the oil reserves be?
c. If the rate at which the reserves are decreasing is constant, when will the world’s oil reserves be depleted?
Solution
a.
[latex]\begin{array}{l}\text{The year 2014 corresponds to }t=0.\\ \text{We have }m=-25\text{ and }b\text{ at the point }(0,1820)\\ \begin{array}{rcl}y&=&mx+b\\y&=&-25x+1820\\\text{or }R(t)&=&-25t+1820\end{array}\end{array}[/latex]
b.
[latex]\begin{array}{rcl}R(7)&=&-25(7)+1820\\ &=& 1645\text{ billion cubic feet}\end{array}[/latex]
c.
[latex]\begin{array}{rcl}0&=&-25t+1820\\-1820&=&-25t\\72.8&=&t\;⇒\;2014+72.8=2086.8\text{. So, in the year 2086}\end{array}[/latex]
Option A: Base salary of [latex]$17\text{,}000[/latex] a year with a commission of [latex]12\%[/latex] of your sales
Option B: Base salary of [latex]$20\text{,}000[/latex] a year with a commission of [latex]5\%[/latex] of your sales
How much jewelry would you need to sell for option A to produce a larger income?
Solution
[latex]\begin{array}{l}\text{Plan 1: }y=5x\text{ where }x\text{ is number of windows}\\ \text{Plan 2: }y=3x+40\text{ where }x\text{ is number of windows}\\ \begin{array}{rcl}3x+40&\le&5x\\40&\le&2x\\20&\le&x\end{array}\\ \text{So, more than 20 windows}\end{array}[/latex]
Option A: Base salary of [latex]$20\text{,}000[/latex] a year with a commission of [latex]12\%[/latex] of your sales
Option B: Base salary of [latex]$26\text{,}000[/latex] a year with a commission of [latex]3\%[/latex] of your sales
How many electronics would you need to sell for option A to produce a larger income?
Option A: Base salary of [latex]$14\text{,}000[/latex] a year with a commission of [latex]10\%[/latex] of your sales
Option B: Base salary of [latex]$19\text{,}000[/latex] a year with a commission of [latex]4\%[/latex] of your sales
How many electronics would you need to sell for option A to produce a larger income?
Solution
[latex]\begin{array}{l}\text{Option A: }y=0.10x+14\text{,}000\text{ where }x\text{ is dollars of sales.}\\\text{Option B: }y=0.04x+19\text{,}000\text{ where }x\text{ is dollars of sales.}\\ \begin{array}{rcl}0.10x+14\text{,}000&\ge&0.04x+19\text{,}000\\0.06x+14\text{,}000&\ge&19\text{,}000\\0.06x&\ge&5\text{,}000\\x&\ge&83\text{,}333.33\end{array}\\\text{So, more than }$83\text{,}333.33\text{ in sales.}\end{array}[/latex]
Option A: Base salary of [latex]$10\text{,}000[/latex] a year with a commission of [latex]9\%[/latex] of your sales
Option B: Base salary of [latex]$20\text{,}000[/latex] a year with a commission of [latex]4\%[/latex] of your sales
How much electronics would you need to sell for option A to produce a larger income?
a function with a constant rate of change that is a polynomial of degree 1, and whose graph is a straight line
a function with a negative slope: If f(x)=mx+b, m<0.
a function with a positive slope: If f(x)=mx+b, m>0.