3.8 Solve Mixture and Uniform Motion Applications
Learning Objectives
By the end of this section, you will be able to:
- Solve coin word problems
- Solve ticket and stamp word problems
- Solve mixture word problems
- Solve uniform motion applications
Try It
Before you get started, take this readiness quiz:
1) Multiply: [latex]14(0.25)[/latex].
2) Solve: [latex](0.25x)+0.10(x+4)=2.5[/latex]
3) The number of dimes is three more than the number of quarters. Let [latex]q[/latex] represent the number of quarters. Write an expression for the number of dimes.
4) Find the distance travelled by a car going [latex]70[/latex] miles per hour for [latex]3[/latex] hours.
5) Solve [latex]x+1.2(x-10)=98[/latex].
6) Convert [latex]90[/latex] minutes to hours.
Solve Coin Word Problems
In mixture problems, we will have two or more items with different values to combine. The mixture model is used by grocers and bartenders to make sure they set fair prices for the products they sell. Many other professionals, like chemists, investment bankers, and landscapers also use the mixture model. Doing the Manipulative Mathematics activity Coin Lab will help you develop a better understanding of mixture word problems.
We will start by looking at an application everyone is familiar with—money!
Imagine that we take a handful of coins from a pocket or purse and place them on a desk. How would we determine the value of that pile of coins? If we can form a step-by-step plan for finding the total value of the coins, it will help us as we begin solving coin word problems.
So what would we do? To get some order to the mess of coins, we could separate the coins into piles according to their value. Quarters would go with quarters, dimes with dimes, nickels with nickels, and so on. To get the total value of all the coins, we would add the total value of each pile.

How would we determine the value of each pile? Think about the dime pile—how much is it worth? If we count the number of dimes, we’ll know how many we have—the number of dimes.
But this does not tell us the value of all the dimes. Say we counted 17 dimes, how much are they worth? Each dime is worth $0.10—that is the value of one dime. To find the total value of the pile of 17 dimes, multiply 17 by $0.10 to get $1.70. This is the total value of all 17 dimes. This method leads to the following model.
How To
Total Value of Coins
For the same type of coin, the total value of several coins is found by using the model
Where
number is the number of coins
value is the value of each coin
total value is the total value of all the coins
The number of dimes times the value of each dime equals the total value of the dimes.
We could continue this process for each type of coin, and then we would know the total value of each type of coin. To get the total value of all the coins, add the total value of each type of coin.
Let’s look at a specific case. Suppose there are [latex]14[/latex] quarters, [latex]17[/latex] dimes, [latex]21[/latex] nickels, and [latex]39[/latex] pennies.
| Type | Number · | Value($) | = Total Value ($) |
|---|---|---|---|
| Quarters | 14 | 0.25 | 3.50 |
| Dimes | 17 | 0.10 | 1.70 |
| Nickels | 21 | 0.05 | 1.05 |
| Pennies | 39 | 0.01 | 0.39 |
| 6.64 | |||
The total value of all the coins is [latex]$6.64[/latex].
Notice how the chart helps organize all the information! Let’s see how we use this method to solve a coin word problem.
Example 1
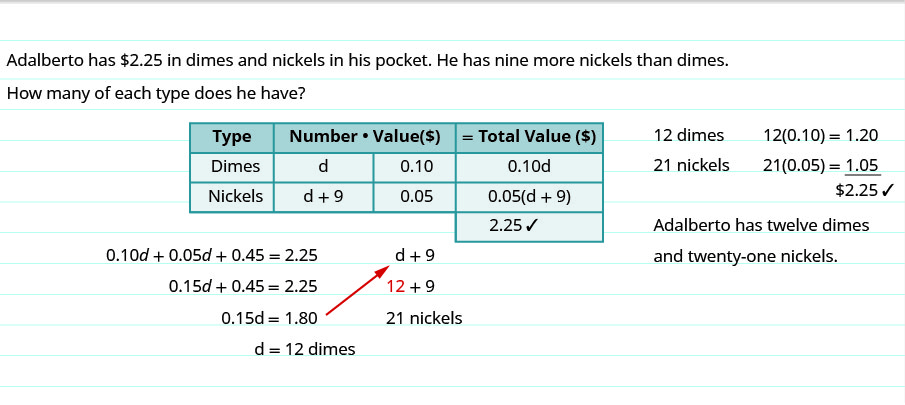
Adalberto has [latex]$2.25[/latex] in dimes and nickels in his pocket. He has nine more nickels than dimes. How many of each type of coin does he have?
Solution
Step 1: Read the problem. Make sure all the words and ideas are understood.
- Determine the types of coins involved.
Think about the strategy we used to find the value of the handful of coins. The first thing we need is to notice what types of coins are involved. Adalberto has dimes and nickels. - Create a table to organize the information. See chart below.
- Label the columns “type,” “number,” “value,” “total value.”
- List the types of coins.
- Write in the value of each type of coin.
- Write in the total value of all the coins.
| Type | Number · | Value ($) | = Total Value ($) |
|---|---|---|---|
| Dimes | [latex]0.10[/latex] | ||
| Nickels | [latex]0.05[/latex] | ||
| [latex]2.25[/latex] | |||
We can work this problem all in cents or in dollars. Here we will do it in dollars and put in the dollar sign ($) in the table as a reminder.
The value of a dime is [latex]$0.10[/latex] and the value of a nickel is [latex]$0.05[/latex]. The total value of all the coins is [latex]$2.25[/latex]. The table below shows this information.
Step 2: Identify what we are looking for.
- We are asked to find the number of dimes and nickels Adalberto has.
Step 3: Name what we are looking for. Choose a variable to represent that quantity.
- Use variable expressions to represent the number of each type of coin and write them in the table.
- Multiply the number times the value to get the total value of each type of coin.
Next we counted the number of each type of coin. In this problem we cannot count each type of coin—that is what you are looking for—but we have a clue. There are nine more nickels than dimes. The number of nickels is nine more than the number of dimes.
Let [latex]d =[/latex] number of dimes.
[latex]d + 9 =[/latex] number of nickles
Fill in the “number” column in the table to help get everything organized.
| Type | Number · | Value ($) | = Total Value ($) |
|---|---|---|---|
| Dimes | [latex]d[/latex] | [latex]0.10[/latex] | |
| Nickels | [latex]d+9[/latex] | [latex]0.05[/latex] | |
| [latex]2.25[/latex] | |||
Now we have all the information we need from the problem!
We multiply the number times the value to get the total value of each type of coin. While we do not know the actual number, we do have an expression to represent it.
And so now multiply [latex]{number}\times {value} = {total\hspace{0.15cm}value}[/latex] See how this is done in the table below.
| Type | Number · | Value ($) | = Total Value ($) |
|---|---|---|---|
| Dimes | [latex]d[/latex] | [latex]0.10[/latex] | [latex]0.10d[/latex] |
| Nickels | [latex]d+9[/latex] | [latex]0.05[/latex] | [latex]0.05(d+9)[/latex] |
| [latex]2.25[/latex] | |||
Notice that we made the heading of the table show the model.
Step 4: Translate into an equation. It may be helpful to restate the problem in one sentence. Translate the English sentence into an algebraic equation.
Write the equation by adding the total values of all the types of coins.
[latex]{\small\begin{align*} &\;&\underbrace{\text{Value of dimes}}\;&\;\;+\;&\underbrace{\text{Value of nickels}}\;&\;\;=\;&\underbrace{\text{Total value of coins}}\\ &\text{Translate to an equation}&0.10d\;\;\;\;\;\;\;\;&\;\;+\;&\;0.50(d+9)\;\;\;&\;\;=\;&\;2.25\;\;\;\;\;\;\;\;\;\;\;\;\;\; \end{align*}}[/latex]
Step 5: Solve the equation using good algebra techniques.
[latex]\begin{align*} &\text{Now solve this equation}\;&0.10d+0.05(d+9)&=2.25\\ &\text{Distribute}\;&0.10d+0.05d+0.45&=2.25\\ &\text{Combine like terms}\;&0.15d+0.45&=2.25\\ &\text{Subtract 0.45 from each side}\;&0.15d&=2.25\\ &\text{Divide}\;&d&=12\\ &\text{So there are 12 dimes}\;&\;\\ &\text{The number of nickels is (}{\color{red}{d}}+9\text{)}\;&{\color{red}{d}}&+9\\ &\;&{\color{red}{12}}+9&=21 \end{align*}[/latex]
Step 6: Check the answer in the problem and make sure it makes sense.
Does this check?
| [latex]12[/latex] dimes | [latex]12(0.10) = 1.20[/latex] |
| [latex]21[/latex] nickels | [latex]21(0.05)=2.25[/latex]✓ |
Step 7: Answer the question with a complete sentence.
- Adalberto has twelve dimes and twenty-one nickels.
If this were a homework exercise, our work might look like the following.
Try It
7) Michaela has [latex]$2.05[/latex] in dimes and nickels in her change purse. She has seven more dimes than nickels. How many coins of each type does she have?
Solution
[latex]9[/latex] nickels, [latex]16[/latex] dimes
8) Liliana has [latex]$2.10[/latex] in nickels and quarters in her backpack. She has [latex]12[/latex] more nickels than quarters. How many coins of each type does she have?
Solution
[latex]17[/latex] nickels, [latex]5[/latex] quarters
Example 2
Maria has [latex]$2.43[/latex] in quarters and pennies in her wallet. She has twice as many pennies as quarters. How many coins of each type does she have?
Solution
Step 1: Read the problem.
Determine the types of coins involved.
We know that Maria has quarters and pennies.
Create a table to organize the information.
-
- Label the columns “type,” “number,” “value,” “total value.”
- List the types of coins.
- Write in the value of each type of coin.
- Write in the total value of all the coins.
| Type | Number · | Value ($) | = Total Value ($) |
|---|---|---|---|
| Quarters | [latex]0.25[/latex] | ||
| Pennies | [latex]0.01[/latex] | ||
| [latex]2.43[/latex] | |||
Step 2: Identify what you are looking for.
- We are looking for the number of quarters and pennies.
Step 3: Name. Represent the number of quarters and pennies using variables.
- We know Maria has twice as many pennies as quarters. The number of pennies is defined in terms of quarters.
- Let [latex]q[/latex] represent the number of quarters.
- Then the number of pennies is [latex]2q[/latex].
| Type | Number · | Value ($) | = Total Value ($) |
|---|---|---|---|
| Quarters | [latex]q[/latex] | [latex]0.25[/latex] | |
| Pennies | [latex]2q[/latex] | [latex]0.01[/latex] | |
| [latex]2.43[/latex] | |||
Multiply the ‘number’ and the ‘value’ to get the ‘total value’ of each type of coin.
| Type | Number · | Value ($) | = Total Value ($) |
|---|---|---|---|
| Quarters | [latex]q[/latex] | [latex]0.25[/latex] | [latex]0.25q[/latex] |
| Pennies | [latex]2q[/latex] | [latex]0.01[/latex] | [latex]0.01(2q)[/latex] |
| [latex]2.43[/latex] | |||
Step 4: Translate. Write the equation by adding the ‘total value’ of all the types of coins.
Step 5: Solve the equation.
[latex]\begin{align*}&\;&0.25q+0.01(2q)&=2.43\\ &\text{Multiply}\;&0.25q+0.02q&=2.43\\ &\text{Combine like terms}\;&0.27q&=2.43\\ &\text{Divide by 0.27}\;&d&=9\\ &\text{The number of pennies is 2q}\;&\;&2{\color{red}{q}}\\ &\;&2\cdot{\color{red}{9}}&=18\;\text{pennies} \end{align*}[/latex]
Step 6: Check the answer in the problem.
Maria has [latex]9[/latex] quarters and [latex]18[/latex] pennies. Does this make [latex]$2.43[/latex]?
[latex]\begin{align*}&9\;\text{quarters}\;&9(0.25)&=2.25\\ &18\;\text{pennies}\;&18(0.01)&=0.18\\ &\text{Total}\;&\;&\$2.43\checkmark \end{align*}[/latex]
Step 7: Answer the question.
Maria has nine quarters and eighteen pennies.
Try It
9) Sumanta has [latex]$4.20[/latex] in nickels and dimes in her piggy bank. She has twice as many nickels as dimes. How many coins of each type does she have?
Solution
[latex]42[/latex] nickels, [latex]21[/latex] dimes.
10) Alison has three times as many dimes as quarters in her purse. She has [latex]$9.35[/latex] altogether. How many coins of each type does she have?
Solution
[latex]51[/latex] dimes, [latex]17[/latex] quarters.
In the next example, we’ll show only the completed table—remember the steps we take to fill in the table.
How To
Solve Coin Word Problems.
Step 1: Read the problem. Make sure all the words and ideas are understood.
- Determine the types of coins involved.
- Create a table to organize the information.
- Label the columns “type,” “number,” “value,” and “total value.”
- List the types of coins.
- Write in the value of each type of coin.
- Write in the total value of all the coins.
Step 2: Identify what we are looking for.
Step 3: Name what we are looking for. Choose a variable to represent that quantity.
Use variable expressions to represent the number of each type of coin and write them in the table.
Multiply the number times the value to get the total value of each type of coin.
Step 4: Translate into an equation.
It may be helpful to restate the problem in one sentence with all the important information. Then, translate the sentence into an equation.
Write the equation by adding the total values of all the types of coins.
Step 5: Solve the equation using good algebra techniques.
Step 6: Check the answer in the problem and make sure it makes sense.
Step 7: Answer the question with a complete sentence.
Example 3
Danny has [latex]$2.14[/latex] worth of pennies and nickels in his piggy bank. The number of nickels is two more than ten times the number of pennies. How many nickels and how many pennies does Danny have?
Solution
Step 1: Read the problem.
Determine the types of coins involved.
pennies and nickels
Create a table. Write in the value of each type of coin.
Pennies are worth [latex]$0.01[/latex].
Nickels are worth [latex]$0.05[/latex].
Step 2: Identify what we are looking for.
the number of pennies and nickels
Step 3: Name. Represent the number of each type of coin using variables.
The number of nickels is defined in terms of the number of pennies, so start with pennies.
Let [latex]p[/latex] = number of pennies
The number of nickels is two more than ten times the number of pennies.
Let [latex]10p+2[/latex] = number of nickels
Multiply the number and the value to get the total value of each type of coin.
| Type | Number · | Value ($) | = Total Value ($) |
|---|---|---|---|
| Pennies | [latex]p[/latex] | [latex]0.01[/latex] | [latex]0.01p[/latex] |
| Nickels | [latex]10p+2[/latex] | [latex]0.05[/latex] | [latex]0.05(10p+2)[/latex] |
| [latex]2.14[/latex] | |||
Step 4: Translate. Write the equation by adding the total value of all the types of coins.
[latex]0.01p\;+\;0.05(10p\;+\;2)\;=\;2.14[/latex]
Step 5: Solve the equation.
[latex]\begin{eqnarray*}0.01p\;+\;0.50p\;+\;0.10\;&=&\;2.14\\0.51p\;+\;0.10\;&=&\;2.14\\0.51p\;&=&\;2.04\\p\;&=&\;4\;\text{pennies}\end{eqnarray*}[/latex]
How many nickels?
[latex]\begin{align*}10p\;+\;2\\10({\color{red}{4}})\;+\;2\\42\;\text{nickles}\end{align*}[/latex]
Step 7: Answer the question.
Danny has four pennies and [latex]42[/latex] nickels.
Try It
11) Jesse has [latex]$6.55[/latex] worth of quarters and nickels in his pocket. The number of nickels is five more than two times the number of quarters. How many nickels and how many quarters does Jesse have?
Solution
[latex]41[/latex] nickels, [latex]18[/latex] quarters
12) Elane has [latex]$7.00[/latex] total in dimes and nickels in her coin jar. The number of dimes that Elane has is seven less than three times the number of nickels. How many of each coin does Elane have?
Solution
[latex]22[/latex] nickels, [latex]59[/latex] dimes
Solve Ticket and Stamp Word Problems
Problems involving tickets or stamps are very much like coin problems. Each type of ticket and stamp has a value, just like each type of coin does. So to solve these problems, we will follow the same steps we used to solve coin problems.
Example 4
At a school concert, the total value of tickets sold was [latex]$1,506[/latex]. Student tickets sold for [latex]$6[/latex] each and adult tickets sold for [latex]$9[/latex] each. The number of adult tickets sold was five less than three times the number of student tickets sold. How many student tickets and how many adult tickets were sold?
Solution
Step 1: Read the problem.
- Determine the types of tickets involved. There are student tickets and adult tickets.
- Create a table to organize the information.
| Type | Number · | Value ($) | = Total Value ($) |
|---|---|---|---|
| Student | [latex]6[/latex] | ||
| Adult | [latex]9[/latex] | ||
| 1506 | |||
Step 2: Identify what we are looking for.
- We are looking for the number of student and adult tickets.
Step 3: Name. Represent the number of each type of ticket using variables.
We know the number of adult tickets sold was five less than three times the number of student tickets sold.
- Let [latex]s[/latex] be the number of student tickets.
- Then [latex]3s-5[/latex] is the number of adult tickets
Multiply the number times the value to get the total value of each type of ticket.
| Type | Number · | Value ($) | = Total Value ($) |
|---|---|---|---|
| Student | [latex]s[/latex] | [latex]6[/latex] | [latex]6s[/latex] |
| Adult | [latex]3s-5[/latex] | [latex]9[/latex] | [latex]9(3s-5)[/latex] |
| [latex]1506[/latex] | |||
Step 4: Translate. Write the equation by adding the total values of each type of ticket.
Step 5: Solve the equation.
[latex]\begin{eqnarray}6s+27s-45 &=& 1506\\33s-45 &=& 1506 \\s &=& 47 \\ &=& 3s-5 \\ &=& 3(47)-5 \end{eqnarray}[/latex]
[latex]136[/latex] adult tickets.
Step 6: Check the answer.
There were [latex]47[/latex] student tickets at [latex]$6[/latex] each and [latex]136[/latex] adult tickets at [latex]$9[/latex] each. Is the total value [latex]$1,506[/latex]? We find the total value of each type of ticket by multiplying the number of tickets times its value then add to get the total value of all the tickets sold.
[latex]\begin{eqnarray*}47\;\times\;6\;&=&\;282\\136\;\times\;9\;&=&\;1,224\\&=&\;1,506\;\checkmark\end{eqnarray*}[/latex]
Step 7: Answer the question. They sold [latex]47[/latex] student tickets and [latex]136[/latex] adult tickets.
Try It
13) On The first day of a water polo tournament the total value of tickets sold was [latex]$17,610[/latex]. One-day passes sold for [latex]$20[/latex] and tournament passes sold for [latex]$30[/latex]. The number of tournament passes sold was [latex]37[/latex] more than the number of day passes sold. How many day passes and how many tournament passes were sold?
Solution
[latex]330[/latex] day passes, [latex]367[/latex] tournament passes
14) At the movie theatre, the total value of tickets sold was [latex]$2,612.50[/latex]. Adult tickets sold for [latex]$10[/latex] each and senior/child tickets sold for [latex]$7.50[/latex] each. The number of senior/child tickets sold was [latex]25[/latex] less than twice the number of adult tickets sold. How many senior/child tickets and how many adult tickets were sold?
Solution
[latex]112[/latex] adult tickets, [latex]199[/latex] senior/child tickets
We have learned how to find the total number of tickets when the number of one type of ticket is based on the number of the other type. Next, we’ll look at an example where we know the total number of tickets and have to figure out how the two types of tickets relate.
Suppose Bianca sold a total of [latex]100[/latex] tickets. Each ticket was either an adult ticket or a child ticket. If she sold [latex]20[/latex] child tickets, how many adult tickets did she sell?
- Did you say ‘[latex]80[/latex]’? How did you figure that out? Did you subtract [latex]20[/latex] from [latex]100[/latex]?
If she sold [latex]45[/latex] child tickets, how many adult tickets did she sell?
- Did you say ‘[latex]55[/latex]’? How did you find it? By subtracting [latex]45[/latex] from [latex]100[/latex]?
What if she sold [latex]75[/latex] child tickets? How many adult tickets did she sell?
- The number of adult tickets must be [latex]100-75[/latex]. She sold [latex]25[/latex] adult tickets.
Now, suppose Bianca sold [latex]x[/latex] child tickets. Then how many adult tickets did she sell? To find out, we would follow the same logic we used above. In each case, we subtracted the number of child tickets from [latex]100[/latex] to get the number of adult tickets. We now do the same with [latex]x[/latex].
We have summarized this below.
| Child tickets | Adult tickets |
|---|---|
| [latex]20[/latex] | [latex]80[/latex] |
| [latex]45[/latex] | [latex]55[/latex] |
| [latex]75[/latex] | [latex]25[/latex] |
| [latex]{\color{red}{x}}[/latex] | [latex]{\color{red}{100-x}}[/latex] |
We can apply these techniques to other examples
Example 5
Galen sold [latex]810[/latex] tickets for his church’s carnival for a total of [latex]$2,820[/latex]. Children’s tickets cost [latex]$3[/latex] each and adult tickets cost [latex]$5[/latex] each. How many children’s tickets and how many adult tickets did he sell?
Solution
Step 1: Read the problem.
- Determine the types of tickets involved. There are children tickets and adult tickets.
- Create a table to organize the information.
| Type | Number · | Value ($) | = Total Value ($) |
|---|---|---|---|
| Children | [latex]3[/latex] | ||
| Adult | [latex]5[/latex] | ||
| [latex]2820[/latex] | |||
Step 2: Identify what we are looking for.
- We are looking for the number of children and adult tickets.
Step 3: Name. Represent the number of each type of ticket using variables.
- We know the total number of tickets sold was 810. This means the number of children’s tickets plus the number of adult tickets must add up to 810.
- Let [latex]c[/latex] be the number of children tickets.
- Then [latex]810-c[/latex] is the number of adult tickets.
- Multiply the number times the value to get the total value of each type of ticket.
| Type | Number · | Value ($) | = Total Value ($) |
|---|---|---|---|
| Children | [latex]c[/latex] | [latex]3[/latex] | [latex]3c[/latex] |
| Adult | [latex]810-c[/latex] | [latex]5[/latex] | [latex]5(810-c)[/latex] |
| [latex]2820[/latex] |
Step 4: Translate.
Write the equation by adding the total values of each type of ticket.
Step 5: Solve the equation.
[latex]\begin{eqnarray}3c+5(810-c)&=&2,820\\3c+5(810-c)&=&2,820\\-2c&=&-1,230\\c&=&615 \;\text{children tickets}\end{eqnarray}[/latex]
How many adults?
[latex]\begin{align*} 810&-c\\ 810&-615 \end{align*}[/latex]
[latex]195[/latex] adult tickets
Step 6: Check the answer. There were [latex]615[/latex] children’s tickets at [latex]$3[/latex] each and [latex]195[/latex] adult tickets at [latex]$5[/latex] each. Is the total value [latex]$2,820[/latex]?
[latex]\begin{eqnarray*}615\;\times\;3\;&=&\;1,845\\195\;\times\;5\;&=&\;975\\&=&\;2,820\;\checkmark\end{eqnarray*}[/latex]
Step 7: Answer the question. Galen sold [latex]615[/latex] children’s tickets and [latex]195[/latex] adult tickets.
Try It
15) During her shift at the museum ticket booth, Leah sold [latex]115[/latex] tickets for a total of [latex]$1,163[/latex]. Adult tickets cost [latex]$12[/latex] and student tickets cost [latex]$5[/latex]. How many adult tickets and how many student tickets did Leah sell?
Solution
[latex]84[/latex] adult tickets, [latex]31[/latex] student tickets
16) A whale-watching ship had [latex]40[/latex] paying passengers on board. The total collected from tickets was [latex]$1,196[/latex]. Full-fare passengers paid [latex]$32[/latex] each and reduced-fare passengers paid [latex]$26[/latex] each. How many full-fare passengers and how many reduced-fare passengers were on the ship?
Solution
[latex]26[/latex] full-fare, [latex]14[/latex] reduced fare
Now, we’ll do one where we fill in the table all at once.
Example 6
Monica paid $8.36 for stamps. The number of 41-cent stamps was four more than twice the number of two-cent stamps. How many 41-cent stamps and how many two-cent stamps did Monica buy?
Solution
The types of stamps are [latex]41[/latex]-cent stamps and two-cent stamps. Their names also give the value!
“The number of [latex]41[/latex]-cent stamps was four more than twice the number of two-cent stamps.”
| Type | Number · | Value ($) | = Total Value ($) |
|---|---|---|---|
| 41 cent stamps | [latex]2x+4[/latex] | [latex]0.41[/latex] | [latex]0.41(2x+4)[/latex] |
| 2 cent stamps | [latex]x[/latex] | [latex]0.02[/latex] | [latex]0.02x[/latex] |
| [latex]8.36[/latex] | |||
Step 1: Write the equation from the total values.
[latex]0.41(2x+4)+0.02x=8.36[/latex]
Step 2: Solve the equation.
[latex]\begin{align*}0.82x+1.64+0.02x&=8.36\\0.84x+1.64&=8.36\\0.84x&=6.72\\x&=8 \end{align*}[/latex]
Monica bought eight two-cent stamps.
[latex]2x+4[/latex] for [latex]x=8[/latex]
Step 3: Find the number of 41-cent stamps she bought by evaluating.
[latex]\begin{align*} 2x+4\\ 2(8)+4\\ 20 \end{align*}[/latex]
Step 4: Check.
[latex]\begin{align*} 8(0.02)+20(0.41)&\overset?=8.36\\ 0.16+8.20&\overset?=8.36\\ 8.36&=8.36\checkmark \end{align*}[/latex]
Monica bought eight two-cent stamps and 20 41-cent stamps.
Try It
17) Eric paid [latex]$13.36[/latex] for stamps. The number of [latex]41[/latex]-cent stamps was eight more than twice the number of two-cent stamps. How many [latex]41[/latex]-cent stamps and how many two-cent stamps did Eric buy?
Solution
[latex]32[/latex] at [latex]$0.41[/latex], [latex]12[/latex] at [latex]$0.02[/latex]
18) Kailee paid [latex]$12.66[/latex] for stamps. The number of [latex]41[/latex]-cent stamps was four less than three times the number of [latex]20[/latex]-cent stamps. How many [latex]41[/latex]-cent stamps and how many [latex]20[/latex]-cent stamps did Kailee buy?
Solution
[latex]26[/latex] at [latex]$0.41[/latex], [latex]10[/latex] at [latex]$0.20[/latex]
Solve Mixture Word Problems
Now we’ll solve some more general applications of the mixture model. Grocers and bartenders use the mixture model to set a fair price for a product made from mixing two or more ingredients. Financial planners use the mixture model when they invest money in a variety of accounts and want to find the overall interest rate. Landscape designers use the mixture model when they have an assortment of plants and a fixed budget, and event coordinators do the same when choosing appetizers and entrees for a banquet.
Our first mixture word problem will be making trail mix from raisins and nuts.
Example 7
Henning is mixing raisins and nuts to make [latex]10[/latex] pounds of trail mix. Raisins cost [latex]$2[/latex] a pound and nuts cost [latex]$6[/latex] a pound. If Henning wants his cost for the trail mix to be [latex]$5.20[/latex] a pound, how many pounds of raisins and how many pounds of nuts should he use?
Solution
As before, we fill in a chart to organize our information.
The [latex]10[/latex] pounds of trail mix will come from mixing raisins and nuts.
[latex]\begin{eqnarray*} x &=& \text{number of pounds of raisins} \\ 10 - x &=& \text{number of pounds of nuts} \end{eqnarray*}[/latex]
We enter the price per pound for each item.
We multiply the number times the value to get the total value.
| Type | Number of pounds · | Price per pound ($) | = Total Value ($) |
|---|---|---|---|
| Raisins | [latex]x[/latex] | [latex]2[/latex] | [latex]2x[/latex] |
| Nuts | [latex]10-x[/latex] | [latex]6[/latex] | [latex]6(10-x)[/latex] |
| Trail mix | [latex]10[/latex] | [latex]5.20[/latex] | [latex]10(5.20)[/latex] |
Notice that the last line in the table gives the information for the total amount of the mixture.
We know the value of the raisins plus the value of the nuts will be the value of the trail mix.
Step 1: Write the equation from the total values.
[latex]2x\;+\;6(10\;+\;x)\;=\;10(5.20)[/latex]
Step 2: Solve the equation.
[latex]\begin{eqnarray*}2x\;+\;60\;-\;6x\;&=&\;52\\-4x\;&=&\;-8\\x\;&=&\;2\;\text{pounds of raisins}\end{eqnarray*}[/latex]
Step 3: Find the number of pounds of nuts.
[latex]\begin{eqnarray*}10\;-\;x\\10\;-\;{\color{red}{2}}\\{\color{black}{8}}\;\text{pounds of nuts}\end{eqnarray*}[/latex]
Step 4: Check.
[latex]\begin{align*} 2(\$2)+8(\$6)&\overset?=10(\$5.20)\\ \$4+48&\overset?=\$52\\ \$52&=\$52\checkmark \end{align*}[/latex]
Henning mixed two pounds of raisins with eight pounds of nuts.
Try It
19) Orlando is mixing nuts and cereal squares to make a party mix. Nuts sell for [latex]$7[/latex] a pound and cereal squares sell for [latex]$4[/latex] a pound. Orlando wants to make [latex]30[/latex] pounds of party mix at a cost of [latex]$6.50[/latex] a pound, how many pounds of nuts and how many pounds of cereal squares should he use?
Solution
[latex]5[/latex] pounds cereal squares, [latex]25[/latex] pounds nuts
20) Becca wants to mix fruit juice and soda to make a punch. She can buy fruit juice for [latex]$3[/latex] a gallon and soda for [latex]$4[/latex] a gallon. If she wants to make [latex]28[/latex] gallons of punch at a cost of [latex]$3.25[/latex] a gallon, how many gallons of fruit juice and how many gallons of soda should she buy?
Solution
[latex]21[/latex] gallons of fruit punch, [latex]7[/latex] gallons of soda
We can also use the mixture model to solve investment problems using simple interest. We have used the simple interest formula, [latex]I=Prt[/latex], where [latex]t[/latex] represented the number of years. When we just need to find the interest for one year, [latex]t=1[/latex], so then [latex]I=Pr[/latex].
Example 8
Stacey has [latex]$20,000[/latex] to invest in two different bank accounts. One account pays interest at [latex]3%[/latex] per year and the other account pays interest at [latex]5%[/latex] per year. How much should she invest in each account if she wants to earn [latex]4.5%[/latex] interest per year on the total amount?
Solution
We will fill in a chart to organize our information. We will use the simple interest formula to find the interest earned in the different accounts.
The interest on the mixed investment will come from adding the interest from the account earning [latex]3%[/latex] and the interest from the account earning [latex]5%[/latex] to get the total interest on the [latex]$20,000[/latex].
[latex]\begin{align*}\text{Let }x&=\text{amount invested at 3}\%\\20,000-x&=\text{amount invested at 5}\%\end{align*}[/latex]
The amount invested is the principal for each account.
We enter the interest rate for each account.
We multiply the amount invested times the rate to get the interest.
| Type | Amount Invested · | Rate | = Interest |
|---|---|---|---|
| 3% | [latex]x[/latex] | [latex]0.03[/latex] | [latex]0.03x[/latex] |
| 5% | [latex]20,000-x[/latex] | [latex]0.05[/latex] | [latex]0.05(20,000-x)[/latex] |
| 4.5% | [latex]20,000[/latex] | [latex]0.045[/latex] | [latex]0.045(20,000)[/latex] |
Notice that the total amount invested, [latex]20,000[/latex], is the sum of the amount invested at [latex]3%[/latex] and the amount invested at [latex]5%[/latex]. The total interest, [latex]0.045(20,000)[/latex] is the sum of the interest earned in the [latex]3%[/latex] account and the interest earned in the 5% account.
As with the other mixture applications, the last column in the table gives us the equation to solve.
Step 1: Write the equation from the interest earned.
[latex]0.03x + 0.05(20,000 - x)= 0.045(20,000)[/latex]
Step 2: Solve the equation.
[latex]\begin{align*} 0.03x + 0.05(20,000-x)&= 0.045(20,000)\\ 0.03x + 1000 - 0.05x&= 900\\ -0.02x + 1000&=900\\ -0.02x&-100\\ x&=5,000\;\text{amount invested at 3%} \end{align*}[/latex]
Step 3: Find the amount invested at 5%.
[latex]\begin{align*} 20,000&-{\color{red}{x}}\\ 20,000&-{\color{red}{5}}{\color{red}{,}}{\color{red}{000}}\\ 15,000&=\text{amount invested at 5%} \end{align*}[/latex]
Step 4: Check.
[latex]\begin{align*} 0.03x+0.05(15,000+x)&\overset?=0.045(20,000)\\ 150+750&\overset?=-900\\ 900&=900\checkmark\\ \end{align*}[/latex]
Stacey should invest $5,000 in the account that earns 3% and $15,000 in the account that earns 5%.
Try It
21) Remy has [latex]$14,000[/latex] to invest in two mutual funds. One fund pays interest at [latex]4%[/latex] per year and the other fund pays interest at [latex]7%[/latex] per year. How much should she invest in each fund if she wants to earn [latex]6.1%[/latex] interest on the total amount?
Solution
[latex]$4,200[/latex] at [latex]4%[/latex], [latex]$9,800[/latex] at [latex]7%[/latex]
22) Marco has [latex]$8,000[/latex] to save for his daughter’s college education. He wants to divide it between one account that pays [latex]3.2%[/latex] interest per year and another account that pays [latex]8%[/latex] interest per year. How much should he invest in each account if he wants the interest on the total investment to be [latex]6.5%[/latex]?
Solution
[latex]$2,500[/latex] at [latex]3.2%[/latex], [latex]$5,500[/latex] at [latex]8%[/latex]
Solve Uniform Motion Applications
When planning a road trip, it often helps to know how long it will take to reach the destination or how far to travel each day. We would use the distance, rate, and time formula, [latex]D=rt[/latex], which we have already seen.
In this section, we will use this formula in situations that require a little more algebra to solve than the ones we saw earlier. Generally, we will be looking at comparing two scenarios, such as two vehicles travelling at different rates or in opposite directions. When the speed of each vehicle is constant, we call applications like this uniform motion problems.
Our problem-solving strategies will still apply here, but we will add to the first step. The first step will include drawing a diagram that shows what is happening in the example. Drawing the diagram helps us understand what is happening so that we can write an appropriate equation. Then we will make a table to organize the information, like we did for the money applications.
The steps are listed here for easy reference:
How To
Use a Problem-Solving Strategy in Distance, Rate, and Time Applications.
Step 1: Read the problem. Make sure all the words and ideas are understood.
- Draw a diagram to illustrate what is happening.
- Create a table to organize the information.
- Label the column’s rate, time, and distance.
- List the two scenarios.
- Write in the information you know.
Step 2: Identify what we are looking for.
Step 3: Name what we are looking for. Choose a variable to represent that quantity.
- Complete the chart.
- Use variable expressions to represent that quantity in each row.
- Multiply the rate times the time to get the distance.
Step 4: Translate into an equation.
- Restate the problem in one sentence with all the important information.
- Then, translate the sentence into an equation.
Step 5: Solve the equation using good algebra techniques.
Step 6: Check the answer in the problem and make sure it makes sense.
Step 7: Answer the question with a complete sentence.
Example 9
An express train and a local train leave Pittsburgh to travel to Washington, D.C. The express train can make the trip in [latex]4[/latex] hours and the local train takes [latex]5[/latex] hours for the trip. The speed of the express train is [latex]12[/latex] miles per hour faster than the speed of the local train. Find the speed of both trains.
Solution
Step 1: Read the problem. Make sure all the words and ideas are understood.
- Draw a diagram to illustrate what it happening. Shown below is a sketch of what is happening in the example.
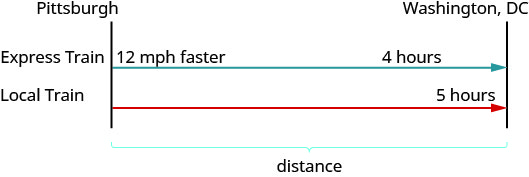
Figure 3.8.5 Rate (mph) · Time (hrs) = Distance (miles) Express [latex]{\color{red}{4}}[/latex] Local [latex]{\color{red}{5}}[/latex] - Create a table to organize the information.
- Label the columns “Rate,” “Time,” and “Distance.”
- List the two scenarios.
- Write in the information you know.
Step 2: Identify what we are looking for.
- We are asked to find the speed of both trains.
- Notice that the distance formula uses the word “rate,” but it is more common to use “speed” when we talk about vehicles in everyday English.
Step 3: Name what we are looking for. Choose a variable to represent that quantity.
- Complete the chart
- Use variable expressions to represent that quantity in each row.
- We are looking for the speed of the trains. Let’s let [latex]r[/latex] represent the speed of the local train. Since the speed of the express train is [latex]12[/latex] mph faster, we represent that as [latex]r+12[/latex].
[latex]r =[/latex] speed of the local train
[latex]r+12 =[/latex] speed of the express train
Fill in the speeds on the chart.
| Rate (mph) · | Time (hrs) | = Distance (miles) | |
|---|---|---|---|
| Express | [latex]{\color{red}{r+12}}[/latex] | [latex]{\color{red}{4}}[/latex] | |
| Local | [latex]{\color{red}{r}}[/latex] | [latex]{\color{red}{5}}[/latex] |
Multiply the rate times the time to get the distance.
| Rate (mph) · | Time (hrs) | = Distance (miles) | |
|---|---|---|---|
| Express | [latex]r+12[/latex] | [latex]4[/latex] | [latex]{\color{red}{4(r+12)}}[/latex] |
| Local | [latex]r[/latex] | [latex]5[/latex] | [latex]{\color{red}{5r}}[/latex] |
Step 4: Translate into an equation.
- Restate the problem in one sentence with all the important information.
- Then, translate the sentence into an equation.
- The equation to model this situation will come from the relation between the distances. Look at the diagram we drew above. How is the distance travelled by the express train related to the distance travelled by the local train?
- Since both trains leave from Pittsburgh and travel to Washington, D.C. they travel the same distance. So we write:
[latex]{\small\begin{align*} &\;&\underbrace{\text{distance travelled by express train}}\;&\;\;=\;&\underbrace{\text{distance travelled by local train}}\\ &\text{Translate to an equation}&4(r+12)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;&\;\;=\;&\;5r\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\end{align*}}[/latex]
Step 5: Solve the equation using good algebra techniques.
Now solve this equation.
[latex]\begin{eqnarray*}4(r\;+\;12)\;&=&\;5r\\4r\;+\;48\;&=&\;5r\\48\;&=&\;r\end{eqnarray*}[/latex]
So the speed of the local train is [latex]48[/latex] mph.
Find the speed of the express train.
[latex]\begin{eqnarray*}{\color{red}{r}}\;+\;12\\{\color{red}{48}}\;+\;12\\60\end{eqnarray*}[/latex]
The speed of the express train is [latex]60[/latex] mph.
Step 6: Check the answer in the problem and make sure it makes sense.
[latex]\begin{align*} &\text{express train}\;&60\;mph(4\;hours)&=240\;miles\\ &\text{local train}\;&48\;mph(5\;hour)&=240\;miles \end{align*}[/latex]
Step 7: Answer the question with a complete sentence.
- The speed of the local train is [latex]48[/latex] mph and the speed of the express train is [latex]60[/latex] mph.
Try It
23) Wayne and Dennis like to ride the bike path from Riverside Park to the beach. Dennis’s speed is seven miles per hour faster than Wayne’s speed, so it takes Wayne [latex]2[/latex] hours to ride to the beach while it takes Dennis [latex]1.5[/latex] hours for the ride. Find the speed of both bikers.
Solution
Wayne [latex]21[/latex] mph, Dennis [latex]28[/latex] mph
24) Jeromy can drive from his house in Cleveland to his college in Chicago in [latex]4.5[/latex] hours. It takes his mother [latex]6[/latex] hours to make the same drive. Jeromy drives [latex]20[/latex] miles per hour faster than his mother. Find Jeromy’s speed and his mother’s speed.
Solution
Jeromy [latex]80[/latex] mph, mother [latex]60[/latex] mph
The diagram and the chart helped us write the equation we solved. Let’s see how this works in another case.
Example 10
Christopher and his parents live 115 miles apart. They met at a restaurant between their homes to celebrate his mother’s birthday. Christopher drove 1.5 hours while his parents drove 1 hour to get to the restaurant. Christopher’s average speed was 10 miles per hour faster than his parents’ average speed. What were the average speeds of Christopher and his parents as they drove to the restaurant?
Solution
Step 1: Read the problem. Make sure all the words and ideas are understood.
- Draw a diagram to illustrate what is happening. Below is a sketch of what is happening in the example.
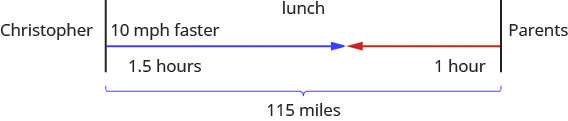
- Create a table to organize the information.
- Label the columns’ rate, time, and distance.
- List the two scenarios.
- Write in the information you know.
| Rate (mph) · | Time (hrs) | = Distance (miles) | |
|---|---|---|---|
| Christopher | [latex]{\color{red}{1.5}}[/latex] | ||
| Parents | [latex]{\color{red}{1}}[/latex] | ||
| [latex]{\color{red}{115}}[/latex] | |||
Step 2: Identify what we are looking for.
- We are asked to find the average speeds of Christopher and his parents.
Step 3: Name what we are looking for. Choose a variable to represent that quantity.
- Complete the chart.
- Use variable expressions to represent that quantity in each row.
- We are looking for their average speeds. Let’s let [latex]r[/latex] represent the average speed of the parents. Since the Christopher’s speed is [latex]10[/latex] mph faster, we represent that as [latex]r+10[/latex].
Fill in the speeds on the chart.
| Rate (mph) · | Time (hrs) | = Distance (miles) | |
|---|---|---|---|
| Christopher | [latex]r+10[/latex] | [latex]1.5[/latex] | [latex]{\color{red}{1.5(r+10)}}[/latex] |
| Parents | [latex]r[/latex] | [latex]1[/latex] | [latex]{\color{red}{r}}[/latex] |
| [latex]{\color{red}{115}}[/latex] | |||
Multiply the rate times the time to get the distance.
Step 4: Translate into an equation.
- Restate the problem in one sentence with all the important information.
- Then, translate the sentence into an equation.
- Again, we need to identify a relationship between the distances to write an equation. Look at the diagram we created above and notice the relationship between the distance Christopher travelled and the distance his parents travelled.
The distance Christopher travelled plus the distance his parents travelled must add up to 115 miles. So we write:
[latex]{\small\begin{align*} &\;&\underbrace{\text{distance travelled by Christopher}}&\;+&\underbrace{\text{distance travelled by his parents}}&\;=&115\\ &\text{Translate to an equation}&1.5(r+10)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;&\;+&\;r\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;&\;=&115\end{align*}}[/latex]
Step 5: Solve the equation using good algebra techniques.
Now solve this equation.
[latex]\begin{align*} 1.5(r+10)+r&=115\\ 1.5r+15+r&=115\\ 2.5r+15&=115\\ 2.5r&=100\\ r&=40 \end{align*}[/latex]
So the parents’ speed was [latex]40[/latex] mph.
Christopher’s speed is [latex]r+10[/latex].
[latex]\begin{align*}{\color{red}{r}}&+10\\ {\color{red}{40}}+10&=50 \end{align*}[/latex]
Step 6: Check the answer in the problem and make sure it makes sense.
[latex]\begin{align*} &\text{Christopher drove}\;&50\;mph(1.5\;hours)&=75\;miles\\ &\text{His parents drove}\;&40\;mph(1\;hour)&=40\;miles\\ &\;&\;&=115\;miles \end{align*}[/latex]
Step 7: Answer the question with a complete sentence.
Christopher’s speed was [latex]50[/latex] mph.
His parents’ speed was [latex]40[/latex] mph.
Try It
25) Carina is driving from her home in Anaheim to Berkeley on the same day her brother is driving from Berkeley to Anaheim, so they decide to meet for lunch along the way in Buttonwillow. The distance from Anaheim to Berkeley is [latex]410[/latex] miles. It takes Carina [latex]3[/latex] hours to get to Buttonwillow, while her brother drives [latex]4[/latex] hours to get there. The average speed Carina’s brother drove was [latex]15[/latex] miles per hour faster than Carina’s average speed. Find Carina’s and her brother’s average speeds.
Solution
Carina [latex]50[/latex] mph, brother [latex]65[/latex] mph
26) Ashley goes to college in Minneapolis, [latex]234[/latex] miles from her home in Sioux Falls. She wants her parents to bring her more winter clothes, so they decide to meet at a restaurant on the road between Minneapolis and Sioux Falls. Ashley and her parents both drove [latex]2[/latex] hours to the restaurant. Ashley’s average speed was seven miles per hour faster than her parents’ average speed. Find Ashley’s and her parents’ average speed.
Solution
Parents [latex]55[/latex] mph, Ashley [latex]62[/latex] mph
As you read the next example, think about the relationship between the distances travelled. Which of the previous two examples is more similar to this situation?
Example 11
Two truck drivers leave a rest area on the interstate at the same time. One truck travels east and the other one travels west. The truck travelling west travels at [latex]70[/latex] mph and the truck travelling east has an average speed of [latex]60[/latex] mph. How long will they travel before they are [latex]325[/latex] miles apart?
Solution
Step 1: Read the problem. Make sure all the words and ideas are understood.
- Draw a diagram to illustrate what is happening.
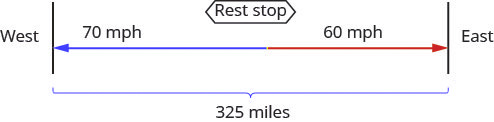
Figure 3.8.7 - Create a table to organize the information.
| Rate (mph) · | Time (hrs) | = Distance (miles) | |
|---|---|---|---|
| West | [latex]{\color{red}{70}}[/latex] | ||
| East | [latex]{\color{red}{60}}[/latex] | ||
| [latex]{\color{red}{325}}[/latex] | |||
Step 2: Identify what we are looking for.
- We are asked to find the amount of time the trucks will travel until they are [latex]325[/latex] miles apart.
Step 3: Name what we are looking for. Choose a variable to represent that quantity.
- We are looking for the time travelled. Both trucks will travel the same amount of time. Let’s call the time [latex]t[/latex]. Since their speeds are different, they will travel different distances.
- Complete the chart.
| Rate (mph) · | Time (hrs) | = Distance (miles) | |
|---|---|---|---|
| West | [latex]70[/latex] | [latex]{\color{red}{t}}[/latex] | [latex]{\color{red}{70t}}[/latex] |
| East | [latex]60[/latex] | [latex]{\color{red}{t}}[/latex] | [latex]{\color{red}{60t}}[/latex] |
| [latex]325[/latex] | |||
Step 4: Translate into an equation.
- We need to find a relation between the distances to write an equation. Looking at the diagram, what is the relationship between the distance each of the trucks will travel?
- The distance travelled by truck going west plus the distance travelled by the truck going east must add up to 325 miles. So we write:
[latex]\begin{align*} &\underbrace{\text{distance travelled by westbound truck}}\;&\;+&\underbrace{\text{distance travelled by eastbound truck}}&\;=&32\\ &\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;70t\;&\;+&\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;60t\;&\;=&32\end{align*}[/latex]
Step 5: Solve the equation using good algebra techniques.
[latex]\begin{align*} 70t+60t&=325\\ 130t&=325\\ t&=2.5 \end{align*}[/latex]
So it will take the trucks [latex]2.5[/latex] hours to be [latex]325[/latex] miles apart.
Step 6: Check the answer in the problem and make sure it makes sense.
[latex]\begin{align*} &\text{Truck going West}\;&70\;mph(2.5\;hours)&=175\;miles\\ &\text{Truck going East}\;&60\;mph(2.5\;hour)&=150\;miles\\ &\;&\;&=325\;miles \end{align*}[/latex]
Step 7: Answer the question with a complete sentence.
It will take the trucks [latex]2.5[/latex] hours to be [latex]325[/latex] miles apart.
Try It
27) Pierre and Monique leave their home in Portland at the same time. Pierre drives north on the turnpike at a speed of [latex]75[/latex] miles per hour while Monique drives south at a speed of [latex]68[/latex] miles per hour. How long will it take them to be [latex]429[/latex] miles apart?
Solution
[latex]3[/latex] hours
28) Thanh and Nhat leave their office in Sacramento at the same time. Thanh drives north on I-5 at a speed of [latex]72[/latex] miles per hour. Nhat drives south on I-5 at a speed of [latex]76[/latex] miles per hour. How long will it take them to be [latex]330[/latex] miles apart?
Solution
[latex]2.2[/latex] hours
Matching Units in Problems
It is important to make sure the units match when we use the distance rate and time formula. For instance, if the rate is in miles per hour, then the time must be in hours.
Example 12
When Katie Mae walks to school, it takes her [latex]30[/latex] minutes. If she rides her bike, it takes her [latex]15[/latex] minutes. Her speed is three miles per hour faster when she rides her bike than when she walks. What are her walking speed and her speed riding her bike?
Solution
First, we draw a diagram that represents the situation to help us see what is happening.
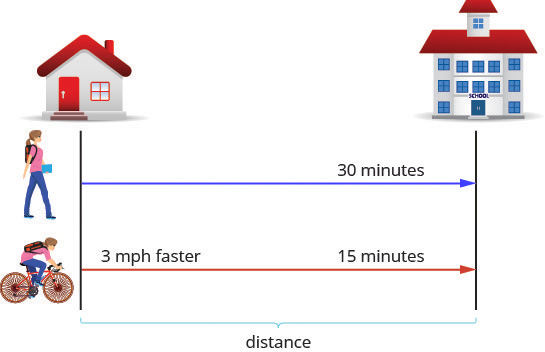
We are asked to find her speed walking and riding her bike. Let’s call her walking speed [latex]r[/latex]. Since her biking speed is three miles per hour faster, we will call that speed [latex]r+3[/latex]. We write the speeds in the chart.
The speed is in miles per hour, so we need to express the times in hours, too, in order for the units to be the same. Remember, one hour is 60 minutes. So:
30 minutes is [latex]\frac{30}{60}[/latex] or [latex]\frac{1}{2}[/latex] hour
| Rate (mph) · | Time (hrs) | = Distance (miles) | |
|---|---|---|---|
| Walk | [latex]r[/latex] | [latex]\frac12[/latex] | [latex]\frac12r[/latex] |
| Bike | [latex]r+3[/latex] | [latex]\frac14[/latex] | [latex]\frac14(r+3)[/latex] |
The equation will come from the fact that the distance from Katie Mae’s home to her school is the same whether she is walking or riding her bike.
So we say:
[latex]\underbrace{\text{distance walked}}\;=\;\underbrace{\text{distance covered by bike}}[/latex]
Step 1: Translate into an equation.
[latex]\frac12r\;=\;\frac14(r\;+\;3)[/latex]
Step 2: Solve this equation.
[latex]\frac12r\;=\;\frac14(r\;+\;3)[/latex]
Step 3: Clear the fractions by multiplying by the LCD of all the fractions in the equation.
[latex]8\;\times\;\frac12r\;=\;8\;\times\;\frac14(r\;+\;3)[/latex]
Step 4: Simplify.
[latex]\begin{eqnarray*}4r\;&=&\;2(r\;+\;3)\\4r\;&=&\;2r\;+\;6\\2r\;&=&\;6\\r\;&=&\;3\;mph\end{eqnarray*}[/latex]
3 mph is Katie Mae’s walking speed
[latex]{\color{red}{r}}{+3}[/latex] biking speed
[latex]{\color{red}{3}}{\;+\;3}[/latex]
[latex]6[/latex] mph (Katie Mae’s biking speed)
Step 5: Let’s check if this works.
[latex]\begin{align*} &\text{Walk}\;&3\;mph(0.5\;hours)&=1.5\;miles\\ &\text{Bike}\;&6\;mph(0.25\;hour)&=1.5\;miles\end{align*}[/latex]
Yes, either way, Katie Mae travels [latex]1.5[/latex] miles to school.
Katie Mae’s walking speed is [latex]3[/latex] mph.
Her speed riding her bike is [latex]6[/latex] mph.
Try It
29) Suzy takes [latex]50[/latex] minutes to hike uphill from the parking lot to the lookout tower. It takes her [latex]30[/latex] minutes to hike back down to the parking lot. Her speed going downhill is [latex]1.2[/latex] miles per hour faster than her speed going uphill. Find Suzy’s uphill and downhill speeds.
Solution
Uphill [latex]1.8[/latex] mph, downhill [latex]3[/latex] mph
30) Llewyn takes [latex]45[/latex] minutes to drive his boat upstream from the dock to his favorite fishing spot. It takes him [latex]30[/latex] minutes to drive the boat back downstream to the dock. The boat’s speed going downstream is four miles per hour faster than its speed going upstream. Find the boat’s upstream and downstream speeds.
Solution
Upstream [latex]8[/latex] mph, downstream [latex]12[/latex] mph
In the distance, rate, and time formula, time represents the actual amount of elapsed time (in hours, minutes, etc.). If a problem gives us starting and ending times as clock times, we must find the elapsed time in order to use the formula.
Example 13
Hamilton loves to travel to Las Vegas, [latex]255[/latex] miles from his home in Orange County. On his last trip, he left his house at 2:00 pm. The first part of his trip was on congested city freeways. At 4:00 pm, the traffic cleared and he was able to drive through the desert at a speed [latex]1.75[/latex] times faster than when he drove in the congested area. He arrived in Las Vegas at 6:30 pm. How fast was he driving during each part of his trip?
Solution
A diagram will help us model this trip.
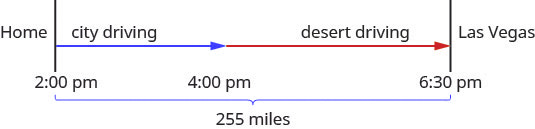
Next, we create a table to organize the information.
We know the total distance is [latex]255[/latex] miles. We are looking for the rate of speed for each part of the trip. The rate in the desert is [latex]1.75[/latex] times the rate in the city. If we let [latex]r=[/latex] the rate in the city, then the rate in the desert is [latex]1.75r[/latex].
The times here are given as clock times. Hamilton started from home at 2:00 pm and entered the desert at 4:30 pm. So he spent two hours driving the congested freeways in the city. Then he drove faster from 4:00 pm until 6:30 pm in the desert. So he drove [latex]2.5[/latex] hours in the desert.
Now, we multiply the rates by the times.
| Rate (mph) · | Time (hrs) | = Distance (miles) | |
|---|---|---|---|
| City | [latex]r[/latex] | [latex]2[/latex] | [latex]2r[/latex] |
| Desert | [latex]1.75r[/latex] | [latex]2.5[/latex] | [latex]2.5(1.5r)[/latex] |
| [latex]225[/latex] | |||
By looking at the diagram below, we can see that the sum of the distance driven in the city and the distance driven in the desert is [latex]255[/latex] miles.
[latex]\underbrace{\text{distance driven in the city}}\;+\;\underbrace{\text{distance driven in desert}}\;=255[/latex]
Step 1: Translate into an equation.
[latex]2r\;+\;2.5(1.75r)\;=\;255[/latex]
Step 2: Solve this equation.
[latex]\begin{eqnarray*}2r\;+\;2.5(1.75r)\;&=&\;255\\2r\;+\;4.375r\;&=&\;255\\6.375r\;&=&\;255\\r\;&=&\;40\;mph\;city\end{eqnarray*}[/latex]
[latex]\begin{align*}&1.75{\color{red}{r}}\;\text{desert speed}\\&1.75({\color{red}{40}})\\&70\;mph\end{align*}[/latex]
Step 3: Check.
[latex]\begin{align*}\text{City }40\;mph\;(2\;\text{hours})&= 80\;miles\\\text{Desert }70\;mph\;(2.5\;\text{hours})&= \frac{175\;miles}{255\;miles}\end{align*}[/latex]
Hamilton drove [latex]40[/latex] mph in the city and [latex]70[/latex] mph in the desert.
Try It
31) Cruz is training to compete in a triathlon. He left his house at 6:00 and ran until 7:30. Then he rode his bike until 9:45. He covered a total distance of [latex]51[/latex] miles. His speed when biking was [latex]1.6[/latex] times his speed when running. Find Cruz’s biking and running speeds.
Solution
Biking [latex]16[/latex] mph, running [latex]10[/latex] mph
32) Phuong left home on his bicycle at 10:00. He rode on the flat street until 11:15, then rode uphill until 11:45. He rode a total of [latex]31[/latex] miles. His speed riding uphill was [latex]0.6[/latex] times his speed on the flat street. Find his speed biking uphill and on the flat street.
Solution
Uphill [latex]12[/latex] mph, flat street [latex]20[/latex] mph
Key Concepts
- Total Value of Coins For the same type of coin, the total value of a number of coins is found by using the model.
- number × value=total value where number is the number of coins and value is the value of each coin; total value is the total value of all the coins
- Problem-Solving Strategy—Coin Word Problems
- Read the problem. Make all the words and ideas are understood. Determine the types of coins involved.
- Create a table to organize the information.
- Label the columns type, number, value, total value.
- List the types of coins.
- Write in the value of each type of coin.
- Write in the total value of all the coins.
- Identify what we are looking for.
- Name what we are looking for. Choose a variable to represent that quantity.
Use variable expressions to represent the number of each type of coin and write them in the table.
Multiply the number times the value to get the total value of each type of coin. - Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the sentence into an equation.
Write the equation by adding the total values of all the types of coins. - Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
- Read the problem. Make all the words and ideas are understood. Determine the types of coins involved.
- Distance, Rate, and Time
- [latex]D = rt[/latex] where [latex]D =[/latex] distance, [latex]r =[/latex] rate, [latex]t =[/latex] time
- Problem-Solving Strategy—Distance, Rate, and Time Applications
- Read the problem. Make sure all the words and ideas are understood.
Draw a diagram to illustrate what it happening.
Create a table to organize the information: Label the columns rate, time, distance. List the two scenarios. Write in the information you know. - Identify what we are looking for.
- Name what we are looking for. Choose a variable to represent that quantity.
Complete the chart.
Use variable expressions to represent that quantity in each row.
Multiply the rate times the time to get the distance. - Translate into an equation.
Restate the problem in one sentence with all the important information.
Then, translate the sentence into an equation. - Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
- Read the problem. Make sure all the words and ideas are understood.
Glossary
- Mixture problems
- Mixture problems combine two or more items with different values together.
Exercises: Solve Coin Word Problems
Instructions: For questions 1-18, solve each coin word problem.
Solution
[latex]8[/latex] nickels, [latex]22[/latex] dimes
Solution
[latex]15[/latex] dimes, [latex]8[/latex] quarters
Solution
[latex]10[/latex] at [latex]$1[/latex], [latex]7[/latex] at [latex]$5[/latex]
Solution
[latex]18[/latex] quarters, [latex]36[/latex] nickels
Solution
[latex]30[/latex] pennies, [latex]90[/latex] dimes
Solution
[latex]10[/latex] at [latex]$10[/latex], [latex]5[/latex] at [latex]$5[/latex]
Solution
[latex]12[/latex] dimes and [latex]27[/latex] nickels
Solution
[latex]63[/latex] dimes, [latex]20[/latex] quarters
Solution
16 nickels, 12 dimes, 7 quarters
Exercises: Solve Ticket and Stamp Word Problems
Instructions: For questions 19-32, solve each ticket or stamp word problem.
Solution
[latex]30[/latex] child tickets, [latex]50[/latex] adult tickets
Solution
[latex]110[/latex] child tickets, [latex]50[/latex] adult tickets
Solution
[latex]34[/latex] general, [latex]61[/latex] youth
Solution
[latex]114[/latex] general, [latex]246[/latex] student
Solution
[latex]40[/latex] postcards, [latex]100[/latex] stamps
Solution
[latex]30[/latex] at [latex]$0.41[/latex], [latex]10[/latex] at [latex]$0.02[/latex]
Solution
[latex]15[/latex] [latex]$10[/latex] shares, [latex]5[/latex] [latex]$12[/latex] shares
Exercises: Solve Mixture Word Problems
Instructions: For questions 33-44, solve each mixture word problem.
Solution
[latex]5[/latex] liters champagne, [latex]10[/latex] liters orange juice
Solution
[latex]7.5[/latex] lbs Maui beans, [latex]17.5[/latex] Kona beans
Solution
[latex]800[/latex] at [latex]$1.50[/latex], [latex]200[/latex] at [latex]$9.00[/latex]
Solution
[latex]$8\text{,}000[/latex] at [latex]4\%[/latex], [latex]$17\text{,}000[/latex] at [latex]9\%[/latex]
Solution
[latex]$10\text{,}000[/latex] in CD, [latex]$30\text{,}000[/latex] in mutual fund
Solution
[latex]9.1\%[/latex]
44. Liam borrowed a total of [latex]$35\text{,}000[/latex] to pay for college. He pays his parents [latex]3\%[/latex] interest on the [latex]$8\text{,}000[/latex] he borrowed from them and pays the bank [latex]6.8\%[/latex] on the rest. What average interest rate does he pay on the total [latex]$35\text{,}000[/latex]? (Round your answer to the nearest tenth of a percent.)
Exercises: Solve Uniform Motion Applications
Instructions: For questions 45-66, solve.
Solution
Mason [latex]75[/latex] mph, train [latex]60[/latex] mph
Solution
express bus [latex]75[/latex] mph, local [latex]50[/latex] mph
Solution
Saul [latex]82[/latex] mph, Erwin [latex]74[/latex] mph
Solution
Helen [latex]67[/latex] mph, Anne [latex]53[/latex] mph
Solution
Aletheia [latex]2.4[/latex] mph, Elvira [latex]3[/latex] mph
54. DaMarcus and Fabian live [latex]23[/latex] miles apart and play soccer at a park between their homes. DaMarcus rode his bike for three-quarters of an hour and Fabian rode his bike for half an hour to get to the park. Fabian’s speed was six miles per hour faster than DaMarcus’ speed. Find the speed of both soccer players.
Solution
[latex]3[/latex] hours
57. Two buses leave Billings at the same time. The Seattle bus heads west on I-90 at a speed of [latex]73[/latex] miles per hour while the Chicago bus heads east at a speed of [latex]79[/latex] miles an hour. How many hours will it take them to be [latex]532[/latex] miles apart?
Solution
[latex]3.5[/latex] hours
Solution
walking [latex]3[/latex] mph, jogging [latex]4.5[/latex] mph
60. Julian rides his bike uphill for [latex]45[/latex] minutes, then turns around and rides back downhill. It takes him [latex]15[/latex] minutes to get back to where he started. His uphill speed is [latex]3.2[/latex] miles per hour slower than his downhill speed. Find Julian’s uphill and downhill speed.
Solution
upstream [latex]6[/latex] mph, downstream [latex]9[/latex] mph
Solution
skateboarding [latex]7.2[/latex] mph, walking [latex]2.9[/latex] mph
Solution
heavy traffic [latex]30[/latex] mph, light traffic [latex]70[/latex] mph
Exercises: Everyday Math
Instructions: For questions 67-70, answer the given everyday math word problems.
Solution
[latex]9[/latex] girls, [latex]3[/latex] adults
68. Laurie was completing the treasurer’s report for her son’s Boy Scout troop at the end of the school year. She didn’t remember how many boys had paid the [latex]$15[/latex] full-year registration fee and how many had paid the [latex]$10[/latex] partial-year fee. She knew that the number of boys who paid for a full-year was ten more than the number who paid for a partial-year. If [latex]$250[/latex] was collected for all the registrations, how many boys had paid the full-year fee and how many had paid the partial-year fee?
69. John left his house in Irvine at 8:35 am to drive to a meeting in Los Angeles, [latex]45[/latex] miles away. He arrived at the meeting at 9:50. At 3:30 pm, he left the meeting and drove home. He arrived home at 5:18.
a. What was his average speed on the drive from Irvine to Los Angeles?
b. What was his average speed on the drive from Los Angeles to Irvine?
c. What was the total time he spent driving to and from this meeting?
d. John drove a total of [latex]90[/latex] miles roundtrip. Find his average speed. (Round to the nearest tenth.)
Solution
a. [latex]36[/latex] mph
b. [latex]25[/latex] mph
c. [latex]3.05[/latex] hours
d. [latex]29.5[/latex] mph
70. Sarah wants to arrive at her friend’s wedding at 3:00. The distance from Sarah’s house to the wedding is [latex]95[/latex] miles. Based on usual traffic patterns, Sarah predicts she can drive the first [latex]15[/latex] miles at [latex]60[/latex] miles per hour, the next [latex]10[/latex] miles at [latex]30[/latex] miles per hour, and the remainder of the drive at [latex]70[/latex] miles per hour.
a. How long will it take Sarah to drive the first [latex]15[/latex] miles?
b. How long will it take Sarah to drive the next [latex]10[/latex] miles?
c. How long will it take Sarah to drive the rest of the trip?
d. What time should Sarah leave her house?
Exercises: Writing Exercises
Instructions: For questions 71-76, answer the given writing exercises.
Solution
Answers will vary.
Solution
Answers will vary.
74. What similarities and differences did you see between solving the coin problems and the ticket and stamp problems?
Solution
Answers will vary.
Mixture problems combine two or more items with different values together.

