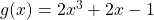Chapter 4.7: The Chain Rule
Learning Objectives
- State the chain rule for the composition of two functions.
- Apply the chain rule together with the power rule.
- Apply the chain rule and the product/quotient rules correctly in combination when both are necessary.
- Recognize the chain rule for a composition of three or more functions.
- Describe the proof of the chain rule.
We have seen the techniques for differentiating basic functions ( ![]() , etc.) as well as sums, differences, products, quotients, and constant multiples of these functions. However, these techniques do not allow us to differentiate compositions of functions, such as
, etc.) as well as sums, differences, products, quotients, and constant multiples of these functions. However, these techniques do not allow us to differentiate compositions of functions, such as ![]() or
or ![]() . In this section, we study the rule for finding the derivative of the composition of two or more functions.
. In this section, we study the rule for finding the derivative of the composition of two or more functions.
Deriving the Chain Rule
When we have a function that is a composition of two or more functions, we could use all of the techniques we have already learned to differentiate it. However, using all of those techniques to break down a function into simpler parts that we are able to differentiate can get cumbersome. Instead, we use the chain rule, which states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function times the derivative of the inner function.
To put this rule into context, let’s take a look at an example: ![]() . We can think of the derivative of this function with respect to
. We can think of the derivative of this function with respect to ![]() as the rate of change of
as the rate of change of ![]() relative to the change in
relative to the change in ![]() . Consequently, we want to know how
. Consequently, we want to know how ![]() changes as
changes as ![]() changes. We can think of this event as a chain reaction: As
changes. We can think of this event as a chain reaction: As ![]() changes,
changes, ![]() changes, which leads to a change in
changes, which leads to a change in ![]() . This chain reaction gives us hints as to what is involved in computing the derivative of
. This chain reaction gives us hints as to what is involved in computing the derivative of ![]() . First of all, a change in
. First of all, a change in ![]() forcing a change in
forcing a change in ![]() suggests that somehow the derivative of
suggests that somehow the derivative of ![]() is involved. In addition, the change in
is involved. In addition, the change in ![]() forcing a change in
forcing a change in ![]() suggests that the derivative of
suggests that the derivative of ![]() with respect to
with respect to ![]() , where
, where ![]() , is also part of the final derivative.
, is also part of the final derivative.
We can take a more formal look at the derivative of ![]() by setting up the limit that would give us the derivative at a specific value
by setting up the limit that would give us the derivative at a specific value ![]() in the domain of
in the domain of ![]() .
.
This expression does not seem particularly helpful; however, we can modify it by multiplying and dividing by the expression ![]() to obtain
to obtain
From the definition of the derivative, we can see that the second factor is the derivative of ![]() at
at ![]() . That is,
. That is,
However, it might be a little more challenging to recognize that the first term is also a derivative. We can see this by letting ![]() and observing that as
and observing that as ![]() :
:
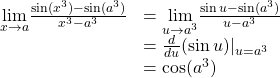
Thus, ![]() .
.
In other words, if ![]() , then
, then ![]() . Thus, if we think of
. Thus, if we think of ![]() as the composition
as the composition ![]() where
where ![]() and
and ![]() , then the derivative of
, then the derivative of ![]() is the product of the derivative of
is the product of the derivative of ![]() and the derivative of the function
and the derivative of the function ![]() evaluated at the function
evaluated at the function ![]() . At this point, we anticipate that for
. At this point, we anticipate that for ![]() , it is quite likely that
, it is quite likely that ![]() . As we determined above, this is the case for
. As we determined above, this is the case for ![]() .
.
Now that we have derived a special case of the chain rule, we state the general case and then apply it in a general form to other composite functions. An informal proof is provided at the end of the section.
Rule: The Chain Rule
Let ![]() and
and ![]() be functions. For all
be functions. For all ![]() in the domain of
in the domain of ![]() for which
for which ![]() is differentiable at
is differentiable at ![]() and
and ![]() is differentiable at
is differentiable at ![]() , the derivative of the composite function
, the derivative of the composite function
is given by
Alternatively, if ![]() is a function of
is a function of ![]() , and
, and ![]() is a function of
is a function of ![]() , then
, then
Watch an animation of the chain rule.
Problem-Solving Strategy: Applying the Chain Rule
- To differentiate
 , begin by identifying
, begin by identifying 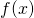 and
and 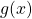 .
. - Find
 and evaluate it at
and evaluate it at 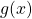 to obtain
to obtain 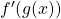 .
. - Find
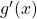 .
. - Write
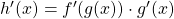 .
.
Note: When applying the chain rule to the composition of two or more functions, keep in mind that we work our way from the outside function in. It is also useful to remember that the derivative of the composition of two functions can be thought of as having two parts; the derivative of the composition of three functions has three parts; and so on. Also, remember that we never evaluate a derivative at a derivative.
The Chain and Power Rules Combined
We can now apply the chain rule to composite functions, but note that we often need to use it with other rules. For example, to find derivatives of functions of the form ![]() , we need to use the chain rule combined with the power rule. To do so, we can think of
, we need to use the chain rule combined with the power rule. To do so, we can think of ![]() as
as ![]() where
where ![]() . Then
. Then ![]() . Thus,
. Thus, ![]() . This leads us to the derivative of a power function using the chain rule,
. This leads us to the derivative of a power function using the chain rule,
Rule: Power Rule for Composition of Functions
For all values of ![]() for which the derivative is defined, if
for which the derivative is defined, if
Then
Using the Chain and Power Rules
Find the derivative of ![]() .
.
Solution
First, rewrite ![]() .
.
Applying the power rule with ![]() , we have
, we have
Rewriting back to the original form gives us
Find the derivative of ![]() .
.
Solution
![]()
Using the Chain and Power Rules with a Trigonometric Function
Find the derivative of ![]() .
.
Solution
First recall that ![]() , so we can rewrite
, so we can rewrite ![]() as
as ![]() .
.
Applying the power rule with ![]() , we obtain
, we obtain
Finding the Equation of a Tangent Line
Find the equation of a line tangent to the graph of ![]() at
at ![]() .
.
Solution
Because we are finding an equation of a line, we need a point. The ![]() -coordinate of the point is 2. To find the
-coordinate of the point is 2. To find the ![]() -coordinate, substitute 2 into
-coordinate, substitute 2 into ![]() . Since
. Since ![]() , the point is
, the point is ![]() .
.
For the slope, we need ![]() . To find
. To find ![]() , first we rewrite
, first we rewrite ![]() and apply the power rule to obtain
and apply the power rule to obtain
By substituting, we have ![]() . Therefore, the line has equation
. Therefore, the line has equation ![]() . Rewriting, the equation of the line is
. Rewriting, the equation of the line is ![]() .
.
Find the equation of the line tangent to the graph of ![]() at
at ![]() .
.
Solution
![]()
Hint
Use the preceding example as a guide.
Combining the Chain Rule with Other Rules
Now that we can combine the chain rule and the power rule, we examine how to combine the chain rule with the other rules we have learned. In particular, we can use it with the formulas for the derivatives of trigonometric functions or with the product rule.
Using the Chain Rule on a General Cosine Function
Find the derivative of ![]() .
.
Solution
Think of ![]() as
as ![]() where
where ![]() . Since
. Since ![]() we have
we have ![]() . Then we do the following calculation.
. Then we do the following calculation.
Thus, the derivative of ![]() is given by
is given by ![]() .
.
In the following example we apply the rule that we have just derived.
Using the Chain Rule on a Cosine Function
Find the derivative of ![]() .
.
Show Solution
Let ![]() . Then
. Then ![]() .
.
Using the result from the previous example, ![]()
Using the Chain Rule on Another Trigonometric Function
Find the derivative of ![]() .
.
Solution
Apply the chain rule to ![]() to obtain
to obtain
In this problem, ![]() , so we have
, so we have ![]() . Therefore, we obtain
. Therefore, we obtain
Find the derivative of ![]() .
.
Show Solution
![]()
Hint
Apply the chain rule to ![]() first and then use
first and then use ![]() .
.
At this point we provide a list of derivative formulas that may be obtained by applying the chain rule in conjunction with the formulas for derivatives of trigonometric functions. Their derivations are similar to those used in (Figure) and (Figure). For convenience, formulas are also given in Leibniz’s notation, which some students find easier to remember. (We discuss the chain rule using Leibniz’s notation at the end of this section.) It is not absolutely necessary to memorize these as separate formulas as they are all applications of the chain rule to previously learned formulas.
Using the Chain Rule with Trigonometric Functions
For all values of ![]() for which the derivative is defined,
for which the derivative is defined,

Combining the Chain Rule with the Product Rule
Find the derivative of ![]() .
.
Solution
First apply the product rule, then apply the chain rule to each term of the product.
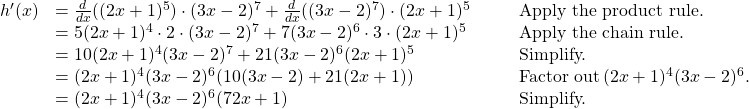
Find the derivative of ![]() .
.
Solution
![]()
Hint
Start out by applying the quotient rule. Remember to use the chain rule to differentiate the denominator.
Composites of Three or More Functions
We can now combine the chain rule with other rules for differentiating functions, but when we are differentiating the composition of three or more functions, we need to apply the chain rule more than once. If we look at this situation in general terms, we can generate a formula, but we do not need to remember it, as we can simply apply the chain rule multiple times.
In general terms, first we let
Then, applying the chain rule once we obtain
Applying the chain rule again, we obtain
Rule: Chain Rule for a Composition of Three Functions
For all values of ![]() for which the function is differentiable, if
for which the function is differentiable, if
then
In other words, we are applying the chain rule twice.
Notice that the derivative of the composition of three functions has three parts. (Similarly, the derivative of the composition of four functions has four parts, and so on.) Also, remember, we always work from the outside in, taking one derivative at a time.
Differentiating a Composite of Three Functions
Find the derivative of ![]() .
.
Solution
First, rewrite ![]() as
as
Then apply the chain rule several times.
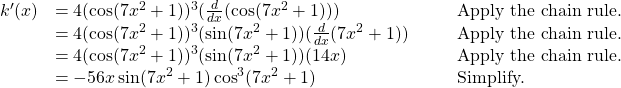
Using the Chain Rule in a Velocity Problem
A particle moves along a coordinate axis. Its position at time ![]() is given by
is given by ![]() . What is the velocity of the particle at time
. What is the velocity of the particle at time ![]() ?
?
Solution
To find ![]() , the velocity of the particle at time
, the velocity of the particle at time ![]() , we must differentiate
, we must differentiate ![]() . Thus,
. Thus,
Substituting ![]() into
into ![]() , we obtain
, we obtain ![]() .
.
A particle moves along a coordinate axis. Its position at time ![]() is given by
is given by ![]() . Find its acceleration at time
. Find its acceleration at time ![]() .
.
Solution
![]()
Hint
Acceleration is the second derivative of position.
Proof of the Chain Rule
At this point, we present a very informal proof of the chain rule. For simplicity’s sake we ignore certain issues: For example, we assume that ![]() for
for ![]() in some open interval containing
in some open interval containing ![]() . We begin by applying the limit definition of the derivative to the function
. We begin by applying the limit definition of the derivative to the function ![]() to obtain
to obtain ![]() :
:
Rewriting, we obtain
Although it is clear that
it is not obvious that
To see that this is true, first recall that since ![]() is differentiable at
is differentiable at ![]() is also continuous at
is also continuous at ![]() . Thus,
. Thus,
Next, make the substitution ![]() and
and ![]() and use change of variables in the limit to obtain
and use change of variables in the limit to obtain
Finally,
Using the Chain Rule with Functional Values
Let ![]() . If
. If ![]() , and
, and ![]() , find
, find ![]() .
.
Solution
Use the chain rule, then substitute.

The Chain Rule Using Leibniz’s Notation
As with other derivatives that we have seen, we can express the chain rule using Leibniz’s notation. This notation for the chain rule is used heavily in physics applications.
For ![]() , let
, let ![]() and
and ![]() . Thus,
. Thus,
Consequently,
Rule: Chain Rule Using Leibniz’s Notation
If ![]() is a function of
is a function of ![]() , and
, and ![]() is a function of
is a function of ![]() , then
, then
Taking a Derivative Using Leibniz’s Notation, Example 1
Find the derivative of ![]() .
.
Solution
First, let ![]() . Thus,
. Thus, ![]() . Next, find
. Next, find ![]() and
and ![]() . Using the quotient rule,
. Using the quotient rule,
and
Finally, we put it all together.

It is important to remember that, when using the Leibniz form of the chain rule, the final answer must be expressed entirely in terms of the original variable given in the problem.
Taking a Derivative Using Leibniz’s Notation, Example 2
Find the derivative of ![]() .
.
Solution
First, let ![]() . Then
. Then ![]() . Next, find
. Next, find ![]() and
and ![]() :
:
Finally, we put it all together.

Use Leibniz’s notation to find the derivative of ![]() . Make sure that the final answer is expressed entirely in terms of the variable
. Make sure that the final answer is expressed entirely in terms of the variable ![]() .
.
Solution
![]()
Hint
Let ![]() .
.
Key Concepts
- The chain rule allows us to differentiate compositions of two or more functions. It states that for
 ,
,
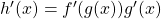 .
.In Leibniz’s notation this rule takes the form
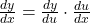 .
. - We can use the chain rule with other rules that we have learned, and we can derive formulas for some of them.
- The chain rule combines with the power rule to form a new rule:
If
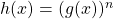 , then
, then 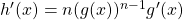 .
. - When applied to the composition of three functions, the chain rule can be expressed as follows: If
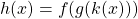 , then
, then  .
.
Key Equations
- The chain rule
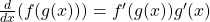
- The power rule for functions
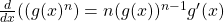
For the following exercises, given ![]() and
and ![]() , find
, find ![]() by using Leibniz’s notation for the chain rule:
by using Leibniz’s notation for the chain rule: ![]() .
.
1. ![]()
2. ![]()
Solution
![]()
3. ![]()
4. ![]()
Solution
![]()
5. ![]()
6. ![]()
Solution
![]()
For each of the following exercises,
- decompose each function in the form
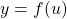 and
and 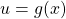 , and
, and - find
 as a function of
as a function of  .
.
7. ![]()
8. ![]()
Solution
a. ![]() ;
;
b. ![]()
9. ![]()
10. ![]()
Solution
a. ![]() ;
;
b. ![]()
11. ![]()
12. ![]()
Solution
a. ![]() ;
;
b. ![]()
13. ![]()
14. ![]()
Solution
a. ![]() ;
;
b. ![]()
For the following exercises, find ![]() for each function.
for each function.
15. ![]()
16. ![]()
Solution
![]()
17. ![]()
18. ![]()
Solution
![]()
19. ![]()
20. ![]()
Solution
![]()
21. ![]()
22. ![]()
Solution
![]()
23. ![]()
24. ![]()
Solution
![]()
25. Let ![]() and suppose that
and suppose that ![]() and
and ![]() for
for ![]() . Find
. Find ![]() .
.
26. Let ![]() and suppose that
and suppose that ![]() and
and ![]() when
when ![]() . Find
. Find ![]()
Solution
![]()
27. Let ![]() and
and ![]() . If
. If ![]() and
and ![]() when
when ![]() , find
, find ![]() .
.
28. [T] Find the equation of the tangent line to ![]() at the origin. Use a calculator to graph the function and the tangent line together.
at the origin. Use a calculator to graph the function and the tangent line together.
Solution
![]()
29. [T] Find the equation of the tangent line to ![]() at the point
at the point ![]() . Use a calculator to graph the function and the tangent line together.
. Use a calculator to graph the function and the tangent line together.
30. Find the ![]() -coordinates at which the tangent line to
-coordinates at which the tangent line to ![]() is horizontal.
is horizontal.
Solution
![]()
31. [T] Find an equation of the line that is normal to ![]() at the point
at the point ![]() . Use a calculator to graph the function and the normal line together.
. Use a calculator to graph the function and the normal line together.
For the following exercises, use the information in the following table to find ![]() at the given value for
at the given value for ![]() .
.
| |
|
|
|
|
|---|---|---|---|---|
| 0 | 2 | 5 | 0 | 2 |
| 1 | 1 | −2 | 3 | 0 |
| 2 | 4 | 4 | 1 | −1 |
| 3 | 3 | −3 | 2 | 3 |
32. ![]()
Solution
10
33. ![]()
34. ![]()
Solution
![]()
35. ![]()
36. ![]()
Solution
-4
37. ![]()
38. ![]()
Solution
-12
39. ![]()
40. [T] The position function of a freight train is given by ![]() , with
, with ![]() in meters and
in meters and ![]() in seconds. At time
in seconds. At time ![]() s, find the train’s
s, find the train’s
- velocity and
- acceleration.
- Using a. and b. is the train speeding up or slowing down?
Solution
a. ![]() m/s;
m/s;
b. ![]() ;
;
c. The train is slowing down since velocity and acceleration have opposite signs.
41. [T] A mass hanging from a vertical spring is in simple harmonic motion as given by the following position function, where ![]() is measured in seconds and
is measured in seconds and ![]() is in inches:
is in inches:
![]() .
.
- Determine the position of the spring at
 s.
s. - Find the velocity of the spring at
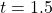 s.
s.
42. [T] The total cost to produce ![]() boxes of Thin Mint Girl Scout cookies is
boxes of Thin Mint Girl Scout cookies is ![]() dollars, where
dollars, where ![]() . In
. In ![]() weeks production is estimated to be
weeks production is estimated to be ![]() boxes.
boxes.
- Find the marginal cost
 .
. - Use Leibniz’s notation for the chain rule,
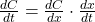 , to find the rate with respect to time
, to find the rate with respect to time 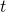 that the cost is changing.
that the cost is changing. - Use b. to determine how fast costs are increasing when
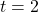 weeks. Include units with the answer.
weeks. Include units with the answer.
Solution
a. ![]()
b. ![]()
c. Approximately $90,300 per week
43. [T] The formula for the area of a circle is ![]() , where
, where ![]() is the radius of the circle. Suppose a circle is expanding, meaning that both the area
is the radius of the circle. Suppose a circle is expanding, meaning that both the area ![]() and the radius
and the radius ![]() (in inches) are expanding.
(in inches) are expanding.
- Suppose
 where
where 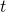 is time in seconds. Use the chain rule
is time in seconds. Use the chain rule 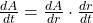 to find the rate at which the area is expanding.
to find the rate at which the area is expanding. - Use a. to find the rate at which the area is expanding at
 s.
s.
44. [T] The formula for the volume of a sphere is ![]() , where
, where ![]() (in feet) is the radius of the sphere. Suppose a spherical snowball is melting in the sun.
(in feet) is the radius of the sphere. Suppose a spherical snowball is melting in the sun.
- Suppose
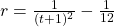 where
where 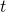 is time in minutes. Use the chain rule
is time in minutes. Use the chain rule 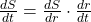 to find the rate at which the snowball is melting.
to find the rate at which the snowball is melting. - Use a. to find the rate at which the volume is changing at
 min.
min.
Solution
a. ![]()
b. The volume is decreasing at a rate of ![]() .
.
45. [T] The daily temperature in degrees Fahrenheit of Phoenix in the summer can be modeled by the function ![]() , where
, where ![]() is hours after midnight. Find the rate at which the temperature is changing at 4 p.m.
is hours after midnight. Find the rate at which the temperature is changing at 4 p.m.
46. [T] The depth (in feet) of water at a dock changes with the rise and fall of tides. The depth is modeled by the function ![]() , where
, where ![]() is the number of hours after midnight. Find the rate at which the depth is changing at 6 a.m.
is the number of hours after midnight. Find the rate at which the depth is changing at 6 a.m.
Solution
![]() ft/hr
ft/hr
Glossary
- chain rule
- the chain rule defines the derivative of a composite function as the derivative of the outer function evaluated at the inner function times the derivative of the inner function


Hint
Use (Figure) with