Chapter 1.9: Solving Systems with Inverses
Learning Objectives
In this section, you will:
- Find the inverse of a matrix.
- Solve a system of linear equations using an inverse matrix.
Nancy plans to invest $10,500 into two different bonds to spread out her risk. The first bond has an annual return of 10%, and the second bond has an annual return of 6%. In order to receive an 8.5% return from the two bonds, how much should Nancy invest in each bond? What is the best method to solve this problem?
There are several ways we can solve this problem. As we have seen in previous sections, systems of equations and matrices are useful in solving real-world problems involving finance. After studying this section, we will have the tools to solve the bond problem using the inverse of a matrix.
Finding the Inverse of a Matrix
We know that the multiplicative inverse of a real number ![]() is
is ![]() and
and ![]() For example,
For example, ![]() and
and ![]() The multiplicative inverse of a matrix is similar in concept, except that the product of matrix
The multiplicative inverse of a matrix is similar in concept, except that the product of matrix ![]() and its inverse
and its inverse ![]() equals the identity matrix. The identity matrix is a square matrix containing ones down the main diagonal and zeros everywhere else. We identify identity matrices by
equals the identity matrix. The identity matrix is a square matrix containing ones down the main diagonal and zeros everywhere else. We identify identity matrices by ![]() where
where ![]() represents the dimension of the matrix. (Figure) and (Figure) are the identity matrices for a
represents the dimension of the matrix. (Figure) and (Figure) are the identity matrices for a ![]() matrix and a
matrix and a ![]() matrix, respectively.
matrix, respectively.
![Rendered by QuickLaTeX.com {I}_{3}=\left[\begin{array}{rrrrr}\hfill 1& \hfill & \hfill 0& \hfill & \hfill 0\\ \hfill 0& \hfill & \hfill 1& \hfill & \hfill 0\\ \hfill 0& \hfill & \hfill 0& \hfill & \hfill 1\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-1286e75343913af279a69f64da6387de_l3.png)
The identity matrix acts as a 1 in matrix algebra. For example, ![]()
A matrix that has a multiplicative inverse has the properties
A matrix that has a multiplicative inverse is called an invertible matrix. Only a square matrix may have a multiplicative inverse, as the reversibility, ![]() is a requirement. Not all square matrices have an inverse, but if
is a requirement. Not all square matrices have an inverse, but if ![]() is invertible, then
is invertible, then ![]() is unique. We will look at two methods for finding the inverse of a
is unique. We will look at two methods for finding the inverse of a ![]() matrix and a third method that can be used on both
matrix and a third method that can be used on both ![]() and
and ![]() matrices.
matrices.
The Identity Matrix and Multiplicative Inverse
The identity matrix, ![]() is a square matrix containing ones down the main diagonal and zeros everywhere else.
is a square matrix containing ones down the main diagonal and zeros everywhere else.
![Rendered by QuickLaTeX.com \begin{array}{l}\hfill \\ \begin{array}{l}\begin{array}{l}\hfill \\ {I}_{2}=\left[\begin{array}{rr}\hfill 1& \hfill 0\\ \hfill 0& \hfill 1\end{array}\right]\begin{array}{cccc}& & & \end{array}{I}_{3}=\left[\begin{array}{rrr}\hfill 1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 1& \hfill 0\\ \hfill 0& \hfill 0& \hfill 1\end{array}\right]\hfill \end{array}\hfill \\ \text{2×2}\,\,\,\,\,\,\,\,\,\,\,\text{ 3×3}\hfill \end{array}\hfill \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-d2f6bf2496abf9c4093505afd1dc4c7f_l3.png)
If ![]() is an
is an ![]()
matrix and ![]() is an
is an ![]()
matrix such that ![]() then
then ![]() the multiplicative inverse of a matrix
the multiplicative inverse of a matrix ![]()
Showing That the Identity Matrix Acts as a 1
Given matrix A, show that ![]()
Show Solution
Use matrix multiplication to show that the product of ![]() and the identity is equal to the product of the identity and A.
and the identity is equal to the product of the identity and A.
![Rendered by QuickLaTeX.com AI=\left[\begin{array}{rrr}\hfill 3& \hfill & \hfill 4\\ \hfill -2& \hfill & \hfill 5\end{array}\right]\,\,\begin{array}{r}\hfill \end{array}\,\,\left[\begin{array}{rrr}\hfill 1& \hfill & \hfill 0\\ \hfill 0& \hfill & \hfill 1\end{array}\right]=\left[\begin{array}{rrrr}\hfill 3\cdot 1+4\cdot 0& \hfill & \hfill & \hfill 3\cdot 0+4\cdot 1\\ \hfill -2\cdot 1+5\cdot 0& \hfill & \hfill & \hfill -2\cdot 0+5\cdot 1\end{array}\right]=\left[\begin{array}{rrr}\hfill 3& \hfill & \hfill 4\\ \hfill -2& \hfill & \hfill 5\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-6ebf1d357135732eb0d6526459cf40ab_l3.png)
![Rendered by QuickLaTeX.com AI=\left[\begin{array}{rrr}\hfill 1& \hfill & \hfill 0\\ \hfill 0& \hfill & \hfill 1\end{array}\right]\,\,\begin{array}{r}\hfill \end{array}\,\,\left[\begin{array}{rrr}\hfill 3& \hfill & \hfill 4\\ \hfill -2& \hfill & \hfill 5\end{array}\right]=\left[\begin{array}{rrrr}\hfill 1\cdot 3+0\cdot \left(-2\right)& \hfill & \hfill & \hfill 1\cdot 4+0\cdot 5\\ \hfill 0\cdot 3+1\cdot \left(-2\right)& \hfill & \hfill & \hfill 0\cdot 4+1\cdot 5\end{array}\right]=\left[\begin{array}{rrr}\hfill 3& \hfill & \hfill 4\\ \hfill -2& \hfill & \hfill 5\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-5d3db6180ab1d9fe4ea6766b56b584db_l3.png)
How To
Given two matrices, show that one is the multiplicative inverse of the other.
- Given matrix
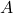 of order
of order 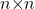 and matrix
and matrix 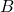 of order
of order 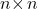 multiply
multiply 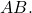
- If
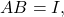 then find the product
then find the product 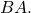 If
If 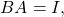 then
then 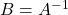 and
and 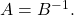
Showing That Matrix A Is the Multiplicative Inverse of Matrix B
Show that the given matrices are multiplicative inverses of each other.
Show Solution
Multiply ![]() and
and ![]() If both products equal the identity, then the two matrices are inverses of each other.
If both products equal the identity, then the two matrices are inverses of each other.
![Rendered by QuickLaTeX.com \begin{array}{l}AB=\left[\begin{array}{rrr}\hfill 1& \hfill & \hfill 5\\ \hfill -2& \hfill & \hfill -9\end{array}\right]\text{·}\left[\begin{array}{rrr}\hfill -9& \hfill & \hfill -5\\ \hfill 2& \hfill & \hfill 1\end{array}\right]\hfill \\ \,\,\,\,\,\,\,\,=\left[\begin{array}{rrr}\hfill 1\left(-9\right)+5\left(2\right)& \hfill & \hfill 1\left(-5\right)+5\left(1\right)\\ \hfill -2\left(-9\right)-9\left(2\right)& \hfill & \hfill -2\left(-5\right)-9\left(1\right)\end{array}\right]\hfill \\ \,\,\,\,\,\,\,\,=\left[\begin{array}{ccc}1& & 0\\ 0& & 1\end{array}\right]\hfill \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-ad6f548296bab8cb8ca26d6571167220_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{l}BA=\left[\begin{array}{rrr}\hfill -9& \hfill & \hfill -5\\ \hfill 2& \hfill & \hfill 1\end{array}\right]\text{·}\left[\begin{array}{rrr}\hfill 1& \hfill & \hfill 5\\ \hfill -2& \hfill & \hfill -9\end{array}\right]\hfill \\ \,\,\,\,\,\,\,\,=\left[\begin{array}{rrr}\hfill -9\left(1\right)-5\left(-2\right)& \hfill & \hfill -9\left(5\right)-5\left(-9\right)\\ \hfill 2\left(1\right)+1\left(-2\right)& \hfill & \hfill 2\left(-5\right)+1\left(-9\right)\end{array}\right]\hfill \\ \,\,\,\,\,\,\,\,=\left[\begin{array}{ccc}1& & 0\\ 0& & 1\end{array}\right]\hfill \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-0cd1f8eddb90f3d6093caf00c2c8ed40_l3.png)
![]() and
and ![]() are inverses of each other.
are inverses of each other.
Try It
Show that the following two matrices are inverses of each other.
Show Solution
![Rendered by QuickLaTeX.com \begin{array}{l}AB=\left[\begin{array}{rrr}\hfill 1& \hfill & \hfill 4\\ \hfill -1& \hfill & \hfill -3\end{array}\right]\begin{array}{r}\hfill \end{array}\left[\begin{array}{rrr}\hfill -3& \hfill & \hfill -4\\ \hfill 1& \hfill & \hfill 1\end{array}\right]=\left[\begin{array}{rrr}\hfill 1\left(-3\right)+4\left(1\right)& \hfill & \hfill 1\left(-4\right)+4\left(1\right)\\ \hfill -1\left(-3\right)+-3\left(1\right)& \hfill & \hfill -1\left(-4\right)+-3\left(1\right)\end{array}\right]=\left[\begin{array}{rrr}\hfill 1& \hfill & \hfill 0\\ \hfill 0& \hfill & \hfill 1\end{array}\right]\hfill \\ BA=\left[\begin{array}{rrr}\hfill -3& \hfill & \hfill -4\\ \hfill 1& \hfill & \hfill 1\end{array}\right]\begin{array}{r}\hfill \end{array}\left[\begin{array}{rrr}\hfill 1& \hfill & \hfill 4\\ \hfill -1& \hfill & \hfill -3\end{array}\right]=\left[\begin{array}{rrr}\hfill -3\left(1\right)+-4\left(-1\right)& \hfill & \hfill -3\left(4\right)+-4\left(-3\right)\\ \hfill 1\left(1\right)+1\left(-1\right)& \hfill & \hfill 1\left(4\right)+1\left(-3\right)\end{array}\right]=\left[\begin{array}{rrr}\hfill 1& \hfill & \hfill 0\\ \hfill 0& \hfill & \hfill 1\end{array}\right]\hfill \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-5f3eeb73958047083db6201a60bfd9fe_l3.png)
Finding the Multiplicative Inverse Using Matrix Multiplication
We can now determine whether two matrices are inverses, but how would we find the inverse of a given matrix? Since we know that the product of a matrix and its inverse is the identity matrix, we can find the inverse of a matrix by setting up an equation using matrix multiplication.
Finding the Multiplicative Inverse Using Matrix Multiplication
Use matrix multiplication to find the inverse of the given matrix.
Show Solution
For this method, we multiply ![]() by a matrix containing unknown constants and set it equal to the identity.
by a matrix containing unknown constants and set it equal to the identity.
Find the product of the two matrices on the left side of the equal sign.
Next, set up a system of equations with the entry in row 1, column 1 of the new matrix equal to the first entry of the identity, 1. Set the entry in row 2, column 1 of the new matrix equal to the corresponding entry of the identity, which is 0.
Using row operations, multiply and add as follows: ![]() Add the equations, and solve for
Add the equations, and solve for ![]()
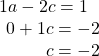
Back-substitute to solve for ![]()
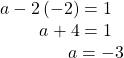
Write another system of equations setting the entry in row 1, column 2 of the new matrix equal to the corresponding entry of the identity, 0. Set the entry in row 2, column 2 equal to the corresponding entry of the identity.
Using row operations, multiply and add as follows: ![]() Add the two equations and solve for
Add the two equations and solve for ![]()
Once more, back-substitute and solve for ![]()
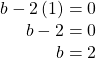
Finding the Multiplicative Inverse by Augmenting with the Identity
Another way to find the multiplicative inverse is by augmenting with the identity. When matrix ![]() is transformed into
is transformed into ![]() the augmented matrix
the augmented matrix ![]() transforms into
transforms into ![]()
For example, given
augment ![]() with the identity
with the identity
Perform row operations with the goal of turning ![]() into the identity.
into the identity.
- Switch row 1 and row 2.
![Rendered by QuickLaTeX.com \left[\begin{array}{rr}\hfill 5& \hfill 3\\ \hfill 2& \hfill 1\end{array}\text{ }|\text{ }\begin{array}{rr}\hfill 0& \hfill 1\\ \hfill 1& \hfill 0\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-6e1955ed5f0763105fb0dde8b3144b95_l3.png)
- Multiply row 2 by
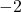 and add to row 1.
and add to row 1.
![Rendered by QuickLaTeX.com \left[\begin{array}{rr}\hfill 1& \hfill 1\\ \hfill 2& \hfill 1\end{array}\text{ }|\text{ }\begin{array}{rr}\hfill -2& \hfill 1\\ \hfill 1& \hfill 0\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-89d9a6f208d58bc78e512404031b20c2_l3.png)
- Multiply row 1 by
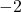 and add to row 2.
and add to row 2.
![Rendered by QuickLaTeX.com \left[\begin{array}{rr}\hfill 1& \hfill 1\\ \hfill 0& \hfill -1\end{array}\text{ }|\text{ }\begin{array}{rr}\hfill -2& \hfill 1\\ \hfill 5& \hfill -2\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-6e4d396911e509cd102c45721fdf3597_l3.png)
- Add row 2 to row 1.
![Rendered by QuickLaTeX.com \left[\begin{array}{rr}\hfill 1& \hfill 0\\ \hfill 0& \hfill -1\end{array}\text{ }|\text{ }\begin{array}{rr}\hfill 3& \hfill -1\\ \hfill 5& \hfill -2\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-09961d29cd45dbe0bb5819d0da6fca9e_l3.png)
- Multiply row 2 by
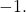
![Rendered by QuickLaTeX.com \left[\begin{array}{rr}\hfill 1& \hfill 0\\ \hfill 0& \hfill 1\end{array}\text{ }|\text{ }\begin{array}{rr}\hfill 3& \hfill -1\\ \hfill -5& \hfill 2\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-cb861386935db6c0fda14d75522a2087_l3.png)
The matrix we have found is ![]()
Finding the Multiplicative Inverse of 2×2 Matrices Using a Formula
When we need to find the multiplicative inverse of a ![]() matrix, we can use a special formula instead of using matrix multiplication or augmenting with the identity.
matrix, we can use a special formula instead of using matrix multiplication or augmenting with the identity.
If ![]() is a
is a ![]() matrix, such as
matrix, such as
the multiplicative inverse of ![]() is given by the formula
is given by the formula
where ![]() If
If ![]() then
then ![]() has no inverse.
has no inverse.
Using the Formula to Find the Multiplicative Inverse of Matrix A
Use the formula to find the multiplicative inverse of
Show Solution
Using the formula, we have
![Rendered by QuickLaTeX.com \begin{array}{l}{A}^{-1}=\frac{1}{\left(1\right)\left(-3\right)-\left(-2\right)\left(2\right)}\left[\begin{array}{cc}-3& 2\\ -2& 1\end{array}\right]\hfill \\ \,\,\,\,\,\,\,\,\,\,=\frac{1}{-3+4}\left[\begin{array}{cc}-3& 2\\ -2& 1\end{array}\right]\hfill \\ \,\,\,\,\,\,\,\,\,\,=\left[\begin{array}{cc}-3& 2\\ -2& 1\end{array}\right]\hfill \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-64e76123b53499182c10c1e456ba716c_l3.png)
Analysis
We can check that our formula works by using one of the other methods to calculate the inverse. Let’s augment ![]() with the identity.
with the identity.
Perform row operations with the goal of turning ![]() into the identity.
into the identity.
- Multiply row 1 by
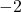 and add to row 2.
and add to row 2.
![Rendered by QuickLaTeX.com \left[\begin{array}{cc}1& -2\\ 0& 1\end{array}\,\,\,|\,\,\begin{array}{cc}1& 0\\ -2& 1\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-d6851a80be476b0ac5fe63e26e8cdd9b_l3.png)
- Multiply row 1 by 2 and add to row 1.
![Rendered by QuickLaTeX.com \left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\,\,\,|\,\,\begin{array}{cc}-3& 2\\ -2& 1\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-53c4856e9cec6c2948e116f69815d2f2_l3.png)
So, we have verified our original solution.
Try It
Use the formula to find the inverse of matrix ![]() Verify your answer by augmenting with the identity matrix.
Verify your answer by augmenting with the identity matrix.
Show Solution
![]()
Finding the Inverse of the Matrix, If It Exists
Find the inverse, if it exists, of the given matrix.
Show Solution
We will use the method of augmenting with the identity.
- Switch row 1 and row 2.
![Rendered by QuickLaTeX.com \left[\begin{array}{cc}1& 3\\ 3& 6\,\text{}\end{array}\text{}\,\,\text{}\text{}|\,\,\,\begin{array}{cc}0& 1\\ 1& 0\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-a6cfb1fb765e9471bb8ed2a52d515489_l3.png)
- Multiply row 1 by −3 and add it to row 2.
![Rendered by QuickLaTeX.com \left[\begin{array}{cc}1& 2\\ 0& 0\end{array}\,\,\,|\,\,\,\begin{array}{cc}1& 0\\ -3& 1\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-c80fa0330431f96d25ec3c82d74d4780_l3.png)
- There is nothing further we can do. The zeros in row 2 indicate that this matrix has no inverse.
Finding the Multiplicative Inverse of 3×3 Matrices
Unfortunately, we do not have a formula similar to the one for a ![]() matrix to find the inverse of a
matrix to find the inverse of a ![]() matrix. Instead, we will augment the original matrix with the identity matrix and use row operations to obtain the inverse.
matrix. Instead, we will augment the original matrix with the identity matrix and use row operations to obtain the inverse.
Given a ![]()
matrix
![Rendered by QuickLaTeX.com A=\left[\begin{array}{ccc}2& 3& 1\\ 3& 3& 1\\ 2& 4& 1\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-a07cde26208c1603aa90d4bb807a285d_l3.png)
augment ![]() with the identity matrix
with the identity matrix
![Rendered by QuickLaTeX.com A|I=\left[\begin{array}{ccc}2& 3& 1\\ 3& 3& 1\\ 2& 4& 1\end{array}\text{ }|\text{ }\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-b134ae30828ccfef66f47b680749658e_l3.png)
To begin, we write the augmented matrix with the identity on the right and ![]() on the left. Performing elementary row operations so that the identity matrix appears on the left, we will obtain the inverse matrix on the right. We will find the inverse of this matrix in the next example.
on the left. Performing elementary row operations so that the identity matrix appears on the left, we will obtain the inverse matrix on the right. We will find the inverse of this matrix in the next example.
How To
Given a ![]() matrix, find the inverse
matrix, find the inverse
- Write the original matrix augmented with the identity matrix on the right.
- Use elementary row operations so that the identity appears on the left.
- What is obtained on the right is the inverse of the original matrix.
- Use matrix multiplication to show that
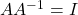 and
and 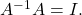
Finding the Inverse of a 3 × 3 Matrix
Given the ![]() matrix
matrix ![]() find the inverse.
find the inverse.
![Rendered by QuickLaTeX.com A=\left[\begin{array}{ccc}2& 3& 1\\ 3& 3& 1\\ 2& 4& 1\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-a07cde26208c1603aa90d4bb807a285d_l3.png)
Show Solution
Augment ![]() with the identity matrix, and then begin row operations until the identity matrix replaces
with the identity matrix, and then begin row operations until the identity matrix replaces ![]() The matrix on the right will be the inverse of
The matrix on the right will be the inverse of ![]()
![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}2& 3& 1\\ 3& 3& 1\\ 2& 4& 1\end{array}\,\,\,|\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ \,\,0& 0& 1\end{array}\right]\stackrel{\text{Interchange }{R}_{2}\,\text{and }{R}_{1}}{\to }\left[\begin{array}{ccc}3& 3& 1\\ 2& 3& 1\\ 2& 4& 1\end{array}\,\,\,|\begin{array}{ccc}0& 1& 0\\ 1& 0& 0\\ \,\,\,0& 0& 1\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-0ba228f2cb241356ac0ae5a66afc8a53_l3.png)
![Rendered by QuickLaTeX.com -{R}_{2}+{R}_{1}={R}_{1}\to \left[\begin{array}{ccc}1& 0& 0\\ 2& 3& 1\\ 2& 4& 1\end{array}\,\,|\,\,\begin{array}{rrr}\hfill -1& \hfill 1& \hfill 0\\ \hfill 1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 1\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-51a339ca782f41e6c21c86b9639674d2_l3.png)
![Rendered by QuickLaTeX.com -{R}_{2}+{R}_{3}={R}_{3}\to \left[\begin{array}{ccc}1& 0& 0\\ 2& 3& 1\\ 0& 1& 0\end{array}\,\,|\,\,\begin{array}{rrr}\hfill -1& \hfill 1& \hfill 0\\ \hfill 1& \hfill 0& \hfill 0\\ \hfill -1& \hfill 0& \hfill 1\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-05600632cc5188ca3760606e78fe0f3a_l3.png)
![Rendered by QuickLaTeX.com {R}_{3}\,↔ {R}_{2}\to \left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 2& 3& 1\end{array}\,\,|\,\,\begin{array}{rrr}\hfill -1& \hfill 1& \hfill 0\\ \hfill -1& \hfill 0& \hfill 1\\ \hfill 1& \hfill 0& \hfill 0\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-fad24bfcce4fd1ec0a948a96279f0fc3_l3.png)
![Rendered by QuickLaTeX.com -2{R}_{1}+{R}_{3}={R}_{3}\to \left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 3& 1\end{array}\,\,|\,\,\begin{array}{rrr}\hfill -1& \hfill 1& \hfill 0\\ \hfill -1& \hfill 0& \hfill 1\\ \hfill 3& \hfill -2& \hfill 0\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-adbd575248290682041e01ec1446ef0f_l3.png)
![Rendered by QuickLaTeX.com -3{R}_{2}+{R}_{3}={R}_{3}\to \left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\,\,|\,\,\begin{array}{rrr}\hfill -1& \hfill 1& \hfill 0\\ \hfill -1& \hfill 0& \hfill 1\\ \hfill 6& \hfill -2& \hfill -3\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-8e9cf445a3a055970e294cd74ae981ce_l3.png)
Thus,
![Rendered by QuickLaTeX.com {A}^{-1}=B=\left[\begin{array}{ccc}-1& \,1& \,0\\ -1& \,\,0& \,\,1\\ \,\,6& -2& -3\end{array}\,\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-c562ef6ee95c36c4ecf292f7c689aff3_l3.png)
Analysis
To prove that ![]() let’s multiply the two matrices together to see if the product equals the identity, if
let’s multiply the two matrices together to see if the product equals the identity, if ![]() and
and ![]()
![Rendered by QuickLaTeX.com \begin{array}{l}\begin{array}{l}\begin{array}{l}\hfill \\ \hfill \end{array}\hfill \\ A{A}^{-1}=\left[\begin{array}{ccc}2& 3& 1\\ 3& 3& 1\\ 2& 4& 1\end{array}\right]\text{ }\left[\begin{array}{rrr}\hfill -1& \hfill 1& \hfill 0\\ \hfill -1& \hfill 0& \hfill 1\\ \hfill 6& \hfill -2& \hfill -3\end{array}\right]\hfill \end{array}\hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,=\left[\begin{array}{ccc}2\left(-1\right)+3\left(-1\right)+1\left(6\right)& \,\,2\left(1\right)+3\left(0\right)+1\left(-2\right)& \,\,2\left(0\right)+3\left(1\right)+1\left(-3\right)\\ 3\left(-1\right)+3\left(-1\right)+1\left(6\right)& \,\,3\left(1\right)+3\left(0\right)+1\left(-2\right)& \,\,3\left(0\right)+3\left(1\right)+1\left(-3\right)\\ 2\left(-1\right)+4\left(-1\right)+1\left(6\right)& \,\,2\left(1\right)+4\left(0\right)+1\left(-2\right)& \,\,2\left(0\right)+4\left(1\right)+1\left(-3\right)\end{array}\right]\hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]\hfill \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-2311de7e5ffb668c6bd66d4c094342a6_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{l}\begin{array}{l}\begin{array}{l}\hfill \\ \hfill \end{array}\hfill \\ {A}^{-1}A=\left[\begin{array}{rrr}\hfill -1& \hfill 1& \hfill 0\\ \hfill -1& \hfill 0& \hfill 1\\ \hfill 6& \hfill -2& \hfill -3\end{array}\right]\text{ }\left[\begin{array}{ccc}2& 3& 1\\ 3& 3& 1\\ 2& 4& 1\end{array}\right]\hfill \end{array}\hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\left[\begin{array}{rrr}\hfill -1\left(2\right)+1\left(3\right)+0\left(2\right)& \hfill \,\,-1\left(3\right)+1\left(3\right)+0\left(4\right)& \hfill \,\,-1\left(1\right)+1\left(1\right)+0\left(1\right)\\ \hfill -1\left(2\right)+0\left(3\right)+1\left(2\right)& \hfill \,\,-1\left(3\right)+0\left(3\right)+1\left(4\right)& \hfill \,\,-1\left(1\right)+0\left(1\right)+1\left(1\right)\\ \hfill 6\left(2\right)+-2\left(3\right)+-3\left(2\right)& \hfill \,\,6\left(3\right)+-2\left(3\right)+-3\left(4\right)& \hfill \,\,6\left(1\right)+-2\left(1\right)+-3\left(1\right)\end{array}\right]\hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\left[\begin{array}{rrr}\hfill 1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 1& \hfill 0\\ \hfill 0& \hfill 0& \hfill 1\end{array}\right]\hfill \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-99688a63b91719e1ed463b6343ad622b_l3.png)
Try It
Find the inverse of the ![]() matrix.
matrix.
![Rendered by QuickLaTeX.com A=\left[\begin{array}{ccc}\,\,2& -17& 11\\ -1& \,\,\,11& -7\\ \,\,\,0& \,\,\,\,\,3& -2\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-f94122ededfbc341c3ba13872983ee1f_l3.png)
Show Solution
![Rendered by QuickLaTeX.com {A}^{-1}=\left[\begin{array}{ccc}1& 1& \,\,2\\ 2& 4& -3\\ 3& 6& -5\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-e2c172050430af7509c32de557406241_l3.png)
Solving a System of Linear Equations Using the Inverse of a Matrix
Solving a system of linear equations using the inverse of a matrix requires the definition of two new matrices: ![]() is the matrix representing the variables of the system, and
is the matrix representing the variables of the system, and ![]() is the matrix representing the constants. Using matrix multiplication, we may define a system of equations with the same number of equations as variables as
is the matrix representing the constants. Using matrix multiplication, we may define a system of equations with the same number of equations as variables as
To solve a system of linear equations using an inverse matrix, let ![]() be the coefficient matrix, let
be the coefficient matrix, let ![]() be the variable matrix, and let
be the variable matrix, and let ![]() be the constant matrix. Thus, we want to solve a system
be the constant matrix. Thus, we want to solve a system ![]() For example, look at the following system of equations.
For example, look at the following system of equations.
From this system, the coefficient matrix is
The variable matrix is
And the constant matrix is
Then ![]() looks like
looks like
Recall the discussion earlier in this section regarding multiplying a real number by its inverse, ![]() To solve a single linear equation
To solve a single linear equation ![]() for
for ![]() we would simply multiply both sides of the equation by the multiplicative inverse (reciprocal) of
we would simply multiply both sides of the equation by the multiplicative inverse (reciprocal) of ![]() Thus,
Thus,
![Rendered by QuickLaTeX.com \begin{array}{c}\text{ }ax=b\\ \text{ }\left(\frac{1}{a}\right)ax=\left(\frac{1}{a}\right)b\\ \left({a}^{-1}\text{ }\right)ax=\left({a}^{-1}\right)b\\ \left[\left({a}^{-1}\right)a\right]x=\left({a}^{-1}\right)b\\ \text{ }1x=\left({a}^{-1}\right)b\\ \text{ }x=\left({a}^{-1}\right)b\end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-6945abdb88b733ab3df900beaa1541e4_l3.png)
The only difference between solving a linear equation and a system of equations written in matrix form is that finding the inverse of a matrix is more complicated, and matrix multiplication is a longer process. However, the goal is the same—to isolate the variable.
We will investigate this idea in detail, but it is helpful to begin with a ![]() system and then move on to a
system and then move on to a ![]() system.
system.
Solving a System of Equations Using the Inverse of a Matrix
Given a system of equations, write the coefficient matrix ![]() the variable matrix
the variable matrix ![]() and the constant matrix
and the constant matrix ![]() Then
Then
Multiply both sides by the inverse of ![]() to obtain the solution.
to obtain the solution.
![Rendered by QuickLaTeX.com \begin{array}{r}\hfill \left({A}^{-1}\right)AX=\left({A}^{-1}\right)B\\ \hfill \left[\left({A}^{-1}\right)A\right]X=\left({A}^{-1}\right)B\\ \hfill IX=\left({A}^{-1}\right)B\\ \hfill X=\left({A}^{-1}\right)B\end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-b9ae1eac8ad88d9d6bb90585d06476ff_l3.png)
If the coefficient matrix does not have an inverse, does that mean the system has no solution?
No, if the coefficient matrix is not invertible, the system could be inconsistent and have no solution, or be dependent and have infinitely many solutions.
Solving a 2 × 2 System Using the Inverse of a Matrix
Solve the given system of equations using the inverse of a matrix.
Show Solution
Write the system in terms of a coefficient matrix, a variable matrix, and a constant matrix.
Then
First, we need to calculate ![]() Using the formula to calculate the inverse of a 2 by 2 matrix, we have:
Using the formula to calculate the inverse of a 2 by 2 matrix, we have:
![Rendered by QuickLaTeX.com \begin{array}{l}{A}^{-1}=\frac{1}{ad-bc}\left[\begin{array}{cc}d& -b\\ -c& a\end{array}\right]\hfill \\ \text{ }=\frac{1}{3\left(11\right)-8\left(4\right)}\left[\begin{array}{cc}11& -8\\ -4& 3\end{array}\right]\hfill \\ \text{ }=\frac{1}{1}\left[\begin{array}{cc}11& -8\\ -4& 3\end{array}\right]\hfill \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-3aea19861c2a98d8bacbc9f03c3d3978_l3.png)
So,
Now we are ready to solve. Multiply both sides of the equation by ![]()
![Rendered by QuickLaTeX.com \begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left({A}^{-1}\right)AX=\left({A}^{-1}\right)B\hfill \\ \left[\begin{array}{rr}\hfill 11& \hfill -8\\ \hfill -4& \hfill 3\end{array}\right]\text{ }\left[\begin{array}{cc}3& 8\\ 4& 11\end{array}\right]\text{ }\left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{rr}\hfill 11& \hfill -8\\ \hfill -4& \hfill 3\end{array}\right]\text{ }\left[\begin{array}{c}5\\ 7\end{array}\right]\hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\text{ }\left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{r}\hfill 11\left(5\right)+\left(-8\right)7\\ \hfill -4\left(5\right)+3\left(7\right)\end{array}\right]\hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{r}\hfill -1\\ \hfill 1\end{array}\right]\hfill \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-4d659a7e8c9849fafd2317f5489de05f_l3.png)
The solution is ![]()
Can we solve for ![]() by finding the product
by finding the product ![]()
No, recall that matrix multiplication is not commutative, so ![]() Consider our steps for solving the matrix equation.
Consider our steps for solving the matrix equation.
![Rendered by QuickLaTeX.com \begin{array}{r}\hfill \left({A}^{-1}\right)AX=\left({A}^{-1}\right)B\\ \hfill \left[\left({A}^{-1}\right)A\right]X=\left({A}^{-1}\right)B\\ \hfill IX=\left({A}^{-1}\right)B\\ \hfill X=\left({A}^{-1}\right)B\end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-b9ae1eac8ad88d9d6bb90585d06476ff_l3.png)
Notice in the first step we multiplied both sides of the equation by ![]() but the
but the ![]() was to the left of
was to the left of ![]() on the left side and to the left of
on the left side and to the left of ![]() on the right side. Because matrix multiplication is not commutative, order matters.
on the right side. Because matrix multiplication is not commutative, order matters.
Solving a 3 × 3 System Using the Inverse of a Matrix
Solve the following system using the inverse of a matrix.
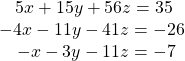
Show Solution
Write the equation ![]()
![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}5& 15& 56\\ -4& -11& -41\\ -1& -3& -11\end{array}\right]\text{ }\left[\begin{array}{c}x\\ y\\ z\end{array}\right]=\left[\begin{array}{r}\hfill 35\\ \hfill -26\\ \hfill -7\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-e1043efbdb4d3676884b99295fe70fa7_l3.png)
First, we will find the inverse of ![]() by augmenting with the identity.
by augmenting with the identity.
![Rendered by QuickLaTeX.com \left[\begin{array}{rrr}\hfill 5& \hfill 15& \hfill 56\\ \hfill -4& \hfill -11& \hfill -41\\ \hfill -1& \hfill -3& \hfill -11\end{array}\,\,|\,\,\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-494d2487679268db3c051af0b51acfc0_l3.png)
Multiply row 1 by ![]()
![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}1& 3& \frac{56}{5}\\ -4& -11& -41\\ -1& -3& -11\end{array}\,\,|\,\,\begin{array}{ccc}\frac{1}{5}& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-a1b9fbf92f69b6c31270f3f80e5954ab_l3.png)
Multiply row 1 by 4 and add to row 2.
![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}1& 3& \frac{56}{5}\\ 0& 1& \frac{19}{5}\\ -1& -3& -11\end{array}\,\,|\,\,\begin{array}{ccc}\frac{1}{5}& 0& 0\\ \frac{4}{5}& 1& 0\\ 0& 0& 1\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-785d7c3198be1b27c37605c4b24c134f_l3.png)
Add row 1 to row 3.
![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}1& 3& \frac{56}{5}\\ 0& 1& \frac{19}{5}\\ 0& 0& \frac{1}{5}\end{array}\,\,|\,\,\begin{array}{ccc}\frac{1}{5}& 0& 0\\ \frac{4}{5}& 1& 0\\ \frac{1}{5}& 0& 1\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-f8dd646db150422a2ec17c7e2af616be_l3.png)
Multiply row 2 by −3 and add to row 1.
![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}1& 0& -\frac{1}{5}\\ 0& 1& \frac{19}{5}\\ 0& 0& \frac{1}{5}\end{array}\,\,|\,\,\begin{array}{ccc}-\frac{11}{5}& -3& 0\\ \frac{4}{5}& 1& 0\\ \frac{1}{5}& 0& 1\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-78075b7cab97b457df64e3996898aeaa_l3.png)
Multiply row 3 by 5.
![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}1& 0& -\frac{1}{5}\\ 0& 1& \frac{19}{5}\\ 0& 0& 1\end{array}\,\,|\,\,\begin{array}{ccc}-\frac{11}{5}& -3& 0\\ \frac{4}{5}& 1& 0\\ 1& 0& 5\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-f8e5b28e549642be11e6683c71ed36b9_l3.png)
Multiply row 3 by ![]() and add to row 1.
and add to row 1.
![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}1& 0& 0\\ 0& 1& \frac{19}{5}\\ 0& 0& 1\end{array}\,\,|\,\,\begin{array}{ccc}-2& -3& 1\\ \frac{4}{5}& 1& 0\\ 1& 0& 5\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-03e50165692bb9cc26638f8d07c3fef9_l3.png)
Multiply row 3 by ![]() and add to row 2.
and add to row 2.
![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\,\,|\,\,\begin{array}{ccc}-2& -3& 1\\ -3& 1& -19\\ 1& 0& 5\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-085e4d27f03a0c597fc4d861e91673f3_l3.png)
So,
![Rendered by QuickLaTeX.com {A}^{-1}=\left[\begin{array}{ccc}-2& -3& 1\\ -3& 1& -19\\ 1& 0& 5\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-0a38f1d75510712e91dbc0dd0365f6a9_l3.png)
Multiply both sides of the equation by ![]() We want
We want ![]()
![Rendered by QuickLaTeX.com \left[\begin{array}{rrr}\hfill -2& \hfill -3& \hfill 1\\ \hfill -3& \hfill 1& \hfill -19\\ \hfill 1& \hfill 0& \hfill 5\end{array}\right]\text{ }\left[\begin{array}{rrr}\hfill 5& \hfill 15& \hfill 56\\ \hfill -4& \hfill -11& \hfill -41\\ \hfill -1& \hfill -3& \hfill -11\end{array}\right]\text{ }\left[\begin{array}{c}x\\ y\\ z\end{array}\right]=\left[\begin{array}{rrr}\hfill -2& \hfill -3& \hfill 1\\ \hfill -3& \hfill 1& \hfill -19\\ \hfill 1& \hfill 0& \hfill 5\end{array}\right]\text{ }\left[\begin{array}{r}\hfill 35\\ \hfill -26\\ \hfill -7\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-17355f2c4f670c8e707d90856f426404_l3.png)
Thus,
![Rendered by QuickLaTeX.com {A}^{-1}B=\left[\begin{array}{r}\hfill -70+78-7\\ \hfill -105-26+133\\ \hfill 35+0-35\end{array}\right]=\left[\begin{array}{c}1\\ 2\\ 0\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-c1e0a8099cfd306cd49173db761d67cc_l3.png)
The solution is ![]()
Try It
Solve the system using the inverse of the coefficient matrix.
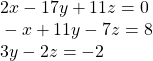
Show Solution
![Rendered by QuickLaTeX.com X=\left[\begin{array}{c}4\\ 38\\ 58\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-6ba3c0aba9d0aedfbb949633fdd91b6e_l3.png)
How To
Given a system of equations, solve with matrix inverses using a calculator.
- Save the coefficient matrix and the constant matrix as matrix variables
![Rendered by QuickLaTeX.com \,\left[A\right]\,](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-8a6d539f00b1e651ee4bea580239542a_l3.png) and
and ![Rendered by QuickLaTeX.com \,\left[B\right].](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-c0775245ad701c522952b50edd0b20a6_l3.png)
- Enter the multiplication into the calculator, calling up each matrix variable as needed.
- If the coefficient matrix is invertible, the calculator will present the solution matrix; if the coefficient matrix is not invertible, the calculator will present an error message.
Using a Calculator to Solve a System of Equations with Matrix Inverses
Solve the system of equations with matrix inverses using a calculator
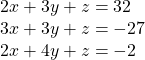
Show Solution
On the matrix page of the calculator, enter the coefficient matrix as the matrix variable ![]() and enter the constant matrix as the matrix variable
and enter the constant matrix as the matrix variable ![]()
![Rendered by QuickLaTeX.com \left[A\right]=\left[\begin{array}{ccc}2& 3& 1\\ 3& 3& 1\\ 2& 4& 1\end{array}\right],\text{ }\left[B\right]=\left[\begin{array}{c}32\\ -27\\ -2\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-bb47e0cdb6f72f2f21b7352531ba023b_l3.png)
On the home screen of the calculator, type in the multiplication to solve for ![]() calling up each matrix variable as needed.
calling up each matrix variable as needed.
Evaluate the expression.
![Rendered by QuickLaTeX.com \left[\begin{array}{c}-59\\ -34\\ 252\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-fa8866c191c96c09425143f46b977829_l3.png)
Access these online resources for additional instruction and practice with solving systems with inverses.
Key Equations
| Identity matrix for a |
|
| Identity matrix for a |
![Rendered by QuickLaTeX.com {I}_{3}=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-70ef03caf5c47f982175c98b70a96c66_l3.png) |
| Multiplicative inverse of a |
|
Key Concepts
- An identity matrix has the property
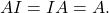 See (Figure).
See (Figure). - An invertible matrix has the property
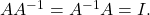 See (Figure).
See (Figure). - Use matrix multiplication and the identity to find the inverse of a
 matrix. See (Figure).
matrix. See (Figure). - The multiplicative inverse can be found using a formula. See (Figure).
- Another method of finding the inverse is by augmenting with the identity. See (Figure).
- We can augment a
 matrix with the identity on the right and use row operations to turn the original matrix into the identity, and the matrix on the right becomes the inverse. See (Figure).
matrix with the identity on the right and use row operations to turn the original matrix into the identity, and the matrix on the right becomes the inverse. See (Figure). - Write the system of equations as
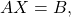 and multiply both sides by the inverse of
and multiply both sides by the inverse of 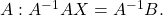 See (Figure) and (Figure).
See (Figure) and (Figure). - We can also use a calculator to solve a system of equations with matrix inverses. See (Figure).
Section Exercises
Verbal
1. In a previous section, we showed that matrix multiplication is not commutative, that is, ![]() in most cases. Can you explain why matrix multiplication is commutative for matrix inverses, that is,
in most cases. Can you explain why matrix multiplication is commutative for matrix inverses, that is, ![]()
Show Solution
If ![]() is the inverse of
is the inverse of ![]() then
then ![]() the identity matrix. Since
the identity matrix. Since ![]() is also the inverse of
is also the inverse of ![]() You can also check by proving this for a
You can also check by proving this for a ![]() matrix.
matrix.
2. Does every ![]() matrix have an inverse? Explain why or why not. Explain what condition is necessary for an inverse to exist.
matrix have an inverse? Explain why or why not. Explain what condition is necessary for an inverse to exist.
3. Can you explain whether a ![]() matrix with an entire row of zeros can have an inverse?
matrix with an entire row of zeros can have an inverse?
Show Solution
No, because ![]() and
and ![]() are both 0, so
are both 0, so ![]() which requires us to divide by 0 in the formula.
which requires us to divide by 0 in the formula.
4. Can a matrix with an entire column of zeros have an inverse? Explain why or why not.
5. Can a matrix with zeros on the diagonal have an inverse? If so, find an example. If not, prove why not. For simplicity, assume a ![]() matrix.
matrix.
Show Solution
Yes. Consider the matrix ![]() The inverse is found with the following calculation:
The inverse is found with the following calculation: ![]()
Algebraic
In the following exercises, show that matrix ![]() is the inverse of matrix
is the inverse of matrix ![]()
6. ![]()
7. ![]()
Show Solution
![]()
8. ![]()
9. ![]()
Show Solution
![]()
10. ![Rendered by QuickLaTeX.com A=\left[\begin{array}{ccc}1& 0& 1\\ 0& 1& -1\\ 0& 1& 1\end{array}\right],\,B=\frac{1}{2}\left[\begin{array}{ccc}2& 1& -1\\ 0& 1& 1\\ 0& -1& 1\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-2bec278f444d80c4135a7205a2b1cb81_l3.png)
11. ![Rendered by QuickLaTeX.com A=\left[\begin{array}{ccc}1& 2& 3\\ 4& 0& 2\\ 1& 6& 9\end{array}\right],\,B=\frac{1}{4}\left[\begin{array}{ccc}6& 0& -2\\ 17& -3& -5\\ -12& 2& 4\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-b8ad72385f0eb8c877f192a339bce76c_l3.png)
Show Solution
![Rendered by QuickLaTeX.com AB=BA=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]=I](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-0d73160c5f65a5a9caaf8567e5d80c09_l3.png)
12. ![Rendered by QuickLaTeX.com A=\left[\begin{array}{ccc}3& 8& 2\\ 1& 1& 1\\ 5& 6& 12\end{array}\right],\,B=\frac{1}{36}\left[\begin{array}{ccc}-6& 84& -6\\ 7& -26& 1\\ -1& -22& 5\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-872c06442284637d537eab7413501f00_l3.png)
For the following exercises, find the multiplicative inverse of each matrix, if it exists.
13. ![]()
Show Solution
![]()
15. ![]()
Show Solution
![]()
16. ![]()
Show Solution
There is no inverse
18. ![]()
19. ![]()
Show Solution
![]()
20. ![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}1& 0& 6\\ -2& 1& 7\\ 3& 0& 2\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-561891bd31f7453cd79ddebf46e204de_l3.png)
21. ![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}0& 1& -3\\ 4& 1& 0\\ 1& 0& 5\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-7030c8e7cc267fc727408cb192aa9634_l3.png)
Show Solution
![Rendered by QuickLaTeX.com \frac{1}{17}\left[\begin{array}{ccc}-5& 5& -3\\ 20& -3& 12\\ 1& -1& 4\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-b88952adadfd72184b3ac2a3f2012c3f_l3.png)
22. ![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}1& 2& -1\\ -3& 4& 1\\ -2& -4& -5\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-00c5f6c459f8df07124e598f58e039d1_l3.png)
![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}1& 9& -3\\ 2& 5& 6\\ 4& -2& 7\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-191e1d10916b39013009318a49493f62_l3.png)
Show Solution
![Rendered by QuickLaTeX.com \frac{1}{209}\left[\begin{array}{ccc}47& -57& 69\\ 10& 19& -12\\ -24& 38& -13\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-c371f9454f7662c31063ae6a073dc1dd_l3.png)
24. ![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}1& -2& 3\\ -4& 8& -12\\ 1& 4& 2\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-ebf88137f7d740ed276a55e2b3698c16_l3.png)
25. ![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}\frac{1}{2}& \frac{1}{2}& \frac{1}{2}\\ \frac{1}{3}& \frac{1}{4}& \frac{1}{5}\\ \frac{1}{6}& \frac{1}{7}& \frac{1}{8}\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-2f0022ea975775200fedb3ff7bd5ae09_l3.png)
Show Solution
![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}18& 60& -168\\ -56& -140& 448\\ 40& 80& -280\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-a76f6a4daad65a8182342c83a88bd8bb_l3.png)
26. ![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\\ 7& 8& 9\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-b11051c5e83c70242a84977c89989b76_l3.png)
For the following exercises, solve the system using the inverse of a ![]() matrix.
matrix.
27. ![]()
Show Solution
![]()
28. ![]()
29. ![]()
Show Solution
![]()
30. ![]()
31. ![]()
Show Solution
![]()
Show Solution
![]()
34. ![]()
For the following exercises, solve a system using the inverse of a ![]()
matrix.
35. 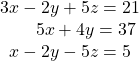
Show Solution
![]()
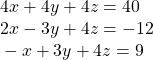
37. 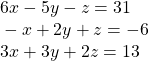
Show Solution
![]()
38. 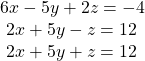
39. 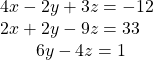
Show Solution
![]()
40. 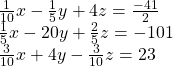
41. 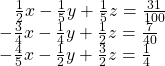
Show Solution
![]()
42. 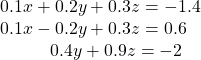
Technology
For the following exercises, use a calculator to solve the system of equations with matrix inverses.
43. ![]()
Show Solution
![]()
44. ![]()
45. 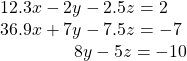
Show Solution
![]()
46. 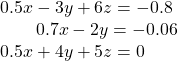
Extensions
For the following exercises, find the inverse of the given matrix.
47. ![Rendered by QuickLaTeX.com \left[\begin{array}{cccc}1& 0& 1& 0\\ 0& 1& 0& 1\\ 0& 1& 1& 0\\ 0& 0& 1& 1\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-bdf281eb98e4b9ae6463fe73253a613e_l3.png)
Show Solution
![Rendered by QuickLaTeX.com \frac{1}{2}\left[\begin{array}{rrrr}\hfill 2& \hfill 1& \hfill -1& \hfill -1\\ \hfill 0& \hfill 1& \hfill 1& \hfill -1\\ \hfill 0& \hfill -1& \hfill 1& \hfill 1\\ \hfill 0& \hfill 1& \hfill -1& \hfill 1\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-969bcfc614e165e757c2805e0bcd1137_l3.png)
48. ![Rendered by QuickLaTeX.com \left[\begin{array}{rrrr}\hfill -1& \hfill 0& \hfill 2& \hfill 5\\ \hfill 0& \hfill 0& \hfill 0& \hfill 2\\ \hfill 0& \hfill 2& \hfill -1& \hfill 0\\ \hfill 1& \hfill -3& \hfill 0& \hfill 1\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-9a28bdac95bce0b886cdeabe1d2f7caa_l3.png)
49. ![Rendered by QuickLaTeX.com \left[\begin{array}{rrrr}\hfill 1& \hfill -2& \hfill 3& \hfill 0\\ \hfill 0& \hfill 1& \hfill 0& \hfill 2\\ \hfill 1& \hfill 4& \hfill -2& \hfill 3\\ \hfill -5& \hfill 0& \hfill 1& \hfill 1\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-78bab1f2ef1ec1b8fe8e096f48f0897a_l3.png)
Show Solution
![Rendered by QuickLaTeX.com \frac{1}{39}\left[\begin{array}{rrrr}\hfill 3& \hfill 2& \hfill 1& \hfill -7\\ \hfill 18& \hfill -53& \hfill 32& \hfill 10\\ \hfill 24& \hfill -36& \hfill 21& \hfill 9\\ \hfill -9& \hfill 46& \hfill -16& \hfill -5\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-6926df103b1377d4d9bffea833a0c0f6_l3.png)
50. ![Rendered by QuickLaTeX.com \left[\begin{array}{rrrrr}\hfill 1& \hfill 2& \hfill 0& \hfill 2& \hfill 3\\ \hfill 0& \hfill 2& \hfill 1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 3& \hfill 0& \hfill 1\\ \hfill 0& \hfill 2& \hfill 0& \hfill 0& \hfill 1\\ \hfill 0& \hfill 0& \hfill 1& \hfill 2& \hfill 0\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-2478bac74ef444f1a3067c4fbc429247_l3.png)
51. ![Rendered by QuickLaTeX.com \left[\begin{array}{rrrrrr}\hfill 1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill 0\\ \hfill 1& \hfill 1& \hfill 1& \hfill 1& \hfill 1& \hfill 1\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-fdfae56d5e8c864e1cf0e23c2d76af83_l3.png)
Show Solution
![Rendered by QuickLaTeX.com \left[\begin{array}{rrrrrr}\hfill 1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill 0\\ \hfill -1& \hfill -1& \hfill -1& \hfill -1& \hfill -1& \hfill 1\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-bc7521805197fba1ed4df5e2b8b68463_l3.png)
Real-World Applications
For the following exercises, write a system of equations that represents the situation. Then, solve the system using the inverse of a matrix.
52. 2,400 tickets were sold for a basketball game. If the prices for floor 1 and floor 2 were different, and the total amount of money brought in is $64,000, how much was the price of each ticket?
53. In the previous exercise, if you were told there were 400 more tickets sold for floor 2 than floor 1, how much was the price of each ticket?
Show Solution
Infinite solutions.
54. A food drive collected two different types of canned goods, green beans and kidney beans. The total number of collected cans was 350 and the total weight of all donated food was 348 lb, 12 oz. If the green bean cans weigh 2 oz less than the kidney bean cans, how many of each can was donated?
55. Students were asked to bring their favorite fruit to class. 95% of the fruits consisted of banana, apple, and oranges. If oranges were twice as popular as bananas, and apples were 5% less popular than bananas, what are the percentages of each individual fruit?
Show Solution
50% oranges, 25% bananas, 20% apples
56. A sorority held a bake sale to raise money and sold brownies and chocolate chip cookies. They priced the brownies at $1 and the chocolate chip cookies at $0.75. They raised $700 and sold 850 items. How many brownies and how many cookies were sold?
57. A clothing store needs to order new inventory. It has three different types of hats for sale: straw hats, beanies, and cowboy hats. The straw hat is priced at $13.99, the beanie at $7.99, and the cowboy hat at $14.49. If 100 hats were sold this past quarter, $1,119 was taken in by sales, and the amount of beanies sold was 10 more than cowboy hats, how many of each should the clothing store order to replace those already sold?
Show Solution
10 straw hats, 50 beanies, 40 cowboy hats
58. Anna, Ashley, and Andrea weigh a combined 370 lb. If Andrea weighs 20 lb more than Ashley, and Anna weighs 1.5 times as much as Ashley, how much does each girl weigh?
59. Three roommates shared a package of 12 ice cream bars, but no one remembers who ate how many. If Tom ate twice as many ice cream bars as Joe, and Albert ate three less than Tom, how many ice cream bars did each roommate eat?
Show Solution
Tom ate 6, Joe ate 3, and Albert ate 3.
60. A farmer constructed a chicken coop out of chicken wire, wood, and plywood. The chicken wire cost $2 per square foot, the wood $10 per square foot, and the plywood $5 per square foot. The farmer spent a total of $51, and the total amount of materials used was ![]() He used
He used ![]() more chicken wire than plywood. How much of each material in did the farmer use?
more chicken wire than plywood. How much of each material in did the farmer use?
61. Jay has lemon, orange, and pomegranate trees in his backyard. An orange weighs 8 oz, a lemon 5 oz, and a pomegranate 11 oz. Jay picked 142 pieces of fruit weighing a total of 70 lb, 10 oz. He picked 15.5 times more oranges than pomegranates. How many of each fruit did Jay pick?
Show Solution
124 oranges, 10 lemons, 8 pomegranates
Glossary
- identity matrix
- a square matrix containing ones down the main diagonal and zeros everywhere else; it acts as a 1 in matrix algebra
- multiplicative inverse of a matrix
- a matrix that, when multiplied by the original, equals the identity matrix

