Chapter 5.1 Related Rates
Learning Objectives
- Express changing quantities in terms of derivatives.
- Find relationships among the derivatives in a given problem.
- Use the chain rule to find the rate of change of one quantity that depends on the rate of change of other quantities.
We have seen that for quantities that are changing over time, the rates at which these quantities change are given by derivatives. If two related quantities are changing over time, the rates at which the quantities change are related. For example, if a balloon is being filled with air, both the radius of the balloon and the volume of the balloon are increasing. In this section, we consider several problems in which two or more related quantities are changing and we study how to determine the relationship between the rates of change of these quantities.
Setting up Related-Rates Problems
In many real-world applications, related quantities are changing with respect to time. For example, if we consider the balloon example again, we can say that the rate of change in the volume, ![]() , is related to the rate of change in the radius,
, is related to the rate of change in the radius, ![]() . In this case, we say that
. In this case, we say that ![]() and
and ![]() are related rates because
are related rates because ![]() is related to
is related to ![]() . Here we study several examples of related quantities that are changing with respect to time and we look at how to calculate one rate of change given another rate of change.
. Here we study several examples of related quantities that are changing with respect to time and we look at how to calculate one rate of change given another rate of change.
Inflating a Balloon
A spherical balloon is being filled with air at the constant rate of ![]() ((Figure)). How fast is the radius increasing when the radius is
((Figure)). How fast is the radius increasing when the radius is ![]() ?
?
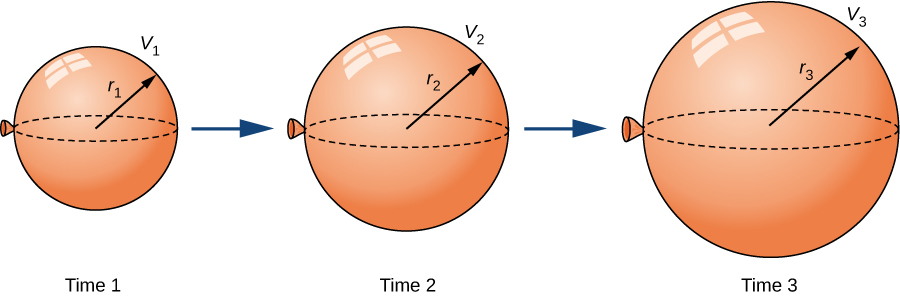
Solution
The volume of a sphere of radius ![]() centimeters is
centimeters is
Since the balloon is being filled with air, both the volume and the radius are functions of time. Therefore, ![]() seconds after beginning to fill the balloon with air, the volume of air in the balloon is
seconds after beginning to fill the balloon with air, the volume of air in the balloon is
Differentiating both sides of this equation with respect to time and applying the chain rule, we see that the rate of change in the volume is related to the rate of change in the radius by the equation
The balloon is being filled with air at the constant rate of 2 cm3/sec, so ![]() . Therefore,
. Therefore,
which implies
When the radius ![]() ,
,
What is the instantaneous rate of change of the radius when ![]() ?
?
Solution
![]() , or approximately 0.0044 cm/sec
, or approximately 0.0044 cm/sec
Before looking at other examples, let’s outline the problem-solving strategy we will be using to solve related-rates problems.
Problem-Solving Strategy: Solving a Related-Rates Problem
- Assign symbols to all variables involved in the problem. Draw a figure if applicable.
- State, in terms of the variables, the information that is given and the rate to be determined.
- Find an equation relating the variables introduced in step 1.
- Using the chain rule, differentiate both sides of the equation found in step 3 with respect to the independent variable. This new equation will relate the derivatives.
- Substitute all known values into the equation from step 4, then solve for the unknown rate of change.
Note that when solving a related-rates problem, it is crucial not to substitute known values too soon. For example, if the value for a changing quantity is substituted into an equation before both sides of the equation are differentiated, then that quantity will behave as a constant and its derivative will not appear in the new equation found in step 4. We examine this potential error in the following example.
Examples of the Process
Let’s now implement the strategy just described to solve several related-rates problems. The first example involves a plane flying overhead. The relationship we are studying is between the speed of the plane and the rate at which the distance between the plane and a person on the ground is changing.
An Airplane Flying at a Constant Elevation
An airplane is flying overhead at a constant elevation of ![]() ft. A man is viewing the plane from a position
ft. A man is viewing the plane from a position ![]() ft from the base of a radio tower. The airplane is flying horizontally away from the man. If the plane is flying at the rate of
ft from the base of a radio tower. The airplane is flying horizontally away from the man. If the plane is flying at the rate of ![]() ft/sec, at what rate is the distance between the man and the plane increasing when the plane passes over the radio tower?
ft/sec, at what rate is the distance between the man and the plane increasing when the plane passes over the radio tower?
Solution
Step 1. Draw a picture, introducing variables to represent the different quantities involved.
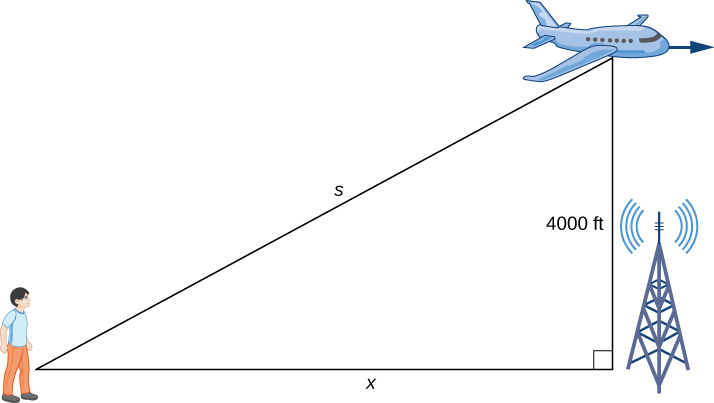
As shown, ![]() denotes the distance between the man and the position on the ground directly below the airplane. The variable
denotes the distance between the man and the position on the ground directly below the airplane. The variable ![]() denotes the distance between the man and the plane. Note that both
denotes the distance between the man and the plane. Note that both ![]() and
and ![]() are functions of time. We do not introduce a variable for the height of the plane because it remains at a constant elevation of
are functions of time. We do not introduce a variable for the height of the plane because it remains at a constant elevation of ![]() ft. Since an object’s height above the ground is measured as the shortest distance between the object and the ground, the line segment of length
ft. Since an object’s height above the ground is measured as the shortest distance between the object and the ground, the line segment of length ![]() ft is perpendicular to the line segment of length
ft is perpendicular to the line segment of length ![]() feet, creating a right triangle.
feet, creating a right triangle.
Step 2. Since ![]() denotes the horizontal distance between the man and the point on the ground below the plane,
denotes the horizontal distance between the man and the point on the ground below the plane, ![]() represents the speed of the plane. We are told the speed of the plane is 600 ft/sec. Therefore,
represents the speed of the plane. We are told the speed of the plane is 600 ft/sec. Therefore, ![]() ft/sec. Since we are asked to find the rate of change in the distance between the man and the plane when the plane is directly above the radio tower, we need to find
ft/sec. Since we are asked to find the rate of change in the distance between the man and the plane when the plane is directly above the radio tower, we need to find ![]() when
when ![]() ft.
ft.
Step 3. From the figure, we can use the Pythagorean theorem to write an equation relating ![]() and
and ![]() :
:
![]() .
.
Step 4. Differentiating this equation with respect to time and using the fact that the derivative of a constant is zero, we arrive at the equation
![]() .
.
Step 5. Find the rate at which the distance between the man and the plane is increasing when the plane is directly over the radio tower. That is, find ![]() when
when ![]() ft. Since the speed of the plane is
ft. Since the speed of the plane is ![]() ft/sec, we know that
ft/sec, we know that ![]() ft/sec. We are not given an explicit value for
ft/sec. We are not given an explicit value for ![]() ; however, since we are trying to find
; however, since we are trying to find ![]() when
when ![]() ft, we can use the Pythagorean theorem to determine the distance
ft, we can use the Pythagorean theorem to determine the distance ![]() when
when ![]() and the height is
and the height is ![]() ft. Solving the equation
ft. Solving the equation
for ![]() , we have
, we have ![]() ft at the time of interest. Using these values, we conclude that
ft at the time of interest. Using these values, we conclude that ![]() is a solution of the equation
is a solution of the equation
Therefore,
![]() ft/sec.
ft/sec.
Note: When solving related-rates problems, it is important not to substitute values for the variables too soon. For example, in step 3, we related the variable quantities ![]() and
and ![]() by the equation
by the equation
Since the plane remains at a constant height, it is not necessary to introduce a variable for the height, and we are allowed to use the constant 4000 to denote that quantity. However, the other two quantities are changing. If we mistakenly substituted ![]() into the equation before differentiating, our equation would have been
into the equation before differentiating, our equation would have been
After differentiating, our equation would become
As a result, we would incorrectly conclude that ![]() .
.
What is the speed of the plane if the distance between the person and the plane is increasing at the rate of ![]() ft/sec?
ft/sec?
Solution
![]() ft/sec
ft/sec
Hint
![]() ft/sec
ft/sec
We now return to the problem involving the rocket launch from the beginning of the chapter.
Chapter Opener: A Rocket Launch

Solution
Step 1. Draw a picture introducing the variables.
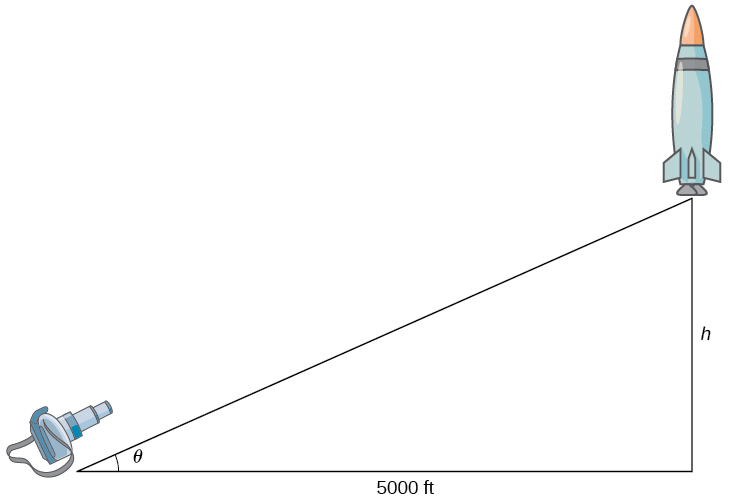
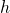 and
and 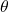 , respectively.
, respectively.Let ![]() denote the height of the rocket above the launch pad and
denote the height of the rocket above the launch pad and ![]() be the angle between the camera lens and the ground.
be the angle between the camera lens and the ground.
Step 2. We are trying to find the rate of change in the angle of the camera with respect to time when the rocket is ![]() ft off the ground. That is, we need to find
ft off the ground. That is, we need to find ![]() when
when ![]() ft. At that time, we know the velocity of the rocket is
ft. At that time, we know the velocity of the rocket is ![]() ft/sec.
ft/sec.
Step 3. Now we need to find an equation relating the two quantities that are changing with respect to time: ![]() and
and ![]() . How can we create such an equation? Using the fact that we have drawn a right triangle, it is natural to think about trigonometric functions. Recall that
. How can we create such an equation? Using the fact that we have drawn a right triangle, it is natural to think about trigonometric functions. Recall that ![]() is the ratio of the length of the opposite side of the triangle to the length of the adjacent side. Thus, we have
is the ratio of the length of the opposite side of the triangle to the length of the adjacent side. Thus, we have
This gives us the equation
![]() .
.
Step 4. Differentiating this equation with respect to time ![]() , we obtain
, we obtain
![]() .
.
Step 5. We want to find ![]() when
when ![]() ft. At this time, we know that
ft. At this time, we know that ![]() ft/sec. We need to determine
ft/sec. We need to determine ![]() . Recall that
. Recall that ![]() is the ratio of the length of the hypotenuse to the length of the adjacent side. We know the length of the adjacent side is
is the ratio of the length of the hypotenuse to the length of the adjacent side. We know the length of the adjacent side is ![]() ft. To determine the length of the hypotenuse, we use the Pythagorean theorem, where the length of one leg is
ft. To determine the length of the hypotenuse, we use the Pythagorean theorem, where the length of one leg is ![]() ft, the length of the other leg is
ft, the length of the other leg is ![]() ft, and the length of the hypotenuse is
ft, and the length of the hypotenuse is ![]() feet as shown in the following figure.
feet as shown in the following figure.
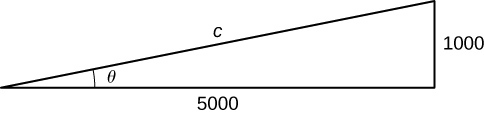
We see that
and we conclude that the hypotenuse is
Therefore, when ![]() , we have
, we have
Recall from step 4 that the equation relating ![]() to our known values is
to our known values is
When ![]() ft, we know that
ft, we know that ![]() ft/sec and
ft/sec and ![]() . Substituting these values into the previous equation, we arrive at the equation
. Substituting these values into the previous equation, we arrive at the equation
Therefore, ![]() rad/sec.
rad/sec.
What rate of change is necessary for the elevation angle of the camera if the camera is placed on the ground at a distance of ![]() ft from the launch pad and the velocity of the rocket is
ft from the launch pad and the velocity of the rocket is ![]() ft/sec when the rocket is
ft/sec when the rocket is ![]() ft off the ground?
ft off the ground?
Solution
![]() rad/sec
rad/sec
Hint
Find ![]() when
when ![]() ft. At that time,
ft. At that time, ![]() ft/sec.
ft/sec.
In the next example, we consider water draining from a cone-shaped funnel. We compare the rate at which the level of water in the cone is decreasing with the rate at which the volume of water is decreasing.
Water Draining from a Funnel
Water is draining from the bottom of a cone-shaped funnel at the rate of ![]() . The height of the funnel is
. The height of the funnel is ![]() ft and the radius at the top of the funnel is
ft and the radius at the top of the funnel is ![]() ft. At what rate is the height of the water in the funnel changing when the height of the water is
ft. At what rate is the height of the water in the funnel changing when the height of the water is ![]() ft?
ft?
Solution
Step 1: Draw a picture introducing the variables.
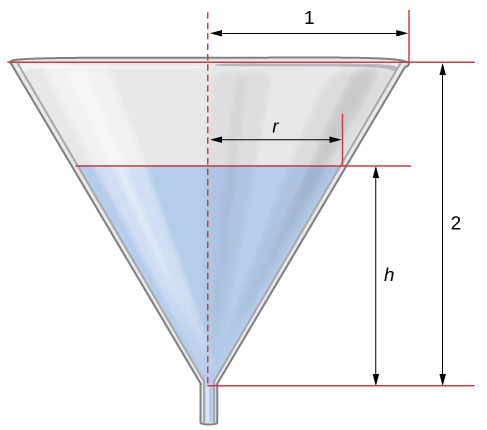
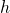 and
and 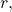 respectively.
respectively.Let ![]() denote the height of the water in the funnel,
denote the height of the water in the funnel, ![]() denote the radius of the water at its surface, and
denote the radius of the water at its surface, and ![]() denote the volume of the water.
denote the volume of the water.
Step 2: We need to determine ![]() when
when ![]() ft. We know that
ft. We know that ![]() .
.
Step 3: The volume of water in the cone is
From the figure, we see that we have similar triangles. Therefore, the ratio of the sides in the two triangles is the same. Therefore, ![]() or
or ![]() . Using this fact, the equation for volume can be simplified to
. Using this fact, the equation for volume can be simplified to
![]() .
.
Step 4: Applying the chain rule while differentiating both sides of this equation with respect to time ![]() , we obtain
, we obtain
![]() .
.
Step 5: We want to find ![]() when
when ![]() ft. Since water is leaving at the rate of
ft. Since water is leaving at the rate of ![]() , we know that
, we know that ![]() . Therefore,
. Therefore,
which implies
It follows that
At what rate is the height of the water changing when the height of the water is ![]() ft?
ft?
Solution
![]() ft/sec
ft/sec
Hint
We need to find ![]() when
when ![]() .
.
Key Concepts
- To solve a related rates problem, first draw a picture that illustrates the relationship between the two or more related quantities that are changing with respect to time.
- In terms of the quantities, state the information given and the rate to be found.
- Find an equation relating the quantities.
- Use differentiation, applying the chain rule as necessary, to find an equation that relates the rates.
- Be sure not to substitute a variable quantity for one of the variables until after finding an equation relating the rates.
For the following exercises, find the quantities for the given equation.
1. Find ![]() at
at ![]() and
and ![]() if
if ![]() .
.
Solution
8
2. Find ![]() at
at ![]() and
and ![]() if
if ![]() .
.
3. Find ![]() at
at ![]() and
and ![]() if
if ![]() and
and ![]() .
.
Solution
![]()
For the following exercises, sketch the situation if necessary and used related rates to solve for the quantities.
4. [T] If two electrical resistors are connected in parallel, the total resistance (measured in ohms, denoted by the Greek capital letter omega, ![]() ) is given by the equation
) is given by the equation ![]() . If
. If ![]() is increasing at a rate of
is increasing at a rate of ![]() and
and ![]() decreases at a rate of
decreases at a rate of ![]() , at what rate does the total resistance change when
, at what rate does the total resistance change when ![]() and
and ![]() ?
?
5. A 10 ft ladder is leaning against a wall. If the top of the ladder slides down the wall at a rate of 2 ft/sec, how fast is the bottom moving along the ground when the bottom of the ladder is 5 ft from the wall?
Solution
![]() ft/sec
ft/sec
6. A 25 ft ladder is leaning against a wall. If we push the ladder toward the wall at a rate of 1 ft/sec, and the bottom of the ladder is initially ![]() ft away from the wall, how fast does the ladder move up the wall
ft away from the wall, how fast does the ladder move up the wall ![]() sec after we start pushing?
sec after we start pushing?
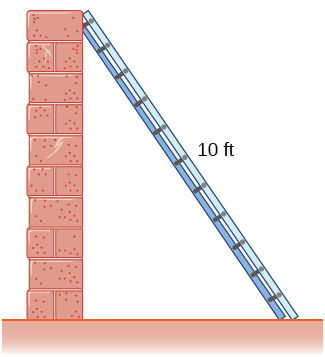
7. Two airplanes are flying in the air at the same height: airplane ![]() is flying east at 250 mi/h and airplane
is flying east at 250 mi/h and airplane ![]() is flying north at
is flying north at ![]() mi/h. If they are both heading to the same airport, located 30 miles east of airplane
mi/h. If they are both heading to the same airport, located 30 miles east of airplane ![]() and 40 miles north of airplane
and 40 miles north of airplane ![]() , at what rate is the distance between the airplanes changing?
, at what rate is the distance between the airplanes changing?
Solution
The distance is decreasing at ![]() mi/h.
mi/h.
8. You and a friend are riding your bikes to a restaurant that you think is east; your friend thinks the restaurant is north. You both leave from the same point, with you riding at 16 mph east and your friend riding ![]() mph north. After you traveled
mph north. After you traveled ![]() mi, at what rate is the distance between you changing?
mi, at what rate is the distance between you changing?
9. Two buses are driving along parallel freeways that are ![]() mi apart, one heading east and the other heading west. Assuming that each bus drives a constant
mi apart, one heading east and the other heading west. Assuming that each bus drives a constant ![]() mph, find the rate at which the distance between the buses is changing when they are
mph, find the rate at which the distance between the buses is changing when they are ![]() mi apart, heading toward each other.
mi apart, heading toward each other.
Solution
The distance between them shrinks at a rate of ![]() mph.
mph.
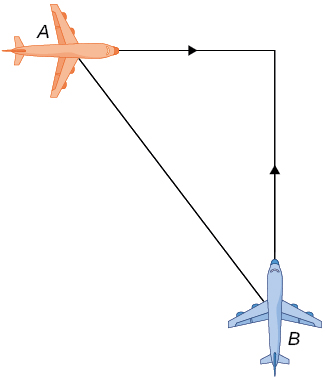
10. A 6-ft-tall person walks away from a 10 ft lamppost at a constant rate of ![]() ft/sec. What is the rate that the tip of the shadow moves away from the pole when the person is
ft/sec. What is the rate that the tip of the shadow moves away from the pole when the person is ![]() ft away from the pole?
ft away from the pole?
11. Using the previous problem, what is the rate at which the tip of the shadow moves away from the person when the person is 10 ft from the pole?
Solution
![]() ft/sec
ft/sec
12. A 5-ft-tall person walks toward a wall at a rate of 2 ft/sec. A spotlight is located on the ground 40 ft from the wall. How fast does the height of the person’s shadow on the wall change when the person is 10 ft from the wall?
13. Using the previous problem, what is the rate at which the shadow changes when the person is 10 ft from the wall, if the person is walking away from the wall at a rate of 2 ft/sec?
Solution
It grows at a rate ![]() ft/sec
ft/sec
14. A helicopter starting on the ground is rising directly into the air at a rate of 25 ft/sec. You are running on the ground starting directly under the helicopter at a rate of 10 ft/sec. Find the rate of change of the distance between the helicopter and yourself after 5 sec.
15. Using the previous problem, what is the rate at which the distance between you and the helicopter is changing when the helicopter has risen to a height of 60 ft in the air, assuming that, initially, it was 30 ft above you?
Solution
The distance is increasing at ![]() ft/sec
ft/sec
For the following exercises, draw and label diagrams to help solve the related-rates problems.
16. The side of a cube increases at a rate of ![]() m/sec. Find the rate at which the volume of the cube increases when the side of the cube is 4 m.
m/sec. Find the rate at which the volume of the cube increases when the side of the cube is 4 m.
17. The volume of a cube decreases at a rate of 10 m/sec. Find the rate at which the side of the cube changes when the side of the cube is 2 m.
Solution
![]() m/sec
m/sec
18. The radius of a circle increases at a rate of 2 m/sec. Find the rate at which the area of the circle increases when the radius is 5 m.
19. The radius of a sphere decreases at a rate of 3 m/sec. Find the rate at which the surface area decreases when the radius is 10 m.
Solution
![]() /sec
/sec
20. The radius of a sphere increases at a rate of 1 m/sec. Find the rate at which the volume increases when the radius is 20 m.
21. The radius of a sphere is increasing at a rate of 9 cm/sec. Find the radius of the sphere when the volume and the radius of the sphere are increasing at the same numerical rate.
Solution
![]() cm
cm
22. The base of a triangle is shrinking at a rate of 1 cm/min and the height of the triangle is increasing at a rate of 5 cm/min. Find the rate at which the area of the triangle changes when the height is 22 cm and the base is 10 cm.
23. A triangle has two constant sides of length 3 ft and 5 ft. The angle between these two sides is increasing at a rate of 0.1 rad/sec. Find the rate at which the area of the triangle is changing when the angle between the two sides is ![]() .
.
Solution
The area is increasing at a rate ![]() .
.
24. A triangle has a height that is increasing at a rate of 2 cm/sec and its area is increasing at a rate of 4 ![]() . Find the rate at which the base of the triangle is changing when the height of the triangle is 4 cm and the area is 20
. Find the rate at which the base of the triangle is changing when the height of the triangle is 4 cm and the area is 20 ![]() .
.
For the following exercises, consider a right cone that is leaking water. The dimensions of the conical tank are a height of 16 ft and a radius of 5 ft.
25. How fast does the depth of the water change when the water is 10 ft high if the cone leaks water at a rate of 10 ![]() /min?
/min?
Solution
The depth of the water decreases at ![]() ft/min.
ft/min.
26. Find the rate at which the surface area of the water changes when the water is 10 ft high if the cone leaks water at a rate of 10 ![]() /min.
/min.
27. If the water level is decreasing at a rate of 3 in./min when the depth of the water is 8 ft, determine the rate at which water is leaking out of the cone.
Solution
The volume is decreasing at a rate of ![]()
28. A vertical cylinder is leaking water at a rate of 1 ![]() /sec. If the cylinder has a height of 10 ft and a radius of 1 ft, at what rate is the height of the water changing when the height is 6 ft?
/sec. If the cylinder has a height of 10 ft and a radius of 1 ft, at what rate is the height of the water changing when the height is 6 ft?
29. A cylinder is leaking water but you are unable to determine at what rate. The cylinder has a height of 2 m and a radius of 2 m. Find the rate at which the water is leaking out of the cylinder if the rate at which the height is decreasing is 10 cm/min when the height is 1 m.
Solution
The water flows out at rate ![]() /min.
/min.
30. A trough has ends shaped like isosceles triangles, with width 3 m and height 4 m, and the trough is 10 m long. Water is being pumped into the trough at a rate of ![]() /min. At what rate does the height of the water change when the water is 1 m deep?
/min. At what rate does the height of the water change when the water is 1 m deep?
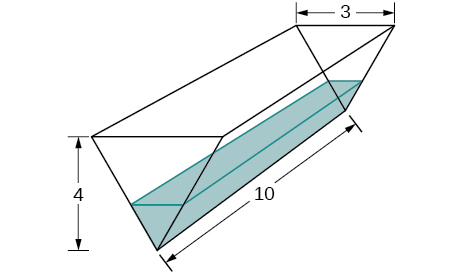
31. A tank is shaped like an upside-down square pyramid, with base of 4 m by 4 m and a height of 12 m (see the following figure). How fast does the height increase when the water is 2 m deep if water is being pumped in at a rate of ![]() /sec?
/sec?
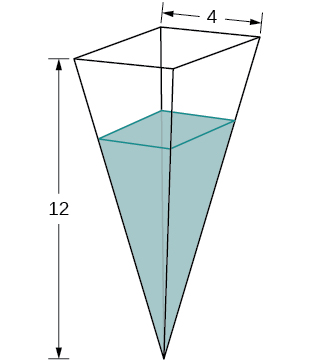
Solution
![]() m/sec
m/sec
For the following problems, consider a pool shaped like the bottom half of a sphere, that is being filled at a rate of 25 ![]() /min. The radius of the pool is 10 ft.
/min. The radius of the pool is 10 ft.
32. Find the rate at which the depth of the water is changing when the water has a depth of 5 ft.
33. Find the rate at which the depth of the water is changing when the water has a depth of 1 ft.
Solution
![]() ft/min
ft/min
34. If the height is increasing at a rate of 1 in/sec when the depth of the water is 2 ft, find the rate at which water is being pumped in.
35. Gravel is being unloaded from a truck and falls into a pile shaped like a cone at a rate of 10 ![]() /min. The radius of the cone base is three times the height of the cone. Find the rate at which the height of the gravel changes when the pile has a height of 5 ft.
/min. The radius of the cone base is three times the height of the cone. Find the rate at which the height of the gravel changes when the pile has a height of 5 ft.
Solution
![]() ft/min
ft/min
36. Using a similar setup from the preceding problem, find the rate at which the gravel is being unloaded if the pile is 5 ft high and the height is increasing at a rate of 4 in/min.
For the following exercises, draw the situations and solve the related-rate problems.
37. You are stationary on the ground and are watching a bird fly horizontally at a rate of 10 m/sec. The bird is located 40 m above your head. How fast does the angle of elevation change when the horizontal distance between you and the bird is 9 m?
Solution
The angle decreases at ![]() rad/sec.
rad/sec.
38. You stand 40 ft from a bottle rocket on the ground and watch as it takes off vertically into the air at a rate of 20 ft/sec. Find the rate at which the angle of elevation changes when the rocket is 30 ft in the air.
39. A lighthouse, ![]() , is on an island 4 mi away from the closest point,
, is on an island 4 mi away from the closest point, ![]() , on the beach (see the following image). If the lighthouse light rotates clockwise at a constant rate of 10 revolutions/min, how fast does the beam of light move across the beach 2 mi away from the closest point on the beach?
, on the beach (see the following image). If the lighthouse light rotates clockwise at a constant rate of 10 revolutions/min, how fast does the beam of light move across the beach 2 mi away from the closest point on the beach?
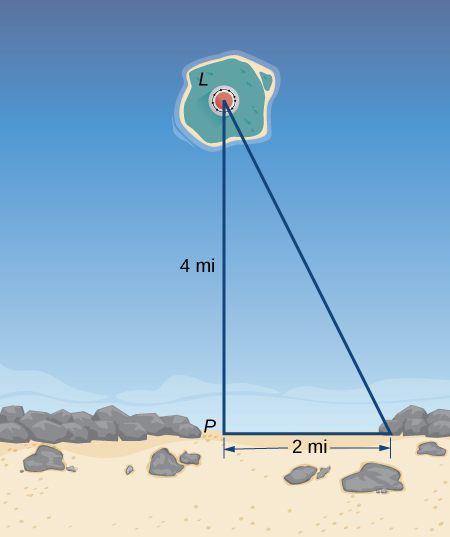
Solution
![]() mi/min
mi/min
40. Using the same setup as the previous problem, determine at what rate the beam of light moves across the beach 1 mi away from the closest point on the beach.
41. You are walking to a bus stop at a right-angle corner. You move north at a rate of 2 m/sec and are 20 m south of the intersection. The bus travels west at a rate of 10 m/sec away from the intersection – you have missed the bus! What is the rate at which the angle between you and the bus is changing when you are 20 m south of the intersection and the bus is 10 m west of the intersection?
Solution
The angle is changing at a rate of ![]() rad/sec.
rad/sec.
For the following exercises, refer to the figure of baseball diamond, which has sides of 90 ft.
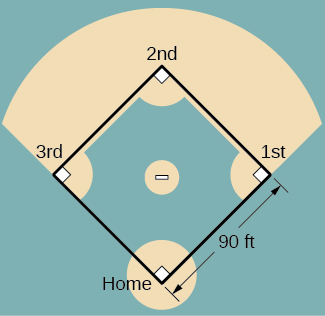
42. [T] A batter hits a ball toward third base at 75 ft/sec and runs toward first base at a rate of 24 ft/sec. At what rate does the distance between the ball and the batter change when 2 sec have passed?
43. [T] A batter hits a ball toward second base at 80 ft/sec and runs toward first base at a rate of 30 ft/sec. At what rate does the distance between the ball and the batter change when the runner has covered one-third of the distance to first base? (Hint: Recall the law of cosines.)
Solution
The distance is increasing at a rate of 62.50 ft/sec.
44. [T] A batter hits the ball and runs toward first base at a speed of 22 ft/sec. At what rate does the distance between the runner and second base change when the runner has run 30 ft?
45. [T] Runners start at first and second base. When the baseball is hit, the runner at first base runs at a speed of 18 ft/sec toward second base and the runner at second base runs at a speed of 20 ft/sec toward third base. How fast is the distance between runners changing 1 sec after the ball is hit?
Solution
The distance is decreasing at a rate of 11.99 ft/sec.
Glossary
- related rates
- are rates of change associated with two or more related quantities that are changing over time


Hint