Chapter 3.5: Continuity
Learning Objectives
- Explain the three conditions for continuity at a point.
- Describe three kinds of discontinuities.
- Define continuity on an interval.
- State the theorem for limits of composite functions.
- Provide an example of the intermediate value theorem.
Many functions have the property that their graphs can be traced with a pencil without lifting the pencil from the page. Such functions are called continuous. Other functions have points at which a break in the graph occurs, but satisfy this property over intervals contained in their domains. They are continuous on these intervals and are said to have a discontinuity at a point where a break occurs.
We begin our investigation of continuity by exploring what it means for a function to have continuity at a point. Intuitively, a function is continuous at a particular point if there is no break in its graph at that point.
Continuity at a Point
Before we look at a formal definition of what it means for a function to be continuous at a point, let’s consider various functions that fail to meet our intuitive notion of what it means to be continuous at a point. We then create a list of conditions that prevent such failures.
Our first function of interest is shown in (Figure). We see that the graph of ![]() has a hole at
has a hole at ![]() . In fact,
. In fact, ![]() is undefined. At the very least, for
is undefined. At the very least, for ![]() to be continuous at
to be continuous at ![]() , we need the following conditions:
, we need the following conditions:
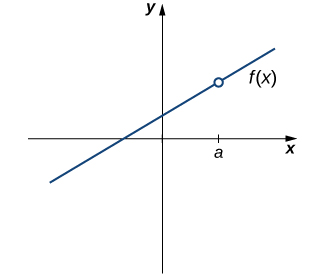
 is not continuous at a because
is not continuous at a because  is undefined.
is undefined.However, as we see in (Figure), this condition alone is insufficient to guarantee continuity at the point ![]() . Although
. Although ![]() is defined, the function has a gap at
is defined, the function has a gap at ![]() . In this example, the gap exists because
. In this example, the gap exists because ![]() does not exist. We must add another condition for continuity at
does not exist. We must add another condition for continuity at ![]() —namely,
—namely,
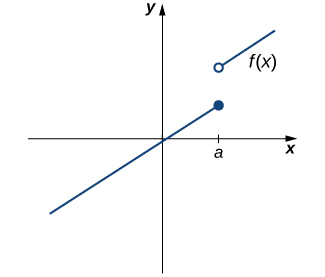
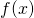 is not continuous at a because
is not continuous at a because  does not exist.
does not exist.However, as we see in (Figure), these two conditions by themselves do not guarantee continuity at a point. The function in this figure satisfies both of our first two conditions, but is still not continuous at ![]() . We must add a third condition to our list:
. We must add a third condition to our list:
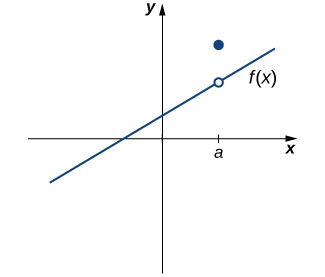
 is not continuous at a because
is not continuous at a because 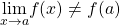 .
.Now we put our list of conditions together and form a definition of continuity at a point.
Definition
A function ![]() is continuous at a point
is continuous at a point ![]() if and only if the following three conditions are satisfied:
if and only if the following three conditions are satisfied:
-
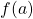 is defined
is defined -
 exists
exists -
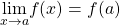
A function is discontinuous at a point ![]() if it fails to be continuous at
if it fails to be continuous at ![]() .
.
The following procedure can be used to analyze the continuity of a function at a point using this definition.
Problem-Solving Strategy: Determining Continuity at a Point
- Check to see if
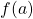 is defined. If
is defined. If 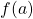 is undefined, we need go no further. The function is not continuous at
is undefined, we need go no further. The function is not continuous at  . If
. If 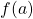 is defined, continue to step 2.
is defined, continue to step 2. - Compute
 . In some cases, we may need to do this by first computing
. In some cases, we may need to do this by first computing 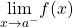 and
and 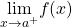 . If
. If  does not exist (that is, it is not a real number), then the function is not continuous at
does not exist (that is, it is not a real number), then the function is not continuous at  and the problem is solved. If
and the problem is solved. If  exists, then continue to step 3.
exists, then continue to step 3. - Compare
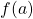 and
and  . If
. If 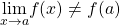 , then the function is not continuous at
, then the function is not continuous at  . If
. If 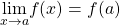 , then the function is continuous at
, then the function is continuous at  .
.
The next three examples demonstrate how to apply this definition to determine whether a function is continuous at a given point. These examples illustrate situations in which each of the conditions for continuity in the definition succeed or fail.
Determining Continuity at a Point, Condition 1
Using the definition, determine whether the function ![]() is continuous at
is continuous at ![]() . Justify the conclusion.
. Justify the conclusion.
Solution
Let’s begin by trying to calculate ![]() . We can see that
. We can see that ![]() , which is undefined. Therefore,
, which is undefined. Therefore, ![]() is discontinuous at 2 because
is discontinuous at 2 because ![]() is undefined. The graph of
is undefined. The graph of ![]() is shown in (Figure).
is shown in (Figure).

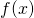 is discontinuous at 2 because
is discontinuous at 2 because 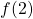 is undefined.
is undefined.Determining Continuity at a Point, Condition 2
Using the definition, determine whether the function 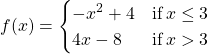 is continuous at
is continuous at ![]() . Justify the conclusion.
. Justify the conclusion.
Solution
Let’s begin by trying to calculate ![]() .
.
Thus, ![]() is defined. Next, we calculate
is defined. Next, we calculate ![]() . To do this, we must compute
. To do this, we must compute ![]() and
and ![]() :
:
and
Therefore, ![]() does not exist. Thus,
does not exist. Thus, ![]() is not continuous at 3. The graph of
is not continuous at 3. The graph of ![]() is shown in (Figure).
is shown in (Figure).

Determining Continuity at a Point, Condition 3
Using the definition, determine whether the function 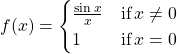 is continuous at
is continuous at ![]() .
.
Solution
First, observe that
Next,
Last, compare ![]() and
and ![]() . We see that
. We see that
Since all three of the conditions in the definition of continuity are satisfied, ![]() is continuous at
is continuous at ![]() .
.
Using the definition, determine whether the function 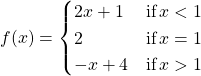 is continuous at
is continuous at ![]() . If the function is not continuous at 1, indicate the condition for continuity at a point that fails to hold.
. If the function is not continuous at 1, indicate the condition for continuity at a point that fails to hold.
Solution
![]() is not continuous at 1 because
is not continuous at 1 because ![]() .
.
By applying the definition of continuity and previously established theorems concerning the evaluation of limits, we can state the following theorem.
Continuity of Polynomials and Rational Functions
Polynomials and rational functions are continuous at every point in their domains.
Proof
Previously, we showed that if ![]() and
and ![]() are polynomials,
are polynomials, ![]() for every polynomial
for every polynomial ![]() and
and ![]() as long as
as long as ![]() . Therefore, polynomials and rational functions are continuous on their domains.
. Therefore, polynomials and rational functions are continuous on their domains. ![]()
We now apply (Figure) to determine the points at which a given rational function is continuous.
Continuity of a Rational Function
For what values of ![]() is
is ![]() continuous?
continuous?
Solution
The rational function ![]() is continuous for every value of
is continuous for every value of ![]() except
except ![]() .
.
Types of Discontinuities
As we have seen in (Figure) and (Figure), discontinuities take on several different appearances. We classify the types of discontinuities we have seen thus far as removable discontinuities, infinite discontinuities, or jump discontinuities. Intuitively, a removable discontinuity is a discontinuity for which there is a hole in the graph, a jump discontinuity is a noninfinite discontinuity for which the sections of the function do not meet up, and an infinite discontinuity is a discontinuity located at a vertical asymptote. (Figure) illustrates the differences in these types of discontinuities. Although these terms provide a handy way of describing three common types of discontinuities, keep in mind that not all discontinuities fit neatly into these categories.
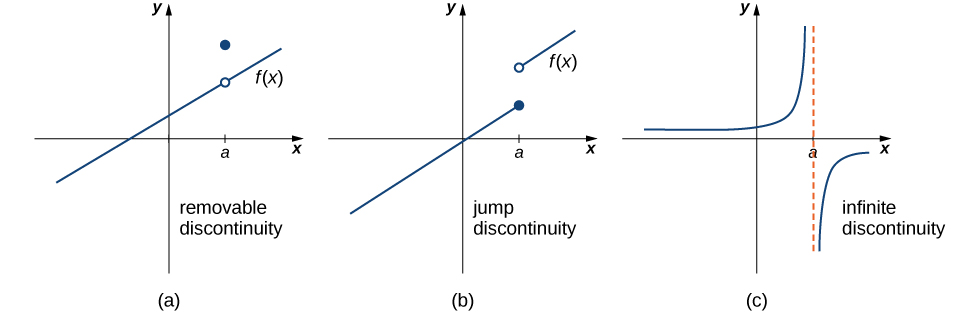
These three discontinuities are formally defined as follows:
Definition
If ![]() is discontinuous at
is discontinuous at ![]() , then
, then
-
 has a removable discontinuity at
has a removable discontinuity at  if
if  exists. (Note: When we state that
exists. (Note: When we state that  exists, we mean that
exists, we mean that 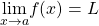 , where
, where 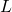 is a real number.)
is a real number.) -
 has a jump discontinuity at
has a jump discontinuity at  if
if 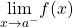 and
and 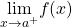 both exist, but
both exist, but 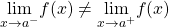 . (Note: When we state that
. (Note: When we state that 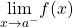 and
and 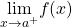 both exist, we mean that both are real-valued and that neither take on the values
both exist, we mean that both are real-valued and that neither take on the values  .)
.) -
 has an infinite discontinuity at
has an infinite discontinuity at  if
if 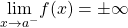 or
or  .
.
Classifying a Discontinuity
In (Figure), we showed that ![]() is discontinuous at
is discontinuous at ![]() . Classify this discontinuity as removable, jump, or infinite.
. Classify this discontinuity as removable, jump, or infinite.
Solution
To classify the discontinuity at 2 we must evaluate ![]() :
:
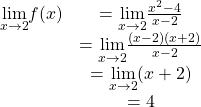
Since ![]() is discontinuous at 2 and
is discontinuous at 2 and ![]() exists,
exists, ![]() has a removable discontinuity at
has a removable discontinuity at ![]() .
.
Classifying a Discontinuity
In (Figure), we showed that 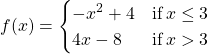 is discontinuous at
is discontinuous at ![]() . Classify this discontinuity as removable, jump, or infinite.
. Classify this discontinuity as removable, jump, or infinite.
Solution
Earlier, we showed that ![]() is discontinuous at 3 because
is discontinuous at 3 because ![]() does not exist. However, since
does not exist. However, since ![]() and
and ![]() both exist, we conclude that the function has a jump discontinuity at 3.
both exist, we conclude that the function has a jump discontinuity at 3.
Classifying a Discontinuity
Determine whether ![]() is continuous at −1. If the function is discontinuous at −1, classify the discontinuity as removable, jump, or infinite.
is continuous at −1. If the function is discontinuous at −1, classify the discontinuity as removable, jump, or infinite.
Solution
The function value ![]() is undefined. Therefore, the function is not continuous at −1. To determine the type of discontinuity, we must determine the limit at −1. We see that
is undefined. Therefore, the function is not continuous at −1. To determine the type of discontinuity, we must determine the limit at −1. We see that ![]() and
and ![]() . Therefore, the function has an infinite discontinuity at −1.
. Therefore, the function has an infinite discontinuity at −1.
For 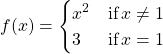 , decide whether
, decide whether ![]() is continuous at 1. If
is continuous at 1. If ![]() is not continuous at 1, classify the discontinuity as removable, jump, or infinite.
is not continuous at 1, classify the discontinuity as removable, jump, or infinite.
Solution
Discontinuous at 1; removable
Hint
Follow the steps in (Figure). If the function is discontinuous at 1, look at ![]() and use the definition to determine the type of discontinuity.
and use the definition to determine the type of discontinuity.
Continuity over an Interval
Now that we have explored the concept of continuity at a point, we extend that idea to continuity over an interval. As we develop this idea for different types of intervals, it may be useful to keep in mind the intuitive idea that a function is continuous over an interval if we can use a pencil to trace the function between any two points in the interval without lifting the pencil from the paper. In preparation for defining continuity on an interval, we begin by looking at the definition of what it means for a function to be continuous from the right at a point and continuous from the left at a point.
Continuity from the Right and from the Left
A function ![]() is said to be continuous from the right at
is said to be continuous from the right at ![]() if
if ![]() .
.
A function ![]() is said to be continuous from the left at
is said to be continuous from the left at ![]() if
if ![]() .
.
A function is continuous over an open interval if it is continuous at every point in the interval. A function ![]() is continuous over a closed interval of the form
is continuous over a closed interval of the form ![]() if it is continuous at every point in
if it is continuous at every point in ![]() and is continuous from the right at
and is continuous from the right at ![]() and is continuous from the left at
and is continuous from the left at ![]() . Analogously, a function
. Analogously, a function ![]() is continuous over an interval of the form
is continuous over an interval of the form ![]() if it is continuous over
if it is continuous over ![]() and is continuous from the left at
and is continuous from the left at ![]() . Continuity over other types of intervals are defined in a similar fashion.
. Continuity over other types of intervals are defined in a similar fashion.
Requiring that ![]() and
and ![]() ensures that we can trace the graph of the function from the point
ensures that we can trace the graph of the function from the point ![]() to the point
to the point ![]() without lifting the pencil. If, for example,
without lifting the pencil. If, for example, ![]() , we would need to lift our pencil to jump from
, we would need to lift our pencil to jump from ![]() to the graph of the rest of the function over
to the graph of the rest of the function over ![]() .
.
Continuity on an Interval
State the interval(s) over which the function ![]() is continuous.
is continuous.
Solution
Since ![]() is a rational function, it is continuous at every point in its domain. The domain of
is a rational function, it is continuous at every point in its domain. The domain of ![]() is the set
is the set ![]() . Thus,
. Thus, ![]() is continuous over each of the intervals
is continuous over each of the intervals ![]() , and
, and ![]() .
.
Continuity over an Interval
State the interval(s) over which the function ![]() is continuous.
is continuous.
Solution
From the limit laws, we know that ![]() for all values of
for all values of ![]() in
in ![]() . We also know that
. We also know that ![]() exists and
exists and ![]() exists. Therefore,
exists. Therefore, ![]() is continuous over the interval
is continuous over the interval ![]() .
.
State the interval(s) over which the function ![]() is continuous.
is continuous.
Solution
![]()
Hint
Use (Figure) as a guide for solving.
The (Figure) allows us to expand our ability to compute limits. In particular, this theorem ultimately allows us to demonstrate that trigonometric functions are continuous over their domains.
Composite Function Theorem
If ![]() is continuous at
is continuous at ![]() and
and ![]() , then
, then
Before we move on to (Figure), recall that earlier, in the section on limit laws, we showed ![]() . Consequently, we know that
. Consequently, we know that ![]() is continuous at 0. In (Figure) we see how to combine this result with the composite function theorem.
is continuous at 0. In (Figure) we see how to combine this result with the composite function theorem.
Limit of a Composite Cosine Function
Evaluate ![]() .
.
Solution
The given function is a composite of ![]() and
and ![]() . Since
. Since ![]() and
and ![]() is continuous at 0, we may apply the composite function theorem. Thus,
is continuous at 0, we may apply the composite function theorem. Thus,
The proof of the next theorem uses the composite function theorem as well as the continuity of ![]() and
and ![]() at the point 0 to show that trigonometric functions are continuous over their entire domains.
at the point 0 to show that trigonometric functions are continuous over their entire domains.
Continuity of Trigonometric Functions
Trigonometric functions are continuous over their entire domains.
Proof
We begin by demonstrating that ![]() is continuous at every real number. To do this, we must show that
is continuous at every real number. To do this, we must show that ![]() for all values of
for all values of ![]() .
.

The proof that ![]() is continuous at every real number is analogous. Because the remaining trigonometric functions may be expressed in terms of
is continuous at every real number is analogous. Because the remaining trigonometric functions may be expressed in terms of ![]() and
and ![]() their continuity follows from the quotient limit law.
their continuity follows from the quotient limit law. ![]()
As you can see, the composite function theorem is invaluable in demonstrating the continuity of trigonometric functions. As we continue our study of calculus, we revisit this theorem many times.
The Intermediate Value Theorem
Functions that are continuous over intervals of the form ![]() , where
, where ![]() and
and ![]() are real numbers, exhibit many useful properties. Throughout our study of calculus, we will encounter many powerful theorems concerning such functions. The first of these theorems is the Intermediate Value Theorem.
are real numbers, exhibit many useful properties. Throughout our study of calculus, we will encounter many powerful theorems concerning such functions. The first of these theorems is the Intermediate Value Theorem.
The Intermediate Value Theorem
Let ![]() be continuous over a closed, bounded interval
be continuous over a closed, bounded interval ![]() . If
. If ![]() is any real number between
is any real number between ![]() and
and ![]() , then there is a number
, then there is a number ![]() in
in ![]() satisfying
satisfying ![]() . (See (Figure)).
. (See (Figure)).
![A diagram illustrating the intermediate value theorem. There is a generic continuous curved function shown over the interval [a,b]. The points fa. and fb. are marked, and dotted lines are drawn from a, b, fa., and fb. to the points (a, fa.) and (b, fb.). A third point, c, is plotted between a and b. Since the function is continuous, there is a value for fc. along the curve, and a line is drawn from c to (c, fc.) and from (c, fc.) to fc., which is labeled as z on the y axis.](https://s3-us-west-2.amazonaws.com/courses-images/wp-content/uploads/sites/2332/2018/01/11203518/CNX_Calc_Figure_02_04_007.jpg)
![Rendered by QuickLaTeX.com c \in [a,b]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-28289cc7f228a5994a26b387092e07a1_l3.png) that satisfies
that satisfies 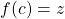 .
.Application of the Intermediate Value Theorem
Show that ![]() has at least one zero.
has at least one zero.
Solution
Since ![]() is continuous over
is continuous over ![]() , it is continuous over any closed interval of the form
, it is continuous over any closed interval of the form ![]() . If you can find an interval
. If you can find an interval ![]() such that
such that ![]() and
and ![]() have opposite signs, you can use the Intermediate Value Theorem to conclude there must be a real number
have opposite signs, you can use the Intermediate Value Theorem to conclude there must be a real number ![]() in
in ![]() that satisfies
that satisfies ![]() . Note that
. Note that
and
Using the Intermediate Value Theorem, we can see that there must be a real number ![]() in
in ![]() that satisfies
that satisfies ![]() . Therefore,
. Therefore, ![]() has at least one zero.
has at least one zero.
When Can You Apply the Intermediate Value Theorem?
If ![]() is continuous over
is continuous over ![]() , and
, and ![]() can we use the Intermediate Value Theorem to conclude that
can we use the Intermediate Value Theorem to conclude that ![]() has no zeros in the interval
has no zeros in the interval ![]() ? Explain.
? Explain.
Solution
No. The Intermediate Value Theorem only allows us to conclude that we can find a value between ![]() and
and ![]() ; it doesn’t allow us to conclude that we can’t find other values. To see this more clearly, consider the function
; it doesn’t allow us to conclude that we can’t find other values. To see this more clearly, consider the function ![]() . It satisfies
. It satisfies ![]() , and
, and ![]() .
.
When Can You Apply the Intermediate Value Theorem?
For ![]() and
and ![]() . Can we conclude that
. Can we conclude that ![]() has a zero in the interval
has a zero in the interval ![]() ?
?
Solution
No. The function is not continuous over ![]() . The Intermediate Value Theorem does not apply here.
. The Intermediate Value Theorem does not apply here.
Show that ![]() has a zero over the interval
has a zero over the interval ![]() .
.
Solution
![]() ;
; ![]() is continuous over
is continuous over ![]() . It must have a zero on this interval.
. It must have a zero on this interval.
Hint
Find ![]() and
and ![]() . Apply the Intermediate Value Theorem.
. Apply the Intermediate Value Theorem.
Key Concepts
- For a function to be continuous at a point, it must be defined at that point, its limit must exist at the point, and the value of the function at that point must equal the value of the limit at that point.
- Discontinuities may be classified as removable, jump, or infinite.
- A function is continuous over an open interval if it is continuous at every point in the interval. It is continuous over a closed interval if it is continuous at every point in its interior and is continuous at its endpoints.
- The composite function theorem states: If
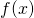 is continuous at
is continuous at 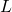 and
and 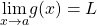 , then
, then 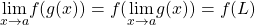 .
. - The Intermediate Value Theorem guarantees that if a function is continuous over a closed interval, then the function takes on every value between the values at its endpoints.
For the following exercises, determine the point(s), if any, at which each function is discontinuous. Classify any discontinuity as jump, removable, infinite, or other.
1. ![]()
Show Solution
The function is defined for all ![]() in the interval
in the interval ![]() .
.
2. ![]()
3. ![]()
Solution
Removable discontinuity at ![]() ; infinite discontinuity at
; infinite discontinuity at ![]()
4. ![]()
5. ![]()
Solution
Infinite discontinuity at ![]()
6. ![]()
7. ![]()
Solution
Infinite discontinuities at ![]() , for
, for ![]()
8. ![]()
For the following exercises, decide if the function continuous at the given point. If it is discontinuous, what type of discontinuity is it?
9. ![]() at
at ![]()
Solution
No. It is a removable discontinuity.
10. ![]() at
at ![]()
11. 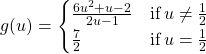 at
at ![]()
Solution
Yes. It is continuous.
12. ![]() , at
, at ![]()
13. 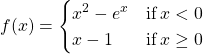 at
at ![]()
Solution
Yes. It is continuous.
14. 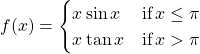 at
at ![]()
In the following exercises, find the value(s) of ![]() that makes each function continuous over the given interval.
that makes each function continuous over the given interval.
15. 
Solution
![]()
16. 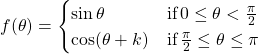
17. 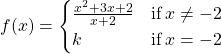
Solution
![]()
18. 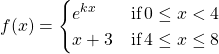
19. 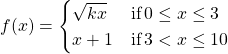
Solution
![]()
In the following exercises, use the Intermediate Value Theorem (IVT).
20. Let 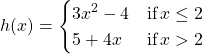 Over the interval
Over the interval ![]() , there is no value of
, there is no value of ![]() such that
such that ![]() , although
, although ![]() and
and ![]() . Explain why this does not contradict the IVT.
. Explain why this does not contradict the IVT.
21. A particle moving along a line has at each time ![]() a position function
a position function ![]() , which is continuous. Assume
, which is continuous. Assume ![]() and
and ![]() . Another particle moves such that its position is given by
. Another particle moves such that its position is given by ![]() . Explain why there must be a value
. Explain why there must be a value ![]() for
for ![]() such that
such that ![]() .
.
Solution
Since both ![]() and
and ![]() are continuous everywhere, then
are continuous everywhere, then ![]() is continuous everywhere and, in particular, it is continuous over the closed interval
is continuous everywhere and, in particular, it is continuous over the closed interval ![]() . Also,
. Also, ![]() and
and ![]() . Therefore, by the IVT, there is a value
. Therefore, by the IVT, there is a value ![]() such that
such that ![]() .
.
22. [T] Use the statement “The cosine of ![]() is equal to
is equal to ![]() cubed.”
cubed.”
- Write the statement as a mathematical equation.
- Prove that the equation in part a. has at least one real solution.
- Use a calculator to find an interval of length 0.01 that contains a solution of the equation.
23. Apply the IVT to determine whether ![]() has a solution in one of the intervals
has a solution in one of the intervals ![]() or
or ![]() . Briefly explain your response for each interval.
. Briefly explain your response for each interval.
Solution
The function ![]() is continuous over the interval
is continuous over the interval ![]() and has opposite signs at the endpoints.
and has opposite signs at the endpoints.
24. Consider the graph of the function ![]() shown in the following graph.
shown in the following graph.
![A diagram illustrating the intermediate value theorem. There is a generic continuous curved function shown over the interval [a,b]. The points fa. and fb. are marked, and dotted lines are drawn from a, b, fa., and fb. to the points (a, fa.) and (b, fb.). A third point, c, is plotted between a and b. Since the function is continuous, there is a value for fc. along the curve, and a line is drawn from c to (c, fc.) and from (c, fc.) to fc., which is labeled as z on the y axis.](https://s3-us-west-2.amazonaws.com/courses-images/wp-content/uploads/sites/2332/2018/01/11203520/CNX_Calc_Figure_02_04_201.jpg)
- Find all values for which the function is discontinuous.
- For each value in part a., use the formal definition of continuity to explain why the function is discontinuous at that value.
- Classify each discontinuity as either jump, removable, or infinite.
25. Let 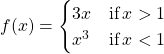
- Sketch the graph of
 .
. - Is it possible to find a value
 such that
such that 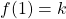 , which makes
, which makes 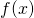 continuous for all real numbers? Briefly explain.
continuous for all real numbers? Briefly explain.
Solution
a.
b. It is not possible to redefine ![]() since the discontinuity is a jump discontinuity.
since the discontinuity is a jump discontinuity.
26. Let ![]() for
for ![]() .
.
- Sketch the graph of
 .
. - Is it possible to find values
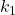 and
and  such that
such that 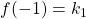 and
and  , and that makes
, and that makes 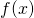 continuous for all real numbers? Briefly explain.
continuous for all real numbers? Briefly explain.
27. Sketch the graph of the function ![]() with properties i. through vii.
with properties i. through vii.
- The domain of
 is
is 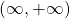 .
. -
 has an infinite discontinuity at
has an infinite discontinuity at 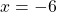 .
. -
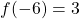
-

-
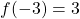
-
 is left continuous but not right continuous at
is left continuous but not right continuous at 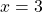 .
. -
 and
and 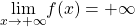
Solution
Answers may vary; see the following example:

28. Sketch the graph of the function ![]() with properties i. through iv.
with properties i. through iv.
- The domain of
 is
is ![Rendered by QuickLaTeX.com [0,5]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-89b821eefc8fc303d9028c7e6072e2df_l3.png) .
. -
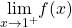 and
and 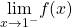 exist and are equal.
exist and are equal. -
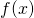 is left continuous but not continuous at
is left continuous but not continuous at  , and right continuous but not continuous at
, and right continuous but not continuous at 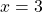 .
. -
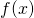 has a removable discontinuity at
has a removable discontinuity at 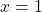 , a jump discontinuity at
, a jump discontinuity at  , and the following limits hold:
, and the following limits hold: 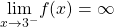 and
and 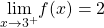 .
.
In the following exercises, suppose ![]() is defined for all
is defined for all ![]() . For each description, sketch a graph with the indicated property.
. For each description, sketch a graph with the indicated property.
29. Discontinuous at ![]() with
with ![]() and
and ![]()
Solution
Answers may vary; see the following example:

30. Discontinuous at ![]() but continuous elsewhere with
but continuous elsewhere with ![]()
Determine whether each of the given statements is true. Justify your response with an explanation or counterexample.
31. ![]() is continuous everywhere.
is continuous everywhere.
Solution
False. It is continuous over ![]() .
.
32. If the left- and right-hand limits of ![]() as
as ![]() exist and are equal, then
exist and are equal, then ![]() cannot be discontinuous at
cannot be discontinuous at ![]() .
.
33. If a function is not continuous at a point, then it is not defined at that point.
Solution
False. Consider 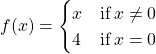
34. According to the IVT, ![]() has a solution over the interval
has a solution over the interval ![]() .
.
35. If ![]() is continuous such that
is continuous such that ![]() and
and ![]() have opposite signs, then
have opposite signs, then ![]() has exactly one solution in
has exactly one solution in ![]() .
.
Solution
False. Consider ![]() on
on ![]() .
.
36. The function ![]() is continuous over the interval
is continuous over the interval ![]() .
.
37. If ![]() is continuous everywhere and
is continuous everywhere and ![]() , then there is no root of
, then there is no root of ![]() in the interval
in the interval ![]() .
.
Solution
False. The IVT does not work in reverse! Consider ![]() over the interval
over the interval ![]() .
.
The following problems consider the scalar form of Coulomb’s law, which describes the electrostatic force between two point charges, such as electrons. It is given by the equation ![]() , where
, where ![]() is Coulomb’s constant,
is Coulomb’s constant, ![]() are the magnitudes of the charges of the two particles, and
are the magnitudes of the charges of the two particles, and ![]() is the distance between the two particles.
is the distance between the two particles.
38. [T] To simplify the calculation of a model with many interacting particles, after some threshold value ![]() , we approximate
, we approximate ![]() as zero.
as zero.
- Explain the physical reasoning behind this assumption.
- What is the force equation?
- Evaluate the force
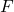 using both Coulomb’s law and our approximation, assuming two protons with a charge magnitude of
using both Coulomb’s law and our approximation, assuming two protons with a charge magnitude of 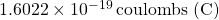 , and the Coulomb constant
, and the Coulomb constant 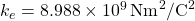 are 1 m apart. Also, assume
are 1 m apart. Also, assume 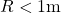 . How much inaccuracy does our approximation generate? Is our approximation reasonable?
. How much inaccuracy does our approximation generate? Is our approximation reasonable? - Is there any finite value of
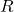 for which this system remains continuous at
for which this system remains continuous at 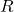 ?
?
39. [T] Instead of making the force 0 at ![]() , instead we let the force be
, instead we let the force be ![]() for
for ![]() . Assume two protons, which have a magnitude of charge
. Assume two protons, which have a magnitude of charge ![]() , and the Coulomb constant
, and the Coulomb constant ![]() . Is there a value
. Is there a value ![]() that can make this system continuous? If so, find it.
that can make this system continuous? If so, find it.
Solution
![]()
Recall the discussion on spacecraft from the chapter opener. The following problems consider a rocket launch from Earth’s surface. The force of gravity on the rocket is given by ![]() , where
, where ![]() is the mass of the rocket,
is the mass of the rocket, ![]() is the distance of the rocket from the center of Earth, and
is the distance of the rocket from the center of Earth, and ![]() is a constant.
is a constant.
40. [T] Determine the value and units of ![]() given that the mass of the rocket on Earth is 3 million kg. (Hint: The distance from the center of Earth to its surface is 6378 km.)
given that the mass of the rocket on Earth is 3 million kg. (Hint: The distance from the center of Earth to its surface is 6378 km.)
41. [T] After a certain distance ![]() has passed, the gravitational effect of Earth becomes quite negligible, so we can approximate the force function by
has passed, the gravitational effect of Earth becomes quite negligible, so we can approximate the force function by 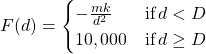 Find the necessary condition
Find the necessary condition ![]() such that the force function remains continuous.
such that the force function remains continuous.
Solution
![]() km
km
42. As the rocket travels away from Earth’s surface, there is a distance ![]() where the rocket sheds some of its mass, since it no longer needs the excess fuel storage. We can write this function as
where the rocket sheds some of its mass, since it no longer needs the excess fuel storage. We can write this function as  Is there a
Is there a ![]() value such that this function is continuous, assuming
value such that this function is continuous, assuming ![]() ?
?
Prove the following functions are continuous everywhere
43. ![]()
Solution
For all values of ![]() is defined,
is defined, ![]() exists, and
exists, and ![]() . Therefore,
. Therefore, ![]() is continuous everywhere.
is continuous everywhere.
44. ![]()
45. Where is 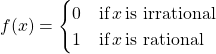 continuous?
continuous?
Solution
Nowhere
Glossary
- continuity at a point
- A function
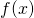 is continuous at a point
is continuous at a point  if and only if the following three conditions are satisfied: (1)
if and only if the following three conditions are satisfied: (1) 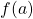 is defined, (2)
is defined, (2)  exists, and (3)
exists, and (3) 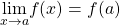
- continuity from the left
- A function is continuous from the left at
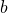 if
if 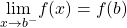
- continuity from the right
- A function is continuous from the right at
 if
if 
- continuity over an interval
- a function that can be traced with a pencil without lifting the pencil; a function is continuous over an open interval if it is continuous at every point in the interval; a function
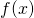 is continuous over a closed interval of the form
is continuous over a closed interval of the form ![Rendered by QuickLaTeX.com [a,b]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-fcda5ef4ae327e1afef79dc73df91703_l3.png) if it is continuous at every point in
if it is continuous at every point in 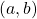 , and it is continuous from the right at
, and it is continuous from the right at  and from the left at
and from the left at 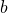
- discontinuity at a point
- A function is discontinuous at a point or has a discontinuity at a point if it is not continuous at the point
- infinite discontinuity
- An infinite discontinuity occurs at a point
 if
if 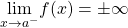 or
or 
- Intermediate Value Theorem
- Let
 be continuous over a closed bounded interval
be continuous over a closed bounded interval ![Rendered by QuickLaTeX.com [a,b]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-fcda5ef4ae327e1afef79dc73df91703_l3.png) ; if
; if  is any real number between
is any real number between 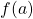 and
and 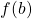 , then there is a number
, then there is a number  in
in ![Rendered by QuickLaTeX.com [a,b]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-fcda5ef4ae327e1afef79dc73df91703_l3.png) satisfying
satisfying 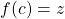
- jump discontinuity
- A jump discontinuity occurs at a point
 if
if 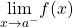 and
and 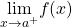 both exist, but
both exist, but 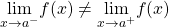
- removable discontinuity
- A removable discontinuity occurs at a point
 if
if 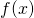 is discontinuous at
is discontinuous at  , but
, but  exists
exists


Hint
Check each condition of the definition.