Chapter 3 Review Exercises

Mike LePine

Chapter 3 Review Exercises

True or False. In the following exercises, justify your answer with a proof or a counterexample.

1. A function has to be continuous at $x=a$ if the $\underset{x\to a}{\lim}f(x)$ exists.

2. You can use the quotient rule to evaluate $\underset{x\to 0}{\lim}\frac{\sin x}{x}$ .

Solution

False

3. If there is a vertical asymptote at $x=a$ for the function $f(x)$ , then $f$ is undefined at the point $x=a$ .

4. If $\underset{x\to a}{\lim}f(x)$ does not exist, then $f$ is undefined at the point $x=a$ .

Solution

False. A removable discontinuity is possible.

5. Using the graph, find each limit or explain why the limit does not exist.

$\underset{x\to -1}{\lim}f(x)$
$\underset{x\to 1}{\lim}f(x)$
$\underset{x\to 0^+}{\lim}f(x)$
$\underset{x\to 2}{\lim}f(x)$

A graph of a piecewise function with several segments. The first is a decreasing concave up curve existing for x 1, starting at the open circle at (1,1).

In the following exercises, evaluate the limit algebraically or explain why the limit does not exist.

6. $\underset{x\to 2}{\lim}\frac{2x^2-3x-2}{x-2}$

Solution

5

7. $\underset{x\to 0}{\lim}3x^2-2x+4$

8. $\underset{x\to 3}{\lim}\frac{x^3-2x^2-1}{3x-2}$

Solution

$8/7$

9. $\underset{x\to \pi/2}{\lim}\frac{\cot x}{\cos x}$

10. $\underset{x\to -5}{\lim}\frac{x^2+25}{x+5}$

Solution

DNE

11. $\underset{x\to 2}{\lim}\frac{3x^2-2x-8}{x^2-4}$

12. $\underset{x\to 1}{\lim}\frac{x^2-1}{x^3-1}$

Solution

$2/3$

13. $\underset{x\to 1}{\lim}\frac{x^2-1}{\sqrt{x}-1}$

14. $\underset{x\to 4}{\lim}\frac{4-x}{\sqrt{x}-2}$

Solution

−4

15. $\underset{x\to 4}{\lim}\frac{1}{\sqrt{x}-2}$

In the following exercises, use the squeeze theorem to prove the limit.

16. $\underset{x\to 0}{\lim}x^2\cos(2\pi x)=0$

Solution

Since $-1\le \cos (2\pi x)\le 1$ , then $-x^2\le x^2\cos(2\pi x)\le x^2$ . Since $\underset{x\to 0}{\lim}x^2=0=\underset{x\to 0}{\lim}-x^2$ , it follows that $\underset{x\to 0}{\lim}x^2\cos(2\pi x)=0$ .

17. $\underset{x\to 0}{\lim}x^3\sin(\frac{\pi}{x})=0$

18. Determine the domain such that the function $f(x)=\sqrt{x-2}+xe^x$ is continuous over its domain.

Solution

$[2,\infty)$

In the following exercises, determine the value of $c$ such that the function remains continuous. Draw your resulting function to ensure it is continuous.

19. $f(x)=\begin{cases} x^2+1 & \text{if} \, x>c \\ 2x & \text{if} \, x \le c \end{cases}$

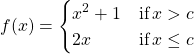
20. $f(x)=\begin{cases} \sqrt{x+1} & \text{if} \, x > -1 \\ x^2+c & \text{if} \, x \le -1 \end{cases}$

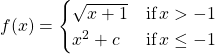
Solution

$c=-1$

In the following exercises, use the precise definition of limit to prove the limit.

21. $\underset{x\to 1}{\lim}(8x+16)=24$

22. $\underset{x\to 0}{\lim}x^3=0$

Solution

$\delta =\sqrt[3]{\epsilon}$

23. A ball is thrown into the air and the vertical position is given by $x(t)=-4.9t^2+25t+5$ . Use the Intermediate Value Theorem to show that the ball must land on the ground sometime between 5 sec and 6 sec after the throw.

24. A particle moving along a line has a displacement according to the function $x(t)=t^2-2t+4$ , where $x$ is measured in meters and $t$ is measured in seconds. Find the average velocity over the time period $t=[0,2]$ .