Chapter 1.7: Matrices and Matrix Operations
Learning Objectives
In this section, you will:
- Find the sum and difference of two matrices.
- Find scalar multiples of a matrix.
- Find the product of two matrices.

Two club soccer teams, the Wildcats and the Mud Cats, are hoping to obtain new equipment for an upcoming season. (Figure) shows the needs of both teams.
| Wildcats | Mud Cats | |
|---|---|---|
| Goals | 6 | 10 |
| Balls | 30 | 24 |
| Jerseys | 14 | 20 |
A goal costs $300; a ball costs $10; and a jersey costs $30. How can we find the total cost for the equipment needed for each team? In this section, we discover a method in which the data in the soccer equipment table can be displayed and used for calculating other information. Then, we will be able to calculate the cost of the equipment.
Finding the Sum and Difference of Two Matrices
To solve a problem like the one described for the soccer teams, we can use a matrix, which is a rectangular array of numbers. A row in a matrix is a set of numbers that are aligned horizontally. A column in a matrix is a set of numbers that are aligned vertically. Each number is an entry, sometimes called an element, of the matrix. Matrices (plural) are enclosed in [ ] or ( ), and are usually named with capital letters. For example, three matrices named ![]() and
and ![]() are shown below.
are shown below.
![Rendered by QuickLaTeX.com A=\left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right],B=\left[\begin{array}{ccc}1& 2& 7\\ 0& -5& 6\\ 7& 8& 2\end{array}\right],C=\left[\begin{array}{c}-1\\ \,\,\,0\\ \,\,\,3\end{array}\,\,\,\,\begin{array}{c}3\\ 2\\ 1\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-cd4567a1d70a386c7f48b4f0965532fa_l3.png)
Describing Matrices
A matrix is often referred to by its size or dimensions: ![]() indicating
indicating ![]() rows and
rows and ![]() columns. Matrix entries are defined first by row and then by column. For example, to locate the entry in matrix
columns. Matrix entries are defined first by row and then by column. For example, to locate the entry in matrix ![]() identified as
identified as ![]() we look for the entry in row
we look for the entry in row ![]() column
column ![]() In matrix
In matrix ![]() shown below, the entry in row 2, column 3 is
shown below, the entry in row 2, column 3 is ![]()
![Rendered by QuickLaTeX.com A=\left[\begin{array}{ccc}{a}_{11}& {a}_{12}& {a}_{13}\\ {a}_{21}& {a}_{22}& {a}_{23}\\ {a}_{31}& {a}_{32}& {a}_{33}\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-0fcc0b1448aa33d56fab1e49ab8e8138_l3.png)
A square matrix is a matrix with dimensions ![]() meaning that it has the same number of rows as columns. The
meaning that it has the same number of rows as columns. The ![]() matrix above is an example of a square matrix.
matrix above is an example of a square matrix.
A row matrix is a matrix consisting of one row with dimensions ![]()
A column matrix is a matrix consisting of one column with dimensions ![]()
![Rendered by QuickLaTeX.com \left[\begin{array}{c}{a}_{11}\\ {a}_{21}\\ {a}_{31}\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-7054997e62c863d885debf95a9c1d6cf_l3.png)
A matrix may be used to represent a system of equations. In these cases, the numbers represent the coefficients of the variables in the system. Matrices often make solving systems of equations easier because they are not encumbered with variables. We will investigate this idea further in the next section, but first we will look at basic matrix operations.
Matrices
A matrix is a rectangular array of numbers that is usually named by a capital letter: ![]() and so on. Each entry in a matrix is referred to as
and so on. Each entry in a matrix is referred to as ![]() such that
such that ![]() represents the row and
represents the row and ![]() represents the column. Matrices are often referred to by their dimensions:
represents the column. Matrices are often referred to by their dimensions: ![]() indicating
indicating ![]() rows and
rows and ![]() columns.
columns.
Finding the Dimensions of the Given Matrix and Locating Entries
Given matrix ![]()
- What are the dimensions of matrix
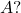
- What are the entries at
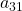 and
and 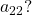
![Rendered by QuickLaTeX.com A=\left[\begin{array}{rrrr}\hfill 2& \hfill & \hfill 1& \hfill 0\\ \hfill 2& \hfill & \hfill 4& \hfill 7\\ \hfill 3& \hfill & \hfill 1& \hfill -2\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-598f143987a974401555d636c7313836_l3.png)
Show Solution
- The dimensions are
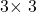 because there are three rows and three columns.
because there are three rows and three columns. - Entry
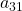 is the number at row 3, column 1, which is 3. The entry
is the number at row 3, column 1, which is 3. The entry 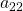 is the number at row 2, column 2, which is 4. Remember, the row comes first, then the column.
is the number at row 2, column 2, which is 4. Remember, the row comes first, then the column.
Adding and Subtracting Matrices
We use matrices to list data or to represent systems. Because the entries are numbers, we can perform operations on matrices. We add or subtract matrices by adding or subtracting corresponding entries.
In order to do this, the entries must correspond. Therefore, addition and subtraction of matrices is only possible when the matrices have the same dimensions. We can add or subtract a ![]() matrix and another
matrix and another ![]() matrix, but we cannot add or subtract a
matrix, but we cannot add or subtract a ![]() matrix and a
matrix and a ![]() matrix because some entries in one matrix will not have a corresponding entry in the other matrix.
matrix because some entries in one matrix will not have a corresponding entry in the other matrix.
Adding and Subtracting Matrices
Given matrices ![]() and
and ![]() of like dimensions, addition and subtraction of
of like dimensions, addition and subtraction of ![]() and
and ![]() will produce matrix
will produce matrix ![]() or
or
![]()
![]()
Matrix addition is commutative.
![]()
It is also associative.
![]()
Finding the Sum of Matrices
Find the sum of ![]() and
and ![]() given
given
Show Solution
Add corresponding entries.
![Rendered by QuickLaTeX.com \begin{array}{l}A+B=\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]+\left[\begin{array}{cc}e& f\\ g& h\end{array}\right]\hfill \\ \text{ }=\left[\begin{array}{ccc}a+e& & b+f\\ c+g& & d+h\end{array}\right]\hfill \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-27b94128e91db09c8271c569f7a287f7_l3.png)
Adding Matrix A and Matrix B
Find the sum of ![]() and
and ![]()
Show Solution
Add corresponding entries. Add the entry in row 1, column 1, ![]() of matrix
of matrix ![]() to the entry in row 1, column 1,
to the entry in row 1, column 1, ![]() of
of ![]() Continue the pattern until all entries have been added.
Continue the pattern until all entries have been added.
![Rendered by QuickLaTeX.com \begin{array}{l}A+B=\left[\begin{array}{cc}4& 1\\ 3& 2\end{array}\right]+\left[\begin{array}{cc}5& 9\\ 0& 7\end{array}\right]\hfill \\ \text{ }=\left[\begin{array}{ccc}4+5& & 1+9\\ 3+0& & 2+7\end{array}\right]\hfill \\ \text{ }=\left[\begin{array}{cc}9& 10\\ 3& 9\end{array}\right]\hfill \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-66c9657baf30e14bb45a8c93aeed43f0_l3.png)
Finding the Difference of Two Matrices
Find the difference of ![]() and
and ![]()
Show Solution
We subtract the corresponding entries of each matrix.
![Rendered by QuickLaTeX.com \begin{array}{l}A-B=\left[\begin{array}{rr}\hfill -2& \hfill 3\\ \hfill 0& \hfill 1\end{array}\right]-\left[\begin{array}{rr}\hfill 8& \hfill 1\\ \hfill 5& \hfill 4\end{array}\right]\hfill \\ \text{ }=\left[\begin{array}{rrr}\hfill -2-8& \hfill & \hfill 3-1\\ \hfill 0-5& \hfill & \hfill 1-4\end{array}\right]\hfill \\ \text{ }=\left[\begin{array}{rrr}\hfill -10& \hfill & \hfill 2\\ \hfill -5& \hfill & \hfill -3\end{array}\right]\hfill \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-38b5568ebd75f41cc39ea2c8e365312b_l3.png)
Finding the Sum and Difference of Two 3 x 3 Matrices
Given ![]() and
and ![]()
- Find the sum.
- Find the difference.
![Rendered by QuickLaTeX.com A=\left[\begin{array}{rrr}\hfill 2& \hfill -10& \hfill -2\\ \hfill 14& \hfill 12& \hfill 10\\ \hfill 4& \hfill -2& \hfill 2\end{array}\right]\text{ and }B=\left[\begin{array}{rrr}\hfill 6& \hfill 10& \hfill -2\\ \hfill 0& \hfill -12& \hfill -4\\ \hfill -5& \hfill 2& \hfill -2\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-491b064edce7950b6bc1cdb0af92e852_l3.png)
Show Solution
- Add the corresponding entries.
![Rendered by QuickLaTeX.com \begin{array}{l}\hfill \\ A+B=\left[\begin{array}{rrr}\hfill 2& \hfill \,\,-10& \hfill \,\,-2\\ \hfill 14& \hfill \,\,12& \hfill \,\,10\\ \hfill 4& \hfill \,\,-2& \hfill \,\,2\end{array}\right]+\left[\begin{array}{rrr}\hfill 6& \hfill \,\,10& \hfill \,\,-2\\ \hfill 0& \hfill \,\,-12& \hfill \,\,-4\\ \hfill -5& \hfill \,\,2& \hfill \,\,-2\end{array}\right]\hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\left[\begin{array}{rrr}\hfill 2+6& \hfill \,\,-10+10& \hfill \,\,-2-2\\ \hfill 14+0& \hfill \,\,12-12& \hfill \,\,10-4\\ \hfill 4-5& \hfill \,\,-2+2& \hfill \,\,2-2\end{array}\right]\hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\left[\begin{array}{rrr}\hfill 8& \hfill \,\,0& \hfill \,\,-4\\ \hfill 14& \hfill \,\,0& \hfill \,\,6\\ \hfill -1& \hfill \,\,0& \hfill \,\,0\end{array}\right]\hfill \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-0482f287878cc2151717d62baa0780f9_l3.png)
- Subtract the corresponding entries.
![Rendered by QuickLaTeX.com \begin{array}{l}\hfill \\ A-B=\left[\begin{array}{rrr}\hfill 2& \hfill -10& \hfill -2\\ \hfill 14& \hfill 12& \hfill 10\\ \hfill 4& \hfill -2& \hfill 2\end{array}\right]-\left[\begin{array}{rrr}\hfill 6& \hfill 10& \hfill -2\\ \hfill 0& \hfill -12& \hfill -4\\ \hfill -5& \hfill 2& \hfill -2\end{array}\right]\hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\left[\begin{array}{rrr}\hfill 2-6& \hfill \,\,-10-10& \hfill \,\,-2+2\\ \hfill 14-0& \hfill \,\,12+12& \hfill \,\,10+4\\ \hfill 4+5& \hfill \,\,-2-2& \hfill \,\,2+2\end{array}\right]\hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\left[\begin{array}{rrr}\hfill -4& \hfill \,\,-20& \hfill \,\,0\\ \hfill 14& \hfill \,\,24& \hfill \,\,14\\ \hfill 9& \hfill \,\,-4& \hfill \,\,4\end{array}\right]\hfill \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-f11bbe59fcadfa3a683c5a44501c6fe6_l3.png)
Try It
Add matrix ![]() and matrix
and matrix ![]()
![Rendered by QuickLaTeX.com A=\left[\begin{array}{rr}\hfill 2& \hfill 6\\ \hfill 1& \hfill 0\\ \hfill 1& \hfill -3\end{array}\right]\text{ and }B=\left[\begin{array}{rr}\hfill 3& \hfill -2\\ \hfill 1& \hfill 5\\ \hfill -4& \hfill 3\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-85425392abd45192a4897096385f8f3f_l3.png)
Show Solution
![Rendered by QuickLaTeX.com A+B=\left[\begin{array}{c}2\\ 1\\ 1\end{array}\begin{array}{c}\,\,\,\,6\\ \text{}\text{}\text{}\,\,\,\,\,0\\ \,\,\,-3\end{array}\right]+\left[\,\begin{array}{c}\,3\\ \,1\\ -4\end{array}\begin{array}{c}\,\,-2\\ \,\,\,\,\,5\\ \,\,\,\,\,\,3\end{array}\right]=\left[\begin{array}{c}2\,\,+\,3\\ 1\,\,\,+\,\,\,1\\ 1+\left(-4\right)\end{array}\,\,\,\,\,\,\begin{array}{c}6+\left(-2\right)\\ 0\,\,+\,\,5\\ -3\,\,\,+\,\,\,3\end{array}\right]=\left[\begin{array}{c}\,5\\ \,\,2\\ -3\end{array}\,\,\,\,\,\,\begin{array}{c}4\\ 5\\ 0\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-26f67be5937b6aa36051e6290f3428b5_l3.png)
Finding Scalar Multiples of a Matrix
Besides adding and subtracting whole matrices, there are many situations in which we need to multiply a matrix by a constant called a scalar. Recall that a scalar is a real number quantity that has magnitude, but not direction. For example, time, temperature, and distance are scalar quantities. The process of scalar multiplication involves multiplying each entry in a matrix by a scalar. A scalar multiple is any entry of a matrix that results from scalar multiplication.
Consider a real-world scenario in which a university needs to add to its inventory of computers, computer tables, and chairs in two of the campus labs due to increased enrollment. They estimate that 15% more equipment is needed in both labs. The school’s current inventory is displayed in (Figure).
| Lab A | Lab B | |
|---|---|---|
| Computers | 15 | 27 |
| Computer Tables | 16 | 34 |
| Chairs | 16 | 34 |
Converting the data to a matrix, we have
![Rendered by QuickLaTeX.com {C}_{2013}=\left[\begin{array}{c}15\\ 16\\ 16\end{array}\,\,\,\,\,\,\,\begin{array}{c}27\\ 34\\ 34\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-9c386876e1ac7cdc71b10d223ab8117d_l3.png)
To calculate how much computer equipment will be needed, we multiply all entries in matrix ![]() by 0.15.
by 0.15.
![Rendered by QuickLaTeX.com \left(0.15\right){C}_{2013}=\left[\begin{array}{c}\left(0.15\right)15\\ \left(0.15\right)16\\ \left(0.15\right)16\end{array}\,\,\,\,\,\,\,\,\begin{array}{c}\left(0.15\right)27\\ \left(0.15\right)34\\ \left(0.15\right)34\end{array}\right]=\left[\begin{array}{c}2.25\\ 2.4\\ 2.4\end{array}\,\,\,\,\,\begin{array}{c}4.05\\ 5.1\\ 5.1\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-273381ccb09b0d6b42697d3c8e96f8f0_l3.png)
We must round up to the next integer, so the amount of new equipment needed is
![Rendered by QuickLaTeX.com \left[\begin{array}{c}3\\ 3\\ 3\end{array}\,\,\,\,\,\begin{array}{c}5\\ 6\\ 6\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-d845116d95b96aec2aaa10018e74f54b_l3.png)
Adding the two matrices as shown below, we see the new inventory amounts.
![Rendered by QuickLaTeX.com \left[\begin{array}{c}15\\ 16\\ 16\end{array}\,\,\,\,\,\,\,\begin{array}{c}27\\ 34\\ 34\end{array}\right]+\left[\begin{array}{c}3\\ 3\\ 3\end{array}\,\,\,\,\,\begin{array}{c}5\\ 6\\ 6\end{array}\right]=\left[\begin{array}{c}18\\ 19\\ 19\end{array}\,\,\,\,\,\begin{array}{c}32\\ 40\\ 40\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-d67be09fcdc54df147e4fa3369760f36_l3.png)
This means
![Rendered by QuickLaTeX.com {C}_{2014}=\left[\begin{array}{c}18\\ 19\\ 19\end{array}\,\,\,\,\,\begin{array}{c}32\\ 40\\ 40\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-0ce50ef4c1a0398385e1dfba8bc45bad_l3.png)
Thus, Lab A will have 18 computers, 19 computer tables, and 19 chairs; Lab B will have 32 computers, 40 computer tables, and 40 chairs.
Scalar Multiplication
Scalar multiplication involves finding the product of a constant by each entry in the matrix. Given
the scalar multiple ![]() is
is
![Rendered by QuickLaTeX.com \begin{array}{l}cA=c\left[\begin{array}{ccc}{a}_{11}& & {a}_{12}\\ {a}_{21}& & {a}_{22}\end{array}\right]\hfill \\ \text{ }=\left[\begin{array}{ccc}c{a}_{11}& & c{a}_{12}\\ c{a}_{21}& & c{a}_{22}\end{array}\right]\hfill \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-841f991897e450c1156e029b77021622_l3.png)
Scalar multiplication is distributive. For the matrices ![]() and
and ![]() with scalars
with scalars ![]() and
and ![]()
Multiplying the Matrix by a Scalar
Multiply matrix ![]() by the scalar 3.
by the scalar 3.
Show Solution
Multiply each entry in ![]() by the scalar 3.
by the scalar 3.
![Rendered by QuickLaTeX.com \begin{array}{l}3A=3\left[\begin{array}{rr}\hfill 8& \hfill \,\,1\\ \hfill 5& \hfill \,\,4\end{array}\right]\hfill \\ \,\,\,\,\,\,\,\,= \left[\begin{array}{rr}\hfill 3\cdot 8& \hfill \,\,3\cdot 1\\ \hfill 3\cdot 5& \hfill \,\,3\cdot 4\end{array}\right]\hfill \\ \,\,\,\,\,\,\,\,= \left[\begin{array}{rr}\hfill 24& \hfill 3\\ \hfill 15& \hfill 12\end{array}\right]\hfill \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-fa1dc74c89d2015ca96672a6e0c02f7e_l3.png)
Try It
Given matrix ![]() find
find ![]() where
where
Show Solution
![]()
Finding the Sum of Scalar Multiples
Find the sum ![]()
![Rendered by QuickLaTeX.com A=\left[\begin{array}{rrr}\hfill 1& \hfill -2& \hfill 0\\ \hfill 0& \hfill -1& \hfill 2\\ \hfill 4& \hfill 3& \hfill -6\end{array}\right]\text{ and }B=\left[\begin{array}{rrr}\hfill -1& \hfill 2& \hfill 1\\ \hfill 0& \hfill -3& \hfill 2\\ \hfill 0& \hfill 1& \hfill -4\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-2647adc4465d77a9821c64604001d24d_l3.png)
Show Solution
First, find ![]() then
then ![]()
![Rendered by QuickLaTeX.com \begin{array}{l}\begin{array}{l}\hfill \\ \hfill \\ 3A=\left[\begin{array}{lll}3\cdot 1\hfill & \,\,3\left(-2\right)\hfill & \,\,3\cdot 0\hfill \\ 3\cdot 0\hfill & \,\,3\left(-1\right)\hfill & \,\,3\cdot 2\hfill \\ 3\cdot 4\hfill & \,\,3\cdot 3\hfill & \,\,3\left(-6\right)\hfill \end{array}\right]\hfill \end{array}\hfill \\ \,\,\,\,\,\,\,=\left[\begin{array}{rrr}\hfill 3& \hfill \,\,-6& \hfill \,\,0\\ \hfill 0& \hfill \,\,-3& \hfill \,\,6\\ \hfill 12& \hfill \,\,9& \hfill \,\,-18\end{array}\right]\hfill \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-5b4128f3ed8d6e8d61967eaac6d3cae0_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{l}\begin{array}{l}\hfill \\ \hfill \\ 2B=\left[\begin{array}{lll}2\left(-1\right)\hfill & \,\,2\cdot 2\hfill & \,\,2\cdot 1\hfill \\ 2\cdot 0\hfill & \,\,2\left(-3\right)\hfill & \,\,2\cdot 2\hfill \\ 2\cdot 0\hfill & \,\,2\cdot 1\hfill & \,\,2\left(-4\right)\hfill \end{array}\right]\hfill \end{array}\hfill \\ \,\,\,\,\,\,\,=\left[\begin{array}{rrr}\hfill -2& \hfill 4& \hfill 2\\ \hfill 0& \hfill -6& \hfill 4\\ \hfill 0& \hfill 2& \hfill -8\end{array}\right]\hfill \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-8d2a5edaaeb6d57fa862d302085183fd_l3.png)
Now, add ![]()
![Rendered by QuickLaTeX.com \begin{array}{l}\hfill \\ \hfill \\ 3A+2B=\left[\begin{array}{rrr}\hfill 3& \hfill -6& \hfill 0\\ \hfill 0& \hfill -3& \hfill 6\\ \hfill 12& \hfill 9& \hfill -18\end{array}\right]+\left[\begin{array}{rrr}\hfill -2& \hfill 4& \hfill 2\\ \hfill 0& \hfill -6& \hfill 4\\ \hfill 0& \hfill 2& \hfill -8\end{array}\right]\hfill \\ \text{ }=\left[\begin{array}{rrr}\hfill 3-2& \hfill \,\,-6+4& \hfill 0+2\\ \hfill 0+0& \hfill \,\,-3-6& \hfill 6+4\\ \hfill 12+0& \hfill \,\,9+2& \hfill -18-8\end{array}\right]\hfill \\ \text{ }=\left[\begin{array}{rrr}\hfill 1& \hfill \,\,-2& \hfill 2\\ \hfill 0& \hfill \,\,-9& \hfill 10\\ \hfill 12& \hfill \,\,11& \hfill -26\end{array}\right]\hfill \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-3ebff7dea19007e5202b192b895488a4_l3.png)
Finding the Product of Two Matrices
In addition to multiplying a matrix by a scalar, we can multiply two matrices. Finding the product of two matrices is only possible when the inner dimensions are the same, meaning that the number of columns of the first matrix is equal to the number of rows of the second matrix. If ![]() is an
is an ![]() matrix and
matrix and ![]() is an
is an ![]() matrix, then the product matrix
matrix, then the product matrix ![]() is an
is an ![]() matrix. For example, the product
matrix. For example, the product ![]() is possible because the number of columns in
is possible because the number of columns in ![]() is the same as the number of rows in
is the same as the number of rows in ![]() If the inner dimensions do not match, the product is not defined.
If the inner dimensions do not match, the product is not defined.

We multiply entries of ![]() with entries of
with entries of ![]() according to a specific pattern as outlined below. The process of matrix multiplication becomes clearer when working a problem with real numbers.
according to a specific pattern as outlined below. The process of matrix multiplication becomes clearer when working a problem with real numbers.
To obtain the entries in row ![]() of
of ![]() we multiply the entries in row
we multiply the entries in row ![]() of
of ![]() by column
by column ![]() in
in ![]() and add. For example, given matrices
and add. For example, given matrices ![]() and
and ![]() where the dimensions of
where the dimensions of ![]() are
are ![]() and the dimensions of
and the dimensions of ![]() are
are ![]() the product of
the product of ![]() will be a
will be a ![]() matrix.
matrix.
![Rendered by QuickLaTeX.com A=\left[\begin{array}{rrr}\hfill {a}_{11}& \hfill {a}_{12}& \hfill {a}_{13}\\ \hfill {a}_{21}& \hfill {a}_{22}& \hfill {a}_{23}\end{array}\right]\text{ and }B=\left[\begin{array}{rrr}\hfill {b}_{11}& \hfill {b}_{12}& \hfill {b}_{13}\\ \hfill {b}_{21}& \hfill {b}_{22}& \hfill {b}_{23}\\ \hfill {b}_{31}& \hfill {b}_{32}& \hfill {b}_{33}\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-64e73ef72552b34c7d535605dc1a95b2_l3.png)
Multiply and add as follows to obtain the first entry of the product matrix ![]()
- To obtain the entry in row 1, column 1 of
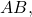 multiply the first row in
multiply the first row in 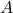 by the first column in
by the first column in 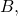 and add.
and add.
![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}{a}_{11}& {a}_{12}& {a}_{13}\end{array}\right]\cdot \left[\begin{array}{c}{b}_{11}\\ {b}_{21}\\ {b}_{31}\end{array}\right]={a}_{11}\cdot {b}_{11}+{a}_{12}\cdot {b}_{21}+{a}_{13}\cdot {b}_{31}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-ca23589c6f262250a4d254e1d2500b65_l3.png)
- To obtain the entry in row 1, column 2 of
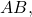 multiply the first row of
multiply the first row of 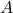 by the second column in
by the second column in 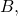 and add.
and add.
![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}{a}_{11}& {a}_{12}& {a}_{13}\end{array}\right]\cdot \left[\begin{array}{c}{b}_{12}\\ {b}_{22}\\ {b}_{32}\end{array}\right]={a}_{11}\cdot {b}_{12}+{a}_{12}\cdot {b}_{22}+{a}_{13}\cdot {b}_{32}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-e7bf6d1070f500d13d93bd3efe7a90de_l3.png)
- To obtain the entry in row 1, column 3 of
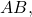 multiply the first row of
multiply the first row of 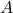 by the third column in
by the third column in 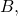 and add.
and add.
![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}{a}_{11}& {a}_{12}& {a}_{13}\end{array}\right]\cdot \left[\begin{array}{c}{b}_{13}\\ {b}_{23}\\ {b}_{33}\end{array}\right]={a}_{11}\cdot {b}_{13}+{a}_{12}\cdot {b}_{23}+{a}_{13}\cdot {b}_{33}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-70a60d8f61a7331d42cb390e7e4795ef_l3.png)
We proceed the same way to obtain the second row of ![]() In other words, row 2 of
In other words, row 2 of ![]() times column 1 of
times column 1 of ![]() row 2 of
row 2 of ![]() times column 2 of
times column 2 of ![]() row 2 of
row 2 of ![]() times column 3 of
times column 3 of ![]() When complete, the product matrix will be
When complete, the product matrix will be
Properties of Matrix Multiplication
For the matrices ![]() and
and ![]() the following properties hold.
the following properties hold.
- Matrix multiplication is associative:
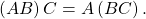
- Matrix multiplication is distributive:
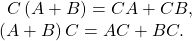
Note that matrix multiplication is not commutative.
Multiplying Two Matrices
Multiply matrix ![]() and matrix
and matrix ![]()
Show Solution
First, we check the dimensions of the matrices. Matrix ![]() has dimensions
has dimensions ![]() and matrix
and matrix ![]() has dimensions
has dimensions ![]() The inner dimensions are the same so we can perform the multiplication. The product will have the dimensions
The inner dimensions are the same so we can perform the multiplication. The product will have the dimensions ![]()
We perform the operations outlined previously.

Multiplying Two Matrices
Given ![]() and
and ![]()
- Find
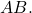
- Find
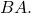
![Rendered by QuickLaTeX.com A=\left[\begin{array}{l}\begin{array}{ccc}-1& 2& 3\end{array}\hfill \\ \begin{array}{ccc}\,\,\,4& 0& 5\end{array}\hfill \end{array}\right]\text{ and }B=\left[\begin{array}{c}\,\,5\\ -4\\ \,\,2\end{array}\,\,\,\begin{array}{c}-1\\ \,\,0\\ \,\,3\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-d5f39c775294f2585a710952c912b063_l3.png)
Show Solution
- As the dimensions of
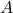 are
are 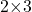 and the dimensions of
and the dimensions of 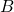 are
are 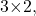 these matrices can be multiplied together because the number of columns in
these matrices can be multiplied together because the number of columns in 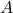 matches the number of rows in
matches the number of rows in 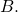 The resulting product will be a
The resulting product will be a 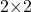 matrix, the number of rows in
matrix, the number of rows in 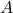 by the number of columns in
by the number of columns in 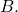
![Rendered by QuickLaTeX.com \begin{array}{l}\hfill \\ AB=\left[\begin{array}{rrr}\hfill -1& \hfill 2& \hfill 3\\ \hfill 4& \hfill 0& \hfill 5\end{array}\right]\text{ }\left[\begin{array}{rr}\hfill 5& \hfill -1\\ \hfill -4& \hfill 0\\ \hfill 2& \hfill 3\end{array}\right]\hfill \\ \text{ }=\left[\begin{array}{rr}\hfill -1\left(5\right)+2\left(-4\right)+3\left(2\right)& \hfill \,\,-1\left(-1\right)+2\left(0\right)+3\left(3\right)\\ \hfill 4\left(5\right)+0\left(-4\right)+5\left(2\right)& \hfill \,\,4\left(-1\right)+0\left(0\right)+5\left(3\right)\end{array}\right]\hfill \\ \text{ }=\left[\begin{array}{rr}\hfill -7& \hfill 10\\ \hfill 30& \hfill 11\end{array}\right]\hfill \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-26f8ad286f3ae6f34302beb07d188d33_l3.png)
- The dimensions of
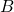 are
are 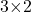 and the dimensions of
and the dimensions of 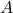 are
are 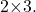 The inner dimensions match so the product is defined and will be a
The inner dimensions match so the product is defined and will be a 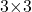 matrix.
matrix.
![Rendered by QuickLaTeX.com \begin{array}{l}\hfill \\ BA=\left[\begin{array}{rr}\hfill 5& \hfill -1\\ \hfill -4& \hfill 0\\ \hfill 2& \hfill 3\end{array}\right]\text{ }\left[\begin{array}{rrr}\hfill -1& \hfill 2& \hfill 3\\ \hfill 4& \hfill 0& \hfill 5\end{array}\right]\hfill \\ \text{ }=\left[\begin{array}{rrr}\hfill 5\left(-1\right)+-1\left(4\right)& \hfill \,\,5\left(2\right)+-1\left(0\right)& \hfill \,\,5\left(3\right)+-1\left(5\right)\\ \hfill -4\left(-1\right)+0\left(4\right)& \hfill \,\,-4\left(2\right)+0\left(0\right)& \hfill \,\,-4\left(3\right)+0\left(5\right)\\ \hfill 2\left(-1\right)+3\left(4\right)& \hfill \,\,2\left(2\right)+3\left(0\right)& \hfill \,\,2\left(3\right)+3\left(5\right)\end{array}\right]\hfill \\ \text{ }=\left[\begin{array}{rrr}\hfill -9& \hfill 10& \hfill 10\\ \hfill 4& \hfill -8& \hfill -12\\ \hfill 10& \hfill 4& \hfill 21\end{array}\right]\hfill \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-32c79cbf4465f1da1878d6ddf84d6796_l3.png)
Analysis
Notice that the products ![]() and
and ![]() are not equal.
are not equal.
![Rendered by QuickLaTeX.com AB=\left[\begin{array}{cc}-7& 10\\ 30& 11\end{array}\right]\ne \left[\begin{array}{ccc}-9& 10& 10\\ 4& -8& -12\\ 10& 4& 21\end{array}\right]=BA](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-f1b5241713f29aa1faf3141b12cb1080_l3.png)
This illustrates the fact that matrix multiplication is not commutative.
Is it possible for AB to be defined but not BA?
Yes, consider a matrix A with dimension ![]() and matrix B with dimension
and matrix B with dimension ![]() For the product AB the inner dimensions are 4 and the product is defined, but for the product BA the inner dimensions are 2 and 3 so the product is undefined.
For the product AB the inner dimensions are 4 and the product is defined, but for the product BA the inner dimensions are 2 and 3 so the product is undefined.
Using Matrices in Real-World Problems
Let’s return to the problem presented at the opening of this section. We have (Figure), representing the equipment needs of two soccer teams.
| Wildcats | Mud Cats | |
|---|---|---|
| Goals | 6 | 10 |
| Balls | 30 | 24 |
| Jerseys | 14 | 20 |
We are also given the prices of the equipment, as shown in (Figure).
| Goal | $300 |
| Ball | $10 |
| Jersey | $30 |
We will convert the data to matrices. Thus, the equipment need matrix is written as
![Rendered by QuickLaTeX.com E=\left[\begin{array}{c}6\\ 30\\ 14\end{array}\,\,\,\,\,\begin{array}{c}10\\ 24\\ 20\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-520712667741d2cca7446403250f039c_l3.png)
The cost matrix is written as
We perform matrix multiplication to obtain costs for the equipment.
![Rendered by QuickLaTeX.com \begin{array}{l}\hfill \\ \hfill \\ CE=\left[\begin{array}{rrr}\hfill 300& \hfill 10& \hfill 30\end{array}\right]\cdot \left[\begin{array}{rr}\hfill 6& \hfill 10\\ \hfill 30& \hfill 24\\ \hfill 14& \hfill 20\end{array}\right]\hfill \\ \text{ }=\left[\begin{array}{rr}\hfill 300\left(6\right)+10\left(30\right)+30\left(14\right)& \hfill 300\left(10\right)+10\left(24\right)+30\left(20\right)\end{array}\right]\hfill \\ \text{ }=\left[\begin{array}{rr}\hfill 2,520& \hfill 3,840\end{array}\right]\hfill \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-81ad721ef926ecbec8a6bc0e430df7b5_l3.png)
The total cost for equipment for the Wildcats is $2,520, and the total cost for equipment for the Mud Cats is $3,840.
How To
Given a matrix operation, evaluate using a calculator.
- Save each matrix as a matrix variable
![Rendered by QuickLaTeX.com \,\left[A\right],\left[B\right],\left[C\right],...](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-f018daeaaf1e6fc9a8b9fd2de5dd657b_l3.png)
- Enter the operation into the calculator, calling up each matrix variable as needed.
- If the operation is defined, the calculator will present the solution matrix; if the operation is undefined, it will display an error message.
Using a Calculator to Perform Matrix Operations
Find ![]() given
given
![Rendered by QuickLaTeX.com A=\left[\begin{array}{rrr}\hfill -15& \hfill 25& \hfill 32\\ \hfill 41& \hfill -7& \hfill -28\\ \hfill 10& \hfill 34& \hfill -2\end{array}\right],B=\left[\begin{array}{rrr}\hfill 45& \hfill 21& \hfill -37\\ \hfill -24& \hfill 52& \hfill 19\\ \hfill 6& \hfill -48& \hfill -31\end{array}\right],\text{and }C=\left[\begin{array}{rrr}\hfill -100& \hfill -89& \hfill -98\\ \hfill 25& \hfill -56& \hfill 74\\ \hfill -67& \hfill 42& \hfill -75\end{array}\right].](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-3228fac672e1a16ac1662e9c7b0bee8a_l3.png)
Show Solution
On the matrix page of the calculator, we enter matrix ![]() above as the matrix variable
above as the matrix variable ![]() matrix
matrix ![]() above as the matrix variable
above as the matrix variable ![]() and matrix
and matrix ![]() above as the matrix variable
above as the matrix variable ![]()
On the home screen of the calculator, we type in the problem and call up each matrix variable as needed.
The calculator gives us the following matrix.
![Rendered by QuickLaTeX.com \left[\begin{array}{rrr}\hfill -983& \hfill \,\,-462& \hfill \,\,136\\ \hfill 1,820& \hfill \,\,1,897& \hfill \,\,-856\\ \hfill -311& \hfill \,\,2,032& \hfill \,\,413\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-8b1278c6975f4ffc9d592915ed403257_l3.png)
Access these online resources for additional instruction and practice with matrices and matrix operations.
Key Concepts
- A matrix is a rectangular array of numbers. Entries are arranged in rows and columns.
- The dimensions of a matrix refer to the number of rows and the number of columns. A
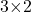 matrix has three rows and two columns. See (Figure).
matrix has three rows and two columns. See (Figure). - We add and subtract matrices of equal dimensions by adding and subtracting corresponding entries of each matrix. See (Figure), (Figure), (Figure), and (Figure).
- Scalar multiplication involves multiplying each entry in a matrix by a constant. See (Figure).
- Scalar multiplication is often required before addition or subtraction can occur. See (Figure).
- Multiplying matrices is possible when inner dimensions are the same—the number of columns in the first matrix must match the number of rows in the second.
- The product of two matrices,
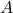 and
and 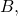 is obtained by multiplying each entry in row 1 of
is obtained by multiplying each entry in row 1 of 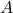 by each entry in column 1 of
by each entry in column 1 of 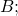 then multiply each entry of row 1 of
then multiply each entry of row 1 of 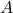 by each entry in columns 2 of
by each entry in columns 2 of 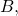 and so on. See (Figure) and (Figure).
and so on. See (Figure) and (Figure). - Many real-world problems can often be solved using matrices. See (Figure).
- We can use a calculator to perform matrix operations after saving each matrix as a matrix variable. See (Figure).
Section Exercises
Verbal
1. Can we add any two matrices together? If so, explain why; if not, explain why not and give an example of two matrices that cannot be added together.
Show Solution
No, they must have the same dimensions. An example would include two matrices of different dimensions. One cannot add the following two matrices because the first is a ![]() matrix and the second is a
matrix and the second is a ![]() matrix.
matrix. ![]() has no sum.
has no sum.
2. Can we multiply any column matrix by any row matrix? Explain why or why not.
3. Can both the products ![]() and
and ![]() be defined? If so, explain how; if not, explain why.
be defined? If so, explain how; if not, explain why.
Show Solution
Yes, if the dimensions of ![]() are
are ![]() and the dimensions of
and the dimensions of ![]() are
are ![]() both products will be defined.
both products will be defined.
4. Can any two matrices of the same size be multiplied? If so, explain why, and if not, explain why not and give an example of two matrices of the same size that cannot be multiplied together.
5. Does matrix multiplication commute? That is, does ![]() If so, prove why it does. If not, explain why it does not.
If so, prove why it does. If not, explain why it does not.
Show Solution
Not necessarily. To find ![]() we multiply the first row of
we multiply the first row of ![]() by the first column of
by the first column of ![]() to get the first entry of
to get the first entry of ![]() To find
To find ![]() we multiply the first row of
we multiply the first row of ![]() by the first column of
by the first column of ![]() to get the first entry of
to get the first entry of ![]() Thus, if those are unequal, then the matrix multiplication does not commute.
Thus, if those are unequal, then the matrix multiplication does not commute.
Algebraic
For the following exercises, use the matrices below and perform the matrix addition or subtraction. Indicate if the operation is undefined.
![Rendered by QuickLaTeX.com A=\left[\begin{array}{cc}1& 3\\ 0& 7\end{array}\right],B=\left[\begin{array}{cc}2& 14\\ 22& 6\end{array}\right],C=\left[\begin{array}{cc}1& 5\\ 8& 92\\ 12& 6\end{array}\right],D=\left[\begin{array}{cc}10& 14\\ 7& 2\\ 5& 61\end{array}\right],E=\left[\begin{array}{cc}6& 12\\ 14& 5\end{array}\right],F=\left[\begin{array}{cc}0& 9\\ 78& 17\\ 15& 4\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-87e62aab693bc672127f1c53aa4af375_l3.png)
6. ![]()
7. ![]()
Show Solution
![Rendered by QuickLaTeX.com \left[\begin{array}{cc}11& 19\\ 15& 94\\ 17& 67\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-8c3bb24f03e9165462297b764444dccd_l3.png)
8. ![]()
9. ![]()
Show Solution
![]()
10. ![]()
11. ![]()
Show Solution
Undidentified; dimensions do not match
For the following exercises, use the matrices below to perform scalar multiplication.
![Rendered by QuickLaTeX.com A=\left[\begin{array}{rr}\hfill 4& \hfill 6\\ \hfill 13& \hfill 12\end{array}\right],B=\left[\begin{array}{rr}\hfill 3& \hfill 9\\ \hfill 21& \hfill 12\\ \hfill 0& \hfill 64\end{array}\right],C=\left[\begin{array}{rrrr}\hfill 16& \hfill 3& \hfill 7& \hfill 18\\ \hfill 90& \hfill 5& \hfill 3& \hfill 29\end{array}\right],D=\left[\begin{array}{rrr}\hfill 18& \hfill 12& \hfill 13\\ \hfill 8& \hfill 14& \hfill 6\\ \hfill 7& \hfill 4& \hfill 21\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-241816b5013c1c0e7d798d49a67a5ffb_l3.png)
Show Solution
![Rendered by QuickLaTeX.com \left[\begin{array}{cc}9& 27\\ 63& 36\\ 0& 192\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-c08de4df34c7865ceea8faf56b91621c_l3.png)
14. ![]()
15. ![]()
Show Solution
![]()
16. ![]()
Show Solution
![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}1,800& 1,200& 1,300\\ 800& 1,400& 600\\ 700& 400& 2,100\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-459631809679c63a183505bc8b1d9480_l3.png)
For the following exercises, use the matrices below to perform matrix multiplication.
![Rendered by QuickLaTeX.com A=\left[\begin{array}{rr}\hfill -1& \hfill 5\\ \hfill 3& \hfill 2\end{array}\right],B=\left[\begin{array}{rrr}\hfill 3& \hfill 6& \hfill 4\\ \hfill -8& \hfill 0& \hfill 12\end{array}\right],C=\left[\begin{array}{rr}\hfill 4& \hfill 10\\ \hfill -2& \hfill 6\\ \hfill 5& \hfill 9\end{array}\right],D=\left[\begin{array}{rrr}\hfill 2& \hfill -3& \hfill 12\\ \hfill 9& \hfill 3& \hfill 1\\ \hfill 0& \hfill 8& \hfill -10\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-3f3c0bd177e442ce3ad58da1644a34cc_l3.png)
18. ![]()
Show Solution
![]()
20. ![]()
21. ![]()
Show Solution
![]()
22. ![]()
23. ![]()
Show Solution
![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}-68& 24& 136\\ -54& -12& 64\\ -57& 30& 128\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-f990b848076fb277abb95caea3f53ca7_l3.png)
For the following exercises, use the matrices below to perform the indicated operation if possible. If not possible, explain why the operation cannot be performed.
![Rendered by QuickLaTeX.com A=\left[\begin{array}{rr}\hfill 2& \hfill -5\\ \hfill 6& \hfill 7\end{array}\right],B=\left[\begin{array}{rr}\hfill -9& \hfill 6\\ \hfill -4& \hfill 2\end{array}\right],C=\left[\begin{array}{rr}\hfill 0& \hfill 9\\ \hfill 7& \hfill 1\end{array}\right],D=\left[\begin{array}{rrr}\hfill -8& \hfill 7& \hfill -5\\ \hfill 4& \hfill 3& \hfill 2\\ \hfill 0& \hfill 9& \hfill 2\end{array}\right],E=\left[\begin{array}{rrr}\hfill 4& \hfill 5& \hfill 3\\ \hfill 7& \hfill -6& \hfill -5\\ \hfill 1& \hfill 0& \hfill 9\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-ba35d38e09b35b4ee78691136d6de57d_l3.png)
24. ![]()
25. ![]()
Show Solution
Undefined; dimensions do not match.
26. ![]()
27. ![]()
Show Solution
![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}-8& 41& -3\\ 40& -15& -14\\ 4& 27& 42\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-67915bf3485baf2566f623d2ace4ada4_l3.png)
28. ![]()
29. ![]()
Show Solution
![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}-840& 650& -530\\ 330& 360& 250\\ -10& 900& 110\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-d5f2c206d4dfbb00c15ebefa15221236_l3.png)
For the following exercises, use the matrices below to perform the indicated operation if possible. If not possible, explain why the operation cannot be performed. (Hint: ![]() )
)
![Rendered by QuickLaTeX.com A=\left[\begin{array}{rr}\hfill -10& \hfill 20\\ \hfill 5& \hfill 25\end{array}\right],B=\left[\begin{array}{rr}\hfill 40& \hfill 10\\ \hfill -20& \hfill 30\end{array}\right],C=\left[\begin{array}{rr}\hfill -1& \hfill 0\\ \hfill 0& \hfill -1\\ \hfill 1& \hfill 0\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-1487db40505a462ff59a9c4801a1dd1e_l3.png)
31. ![]()
Show Solution
![]()
32. ![]()
33. ![]()
Show Solution
Undefined; inner dimensions do not match.
35. ![]()
Show Solution
![]()
36. ![]()
37. ![]()
Show Solution
![]()
38. ![]()
39. ![]()
Show Solution
![]()
40. ![]()
For the following exercises, use the matrices below to perform the indicated operation if possible. If not possible, explain why the operation cannot be performed. (Hint: ![]() )
)
![Rendered by QuickLaTeX.com A=\left[\begin{array}{rr}\hfill 1& \hfill 0\\ \hfill 2& \hfill 3\end{array}\right],B=\left[\begin{array}{rrr}\hfill -2& \hfill 3& \hfill 4\\ \hfill -1& \hfill 1& \hfill -5\end{array}\right],C=\left[\begin{array}{rr}\hfill 0.5& \hfill 0.1\\ \hfill 1& \hfill 0.2\\ \hfill -0.5& \hfill 0.3\end{array}\right],D=\left[\begin{array}{rrr}\hfill 1& \hfill 0& \hfill -1\\ \hfill -6& \hfill 7& \hfill 5\\ \hfill 4& \hfill 2& \hfill 1\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-b28fb667d716dbefa9e0ed8539869772_l3.png)
41. ![]()
Show Solution
![]()
42. ![]()
43. ![]()
Show Solution
![]()
44. ![]()
45. ![]()
Show Solution
![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}-3& -2& -2\\ -28& 59& 46\\ -4& 16& 7\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-8e7240f5c7952035edbc579db5031650_l3.png)
46. ![]()
47. ![]()
Show Solution
![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}1& -18& -9\\ -198& 505& 369\\ -72& 126& 91\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-d4033a3b9d11813b4d932cbb7661a8fe_l3.png)
48. ![]()
49. ![]()
Show Solution
![]()
Technology
For the following exercises, use the matrices below to perform the indicated operation if possible. If not possible, explain why the operation cannot be performed. Use a calculator to verify your solution.
![Rendered by QuickLaTeX.com A=\left[\begin{array}{rrr}\hfill -2& \hfill 0& \hfill 9\\ \hfill 1& \hfill 8& \hfill -3\\ \hfill 0.5& \hfill 4& \hfill 5\end{array}\right],B=\left[\begin{array}{rrr}\hfill 0.5& \hfill 3& \hfill 0\\ \hfill -4& \hfill 1& \hfill 6\\ \hfill 8& \hfill 7& \hfill 2\end{array}\right],C=\left[\begin{array}{rrr}\hfill 1& \hfill 0& \hfill 1\\ \hfill 0& \hfill 1& \hfill 0\\ \hfill 1& \hfill 0& \hfill 1\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-69744051b82ea4cef2365369ec6c94d1_l3.png)
50. ![]()
51. ![]()
Show Solution
![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}2& 24& -4.5\\ 12& 32& -9\\ -8& 64& 61\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-2a9a5fc3f0688fe635d5353fc8db0f9b_l3.png)
52. ![]()
53. ![]()
Show Solution
![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}0.5& 3& 0.5\\ 2& 1& 2\\ 10& 7& 10\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-7a81c294eaa7816911aee8825eb878fb_l3.png)
54. ![]()
Extensions
For the following exercises, use the matrix below to perform the indicated operation on the given matrix.
![Rendered by QuickLaTeX.com B=\left[\begin{array}{rrr}\hfill 1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 1\\ \hfill 0& \hfill 1& \hfill 0\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-b10f16bc7d9d59f4503d18bc76e43d32_l3.png)
55. ![]()
Show Solution
![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-15b718d2f600cc4e0f4da22de1888d13_l3.png)
56. ![]()
57. ![]()
Show Solution
![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-15b718d2f600cc4e0f4da22de1888d13_l3.png)
58. ![]()
Glossary
- column
- a set of numbers aligned vertically in a matrix
- entry
- an element, coefficient, or constant in a matrix
- matrix
- a rectangular array of numbers
- row
- a set of numbers aligned horizontally in a matrix
- scalar multiple
- an entry of a matrix that has been multiplied by a scalar

