5.3 Risk Analysis Techniques
Net Present Value (NPV)
Present Value
Risk managers will be faced with situations where they will need to know the current or present value of money that will be received or paid out in the future. For example, how much money must be invested today to generate funds that are sufficient to pay a sprinkler system at a specific time in the future.
Money that is invested at a given interest rate will increase in value over a given period. For this reason, its present value will be less than its future value. The future value of a sum of money that is to be received is dependent on the rate of return and the number of periods over which it would receive that rate of return.
Simply put, the present value is today’s value of money that is to be received in the future. Discounting is the process that is used to calculate present values.
A dollar today is worth more than a dollar tomorrow!
The formula to calculate present value is as follows:
[latex]PV=\frac{FV_{n}}{(1+r)^{n}}[/latex]
n = Number of periods
r = Rate of return
FVn = Future value of money that must be discounted
Example
At the end of one year, $11,500 needs to be in a savings account that pays 3 percent interest compounded annually. Using the present value table, determine how much must be deposited in the account today to have $11,500 in one year.
Solution
[latex]PV=\frac{FV_{n}}{(1+r)^{n}}[/latex]
[latex]PV=\frac{$11,500}{(1+0.03)^{1}}[/latex]
[latex]PV=\frac{$11,500}{1.03}[/latex]
[latex]PV=$11,165[/latex]
$11,165 must be deposited in the account today to have $11,500 in the account in one year.
Net Present Value
Net present value is the difference between the present value of all future cash inflows, including the salvage value of assets, and the present value of cash outflows over a period.
For example, a risk manager may want to know whether investing in an initiative today, which is a cash outflow, will save money on future costs, which are cash inflows based on saving expenses.
The Net Present Value Equation is expressed as:
[latex]NPV=-C_{o}+\frac{C_{t}}{\lgroup 1+r\rgroup^{t}}+…+\frac{C_{n}}{\lgroup 1+r\rgroup^{n}}[/latex]
Co = Cash flow at beginning of project
Ct = Payment at period t for t = 1, through t = n
r = Discount rate
n = Number of periods
Net present value (NPV) is the difference between the present value of cash inflows and the present value of cash outflows.
NPV = PV (sum of the benefits) – PV (initial costs)
An investment should not be made when the Net Present Value (NPV) is negative. In contrast, a positive NPV would be indicative of an investment that should be made.
Example
A risk manager overseeing a chain of fitness clubs is deciding if an investment of $50,000 on a 2-year preventive maintenance program for the equipment in the clubs is a good idea. The fitness clubs require a return on investment of 6% and expect to save $15,000 on maintenance costs at the end of the first year and $20,000 on maintenance costs at the end of the second year.
Solution
[latex]NPV=-C_{o}+\frac{C_{t}}{\lgroup 1+r\rgroup^{t}}+…+\frac{C_{n}}{\lgroup 1+r\rgroup^{n}}[/latex]
[latex]NPV=-$50,000+\frac{$15,000}{\lgroup 1+0.06\rgroup^{1}}+\frac{$20,000}{\lgroup 1+0.06\rgroup^{2}}[/latex]
[latex]NPV=-$50,000+$14,150+$17,800[/latex]
[latex]NPV=-$18,050[/latex]
Since the NPV is negative the investment in the preventive maintenance program should not be made
Probability Analysis
Probability analysis involves quantifying uncertainties associated with various events or scenarios. By assigning probabilities to different outcomes, risk analysts can assess the likelihood of specific events occurring and their potential impact on a system, process, or project.
Several methods/concepts can be used to calculate probability, such as the law of large numbers, theoretical probability, empirical probability, and probability distributions (Hillson & Hulett, 2004).
However, there are two main ways to do this: the empirical approach and the theoretical approach.
The Empirical Approach uses real-world data and past experiences. It looks at what has happened before to guess what might happen in the future. This method works well when we have lots of information about past events. It’s like learning from history to predict the future (Halton, 2024).
On the other hand, the Theoretical approach uses math and models to calculate probabilities. It doesn’t need past data. Instead, it uses logical reasoning to figure out what might happen. This method is useful when we’re dealing with new situations or when we don’t have much historical information.
Both approaches have their strengths and weaknesses. The empirical approach is great when we have lots of past data, but it might not work well for new or quickly changing situations. The theoretical approach can handle new scenarios, but it might need complex math and could be wrong if its basic assumptions are incorrect (Halton, 2024).
Let’s examine how each approach would determine the probability of getting heads when flipping a fair coin.
Example
Empirical Approach
In this approach, we would actually flip a coin multiple times and record the results. Let’s say we flip a coin 100 times and get the following results:
- Heads: 52 times
- Tails: 48 times
Using the empirical approach, we would calculate the probability of getting heads as:
Probability of Heads = Number of Heads ÷ Total Number of Flips
= 52 ÷ 100 = 0.52 or 52%
This probability is based on actual observed data. If we increased the number of flips to 1000 or 10,000, we would expect the result to get closer to 50%.
Theoretical Approach
In the theoretical approach, we would analyze the coin and the flipping process without actually flipping the coin. We know that a fair coin has two sides: heads and tails. Assuming the coin is perfectly balanced and the flip is fair, we can deduce that:
- There are two possible outcomes (heads or tails)
- Each outcome is equally likely
Using probability theory, we can calculate:
Probability of Heads = Number of favourable outcomes ÷ Total number of possible outcomes
= 1 ÷ 2 = 0.5 or 50%
This theoretical probability is based on logical reasoning and the assumption of a fair coin and fair flip without needing to actually perform any coin flips.
Comparison
The theoretical approach gives us the exact 50% probability we expect from a fair coin. The empirical approach gave us 52%, which is close to but not exactly 50%. This difference illustrates a key point: empirical results can vary due to random chance, especially with smaller sample sizes. As we increase the number of flips in the empirical approach, we would expect the result to converge toward the theoretical 50% probability (Halton, 2024).
In real life, risk managers often use both approaches together. This helps them get a fuller picture of possible risks. They might use empirical data where it’s available and theoretical models where it’s not.
Regression Analysis
Regression analysis is a statistical technique employed in risk assessment to identify relationships between variables and ultimately predict the potential severity of loss events. It is one of the most widely used associative forecasting methods, which involves constructing a mathematical equation that relates the dependent variable to one or more independent variables. This statistical technique estimates the relationships between variables. It encompasses a diverse set of methods for modelling and analyzing the interplay between a dependent variable (the variable being forecast) and one or more independent variables (factors believed to influence the dependent variable). Regression analysis is particularly valuable for understanding how changes in independent variables impact the average value of the dependent variable while holding all other independent variables constant.
The coefficients of the independent variables in the regression equation represent the magnitude and direction of their impact on the dependent variable.
Image Description
The image is a scatter plot depicting data points and a linear regression line. The x-axis ranges from 0 to 4. The y-axis ranges from 0 to 10. The red diamonds represent the data points. The blue line represents the linear regression line, showing the best-fit line through the data points.
The data points follow an upward trend, indicating a positive correlation between the variables. The linear regression line slopes upward from left to right, suggesting a strong linear relationship. The legend in the plot identifies the red diamonds as “Data points” and the blue line as “Linear regression.”
Regression analysis provides several benefits in risk assessment, including:
- Quantifying the influence of multiple risk factors simultaneously
- Identifying the most significant risk drivers
- Developing predictive risk models for forecasting purposes
- Supporting risk-based decision-making through quantitative risk estimates
Regression models’ accuracy depends on data quality, assumptions’ validity, and the appropriate selection of techniques. Residual analysis, model diagnostics, and expert judgment are often used to evaluate and refine regression models in risk assessment applications (Edwards, 2024).
Loss Exposures
Loss exposures refer to situations or circumstances that may lead to financial losses for an individual, organization, or entity. These exposures can arise from various sources, such as property damage, liability claims, or other risks. Analyzing loss exposures is a critical step in risk management, as it helps identify potential risks and develop strategies to mitigate them.
Dimensions of Loss Exposures
When analyzing loss exposures, risk management professionals consider four key dimensions:
- Loss Frequency is the number of losses during a specific period.
- Loss Severity is the seriousness of a specific occurrence.
- Total Dollar Losses is the total dollar amount of losses incurred across all occurrences during a specific period.
- Timing refers to the points at which losses occur and when loss payments are made. Importance of Analyzing Loss Severity
Analyzing loss severity helps to understand the potential financial impact of a loss event. By assessing severity, they can prioritize risks and allocate resources effectively. For instance, a high-severity risk may require more attention and preventive measures than a low-severity risk.
Approaches for Jointly Analyzing Loss Frequency and Severity
The Prouty Approach is a qualitative technique used in risk assessment to determine how to treat different risks based on their potential frequency (likelihood) and severity (impact) of loss.
This approach is typically depicted using a risk matrix that maps the probability of a loss occurring (frequency) on one axis against its potential consequence (severity) on the other axis. Risks are then plotted on this matrix and treated according to which zone they fall into.
| The Prouty Approach | |||||
|---|---|---|---|---|---|
| Loss Frequency | |||||
| Almost Nil | Slight | Moderate | Definite | ||
| Loss Severity | Severe | Transfer | Reduce/Prevent | Reduce/Prevent | Avoid |
| Significant | Retain | Transfer | Reduce/Prevent | Avoid | |
| Slight | Retain | Transfer | Prevent | Prevent | |
Events Consequences Analysis
Decision Tree Analysis
Decision trees provide a graphical framework for depicting a decision-maker’s available choices (actions), potential outcomes (events), and interdependencies between these. They excel in analyzing situations involving a sequence of interrelated decisions.
Following the tree’s construction, the analysis proceeds from right to left, aiming to identify the optimal decision strategy, which translates to a sequence of decisions that maximizes utility. This analysis necessitates three key elements:
- Decision Criterion: The benchmark used to assess the desirability of outcomes, often expressed in terms of profit, cost, or a risk-adjusted measure.
- Event Probabilities: The likelihood assigned to each potential outcome is crucial for calculating expected values.
- Outcome Values: The monetary consequence (revenue or cost) of each decision alternative and chance event.
Example: New Product Launch
Consider a firm contemplating launching a new product versus continuing its existing offering. Launching the new product entails uncertain outcomes contingent upon market demand. High demand translates to a projected profit of $140, while low demand translates to $80. The firm estimates high and low demand probabilities to be 0.7 and 0.3, respectively. Maintaining the existing product guarantees a profit of $110. These estimated profits are depicted at the terminal nodes of the chance branches. Probabilities of high and low demand for the new product are indicated below the corresponding branches emanating from the chance node.
Expected values are calculated by averaging the profits weighted by their respective probabilities. For instance, the expected value at chance node (2) is calculated as (0.7×$140) + (0.3×$80) = $122, which is then inscribed above node (2). Arriving at the decision node (1), we select the alternative with the superior expected value. Since max ($122, $110) = $122, launching the new product is the more profitable course of action.
Procedure
- List the possible alternatives (actions/decisions).
- Identify the possible outcomes.
- List the payoff or profit or reward.
- Select one of the decision theory models.
- Apply the model and make your decision (Borrelli, 2015).
Event Tree Analysis
Event tree analysis (ETA) is a forward-looking, inductive technique employed in risk assessment. It systematically explores the potential consequences of a single initiating event, branching out to depict various sequences of successes and failures that can culminate in different accident scenarios. This approach facilitates the identification of critical pathways that contribute most significantly to system failure.
Key Advantages of Event Tree Analysis
- Comprehensive Coverage: ETAs provide a structured framework for analyzing the temporal progression of events, encompassing the interplay between system functionalities, protective safeguards, operator responses, and potential accident outcomes.
- Probabilistic Assessment: By assigning probabilities to each branch within the event tree, analysts can quantify the likelihood of various accident scenarios, enabling a more informed risk evaluation.
- Identification of Critical Pathways: ETAs pinpoint the sequence of events with the highest probability of leading to system failure, guiding efforts towards targeted risk mitigation strategies.
Applications and Effectiveness
While broadly applicable to diverse risk assessment scenarios, ETAs are particularly well-suited for analyzing complex systems equipped with multiple safety barriers. Their strength lies in systematically dissecting the potential consequences of an initiating event, revealing the interplay
between system behaviour, safeguard effectiveness, and human intervention. This facilitates the identification of critical vulnerabilities and the development of effective risk mitigation strategies.
Overall, event tree analysis is a valuable tool within the probabilistic risk assessment framework, offering a structured and systematic approach to identifying and evaluating potential accident scenarios (Borrelli, 2015).

Image Description
It starts with an “Initiating Event (IE)” at the bottom, which branches into two possible events labelled “Event 1” with outcomes “Success (1s)” and “Failure (1f).” Each of these outcomes leads to further events, numbered 2 to 4, each also having success and failure branches. The final column lists the overall outcome as either “Success Outcome (S)” or “Failure Outcome (F),” with associated probabilities P(S|E) and P(F|E) for success and failure given event E, respectively.
Success Outcome A: PA=(PIE)(P1s)(P2s)(P3s)(P4s)
Failure Outcome B: PB=(PIE)(P1s)(P2s)(P3s)(P4f)
Success Outcome C: PC=(PIE)(P1s)(P2s)(P3f)(P4s)
Failure Outcome D: PD=(PIE)(P1s)(P2s)(P3f)(P4f)
Failure Outcome E: PE=(PIE)(P1s)(P2f)
Failure Outcome F: PF=(PIE)(P1f)(P2f)
Steps
- Define the system.
- Identify the accident scenarios.
- Identify the initiating events.
- Identify intermediate events.
- Build the event tree diagram.
- Obtain event failure probabilities.
- Identify the outcome risk.
- Evaluate the outcome risk.
- Recommend corrective action.
- Document the entire process.
Video: “RENO 9 Quick Start Guide Chapter 9: Risk Analysis ‐ Event Tree for Risk of Fire Damage” by ReliaSoft Software [13:49] is licensed under the Standard YouTube License. Transcript.
Business Impact & Strategic Analysis
Fault Tree Analysis – FTA
Fault tree analysis (FTA) is a deductive, top-down approach to system reliability and safety analysis. Pioneered by Bell Laboratories, FTA systematically decomposes an undesired top-level event (failure) into its constituent basic events. Figure 5.3.2 is an example of a Fault-Tree analysis that goes from the system failure or consequences and follows the sequence of events backward to determine the system failure. The fish-tailed shape symbols are designated ‘or gates,’ meaning that only one event below them is required to occur to cause the event. The dome-shaped symbols are designated ‘and gates,’ meaning that an event can occur only if all events below them occur in sequence. For example, for the top event shown in the figure to occur, one of the events identified under the ‘or gates’ as 1, 2 or 6 must occur first. In comparison, for the top event in the figure to occur, all of the events identified under the ‘and gates’ as 3, 4, 5 or 7 and 8 must occur.
This methodology facilitates the identification of all possible combinations of hardware failures, software malfunctions, and human errors that could lead to the undesired outcome (Borrelli, 2015).
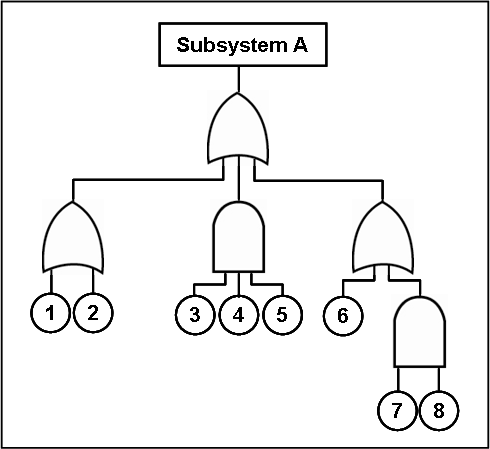
Image Description
The diagram starts with “Subsystem A” at the top, followed by an “OR” gate directly below it. Below the “OR” gate, there are three symbols arranged horizontally from left to right: an “OR” gate, an “AND” gate, and another “OR” gate. The first “OR” gate has two base events numbered 1 and 2. The second “AND” gate has three base events numbered 3, 4, and 5. The third “OR” gate has one base event numbered 6 and an “AND” gate with two base events numbered 7 and 8.
Methodology
- Define undesired events.
- Resolved into immediate causes.
- Continue resolution until basic events are identified.
- Construct a fault tree to demonstrate the logical relationships.
Software Tool
Business Continuity Planning
Business Continuity Planning (BCP) is an organization’s comprehensive process to identify potential threats and develop strategies to ensure the continuity of critical business operations and services during disruptions or disasters. In risk assessment, BCP is crucial in mitigating risks and minimizing their impact on the organization.
BCP involves several key steps that are closely tied to risk assessment:
- Risk Identification: The first step is identifying potential risks that could disrupt business operations. This includes risks from natural disasters (e.g., earthquakes, floods, hurricanes), technological failures (e.g., cyber-attacks, system outages), human-caused events (e.g., terrorism, civil unrest), and other sources.
- Risk Analysis: Once risks are identified, organizations conduct a thorough analysis to understand the likelihood of occurrence and the potential impact on critical business functions, assets, and resources. This analysis helps prioritize risks based on their severity and probability.
- Business Impact Analysis (BIA): A BIA is performed to determine the potential consequences of disruptions on the organization’s operations, processes, and resources. It identifies critical business functions, dependencies, and recovery time objectives, providing insights into risks’ potential financial and operational impacts.
- Risk Mitigation Strategies: Based on the risk analysis and BIA, organizations develop strategies to mitigate or minimize the identified risks. These strategies may include preventive measures, contingency plans, recovery procedures, and continuity plans to ensure the continuation of critical business functions during and after a disruptive event.
- Plan Development: A comprehensive BCP is developed, documenting the strategies, procedures, and resources required to respond to and recover from disruptions. The plan outlines roles, responsibilities, communication protocols, resource allocation, and testing and maintenance procedures.
- Testing and Maintenance: Regular testing and exercising of the BCP are essential to validate its effectiveness and identify areas for improvement. The plan should be reviewed and updated periodically to reflect changes in the organization’s operations, risks, and regulatory requirements.
By integrating risk assessment into the BCP process, organizations can proactively identify and mitigate potential risks, minimize the impact of disruptions, and ensure the continuity of critical business operations, ultimately enhancing their resilience and competitiveness (Setiawan et al., 2017).
SWOT Analysis
SWOT stands for Strengths, Weaknesses, Opportunities, and Threats. It was explained in Chapter 4 as an effective risk identification strategy, but it should be noted that it is also effective in analyzing risks. In risk analysis, SWOT analysis helps identify and categorize potential risks and risk factors into these four categories:
- Strengths: Internal factors or capabilities that can help mitigate risks or enhance the ability to manage risks effectively. These could include skilled personnel, robust processes, financial resources, environment, or competitive advantages.
- Weaknesses: Internal vulnerabilities or deficiencies that can increase the likelihood or impact of risks. Examples include lack of expertise, outdated technology, limited resources, or inefficient processes.
- Opportunities: External factors or situations that, if capitalized upon, can help reduce risks or create new opportunities for risk mitigation. These could include favourable market conditions, new technologies, strategic partnerships, or regulatory changes.
- Threats: External factors or events that can pose risks or challenges to the project or organization. Examples include competition, economic downturns, political instability, natural disasters, or changes in customer preferences.
The SWOT Analysis Process in Risk Analysis Typically Involves The Following Steps
- Identify Risks: Conduct a brainstorming session or use other risk identification techniques to list potential risks that could impact the project or organization.
- Categorize Risks: Classify the identified risks into the four SWOT categories (Strengths, Weaknesses, Opportunities, and Threats) based on their nature and source (internal or external).
- Analyze Interactions: Examine how the identified strengths, weaknesses, opportunities, and threats interact and influence the overall risk landscape. For example, strengths can help mitigate weaknesses or threats, while opportunities can be leveraged to address weaknesses or capitalize on strengths.
- Develop Risk Strategies: Based on the SWOT analysis, develop risk response strategies that leverage strengths, address weaknesses, exploit opportunities, and mitigate threats. These strategies may include risk avoidance, mitigation, transfer, or acceptance.
- Monitor and Review: Monitor the SWOT factors and update the risk analysis as the project or organizational environment changes. Adjust risk strategies accordingly.
By conducting a SWOT analysis in risk analysis, organizations can comprehensively understand their internal and external risk factors, identify potential risk interactions, and develop effective risk management strategies tailored to their specific strengths, weaknesses, opportunities, and threats (Hall, 2024).
Cause and Effect Analysis
Fishbone Diagram
The Fishbone Diagram, or Ishikawa Diagram, is an analytical tool that investigates the causes of an event. It provides a systematic way to explore and visualize the root causes contributing to a specific effect or undesirable outcome.
Fishbone Diagram is a powerful tool that helps organizations identify and analyze the potential causes of risks or failures in a project or process. The diagram resembles a fish skeleton, with the “effect” or problem represented by the fish’s head and the potential causes branching off like bones from the backbone (Oktaviani et al., 2021).
The Main Steps Involved in Fishbone Diagram
- Define the Effect or Problem
- Identify Main Cause Categories
- Brainstorm Potential Causes
- Analyze and Prioritize Causes
- Develop Countermeasures
- Monitor and Review
A critical component of the Fishbone Diagram is the 5-Whys Analysis. The 5-Why Analysis is a structured problem-solving technique used in risk assessment to identify the root causes of potential risks or undesirable events. It involves repeatedly asking the question “Why?” to peel back layers of symptoms and uncover the underlying root causes.
The 5-Why Analysis is instrumental during risk assessment’s risk identification and analysis phases. Systematically exploring the causal relationships behind a potential risk event helps organizations gain a deeper understanding of the root causes and develop effective mitigation strategies.
The Main Steps Involved in The 5-Why Analysis in A Risk Assessment Context
- Define the Risk Event
- Ask “Why?” and Record the Answer
- Repeat the “Why?” Question
- Identify Root Causes
- Develop Countermeasures
- Monitor and Review
Software
Future State Analysis
Scenario Analysis
Scenario analysis is a technique used in risk analysis to evaluate and quantify the potential impacts of uncertainties and risks on desired outcomes or objectives.
It involves creating and analyzing multiple plausible scenarios or future states of the world, each defined by a unique set of assumptions, trends, and events. It helps decision-makers understand how different factors and uncertainties could interact and influence outcomes.
The Following Steps Are Usually Taken in This Technique For Risk Analysis
- Identify Key Uncertainties
- Develop Scenarios
- Assess Impacts
- Quantify Risks
- Analyze and Communicate
Scenario analysis is used in various situations for risk analysis, including:
- Financial Risk Assessment for banks and financial institutions.
- Climate Change Risk for insurance companies and environmental agencies employ scenario analysis to understand the potential impacts of climate change, such as extreme weather events, sea-level rise, and regulatory changes.
- Supply Chain Risk for manufacturers and logistics companies analyzes scenarios related to supplier disruptions, natural disasters, or geopolitical events.
- Pandemic Preparedness for healthcare organizations and public health agencies uses scenario analysis to plan for potential disease outbreaks and assess hospital capacity.
- Strategic Planning for businesses to leverage scenario analysis to evaluate the risks and opportunities associated with different strategic decisions.
By considering multiple scenarios and quantifying their impacts, scenario analysis provides a structured approach to risk assessment, enabling organizations to make informed decisions, develop risk mitigation strategies, and enhance resilience in the face of uncertainty (Hayes, 2023; Airmic, 2016).
Monte-Carlo Analysis
Monte Carlo analysis is a technique used in risk analysis to quantify the potential impact of uncertainty on a project or decision. It simulates various possible scenarios by considering the randomness or variability of different factors.
Monte Carlo Analysis provides a more comprehensive risk picture than traditional point estimates (best-case, worst-case scenarios). It also helps to identify potential risks that might not have been considered before, allowing better decision-making by understanding the probabilities of various outcomes (Stammers, 2024; Agarwal, 2024).
Human Reliability Analysis
Human Reliability and Error Analysis
Human reliability plays a critical role in the resilience of complex systems, given the potential consequences of human errors or oversights. Whether operating a nuclear reactor, flying an aircraft, driving a car, or managing an industrial plant, understanding human reliability is essential.
Various methods can be employed to analyze human reliability. These include hierarchical task analysis, focusing on critical activities that could lead to hazardous events. The process begins by identifying individual tasks and steps within an activity, highlighting potential errors associated with specific steps, and using prompts to identify error mechanisms (such as skipping a step, performing the right action on the wrong object, or transposing digits).
Once potential error sources are identified, actions are developed to minimize their impact and enhance human performance reliability.
Key steps include evaluating necessary information, identifying pre- and post-task states, understanding information transmission, classifying tasks adequately, recognizing interconnections among staff and actions, and screening critical actions. Additionally, practice-oriented methods help estimate failure probabilities.
Finally, constructing a quantitative fault/event tree—incorporating both component failures and human action failures—allows us to perform dominance analyses, further improving system reliability (Borrelli, 2015).
Failure Modes and Effects Analysis
Failure Modes and Effects Analysis (FMEA) is a foundational technique for quantifying potential risks associated with a system’s design. It fosters a systematic approach to analyzing how components or the entire system might fail and the resultant consequences of such failures, and ultimately, guides design revisions to minimize risk. Notably, risk mitigation can be achieved by reducing the occurrence of failures, mitigating their consequences, or, ideally, both. The difference between a fault-tree analysis and failure mode and effects analysis is that fault-tree analysis goes from consequences to causes. In contrast, failure mode and effects analysis go from causes to consequences.
From an engineering design perspective, FMEA empowers the implementation of robust risk mitigation strategies. This can involve incorporating multiple failure barriers, a concept often called defence-in-depth. Additionally, FMEA can inform the system’s strategic use of redundancy and diversity to enhance fault tolerance (Borrelli, 2015).
FMEA Procedure
- Construct a detailed flow chart of the process.
- Determine how each step could possibly fail.
- Determine the “effects” of each possible failure.
- Assign a Severity Rating for each effect.
- Assign an Occurrence Rating for each failure.
- Calculate and prioritize a Risk Priority Number (RPN) for each failure.
- Review the process and conduct a root cause analysis.
- Take action to eliminate or reduce the Risk Priority Number.
- Recalculate the resulting RPN as the failure modes are reduced or eliminated.
Video: “FMEA – What it is and how it works” by Dr. Cyders [22:12] is licensed under the Standard YouTube License. Transcript and closed captions available on YouTube.

