21 RStudio Workshop : Analyse de la variance mixte tridirectionnelle
Mettons à présent en commun tout ce que nous avons appris jusqu’à présent et exécutons un plan d’expérience complexe (2x2x3).
- Variable dépendante : Notes de l’épreuve
- Facteur entre les participants : Exercice (Pleine conscience x Yoga)
- Facteurs internes aux participants : Boisson (café x placebo) et sommeil (0/5/8 heures)
Dans cette expérience hypothétique, deux groupes sont placés dans un programme d’exercice de trois mois. Un groupe participe à trois séances de yoga par semaine, tandis que l’autre est invité à pratiquer la pleine conscience trois fois par semaine à la maison pendant une heure.
Après un mois d’exercice, les participants sont invités à assister à six conférences données à des moments différents. Après un exposé, il leur est demandé de revenir le lendemain pour répondre à des questions sur le contenu de la conférence après avoir dormi 0, 5 ou 8 heures. Au moment du test, les participant.e.s reçoivent du café ou un placebo (boisson chaude décaféinée). Par conséquent, dans les deux groupes d’exercices, tous les participant.e.s connaissent des niveaux différents de manipulation du sommeil et des boissons.
Nous nous intéressons ici à savoir si le manque de sommeil nuit aux résultats des tests. Nous souhaitons également savoir si les personnes qui pratiquent le yoga sont plus résilientes aux effets négatifs du sommeil sur l’apprentissage. De plus, nous souhaitons savoir si le café peut atténuer l’effet du manque de sommeil sur les performances aux tests.
# Data Prepmydata3 <-read_excel("3way_mixed_Sample_DataFile.xlsx") #importing data file# Set-up factorsmydata3 <- mydata3 %>%convert_as_factor(ID, Gender, Exercise, Beverage, Sleep)str(mydata3) #checking factors/levels
## tibble [1,032 × 7] (S3 : tbl_df/tbl/data.frame)
## $ ID : Facteur avec 172 niveaux "23936", "25440″,.. : 10 71 6 70 147 129 74 62 21 38 …
## $ Gender : Facteur avec trois niveaux « F », « M » (H), « Non-Binary » (Non binaire) : 1 1 1 1 1 1 1 3 1 2 ..
## $ Age : num [1:1032] 22 22 23 22 22 24 22 22 23 22 ..
## $ Exercise : Facteur avec deux niveaux « Mindfulness » (pleine conscience),.. : 1 1 1 1 1 1 1 1 1 1..
## $ Beverage : Facteur avec deux niveaux « Coffee » (café), « Placebo » : 1 1 1 1 1 1 1 1 1 1 …
## $ Sleep : Facteur avec trois niveaux "0", "5″, "8″ : 1 1 1 1 1 1 1 1 1 1 …
## $ TestScore: num [1:1032] 89.3 91.6 88.1 92.1 99 …
Vérifions que nous disposons d’une conception équilibrée. Autrement dit, nous avons un nombre égal de participant.e.s par observations pour chaque combinaison de nos trois variables.
# Generating frequency tables to check balance of designtable(mydata3$Beverage, mydata3$Sleep, mydata3$Exercise)
# we are organizing the number of observations per every combination of the within-subjects factors at either level of the between-subjects variable
## , , = Mindfulness
##
##
## 0 5 8
## Coffee 86 86 86
## Placebo 86 86 86
##
## , , = Yoga
##
##
## 0 5 8
## Coffee 86 86 86
## Placebo 86 86 86
Nous pouvons constater que nous disposons d’un nombre égal d’observations (n=86) pour tous les niveaux de nos trois facteurs (c.-à-d. par cellule) par rapport à un plan déséquilibré qui présente un nombre inégal d’observations. Dans ce cas, les chiffres de votre tableau de fréquences ne seront pas tous égaux.
Si la conception de votre expérience est déséquilibrée, je vous recommande la ressource suivante. Cependant, une fois que vous serez à l’aise avec les codes présentés ici, vous pourrez facilement effectuer les mêmes analyses avec votre modèle déséquilibré, moyennant quelques modifications ou ajustements.
Ressource d’analyse de la variance tridirectionnelle non équilibrée : https://www.r-bloggers.com/2011/02/r-tutorial-series-two-way-anova-with-unequal-sample-sizes/
Statistiques sommaires
Calculons maintenant quelques statistiques de base.
# Computing a summary Statistics table for each independent variableanova3.summary.statistics <-data.frame (mydata3 %>%group_by(Exercise, Beverage, Sleep) %>%get_summary_stats(TestScore, type = "full") )
Je recherche ici la performance moyenne ainsi que l’erreur type des valeurs moyennes, que j’utiliserai plus tard pour mes barres d’erreur lors de l’établissement des chiffres. D’autres mesures que vous pouvez utiliser sont énumérées dans la fiche d’information de la fonction get_summary_stats et comprennent : type = c ("mean_sd", "mean_se", "mean_ci", "median_iqr", "median_mad", "quantile", "mean", "median", "min", "max").
Par exemple, si vous souhaitez utiliser les valeurs de l’écart-type moyen pour vos barres d’erreur, vous pouvez utiliser « mean_sd ». Vous pouvez également utiliser « full » comme type pour obtenir toutes les mesures!
Conseil : Vous pouvez explorer ce que chaque fonction offre à l’aide d’exemples en plaçant un « ? » juste avant la fonction vide, comme indiqué ci-dessous. La fiche d’information de la fonction s’ouvrira dans l’onglet Aide en bas à droite sur RStudio. Essayez-le!
?get_summary_stats ()
Tableaux publiables Bien que ce soit un beau tableau, si vous souhaitez inclure des statistiques récapitulatives dans votre thèse finale, suivez les étapes suivantes pour générer de jolis tableaux imprimables!
# Create a copy and maintain the original with full summary statistics which we # will use for plotsanova3.summary.statistics.print <- anova3.summary.statistics# Deleting the column "variable" by name since we only have one dependent variableanova3.summary.statistics.print <-subset(anova3.summary.statistics.print, select =-c(variable))# Selecting columns by name that we want to include in our final table#colnames(anova3.summary.statistics) #print column names to see options anova3.summary.statistics.print <-subset(anova3.summary.statistics.print, select =c(Exercise, Beverage, Sleep, n, mean, se))# Let’s round our numerical values in select columns to 3 significant figures, # but you may choose to change this depending on your own preferenceanova3.summary.statistics.print$mean <-signif(anova3.summary.statistics.print$mean,3) anova3.summary.statistics.print$se <-signif(anova3.summary.statistics.print$se,3) # Next we will change column names to make them nicer#colnames(T2.summary.statistics) # print all column names in data framecolnames(anova3.summary.statistics.print)[colnames(anova3.summary.statistics.print) =="n"] ="N"colnames(anova3.summary.statistics.print)[colnames(anova3.summary.statistics.print) =="mean"] ="Mean"colnames(anova3.summary.statistics.print)[colnames(anova3.summary.statistics.print) =="se"] ="SEM"colnames(anova3.summary.statistics.print)[colnames(anova3.summary.statistics.print) =="Sleep"] ="Sleep (hrs)"# Generating the Printable Summary Stat Table # Make sure to remove the comments sign "#" from the code below when running to create and view the publishable table#anova3.summary.statistics.print %>% # kbl(caption = "Summary Statistics") %>% # Title of the table# kable_classic(full_width = F, html_font = "Cambria", font_size = 10) %>% # add_header_above(c(" " = 4, "Test Score (%)" = 2)) # adding header to columns #in table by position. E.g., # for the first 5 columns we do not want a header so we leave empty space. # Over the last two columns we specified the header name.
Récapitulation des données démographiques
# Selecting rows of data only if ID value is uniquemydata3unique <- mydata3 %>%distinct(mydata3$ID, .keep_all=TRUE) # Looking at the distribution of "Gender" per grouptable(mydata3unique$Gender, mydata3unique$Exercise)
##
## Pleine conscience Yoga
## F 40 60
## M 39 21
## Non-binaire 7 5
nrow(mydata3unique) # total number of participants
# Mean Age Per Group mydata3unique %>%group_by(Exercise) %>%get_summary_stats(Age, type ="mean")
## # Une trame de données « tibble » : 2 × 4
## Exercice variable moyenne n
## <fct> <fct> <dbl> <dbl>
## 1 Pleine conscience Âge 86 22,6
## 2 Yoga Âge 86 22,2
Taille de l’échantillon Nous avons recruté 172 participant.e.s dans le bassin des étudiant.e.s de premier cycle en introduction à la psychologie de l’Université McMaster, en échange d’un crédit partiel de cours. Les personnes ont été assignées au hasard soit à la condition Pleine conscience (n=86; 39 hommes et 7 non-binaires; Moy. âge = 22,6 ans), soit à la condition Yoga (n=86; 21 hommes et 5 non-binaires; Moy. âge = 22,2 ans).
Visualisation
Vous remarquerez que le code que j’utiliserai pour représenter les données de cet ensemble de données est différent des précédents.
Le premier que nous allons créer est un graphique linéaire. Nous voulons donc spécifier ici le facteur que nous voulons sur notre axe des x, ainsi que la mesure sommaire de la variable dépendante que nous voulons sur notre axe des y. Dans ce cas, nous voulons le facteur Sommeil (avec 3 niveaux) sur l’axe des x, et la moyenne des notes de tests sur l’axe des y. Ensuite, nous voulons choisir une autre caractéristique identifiable du graphique pour représenter nos deux autres variables indépendantes. Dans ce cas, nous avons différencié les deux niveaux de la variable Exercice par la couleur des lignes et le type ou la forme des lignes pour représenter les différentes boissons consommées. Vous pouvez choisir n’importe laquelle des options proposées dans l’aide-mémoire et bien d’autres encore!
Conseil : Vous devez concevoir vos graphiques de manière à ce que les différents facteurs puissent être distingués facilement par une personne daltonienne ou être imprimés en noir et blanc. Par conséquent, nous utiliserons également la forme de nos points pour spécifier la variable BLOCK_TYPE
GRAPHIQUE LINÉAIRE
# Notice that I am using the summary stat table with the full range of data not the printable oneanova3.lineplot <-ggplot(anova3.summary.statistics, aes(x=Sleep, y=mean, color=Exercise, group=interaction(Exercise, Beverage))) +geom_point(data=filter(anova3.summary.statistics, Exercise =="Yoga"),shape=19, size=4.5) +#assigning point type 19 from cheat sheet to one level of factorgeom_point(data=filter(anova3.summary.statistics, Exercise =="Mindfulness"), shape=1, size=4.5) +#assigning point type 1 from cheat sheet to other level of factorgeom_line(data=filter(anova3.summary.statistics, Beverage =="Coffee"),linetype="dashed", linewidth=1.2) +#assigning line type to one level of factorgeom_line(data=filter(anova3.summary.statistics, Beverage =="Placebo"), linetype="solid", linewidth=1.2) +#assigning line type to other level of factorscale_color_manual(values =c("skyblue1", "darkred")) +xlab("Sleep (hrs)") +#add title to x-axisylab("Average Test Score (%)") +#add title to y-axistheme_classic() +#this theme has no background, no bounding box. theme(axis.line=element_line(linewidth=1.5), #thickness of x-axis lineaxis.text =element_text(size = 14, colour ="black"),axis.title =element_text(size = 16, colour = "black"),panel.grid.major.y =element_line(), # adding horizontal grid lineslegend.position = "none") +coord_cartesian(ylim=c(0, 100)) +scale_y_continuous(breaks=seq(00, 100, 10)) +# Ticks on y-axis from 0-100, jumps by 10 geom_errorbar(aes(ymin=mean+se, ymax=mean-se), width = 0.12, size = 1) #adding error bars
## Warning: Using ’size’ aesthetic for lines was deprecated in ggplot2 3.4.0.## ℹ Please use ’linewidth’ instead.## This warning is displayed once every 8 hours.## Call ’lifecycle::last_lifecycle_warnings()’ to see where this warning was## generated.
anova3.lineplot
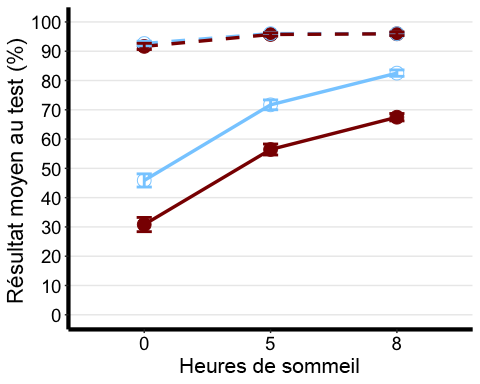
Dans le code suivant, nous pouvons créer une légende personnalisée pour n’importe quelle figure. N’hésitez pas à jouer avec ce code. Je préfère créer ma légende séparément de la fonction que j’utilise pour représenter mes données, car l’esthétique du code interne des graphiques est un peu restreinte, surtout si nous illustrons plus de deux facteurs.
plot.new() legend("center", # location on screen (center, upper right, etc)title=" Exercise Beverage", # bit of a hack here but I put lots of space to align with legend levelslegend=c("Yoga","Mindfulness","Placebo","Coffee"), col=c("skyblue 1", "darkred",’black’,’black’),pch=c(1,19,NA,NA), # assigning point shapes pt.cex = 2, # setting point sizelty =c(0,0,1,2), lwd =c(NA,NA,2,2), # assigning line type bty="o", # border around legend boxbox.lwd = 2, # thickness of border line border=T, # border around legend boxhoriz = T, # title is horizontaltitle.font = 2.5, cex = 0.765# size of the legend box)
Je vous suggère ces options de modification des graphiques à surfaces.
GRAPHIQUE À SURFACES
anova3.bxp <-ggboxplot(mydata3, x = "Sleep", y ="TestScore",color = "Exercise", palette = "grey",facet.by = "Beverage", #specifying grouping variables for faceting the plot # into multiple panelsbxp.errorbar = TRUE, bxp.errorbar.width = 1,xlab = "Sleep (hrs)", ylab ="Judgement of Learning (JOL; %)") +theme(axis.line=element_line(linewidth=1.5), #thickness of x-axis lineaxis.text =element_text(size = 14, colour = "black"),axis.title =element_text(size = 16, colour = "black"),panel.grid.major.y =element_line()) +# adding horizontal grid linesscale_y_continuous(breaks=seq(0, 100, 10)) # Ticks on y-axis from 0-100, # jumps by 10 anova3.bxp
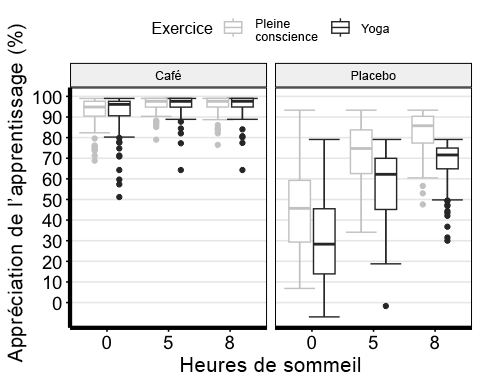
J’ai utilisé la palette de « gris », qui est ennuyeuse si vous voulez mon avis. Même s’il y a bien des façons de choisir les couleurs d’un graphique, voici une librairie super attrayante et utile de couleurs adaptées aux revues scientifiques et inspirées de la science-fiction pour le système ggplot2. Cliquez sur le lien suivant pour voir comment utiliser toutes les options dans vos graphiques.
anova3.bxp.tron <-anova3.bxp +theme_dark() +#changing theme of plottheme (panel.background =element_rect(fill ="#2D2D2D"))+#changing plot# background colorscale_color_tron()
## Scale for colour is already present.## Adding another scale for colour, which will replace the existing scale.
#This palette is inspired by the colours used in Tron Legacy. It is suitable for#displaying data when using a dark themeanova3.bxp.tron
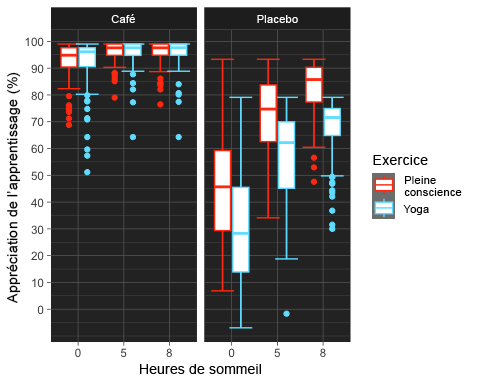
GRAPHIQUE À BARRES
anova3.barplot <-ggplot(anova3.summary.statistics, aes(x =factor(Sleep), y = mean, fill =Beverage:Exercise)) +geom_bar(stat = "identity", position ="dodge") +geom_errorbar(aes(ymax = man + sd, ymin = mean - sd), #standard error barsposition position_dodge(0.9), width = 0.25, color = "Gray25") +xlab("Slep (hrs)") +ylab("Average Test Score (%)") +scale_fill_brewer(palette = "RdPu") +theme_classic() +theme(legend.position = "none", # no legendpanel.grid.major.y =element_line() ) +# addinghorizontal grid linesscale_y_continuous(breaks=seq(0, 100, 10)) # Ticks on y-axis from 0-100, jumps by 10
# Let’s do some exploring with these different colour palettes #This palette is inspired by the colours used in the TV show The Simpsonsanova3.barplot.springfield <- anova3.barplot +scale_fill_simpsons()
## Scale for fill is already present.## Adding another scale for fill, which will replace the existing scale.
#This palette is inspired by the colours used in the TV show Rick and Mortyanova3.barplot.schwifty <- anova3.barplot +scale_fill_rickandmorty()
## Scale for fill is already present.## Adding another scale for fill, which will replace the existing scale.
#This colour palette is inspired by Frontiers:anova3.barplot.default <- anova3.barplot +scale_fill_frontiers()
## Scale for fill is already present.## Adding another scale for fill, which will replace the existing scale.
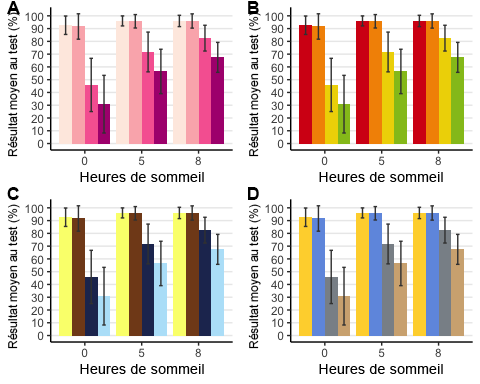
Et si nous voulions publier toutes ces variantes du graphique à barres sur la même page? La fonction suivante permet d’organiser deux ou plusieurs graphiques sur la même page pour l’impression. En spécifiant le nombre de colonnes, vous organisez les graphiques horizontalement, chacun occupant une colonne. En spécifiant le nombre de lignes, vous pouvez organiser les graphiques verticalement. Nous pouvons également ajuster la taille de cette figure avec les trois graphiques. Si les graphiques sont très similaires, vous pouvez créer une légende commune (common legend) en saisissant « T », ce qui permettra au logiciel R de la générer pour vous. Cependant, je préfère créer ma propre légende, ce que nous ferons dans la prochaine section.
barplots <– arrangeGrob (anova3.barplot, anova3.barplot.default,anova3.barplot.schwifty, anova3.barplot.springfield,nrow = 2, ncol = 2)
# Add labels to the arranged plotsbarplots.gg <-as_ggplot(barplots) +#transform to a ggplotdraw_plot_label(label =c("A", "B", "C", "D"), size = 14, #add labelsx =c(0, 0.5, 0, 0.5), #specifying location of labels horizontallyy =c(1.017, 1.017, 0.53, 0.53)) #specifying location of labels #vertically# You can play around with the vertical and horizontal coordinates # (corresponding to the label in the order they are listed).
barplots.gg
Calcul de l’analyse de la variance tridirectionnelle
Il existe de nombreuses façons d’effectuer une analyse de la variance tridirectionnelle. La librairie d’analyse d’expériences factorielle (afex), en particulier, fournit trois fonctions pour le calcul des analyses de la variance. Elles produisent le même résultat, mais le calcul est différent.
- aov_car()
- aov_ez()
- aov_4()
Je vais utiliser la même fonction que pour les analyses de la variance bidirectionnelle. Toutefois, je vous encourage à découvrir laquelle vous convient le mieux ou vous est la plus utile. Voici les ressources suivantes pour commencer à utiliser la librairie afex :
- Analyse de la variance dans le logiciel R : la librairie afex peut être la solution que vous recherchez
- afex : Analyse des expériences factorielles
# Three-Way Mixed ANOVA (2 BLOCK_TYPE x 2 TRIAL-TYPE x 3 SOA)anova3.aov <-anova_test(data = mydata3, dv = TestScore, wid = ID, #factor containing individuals/subjects identifier. Should be unique # per individual.between = Exercise, #(optional) between-subject factor variable(s)within =c(Beverage, Sleep), #(optional) within-subjects factor variablesdetailed = TRUE, #If TRUE, returns extra information (sums of squares columns, #intercept row, etc.)effect.size = "ges"#generalized eta squared or "pes" (partial eta squared), #the option "both" is bugged and currently doesn’t work)# Applies the Greenhouse Geisser correction to effects only when sphericity is violatedanova3.aov <-get_anova_table(anova3.aov, correction = "auto")# ?get_anova_table() to see other viable correction options
Pour le moment, je préfère présenter deux mesures de l’ampleur de l’effet, soit les valeurs partielles et les valeurs de l’eta-carré généralisé. Pour ajouter l’eta-carré partiel, j’ai décidé de le calculer à la main. J’indique également l’erreur type de la valeur moyenne à la main incluse ci-dessous :
# Calculate partial eta square and add it as a new column named "pes"# Codes for MSE and pes retrieved from # https://sherif.io/2014/12/10/ANOVA_in_R.htmlanova3.aov$pes = anova3.aov$SSn/(anova3.aov $ SSn + anova3.aov $ SSd)# Calculate mean sum of error and add it as a new column named "MSE"anova3.aov$MSE = anova3.aov$SSd/anova3.aov$DFd#store ANOVA tables as a dataframeanova3.aov <-data.frame(anova3.aov)# Deleting intercept info (first row)anova3.aov <- anova3.aov[-1,] #removing first row# Okay, let’s make some beautiful printable ANOVA tables# Selecting which values by column name we want to report from the detailed ANOVA tableanova3.aov.printable <- anova3.aov %>%select("Effect", "DFn", "DFd", "F","MSE", "p","p.. 05","pes", "ges")# Rename columnscolnames(anova3.aov.printable)[colnames(anova3.aov.printable) =="pes"] ="η2P"colnames(anova3.aov.printable)[colnames(anova3.aov.printable) =="ges"] ="η2G"colnames(anova3.aov.printable)[colnames(anova3.aov.printable) =="p..05 0] ="sig"#anova3.aov.printable %>%# kbl(caption = "THREE-WAY MIXED ANOVA") %>%# kable_classic(full_width = F, html_font = "Cambria", font_size = 10) %>%# add_header_above(c(" (" = 2, "Test Score (%)" = 8)) %>%# add_footnote("Correction: Greenhouse Geisser")
Analyses post hoc
La méthode empirique consiste à décomposer l’interaction de premier ordre. S’il y a un effet significatif d’interaction tridirectionnelle, vous devez le décomposer en : 1. Interaction bidirectionnelle simple : il s’agit essentiellement d’effectuer deux interactions bidirectionnelles à chaque niveau d’une troisième variable. S’il existe des interactions bidirectionnelles significatives, il faut alors les décomposer en… deux. Effet principal simple : effectuer une analyse de la variance unidirectionnelle à chaque niveau d’une deuxième variable. S’il y a un effet significatif, il faut alors mener… une troisième analyse. Comparaisons simples par paire : effectuer des comparaisons par paire ou d’autres comparaisons post hoc.
Si vous avez lu les modèles d’analyse de la variance birectionnelle et unidirectionnelle plus haut dans le document, les étapes suivantes ne devraient pas vous poser de problème. Comme vous pouvez le constater, la décomposition des interactions d’ordre élevé est très intuitive. Il s’agit simplement de revenir sur ses pas pour découvrir où se situent les différences entre nos groupes et leurs niveaux.
Si vous n’avez pas d’interaction tridirectionnelle significative… ce qui est le cas dans l’exemple actuel, vous devez alors déterminer si vous avez des interactions bidirectionnelles statistiquement significatives. Dans notre cas, nous en avons deux : 1. L’interaction entre la boisson et le sommeil ressemble à une interaction significative d’une analyse de la variance bidirectionnelle entre sujets. L’interaction entre l’exercice et la boisson est comparable à une interaction significative issue d’une analyse de la variance mixte bidirectionnelle. Dans ce cas, nous retracerons nos étapes en effectuant des analyses de la variance unidirectionnelle d’un facteur à chaque niveau de l’autre facteur avec lequel il interagit (c’est-à-dire des analyses d’effets principaux simples), puis des comparaisons par paires si nécessaire.
# Décomposition des interactions « Exercice x Boisson » (Exercise x Beverage) et « Boisson x Sommeil » (Beverage x Sleep)
# Analyse de l’effet principal simple de l’exercice à chaque niveau de boisson :
mydata3.coffee <- anova_test(data = filter(mydata3, Beverage == “Coffee”), wid = ID, within = Sleep, between = Exercise,
dv= TestScore, detailed = TRUE, effect.size = “pes”)
mydata3.placebo <- anova_test(data = filter(mydata3, Beverage == “Placebo”), wid = ID, within = Sleep,
between = Exercise, dv= TestScore, detailed = TRUE, effect.size = “pes”)
#Extraction des tableaux des analyses de la variance sous forme de trames de données
mydata3.coffee <- data.frame (get_anova_table(mydata3.coffee, correction = “auto”) )
mydata3.placebo <– data. frame (get_anova_table (mydata3.placebo, correction = "auto"))
# Faisons de jolis tableaux imprimables; notez que je n’ai pas calculé l’erreur quadratique moyenne (EQM) et que je n’ai pas inclus l’eta-carré généralisé dans mon tableau. # Le but était uniquement d’abréger ce guide. Vous avez les codes des analyses de la variance précédentes pour les calculer vous-mêmes. Suppression des informations d’interception (première ligne)
mydata3.coffee <- mydata3.coffee[–1, ]
mydata3.placebo <- mydata3.placebo[–1, ]
# colnames(mydata3.coffee) #Obtenir tous les noms de colonnes
#Sélectionner les colonnes à conserver par leur nom
mydata3.coffee <- mydata3.coffee %>% Sélectionner(“Effect”, “DFn”, “DFd”, “F”, “p”, “p..05”, “pes”)
mydata3.placebo <- mydata3.placebo %>% Sélectionner(“Effect”, “DFn”, “DFd”, “F”, “p”, “p..05”, “pes”)
#Combiner des tableaux
mydata3.ss.results <- cbind(mydata3.coffee , mydata3.placebo)
# Renommer les colonnes
colnames(mydata3.ss.results)[colnames(mydata3.ss.results) == “pes”] =“η2P”
colnames(mydata3.ss.results)[colnames(mydata3.ss.results) == “ges”] =“η2G”
colnames(mydata3.ss.results)[colnames(mydata3.ss.results) == “p..05”] =“sig”
#Créer une analyse de la variance imprimable en HTML
mydata3.ss.results %>%
kbl(caption = « Effet principal simple de l’exercice à chaque niveau
de boisson ») %>%
kable_classic(full_width = F, html_font = “Cambria”, font_size = 10) %>%
add_header_above(c(” ” = 1, “Coffee” = 7, “Placebo” = 7)) %>%
add_footnote(“Correction: Greenhouse Geisser”)
Étant donné qu’il n’y a pas d’interactions bidirectionnelles significatives, nous ne procéderons pas à des comparaisons par paire.
Rapports Nous avons soumis les résultats des tests à une analyse de la variance tridirectionnelle avec la boisson (café ou placebo) et le sommeil (0/5/8 heures) comme variables intraparticipant et l’exercice (yoga et pleine conscience) comme variable interparticipant. L’analyse de la variance a montré un effet principal significatif de l’exercice [F(1 170) = 33,0, MSE = 472,7, p <0,001, eta-carré partiel = 0,163], boisson [F(1 170) = 1222,8, EQM = 266,3, p <0,001, eta-carré partiel = 0,878], et sommeil [F(1,3-219,3) = 525,1, EQM = 111,2, p <0,001, eta-carré partiel = 0,755]. Il existe également une interaction significative entre l’exercice et la boisson [F(1 170) = 52,2, EQM = 266,3, p <0,001, eta-carré partiel = 0,235] ainsi qu’une interaction entre la boisson et le sommeil [F(1,50-257.3) = 462,1, EQM = 68,8, p <0,001, eta-carré partiel = 0,731]. Ces interactions ont été décomposées en soumettant les résultats des tests des conditions Café et Placebo à des analyses de la variance mixte bidirectionnelle, le sommeil étant un facteur intraparticipant et l’exercice, une variable interparticipant.
Une analyse séparée de la condition Placebo a révélé un effet significatif de l’exercice [F(1 170) = 45,3, p <0,001, eta-carré partiel = 0,210] et un effet du sommeil [F(1,4-238,4) = 238,4, p <0,001, eta-carré partiel = 0,771]. L’analyse de la condition Café n’a révélé qu’un effet significatif du sommeil [F(1,2-206,8) = 46,9, p <0,001, eta-carré partiel = 0,216].
Pratique
Si vous souhaitez mettre à l’épreuve vos nouvelles compétences, j’ai inclus deux ensembles de données ainsi qu’un script séparé contenant toutes les réponses. Je vous recommande vivement d’analyser les données vous-même en utilisant les codes mentionnés ici et de vérifier vos réponses à l’aide du script.
Le premier ensemble de données est nommé « HW1_RTut.xlsx ». Dans cet exemple, nous avons deux échantillons aléatoires, les groupes A et B. Nous avons une certaine mesure numérique dans la colonne « Value ». Nous souhaitons savoir s’il existe une différence significative entre les deux groupes.
Le deuxième ensemble de données est nommé « HW2_RTut.xlsx ». Il se présente comme suit :
- La variable « Participants » représente différentes personnes.
- « WithinSubjectVar » est une variable intrasujet à trois niveaux (mesures répétées).
- « BetweenSubjectVar » est une variable intersujet à deux niveaux (groupe A et groupe B). 4. La réponse est une variable continue.
Nous nous intéressons à l’effet des variables « WithinSubjectVar » et « BetweenSubjectVar » sur la réponse.

