17 Atelier RStudio : Tests T
Les tests T dans le logiciel R comptent parmi les tests les plus courants en statistiques pour déterminer s’il existe une différence réelle entre les moyennes de deux groupes. Il y en a deux types : l’un pour comparer deux groupes distincts et l’autre pour comparer deux groupes apparentés. Pour utiliser correctement un test T, il faut tenir compte de certaines hypothèses que j’ai énumérées ci-dessous, ainsi que des tests appropriés et des codes correspondants pour les vérifier. Cependant, je ne vais pas trop m’y attarder, vous pouvez les lire vous-même. Vous devriez cependant parler de ces hypothèses avec le responsable de recherche et les vérifier si vous craignez que vos données ne les respectent pas. N’oubliez pas que s’il est bon de respecter ces règles, vous pouvez parfois obtenir des résultats utiles même si vous ne les suivez pas à la lettre. Soyez prudent et réfléchissez à la signification de vos chiffres avant de les comparer.
- Normalité : Les données de groupe que vous collectez doivent être réparties d’une manière logique et suivre la distribution à peu près normale d’une courbe en cloche. C’est d’autant plus important lorsque vous ne disposez que d’un petit nombre de points de données (moins de 30).
- Vous pouvez contrôler visuellement la normalité de vos données à l’aide d’histogrammes, de graphiques de densité ou de diagrammes Q-Q. Pour un test plus formel, vous pouvez utiliser la fonction « Test Shapiro-Wilk shapiro.test() » ou la fonction « Test Anderson-Darling ad.test() ad.test() » du paquet « nortest ».
Shapiro-Wilk test for normality shapiro.test(data_vector)
Anderson-Darling test for normality (install and load "nortest" package) ad.test(data_vector)
- Homogénéité de la variance (Variances égales) : Si vous comparez deux éléments différents, la dispersion des chiffres recueillis doit être similaire. Cette hypothèse est essentielle à la vérification de la validité des échantillons indépendants du test T. Certaines variantes du test T permettent de tenir compte des variances inégales.
- Pour tester l’homogénéité des variances entre deux groupes, vous pouvez utiliser la fonction du test de Levene leveneTest() du paquet « car » ou la fonction du test de Bartlett bartlett.test() de la base R. Test de Levene pour l’homogénéité des variances ç) leveneTest(data_vector ~ group_variable).
- Test de Bartlett pour l’homogénéité des variances
bartlett.test(data_vector ~ group_variable)
N’oubliez pas de remplacer « data_vector » par vos données réelles et « group_variable » par la variable ou la colonne du fichier de données qui définit vos groupes. Il est important de noter que ces tests peuvent être influencés par la taille de l’échantillon et qu’ils ne fournissent pas toujours des résultats concluants. Il est conseillé de compléter les tests formels au moyen d’évaluations visuelles de vos données, telles que des graphiques, afin de porter un jugement éclairé sur les hypothèses. De plus, si vos données ne respectent pas les hypothèses, vous pouvez envisager d’autres solutions robustes ou des tests non paramétriques qui y sont moins sensibles.
TEST T À UN ÉCHANTILLON
Ce test sert à comparer la moyenne d’un échantillon à une moyenne standard, théorique ou hypothétique connue (μ). Il vous permet de répondre aux questions de recherche suivantes :
- La moyenne de l’échantillon est-elle égale à la moyenne connue?
- La moyenne de l’échantillon est-elle inférieure à la moyenne connue?
- La moyenne de l’échantillon est-elle supérieure à la moyenne connue?
Par exemple : supposons que nous voulions vérifier si le revenu annuel d’une succursale de Starbucks est inférieur au montant habituel (mu ou μ = 900 K).
En utilisant une fonction de la librairie « readxl », nous chargerons le fichier Excel « OneSampleT_Test.xlsx » dans R sous le nom data_vector « starbucks_rev ».
Conseil : Vous pouvez importer et traiter différents formats de fichiers de données (p. ex., CSV, Excel, JSON) directement dans RStudio à l’aide de fonctions telles que read.csv() ou read_excel().
starbucks_rev <– read_excel(file.choose())# orstarbucks_rev <-read_excel("OneSampleT_Test.xlsx")
Calcul des statistiques sommaires
Calculons d’abord quelques statistiques sommaires de nos données!
# Statistical summaries of monthly revenuesummary(starbucks_rev$monthly_rev)
## Min. 1st Qu. Median Mean 3rd Qu. Max. ## 644201 666112 679089 680923 700306 723093
Ici :
- Min.= la valeur minimale de la colonne
- Q1 = le premier quartile. 25 % des valeurs sont inférieures à ce chiffre.
- Médiane = la valeur médiane. La moitié des valeurs sont inférieures, l’autre moitié est supérieure.
- Q3 = le troisième quartile. 75 % des valeurs sont supérieures à ce chiffre.
- Max. = la valeur maximale
Visualisation
Maintenant que nous avons résumé nos données, traçons des graphiques.
Avant de le faire, consultons le code suivant, c’est un petit aide-mémoire sur l’esthétique des graphiques que j’aime utiliser. Je le copie-colle dans tous mes scripts R, il facilite la conception des graphiques.
Pour une vue d’ensemble plus complète des quelque 600 couleurs, consultez le site : Couleurs dans R
# No margin around chartpar(mar=c(0,0,0,0))# Empty chartplot(0, 0, type = "n", xlim =c(0, 1), ylim =c(0, 1), axes = FALSE, xlab = "", ylab = "")# Settingsline <- 25col <- 5# Add color backgroundrect( rep((0:(col -1)/col),line) , sort(rep((0:(line -1)/line),col),decreasing=T), rep((1:col/col),line) , sort(rep((1:line/line),col),decreasing=T), border = "white" , col=colours()[seq(1,line*col)])# Color namestext( rep((0:(col -1)/col),line)+0.1 , sort(rep((0:(line -1)/line),col),decreasing=T)+0.015 , colors()[seq(1,line*col)] , cex=1)

# This code will generate the chart of shape typesdf_shapes <-data.frame(shape = 0:24)ggplot(df_shapes, aes(0, 0, shape = shape)) +geom_point(aes(shape = shape), size = 5, fill = 'red') +scale_shape_identity() +facet_wrap(~shape) +theme_void()
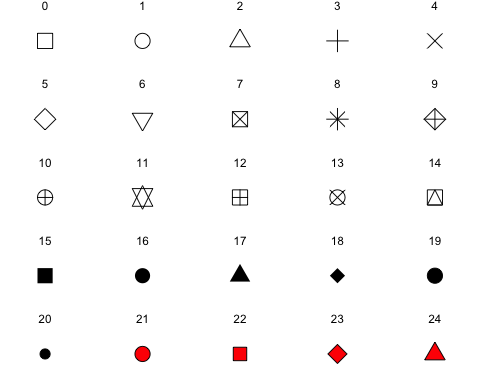
# This code will generate the chart of line typespar(mar=c(0,0,0,0))# Set up the plotting areaplot(NA, xlim=c(0,1), ylim=c(6.5, -0.5),xaxt="n", yaxt="n",xlab=NA, ylab=NA )# Draw the linesfor (i in0:6) {points(c(0.25,1), c(i,i), lty=i, lwd=2, type="l")}# Add labelstext(0, 0, "0. 'blank'" , adj=c(0,.5))text(0, 1, "1. 'solid'" , adj=c(0,.5))text(0, 2, "2. 'dashed'" , adj=c(0,.5))text(0, 3, "3. 'dotted'" , adj=c(0,.5))text(0, 4, "4. 'dotdash'" , adj=c(0,.5))text(0, 5, "5. 'longdash'", adj=c(0,.5))text(0, 6, "6. 'twodash'" , adj=c(0,.5))

ggplot(starbucks_rev, aes(x=Month, y=monthly_rev, group = 1)) +geom_line(color='saddlebrown', linewidth=1, linetype='dashed') +# here we are designing what the lines look like, consult the cheat sheet # above for line optionstheme_pubr() +#changes overall look of the plot there are many theme options geom_point(shape=9, color='seagreen3', size=5) +#here we are designing how # we want each points on the plot to look like. Consult the cheat sheet in the #code chunk above for different point shapes. labs(x = "Month Number", y = "Gross Monthly Revenue (CADs)", title = "Starbucks Branch #4312 Annual Sale")
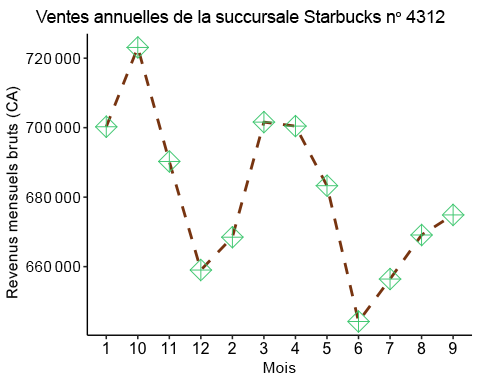
Je vous recommande le guide suivant pour en savoir plus sur la conception, les thèmes, les couleurs d’arrière-plan et les autres options de personnalisation de ggplot2.
# Bar plotggplot(starbucks_rev, aes(x=Month, y=monthly_rev, fill=as.factor(Month)) ) +geom_bar(stat = "identity") +theme_pubr() +theme(legend.position="none") +labs(x = "Month Number", y = "Gross Monthly Revenue (CADs)", title = "Starbucks Branch #4312 Annual Sale")
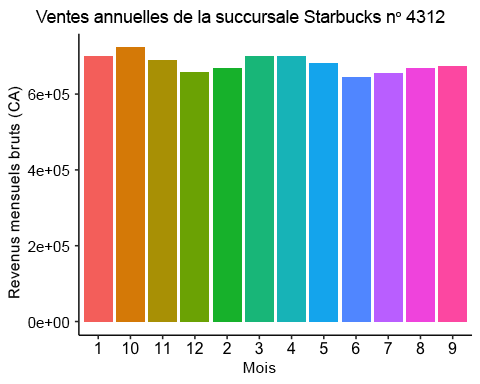
ggboxplot(starbucks_rev$monthly_rev, ylab = "Monthly Revenue (CADs)", xlab = "Months",ggtheme =theme_pubr())
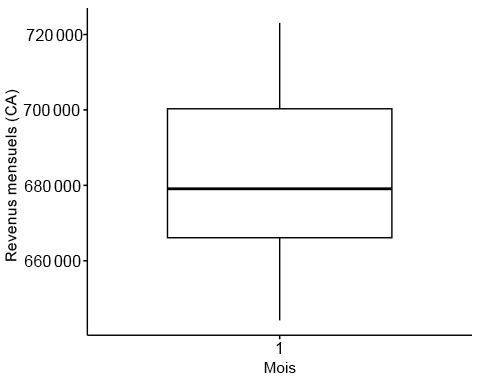
Calcul d’un test T à un échantillon
# Lets compute the t-testt.test(starbucks_rev$monthly_rev, #a numeric vector containing our data valuesmu = 900000, #the theoretical mean. Default is 0 but you can change it. #For our example, in 2022 the average annual revenue for a single store was 900K so we will set#that up. alternative = "less") #the alternative hypothesis. Allowed value is one ## One Sample t-test
## data: starbucks_rev$monthly_rev## t = -33.013, df = 11, p-value = 1.176e-12## alternative hypothesis: true mean is less than 9e+05## 95 percent confidence interval:## -Inf 692840.8## sample estimates:## mean of x ## 680923
# of “two.sided”(default), “greater” or “less”.
Interprétation des résultats Le résultat de la fonction t.test() est une liste contenant les éléments suivants :
- statistic = la valeur de la statistique du test T
- parameter = les degrés de liberté pour les statistiques du test T
- p.value = la valeur p du test
- conf.int = un intervalle de confiance pour la moyenne correspondant à l’autre hypothèse spécifiée.
- estimate = les moyennes des deux groupes comparés (dans le cas d’un test T indépendant) ou la différence de moyennes (dans le cas d’un test T apparié).
Rapport La valeur p du test est de 1,176e-12, ce qui est inférieur au seuil de signification alpha = 0,05. Par conséquent, nous pouvons conclure que le revenu annuel de la succursale Starbucks est significativement inférieur au montant typique (900 000 $) avec une valeur p = 1,18 10^{-12}.
TEST T À DEUX ÉCHANTILLONS NON APPARIÉS
Et si vous vouliez comparer les moyennes de deux échantillons?
Supposons, par exemple, que nous ayons interrogé 100 personnes : 50 adolescents (13 à 18 ans) et 50 adultes (18 ans et plus) ont été invités à indiquer le nombre de leurs visites à Starbucks au cours d’un mois donné. Nous voulons savoir si le nombre moyen de visites des adolescents est significativement différent de celui des adultes.
Un test T sur échantillon non apparié vous permet d’étudier le même type de questions de recherche qu’avec un test T à échantillon unique, mais au lieu d’avoir une moyenne connue, vous comparez la moyenne de deux groupes d’échantillons dont vous avez probablement recueilli les données.
# Importing data sett2data <-read_excel("TwoSampleT_Test.xlsx")# If .txt tab file, use this read.delim()# Or, if .csv file, use this read.csv()
# Lets check our datahead(t2data) #looking at the first 6 rows of data
## # A tibble: 6 × 2## Group StarbucksRun## <chr><dbl>## 1 Adolescents 26## 2 Adolescents 16## 3 Adolescents 16## 4 Adolescents 23## 5 Adolescents 24## 6 Adolescents 20
# Or print all dataprint(t2data)
## # A tibble: 100 × 2## Group StarbucksRun## <chr><dbl>## 1 Adolescents 26## 2 Adolescents 16## 3 Adolescents 16## 4 Adolescents 23## 5 Adolescents 24## 6 Adolescents 20## 7 Adolescents 23## 8 Adolescents 23## 9 Adolescents 22## 10 Adolescents 19## # ℹ 90 more rows
# Compute summary statistics by groups:group_by(t2data, Group) %>%summarise(count =n(),mean =mean(StarbucksRun, na.rm = TRUE),sd =sd(StarbucksRun, na.rm = TRUE) )
## # A tibble: 2 × 4## Group count mean sd## <chr><int><dbl><dbl>## 1 Adolescents 50 21.8 5.14## 2 Adults 50 17.5 9.03
Visualisation
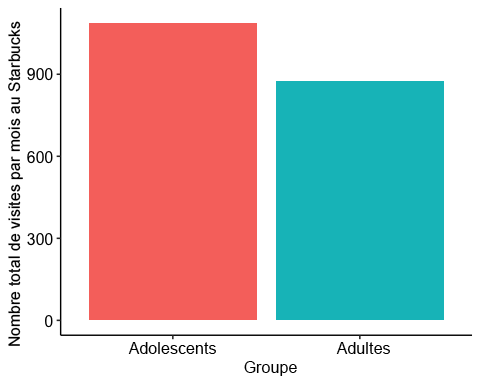
# Bar plotggplot(t2data, aes(x=Group, y=StarbucksRun, fill=as.factor(Group)) ) +geom_bar(stat = "identity") +theme_pubr() +theme(legend.position="none") +labs(x = "Group", y = "Number of Starbucks Runs in a Month")
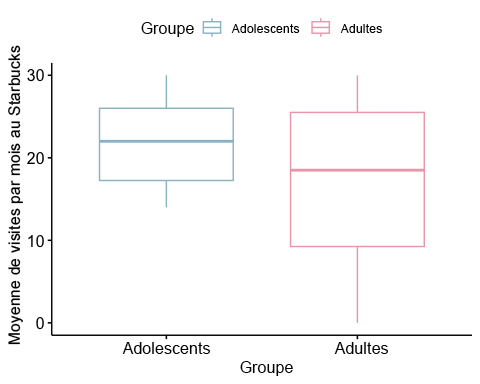
ggboxplot(t2data, x = "Group", y = "StarbucksRun", color = "Group", palette =c("lightblue3", "pink2"),ylab = "Number of Starbucks Runs in a Month", xlab = "Group")
# Compute t-testt.test.2 <-t.test(StarbucksRun ~ Group, data = t2data,alternative ="two.sided", #the alternative hypothesis. #Allowed value is one of “two.sided” (default), “greater” or # “less”. You may choose one depending on the type of # research question you are posing. var.equal = TRUE) #a logical variable indicating whether to # treat the two variances as being equal. If TRUE then the pooled variance is # used to estimate the variance otherwise the Welch test is used.t.test.2
## ## Two Sample t-test## ## data: StarbucksRun by Group## t = 2.9139, df = 98, p-value = 0.004422## alternative hypothesis: true difference in means between group Adolescents and group Adults is not equal to 0## 95 percent confidence interval:## 1.365205 7.194795## sample estimates:## mean in group Adolescents mean in group Adults ## 21.76 17.48
La valeur p du test est de 0,004422, ce qui est inférieur au seuil de signification alpha = 0,05. Nous pouvons conclure que le nombre moyen de visites d’un adolescent à Starbucks est significativement différent de celui d’un adulte avec une valeur p = 0,004.
Notez que nous avons utilisé des tests T pour déterminer si les moyennes des deux échantillons sont différentes, aussi appelés tests bilatéraux. Les exemples suivants sont des tests T unilatéraux :
- Si nous voulions vérifier si la dépense moyenne d’un adolescent dans un Starbucks est inférieure à celle d’un adulte, nous pourrions utiliser le code suivant :
t.test(StarbucksRun ~ Group, data = t2data, var.equal = TRUE, alternative = "less")
- Si nous voulions vérifier si la dépense moyenne d’un adolescent dans un Starbucks est supérieure à celle d’un adulte, nous pourrions utiliser le code suivant :
t.test(StarbucksRun ~ Group, data = t2data, var.equal = TRUE, alternative = "greater")

