20 Atelier RStudio : Analyse de la variance bidirectionnelle
Analyse de la variance bidirectionnelle intraparticipant
La même fonction peut servir au calcul d’une analyse de la variance unidirectionnelle intrasujet et d’une analyse de la variance bidirectionnelle. Je vous encourage fortement à tenter d’effectuer les analyses avant de poursuivre la lecture de ce guide.
Pour cet exercice, nous allons examiner le fichier de données intitulé « Practice_2WayANOVA_Within.xlsx ».
- Variable mesurée : Résultat du test
- Plan à mesures répétées 2 x 3
- Facteurs : « Boisson » et « Sommeil »
Dans cette expérience hypothétique, les participants ont assisté à six conférences à différents moments. Il leur a été demandé d’assister à une conférence, puis de revenir le lendemain pour répondre à un questionnaire à ce sujet après avoir dormi 0 heure, 5 heures ou 8 heures. Au moment du test, ils ont reçu un café ou un placebo (boisson chaude décaféinée).
Nous cherchons à savoir si les résultats des tests diminuent lorsque les participants ne dorment pas suffisamment et si la consommation de café atténue cette baisse de performance.
mydata2w <-read_excel("Practice_2WayANOVA_Within.xlsx") #importing our data file
mydata2w <- mydata2w %>%convert_as_factor(ID, Gender, Beverage, Sleep) #setting up factorsstr(mydata2w) #checking factors
## tibble [516 × 6] (S3: tbl_df/tbl/data.frame)## $ ID : Factor w/ 86 levels "29057","32239",..: 20 48 84 61 22 23 25 29 72 69 ...## $ Gender : Factor w/ 3 levels "F","M","Non-Binary": 1 2 1 1 1 1 1 2 1 1 ...## $ Age : num [1:516] 25 22 22 20 22 20 21 20 19 21 ...## $ Beverage : Factor w/ 2 levels "Coffee","Placebo": 1 1 1 1 1 1 1 1 1 1 ...## $ Sleep : Factor w/ 3 levels "0","5","8": 1 1 1 1 1 1 1 1 1 1 ...## $ TestScore: num [1:516] 99 64.3 93.3 94.8 89.1 ...
# Summary Statistics Tablemydata2w.summarystat <- mydata2w %>%group_by(Beverage, Sleep) %>%get_summary_stats(TestScore, type = "full")
# Selecting rows of data only if ID value is uniquemydata2w.unique <- mydata2w %>%distinct(mydata2w$ID, .keep_all=TRUE) # Looking at the distribution of "Gender" in our sample sizetable(mydata2w.unique$Gender)
## ## F M Non-Binary ## 60 21 5
# Mean Age of Sample Sizemydata2w.unique %>%get_summary_stats(Age, type ="mean")
## # A tibble: 1 × 3## variable n mean## <fct><dbl><dbl>## 1 Age 86 21.5
mydata2w.summarystat
## # A tibble: 6 × 15## Beverage Sleep variable n min max median q1 q3 iqr mad mean## <fct><fct><fct><dbl><dbl><dbl><dbl><dbl><dbl><dbl><dbl><dbl>## 1 Coffee 0 TestSco… 86 51.2 99.0 96.1 90.6 97.6 7.01 4.27 91.7## 2 Coffee 5 TestSco… 86 64.3 99.0 97.6 94.8 99.0 4.22 2.09 95.7## 3 Coffee 8 TestSco… 86 64.3 99.0 97.6 94.8 99.0 4.17 2.06 96.0## 4 Placebo 0 TestSco… 86 -6.95 74.8 23.2 14.2 40.4 26.2 18.8 28.2## 5 Placebo 5 TestSco… 86 -1.67 79.1 62.2 45.1 70.0 24.8 14.8 56.4## 6 Placebo 8 TestSco… 86 30.0 79.1 71.6 64.9 74.9 10.1 6.82 67.5## # ℹ 3 more variables: sd <dbl>, se <dbl>, ci <dbl>
Visualisation
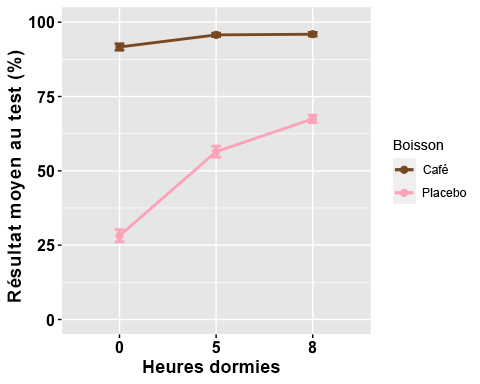
# Line plots with multiple groupsanova2w.lineplot <-ggline(mydata2w, x = "Sleep", y = "TestScore", color = "Beverage",add =c("mean_se"), #adding standard error barspalette =c("tan4", "pink1"),order =c("0", "5", "8"), #organizing order of levelsylab = "Mean Test Score (%)", xlab = "Hours Slept (hrs)", #x- and y-axis title linetype = "solid", font.label =list(size = 20, color = "black"),size = 1,ggtheme =theme_gray(),ylim=c(0,100) #adjusting the min and max value of y-aixs )
# Change the appearance of titles and labelsanova2w.lineplot +font("xlab", size = 14, color = "black", face = "bold")+font("ylab", size = 14, color = "black", face = "bold")+font("xy.text", size = 12, color = "black", face = "bold")
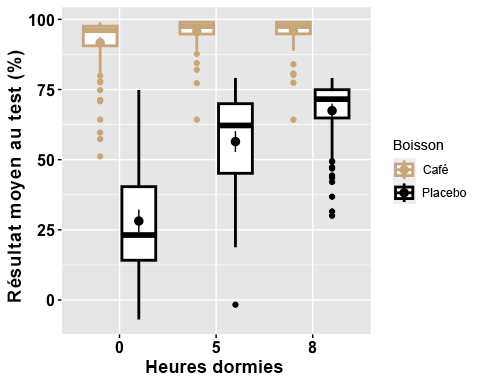
# Box plot with two factor variablesanova2w.boxplot <-ggboxplot(mydata2w, x = "Sleep", y = "TestScore", color = "Beverage",palette =c("tan", "black"),ylab = "Mean Test Score (%)", xlab = "Hours Slept",add = ("mean_ci"), #adding 95% confidence intervalsfont.label =list(size = 20, color = "black"),size = 1,ggtheme =theme_gray())# Change the appearance of titles and labelsanova2w.boxplot +font("xlab", size = 14, color = "black", face = "bold")+font("ylab", size = 14, color = "black", face = "bold")+font("xy.text", size = 12, color = "black", face = "bold")
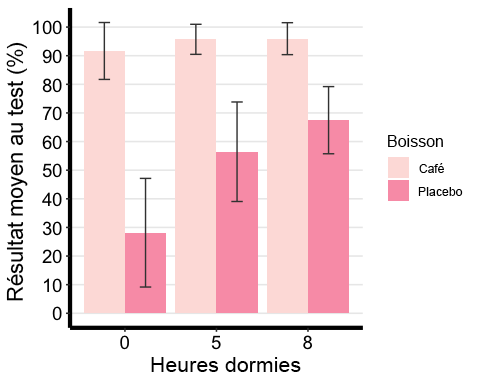
# Bar plot with two-factor variablesanova2w.barplot <-ggplot(mydata2w.summarystat, aes(x =factor(Sleep), y = mean, fill = Beverage) ) +geom_bar(stat = "identity", position = "dodge") +geom_errorbar(aes(ymax = mean + sd, ymin = mean - sd), #adding standard error barsposition =position_dodge(0.9), width = 0.25, color = "Gray25") +xlab("Hours Slept") +ylab("Average Test Score (%)") +scale_fill_brewer(palette = "RdPu") +theme_classic2() +theme(axis.line=element_line(linewidth=1.5), #thickness of x-axis lineaxis.text =element_text(size = 14, colour = "black"),axis.title =element_text(size = 16, colour = "black"),panel.grid.major.y =element_line() ) +# adding horizontal grid linesscale_y_continuous(breaks=seq(0, 100, 10)) # Ticks on y-axis from 0-100, # jumps by 10 anova2w.barplot
Calcul de l’analyse de la variance bidirectionnelle à mesures répétées
mydata2w.2anova <-anova_test(data = mydata2w,dv = TestScore, wid = ID, within =c(Beverage, Sleep), #for more than 2 factors to count you must use c()#it combines 2+ values into a vector/listdetailed = TRUE, effect.size = "ges"#we get the generalized eta squared, enter pes to get ) # partial eta squared# Apply the Greenhouse Geisser correction on an as-needed-basismydata2w.2anova <-get_anova_table(mydata2w.2anova, correction = "auto")
# We can calculate partial eta square and add it as a new column named "pes"mydata2w.2anova$pes = mydata2w.2anova$SSn/(mydata2w.2anova$SSn + mydata2w.2anova$SSd)
# Calculate the mean sum of error and add it as a new column named "MSE"mydata2w.2anova$MSE = mydata2w.2anova$SSd/mydata2w.2anova$DFd
# Convert tables to data framesmydata2w.2anova <-data.frame(mydata2w.2anova)
# Deleting intercept info (first row)mydata2w.2anova <- mydata2w.2anova[-1, ]
# Rename columnscolnames(mydata2w.2anova)[colnames(mydata2w.2anova) =="pes"] ="η2P"colnames(mydata2w.2anova)[colnames(mydata2w.2anova) =="ges"] ="η2G"colnames(mydata2w.2anova)[colnames(mydata2w.2anova) =="p..05"] ="sig"mydata2w.2anova
## Effect DFn DFd SSn SSd F p sig η2G η2P MSE
## 2 Beverage 1.00 85.00 246966.79 18527.547 1133.025 6.47e-51 * 0.752 0.930 217.9711
## 3 Sleep 1.34 113.78 44095.24 12457.452 300.872 8.82e-39 * 0.351 0.779 109.4872
## 4 Beverage:Sleep 1.60 136.23 27663.08 9544.342 246.362 2.23e-41 * 0.254. 0,743-70,0605
Toute interaction bidirectionnelle significative dans cette analyse doit être suivie par d’autres analyses qui examinent l’effet d’un facteur alors que le niveau de l’autre facteur demeure constant.
Dans ces analyses, une interaction bidirectionnelle significative indique que l’impact d’un facteur (p. ex., la boisson) sur la variable de résultat (p. ex., le résultat du test) dépend du niveau de l’autre facteur (p. ex., le sommeil) (et vice-versa). Vous pouvez donc décomposer une interaction significative bidirectionnelle en traitant le facteur A comme une analyse de la variance à un facteur à chaque niveau du facteur B.
Procédure pour une interaction significative bidirectionnelle :
Effet principal simple : exécuter un modèle unidirectionnel d’un facteur alors que le niveau de l’autre facteur demeure constant. Il s’agit d’effectuer deux analyses de la variance unidirectionnelle pour un facteur à chaque niveau de l’autre facteur.
Comparaisons appariées simples : si le résultat de l’une ou l’autre des analyses unidirectionnelles est significatif, par exemple si l’effet principal simple est significatif, vous effectuerez des comparaisons appariées multiples pour déterminer quels groupes sont différents, comme nous l’avons fait précédemment pour le tutoriel sur l’analyse de la variance unidirectionnelle.
# Simple Main Effect# Looking at the effect of Sleep separately for each level of Beverage mydata2w.one.way <- mydata2w %>%group_by(Beverage) %>%anova_test(dv = TestScore, wid = ID, within = Sleep) %>%get_anova_table() %>%adjust_pvalue(method = "bonferroni")mydata2w.one.way
## # A tibble: 2 × 9## Beverage Effect DFn DFd F p `p<.05` ges p.adj## <fct><chr><dbl><dbl><dbl><dbl><chr><dbl><dbl>## 1 Coffee Sleep 1.17 99.4 22.4 2.11e- 6 * 0.07 4.22e- 6## 2 Placebo Sleep 1.51 128. 331 1.76e-45 * 0.51 3.52e-45
L’effet du sommeil est significatif pour les deux niveaux du facteur « Boisson ». Nous devons maintenant procéder à des comparaisons appariées pour déterminer où se situe la différence entre les niveaux de sommeil et les deux niveaux de boisson.
# Pairwise comparisons between Sleep levelsmydata2w.pwc <- mydata2w %>%group_by(Sleep) %>%pairwise_t_test(TestScore ~ Beverage, paired = TRUE,p.adjust.method = "bonferroni")mydata2w.pwc
## # Une trame de données « tibble » : 3 × 11
## Sleep .y. group1 group2 n1 n2 statistic df p p.adj p.adj.signif
## * <fct><chr><chr><chr> <int><int><dbl><dbl><dbl> <dbl><chr>
## 1 0 TestScore Coffee Placebo 86 86 35.1 85 2.32e-52 2.32e-52
## 2 5 TestScore Coffee Placebo 86 86 22.0 85 6.52e-37 6.52e-37
## 3 8 TestScore Coffee Placebo 86 86 25.7 85 8.84e-42 8.84e-42
Interprétation et analyse des résultats
L’analyse de la variance bidirectionnelle à mesures répétées a révélé un effet principal significatif de la boisson [F(1,85) = 1133,0, EQM = 218,0, eta-carré partiel = 0,930] et du sommeil [F(1,3-113,8) = 300,9, EQM = 109,5, eta-carré partiel = 0,780], nuancé par une interaction bidirectionnelle [F(1,6-136,2) = 300,9, EQM = 70,1, eta-carré partiel = 0,743]. Compte tenu de la valeur p ajustée de Bonferroni (p.adj), il semble que l’effet principal simple du sommeil est significatif aux deux niveaux de boisson [Café, p < 0,001; Placebo, p < 0,001]. Les comparaisons appariées montrent que le résultat moyen au test est significativement différent entre le café et le placebo à 0 heure (p < 0,0001), 5 heures (p < 0,0001) et 8 heures (p < 0,0001) de sommeil nocturne.
Notez qu’au lieu de décomposer l’interaction bidirectionnelle Sommeil x Boisson en un simple effet principal de la boisson, vous auriez pu choisir le sommeil. Comme dans le cas de l’analyse pour la variable « Sommeil » à chaque niveau de boisson, il n’est pas forcément nécessaire de réaliser celle-ci. Il suffit d’échanger les facteurs « Sommeil » et « Boisson » avec les codes pour les analyses post hoc.
Que se passerait-il dans les cas suivants? Interaction bidirectionnelle non significative
Il est important de noter que si l’interaction bidirectionnelle n’est pas significative dans l’analyse de la variance globale, mais qu’il existe toujours des effets principaux significatifs (p. ex., l’effet principal du sommeil et l’effet principal de la boisson), vous devez alors interpréter les effets principaux pour chacune des deux variables en effectuant des comparaisons appariées avec le test T.
# Comparisons for Beverage variable
mydata2w %>% pairwise_t_test( TestScore ~ Beverage, paired = TRUE, p.adjust.method = "bonferroni" )
# Comparisons for Sleep variable
mydata2w %>% pairwise_t_test( TestScore ~ Sleep, paired = TRUE, p.adjust.method = "bonferroni" )
Analyse de la variance mixte bidirectionnelle
Pour vous entraîner, je vous invite à calculer une analyse de la variance mixte bidirectionnelle pour le fichier de données « Practice_2WayANOVA_Mixed.xlsx » avec les éléments suivants :
- Variable mesurée : Résultat du test
- Conception mixte 2 x 3
- Interparticipant : « Exercice »
- Intraparticipant : « Sommeil »
Dans cette expérience hypothétique, les participants ont assisté à trois conférences à différents moments. Un groupe de participants a été invité à suivre des cours de yoga trois fois par semaine pendant trois mois avant la série de conférences et pendant l’expérience. Il leur a été demandé d’assister à une conférence, puis de revenir le lendemain pour répondre à un questionnaire à ce sujet après avoir dormi 0 heure, 5 heures ou 8 heures. Un autre groupe de participants a fait l’objet d’un protocole expérimental presque identique sauf qu’au lieu de pratiquer le yoga, il leur a été demandé de faire des exercices de pleine conscience.
Nous nous intéressons aux effets du sommeil sur l’apprentissage. Plus particulièrement, nous cherchons à savoir si les résultats des tests diminuent lorsque les participants ne dorment pas suffisamment. Nous souhaitons aussi vérifier si les personnes qui pratiquent le yoga sont plus résistantes à cette baisse de performance induite par le sommeil. Dans la mesure du possible, visualisez les données, puis calculez les tableaux récapitulatifs et les chiffres appropriés pour les comparer avant d’examiner les réponses ci-dessous.
# Data Prep & Summary Statisticsmydata2m <- read_excel("Practice_2WayANOVA_Mixed.xlsx")
mydata2m <- mydata2m %>% convert_as_factor(ID, Gender, Exercise, Sleep) str(mydata2m)
## tibble [516 × 7] (S3 : tbl_df/tbl/data.frame)## $ ...1 : chr [1:516] "259" "260" "261" "262" ...## $ ID : Factor w/ 172 levels "23936","25440",..: 10 71 6 70 147 129 74 62 21 38 ...## $ Gender : Factor w/ 3 levels "F","M","Non-Binary": 1 1 1 1 1 1 1 3 1 2 ...## $ Age : num [1:516] 22 22 23 22 22 24 22 22 23 22 ...## $ Exercise : Factor w/ 2 levels "Mindfulness",..: 1 1 1 1 1 1 1 1 1 1 ...## $ Sleep : Factor w/ 3 levels "0","5","8": 1 1 1 1 1 1 1 1 1 1 ...## $ TestScore: num [1:516] 32 43 44 46 31 45 21 48 40 32 ...
mydata2m.summarystat <- mydata2m %>%group_by(Exercise, Sleep) %>%get_summary_stats(TestScore, type = "full")
# Selecting rows of data only if ID value is uniquemydata2m.unique <- mydata2m %>%distinct(mydata2m$ID, .keep_all=TRUE) # Looking at the distribution of "Gender" per grouptable(mydata2m.unique$Gender, mydata2m.unique$Exercise)
## Mindfulness Yoga
## F 40 60
## M 39 21
## Non-Binary 7 5
# Mean Age Per Group
mydata2m %>% group_by(Exercise) %>%get_summary_stats(Age, type ="mean")
## # Une trame de données « tibble » : 2 × 4
## Exercise variable n mean
## <fct> <fct> <dbl> <dbl>
## 1 Mindfulness Age 258 22.6
## 2 Yoga Age 258 22.2
mydata2m.summarystat
## # Une trame de données « tibble » : 6 × 15
## Exercise Sleep variable n min max median q1 q3 iqr mad mean sd se ci
## <fct> <fct> <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 Mindful… 0 TestSco… 86 15 48 32 23.2 41.8 18.5 13.3 32.3
## 2 Mindful… 5 TestSco… 86 38 80.8 48 43 53 10 7.41 48.7
## 3 Mindful… 8 TestSco… 86 55 66 59 57 63 6 4.45 60.1
## 4 Yoga 0 TestSco… 86 35 55 44.5 40.2 51 10.8 8.15 45.5
## 5 Yoga 5 TestSco… 86 66 80 72.5 68 76 8 6.67 72.7
## 6 Yoga 8 TestSco… 86 74 100 85.5 79 93.8 14.8 11.1 86.6
Je passerai ici l’étape de visualisation puisque vous pouvez utiliser les mêmes codes que ceux de l’analyse de la variance bidirectionnelle intrasujet. Je vous encourage à vous entraîner à créer des graphiques récapitulatifs.
Calcul de l’analyse de la variance bidirectionnelle
mydata2m.2anova <- anova_test(data = mydata2m,dv = TestScore, wid = ID, between = Exercise, #between-participants factorwithin = Sleep, detailed = TRUE, effect.size = "ges")# Apply the Greenhouse Geisser correction on an as-needed-basismydata2m.2anova <- get_anova_table(mydata2m.2anova, correction = "auto")# Calculate partial eta square and add it as a new column named "pes"mydata2m.2anova$pes = mydata2m.2anova$SSn/(mydata2m.2anova$SSn + mydata2m.2anova$SSd)# Calculate the mean sum of error and add it as a new column named "MSE"mydata2m.2anova$MSE = mydata2m.2anova$SSd/mydata2m.2anova$DFd# Convert tables to data framesmydata2m.2anova <- data.frame(mydata2m.2anova)# Deleting intercept info (first row)mydata2m.2anova <- mydata2m.2anova[-1, ]# Rename columnscolnames(mydata2m.2anova)[colnames(mydata2m.2anova) == "pes"] ="η2P"colnames(mydata2m.2anova)[colnames(mydata2m.2anova) == "ges"] ="η2G"colnames(mydata2m.2anova)[colnames(mydata2m.2anova) == "p..05"] ="sig"mydata2m.2anova
## Effect DFn DFd SSn SSd F p sig η2G η2P MSE
## 2 Exercise 1.00 170.0 57969.259 7475.35 1318.303 5.27e-82 * 0.699 0.8857759 43.97265
## 3 Sleep 1.89 321.9 104622.988 17468.35 1018.179 9.08e-137 * 0.807 0.8569239 54.26638
## 4 Exercise:Sleep 1.89 321.9 4365.807 17468.35 42.488 2.05e-16 * 0.149 0.1999531 54.26638
Procédure pour une interaction significative bidirectionnelle :
# Simple main effect of Exercise at each level of the Sleep factoranova2m.one.way <- mydata2m %>%group_by(Sleep) %>%anova_test(dv = TestScore, wid = ID, between = Exercise) %>%get_anova_table() %>%adjust_pvalue(method = "bonferroni")anova2m.one.way
## # Une trame de données « tibble » : 3 × 9
## Sleep Effect DFn DFd F p `p<.05` ges p.adj
## <fct> <chr> <dbl> <dbl> <dbl> <dbl> <chr> <dbl> <dbl>
## 1 0 Exercise 1 170 109 4.39e-20 * 0.392 1.32e-19
## 2 5 Exercise 1 170 642 1.34e-59 * 0.791 4.02e-59
## 3 8 Exercise 1 170 742 6.34e-64 * 0.814 1.90e-63
OU vous pouvez choisir de décomposer l’interaction Exercice x Sommeil en un simple effet principal du sommeil pour chaque groupe d’exercice (code inclus ci-dessous); cependant, étant donné que nous savons que les résultats des tests diminuent lorsque les participants ne dorment pas suffisamment, ce n’est peut-être pas judicieux. Ici, nous allons plutôt comparer les résultats moyens des tests des deux groupes pour déterminer si le yoga atténue les baisses de performance liées à la durée du sommeil. Vous devez donc définir votre interaction bidirectionnelle afin qu’elle réponde à votre question de recherche.
# Simple main effect of Sleep for each Exercise Group # anova2m.one.way.alt <- mydata2m %>%# group_by(Exercise) %>%# anova_test(dv = TestScore, wid = ID, within = Sleep) %>%# get_anova_table() %>%# adjust_pvalue(method = "bonferroni")#anova2m.one.way.alt
L’effet principal simple de l’exercice étant significatif, nous devons maintenant effectuer des comparaisons appariées multiples pour déterminer quels groupes sont différents.
# Pairwise comparisons between Exercise levelsanova2m.pwc <- mydata2m %>%group_by(Sleep) %>%pairwise_t_test(TestScore ~ Exercise, p.adjust.method = "bonferroni")anova2m.pwc
## # A tibble: 3 × 10## Sleep .y. group1 group2 n1 n2 p p.signif p.adj p.adj.signif## * <fct><chr><chr><chr><int><int><dbl><chr><dbl><chr>## 1 0 TestS… Mindf… Yoga 86 86 4.39e-20 **** 4.39e-20 **** ## 2 5 TestS… Mindf… Yoga 86 86 1.34e-59 **** 1.34e-59 **** ## 3 8 TestS… Mindf… Yoga 86 86 6.34e-64 **** 6.34e-64 ****
# If you computed the simple main effect of sleep the pairwise comparisons would be as such:#anova2m.pwc.alt <- mydata2m %>%# group_by(Exercise) %>%# pairwise_t_test(TestScore ~ Sleep, p.adjust.method = "bonferroni")#anova2m.pwc.alt
Interprétation et rapports
EXEMPLE : L’analyse de la variance mixte bidirectionnelle a révélé un effet principal significatif de l’exercice [F(1,170) = 1318,3, EQM = 44,0, eta-carré partiel = 0,886] et du sommeil [F(1,9-322) = 1018,2, EQM = 54,3, eta-carré partiel = 0,857], nuancé par une interaction bidirectionnelle [F(1,9-322) = 42,5, EQM = 54,3, eta-carré partiel = 0,120]. Compte tenu de la valeur p ajustée de Bonferroni (p.adj), il semble que l’effet principal simple de l’exercice est significatif à tous les niveaux du facteur « Sommeil » [p < 0,001].
Les comparaisons appariées montrent que le résultat moyen au test était significativement différent entre les deux groupes « Exercice » pour tous les niveaux de sommeil, de sorte que le groupe « Yoga » a obtenu un résultat plus élevé au test que le groupe « Pleine conscience » lorsque les participants ont dormi 0 heure (13,1 %, p < 0,0001), 5 heures (24 %, p < 0,0001) ou 8 heures (26,5 %, p < 0,0001) la nuit précédant le test (voir figure 1).
Notez qu’ici, je renvoie mon lectorat à une figure (graphique à barres) afin de constater que le groupe « Yoga » a obtenu de meilleurs résultats que le groupe « Pleine conscience ». J’ai généré un graphique à barres pour ma figure 1 ici. Je vous encourage vivement à recréer ce graphique (avec les barres d’erreur type) ou tout autre type de graphique qui résume bien les données. De plus, à l’aide du tableau récapitulatif des statistiques, j’ai calculé la différence entre les résultats moyens des tests pour les comparaisons appropriées.