19 Atelier Rstudio : Analyse de la variance à un facteur
Analyse de la variance à un facteur entre différents sujets
Dans la première expérience hypothétique, les participants ont assisté à une présentation et ont été invités à passer un test le lendemain sur le contenu après dormi 5 ou 8 heures, ou après une nuit blanche. La variable sommeil est donc manipulée. Dans le cas présent, nous nous intéressons à l’effet des heures de repos sur les résultats en effectuant une analyse de la variance à un facteur,
un volet d’un test-t indépendant à deux échantillons. Les données sont regroupées selon les participants (par exemple, 3 groupes) en fonction d’une seule variable, appelée facteur (par exemple, le sommeil). Le facteur est comme une variable indépendante avec plus de deux niveaux de manipulation. Dans le cas présent, nous avons trois niveaux de manipulation du sommeil.
Par conséquent, dans ce type d’analyse, nous comparons les moyennes dans un contexte de plus de deux niveaux pour un seul facteur. Le tutoriel vise donc à expliquer le fondement d’une analyse de la variance à un facteur et à proposer des exemples pratiques dans le logiciel R.
REMARQUE : si vous n’avez que deux groupes, le test f et le test t sont identiques.
Analyse la variance à un facteur pour deux hypothèses 1. Hypothèse nulle : aucune différence entre les moyennes des différents groupes 2. Hypothèse alternative : une différence de moyennes entre au moins deux groupes.
Il faut dès lors rejeter l’hypothèse nulle en faveur de l’hypothèse alternative, en démontrant la différence notable entre au moins deux groupes de participants.
La première étape est l’importation des données, suivie de l’inspection du fichier.
# Now when it comes to importing your data frame I prefer to do so using the following code which allows me to click on my data frame, but you can also load your data frame by calling on the document's name.mydata1 <- read_excel(file.choose()) # If your data frame is in csv format use read.csv(file.choose())# or # if you already know the name of your data file and have set the working # directory, you can import you data file by namemydata1 =read_excel("OneWay_Sample_DataFile.xlsx") # or read.csv("OneWay_Sample_DataFile.csv")
# Let's inspect our data frameprint(mydata1) # look at the entire data frame
## # A tibble: 258 × 5## ID Gender Age Sleep TestScore## <chr><chr><dbl><chr><dbl>## 1 259 F 27 0 53.3## 2 260 F 22 0 66.0## 3 261 F 19 0 56.3## 4 262 F 25 0 68.7## 5 263 Non-Binary 23 0 77.4## 6 264 F 27 0 19.3## 7 265 F 30 0 31.1## 8 266 Non-Binary 27 0 64.5## 9 267 F 18 0 42.4## 10 268 M 28 0 32.9## # ℹ 248 more rows
# or you can use head(mydata1) #look at the first 6 rows
Notez que dans Rstudio, le fichier de données téléversé sous le nom auquel vous l’avez enregistré, qui dans ce cas est « mydata1 », se trouve dans le coin supérieur droit de votre écran, votre plateforme. Vous y trouverez les travaux, valeurs et fichiers stockés. Cliquez sur le fichier en dessous de l’onglet de données pour l’ouvrir séparément à côté de votre script, afin de le consulter, ou saisissez un code en utilisant « view() ». J’opte souvent pour cette fonction lorsque mon environnement est très encombré et qu’il n’est plus possible de trouver une donnée précise dans toute cette panoplie.
view(mydata1) # to open the entire data file in a separate tab in R studio
Dans ce fichier, le système fait la distinction entre les participants.
Nous disposons également de renseignements démographiques sur l’âge et le genre, que nous résumons et indiquons généralement lorsque nous décrivons la taille de l’échantillon dans la section « Méthodes ». Elles varient en fonction des sujets testés, mais ce sont généralement les éléments que nous rapportons sur les sujets humains.
Dans le fichier de données, la variable dépendante numérique est sous forme de pourcentage sur 100 % (le résultat).
Notre facteur se trouve dans la colonne « Sommeil ». Vérifions s’il est bien configuré en examinant la structure du cadre de données.
str(mydata1) # vérifier la structure du cadre de données
## tibble [258 × 5] (S3: tbl_df/tbl/data.frame)## $ ID : chr [1:258] "259" "260" "261" "262" ...## $ Gender : chr [1:258] "F" "F" "F" "F" ...## $ Age : num [1:258] 27 22 19 25 23 27 30 27 18 28 ...## $ Sleep : chr [1:258] "0" "0" "0" "0" ...## $ TestScore: num [1:258] 53.3 66 56.3 68.7 77.4 ...
Nous pouvons confirmer que la mesure dépendante est configurée comme mesure numérique. Si ce n’est pas le cas, nous devons la corriger en utilisant le code suivant :
mydata1$TestScore <- sapply(mydata1$TestScore, as.numeric)
Notez qu’en utilisant le signe « $ » à côté du nom du cadre de données, nous évoquons un nom de colonne. Lorsque vous tapez, vous remarquerez qu’une liste de tous les noms de colonnes apparaît comme raccourci.
Nous pouvons également constater que l’identité et le sommeil ne sont pas considérés comme des facteurs. Rectifions le tir.
# Lets set up our factormydata1 <- mydata1 %>%convert_as_factor(ID, Sleep)
# Lets double-check to make sure that our factor is set-up correctly. levels(mydata1$Sleep)
## [1] "0" "5" "8"
Statistiques sommaires
Calculons ensuite quelques statistiques sommaires pour chaque groupe selon les différents niveaux de sommeil.
ANOVA1.summary.statistics <-data.frame (mydata1 %>%group_by(Sleep) %>%# enter factor(s)get_summary_stats(TestScore, type = "full") )
ANOVA1.summary.statistics
## Sleep variable n min max median q1 q3 iqr mad mean## 1 0 TestScore 86 6.860 93.301 45.687 29.348 59.249 29.901 23.390 45.873## 2 5 TestScore 86 34.117 93.301 74.726 62.563 83.734 21.171 16.138 71.696## 3 8 TestScore 86 47.587 93.301 85.748 77.358 90.314 12.956 7.858 82.526## sd se ci## 1 20.850 2.248 4.470## 2 15.570 1.679 3.338## 3 10.092 1.088 2.164
Je cherche ici les moyennes des groupes ainsi que l’erreur type des valeurs moyennes, que j’utiliserai par la suite pour mes barres d’erreur lors de la réalisation des figures. D’autres mesures intéressantes sont énumérées dans la fiche d’information de la fonction get_summary_stats et comprennent : type = c ("mean_sd", "mean_se", "mean_ci", "median_iqr", "median_mad", "quantile", "mean", "median", "min", "max").
Par exemple, si vous souhaitez utiliser les valeurs de l’écart-type moyen pour vos barres d’erreur, vous pouvez utiliser « mean_sd ». Vous pouvez également utiliser « full » comme type pour obtenir toutes les mesures!
Conseil de pro : Explorez chaque fonctionnalité avec des exemples en plaçant un « ? » juste avant la fonction vide, comme indiqué ci-dessous. La fiche d’information de la fonction s’ouvrira dans l’onglet Aide en bas à droite sur RStudio. Essayez-le!
?get_summary_stats()
Créer des tableaux publiables
Bien que ce soit un beau tableau, si vous souhaitez inclure des statistiques récapitulatives dans votre thèse finale, suivez les étapes suivantes pour générer des tableaux attrayants imprimables!
# First let's maintain our unedited copy with the full values, which # we will call on when making our plots & figures and a separate copy that # we will edit to make the publishable table. ANOVA1.summarystat.publishable <- ANOVA1.summary.statistics
# We will begin by rounding numerical values in each column to 3 significant # figures, but you may choose to change this depending on your own preferenceANOVA1.summarystat.publishable$mean <-signif(ANOVA1.summarystat.publishable$mean,3) ANOVA1.summarystat.publishable$se <-signif(ANOVA1.summarystat.publishable$se,3)
# Selecting columns by name that we want to include in our final table by nameANOVA1.summarystat.publishable <-subset(ANOVA1.summarystat.publishable, select =c(Sleep, n, mean, se))
# Next we will change column names to make them nicer#colnames(T2.summary.statistics) # to print all column names in data frame if you don't remembercolnames(ANOVA1.summarystat.publishable)[colnames(ANOVA1.summarystat.publishable) =="n"] ="N"colnames(ANOVA1.summarystat.publishable)[colnames(ANOVA1.summarystat.publishable) =="mean"] ="Mean"colnames(ANOVA1.summarystat.publishable)[colnames(ANOVA1.summarystat.publishable) =="se"] ="Standard Error"
# Generating the Printable Summary Stat Table ANOVA1.summarystat.publishable %>%kbl(caption = "Summary Statistics") %>% # Title of the tablekable_classic(full_width = F, html_font = "Cambria", font_size = 10) %>% add_header_above(c(" " = 2, "Test Score (%)" = 2)) # adding header to columns in table by position. # E.g., for the first 2 columns we do not want a header so we leave empty space. # Over the last two column we specified the header name.
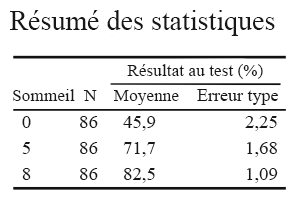
Communiquer des données démographiques Comme je l’ai mentionné, l’une des premières étapes lors de l’élaboration des méthodes est de communiquer quelques renseignements sur la taille de l’échantillon. Plongeons dans le vif du sujet!
# Computing average age by groupmydata1 %>%group_by(Sleep) %>%get_summary_stats(Age, type = "mean")
## # A tibble: 3 × 4## Sleep variable n mean## <fct><fct><dbl><dbl>## 1 0 Age 86 23.7## 2 5 Age 86 24.0## 3 8 Age 86 24.0
Notez que n représente le nombre de participants par groupe. Nous disposons donc des données de 258 participants. De plus, le nombre d’observations par condition est égal : le plan est donc équilibré. Si vous disposez d’un échantillon de taille inégale, consultez le lien suivant pour en savoir plus l’analyse de la variance à un facteur.
Analyse de la variance à un facteur avec des d’échantillons inégaux dans R?
Je vous recommande cependant de lire ce guide pour bien connaître Rstudio. Vous suivrez les mêmes étapes qu’une analyse de la variance, un facteur non équilibré, avec quelques ajustements du code.
# Looking at the distribution of "Gender" across the three groupstable(mydata1$Gender, mydata1$Sleep) %>%#each cell represents the number of subjects in this categoryaddmargins() ## we can add margins to the table to make it clearer
## ## 0 5 8 Sum## F 37 36 45 118## M 39 40 33 112## Non-Binary 10 10 8 28## Sum 86 86 86 258
Données sur les participants
Voici comment présenter des renseignements sur la taille de votre échantillon dans votre section « Méthodes », en vous appuyant sur les tableaux récapitulatifs ci-dessus.
Exemple : Nous avons recruté 258 personnes dans le bassin du premier cycle en introduction à la psychologie de l’Université McMaster, en échange d’un crédit partiel de cours. Elles ont été assignées au hasard à la condition sans sommeil (39 hommes et 10 personnes non binaires; âge moyen = 23,7 ans), à la condition 5 heures de sommeil (n = 86; 40 hommes et 10 personnes non binaires; âge moyen = 24,0 ans), ou à la condition 8 heures de sommeil (n = 86; 33 hommes et 8 personnes non binaires; âge moyen = 24,0 ans)
Visualisation Générer des graphiques et des figures
Avec des statistiques sommaires à l’appui Générons de jolis graphiques récapitulatifs pour visualiser nos données!=
GRAPHIQUE LINÉAIRE
Le premier est un graphique linéaire. Nous voulons donc indiquer le facteur ciblé sur l’axe des x, ainsi que la mesure sommaire de la variable dépendante souhaitée sur l’axe des y. Dans ce cas, le facteur Sommeil (avec 3 niveaux) doit figurer sur l’axe des abscisses, et les résultats moyens aux tests sur l’axe des ordonnées
Conseil : Concevez vos graphiques de sorte que les différents facteurs puissent être distingués par une personne daltonienne ou être imprimés en noir et blanc. Par conséquent, nous utiliserons également la forme de nos points pour spécifier la variable « BLOCK_TYPE »
anova1.lineplot <-ggline(mydata1, x = "Sleep", y = "TestScore",add =c("mean_se", "jitter"), #adding standard error bars and jitter # points representing each individual participant in each group. order =c("0", "5", "8"), #organizing order of levelsylab = "Mean Test Score (%)", xlab = "Hours Slept", #adding x- and y-axis title color = "black", #colour of linelinetype = "dashed", font.label =list(size = 20, color = "black"),size = 1,point.color = "Sleep", #point color differs for each level of the Sleep factorpalette =c("cyan4", "darkgoldenrod1", "deeppink2"),shapes = 1, #point shapespoint.size = 2,ggtheme =theme_gray(),ylim=c(0,100) #adjusting the min and max value of y-aixs)# For more options run the ?ggline() code# Change the appearance of titles and labelsanova1.lineplot +font("xlab", size = 14, color = "black", face = "bold")+font("ylab", size = 14, color = "black", face = "bold")+font("xy.text", size = 12, color = "black", face = "bold")
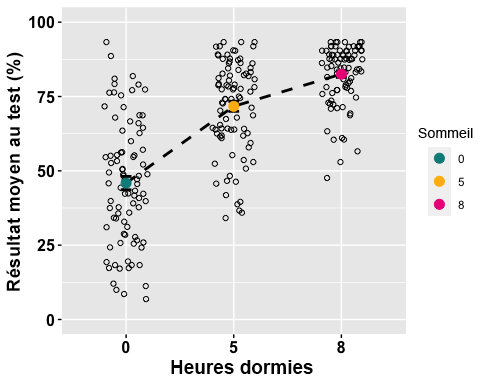
GRAPHIQUE À SURFACES
anova1.boxplot <-ggboxplot(mydata1, x = "Sleep", y = "TestScore", color = "Sleep", palette =c("cyan4", "darkgoldenrod1", "deeppink2"), order =c("0", "5", "8"),ylab = "Mean Test Score (%)", xlab = "Hours Slept",add = ("median_iqr"), #adding median and inner quartile rangefont.label =list(size = 20, color = "black"),size = 1,ggtheme =theme_gray(),ylim=c(0,100) #adjusting the min and max value of y-aixs )
# Change the appearance of titles and labelsanova1.boxplot +font("xlab", size = 14, color = "black", face = "bold")+font("ylab", size = 14, color = "black", face = "bold")+font("xy.text", size = 12, color = "black", face = "bold")
# For more options run the ?ggboxplot() code

GRAPHIQUE À BARRES
Si vous souhaitez explorer les avenues des graphiques à barres, je vous recommande les ressources suivantes :
- L’ABC des diagrammes à barres pour un facteur dans R
- ggplot2 barplots : Guide de démarrage rapide
- Ce billet explique comment concevoir des diagrammes à barres avec R et ggplot2, en utilisant la fonction geom_bar().
- Diagramme à barres attrayant grâce à la fonction ggplot dans R
Le lien suivant vous montrera toutes les palettes de couleurs pour concevoir des graphiques.
# Notice that I am using the summary statistic table with the full range of # summary data not the printable one we made. anova1.barplot <-ggplot(ANOVA1.summary.statistics, aes(x =factor(Sleep), y = mean, fill = Sleep) ) +geom_bar(stat = "identity", position = "dodge") +geom_errorbar(aes(ymax = mean + sd, ymin = mean - sd), #adding standard error barsposition =position_dodge(0.9), width = 0.25, color = "Gray25") +xlab("Hours Slept") +ylab("Average Test Score (%)") +scale_fill_brewer(palette = "RdPu") +theme_classic() +theme(axis.line=element_line(linewidth=1.5), #thickness of x-axis lineaxis.text =element_text(size = 14, colour = "black"),axis.title =element_text(size = 16, colour = "black"),panel.grid.major.y =element_line() ) +# adding horizontal grid linesscale_y_continuous(breaks=seq(0, 100, 10)) # Ticks on y-axis from 0-100, # jumps by 10 anova1.barplot
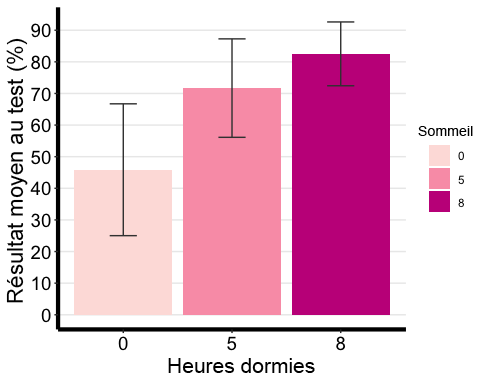
Calcul d’une analyse de la variance à un facteur
# Computing the one-way ANOVAone.aov <-aov(TestScore ~ Sleep, data = mydata1)# Summary of the analysissummary(one.aov)
## Df Sum Sq Mean Sq F value Pr(>F) ## Sleep 2 60991 30496 117.4 <2e-16 ***## Residuals 255 66212 260 ## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Interprétation et rapports
La valeur p (Pr(>F)) est nettement inférieure au seuil de signification de 0,05, comme le montrent les « astérisque » dans le tableau récapitulatif. Nous pouvons donc rejeter l’hypothèse nulle supposant aucune différence entre les groupes. Lorsque nous présentons ces données, il faut généralement indiquer les degrés de liberté, la valeur f, la valeur p et une mesure de l’ampleur de l’effet. Ensuite, il faut calculer les tailles d’effet, en particulier, il faut rapporter l’effet quadratique partiel. Vous devez consulter le chercheur principal sur la mesure de l’ampleur de l’effet jugée appropriée.
Pour en savoir plus sur des options de mesure de l’ampleur de l’effet, veuillez consulter la ressource suivante : Tailles d’effet pour les analyses de la variance à un facteur
options(es.use_symbols = TRUE) # get nice symbols when printing! (On Windows, requires R >= 4.2.0)eta_squared(one.aov, partial = TRUE)
## For one-way between-subjects designs, partial eta squared is equivalent to eta squared. Returning eta squared.
## # Effect Size for ANOVA## ## Parameter | η² | 95% CI## -------------------------------## Sleep | 0.48 | [0.41, 1.00]## ## - One-sided CIs: upper bound fixed at [1.00].
Comparaisons par paires
Bien que l’analyse de la variance à un facteur montre une différence significative entre les groupes, nous ne savons pas quelles paires sont différentes. Néanmoins, en utilisant des comparaisons multiples par paires, nous pouvons les déterminer.
R est doté de plusieurs fonctions pour effectuer les mêmes analyses. Ma préférence à cette étape est TukeyHD(), qui s’appuie sur notre analyse.
TukeyHSD(one.aov, conf.level = 0.95#you may change this, default is 0.95)
## Tukey multiple comparisons of means## 95% family-wise confidence level## ## Fit: aov(formula = TestScore ~ Sleep, data = mydata1)## ## $Sleep## diff lwr upr p adj## 5-0 25.82300 20.029891 31.61610 0.00e+00## 8-0 36.65349 30.860383 42.44659 0.00e+00## 8-5 10.83049 5.037386 16.62360 4.58e-05
Interprétation du résultat :
- diff. : la différence entre les moyennes des deux groupes
- lwr et upr : point inférieur et point supérieur de l’intervalle de confiance à 95 %.
- p adj : valeur p après ajustement pour les comparaisons multiples
Les résultats montrent une différence significative entre toutes les combinaisons de groupes! Cependant, l’avantage le plus important lorsqu’il est question de performance est évident lorsque les participants bénéficient de 8 heures de sommeil par rapport à ceux qui ne dorment pas.
Avec notre tableau récapitulatif, nous disposons maintenant de toute l’information pour présenter nos résultats.
Faire rapport des résultats :
Le résultat du test était statistiquement différent selon la durée du sommeil [F(2, 255) = 117,4, p < 0,001, pη² = 0,48]. Des analyses a posteriori avec ajustement de Bonferroni ont révélé que toutes les différences par paire, entre les niveaux de sommeil, étaient statistiquement significatives (p < 0,001).
Analyse de la variance à un facteur à mesures répétées
Dans la première expérience, nous avons calculé une analyse pour un facteur manipulé entre les sujets, ce qui signifie que nous avons comparé différents groupes. Calculons maintenant une même analyse entre des participants.
Dans cette expérience hypothétique, un groupe de participants est testé à trois moments. Ces derniers subissent tous différentes manipulations du sommeil.
mydata1within <- read_excel("OneWayWithin_Sample_DataFile.xlsx")
# Set-up factormydata1within <- mydata1within %>%convert_as_factor(ID, Sleep)str(mydata1within) #checking data structure and how factor is set-up
## tibble [258 × 5] (S3: tbl_df/tbl/data.frame)## $ ID : Factor w/ 86 levels "29057","32239",..: 20 48 84 61 22 23 25 29 72 69 ...## $ Gender : chr [1:258] "F" "M" "F" "F" ...## $ Age : num [1:258] 23 22 23 23 22 22 22 22 22 22 ...## $ Sleep : Factor w/ 3 levels "0","5","8": 1 1 1 1 1 1 1 1 1 1 ...## $ TestScore: num [1:258] 45.77 17.56 16.6 49.59 8.51 ...
Statistiques sommaires
mydata1within %>%group_by(Sleep) %>%get_summary_stats(TestScore, type = "mean_se")
## # A tibble: 3 × 5## Sleep variable n mean se## <fct><fct><dbl><dbl><dbl>## 1 0 TestScore 86 30.8 2.43## 2 5 TestScore 86 56.4 1.88## 3 8 TestScore 86 67.5 1.26
Je ne m’attarde pas sur certaines étapes, comme la synthèse des renseignements démographiques et la visualisation des données. Mais vous pouvez utiliser les mêmes codes que ceux de l’analyse de la variance à un facteur. La principale différence réside dans le calcul à proprement parler, pour laquelle nous utiliserons une fonction différente.
Calcul de l’analyse de la variance à un facteur à mesures répétées
one.aov.within <-anova_test(data = mydata1within, #data frame dv = TestScore, #(numeric) dependent variable namewid = ID, #subjects identifier; must be unique per participantwithin = Sleep, # within-subjects factor variableseffect.size = "pes", #default is generalized eta square "ges" but here we specify that we want partial eta squared detailed = TRUE, #If TRUE, returns extra information (such as sums of squares columns, intercept row, etc.) in the ANOVA table)# Run ?anova_test() to explore more options for this function.
get_anova_table(one.aov.within, correction = "auto") #automatically apply GG correction to only within-subjects factors violating the sphericity assumption
## ANOVA Table (type III tests)## ## Effect DFn DFd SSn SSd F p p<.05 pes## 1 (Intercept) 1.00 85.00 686279.36 59317.41 983.417 1.71e-48 * 0.92## 2 Sleep 1.37 116.22 60840.19 21389.16 241.777 2.37e-35 * 0.74
Le tableau de l’analyse de la variance à un facteur montre que le sommeil a un effet notable sur les résultats des tests. Ensuite, nous voulons voir où se situent les différences de scores.
Analyses a posteriori
one.anova.within.pwc <- mydata1within %>%pairwise_t_test(TestScore ~ Sleep, paired = TRUE,p.adjust.method = "bonferroni")one.anova.within.pwc
## # A tibble: 3 × 10## .y. group1 group2 n1 n2 statistic df p p.adj p.adj.signif## * <chr><chr><chr><int><int><dbl><dbl><dbl><dbl><chr>## 1 Test… 0 5 86 86 -14.7 85 5.39e-25 1.62e-24 **** ## 2 Test… 0 8 86 86 -17.1 85 2.69e-29 8.07e-29 **** ## 3 Test… 5 8 86 86 -10.3 85 1.15e-16 3.45e-16 ****

