Experiment 6: Fluid Flow – Minor Losses
Purpose
The purpose of this experiment is to find pressure loss (head loss) for several pipe components over a range of flow rates and compare the experimental findings to theoretical calculations.
Introduction
Liquids only flow through pipes if forced to do so by pressure caused by a pump of by gravity. It is found that the pressure measured at any point in the pipe decreases in the direction of flow. This pressure loss is caused by friction in the liquid and between the liquid and the walls of the pipe.
The fluid flow apparatus in room E030, shown in Figure 1 consists of a pump pushing water from a holding tank through a series of pipes and back into the tank, to form a closed loop. The piping contains a number of valves that can be used to force the water to flow through any or all of the five sections shown, depending on which valves are open or closed. If all the valves are closed no water will flow. This would damage some pumps but not the centrifugal pump used in the lab.
The piping system also contains a rotameter (flowmeter), a line with an orifice plate, a line with a venturi, a line with circular and square bends, and line with an expansion / contraction section, and a line with a globe valve and a gate valve. Along the pipes are many pressure tappings where pressure can be measured. This is done via pressure transmitters which report the pressure in inches of H2O.
For fluids flowing in a piping system where the pipes are full, the pressure change from one position to another can be calculated from Bernoulli’s formula which, assuming there is no pump between points 1 and 2, yields:
(1) ![]()
where:
- z1, z2: heights of water in the piping system relative to a common reference height (m)
- V1, V2: velocity of water (m/s)
- P1, P2: static pressure in the pipe (Pa = kg/(m s2))
- ρ: density of water (kg/m3)
- g: gravitational acceleration (9.81 m/s2)
- hL “head loss” which accounts for energy loss due to friction (m)
When the diameter of the pipe does not change, the velocity will also remain constant and Bernoull’s equation reduces to:
(2) ![]()
When there is also no change in elevation (e.g. the piping is horizontal), the height terms can also be eliminated and Bernoulli’s is simplified to:
(3) ![]()
Thus, any change in static pressure is due only to friction loss.
Frictional loss through pipe components
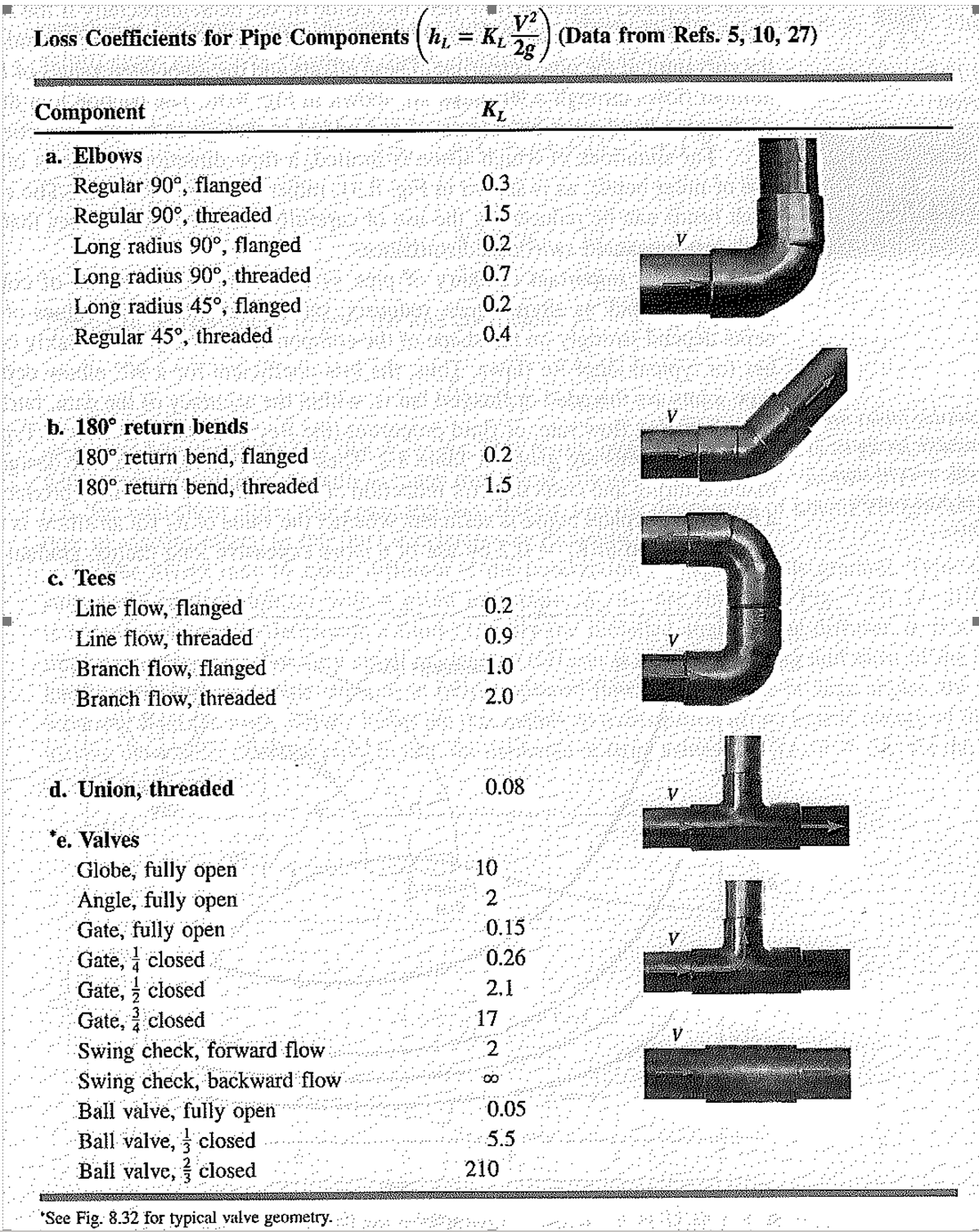
This labs deals with pressure drop through “pipe components”, such a series of elbows, direction changes, and valves. The pressure drops through any pipe component, also called “minor losses”, can be calculated by the following expression:
(4) ![]()
where
- V: the average fluid velocity through the pipe component
- KL the “Head-Loss” or “Kawamura” coefficient of the component
Values for the Kawamura coefficient for different pipe components can be found in the table at the end of this lab manual.
Equipment
The fluid flow system in room E030 consists of a tank, a pump, and five lines in parallel. A photo of the equipment with several key elements is provided below.
Figure 1: Fluid Flow apparatus in E030
The apparatus has been automated and most of the functions are controlled through an operator station. A screenshot of the operator station with key elements is provided below
Figure 2: Operator station for Fluid Flow apparatus in E030
In this experiment, the third line with circular and square bends and the fifth line with a globe and agate valve will be used. Some more details on valves can be obtained from the Visual Encyclopedia of Chemical Engineering: Valves https://encyclopedia.che.engin.umich.edu/Pages/TransportStorage/Valves/Valves.html. The two videos below explain the operation of Globe and Gate valves:
Figure 3: Globe valve operation, by FBV Inc.
Figure 4: Gate valve operation, by FBV Inc.
Procedure
The video of the experimental procedure can be seen here: https://www.macvideo.ca/media/PROCTECH+2EC3+-+Fluid+Flow+Experimental+Procedure/1_13zqdrs1
Only the third (bends) and the fifth (valves) line of the apparatus are used in this part. The calibration of the rotameter can be done simultaneously with measurement of the pressure drop readings. The calibration can be done on either the bend or valve line.
- Preparation
- Make sure the water level in the tank is at least 2/3 full; otherwise air can be drawn into the pump. If the level is low, use the hose on the side (next to the safety shower) to fill the tank.

Figure 5: Tank of fluid-flow experiment - Open the rotameter valve then the inlet and outlet valves of the third line. Make sure all other valves are closed. With the switch behind the rotameter (see figure below), turn on the pump.
- Set the flow of water to 700 (look at the picture below to see how to properly read the flow of water) to allow all the air bubbles stuck inside the pipes to escape. This might take some time… let the water run for a bit.
- Make sure the water level in the tank is at least 2/3 full; otherwise air can be drawn into the pump. If the level is low, use the hose on the side (next to the safety shower) to fill the tank.
- Measurements on third line
For the first line, you will be doing two tasks simultaneously: record the pressure drop on the line and check the rotameter flow rate at different rotameter settings- Set a flow of water of 100 IGPH (imperial gallons per hour) by adjusting the rotameter valve. Make sure there are no air pockets in the line (if there are any, go back to step 3 of the preparation). Record the flow rate shown by the rotameter float (read from the centre shoulder of the float). Write down the units of the rotameter.
- Check (calibrate) this flow rate by diverting the water going back to the tank into a weighed bucket and measuring the mass of water collected over a measured period of time (use 30 seconds or 60 seconds). After your measurement return that water to the tank.
- At the operator’s station, be sure that the appropriate line is selected. Record the pressure drop at each of the tappings as displayed on the operator’s screen and transducers. Wait about 30 seconds after adjusting the flow rate before recording the pressure drop values. The values will still be oscillating; take an average value if possible. Recall that the units of pressure drop are inches of water column (“H2O).
- Repeat seven times, for a total of 8 different flow rates, using different flow rates by adjusting the rotameter valve. Try to obtain eight sets of readings which cover the whole range of rotameter flows as shown by the scale.
- If any result is suspect, repeat the measurement.
- Measurement on fifth line
- Close the valves for the third line and open those for the fifth line. Follow the procedure shown in the video to avoid over-pressurizing any line.
- At the operator’s station, be sure that the fifth (valves) line is selected.
- Turn the rotameter valve to set the flow rate to its maximum. Let the water run for some time to allow all the air bubbles stuck inside the pipes to escape.
- Repeat the pressure drop recording procedure (steps 3, 4, and 5 from first line above) for the fifth line (valves) with the valves fully open, but this time only the pressure drops need to be collected. Make sure you collect pressure drop readings over at least eight flow rates that span the whole range of rotameter values.
- Repeat the measurements with both valves half-way open (to assess when the valves are half open measure the number of revolutions needed to go from fully open to fully closed).
- Repeat the procedure with both valves quarter open.
- Stop Down
- At the end of the experiment, stop the pump. Turn the rotameter to zero and open both the valves for the top line.
- At the operator’s station, select the “none” button.
Report
Useful dimensions
- Bends: pipe diameter = 15 mm
- Valves: pipe diameter = 25 mm
Part I
Present all your data through Tables. Make sure your table contain proper units
- Calibration curve:
- Use your “calibraton data” (i.e. the actual flow rate data collected by diverting the water into a bucket and weighing) to calculate the actual flow rate through the pump in kg/s.
- Create a plot of actual flow rate vs. Rotameter reading.
- Find the equation of the line graph. It must cross the origin. This equation will be used for converting all rotameter readings to actual flow rate.
- Pressure Drop vs Flowrate:
- On a single graph plot pressure drop (on y axis) versus flowrate (on x-axis) for all examined components of the pipe systems (8 lines in total):
- Two different bends
- Globe and Gate valve fully open
- Globe and Gate valve half open
- Globe and Gate valve quarter open
- On a single graph plot pressure drop (on y axis) versus flowrate (on x-axis) for all examined components of the pipe systems (8 lines in total):
Part II
- For each case run, use equations (4) and (5) to calculate the Kawamura coefficient (KL) for each pipe component. This will provide you with 8 KL values for the circular bends, 8 values for the square bends, 8 values for the gate valve fully open, 8 values for the globe valve fully open, and so on for the valves half and a-quarter open. To calculate the KL value for each run you will need to:
- Use the calibration curve of the rotameter to convert the reading to flow rate
- Use the pipe diameter to calculate the fluid’s average speed through the pipe.
The relationship between flow rate and average speed is(5)
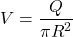
where Q is the flow rate and R the pipe radius.
- Use equations (4) and (5) to convert the pressure drop values to KL values. The video below provides some advice on how to manipulate the data. You are advised to do this part using Excel or another spreadsheet. Include the full Excel Table and a sample calculation for only one case with your report.
- Tabulate the calculated values of the KL coefficient for the bends and the valves for the various flow rates. Average the calculated values and compare the average with the corresponding value given in the tables at the end of the lab manual.
- Comment on the following:
- Are the KL values flow-rate dependent? Should they be?
- What is the % error in the KL values between the calculated and the theoretical values?
Notes:
- To evaluate the theoretical KL value for the circular bend of line 3, approximate it as two 90° and one 180° regular, flanged elbows. Calculate the KL value by adding the tabulated KL values of these components.
- To evaluate the theoretical KL value for the square bend or line 3, approximate it as four flanged Tees with branched flow. Calculate the KL
 value by adding the tabulated KL valued of these components.
value by adding the tabulated KL valued of these components.
Loss Coefficient Tables