Module 24: Volume of Common Solids

sboschman

30 Module 24: Volume of Common Solids — Technical Mathematics

<!– pb_fixme –>

Wanda Ortiz of The Iron Maidens turns up the volume.

You may use a calculator throughout this module.

Note: We will not necessarily follow the rules for rounding (precision and accuracy) in this module. Many of these figures have dimensions with only one significant figure, but we would lose a lot of information if we rounded the results to only one sig fig.

In the answer key, we will often round to the nearest whole number, or to the nearest tenth, or to two or three significant figures as we deem appropriate.

The surface area of a solid is the sum of the areas of all its faces; therefore, surface area is two-dimensional and measured in square units. The volume is the amount of space inside the solid. Volume is three-dimensional, measured in cubic units. You can imagine the volume as the number of cubes required to completely fill up the solid.

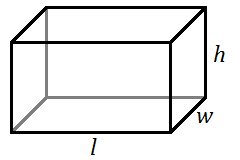
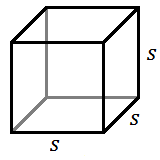
a three-dimensional rectangular box with the bottom front edge labeled l, the bottom right edge labeled w, and the vertical right edge labeled h a three-dimensional square box with the bottom front edge labeled s, the bottom right edge labeled s, and the vertical right edge labeled s

Volume of a Rectangular Solid

For a rectangular solid with length $l$ , width $w$ , and height $h$ :

$V=lwh$

For a cube with side length $s$ :

$V=s^3$

Exercises

Find the volume of each solid.

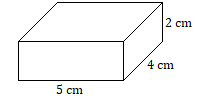
1.

2.

A solid with two equal sized polygons as its bases and rectangular lateral faces is called a right-angle prism. Some examples are shown below. We will refer to them simply as prisms in this textbook. (We will not be working with oblique prisms, which have parallelograms for the lateral faces.)

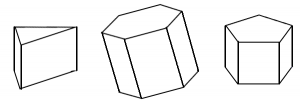
If you know the area of one of the bases, multiplying it by the height gives you the volume of the prism. In the formula below, we are using a capital $B$ to represent the area of the base.

Volume of a Prism

For a prism with base area $B$ and height $h$ :

$V=Bh$

If the prism is lying on its side, the “height” will look like a length. No matter how the prism is oriented, the height is the dimension that is perpendicular to the planes of the two parallel bases.

Exercises

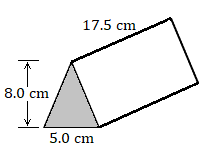
Find the volume of each prism.

3.

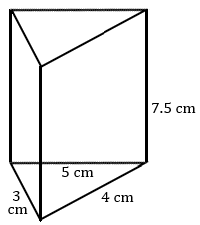
4.

5.
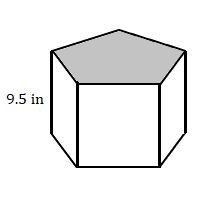
The area of the pentagon is 55 square inches.

A cylinder can be thought of as a prism with bases that are circles, rather than polygons. Just as with a prism, the volume is the area of the base multiplied by the height.

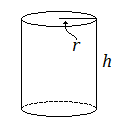
Volume of a Cylinder

For a cylinder with radius $r$ and height $h$ :

$V=\pi{r^2}h$

Exercises

Find the volume of each cylinder.

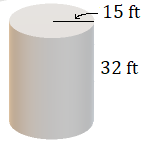
6.

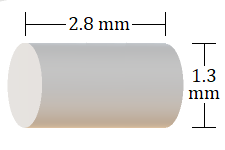
7.

As with surface area, we would need to use calculus to derive the formula for the volume of a sphere. Just believe it.

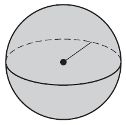
Volume of a Sphere

For a sphere with radius $r$ :

$V=\frac{4}{3}\pi{r^3}$ or $V=4\pi{r^3}\div3$

Exercises

Find the volume of each sphere.

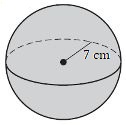
8.

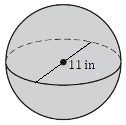
9.

Composite Solids

Of course, not every three-dimensional object is a prism, cylinder, or sphere. A composite solid is made up of two or more simpler solids. As with two-dimensional composite figures, breaking the figure into recognizable solids is a good first step.

Exercises

10. A rivet is formed by topping a cylinder with a hemisphere. The width of the cylindrical part (the rivet pin) is $1.6$ cm and the length is $7$ cm. The width of the hemisphere-shaped top (the rivet head) is $3.2$ cm. Find the rivet’s volume.

<!– pb_fixme –>

<!– pb_fixme –>
<!– pb_fixme –>

30 Module 24: Volume of Common Solids — Technical Mathematics

Module 24: Volume of Common Solids

Composite Solids

License

Share This Book