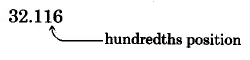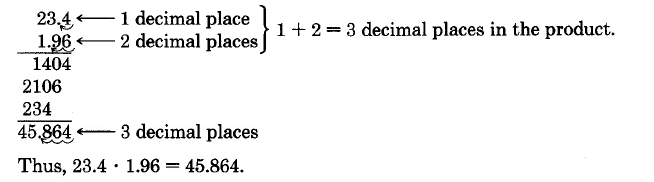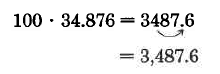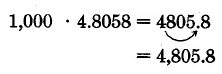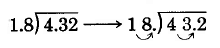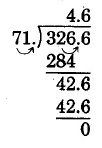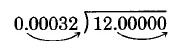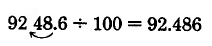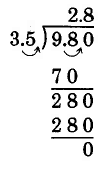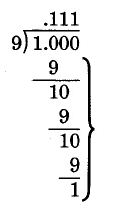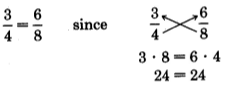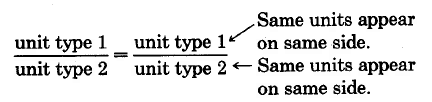127 Fundamentals of Mathematics: Part 9
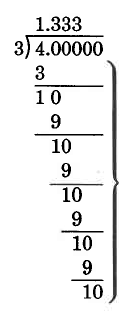
0.219
Exercise 6.3.14
0.811
Exercise 6.3.15
(Solution on p. 405.)
4.8
Exercise 6.3.16
2.6
Exercise 6.3.17
(Solution on p. 405.)
16.12
Exercise 6.3.18
25.88
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 6.3.19
(Solution on p. 405.)
6.0005
Exercise 6.3.20
1.355
Exercise 6.3.21
(Solution on p. 405.)
16.125
Exercise 6.3.22
0.375
Exercise 6.3.23
(Solution on p. 405.)
3.04
Exercise 6.3.24
21.1875
Exercise 6.3.25
(Solution on p. 405.)
8.225
Exercise 6.3.26
1.0055
Exercise 6.3.27
(Solution on p. 405.)
9.99995
Exercise 6.3.28
22.110
For the following 10 problems, convert each complex decimal to a fraction.
Exercise 6.3.29
(Solution on p. 405.)
0.7 12
Exercise 6.3.30
0.012 12
Exercise 6.3.31
(Solution on p. 405.)
2.16 14
Exercise 6.3.32
5.18 23
Exercise 6.3.33
(Solution on p. 405.)
14.11213
Exercise 6.3.34
80.001137
Exercise 6.3.35
(Solution on p. 405.)
1.40 5
16
Exercise 6.3.36
0.8 53
Exercise 6.3.37
(Solution on p. 405.)
1.9 75
Exercise 6.3.38
1.7 37
9
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
350
CHAPTER 6. DECIMALS
6.3.4.1 Exercises for Review
Exercise 6.3.39
(Solution on p. 405.)
(Section 3.6) Find the greatest common factor of 70, 182, and 154.
Exercise 6.3.40
(Section 3.6) Find the greatest common multiple of 14, 26, and 60.
Exercise 6.3.41
(Solution on p. 405.)
(Section 4.5) Find the value of 3 · 15
.
5
18 ÷ 59
Exercise 6.3.42
(Section 5.4) Find the value of 52 + 8 1
3
12 .
Exercise 6.3.43
(Solution on p. 405.)
(Section 6.2) In the decimal number 26.10742, the digit 7 is in what position?
6.4 Rounding Decimals4
6.4.1 Section Overview
• Rounding Decimal Numbers
6.4.2 Rounding Decimal Numbers
We rst considered the concept of rounding numbers in Section 1.4 where our concern with rounding was related to whole numbers only. With a few minor changes, we can apply the same rules of rounding to decimals.
To round a decimal to a particular position:
1. Mark the position of the round-o digit (with an arrow or check).
2. Note whether the digit to the immediate right of the marked digit is (a) less than 5. If so, leave the round-o digit unchanged.
(b) 5 or greater. If so, add 1 to the round-o digit.
3. If the round-o digit is
(a) to the right of the decimal point, eliminate all the digits to its right.
(b) to the left of the decimal point, replace all the digits between it and the decimal point with zeros and eliminate the decimal point and all the decimal digits.
6.4.2.1 Sample Set A
Round each decimal to the specied position. (The numbers in parentheses indicate which step is being used.)
Example 6.15
Round 32.116 to the nearest hundredth.
(1)
4This content is available online at <http://cnx.org/content/m34959/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
351
(2b) The digit immediately to the right is 6, and 6 > 5, so we add 1 to the round-o digit: 1 + 1 = 2
(3a) The round-o digit is to the right of the decimal point, so we eliminate all digits to its right.
32.12
The number 32.116 rounded to the nearest hundredth is 32.12.
Example 6.16
Round 633.14216 to the nearest hundred.
(1)
(2a) The digit immediately to the right is 3, and 3 < 5 so we leave the round-o digit unchanged.
(3b) The round-o digit is to the left of 0, so we replace all the digits between it and the decimal point with zeros and eliminate the decimal point and all the decimal digits. 600
The number 633.14216 rounded to the nearest hundred is 600.
Example 6.17
1,729.63 rounded to the nearest ten is 1,730.
Example 6.18
1.0144 rounded to the nearest tenth is 1.0.
Example 6.19
60.98 rounded to the nearest one is 61.
Sometimes we hear a phrase such as “round to three decimal places.” This phrase means that the round-o digit is the third decimal digit (the digit in the thousandths position).
Example 6.20
67.129 rounded to the second decimal place is 67.13.
Example 6.21
67.129558 rounded to 3 decimal places is 67.130.
6.4.2.2 Practice Set A
Round each decimal to the specied position.
Exercise 6.4.1
(Solution on p. 406.)
4.816 to the nearest hundredth.
Exercise 6.4.2
(Solution on p. 406.)
0.35928 to the nearest ten thousandths.
Exercise 6.4.3
(Solution on p. 406.)
82.1 to the nearest one.
Exercise 6.4.4
(Solution on p. 406.)
753.98 to the nearest hundred.
Exercise 6.4.5
(Solution on p. 406.)
Round 43.99446 to three decimal places.
Exercise 6.4.6
(Solution on p. 406.)
Round 105.019997 to four decimal places.
Exercise 6.4.7
(Solution on p. 406.)
Round 99.9999 to two decimal places.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 6. DECIMALS
6.4.3 Exercises
For the rst 10 problems, complete the chart by rounding each decimal to the indicated positions.
Exercise 6.4.8
(Solution on p. 406.)
20.01071
Tenth Hundredth Thousandth Ten Thousandth
Table 6.1
Exercise 6.4.9
3.52612
Tenth Hundredth Thousandth Ten Thousandth
3.53
Table 6.2
Exercise 6.4.10
(Solution on p. 406.)
531.21878
Tenth Hundredth Thousandth Ten Thousandth
Table 6.3
Exercise 6.4.11
36.109053
Tenth Hundredth Thousandth Ten Thousandth
36.1
Table 6.4
Exercise 6.4.12
(Solution on p. 406.)
1.999994
Tenth Hundredth Thousandth Ten Thousandth
Table 6.5
Exercise 6.4.13
7.4141998
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Tenth Hundredth Thousandth Ten Thousandth
7.414
Table 6.6
Exercise 6.4.14
(Solution on p. 406.)
0.000007
Tenth Hundredth Thousandth Ten Thousandth
Table 6.7
Exercise 6.4.15
0.00008
Tenth Hundredth Thousandth Ten Thousandth
0.0001
Table 6.8
Exercise 6.4.16
(Solution on p. 406.)
9.19191919
Tenth Hundredth Thousandth Ten Thousandth
Table 6.9
Exercise 6.4.17
0.0876543
Tenth Hundredth Thousandth Ten Thousandth
Table 6.10
Calculator Problems
For the following 5 problems, round 18.4168095 to the indicated place.
Exercise 6.4.18
(Solution on p. 407.)
3 decimal places.
Exercise 6.4.19
1 decimal place.
Exercise 6.4.20
(Solution on p. 407.)
5 decimal places.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 6. DECIMALS
Exercise 6.4.21
6 decimal places.
Exercise 6.4.22
(Solution on p. 407.)
2 decimal places.
Calculator Problems
For the following problems, perform each division using a calculator.
Exercise 6.4.23
4 ÷ 3 and round to 2 decimal places.
Exercise 6.4.24
(Solution on p. 407.)
1 ÷ 8 and round to 1 decimal place.
Exercise 6.4.25
1 ÷ 27 and round to 6 decimal places.
Exercise 6.4.26
(Solution on p. 407.)
51 ÷ 61 and round to 5 decimal places.
Exercise 6.4.27
3 ÷ 16 and round to 3 decimal places.
Exercise 6.4.28
(Solution on p. 407.)
16 ÷ 3 and round to 3 decimal places.
Exercise 6.4.29
26 ÷ 7 and round to 5 decimal places.
6.4.3.1 Exercises for Review
Exercise 6.4.30
(Solution on p. 407.)
(Section 1.2) What is the value of 2 in the number 421,916,017?
Exercise 6.4.31
(Section 2.4) Perform the division: 378 ÷ 29.
Exercise 6.4.32
(Solution on p. 407.)
(Section 3.2) Find the value of 44.
Exercise 6.4.33
(Section 4.3) Convert 11 to a mixed number.
3
Exercise 6.4.34
(Solution on p. 407.)
(Section 6.3) Convert 3.16 to a mixed number fraction.
6.5 Addition and Subtraction of Decimals5
6.5.1 Section Overview
• The Logic Behind the Method
• The Method of Adding and Subtracting Decimals
• Calculators
5This content is available online at <http://cnx.org/content/m34960/1.5/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
6.5.2 The Logic Behind the Method
Consider the sum of 4.37 and 3.22. Changing each decimal to a fraction, we have 4 37
100 + 3 22
100 Performing the addition, we get
4.37 + 3.22 = 4 37
100 + 3 22
100
=
4·100+37
100
+ 3·100+22
100
=
437
100 + 322
100
=
437+322
100
=
759
100
=
7 59
100
=
seven and fty-nine hundredths
=
7.59
Thus, 4.37 + 3.22 = 7.59.
6.5.3 The Method of Adding and Subtracting Decimals
When writing the previous addition, we could have written the numbers in columns.
4.37
+3.22
7.59
This agrees with our previous result. From this observation, we can suggest a method for adding and subtracting decimal numbers.
Method of Adding and Subtracting Decimals
To add or subtract decimals:
1. Align the numbers vertically so that the decimal points line up under each other and the corresponding decimal positions are in the same column.
2. Add or subtract the numbers as if they were whole numbers.
3. Place a decimal point in the resulting sum or dierence directly under the other decimal points.
6.5.3.1 Sample Set A
Find the following sums and dierences.
Example 6.22
9.813 + 2.140
9.813
The decimal points are aligned in the same column.
+2.140
11.953
Example 6.23
841.0056 + 47.016 + 19.058
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
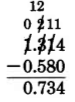
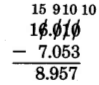

356
CHAPTER 6. DECIMALS
841.0056
47.016
+19.058
To insure that the columns align properly, we can write a 0 in the position at the end of the numbers 47.016 and 19.058 without changing their values.
Example 6.24
1.314 − 0.58
1.314
−0.58
Write a 0 in the thousandths position.
Example 6.25
16.01 − 7.053
16.01
−7.053
Write a 0 in the thousandths position.
Example 6.26
Find the sum of 6.88106 and 3.5219 and round it to three decimal places.
6.88106
+3.5219
Write a 0 in the ten thousandths position.
We need to round the sum to the thousandths position. Since the digit in the position immediately to the right is 9, and 9>5, we get
10.403
Example 6.27
Wendy has $643.12 in her checking account. She writes a check for $16.92. How much is her new account balance?
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
357
To nd the new account balance, we need to nd the dierence between 643.12 and 16.92. We will subtract 16.92 from 643.12.
After writing a check for $16.92, Wendy now has a balance of $626.20 in her checking account.
6.5.3.2 Practice Set A
Find the following sums and dierences.
Exercise 6.5.1
(Solution on p. 407.)
3.187 + 2.992
Exercise 6.5.2
(Solution on p. 407.)
14.987 − 5.341
Exercise 6.5.3
(Solution on p. 407.)
0.5261 + 1.0783
Exercise 6.5.4
(Solution on p. 407.)
1.06 − 1.0535
Exercise 6.5.5
(Solution on p. 407.)
16,521.07 + 9,256.15
Exercise 6.5.6
(Solution on p. 407.)
Find the sum of 11.6128 and 14.07353, and round it to two decimal places.
6.5.4 Calculators
The calculator can be useful for nding sums and dierences of decimal numbers. However, calculators with an eight-digit display cannot be used when working with decimal numbers that contain more than eight digits, or when the sum results in more than eight digits. In practice, an eight-place decimal will seldom be encountered. There are some inexpensive calculators that can handle 13 decimal places.
6.5.4.1 Sample Set B
Use a calculator to nd each sum or dierence.
Example 6.28
42.0638 + 126.551
Display Reads
Type 42.0638 42.0638
Press +
42.0638
Type 126.551 126.551
Press =
168.6148
Table 6.11
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 6. DECIMALS
The sum is 168.6148.
Example 6.29
Find the dierence between 305.0627 and 14.29667.
Display Reads
Type 305.0627 305.0627
Press
305.0627
Type 14.29667 14.29667
Press =
290.76603
Table 6.12
The dierence is 290.76603
Example 6.30
51.07 + 3,891.001786
Since 3,891.001786 contains more than eight digits, we will be unable to use an eight-digit display calculator to perform this addition. We can, however, nd the sum by hand.
51.070000
3891.001786
3942.071786
The sum is 3,942.071786.
6.5.4.2 Practice Set B
Use a calculator to perform each operation.
Exercise 6.5.7
(Solution on p. 407.)
4.286 + 8.97
Exercise 6.5.8
(Solution on p. 407.)
452.0092 − 392.558
Exercise 6.5.9
(Solution on p. 407.)
Find the sum of 0.095 and 0.001862
Exercise 6.5.10
(Solution on p. 407.)
Find the dierence between 0.5 and 0.025
Exercise 6.5.11
(Solution on p. 407.)
Find the sum of 2,776.00019 and 2,009.00012.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
6.5.5 Exercises
For the following 15 problems, perform each addition or subtraction. Use a calculator to check each result.
Exercise 6.5.12
(Solution on p. 407.)
1.84 + 7.11
Exercise 6.5.13
15.015 − 6.527
Exercise 6.5.14
(Solution on p. 407.)
11.842 + 28.004
Exercise 6.5.15
3.16 − 2.52
Exercise 6.5.16
(Solution on p. 407.)
3.55267 + 8.19664
Exercise 6.5.17
0.9162 − 0.0872
Exercise 6.5.18
(Solution on p. 408.)
65.512 − 8.3005
Exercise 6.5.19
761.0808 − 53.198
Exercise 6.5.20
(Solution on p. 408.)
4.305 + 2.119 − 3.817
Exercise 6.5.21
19.1161 + 27.8014 + 39.3161
Exercise 6.5.22
(Solution on p. 408.)
0.41276 − 0.0018 − 0.00011
Exercise 6.5.23
2.181 + 6.05 + 1.167 + 8.101
Exercise 6.5.24
(Solution on p. 408.)
1.0031+6.013106+0.00018+0.0092+2.11
Exercise 6.5.25
27 + 42 + 9.16 − 0.1761 + 81.6
Exercise 6.5.26
(Solution on p. 408.)
10.28 + 11.111 + 0.86 + 5.1
For the following 10 problems, solve as directed. A calculator may be useful.
Exercise 6.5.27
Add 6.1121 and 4.916 and round to 2 decimal places.
Exercise 6.5.28
(Solution on p. 408.)
Add 21.66418 and 18.00184 and round to 4 decimal places.
Exercise 6.5.29
Subtract 5.2121 from 9.6341 and round to 1 decimal place.
Exercise 6.5.30
(Solution on p. 408.)
Subtract 0.918 from 12.006 and round to 2 decimal places.
Exercise 6.5.31
Subtract 7.01884 from the sum of 13.11848 and 2.108 and round to 4 decimal places.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 6. DECIMALS
Exercise 6.5.32
(Solution on p. 408.)
A checking account has a balance of $42.51. A check is written for $19.28. What is the new balance?
Exercise 6.5.33
A checking account has a balance of $82.97. One check is written for $6.49 and another for $39.95.
What is the new balance?
Exercise 6.5.34
(Solution on p. 408.)
A person buys $4.29 worth of hamburger and pays for it with a $10 bill. How much change does this person get?
Exercise 6.5.35
A man buys $6.43 worth of stationary and pays for it with a $20 bill. After receiving his change, he realizes he forgot to buy a pen. If the total price of the pen is $2.12, and he buys it, how much of the $20 bill is left?
Exercise 6.5.36
(Solution on p. 408.)
A woman starts recording a movie on her video cassette recorder with the tape counter set at 21.93. The movie runs 847.44 tape counter units. What is the nal tape counter reading?
6.5.5.1 Exercises for Review
Exercise 6.5.37
(Section 1.6) Find the dierence between 11,206 and 10,884.
Exercise 6.5.38
(Solution on p. 408.)
(Section 2.2) Find the product, 820 · 10,000.
Exercise 6.5.39
√
√
(Section 3.3) Find the value of 121 − 25 + 82 + 16 ÷ 22 .
Exercise 6.5.40
(Solution on p. 408.)
(Section 4.6) Find the value of 81 · 36
.
3
75 ÷ 2 25
Exercise 6.5.41
(Section 6.4) Round 1.08196 to the nearest hundredth.
6.6 Multiplication of Decimals6
6.6.1 Section Overview
• The Logic Behind the Method
• The Method of Multiplying Decimals
• Calculators
• Multiplying Decimals By Powers of 10
• Multiplication in Terms of Of
6This content is available online at <http://cnx.org/content/m34963/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
361
6.6.2 The Logic Behind the Method
Consider the product of 3.2 and 1.46. Changing each decimal to a fraction, we have (3.2) (1.46) =
3 2
10 · 1 46
100
=
32
10 · 146
100
=
32·146
10·100
=
4672
1000
=
4 672
1000
=
four and six hundred seventy-two thousandths
=
4.672
Thus, (3.2) (1.46) = 4.672.
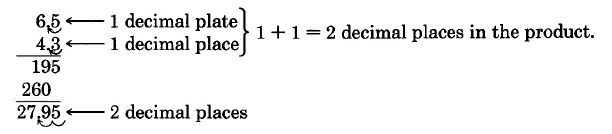
Notice that the factor
3.2 has 1 decimal place,
1.46 has 2 decimal places, }1 + 2 = 3
and the product
4.672 has 3 decimal places.
Using this observation, we can suggest that the sum of the number of decimal places in the factors equals the number of decimal places in the product.
6.6.3 The Method of Multiplying Decimals
Method of Multiplying Decimals
To multiply decimals,
1. Multiply the numbers as if they were whole numbers.
2. Find the sum of the number of decimal places in the factors.
3. The number of decimal places in the product is the sum found in step 2.
6.6.3.1 Sample Set A
Find the following products.
Example 6.31
6.5 · 4.3
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

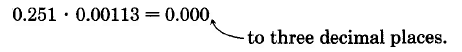
362
CHAPTER 6. DECIMALS
Thus, 6.5 · 4.3 = 27.95.
Example 6.32
23.4 · 1.96
Thus, 23.4 · 1.96 = 45.864.
Example 6.33
Find the product of 0.251 and 0.00113 and round to three decimal places.
Now, rounding to three decimal places, we get
6.6.3.2 Practice Set A
Find the following products.
Exercise 6.6.1
(Solution on p. 408.)
5.3 · 8.6
Exercise 6.6.2
(Solution on p. 408.)
2.12 · 4.9
Exercise 6.6.3
(Solution on p. 408.)
1.054 · 0.16
Exercise 6.6.4
(Solution on p. 408.)
0.00031 · 0.002
Exercise 6.6.5
(Solution on p. 408.)
Find the product of 2.33 and 4.01 and round to one decimal place.
Exercise 6.6.6
(Solution on p. 408.)
10 · 5.394
Exercise 6.6.7
(Solution on p. 408.)
100 · 5.394
Exercise 6.6.8
(Solution on p. 408.)
1000 · 5.394
Exercise 6.6.9
(Solution on p. 408.)
10,000 · 5.394
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
6.6.4 Calculators
Calculators can be used to nd products of decimal numbers. However, a calculator that has only an eight-digit display may not be able to handle numbers or products that result in more than eight digits. But there are plenty of inexpensive ($50 – $75) calculators with more than eight-digit displays.
6.6.4.1 Sample Set B
Find the following products, if possible, using a calculator.
Example 6.34
2.58 · 8.61
Display Reads
Type 2.58 2.58
Press ×
2.58
Type 8.61 8.61
Press =
22.2138
Table 6.13
The product is 22.2138.
Example 6.35
0.006 · 0.0042
Display Reads
Type .006
.006
Press ×
.006
Type .0042 0.0042
Press =
0.0000252
Table 6.14
We know that there will be seven decimal places in the product (since 3 + 4 = 7). Since the display shows 7 decimal places, we can assume the product is correct. Thus, the product is 0.0000252.
Example 6.36
0.0026 · 0.11976
Since we expect 4 + 5 = 9 decimal places in the product, we know that an eight-digit display calculator will not be able to provide us with the exact value. To obtain the exact value, we must use “hand technology.” Suppose, however, that we agree to round o this product to three decimal places. We then need only four decimal places on the display.
Display Reads
Type .0026
.0026
Press ×
.0026
Type .11976 0.11976
Press =
0.0003114
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
364
CHAPTER 6. DECIMALS
Table 6.15
Rounding 0.0003114 to three decimal places we get 0.000. Thus, 0.0026 · 0.11976 = 0.000 to three decimal places.
6.6.4.2 Practice Set B
Use a calculator to nd each product. If the calculator will not provide the exact product, round the result to four decimal places.
Exercise 6.6.10
(Solution on p. 408.)
5.126 · 4.08
Exercise 6.6.11
(Solution on p. 408.)
0.00165 · 0.04
Exercise 6.6.12
(Solution on p. 408.)
0.5598 · 0.4281
Exercise 6.6.13
(Solution on p. 408.)
0.000002 · 0.06
6.6.5 Multiplying Decimals by Powers of 10
There is an interesting feature of multiplying decimals by powers of 10. Consider the following multiplications.
Multiplication
Number of Zeros in the Power of Number of Positions the Decimal
10
Point Has Been Moved to the
Right
10 · 8.315274 = 83.15274
1
1
100 · 8.315274 = 831.5274
2
2
1, 000 · 8.315274 = 8, 315.274
3
3
10, 000 · 8.315274 = 83, 152.74
4
4
Table 6.16
Multiplying a Decimal by a Power of 10
To multiply a decimal by a power of 10, move the decimal place to the right of its current position as many places as there are zeros in the power of 10. Add zeros if necessary.
6.6.5.1 Sample Set C
Find the following products.
Example 6.37
100 · 34.876. Since there are 2 zeros in 100, Move the decimal point in 34.876 two places to the right.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

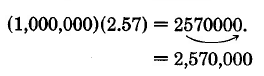

365
Example 6.38
1, 000 · 4.8058. Since there are 3 zeros in 1,000, move the decimal point in 4.8058 three places to the right.
Example 6.39
10, 000 · 56.82. Since there are 4 zeros in 10,000, move the decimal point in 56.82 four places to the right. We will have to add two zeros in order to obtain the four places.
Since there is no fractional part, we can drop the decimal point.
Example 6.40
Example 6.41
6.6.5.2 Practice Set C
Find the following products.
Exercise 6.6.14
(Solution on p. 409.)
100 · 4.27
Exercise 6.6.15
(Solution on p. 409.)
10,000 · 16.52187
Exercise 6.6.16
(Solution on p. 409.)
(10) (0.0188)
Exercise 6.6.17
(Solution on p. 409.)
(10,000,000,000) (52.7)
6.6.6 Multiplication in Terms of Of
Recalling that the word “of” translates to the arithmetic operation of multiplication, let’s observe the following multiplications.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 6. DECIMALS
6.6.6.1 Sample Set D
Example 6.42
Find 4.1 of 3.8.
Translating “of” to “×”, we get
4.1
×3.8
328
123
15.58
Thus, 4.1 of 3.8 is 15.58.
Example 6.43
Find 0.95 of the sum of 2.6 and 0.8.
We rst nd the sum of 2.6 and 0.8.
2.6
+0.8
3.4
Now nd 0.95 of 3.4
3.4
×0.95
170
306
3.230
Thus, 0.95 of (2.6 + 0.8) is 3.230.
6.6.6.2 Practice Set D
Exercise 6.6.18
(Solution on p. 409.)
Find 2.8 of 6.4.
Exercise 6.6.19
(Solution on p. 409.)
Find 0.1 of 1.3.
Exercise 6.6.20
(Solution on p. 409.)
Find 1.01 of 3.6.
Exercise 6.6.21
(Solution on p. 409.)
Find 0.004 of 0.0009.
Exercise 6.6.22
(Solution on p. 409.)
Find 0.83 of 12.
Exercise 6.6.23
(Solution on p. 409.)
Find 1.1 of the sum of 8.6 and 4.2.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
6.6.7 Exercises
For the following 30 problems, nd each product and check each result with a calculator.
Exercise 6.6.24
(Solution on p. 409.)
3.4 · 9.2
Exercise 6.6.25
4.5 · 6.1
Exercise 6.6.26
(Solution on p. 409.)
8.0 · 5.9
Exercise 6.6.27
6.1 · 7
Exercise 6.6.28
(Solution on p. 409.)
(0.1) (1.52)
Exercise 6.6.29
(1.99) (0.05)
Exercise 6.6.30
(Solution on p. 409.)
(12.52) (0.37)
Exercise 6.6.31
(5.116) (1.21)
Exercise 6.6.32
(Solution on p. 409.)
(31.82) (0.1)
Exercise 6.6.33
(16.527) (9.16)
Exercise 6.6.34
(Solution on p. 409.)
0.0021 · 0.013
Exercise 6.6.35
1.0037 · 1.00037
Exercise 6.6.36
(Solution on p. 409.)
(1.6) (1.6)
Exercise 6.6.37
(4.2) (4.2)
Exercise 6.6.38
(Solution on p. 409.)
0.9 · 0.9
Exercise 6.6.39
1.11 · 1.11
Exercise 6.6.40
(Solution on p. 409.)
6.815 · 4.3
Exercise 6.6.41
9.0168 · 1.2
Exercise 6.6.42
(Solution on p. 409.)
(3.5162) (0.0000003)
Exercise 6.6.43
(0.000001) (0.01)
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 6. DECIMALS
Exercise 6.6.44
(Solution on p. 409.)
(10) (4.96)
Exercise 6.6.45
(10) (36.17)
Exercise 6.6.46
(Solution on p. 409.)
10 · 421.8842
Exercise 6.6.47
10 · 8.0107
Exercise 6.6.48
(Solution on p. 409.)
100 · 0.19621
Exercise 6.6.49
100 · 0.779
Exercise 6.6.50
(Solution on p. 409.)
1000 · 3.596168
Exercise 6.6.51
1000 · 42.7125571
Exercise 6.6.52
(Solution on p. 409.)
1000 · 25.01
Exercise 6.6.53
100, 000 · 9.923
Exercise 6.6.54
(Solution on p. 410.)
(4.6) (6.17)
Actual product Tenths Hundreds Thousandths
Table 6.17
Exercise 6.6.55
(8.09) (7.1)
Actual product Tenths Hundreds Thousandths
Table 6.18
Exercise 6.6.56
(Solution on p. 410.)
(11.1106) (12.08)
Actual product Tenths Hundreds Thousandths
Table 6.19
Exercise 6.6.57
0.0083 · 1.090901
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Actual product Tenths Hundreds Thousandths
Table 6.20
Exercise 6.6.58
(Solution on p. 410.)
7 · 26.518
Actual product Tenths Hundreds Thousandths
Table 6.21
For the following 15 problems, perform the indicated operations
Exercise 6.6.59
Find 5.2 of 3.7.
Exercise 6.6.60
(Solution on p. 410.)
Find 12.03 of 10.1
Exercise 6.6.61
Find 16 of 1.04
Exercise 6.6.62
(Solution on p. 410.)
Find 12 of 0.1
Exercise 6.6.63
Find 0.09 of 0.003
Exercise 6.6.64
(Solution on p. 410.)
Find 1.02 of 0.9801
Exercise 6.6.65
Find 0.01 of the sum of 3.6 and 12.18
Exercise 6.6.66
(Solution on p. 410.)
Find 0.2 of the sum of 0.194 and 1.07
Exercise 6.6.67
Find the dierence of 6.1 of 2.7 and 2.7 of 4.03
Exercise 6.6.68
(Solution on p. 410.)
Find the dierence of 0.071 of 42 and 0.003 of 9.2
Exercise 6.6.69
If a person earns $8.55 an hour, how much does he earn in twenty-ve hundredths of an hour?
Exercise 6.6.70
(Solution on p. 410.)
A man buys 14 items at $1.16 each. What is the total cost?
Exercise 6.6.71
In the problem above, how much is the total cost if 0.065 sales tax is added?
Exercise 6.6.72
(Solution on p. 410.)
A river rafting trip is supposed to last for 10 days and each day 6 miles is to be rafted. On the third day a person falls out of the raft after only 2 of that day’s mileage. If this person gets discouraged 5
and quits, what fraction of the entire trip did he complete?
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 6. DECIMALS
Exercise 6.6.73
A woman starts the day with $42.28. She buys one item for $8.95 and another for $6.68. She then buys another item for sixty two-hundredths of the remaining amount. How much money does she have left?
Calculator Problems
For the following 10 problems, use a calculator to determine each product. If the calculator will not provide the exact product, round the results to ve decimal places.
Exercise 6.6.74
(Solution on p. 410.)
0.019 · 0.321
Exercise 6.6.75
0.261 · 1.96
Exercise 6.6.76
(Solution on p. 410.)
4.826 · 4.827
Exercise 6.6.77
(9.46)2
Exercise 6.6.78
(Solution on p. 410.)
(0.012)2
Exercise 6.6.79
0.00037 · 0.0065
Exercise 6.6.80
(Solution on p. 410.)
0.002 · 0.0009
Exercise 6.6.81
0.1286 · 0.7699
Exercise 6.6.82
(Solution on p. 410.)
0.01 · 0.00000471
Exercise 6.6.83
0.00198709 · 0.03
6.6.7.1 Exercises for Review
Exercise 6.6.84
(Solution on p. 410.)
(Section 2.3) Find the value, if it exists, of 0 ÷ 15.
Exercise 6.6.85
(Section 3.5) Find the greatest common factor of 210, 231, and 357.
Exercise 6.6.86
(Solution on p. 411.)
(Section 4.4) Reduce 280
2,156 to lowest terms.
Exercise 6.6.87
(Section 6.2) Write “fourteen and one hundred twenty-one ten-thousandths, using digits.”
Exercise 6.6.88
(Solution on p. 411.)
(Section 6.5) Subtract 6.882 from 8.661 and round the result to two decimal places.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
371
6.7 Division of Decimals7
6.7.1 Section Overview
• The Logic Behind the Method
• A Method of Dividing a Decimal By a Nonzero Whole Number
• A Method of Dividing a Decimal by a Nonzero Decimal
• Dividing Decimals by Powers of 10
6.7.2 The Logic Behind the Method
As we have done with addition, subtraction, and multiplication of decimals, we will study a method of division of decimals by converting them to fractions, then we will make a general rule.
We will proceed by using this example: Divide 196.8 by 6.
32
6)196.8
18
16
12
4
We have, up to this point, divided 196.8 by 6 and have gotten a quotient of 32 with a remainder of 4. If we follow our intuition and bring down the .8, we have the division 4.8 ÷ 6.
4.8 ÷ 6 = 4 8
10 ÷ 6
=
48
10 ÷ 61
8
=
)48
10 · 1
)6
1
=
8
10
Thus, 4.8 ÷ 6 = .8.
Now, our intuition and experience with division direct us to place the .8 immediately to the right of 32.
From these observations, we suggest the following method of division.
7This content is available online at <http://cnx.org/content/m34968/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
372
CHAPTER 6. DECIMALS
6.7.3 A Method of Dividing a Decimal by a Nonzero Whole Number
Method of Dividing a Decimal by a Nonzero Whole Number
To divide a decimal by a nonzero whole number:
1. Write a decimal point above the division line and directly over the decimal point of the dividend.
2. Proceed to divide as if both numbers were whole numbers.
3. If, in the quotient, the rst nonzero digit occurs to the right of the decimal point, but not in the tenths position, place a zero in each position between the decimal point and the rst nonzero digit of the quotient.
6.7.3.1 Sample Set A
Find the decimal representations of the following quotients.
Example 6.44
114.1 ÷ 7 = 7
16.3
7)114.1
7
44
42
2.1
2.1
0
Thus, 114.1 ÷ 7 = 16.3.
Check: If 114.1 ÷ 7 = 16.3, then 7 · 16.3 should equal 114.1.
4 2
16.3
7
114.1
True.
Example 6.45
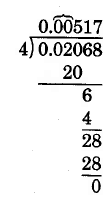
0.02068 ÷ 4
Place zeros in the tenths and hundredths positions. (See Step 3.)
Thus, 0.02068 ÷ 4 = 0.00517.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
373
6.7.3.2 Practice Set A
Find the following quotients.
Exercise 6.7.1
(Solution on p. 411.)
184.5 ÷ 3
Exercise 6.7.2
(Solution on p. 411.)
16.956 ÷ 9
Exercise 6.7.3
(Solution on p. 411.)
0.2964 ÷ 4
Exercise 6.7.4
(Solution on p. 411.)
0.000496 ÷ 8
6.7.4 A Method of Dividing a Decimal By a Nonzero Decimal
Now that we can divide decimals by nonzero whole numbers, we are in a position to divide decimals by a nonzero decimal. We will do so by converting a division by a decimal into a division by a whole number, a process with which we are already familiar. We’ll illustrate the method using this example: Divide 4.32 by 1.8.
Let’s look at this problem as 4 32
100 ÷ 1 8
10 .
4 32
4 32
100
100 ÷ 1 8
10
=
1 8
10
432
=
100
18
10
The divisor is 18
10 . We can convert 18
10 into a whole number if we multiply it by 10.
1
18
)10
10 · 10 = 18 ·
= 18
)10
1
1
But, we know from our experience with fractions, that if we multiply the denominator of a fraction by a nonzero whole number, we must multiply the numerator by that same nonzero whole number. Thus, when converting 18
10 to a whole number by multiplying it by 10, we must also multiply the numerator 432
100 by 10.
1
432
)10
100 · 10 = 432 ·
=
432·1 = 432
)100
1
10·1
10
10
=
43 210
=
43.2
We have converted the division 4.32 ÷ 1.8 into the division 43.2 ÷ 18, that is, 1.8)4.32 → 18)43.2
Notice what has occurred.
If we “move” the decimal point of the divisor one digit to the right, we must also “move” the decimal point of the dividend one place to the right. The word “move” actually indicates the process of multiplication by a power of 10.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

374
CHAPTER 6. DECIMALS
Method of Dividing a Decimal by a Decimal Number
To divide a decimal by a nonzero decimal,
1. Convert the divisor to a whole number by moving the decimal point to the position immediately to the right of the divisor’s last digit.
2. Move the decimal point of the dividend to the right the same number of digits it was moved in the divisor.
3. Set the decimal point in the quotient by placing a decimal point directly above the newly located decimal point in the dividend.
4. Divide as usual.
6.7.4.1 Sample Set B
Find the following quotients.
Example 6.46
32.66 ÷ 7.1
7.1)32.66
The divisor has one decimal place.
Move the decimal point of both the divisor and the dividend 1 place to the right.
Set the decimal point.
Divide as usual.
Thus, 32.66 ÷ 7.1 = 4.6.
Check: 32.66 ÷ 7.1 = 4.6 if 4.6 × 7.1 = 32.66
4.6
×7.1
46
322
32.66
True.
Example 6.47
1.0773 ÷ 0.513
The divisor has 3 decimal places.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
375
Move the decimal point of both the divisor and the dividend 3 places to the right.
Set the decimal place and divide.
Thus, 1.0773 ÷ 0.513 = 2.1.
Checking by multiplying 2.1 and 0.513 will convince us that we have obtained the correct result.
(Try it.)
Example 6.48
12 ÷ 0.00032
0.00032)12.00000
The divisor has 5 decimal places.
Move the decimal point of both the divisor and the dividend 5 places to the right. We will need to add 5 zeros to 12.
Set the decimal place and divide.
This is now the same as the division of whole numbers.
37500.
32)1200000.
96
240
224
160
160
000
Checking assures us that 12 ÷ 0.00032 = 37, 500.
6.7.4.2 Practice Set B
Find the decimal representation of each quotient.
Exercise 6.7.5
(Solution on p. 411.)
9.176 ÷ 3.1
Exercise 6.7.6
(Solution on p. 411.)
5.0838 ÷ 1.11
Exercise 6.7.7
(Solution on p. 411.)
16 ÷ 0.0004
Exercise 6.7.8
(Solution on p. 411.)
8, 162.41 ÷ 10
Exercise 6.7.9
(Solution on p. 411.)
8, 162.41 ÷ 100
Exercise 6.7.10
(Solution on p. 411.)
8, 162.41 ÷ 1, 000
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 6. DECIMALS
Exercise 6.7.11
(Solution on p. 411.)
8, 162.41 ÷ 10, 000
6.7.5 Calculators
Calculators can be useful for nding quotients of decimal numbers. As we have seen with the other calculator operations, we can sometimes expect only approximate results. We are alerted to approximate results when the calculator display is lled with digits. We know it is possible that the operation may produce more digits than the calculator has the ability to show. For example, the multiplication 0.12345 × 0.4567
|
{z
}
|
{z
}
5 decimal
4 decimal
places
places
produces 5 + 4 = 9 decimal places. An eight-digit display calculator only has the ability to show eight digits, and an approximation results. The way to recognize a possible approximation is illustrated in problem 3 of the next sample set.
6.7.5.1 Sample Set C
Find each quotient using a calculator. If the result is an approximation, round to ve decimal places.
Example 6.49
12.596 ÷ 4.7
Display Reads
Type 12.596 12.596
Press ÷
12.596
Type 4.7
4.7
Press =
2.68
Table 6.22
Since the display is not lled, we expect this to be an accurate result.
Example 6.50
0.5696376 ÷ 0.00123
Display Reads
Type .5696376 0.5696376
Press ÷
0.5696376
Type .00123
0.00123
Press =
463.12
Table 6.23
Since the display is not lled, we expect this result to be accurate.
Example 6.51
0.8215199 ÷ 4.113
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Display Reads
Type .8215199 0.8215199
Press ÷
0.8215199
Type 4.113
4.113
Press =
0.1997373
Table 6.24
There are EIGHT DIGITS DISPLAY FILLED! BE AWARE OF POSSIBLE APPROXI-
MATIONS.
3
We can check for a possible approximation in the following way. Since the division 4)12 can be checked by multiplying 4 and 3, we can check our division by performing the multiplication 4.113 × 0.1997373
| {z }
|
{z
}
3 decimal
7 decimal
places
places
This multiplication produces 3 + 7 = 10 decimal digits. But our suspected quotient contains only 8
decimal digits. We conclude that the answer is an approximation. Then, rounding to ve decimal places, we get 0.19974.
6.7.5.2 Practice Set C
Find each quotient using a calculator. If the result is an approximation, round to four decimal places.
Exercise 6.7.12
(Solution on p. 411.)
42.49778 ÷ 14.261
Exercise 6.7.13
(Solution on p. 411.)
0.001455 ÷ 0.291
Exercise 6.7.14
(Solution on p. 411.)
7.459085 ÷ 2.1192
6.7.6 Dividing Decimals By Powers of 10
In problems 4 and 5 of Section 6.7.4.2 (Practice Set B), we found the decimal representations of 8, 162.41÷10
and 8, 162.41 ÷ 100. Let’s look at each of these again and then, from these observations, make a general statement regarding division of a decimal number by a power of 10.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 6. DECIMALS
816.241
10)8162.410
80
16
10
62
60
24
20
41
40
10
10
0
Thus, 8, 162.41 ÷ 10 = 816.241.
Notice that the divisor 10 is composed of one 0 and that the quotient 816.241 can be obtained from the dividend 8,162.41 by moving the decimal point one place to the left.
81.6241
100)8162.4100
800
162
100
62 4
60 0
2 41
2 00
410
400
100
100
0
Thus, 8, 162.41 ÷ 100 = 81.6241.
Notice that the divisor 100 is composed of two 0’s and that the quotient 81.6241 can be obtained from the dividend by moving the decimal point two places to the left.
Using these observations, we can suggest the following method for dividing decimal numbers by powers of 10.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
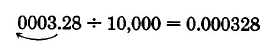
379
Dividing a Decimal Fraction by a Power of 10
To divide a decimal fraction by a power of 10, move the decimal point of the decimal fraction to the left as many places as there are zeros in the power of 10. Add zeros if necessary.
6.7.6.1 Sample Set D
Find each quotient.
Example 6.52
9, 248.6 ÷ 100
Since there are 2 zeros in this power of 10, we move the decimal point 2 places to the left.
Example 6.53
3.28 ÷ 10, 000
Since there are 4 zeros in this power of 10, we move the decimal point 4 places to the left. To do so, we need to add three zeros.
6.7.6.2 Practice Set D
Find the decimal representation of each quotient.
Exercise 6.7.15
(Solution on p. 411.)
182.5 ÷ 10
Exercise 6.7.16
(Solution on p. 411.)
182.5 ÷ 100
Exercise 6.7.17
(Solution on p. 411.)
182.5 ÷ 1, 000
Exercise 6.7.18
(Solution on p. 411.)
182.5 ÷ 10, 000
Exercise 6.7.19
(Solution on p. 411.)
646.18 ÷ 100
Exercise 6.7.20
(Solution on p. 411.)
21.926 ÷ 1, 000
6.7.7 Exercises
For the following 30 problems, nd the decimal representation of each quotient. Use a calculator to check each result.
Exercise 6.7.21
(Solution on p. 411.)
4.8 ÷ 3
Exercise 6.7.22
16.8 ÷ 8
Exercise 6.7.23
(Solution on p. 411.)
18.5 ÷ 5
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 6. DECIMALS
Exercise 6.7.24
12.33 ÷ 3
Exercise 6.7.25
(Solution on p. 411.)
54.36 ÷ 9
Exercise 6.7.26
73.56 ÷ 12
Exercise 6.7.27
(Solution on p. 412.)
159.46 ÷ 17
Exercise 6.7.28
12.16 ÷ 64
Exercise 6.7.29
(Solution on p. 412.)
37.26 ÷ 81
Exercise 6.7.30
439.35 ÷ 435
Exercise 6.7.31
(Solution on p. 412.)
36.98 ÷ 4.3
Exercise 6.7.32
46.41 ÷ 9.1
Exercise 6.7.33
(Solution on p. 412.)
3.6 ÷ 1.5
Exercise 6.7.34
0.68 ÷ 1.7
Exercise 6.7.35
(Solution on p. 412.)
50.301 ÷ 8.1
Exercise 6.7.36
2.832 ÷ 0.4
Exercise 6.7.37
(Solution on p. 412.)
4.7524 ÷ 2.18
Exercise 6.7.38
16.2409 ÷ 4.03
Exercise 6.7.39
(Solution on p. 412.)
1.002001 ÷ 1.001
Exercise 6.7.40
25.050025 ÷ 5.005
Exercise 6.7.41
(Solution on p. 412.)
12.4 ÷ 3.1
Exercise 6.7.42
0.48 ÷ 0.08
Exercise 6.7.43
(Solution on p. 412.)
30.24 ÷ 2.16
Exercise 6.7.44
48.87 ÷ 0.87
Exercise 6.7.45
(Solution on p. 412.)
12.321 ÷ 0.111
Exercise 6.7.46
64, 351.006 ÷ 10
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 6.7.47
(Solution on p. 412.)
64, 351.006 ÷ 100
Exercise 6.7.48
64, 351.006 ÷ 1, 000
Exercise 6.7.49
(Solution on p. 412.)
64, 351.006 ÷ 1, 000, 000
Exercise 6.7.50
0.43 ÷ 100
For the following 5 problems, nd each quotient. Round to the specied position. A calculator may be used.
Exercise 6.7.51
(Solution on p. 412.)
11.2944 ÷ 6.24
Actual Quotient Tenths Hundredths Thousandths
Table 6.25
Exercise 6.7.52
45.32931 ÷ 9.01
Actual Quotient Tenths Hundredths Thousandths
Table 6.26
Exercise 6.7.53
(Solution on p. 412.)
3.18186 ÷ 0.66
Actual Quotient Tenths Hundredths Thousandths
Table 6.27
Exercise 6.7.54
4.3636 ÷ 4
Actual Quotient Tenths Hundredths Thousandths
Table 6.28
Exercise 6.7.55
(Solution on p. 412.)
0.00006318 ÷ 0.018
Actual Quotient Tenths Hundredths Thousandths
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 6. DECIMALS
Table 6.29
For the following 9 problems, nd each solution.
Exercise 6.7.56
Divide the product of 7.4 and 4.1 by 2.6.
Exercise 6.7.57
(Solution on p. 413.)
Divide the product of 11.01 and 0.003 by 2.56 and round to two decimal places.
Exercise 6.7.58
Divide the dierence of the products of 2.1 and 9.3, and 4.6 and 0.8 by 0.07 and round to one decimal place.
Exercise 6.7.59
(Solution on p. 413.)
A ring costing $567.08 is to be paid o in equal monthly payments of $46.84. In how many months will the ring be paid o?
Exercise 6.7.60
Six cans of cola cost $2.58. What is the price of one can?
Exercise 6.7.61
(Solution on p. 413.)
A family traveled 538.56 miles in their car in one day on their vacation. If their car used 19.8
gallons of gas, how many miles per gallon did it get?
Exercise 6.7.62
Three college students decide to rent an apartment together. The rent is $812.50 per month. How much must each person contribute toward the rent?
Exercise 6.7.63
(Solution on p. 413.)
A woman notices that on slow speed her video cassette recorder runs through 296.80 tape units in 10 minutes and at fast speed through 1098.16 tape units. How many times faster is fast speed than slow speed?
Exercise 6.7.64
A class of 34 rst semester business law students pay a total of $1,354.90, disregarding sales tax, for their law textbooks. What is the cost of each book?
Calculator Problems
For the following problems, use calculator to nd the quotients. If the result is approximate (see Sample Set C Example 6.51) round the result to three decimal places.
Exercise 6.7.65
(Solution on p. 413.)
3.8994 ÷ 2.01
Exercise 6.7.66
0.067444 ÷ 0.052
Exercise 6.7.67
(Solution on p. 413.)
14, 115.628 ÷ 484.74
Exercise 6.7.68
219, 709.36 ÷ 9941.6
Exercise 6.7.69
(Solution on p. 413.)
0.0852092 ÷ 0.49271
Exercise 6.7.70
2.4858225 ÷ 1.11611
Exercise 6.7.71
(Solution on p. 413.)
0.123432 ÷ 0.1111
Exercise 6.7.72
2.102838 ÷ 1.0305
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
383
6.7.7.1 Exercises for Review
Exercise 6.7.73
(Solution on p. 413.)
(Section 4.3) Convert 47 to an improper fraction.
8
Exercise 6.7.74
(Section 4.7) 2 of what number is 4?
7
5
Exercise 6.7.75
(Solution on p. 413.)
(Section 5.3) Find the sum. 415 + 710 + 3.
5
Exercise 6.7.76
(Section 6.4) Round 0.01628 to the nearest ten-thousandths.
Exercise 6.7.77
(Solution on p. 413.)
(Section 6.6) Find the product (2.06)(1.39)
6.8 Nonterminating Divisions8
6.8.1 Section Overview
• Nonterminating Divisions
• Denoting Nonterminating Quotients
6.8.2 Nonterminating Divisions
Let’s consider two divisions:
1. 9.8 ÷ 3.5
2. 4 ÷ 3
Terminating Divisions
Previously, we have considered divisions like example 1, which is an example of a terminating division. A terminating division is a division in which the quotient terminates after several divisions (the remainder is zero).
Exact Divisions
The quotient in this problem terminates in the tenths position. Terminating divisions are also called exact divisions.
Nonterminating Division
The division in example 2 is an example of a nonterminating division. A non-terminating division is a division that, regardless of how far we carry it out, always has a remainder.
8This content is available online at <http://cnx.org/content/m34969/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
384
CHAPTER 6. DECIMALS
Repeating Decimal
We can see that the pattern in the brace is repeated endlessly. Such a decimal quotient is called a repeating decimal.
6.8.3 Denoting Nonterminating Quotients
We use three dots at the end of a number to indicate that a pattern repeats itself endlessly.
4 ÷ 3 = 1.333 . . .
Another way, aside from using three dots, of denoting an endlessly repeating pattern is to write a bar ( ) above the repeating sequence of digits.
4 ÷ 3 = 1.3
The bar indicates the repeated pattern of 3.
Repeating patterns in a division can be discovered in two ways:
1. As the division process progresses, should the remainder ever be the same as the dividend, it can be concluded that the division is nonterminating and that the pattern in the quotient repeats. This fact is illustrated in Example 6.54 of Section 6.8.3.1 (Sample Set A).
2. As the division process progresses, should the “product, dierence” pattern ever repeat two consecutive times, it can be concluded that the division is nonterminating and that the pattern in the quotient repeats. This fact is illustrated in Example 6.55 and 4 of Section 6.8.3.1 (Sample Set A).
6.8.3.1 Sample Set A
Carry out each division until the repeating pattern can be determined.
Example 6.54
100 ÷ 27
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
385
3.70370
27)100.00000
81
19 0
18 9
100
81
190
189
When the remainder is identical to the dividend, the division is nonterminating. This implies that the pattern in the quotient repeats.
100 ÷ 27 = 3.70370370 . . . The repeating block is 703.
100 ÷ 27 = 3.703
Example 6.55
1 ÷ 9
We see that this product, dierencepattern repeats. We can conclude that the division is nonterminating and that the quotient repeats.
1 ÷ 9 = 0.111 . . . The repeating block is 1.
1 ÷ 9 = 0.1
Example 6.56
Divide 2 by 11 and round to 3 decimal places.
Since we wish to round the quotient to three decimal places, we’ll carry out the division so that the quotient has four decimal places.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
386
CHAPTER 6. DECIMALS
.1818
11)2.0000
1 1
90
88
20
11
90
The number .1818 rounded to three decimal places is .182. Thus, correct to three decimal places, 2 ÷ 11 = 0.182
Example 6.57
Divide 1 by 6.
We see that this product, dierence pattern repeats. We can conclude that the division is nonterminating and that the quotient repeats at the 6.
1 ÷ 6 = 0.16
6.8.3.2 Practice Set A
Carry out the following divisions until the repeating pattern can be determined.
Exercise 6.8.1
(Solution on p. 413.)
1 ÷ 3
Exercise 6.8.2
(Solution on p. 413.)
5 ÷ 6
Exercise 6.8.3
(Solution on p. 413.)
11 ÷ 9
Exercise 6.8.4
(Solution on p. 413.)
17 ÷ 9
Exercise 6.8.5
(Solution on p. 413.)
Divide 7 by 6 and round to 2 decimal places.
Exercise 6.8.6
(Solution on p. 413.)
Divide 400 by 11 and round to 4 decimal places.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
6.8.4 Exercises
For the following 20 problems, carry out each division until the repeating pattern is determined. If a repeating pattern is not apparent, round the quotient to three decimal places.
Exercise 6.8.7
(Solution on p. 413.)
4 ÷ 9
Exercise 6.8.8
8 ÷ 11
Exercise 6.8.9
(Solution on p. 413.)
4 ÷ 25
Exercise 6.8.10
5 ÷ 6
Exercise 6.8.11
(Solution on p. 413.)
1 ÷ 7
Exercise 6.8.12
3 ÷ 1.1
Exercise 6.8.13
(Solution on p. 413.)
20 ÷ 1.9
Exercise 6.8.14
10 ÷ 2.7
Exercise 6.8.15
(Solution on p. 413.)
1.11 ÷ 9.9
Exercise 6.8.16
8.08 ÷ 3.1
Exercise 6.8.17
(Solution on p. 413.)
51 ÷ 8.2
Exercise 6.8.18
0.213 ÷ 0.31
Exercise 6.8.19
(Solution on p. 413.)
0.009 ÷ 1.1
Exercise 6.8.20
6.03 ÷ 1.9
Exercise 6.8.21
(Solution on p. 413.)
0.518 ÷ 0.62
Exercise 6.8.22
1.55 ÷ 0.27
Exercise 6.8.23
(Solution on p. 413.)
0.333 ÷ 0.999
Exercise 6.8.24
0.444 ÷ 0.999
Exercise 6.8.25
(Solution on p. 414.)
0.555 ÷ 0.27
Exercise 6.8.26
3.8 ÷ 0.99
Calculator Problems
For the following 10 problems, use a calculator to perform each division.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 6. DECIMALS
Exercise 6.8.27
(Solution on p. 414.)
7 ÷ 9
Exercise 6.8.28
8 ÷ 11
Exercise 6.8.29
(Solution on p. 414.)
14 ÷ 27
Exercise 6.8.30
1 ÷ 44
Exercise 6.8.31
(Solution on p. 414.)
2 ÷ 44
Exercise 6.8.32
0.7 ÷ 0.9 (Compare this with Exercise 6.8.27.)
Exercise 6.8.33
(Solution on p. 414.)
80 ÷ 110 (Compare this with Exercise 6.8.28.)
Exercise 6.8.34
0.0707 ÷ 0.7070
Exercise 6.8.35
(Solution on p. 414.)
0.1414 ÷ 0.2020
Exercise 6.8.36
1 ÷ 0.9999999
6.8.4.1 Exercise for Review
Exercise 6.8.37
(Solution on p. 414.)
(Section 1.2) In the number 411,105, how many ten thousands are there?
Exercise 6.8.38
(Section 2.3) Find the quotient, if it exists. 17 ÷ 0.
Exercise 6.8.39
(Solution on p. 414.)
(Section 3.6) Find the least common multiple of 45, 63, and 98.
Exercise 6.8.40
(Section 6.5) Subtract 8.01629 from 9.00187 and round the result to three decimal places.
Exercise 6.8.41
(Solution on p. 414.)
(Section 6.7) Find the quotient. 104.06 ÷ 12.1.
6.9 Converting a Fraction to a Decimal9
Now that we have studied and practiced dividing with decimals, we are also able to convert a fraction to a decimal. To do so we need only recall that a fraction bar can also be a division symbol. Thus, 3 not only 4
means “3 objects out of 4,” but can also mean “3 divided by 4.”
9This content is available online at <http://cnx.org/content/m34970/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
389
6.9.1 Sample Set A
Convert the following fractions to decimals. If the division is nonterminating, round to two decimal places.
Example 6.58
3 . Divide 3 by 4.
4
.75
4)3.00
2 8
20
20
0
Thus, 3 = 0.75.
4
Example 6.59
1 Divide 1 by 5.
5
.2
5)1.0
1.0
0
Thus, 1 = 0.2
5
Example 6.60
5 . Divide 5 by 6.
6
5 = 0.833 · · · We are to round to two decimal places.
6
Thus, 5 = 0.83 to two decimal places.
6
Example 6.61
5 1 . Note that 5 1 = 5 + 1 .
8
8
8
Convert 1 to a decimal.
8
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 6. DECIMALS
.125
8)1.000
8
20
16
40
40
0
1 = .125
8
Thus, 51 = 5 + 1 = 5 + .125 = 5.125.
8
8
Example 6.62
0.16 1 . This is a complex decimal.
4
Note that the 6 is in the hundredths position.
The number 0.161 is read as “sixteen and one-fourth hundredths.”
4
13
16 1
16·4+1
65
0.16 1 =
)65
4
4
4
=
· 1
= 13·1
4
100 =
100
= 100
4
4·20 = 13
80
1
)100
20
Now, convert 13
80 to a decimal.
.1625
80)13.0000
8 0
5 00
4 80
200
160
400
400
0
Thus, 0.161 = 0.1625.
4
6.9.2 Practice Set A
Convert the following fractions and complex decimals to decimals (in which no proper fractions appear). If the divison is nonterminating, round to two decimal places.
Exercise 6.9.1
(Solution on p. 414.)
1
4
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 6.9.2
(Solution on p. 414.)
1
25
Exercise 6.9.3
(Solution on p. 414.)
1
6
Exercise 6.9.4
(Solution on p. 414.)
15
16
Exercise 6.9.5
(Solution on p. 414.)
0.9 12
Exercise 6.9.6
(Solution on p. 414.)
8.0126 38
6.9.3 Exercises
For the following 30 problems, convert each fraction or complex decimal number to a decimal (in which no proper fractions appear).
Exercise 6.9.7
(Solution on p. 414.)
1
2
Exercise 6.9.8
4
5
Exercise 6.9.9
(Solution on p. 414.)
7
8
Exercise 6.9.10
5
8
Exercise 6.9.11
(Solution on p. 414.)
3
5
Exercise 6.9.12
2
5
Exercise 6.9.13
(Solution on p. 414.)
1
25
Exercise 6.9.14
3
25
Exercise 6.9.15
(Solution on p. 414.)
1
20
Exercise 6.9.16
1
15
Exercise 6.9.17
(Solution on p. 414.)
1
50
Exercise 6.9.18
1
75
Exercise 6.9.19
(Solution on p. 414.)
1
3
Exercise 6.9.20
5
6
Exercise 6.9.21
(Solution on p. 414.)
3
16
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 6. DECIMALS
Exercise 6.9.22
9
16
Exercise 6.9.23
(Solution on p. 414.)
1
27
Exercise 6.9.24
5
27
Exercise 6.9.25
(Solution on p. 414.)
7
13
Exercise 6.9.26
9
14
Exercise 6.9.27
(Solution on p. 415.)
7 23
Exercise 6.9.28
8 5
16
Exercise 6.9.29
(Solution on p. 415.)
1 2
15
Exercise 6.9.30
65 522
Exercise 6.9.31
(Solution on p. 415.)
101 625
Exercise 6.9.32
0.1 12
Exercise 6.9.33
(Solution on p. 415.)
0.24 18
Exercise 6.9.34
5.66 23
Exercise 6.9.35
(Solution on p. 415.)
810.3106 516
Exercise 6.9.36
4.1 19
For the following 18 problems, convert each fraction to a decimal. Round to ve decimal places.
Exercise 6.9.37
(Solution on p. 415.)
1
9
Exercise 6.9.38
2
9
Exercise 6.9.39
(Solution on p. 415.)
3
9
Exercise 6.9.40
4
9
Exercise 6.9.41
(Solution on p. 415.)
5
9
Exercise 6.9.42
6
9
Exercise 6.9.43
(Solution on p. 415.)
7
9
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 6.9.44
8
9
Exercise 6.9.45
(Solution on p. 415.)
1
11
Exercise 6.9.46
2
11
Exercise 6.9.47
(Solution on p. 415.)
3
11
Exercise 6.9.48
4
11
Exercise 6.9.49
(Solution on p. 415.)
5
11
Exercise 6.9.50
6
11
Exercise 6.9.51
(Solution on p. 415.)
7
11
Exercise 6.9.52
8
11
Exercise 6.9.53
(Solution on p. 415.)
9
11
Exercise 6.9.54
10
11
Calculator Problems
For the following problems, use a calculator to convert each fraction to a decimal. If no repeating pattern seems to exist, round to four decimal places.
Exercise 6.9.55
(Solution on p. 415.)
16
125
Exercise 6.9.56
85
311
Exercise 6.9.57
(Solution on p. 415.)
192
197
Exercise 6.9.58
1
1469
Exercise 6.9.59
(Solution on p. 415.)
4
21,015
Exercise 6.9.60
81,426
106,001
Exercise 6.9.61
(Solution on p. 415.)
16,501
426
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 6. DECIMALS
6.9.3.1 Exercises for Review
Exercise 6.9.62
(Section 1.4) Round 2,105,106 to the nearest hundred thousand.
Exercise 6.9.63
(Solution on p. 415.)
(Section 4.7) 8 of what number is 3?
5
2
Exercise 6.9.64
(Section 5.5) Arrange 1 916, 15, and 1 7
8
12 in increasing order.
Exercise 6.9.65
(Solution on p. 415.)
(Section 6.3) Convert the complex decimal 3.65 to a fraction.
4
Exercise 6.9.66
(Section 6.8) Find the quotient. 30 ÷ 1.1.
6.10 Combinations of Operations with Decimals and Fractions10
Having considered operations with decimals and fractions, we now consider operations that involve both decimals and fractions.
6.10.1 Sample Set A
Perform the following operations.
Example 6.63
0.38· 1 . Convert both numbers to decimals or both numbers to fractions. We’ll convert to decimals.
4
.25
4)1.00
8
20
20
0
To convert 1 to a decimal, divide 1 by 4.
4
Now multiply 0.38 and .25.
1
4
.3 8
×.25
190
76
.0950
Thus, 0.38 · 1 = 0.095.
4
10This content is available online at <http://cnx.org/content/m34971/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
In the problems that follow, the conversions from fraction to decimal, or decimal to fraction, and some of the additions, subtraction, multiplications, and divisions will be left to you.
Example 6.64
1.85 + 3 · 4.1 Convert 3 to a decimal.
8
8
1.85 + 0.375 · 4.1 Multiply before adding.
1.85 + 1.5375 Now add.
3.3875
Example 6.65
5
4
13
− 0.28 Convert 0.28 to a fraction.
5
5
4
4
13
− 28
=
5
− 7
5
100
13 5
25
=
5
20
13 25 − 7
25
1
1
=
)5 · )13
)13
)25
1
5
=
1
5
Example 6.66
125
0.125 + 1 − 0.1211 =
1000
+ 1 − 0.1211
1 1
16
4
16
3
3
1
=
8
+ 1 − 0.1211
4
16
3
=
1 · 3 + 1 − 0.1211
8
4
16
=
3 + 1 − 0.1211
32
16
=
3 + 2 − 0.1211 = 5 − 0.1211
32
32
32
=
0.15625 − 0.1211
=
0.03515
Convert this to fraction form
=
3515
100,000
=
703
20,000
6.10.2 Practice Set A
Perform the following operations.
Exercise 6.10.1
(Solution on p. 415.)
3 + 1.6
5
Exercise 6.10.2
(Solution on p. 415.)
8.91 + 1 · 1.6
5
Exercise 6.10.3
(Solution on p. 415.)
1 9
16 6.12 + 7
25
Exercise 6.10.4
(Solution on p. 415.)
0.156 − 0.05
1 11
15
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 6. DECIMALS
6.10.3 Exercises
Exercise 6.10.5
(Solution on p. 415.)
3
10 + 0.7
Exercise 6.10.6
1 + 0.1
5
Exercise 6.10.7
(Solution on p. 416.)
5 − 0.513
8
Exercise 6.10.8
0.418 − 67
200
Exercise 6.10.9
(Solution on p. 416.)
0.22 · 14
Exercise 6.10.10
3 · 8.4
5
Exercise 6.10.11
(Solution on p. 416.)
1
25 · 3.19
Exercise 6.10.12
3
20 ÷ 0.05
Exercise 6.10.13
(Solution on p. 416.)
7
40 ÷ 0.25
Exercise 6.10.14
1 1
15 ÷ 0.9 · 0.12
Exercise 6.10.15
(Solution on p. 416.)
9.26 + 1 · 0.81
4
Exercise 6.10.16
0.588 + 1
40 · 0.24
Exercise 6.10.17
(Solution on p. 416.)
1
20 + 3.62 · 38
Exercise 6.10.18
7 + 0.15÷ 3
30
Exercise 6.10.19
(Solution on p. 416.)
15
16 ·
7
10 − 0.5
Exercise 6.10.20
0.2 · 7
20 + 1.1143
Exercise 6.10.21
(Solution on p. 416.)
3 · 0.875 + 1
4
8
Exercise 6.10.22
5.198 − 0.26 · 14
250 + 0.119
Exercise 6.10.23
(Solution on p. 416.)
0.5 1 + (0.3)2
4
Exercise 6.10.24
(1.4)2 − 1.6 12
Exercise 6.10.25
(Solution on p. 416.)
3 2 − 0.000625 + (1.1)2
8
Exercise 6.10.26
(0.6)2 · 1
20 − 1
25
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 6.10.27
(Solution on p. 416.)
1 2 − 0.125
2
Exercise 6.10.28
0.75 + 5
4 1
12
2
Exercise 6.10.29
(Solution on p. 416.)
0.375 − 1
2 1
33
16
Exercise 6.10.30
1 1
8 1 ·
4
3
2.25 + 9
25
Exercise 6.10.31
(Solution on p. 416.)
0.32
12
35
0.35
Exercise
√
6.10.32
“
”
49 −5 0.125
64
1.375
6.10.3.1 Exercises for Review
Exercise 6.10.33
(Solution on p. 416.)
(Section 2.5) Is 21,480 divisible by 3?
Exercise 6.10.34
(Section 3.2) Expand 144. Do not nd the actual value.
Exercise 6.10.35
(Solution on p. 416.)
(Section 3.3) Find the prime factorization of 15,400.
Exercise 6.10.36
(Section 6.3) Convert 8.016 to a fraction.
Exercise 6.10.37
(Solution on p. 416.)
(Section 6.9) Find the quotient. 16 ÷ 27.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 6. DECIMALS
6.11 Summary of Key Concepts11
6.11.1 Summary of Key Concepts
Decimal Point (Section 6.2)
A decimal point is a point that separates the units digit from the tenths digit.
Decimal or Decimal Fraction (Section 6.2)
A decimal fraction is a fraction whose denominator is a power of ten.
Converting a Decimal to a Fraction (Section 6.3)
Decimals can be converted to fractions by saying the decimal number in words, then writing what was said.
Rounding Decimals (Section 6.4)
Decimals are rounded in much the same way whole numbers are rounded.
Addition and Subtraction of Decimals (Section 6.5)
To add or subtract decimals,
1. Align the numbers vertically so that the decimal points line up under each other and the corresponding decimal positions are in the same column.
2. Add or subtract the numbers as if they were whole numbers.
3. Place a decimal point in the resulting sum directly under the other decimal points.
Multiplication of Decimals (Section 6.6)
To multiply two decimals,
1. Multiply the numbers as if they were whole numbers.
2. Find the sum of the number of decimal places in the factors.
3. The number of decimal places in the product is the number found in step 2.
Multiplying Decimals by Powers of 10 (Section 6.6)
To multiply a decimal by a power of 10, move the decimal point to the right as many places as there are zeros in the power of ten. Add zeros if necessary.
Division of a Decimal by a Decimal (Section 6.7)
To divide a decimal by a nonzero decimal,
1. Convert the divisor to a whole number by moving the decimal point until it appears to the right of the divisor’s last digit.
2. Move the decimal point of the dividend to the right the same number of digits it was moved in the divisor.
3. Proceed to divide.
4. Locate the decimal in the answer by bringing it straight up from the dividend.
Dividing Decimals by Powers of 10 (Section 6.7)
To divide a decimal by a power of 10, move the decimal point to the left as many places as there are zeros in the power of ten. Add zeros if necessary.
Terminating Divisions (Section 6.8)
A terminating division is a division in which the quotient terminates after several divisions. Terminating divisions are also called exact divisions.
11This content is available online at <http://cnx.org/content/m34972/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Nonterminating Divisions (Section 6.8)
A nonterminating division is a division that, regardless of how far it is carried out, always has a remainder.
Nonterminating divisions are also called nonexact divisions.
Converting Fractions to Decimals (Section 6.9)
A fraction can be converted to a decimal by dividing the numerator by the denominator.
6.12 Exercise Supplement12
6.12.1 Exercise Supplement
6.12.1.1 Reading and Writing Decimals (Section 6.2)
Exercise 6.12.1
(Solution on p. 416.)
The decimal digit that appears two places to the right of the decimal point is in the position.
Exercise 6.12.2
The decimal digit that appears four places to the right of the decimal point is in the position.
For problems 3-8, read each decimal by writing it in words.
Exercise 6.12.3
(Solution on p. 416.)
7.2
Exercise 6.12.4
8.105
Exercise 6.12.5
(Solution on p. 416.)
16.52
Exercise 6.12.6
5.9271
Exercise 6.12.7
(Solution on p. 416.)
0.005
Exercise 6.12.8
4.01701
For problems 9-13, write each decimal using digits.
Exercise 6.12.9
(Solution on p. 416.)
Nine and twelve-hundredths.
Exercise 6.12.10
Two and one hundred seventy-seven thousandths.
Exercise 6.12.11
(Solution on p. 416.)
Fifty-six and thirty-ve ten-thousandths.
Exercise 6.12.12
Four tenths.
Exercise 6.12.13
(Solution on p. 416.)
Four thousand eighty-one millionths.
12This content is available online at <http://cnx.org/content/m34978/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 6. DECIMALS
6.12.1.2 Converting a Decimal to a Fraction (Section 6.3)
For problem 14-20, convert each decimal to a proper fraction or a mixed number.
Exercise 6.12.14
1.07
Exercise 6.12.15
(Solution on p. 416.)
58.63
Exercise 6.12.16
0.05
Exercise 6.12.17
(Solution on p. 416.)
0.14 23
Exercise 6.12.18
1.09 18
Exercise 6.12.19
(Solution on p. 417.)
4.01 1
27
Exercise 6.12.20
9.11 19
6.12.1.3 Rounding Decimals (Section 6.4)
For problems 21-25, round each decimal to the specied position.
Exercise 6.12.21
(Solution on p. 417.)
4.087 to the nearest hundredth.
Exercise 6.12.22
4.087 to the nearest tenth.
Exercise 6.12.23
(Solution on p. 417.)
16.5218 to the nearest one.
Exercise 6.12.24
817.42 to the nearest ten.
Exercise 6.12.25
(Solution on p. 417.)
0.9811602 to the nearest one.
6.12.1.4 Addition, Subtraction, Multiplication and Division of Decimals, and Nonterminating Divisions (Section 6.5,Section 6.6,Section 6.7,Section 6.8)
For problem 26-45, perform each operation and simplify.
Exercise 6.12.26
7.10 + 2.98
Exercise 6.12.27
(Solution on p. 417.)
14.007 − 5.061
Exercise 6.12.28
1.2 · 8.6
Exercise 6.12.29
(Solution on p. 417.)
41.8 · 0.19
Exercise 6.12.30
57.51 ÷ 2.7
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 6.12.31
(Solution on p. 417.)
0.54003 ÷ 18.001
Exercise 6.12.32
32,051.3585 ÷ 23, 006.9999
Exercise 6.12.33
(Solution on p. 417.)
100 · 1, 816.001
Exercise 6.12.34
1, 000 · 1, 816.001
Exercise 6.12.35
(Solution on p. 417.)
10.000 · 0.14
Exercise 6.12.36
0.135888 ÷ 16.986
Exercise 6.12.37
(Solution on p. 417.)
150.79 ÷ 100
Exercise 6.12.38
4.119 ÷ 10, 000
Exercise 6.12.39
(Solution on p. 417.)
42.7 ÷ 18
Exercise 6.12.40
6.9 ÷ 12
Exercise 6.12.41
(Solution on p. 417.)
0.014 ÷ 47.6. Round to three decimal places.
Exercise 6.12.42
8.8 ÷ 19. Round to one decimal place.
Exercise 6.12.43
(Solution on p. 417.)
1.1 ÷ 9
Exercise 6.12.44
1.1 ÷ 9.9
Exercise 6.12.45
(Solution on p. 417.)
30 ÷ 11.1
6.12.1.5 Converting a Fraction to a Decimal (Section 6.9)
For problems 46-55, convert each fraction to a decimal.
Exercise 6.12.46
3
8
Exercise 6.12.47
(Solution on p. 417.)
43
100
Exercise 6.12.48
82
1000
Exercise 6.12.49
(Solution on p. 417.)
9 47
Exercise 6.12.50
8 5
16
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 6. DECIMALS
Exercise 6.12.51
(Solution on p. 417.)
1.3 13
Exercise 6.12.52
25.623
Exercise 6.12.53
(Solution on p. 417.)
125.12518
Exercise 6.12.54
9.11 19
Exercise 6.12.55
(Solution on p. 417.)
0.0 56
6.12.1.6 Combinations of Operations with Decimals and Fractions (Section 6.10) For problems 56-62, perform each operation.
Exercise 6.12.56
5 · 0.25
8
Exercise 6.12.57
(Solution on p. 417.)
3
16 · 1.36
Exercise 6.12.58
3 · 1 + 1.75
5
2
Exercise 6.12.59
(Solution on p. 417.)
7 · 5 + 0.30
2
4
Exercise 6.12.60
19.375 ÷ 4.375 − 1 1
16
Exercise 6.12.61
(Solution on p. 417.)
15
602 · 2.6 + 3 14
Exercise 6.12.62
4 13
18 ÷ 5 3
14 + 3 5
21
6.13 Prociency Exam13
6.13.1 Prociency Exam
Exercise 6.13.1
(Solution on p. 417.)
(Section 6.2) The decimal digit that appears three places to the right of the decimal point is in the
position.
Exercise 6.13.2
(Solution on p. 417.)
(Section 6.2) Write, using words, 15.036.
Exercise 6.13.3
(Solution on p. 417.)
(Section 6.2) Write eighty-one and twelve hundredths using digits. 81.12
Exercise 6.13.4
(Solution on p. 418.)
(Section 6.2) Write three thousand seventeen millionths using digits.
Exercise 6.13.5
(Solution on p. 418.)
(Section 6.3) Convert 0.78 to a fraction. Reduce.
13This content is available online at <http://cnx.org/content/m34979/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 6.13.6
(Solution on p. 418.)
(Section 6.3) Convert 0.875 to a fraction. Reduce.
Exercise 6.13.7
(Solution on p. 418.)
(Section 6.4) Round 4.8063 to the nearest tenth.
Exercise 6.13.8
(Solution on p. 418.)
(Section 6.4) Round 187.51 to the nearest hundred.
Exercise 6.13.9
(Solution on p. 418.)
(Section 6.4) Round 0.0652 to the nearest hundredth.
For problems 10-20, perform each operation.
Exercise 6.13.10
(Solution on p. 418.)
(Section 6.5) 15.026 + 5.971
Exercise 6.13.11
(Solution on p. 418.)
(Section 6.5) 72.15 − 26.585
Exercise 6.13.12
(Solution on p. 418.)
(Section 6.6) 16.2 · 4.8
Exercise 6.13.13
(Solution on p. 418.)
(Section 6.6) 10, 000 · 0.016
Exercise 6.13.14
(Solution on p. 418.)
(Section 6.7) 44.64 ÷ 18.6
Exercise 6.13.15
(Solution on p. 418.)
(Section 6.7) 0.21387 ÷ 0.19
Exercise 6.13.16
(Solution on p. 418.)
(Section 6.8) 0.27 − 311
Exercise 6.13.17
(Solution on p. 418.)
(Section 6.9) Convert 6 211 to a decimal.
Exercise 6.13.18
(Solution on p. 418.)
(Section 6.9) Convert 0.5 9
16 to a decimal.
Exercise 6.13.19
(Solution on p. 418.)
(Section 6.10) 31 + 2.325
8
Exercise 6.13.20
(Solution on p. 418.)
(Section 6.10) 3 × 0.5625
8
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 6. DECIMALS
Solutions to Exercises in Chapter 6
Solution to Exercise 6.2.1 (p. 343)
twelve and nine tenths
Solution to Exercise 6.2.2 (p. 343)
four and eighty-six hundredths
Solution to Exercise 6.2.3 (p. 343)
seven and two hundred thousandths
Solution to Exercise 6.2.4 (p. 343)
thirty thousand four hundred ve millionths
Solution to Exercise 6.2.5 (p. 344)
306.49
Solution to Exercise 6.2.6 (p. 344)
9.004
Solution to Exercise 6.2.7 (p. 344)
0.000061
Solution to Exercise 6.2.8 (p. 344)
Tenths; hundredths, thousandths
Solution to Exercise 6.2.10 (p. 344)
Hundred thousandths; ten millionths
Solution to Exercise 6.2.12 (p. 344)
eight and one tenth
Solution to Exercise 6.2.14 (p. 344)
fty-ve and six hundredths
Solution to Exercise 6.2.16 (p. 344)
one and nine hundred four thousandths
Solution to Exercise 6.2.18 (p. 345)
3.20
Solution to Exercise 6.2.20 (p. 345)
1.8
Solution to Exercise 6.2.22 (p. 345)
511.004
Solution to Exercise 6.2.24 (p. 345)
0.947
Solution to Exercise 6.2.26 (p. 345)
0.00071
Solution to Exercise 6.2.28 (p. 345)
seventy-ve hundredths
Solution to Exercise 6.2.30 (p. 345)
four tenths
Solution to Exercise 6.2.32 (p. 345)
sixteen hundredths
Solution to Exercise 6.2.34 (p. 345)
one thousand eight hundred seventy-ve ten thousandths
Solution to Exercise 6.2.36 (p. 345)
fty-ve hundredths
Solution to Exercise 6.2.38 (p. 346)
2610
Solution to Exercise 6.2.40 (p. 346)
12
Solution to Exercise 6.2.42 (p. 346)
10
or 11
9
9
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 6.3.1 (p. 347)
1621
25
Solution to Exercise 6.3.2 (p. 347)
513
1,000
Solution to Exercise 6.3.3 (p. 347)
6, 646 107
10,000
Solution to Exercise 6.3.4 (p. 347)
1 1
10
Solution to Exercise 6.3.5 (p. 348)
7
8
Solution to Exercise 6.3.6 (p. 348)
31
250
Solution to Exercise 6.3.7 (p. 348)
6 7
1,200
Solution to Exercise 6.3.8 (p. 348)
18 217
Solution to Exercise 6.3.9 (p. 348)
7
10
Solution to Exercise 6.3.11 (p. 348)
53
100
Solution to Exercise 6.3.13 (p. 348)
219
1,000
Solution to Exercise 6.3.15 (p. 348)
4 45
Solution to Exercise 6.3.17 (p. 348)
16 325
Solution to Exercise 6.3.19 (p. 349)
6 1
2,000
Solution to Exercise 6.3.21 (p. 349)
1618
Solution to Exercise 6.3.23 (p. 349)
3 1
25
Solution to Exercise 6.3.25 (p. 349)
8 9
40
Solution to Exercise 6.3.27 (p. 349)
9 19,999
20,000
Solution to Exercise 6.3.29 (p. 349)
3
4
Solution to Exercise 6.3.31 (p. 349)
2 13
80
Solution to Exercise 6.3.33 (p. 349)
14 337
3,000
Solution to Exercise 6.3.35 (p. 349)
1 129
320
Solution to Exercise 6.3.37 (p. 349)
2 1
25
Solution to Exercise 6.3.39 (p. 350)
14
Solution to Exercise 6.3.41 (p. 350)
9
10
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 6. DECIMALS
Solution to Exercise 6.3.43 (p. 350)
thousandths
Solution to Exercise 6.4.1 (p. 351)
4.82
Solution to Exercise 6.4.2 (p. 351)
0.3593
Solution to Exercise 6.4.3 (p. 351)
82
Solution to Exercise 6.4.4 (p. 351)
800
Solution to Exercise 6.4.5 (p. 351)
43.994
Solution to Exercise 6.4.6 (p. 351)
105.0200
Solution to Exercise 6.4.7 (p. 351)
100.00
Solution to Exercise 6.4.8 (p. 352)
Tenth Hundredth Thousandth Ten Thousandth
20.0
20.01
20.011
20.0107
Table 6.30
Solution to Exercise 6.4.10 (p. 352)
Tenth Hundredth Thousandth Ten Thousandth
531.2
531.22
531.219
531.2188
Table 6.31
Solution to Exercise 6.4.12 (p. 352)
Tenth Hundredth Thousandth Ten Thousandth
2.0
2.00
2.000
2.0000
Table 6.32
Solution to Exercise 6.4.14 (p. 353)
Tenth Hundredth Thousandth Ten Thousandth
0.0
0.00
0.000
0.0000
Table 6.33
Solution to Exercise 6.4.16 (p. 353)
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Tenth Hundredth Thousandth Ten Thousandth
9.2
9.19
9.192
9.1919
Table 6.34
Solution to Exercise 6.4.18 (p. 353)
18.417
Solution to Exercise 6.4.20 (p. 353)
18.41681
Solution to Exercise 6.4.22 (p. 354)
18.42
Solution to Exercise 6.4.24 (p. 354)
0.1
Solution to Exercise 6.4.26 (p. 354)
0.83607
Solution to Exercise 6.4.28 (p. 354)
5.333
Solution to Exercise 6.4.30 (p. 354)
Ten million
Solution to Exercise 6.4.32 (p. 354)
256
Solution to Exercise 6.4.34 (p. 354)
3 4
25
Solution to Exercise 6.5.1 (p. 357)
6.179
Solution to Exercise 6.5.2 (p. 357)
9.646
Solution to Exercise 6.5.3 (p. 357)
1.6044
Solution to Exercise 6.5.4 (p. 357)
0.0065
Solution to Exercise 6.5.5 (p. 357)
25,777.22
Solution to Exercise 6.5.6 (p. 357)
25.69
Solution to Exercise 6.5.7 (p. 358)
13.256
Solution to Exercise 6.5.8 (p. 358)
59.4512
Solution to Exercise 6.5.9 (p. 358)
0.096862
Solution to Exercise 6.5.10 (p. 358)
0.475
Solution to Exercise 6.5.11 (p. 358)
Since each number contains more than eight digits, using some calculators may not be helpful. Adding these by hand technology, we get 4,785.00031
Solution to Exercise 6.5.12 (p. 359)
8.95
Solution to Exercise 6.5.14 (p. 359)
39.846
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 6. DECIMALS
Solution to Exercise 6.5.16 (p. 359)
11.74931
Solution to Exercise 6.5.18 (p. 359)
57.2115
Solution to Exercise 6.5.20 (p. 359)
2.607
Solution to Exercise 6.5.22 (p. 359)
0.41085
Solution to Exercise 6.5.24 (p. 359)
9.135586
Solution to Exercise 6.5.26 (p. 359)
27.351
Solution to Exercise 6.5.28 (p. 359)
39.6660
Solution to Exercise 6.5.30 (p. 359)
11.09
Solution to Exercise 6.5.32 (p. 360)
$23.23
Solution to Exercise 6.5.34 (p. 360)
$5.71
Solution to Exercise 6.5.36 (p. 360)
869.37
Solution to Exercise 6.5.38 (p. 360)
8,200,000
Solution to Exercise 6.5.40 (p. 360)
20 = 5 or 22
9
3
9
Solution to Exercise 6.6.1 (p. 362)
45.58
Solution to Exercise 6.6.2 (p. 362)
10.388
Solution to Exercise 6.6.3 (p. 362)
0.16864
Solution to Exercise 6.6.4 (p. 362)
0.00000062
Solution to Exercise 6.6.5 (p. 362)
9.3
Solution to Exercise 6.6.6 (p. 362)
53.94
Solution to Exercise 6.6.7 (p. 362)
539.4
Solution to Exercise 6.6.8 (p. 362)
5,394
Solution to Exercise 6.6.9 (p. 362)
59,340
Solution to Exercise 6.6.10 (p. 364)
20.91408
Solution to Exercise 6.6.11 (p. 364)
0.000066
Solution to Exercise 6.6.12 (p. 364)
0.2397
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 6.6.13 (p. 364)
0.0000
Solution to Exercise 6.6.14 (p. 365)
427
Solution to Exercise 6.6.15 (p. 365)
165,218.7
Solution to Exercise 6.6.16 (p. 365)
0.188
Solution to Exercise 6.6.17 (p. 365)
527,000,000,000
Solution to Exercise 6.6.18 (p. 366)
17.92
Solution to Exercise 6.6.19 (p. 366)
0.13
Solution to Exercise 6.6.20 (p. 366)
3.636
Solution to Exercise 6.6.21 (p. 366)
0.0000036
Solution to Exercise 6.6.22 (p. 366)
9.96
Solution to Exercise 6.6.23 (p. 366)
14.08
Solution to Exercise 6.6.24 (p. 367)
31.28
Solution to Exercise 6.6.26 (p. 367)
47.20
Solution to Exercise 6.6.28 (p. 367)
0.152
Solution to Exercise 6.6.30 (p. 367)
4.6324
Solution to Exercise 6.6.32 (p. 367)
3.182
Solution to Exercise 6.6.34 (p. 367)
0.0000273
Solution to Exercise 6.6.36 (p. 367)
2.56
Solution to Exercise 6.6.38 (p. 367)
0.81
Solution to Exercise 6.6.40 (p. 367)
29.3045
Solution to Exercise 6.6.42 (p. 367)
0.00000105486
Solution to Exercise 6.6.44 (p. 368)
49.6
Solution to Exercise 6.6.46 (p. 368)
4,218.842
Solution to Exercise 6.6.48 (p. 368)
19.621
Solution to Exercise 6.6.50 (p. 368)
3,596.168
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 6. DECIMALS
Solution to Exercise 6.6.52 (p. 368)
25,010
Solution to Exercise 6.6.54 (p. 368)
Actual product Tenths Hundreds Thousandths
28.382
28.4
28.38
28.382
Table 6.35
Solution to Exercise 6.6.56 (p. 368)
Actual product Tenths Hundreds Thousandths
134.216048
134.2
134.22
134.216
Table 6.36
Solution to Exercise 6.6.58 (p. 369)
Actual product Tenths Hundreds Thousandths
185.626
185.6
185.63
185.626
Table 6.37
Solution to Exercise 6.6.60 (p. 369)
121.503
Solution to Exercise 6.6.62 (p. 369)
1.2
Solution to Exercise 6.6.64 (p. 369)
0.999702
Solution to Exercise 6.6.66 (p. 369)
0.2528
Solution to Exercise 6.6.68 (p. 369)
2.9544
Solution to Exercise 6.6.70 (p. 369)
$16.24
Solution to Exercise 6.6.72 (p. 369)
0.24
Solution to Exercise 6.6.74 (p. 370)
0.006099
Solution to Exercise 6.6.76 (p. 370)
23.295102
Solution to Exercise 6.6.78 (p. 370)
0.000144
Solution to Exercise 6.6.80 (p. 370)
0.0000018
Solution to Exercise 6.6.82 (p. 370)
0.0000000471
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 6.6.84 (p. 370)
0Solution to Exercise 6.6.86 (p. 370)
10
77
Solution to Exercise 6.6.88 (p. 370)
1.78
Solution to Exercise 6.7.1 (p. 373)
61.5
Solution to Exercise 6.7.2 (p. 373)
1.884
Solution to Exercise 6.7.3 (p. 373)
0.0741
Solution to Exercise 6.7.4 (p. 373)
0.000062
Solution to Exercise 6.7.5 (p. 375)
2.96
Solution to Exercise 6.7.6 (p. 375)
4.58
Solution to Exercise 6.7.7 (p. 375)
40,000
Solution to Exercise 6.7.8 (p. 375)
816.241
Solution to Exercise 6.7.9 (p. 375)
81.6241
Solution to Exercise 6.7.10 (p. 375)
8.16241
Solution to Exercise 6.7.11 (p. 376)
0.816241
Solution to Exercise 6.7.12 (p. 377)
2.98
Solution to Exercise 6.7.13 (p. 377)
0.005
Solution to Exercise 6.7.14 (p. 377)
3.5197645 is an approximate result. Rounding to four decimal places, we get 3.5198
Solution to Exercise 6.7.15 (p. 379)
18.25
Solution to Exercise 6.7.16 (p. 379)
1.825
Solution to Exercise 6.7.17 (p. 379)
0.1825
Solution to Exercise 6.7.18 (p. 379)
0.01825
Solution to Exercise 6.7.19 (p. 379)
6.4618
Solution to Exercise 6.7.20 (p. 379)
0.021926
Solution to Exercise 6.7.21 (p. 379)
1.6
Solution to Exercise 6.7.23 (p. 379)
3.7
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 6. DECIMALS
Solution to Exercise 6.7.25 (p. 380)
6.04
Solution to Exercise 6.7.27 (p. 380)
9.38
Solution to Exercise 6.7.29 (p. 380)
0.46
Solution to Exercise 6.7.31 (p. 380)
8.6
Solution to Exercise 6.7.33 (p. 380)
2.4
Solution to Exercise 6.7.35 (p. 380)
6.21
Solution to Exercise 6.7.37 (p. 380)
2.18
Solution to Exercise 6.7.39 (p. 380)
1.001
Solution to Exercise 6.7.41 (p. 380)
4Solution to Exercise 6.7.43 (p. 380)
14
Solution to Exercise 6.7.45 (p. 380)
111
Solution to Exercise 6.7.47 (p. 381)
643.51006
Solution to Exercise 6.7.49 (p. 381)
0.064351006
Solution to Exercise 6.7.51 (p. 381)
Actual Quotient Tenths Hundredths Thousandths
1.81
1.8
1.81
1.810
Table 6.38
Solution to Exercise 6.7.53 (p. 381)
Actual Quotient Tenths Hundredths Thousandths
4.821
4.8
4.82
4.821
Table 6.39
Solution to Exercise 6.7.55 (p. 381)
Actual Quotient Tenths Hundredths Thousandths
0.00351
0.0
0.00
0.004
Table 6.40
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 6.7.57 (p. 382)
0.01
Solution to Exercise 6.7.59 (p. 382)
12.11 months
Solution to Exercise 6.7.61 (p. 382)
27.2 miles per gallon
Solution to Exercise 6.7.63 (p. 382)
3.7
Solution to Exercise 6.7.65 (p. 382)
1.94
Solution to Exercise 6.7.67 (p. 382)
29.120
Solution to Exercise 6.7.69 (p. 382)
0.173
Solution to Exercise 6.7.71 (p. 382)
1.111
Solution to Exercise 6.7.73 (p. 383)
39
8
Solution to Exercise 6.7.75 (p. 383)
47 or 117
30
30
Solution to Exercise 6.7.77 (p. 383)
2.8634
Solution to Exercise 6.8.1 (p. 386)
0.3
Solution to Exercise 6.8.2 (p. 386)
0.83
Solution to Exercise 6.8.3 (p. 386)
1.2
Solution to Exercise 6.8.4 (p. 386)
1.8
Solution to Exercise 6.8.5 (p. 386)
1.17
Solution to Exercise 6.8.6 (p. 386)
36.3636
Solution to Exercise 6.8.7 (p. 387)
0.4
Solution to Exercise 6.8.9 (p. 387)
0.16
Solution to Exercise 6.8.11 (p. 387)
0.142857
Solution to Exercise 6.8.13 (p. 387)
10.526
Solution to Exercise 6.8.15 (p. 387)
0.112
Solution to Exercise 6.8.17 (p. 387)
6.21951
Solution to Exercise 6.8.19 (p. 387)
0.0081
Solution to Exercise 6.8.21 (p. 387)
0.835
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 6. DECIMALS
Solution to Exercise 6.8.23 (p. 387)
0.3
Solution to Exercise 6.8.25 (p. 387)
2.05
Solution to Exercise 6.8.27 (p. 387)
0.7
Solution to Exercise 6.8.29 (p. 388)
0.518
Solution to Exercise 6.8.31 (p. 388)
0.045
Solution to Exercise 6.8.33 (p. 388)
0.72
Solution to Exercise 6.8.35 (p. 388)
0.7
Solution to Exercise 6.8.37 (p. 388)
1Solution to Exercise 6.8.39 (p. 388)
4410
Solution to Exercise 6.8.41 (p. 388)
8.6
Solution to Exercise 6.9.1 (p. 390)
0.25
Solution to Exercise 6.9.2 (p. 391)
0.04
Solution to Exercise 6.9.3 (p. 391)
0.17
Solution to Exercise 6.9.4 (p. 391)
0.9375
Solution to Exercise 6.9.5 (p. 391)
0.95
Solution to Exercise 6.9.6 (p. 391)
8.0126375
Solution to Exercise 6.9.7 (p. 391)
0.5
Solution to Exercise 6.9.9 (p. 391)
0.875
Solution to Exercise 6.9.11 (p. 391)
0.6
Solution to Exercise 6.9.13 (p. 391)
0.04
Solution to Exercise 6.9.15 (p. 391)
0.05
Solution to Exercise 6.9.17 (p. 391)
0.02
Solution to Exercise 6.9.19 (p. 391)
0.3
Solution to Exercise 6.9.21 (p. 391)
0.1875
Solution to Exercise 6.9.23 (p. 392)
0.037
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 6.9.25 (p. 392)
0.538461
Solution to Exercise 6.9.27 (p. 392)
7.6
Solution to Exercise 6.9.29 (p. 392)
1.13
Solution to Exercise 6.9.31 (p. 392)
101.24
Solution to Exercise 6.9.33 (p. 392)
0.24125
Solution to Exercise 6.9.35 (p. 392)
810.31063125
Solution to Exercise 6.9.37 (p. 392)
0.11111
Solution to Exercise 6.9.39 (p. 392)
0.33333
Solution to Exercise 6.9.41 (p. 392)
0.55556
Solution to Exercise 6.9.43 (p. 392)
0.77778
Solution to Exercise 6.9.45 (p. 393)
0.09091
Solution to Exercise 6.9.47 (p. 393)
0.27273
Solution to Exercise 6.9.49 (p. 393)
0.45455
Solution to Exercise 6.9.51 (p. 393)
0.63636
Solution to Exercise 6.9.53 (p. 393)
0.81818
Solution to Exercise 6.9.55 (p. 393)
0.128
Solution to Exercise 6.9.57 (p. 393)
0.9746
Solution to Exercise 6.9.59 (p. 393)
0.0002
Solution to Exercise 6.9.61 (p. 393)
38.7347
Solution to Exercise 6.9.63 (p. 394)
15
16
Solution to Exercise 6.9.65 (p. 394)
3 29
40 or 3.725
Solution to Exercise 6.10.1 (p. 395)
2.2 or 215
Solution to Exercise 6.10.2 (p. 395)
9.23
Solution to Exercise 6.10.3 (p. 395)
10
Solution to Exercise 6.10.4 (p. 395)
1
25 or 0.04
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 6. DECIMALS
Solution to Exercise 6.10.5 (p. 396)
1Solution to Exercise 6.10.7 (p. 396)
0.112
Solution to Exercise 6.10.9 (p. 396)
0.055
Solution to Exercise 6.10.11 (p. 396)
0.1276
Solution to Exercise 6.10.13 (p. 396)
0.7
Solution to Exercise 6.10.15 (p. 396)
9.4625
Solution to Exercise 6.10.17 (p. 396)
1.4075
Solution to Exercise 6.10.19 (p. 396)
0.1875
Solution to Exercise 6.10.21 (p. 396)
0.75
Solution to Exercise 6.10.23 (p. 396)
0.615
Solution to Exercise 6.10.25 (p. 396)
1.35
Solution to Exercise 6.10.27 (p. 397)
0.125
Solution to Exercise 6.10.29 (p. 397)
0.15
Solution to Exercise 6.10.31 (p. 397)
2.6
Solution to Exercise 6.10.33 (p. 397)
yes
Solution to Exercise 6.10.35 (p. 397)
23 · 52 · 7 · 11
Solution to Exercise 6.10.37 (p. 397)
0.592
Solution to Exercise 6.12.1 (p. 399)
hundredths
Solution to Exercise 6.12.3 (p. 399)
seven and two tenths
Solution to Exercise 6.12.5 (p. 399)
sixteen and fty-two hundredths
Solution to Exercise 6.12.7 (p. 399)
ve thousandths
Solution to Exercise 6.12.9 (p. 399)
9.12
Solution to Exercise 6.12.11 (p. 399)
56.0035
Solution to Exercise 6.12.13 (p. 399)
0.004081
Solution to Exercise 6.12.15 (p. 400)
85 63
100
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 6.12.17 (p. 400)
11
75
Solution to Exercise 6.12.19 (p. 400)
4 7
675
Solution to Exercise 6.12.21 (p. 400)
4.09
Solution to Exercise 6.12.23 (p. 400)
17
Solution to Exercise 6.12.25 (p. 400)
1Solution to Exercise 6.12.27 (p. 400)
8.946
Solution to Exercise 6.12.29 (p. 400)
7.942
Solution to Exercise 6.12.31 (p. 401)
0.03
Solution to Exercise 6.12.33 (p. 401)
181,600.1
Solution to Exercise 6.12.35 (p. 401)
1.4
Solution to Exercise 6.12.37 (p. 401)
1.5079
Solution to Exercise 6.12.39 (p. 401)
2.372
Solution to Exercise 6.12.41 (p. 401)
0.000
Solution to Exercise 6.12.43 (p. 401)
0.12
Solution to Exercise 6.12.45 (p. 401)
2.702
Solution to Exercise 6.12.47 (p. 401)
0.43
Solution to Exercise 6.12.49 (p. 401)
9.571428
Solution to Exercise 6.12.51 (p. 402)
1.3
Solution to Exercise 6.12.53 (p. 402)
125.125125 (not repeating)
Solution to Exercise 6.12.55 (p. 402)
0.083
Solution to Exercise 6.12.57 (p. 402)
0.255
Solution to Exercise 6.12.59 (p. 402)
5.425
Solution to Exercise 6.12.61 (p. 402)
0.09343
Solution to Exercise 6.13.1 (p. 402)
thousandth
Solution to Exercise 6.13.2 (p. 402)
fteen and thirty-six thousandths
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 6. DECIMALS
Solution to Exercise 6.13.3 (p. 402)
81.12
Solution to Exercise 6.13.4 (p. 402)
0.003017
Solution to Exercise 6.13.5 (p. 402)
39
50
Solution to Exercise 6.13.6 (p. 403)
7
8
Solution to Exercise 6.13.7 (p. 403)
4.8
Solution to Exercise 6.13.8 (p. 403)
200
Solution to Exercise 6.13.9 (p. 403)
0.07
Solution to Exercise 6.13.10 (p. 403)
20.997
Solution to Exercise 6.13.11 (p. 403)
45.565
Solution to Exercise 6.13.12 (p. 403)
77.76
Solution to Exercise 6.13.13 (p. 403)
16
Solution to Exercise 6.13.14 (p. 403)
2.4
Solution to Exercise 6.13.15 (p. 403)
1.1256
Solution to Exercise 6.13.16 (p. 403)
0Solution to Exercise 6.13.17 (p. 403)
6.18
Solution to Exercise 6.13.18 (p. 403)
0.055625
Solution to Exercise 6.13.19 (p. 403)
5.45
Solution to Exercise 6.13.20 (p. 403)
27
128 or 0.2109375
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Ratios and Rates
7.1 Objectives1
After completing this chapter, you should
Ratios and Rates (Section 7.2)
• be able to distinguish between denominate and pure numbers and between ratios and rates Proportions (Section 7.3)
• be able to describe proportions and nd the missing factor in a proportion
• be able to work with proportions involving rates
Applications of Proportions (Section 7.4)
• solve proportion problems using the ve-step method
Percent (Section 7.5)
• understand the relationship between ratios and percents
• be able to make conversions between fractions, decimals, and percents Fractions of One Percent (Section 7.6)
• understand the meaning of a fraction of one percent
• be able to make conversions involving fractions of one percent
Applications of Percents (Section 7.7)
• be able to distinguish between base, percent, and percentage
• be able to nd the percentage, the percent, and the base
7.2 Ratios and Rates2
7.2.1 Section Overview
• Denominate Numbers and Pure Numbers
• Ratios and Rates
1This content is available online at <http://cnx.org/content/m18895/1.3/>.
2This content is available online at <http://cnx.org/content/m34980/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4> 419
420
CHAPTER 7. RATIOS AND RATES
7.2.2 Denominate Numbers and Pure Numbers
Denominate Numbers, Like and Unlike Denominate Numbers
It is often necessary or convenient to compare two quantities. Denominate numbers are numbers together with some specied unit. If the units being compared are alike, the denominate numbers are called like denominate numbers. If units are not alike, the numbers are called unlike denominate numbers.
Examples of denominate numbers are shown in the diagram:
Pure Numbers
Numbers that exist purely as numbers and do not represent amounts of quantities are called pure numbers.
Examples of pure numbers are 8, 254, 0, 215, 2, and 0.07.
8
5
Numbers can be compared in two ways: subtraction and division.
Comparing Numbers by Subtraction and Division
Comparison of two numbers by subtraction indicates how much more one number is than another.
Comparison by division indicates how many times larger or smaller one number is than another.
Comparing Pure or Like Denominate Numbers by Subtraction
Numbers can be compared by subtraction if and only if they both are like denominate numbers or both pure numbers.
7.2.2.1 Sample Set A
Example 7.1
Compare 8 miles and 3 miles by subtraction.
8 mile − 3 miles = 5 miles
This means that 8 miles is 5 miles more than 3 miles.
Examples of use: I can now jog 8 miles whereas I used to jog only 3 miles. So, I can now jog 5
miles more than I used to.
Example 7.2
Compare 12 and 5 by subtraction.
12 − 5 = 7
This means that 12 is 7 more than 5.
Example 7.3
Comparing 8 miles and 5 gallons by subtraction makes no sense.
8 miles − 5 gallons =?
Example 7.4
Compare 36 and 4 by division.
36 ÷ 4 = 9
This means that 36 is 9 times as large as 4. Recall that 36 ÷ 4 = 9 can be expressed as 36 = 9.
4
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Example 7.5
Compare 8 miles and 2 miles by division.
8 miles
2 miles = 4
This means that 8 miles is 4 times as large as 2 miles.
Example of use: I can jog 8 miles to your 2 miles. Or, for every 2 miles that you jog, I jog 8. So, I jog 4 times as many miles as you jog.
Notice that when like quantities are being compared by division, we drop the units. Another way of looking at this is that the units divide out (cancel).
Example 7.6
Compare 30 miles and 2 gallons by division.
30 miles
2 gallons = 15 miles
1 gallon
Example of use: A particular car goes 30 miles on 2 gallons of gasoline. This is the same as getting 15 miles to 1 gallon of gasoline.
Notice that when the quantities being compared by division are unlike quantities, we do not drop the units.
7.2.2.2 Practice Set A
Make the following comparisons and interpret each one.
Exercise 7.2.1
(Solution on p. 466.)
Compare 10 diskettes to 2 diskettes by
(a) subtraction:
(b) division:
Exercise 7.2.2
(Solution on p. 466.)
Compare, if possible, 16 bananas and 2 bags by
(a) subtraction:
(b) division:
7.2.3 Ratios and Rates
Ratio
A comparison, by division, of two pure numbers or two like denominate numbers is a ratio.
The comparison by division of the pure numbers 36 and the like denominate numbers 8 miles 4
2 miles are examples
of ratios.
Rate
A comparison, by division, of two unlike denominate numbers is a rate.
The comparison by division of two unlike denominate numbers, such as
55 miles
1 gallon and 40 dollars
5 tickets
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 7. RATIOS AND RATES
are examples of rates.
Let’s agree to represent two numbers (pure or denominate) with the letters a and b. This means that we’re letting a represent some number and b represent some, perhaps dierent, number. With this agreement, we can write the ratio of the two numbers a and b as
a or b
b
a
The ratio a is read as ” a to b.”
b
The ratio b is read as ” b to a.”
a
Since a ratio or a rate can be expressed as a fraction, it may be reducible.
7.2.3.1 Sample Set B
Example 7.7
The ratio 30 to 2 can be expressed as 30. Reducing, we get 15.
2
1
The ratio 30 to 2 is equivalent to the ratio 15 to 1.
Example 7.8
The rate “4 televisions to 12 people” can be expressed as 4 televisions 12 people . The meaning of this rate is
that “for every 4 televisions, there are 12 people.”
Reducing, we get 1 television
3 people . The meaning of this rate is that “for every 1 television, there are 3
people.
Thus, the rate of “4 televisions to 12 people” is the same as the rate of “1 television to 3 people.”
7.2.3.2 Practice Set B
Write the following ratios and rates as fractions.
Exercise 7.2.3
(Solution on p. 466.)
3 to 2
Exercise 7.2.4
(Solution on p. 466.)
1 to 9
Exercise 7.2.5
(Solution on p. 466.)
5 books to 4 people
Exercise 7.2.6
(Solution on p. 466.)
120 miles to 2 hours
Exercise 7.2.7
(Solution on p. 466.)
8 liters to 3 liters
Write the following ratios and rates in the form “a to b.” Reduce when necessary.
Exercise 7.2.8
(Solution on p. 466.)
9
5
Exercise 7.2.9
(Solution on p. 466.)
1
3
Exercise 7.2.10
(Solution on p. 466.)
25 miles
2 gallons
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 7.2.11
(Solution on p. 466.)
2 mechanics
4 wrenches
Exercise 7.2.12
(Solution on p. 466.)
15 video tapes
18 video tapes
7.2.4 Exercises
For the following 9 problems, complete the statements.
Exercise 7.2.13
(Solution on p. 466.)
Two numbers can be compared by subtraction if and only if
.
Exercise 7.2.14
A comparison, by division, of two pure numbers or two like denominate numbers is called a
.
Exercise 7.2.15
(Solution on p. 466.)
A comparison, by division, of two unlike denominate numbers is called a
.
Exercise 7.2.16
6
11 is an example of a
. (ratio/rate)
Exercise 7.2.17
(Solution on p. 466.)
5
12 is an example of a
. (ratio/rate)
Exercise 7.2.18
7 erasers
12 pencils is an example of a
. (ratio/rate)
Exercise 7.2.19
(Solution on p. 466.)
20 silver coins
35 gold coins is an example of a
.(ratio/rate)
Exercise 7.2.20
3 sprinklers
5 sprinklers is an example of a
. (ratio/rate)
Exercise 7.2.21
(Solution on p. 466.)
18 exhaust valves
11 exhaust valves is an example of a
.(ratio/rate)
For the following 7 problems, write each ratio or rate as a verbal phrase.
Exercise 7.2.22
8
3
Exercise 7.2.23
(Solution on p. 466.)
2
5
Exercise 7.2.24
8 feet
3 seconds
Exercise 7.2.25
(Solution on p. 466.)
29 miles
2 gallons
Exercise 7.2.26
30,000 stars
300 stars
Exercise 7.2.27
(Solution on p. 466.)
5 yards
2 yards
Exercise 7.2.28
164 trees
28 trees
For the following problems, write the simplied fractional form of each ratio or rate.
Exercise 7.2.29
(Solution on p. 466.)
12 to 5
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 7. RATIOS AND RATES
Exercise 7.2.30
81 to 19
Exercise 7.2.31
(Solution on p. 466.)
42 plants to 5 homes
Exercise 7.2.32
8 books to 7 desks
Exercise 7.2.33
(Solution on p. 466.)
16 pints to 1 quart
Exercise 7.2.34
4 quarts to 1 gallon
Exercise 7.2.35
(Solution on p. 467.)
2.54 cm to 1 in
Exercise 7.2.36
80 tables to 18 tables
Exercise 7.2.37
(Solution on p. 467.)
25 cars to 10 cars
Exercise 7.2.38
37 wins to 16 losses
Exercise 7.2.39
(Solution on p. 467.)
105 hits to 315 at bats
Exercise 7.2.40
510 miles to 22 gallons
Exercise 7.2.41
(Solution on p. 467.)
1,042 characters to 1 page
Exercise 7.2.42
1,245 pages to 2 books
7.2.4.1 Exercises for Review
Exercise 7.2.43
(Solution on p. 467.)
(Section 4.3) Convert 16 to a mixed number.
3
Exercise 7.2.44
(Section 4.7) 15 of 24 is what number?
9
7
Exercise 7.2.45
(Solution on p. 467.)
(Section 5.3) Find the dierence. 11
28 − 7
45 .
Exercise 7.2.46
(Section 6.8) Perform the division. If no repeating patterns seems to exist, round the quotient to three decimal places: 22.35 ÷ 17
Exercise 7.2.47
(Solution on p. 467.)
(Section 6.10) Find the value of 1.85 + 3 · 4.1
8
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
425
7.3 Proportions3
7.3.1 Section Overview
• Ratios, Rates, and Proportions
• Finding the Missing Factor in a Proportion
• Proportions Involving Rates
7.3.2 Ratios, Rates, and Proportions
Ratio, Rate
We have dened a ratio as a comparison, by division, of two pure numbers or two like denominate numbers.
We have dened a rate as a comparison, by division, of two unlike denominate numbers.
Proportion
A proportion is a statement that two ratios or rates are equal. The following two examples show how to read proportions.
7.3.2.1 Sample Set A
Write or read each proportion.
Example 7.9
3 = 12
5
20
3 is to 5 as 12 is to 20
Example 7.10
10 items
5 dollars = 2 items
1 dollar
10 items is to 5 dollars as 2 items is to 1 dollar
Example 7.11
8 is to 12 as 16 is to 24.
8
12 = 16
24
Example 7.12
50 milligrams of vitamin C is to 1 tablet as 300 milligrams of vitamin C is to 6 tablets.
50 = 300
1
6
3This content is available online at <http://cnx.org/content/m34981/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
426
CHAPTER 7. RATIOS AND RATES
7.3.2.2 Practice Set A
Write or read each proportion.
Exercise 7.3.1
(Solution on p. 467.)
3 = 6
8
16
Exercise 7.3.2
(Solution on p. 467.)
2 people
1 window = 10 people
5 windows
Exercise 7.3.3
(Solution on p. 467.)
15 is to 4 as 75 is to 20.
Exercise 7.3.4
(Solution on p. 467.)
2 plates are to 1 tray as 20 plates are to 10 trays.
7.3.3 Finding the Missing Factor in a Proportion
Many practical problems can be solved by writing the given information as proportions. Such proportions will be composed of three specied numbers and one unknown number. It is customary to let a letter, such as x, represent the unknown number. An example of such a proportion is
x = 20
4
16
This proportion is read as ” x is to 4 as 20 is to 16.”
There is a method of solving these proportions that is based on the equality of fractions. Recall that two fractions are equivalent if and only if their cross products are equal. For example, Notice that in a proportion that contains three specied numbers and a letter representing an unknown quantity, that regardless of where the letter appears, the following situation always occurs.
(number) · (letter) = (number) · (number)
|
{z
}
We recognize this as a multiplication statement. Specically, it is a missing factor statement. (See Section 4.7
for a discussion of multiplication statements.) For example,
x = 20
4
16
means that 16 · x = 4 · 20
4 = 16
means that 4 · 20 = 16 · x
x
20
5 = x
means that 5 · 16 = 4 · x
4
16
5 = 20
means that 5 · x = 4 · 20
4
x
Each of these statements is a multiplication statement. Specically, each is a missing factor statement. (The letter used here is x, whereas M was used in Section 4.7.)
Finding the Missing Factor in a Proportion
The missing factor in a missing factor statement can be determined by dividing the product by the known factor, that is, if x represents the missing factor, then
x = (product) ÷ (known factor)
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
7.3.3.1 Sample Set B
Find the unknown number in each proportion.
Example 7.13
x = 20
4
16 . Find the cross product.
16 · x
=
20 · 4
16 · x
=
80
Divide the product 80 by the known factor 16.
x
=
80
16
x
=
5
The unknown number is 5.
This mean that 5 = 20
4
16 , or 5 is to 4 as 20 is to 16.
Example 7.14
5 = 20
x
16 . Find the cross product.
5 · 16
=
20 · x
80
=
20 · x
Divide the product 80 by the known factor 20.
80
=
x
20
4
=
x
The unknown number is 4.
This means that 5 = 20
4
16 , or, 5 is to 4 as 20 is to 6.
Example 7.15
16 = 64 Find the cross product.
3
x
16 · x
=
64 · 3
16 · x
=
192
Divide 192 by 16.
x
=
192
16
x
=
12
The unknown number is 12.
The means that 16 = 64
3
12 , or, 16 is to 3 as 64 is to 12.
Example 7.16
9 = x
8
40 Find the cross products.
9 · 40
=
8 · x
360
=
8 · x
Divide 360 by 8.
360
=
x
8
45
=
x
The unknown number is 45.
7.3.3.2 Practice Set B
Find the unknown number in each proportion.
Exercise 7.3.5
(Solution on p. 467.)
x = 12
8
32
Available for free at Connexions <http://cnx.org/content/col10615/1.4>


428
CHAPTER 7. RATIOS AND RATES
Exercise 7.3.6
(Solution on p. 467.)
7 = 14
x
10
Exercise 7.3.7
(Solution on p. 467.)
9
11 = x
55
Exercise 7.3.8
(Solution on p. 467.)
1 = 8
6
x
7.3.4 Proportions Involving Rates
Recall that a rate is a comparison, by division, of unlike denominate numbers. We must be careful when setting up proportions that involve rates. The form is important. For example, if a rate involves two types of units, say unit type 1 and unit type 2, we can write
or
Both cross products produce a statement of the type
(unit type 1) · (unit type 2) = (unit type 1) · (unit type 2)
which we take to mean the comparison
Examples of correctly expressed proportions are the following:
However, if we write the same type of units on dierent sides, such as,
unit type 1
unit type 2 = unit type 2
unit type 1
the cross product produces a statement of the form
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
429
We can see that this is an incorrect comparison by observing the following example: It is incorrect to write 2 hooks
3 poles = 6 poles
4 hooks
for two reason.
1. The cross product is numerically wrong: (2 · 4 6= 3 · 6).
2. The cross product produces the statement hooks are to hooks as poles are to poles, which makes no sense.
7.3.5 Exercises
Exercise 7.3.9
(Solution on p. 467.)
A statement that two ratios or
are equal is called a
.
For the following 9 problems, write each proportion in fractional form.
Exercise 7.3.10
3 is to 7 as 18 is to 42.
Exercise 7.3.11
(Solution on p. 467.)
1 is to 11 as 3 is to 33.
Exercise 7.3.12
9 is to 14 as 27 is to 42.
Exercise 7.3.13
(Solution on p. 467.)
6 is to 90 as 3 is to 45.
Exercise 7.3.14
5 liters is to 1 bottle as 20 liters is to 4 bottles.
Exercise 7.3.15
(Solution on p. 467.)
18 grams of cobalt is to 10 grams of silver as 36 grams of cobalt is to 20 grams of silver.
Exercise 7.3.16
4 cups of water is to 1 cup of sugar as 32 cups of water is to 8 cups of sugar.
Exercise 7.3.17
(Solution on p. 467.)
3 people absent is to 31 people present as 15 people absent is to 155 people present.
Exercise 7.3.18
6 dollars is to 1 hour as 90 dollars is to 15 hours.
For the following 10 problems, write each proportion as a sentence.
Exercise 7.3.19
(Solution on p. 467.)
3 = 15
4
20
Exercise 7.3.20
1 = 5
8
40
Exercise 7.3.21
(Solution on p. 467.)
3 joggers
100 feet = 6 joggers
200 feet
Exercise 7.3.22
12 marshmallows
3 sticks
= 36 marshmallows
9 sticks
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 7. RATIOS AND RATES
Exercise 7.3.23
(Solution on p. 467.)
40 miles
80 miles = 2 gallons
4 gallons
Exercise 7.3.24
4 couches
10 couches = 2 houses
5 houses
Exercise 7.3.25
(Solution on p. 467.)
1 person
1 job
= 8 people
8 jobs
Exercise 7.3.26
1 popsicle
1 popsicle
2
2 children =
1 child
Exercise 7.3.27
(Solution on p. 467.)
2,000 pounds
1 ton
= 60,000 pounds
30 tons
Exercise 7.3.28
1 table
5 tables = 2 people
10 people
For the following 10 problems, solve each proportion.
Exercise 7.3.29
(Solution on p. 468.)
x = 6
5
15
Exercise 7.3.30
x
10 = 28
40
Exercise 7.3.31
(Solution on p. 468.)
5 = 10
x
16
Exercise 7.3.32
13 = 39
x
60
Exercise 7.3.33
(Solution on p. 468.)
1 = x
3
24
Exercise 7.3.34
7
12 = x
60
Exercise 7.3.35
(Solution on p. 468.)
8 = 72
3
x
Exercise 7.3.36
16 = 48
1
x
Exercise 7.3.37
(Solution on p. 468.)
x
25 = 200
125
Exercise 7.3.38
65
30 = x
60
For the following 5 problems, express each sentence as a proportion then solve the proportion.
Exercise 7.3.39
(Solution on p. 468.)
5 hats are to 4 coats as x hats are to 24 coats.
Exercise 7.3.40
x cushions are to 2 sofas as 24 cushions are to 16 sofas.
Exercise 7.3.41
(Solution on p. 468.)
1 spacecraft is to 7 astronauts as 5 spacecraft are to x astronauts.
Exercise 7.3.42
56 microchips are to x circuit boards as 168 microchips are to 3 circuit boards.
Exercise 7.3.43
(Solution on p. 468.)
18 calculators are to 90 calculators as x students are to 150 students.
Exercise 7.3.44
x dollars are to $40,000 as 2 sacks are to 1 sack.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Indicate whether the proportion is true or false.
Exercise 7.3.45
(Solution on p. 468.)
3
16 = 12
64
Exercise 7.3.46
2
15 = 10
75
Exercise 7.3.47
(Solution on p. 468.)
1 = 3
9
30
Exercise 7.3.48
6 knives
7 forks = 12 knives
15 forks
Exercise 7.3.49
(Solution on p. 468.)
33 miles
1 gallon = 99 miles
3 gallons
Exercise 7.3.50
320 feet
5 seconds = 65 feet
1 second
Exercise 7.3.51
(Solution on p. 468.)
35 students
70 students = 1 class
2 classes
Exercise 7.3.52
9 ml chloride
45 ml chloride = 1 test tube
7 test tubes
7.3.5.1 Exercises for Review
Exercise 7.3.53
(Solution on p. 468.)
(Section 1.7) Use the number 5 and 7 to illustrate the commutative property of addition.
Exercise 7.3.54
(Section 2.7) Use the numbers 5 and 7 to illustrate the commutative property of multiplication.
Exercise 7.3.55
(Solution on p. 468.)
(Section 5.3) Find the dierence. 514 − 322.
Exercise 7.3.56
(Section 6.6) Find the product. 8.06129 · 1, 000.
Exercise 7.3.57
(Solution on p. 468.)
(Section 7.2) Write the simplied fractional form of the rate sixteen sentences to two paragraphs.
7.4 Applications of Proportions4
7.4.1 Section Overview
• The Five-Step Method
• Problem Solving
4This content is available online at <http://cnx.org/content/m34982/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 7. RATIOS AND RATES
7.4.2 The Five-Step Method
In Section 7.3 we noted that many practical problems can be solved by writing the given information as proportions. Such proportions will be composed of three specied numbers and one unknown number represented by a letter.
The rst and most important part of solving a proportion problem is to determine, by careful reading, what the unknown quantity is and to represent it with some letter.
The Five-Step Method
The ve-step method for solving proportion problems:
1. By careful reading, determine what the unknown quantity is and represent it with some letter. There will be only one unknown in a problem.
2. Identify the three specied numbers.
3. Determine which comparisons are to be made and set up the proportion.
4. Solve the proportion (using the methods of Section 7.3).
5. Interpret and write a conclusion in a sentence with the appropriate units of measure.
Step 1 is extremely important. Many problems go unsolved because time is not taken to establish what quantity is to be found.
When solving an applied problem, always begin by determining the unknown quantity and representing it with a letter.
7.4.3 Problem Solving
7.4.3.1 Sample Set A
Example 7.17
On a map, 2 inches represents 25 miles. How many miles are represented by 8 inches?
Step 1: The unknown quantity is miles.
Let x = number of miles represented by 8 inches
Step 2: The three specied numbers are
2 inches
25 miles
8 inches
Step 3: The comparisons are
2 inches to 25 miles → 2 inches
25 miles
8 inches to x miles → 8 inches
x miles
Proportions involving ratios and rates are more readily solved by suspending the units while doing the computations.
2
25 = 8x
Step 4:
2
=
8
Perform the cross multiplication.
25
x
2 · x
=
8 · 25
2 · x
=
200
Divide 200 by 2.
x
=
200
2
x
=
100
In step 1, we let x represent the number of miles. So, x represents 100 miles.
Step 5: If 2 inches represents 25 miles, then 8 inches represents 100 miles.
Try Exercise 7.4.1 in Section 7.4.3.2 (Practice Set A).
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Example 7.18
An acid solution is composed of 7 parts water to 2 parts acid. How many parts of water are there in a solution composed of 20 parts acid?
Step 1: The unknown quantity is the number of parts of water.
Let n = number of parts of water.
Step 2: The three specied numbers are
7 parts water
2 parts acid
20 parts acid
Step 3: The comparisons are
7 parts water to 2 parts acid → 72
n parts water to 20 parts acid → n
20
7 = n
2
20
Step 4: 7 = n Perform the cross multiplication.
2
20
7 · 20
=
2 · n
140
=
2 · n
Divide 140 by 2.
140
=
n
2
70
=
n
In step 1 we let n represent the number of parts of water. So, n represents 70 parts of water.
Step 5: 7 parts water to 2 parts acid indicates 70 parts water to 20 parts acid.
Try Problem 7.4.2 in Section 7.4.3.2 (Practice Set A).
Example 7.19
A 5-foot girl casts a 31-foot shadow at a particular time of the day. How tall is a person who casts 3
a 3-foot shadow at the same time of the day?
Step 1: The unknown quantity is the height of the person.
Let h = height of the person.
Step 2: The three specied numbers are
5 feet ( height of girl)
3 1 feet (length of shadow)
3
3 feet (length of shadow)
Step 3: The comparisons are
5-foot girl is to 31foot shadow → 5
3
3 1
3
h-foot person is to 3-foot shadow → h3
5
= h
3 1
3
3
Step 4:
5
=
h
3 1
3
3
5 · 3
=
3 1 · h
3
15
=
10 · h Divide 15 by 10
3
3
15
=
h
10
3
3
)15 · 3
=
h
1
)10
2
9
=
h
2
h
=
4 12
Step 5: A person who casts a 3-foot shadow at this particular time of the day is 41 feet tall.
2
Try Exercise 7.4.3 in Section 7.4.3.2 (Practice Set A).
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 7. RATIOS AND RATES
Example 7.20
The ratio of men to women in a particular town is 3 to 5. How many women are there in the town if there are 19,200 men in town?
Step 1: The unknown quantity is the number of women in town.
Let x = number of women in town.
Step 2: The three specied numbers are
3519,200
Step 3: The comparisons are 3 men to 5 women → 35
19,200 men to x women → 19,200
x
3 = 19,200
5
x
Step 4: 3 = 19,200
5
x
3 · x
=
19, 200 · 5
3 · x
=
96, 000
x
=
96,000
3
x
=
32, 000
Step 5: There are 32,000 women in town.
Example 7.21
The rate of wins to losses of a particular baseball team is 9 . How many games did this team lose 2
if they won 63 games?
Step 1: The unknown quantity is the number of games lost.
Let n = number of games lost.
Step 2: Since 9→ means 9 wins to 2 losses, the three specied numbers are 2
9 (wins)
2 (losses)
63 (wins)
Step 3: The comparisons are
9 wins to 2 losses→ 92
63 wins to n losses → 63n
9 = 63
2
n
Step 4: 9 = 63
2
n
9 · n
=
2 · 63
9 · n
=
126
n
=
126
9
n
=
14
Step 5: This team had 14 losses.
Try Exercise 7.4.4 in Section 7.4.3.2 (Practice Set A).
7.4.3.2 Practice Set A
Solve each problem.
Exercise 7.4.1
(Solution on p. 468.)
On a map, 3 inches represents 100 miles. How many miles are represented by 15 inches?
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Step 1:
Step 2:
Step 3:
Step 4:
Step 5:
Exercise 7.4.2
(Solution on p. 468.)
An alcohol solution is composed of 14 parts water to 3 parts alcohol. How many parts of alcohol are in a solution that is composed of 112 parts water?
Step 1:
Step 2:
Step 3:
Step 4:
Step 5:
Exercise 7.4.3
(Solution on p. 468.)
A 51 -foot woman casts a 7-foot shadow at a particular time of the day. How long of a shadow 2
does a 3-foot boy cast at that same time of day?
Step 1:
Step 2:
Step 3:
Step 4:
Step 5:
Exercise 7.4.4
(Solution on p. 468.)
The rate of houseplants to outside plants at a nursery is 4 to 9. If there are 384 houseplants in the nursery, how many outside plants are there?
Step 1:
Step 2:
Step 3:
Step 4:
Step 5:
Exercise 7.4.5
(Solution on p. 468.)
The odds for a particular event occurring are 11 to 2. (For every 11 times the event does occur, it will not occur 2 times.) How many times does the event occur if it does not occur 18 times?
Step 1:
Step 2:
Step 3:
Step 4:
Step 5:
Exercise 7.4.6
(Solution on p. 468.)
The rate of passing grades to failing grades in a particular chemistry class is 7 . If there are 21
2
passing grades, how many failing grades are there?
Step 1:
Step 2:
Step 3:
Step 4:
Step 5:
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 7. RATIOS AND RATES
7.4.4 Exercises
For the following 20 problems, use the ve-step method to solve each problem.
Exercise 7.4.7
(Solution on p. 468.)
On a map, 4 inches represents 50 miles. How many inches represent 300 miles?
Exercise 7.4.8
On a blueprint for a house, 2 inches represents 3 feet. How many inches represent 10 feet?
Exercise 7.4.9
(Solution on p. 468.)
A model is built to 215 scale. If a particular part of the model measures 6 inches, how long is the actual structure?
Exercise 7.4.10
An acid solution is composed of 5 parts acid to 9 parts of water. How many parts of acid are there in a solution that contains 108 parts of water?
Exercise 7.4.11
(Solution on p. 468.)
An alloy contains 3 parts of nickel to 4 parts of silver. How much nickel is in an alloy that contains 44 parts of silver?
Exercise 7.4.12
The ratio of water to salt in a test tube is 5 to 2. How much salt is in a test tube that contains 35
ml of water?
Exercise 7.4.13
(Solution on p. 469.)
The ratio of sulfur to air in a container is 445. How many ml of air are there in a container that contains 207 ml of sulfur?
Exercise 7.4.14
A 6-foot man casts a 4-foot shadow at a particular time of the day. How tall is a person that casts a 3-foot shadow at that same time of the day?
Exercise 7.4.15
(Solution on p. 469.)
A 51-foot woman casts a 11-foot shadow at a particular time of the day. How long a shadow does 2
2
her 31-foot niece cast at the same time of the day?
2
Exercise 7.4.16
A man, who is 6 feet tall, casts a 7-foot shadow at a particular time of the day. How tall is a tree that casts an 84-foot shadow at that same time of the day?
Exercise 7.4.17
(Solution on p. 469.)
The ratio of books to shelves in a bookstore is 350 to 3. How many books are there in a store that has 105 shelves?
Exercise 7.4.18
The ratio of algebra classes to geometry classes at a particular community college is 13 to 2. How many geometry classes does this college oer if it oers 13 algebra classes?
Exercise 7.4.19
(Solution on p. 469.)
The odds for a particular event to occur are 16 to 3. If this event occurs 64 times, how many times would you predict it does not occur?
Exercise 7.4.20
The odds against a particular event occurring are 8 to 3. If this event does occur 64 times, how many times would you predict it does not occur?
Exercise 7.4.21
(Solution on p. 469.)
The owner of a stationery store knows that a 1-inch stack of paper contains 300 sheets. The owner wishes to stack the paper in units of 550 sheets. How many inches tall should each stack be?
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 7.4.22
A recipe that requires 6 cups of sugar for 15 servings is to be used to make 45 servings. How much sugar will be needed?
Exercise 7.4.23
(Solution on p. 469.)
A pond loses 71 gallons of water every 2 days due to evaporation. How many gallons of water are 2
lost, due to evaporation, in 1 day?
2
Exercise 7.4.24
A photograph that measures 3 inches wide and 41 inches high is to be enlarged so that it is 5
2
inches wide. How high will it be?
Exercise 7.4.25
(Solution on p. 469.)
If 25 pounds of fertilizer covers 400 square feet of grass, how many pounds will it take to cover 500
square feet of grass?
Exercise 7.4.26
Every 11 teaspoons of a particular multiple vitamin, in granular form, contains 0.65 the minimum 2
daily requirement of vitamin C. How many teaspoons of this vitamin are required to supply 1.25
the minimum daily requirement?
7.4.4.1 Exercises for Review
Exercise 7.4.27
(Solution on p. 469.)
(Section 2.2) Find the product, 818 · 0.
Exercise 7.4.28
(Section 4.4) Determine the missing numerator: 815 = N90.
Exercise 7.4.29
(Solution on p. 469.)
(Section 5.6) Find the value of 3 + 4
10
12
19
.
20
Exercise 7.4.30
(Section 6.5) Subtract 0.249 from the sum of 0.344 and 0.612.
Exercise 7.4.31
(Solution on p. 469.)
(Section 7.3) Solve the proportion: 6 = 36
x
30 .
7.5 Percent5
7.5.1 Section Overview
• Ratios and Percents
• The Relationship Between Fractions, Decimals, and Percents Making Conversions 5This content is available online at <http://cnx.org/content/m34983/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 7. RATIOS AND RATES
7.5.2 Ratios and Percents
Ratio, Percent
We dened a ratio as a comparison, by division, of two pure numbers or two like denominate numbers. A most convenient number to compare numbers to is 100. Ratios in which one number is compared to 100 are called percents. The word percent comes from the Latin word “per centum.” The word “per” means “for each” or “for every,” and the word “centum” means “hundred.” Thus, we have the following denition.
Percent means for each hundred,” or “for every hundred.”
The symbol % is used to represent the word percent.
7.5.2.1 Sample Set A
Example 7.22
The ratio 26 to 100 can be written as 26%. We read 26% as “twenty-six percent.”
Example 7.23
The ratio 165
100 can be written as 165%.
We read 165% as “one hundred sixty-ve percent.”
Example 7.24
The percent 38% can be written as the fraction 38
100 .
Example 7.25
The percent 210% can be written as the fraction 210
100 or the mixed number 2 10
100 or 2.1.
Example 7.26
Since one dollar is 100 cents, 25 cents is 25
100 of a dollar. This implies that 25 cents is 25% of one
dollar.
7.5.2.2 Practice Set A
Exercise 7.5.1
(Solution on p. 469.)
Write the ratio 16 to 100 as a percent.
Exercise 7.5.2
(Solution on p. 469.)
Write the ratio 195 to 100 as a percent.
Exercise 7.5.3
(Solution on p. 469.)
Write the percent 83% as a ratio in fractional form.
Exercise 7.5.4
(Solution on p. 469.)
Write the percent 362% as a ratio in fractional form.
7.5.3 The Relationship Between Fractions, Decimals, and Percents Making Conversions
Since a percent is a ratio, and a ratio can be written as a fraction, and a fraction can be written as a decimal, any of these forms can be converted to any other.
Before we proceed to the problems in Section 7.5.3.1 (Sample Set B) and Section 7.5.3.2 (Practice Set B), let’s summarize the conversion techniques.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Conversion Techniques Fractions, Decimals, Percents
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
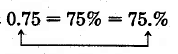
440
CHAPTER 7. RATIOS AND RATES
To Convert a Fraction
To Convert a Decimal
To Convert a Percent
To a decimal: Divide the numer- To a fraction: Read the decimal To a decimal: Move the decimal ator by the denominator
and reduce the resulting fraction
point 2 places to the left and drop
the % symbol
To a percent: Convert the frac- To a percent: Move the decimal To a fraction: Drop the % sign tion rst to a decimal, then move point 2 places to the right and af- and write the number over 100.
the decimal point 2 places to the x the % symbol
Reduce, if possible.
right and ax the % symbol.
Table 7.1
7.5.3.1 Sample Set B
Example 7.27
Convert 12% to a decimal.
12% = 12
100 = 0.12
Note that
The % symbol is dropped, and the decimal point moves 2 places to the left.
Example 7.28
Convert 0.75 to a percent.
0.75 = 75
100 = 75%
Note that
The % symbol is axed, and the decimal point moves 2 units to the right.
Example 7.29
Convert 3 to a percent.
5
We see in Example 7.28 that we can convert a decimal to a percent. We also know that we can convert a fraction to a decimal. Thus, we can see that if we rst convert the fraction to a decimal, we can then convert the decimal to a percent.
.6
5)3.0
3 →
or 3 = 0.6 = 6
5
5
10 = 60
100 = 60%
3 0
0
Example 7.30
Convert 42% to a fraction.
42% = 42
100 = 21
50
or
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
42% = 0.42 = 42
100 = 21
50
7.5.3.2 Practice Set B
Exercise 7.5.5
(Solution on p. 469.)
Convert 21% to a decimal.
Exercise 7.5.6
(Solution on p. 469.)
Convert 461% to a decimal.
Exercise 7.5.7
(Solution on p. 469.)
Convert 0.55 to a percent.
Exercise 7.5.8
(Solution on p. 469.)
Convert 5.64 to a percent.
Exercise 7.5.9
(Solution on p. 469.)
Convert 320 to a percent.
Exercise 7.5.10
(Solution on p. 469.)
Convert 11 to a percent
8
Exercise 7.5.11
(Solution on p. 469.)
Convert 311 to a percent.
7.5.4 Exercises
For the following 12 problems, convert each decimal to a percent.
Exercise 7.5.12
(Solution on p. 469.)
0.25
Exercise 7.5.13
0.36
Exercise 7.5.14
(Solution on p. 469.)
0.48
Exercise 7.5.15
0.343
Exercise 7.5.16
(Solution on p. 469.)
0.771
Exercise 7.5.17
1.42
Exercise 7.5.18
(Solution on p. 469.)
2.58
Exercise 7.5.19
4.976
Exercise 7.5.20
(Solution on p. 470.)
16.1814
Exercise 7.5.21
533.01
Exercise 7.5.22
(Solution on p. 470.)
2
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 7. RATIOS AND RATES
Exercise 7.5.23
14
For the following 10 problems, convert each percent to a decimal.