126 Fundamentals of Mathematics: Part 8
2
Solution to Exercise 4.5.9 (p. 246)
5
18
Solution to Exercise 4.5.10 (p. 248)
7
12
Solution to Exercise 4.5.11 (p. 248)
25
54
Solution to Exercise 4.5.12 (p. 248)
2
3
Solution to Exercise 4.5.13 (p. 248)
2
7
Solution to Exercise 4.5.14 (p. 248)
9
2
Solution to Exercise 4.5.15 (p. 248)
1
Available for free at Connexions <http://cnx.org/content/col10615/1.4>


285
Solution to Exercise 4.5.16 (p. 248)
14
5
Solution to Exercise 4.5.17 (p. 249)
6Solution to Exercise 4.5.18 (p. 249)
22
Solution to Exercise 4.5.19 (p. 249)
8512
Solution to Exercise 4.5.20 (p. 249)
30
Solution to Exercise 4.5.21 (p. 250)
1
64
Solution to Exercise 4.5.22 (p. 250)
9
100
Solution to Exercise 4.5.23 (p. 250)
2
3
Solution to Exercise 4.5.24 (p. 250)
1
2
Solution to Exercise 4.5.25 (p. 250)
1
8
Solution to Exercise 4.5.26 (p. 250)
8 25
Solution to Exercise 4.5.27 (p. 250)
8 12
Solution to Exercise 4.5.28 (p. 250)
1
4
Solution to Exercise 4.5.30 (p. 251)
1
4
Solution to Exercise 4.5.32 (p. 251)
1
64
Solution to Exercise 4.5.34 (p. 251)
2
5
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
Solution to Exercise 4.5.36 (p. 251)
2
9
Solution to Exercise 4.5.38 (p. 252)
4
15
Solution to Exercise 4.5.40 (p. 252)
3
5
Solution to Exercise 4.5.42 (p. 252)
2
Solution to Exercise 4.5.44 (p. 252)
10 or 31
3
3
Solution to Exercise 4.5.46 (p. 252)
52
Solution to Exercise 4.5.48 (p. 252)
4
9
Solution to Exercise 4.5.50 (p. 252)
1
24
Solution to Exercise 4.5.52 (p. 252)
126
Solution to Exercise 4.5.54 (p. 252)
1
4
Solution to Exercise 4.5.56 (p. 252)
1
3
Solution to Exercise 4.5.58 (p. 252)
7
9
Solution to Exercise 4.5.60 (p. 253)
1Solution to Exercise 4.5.62 (p. 253)
28
33
Solution to Exercise 4.5.64 (p. 253)
4
3
Solution to Exercise 4.5.66 (p. 253)
12
Solution to Exercise 4.5.68 (p. 253)
7 13
21 or 160
21
Solution to Exercise 4.5.70 (p. 253)
12
Solution to Exercise 4.5.72 (p. 253)
18
Solution to Exercise 4.5.74 (p. 253)
25 or 81
3
3
Solution to Exercise 4.5.76 (p. 253)
15 =17
8
8
Solution to Exercise 4.5.78 (p. 253)
6Solution to Exercise 4.5.80 (p. 253)
10 =11
9
9
Solution to Exercise 4.5.82 (p. 253)
9 =41
2
2
Solution to Exercise 4.5.84 (p. 254)
85 =141
6
6
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 4.5.86 (p. 254)
72
Solution to Exercise 4.5.88 (p. 254)
4
9
Solution to Exercise 4.5.90 (p. 254)
4
121
Solution to Exercise 4.5.92 (p. 254)
1
4
Solution to Exercise 4.5.94 (p. 254)
1
15
Solution to Exercise 4.5.96 (p. 254)
1
25
Solution to Exercise 4.5.98 (p. 254)
2
3
Solution to Exercise 4.5.100 (p. 254)
9
11
Solution to Exercise 4.5.102 (p. 254)
12 = 22
5
5
Solution to Exercise 4.5.104 (p. 255)
1
3
Solution to Exercise 4.5.106 (p. 255)
7
8
Solution to Exercise 4.5.108 (p. 255)
2Solution to Exercise 4.5.110 (p. 255)
yes
Solution to Exercise 4.5.112 (p. 255)
6
25
Solution to Exercise 4.6.1 (p. 256)
10
3
Solution to Exercise 4.6.2 (p. 256)
3
2
Solution to Exercise 4.6.3 (p. 256)
8
7
Solution to Exercise 4.6.4 (p. 256)
5Solution to Exercise 4.6.5 (p. 256)
7
16
Solution to Exercise 4.6.6 (p. 256)
4
21
Solution to Exercise 4.6.7 (p. 256)
16
163
Solution to Exercise 4.6.8 (p. 258)
4
9
Solution to Exercise 4.6.9 (p. 258)
1Solution to Exercise 4.6.10 (p. 258)
1
2
Solution to Exercise 4.6.11 (p. 258)
15
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
Solution to Exercise 4.6.12 (p. 258)
15
Solution to Exercise 4.6.13 (p. 259)
2Solution to Exercise 4.6.14 (p. 259)
2
5
Solution to Exercise 4.6.15 (p. 259)
16 glasses
Solution to Exercise 4.6.16 (p. 259)
3
2
Solution to Exercise 4.6.17 (p. 259)
8
3
Solution to Exercise 4.6.18 (p. 259)
4
3
Solution to Exercise 4.6.19 (p. 259)
2
5
Solution to Exercise 4.6.20 (p. 259)
is the reciprocal of the fraction.
Solution to Exercise 4.6.21 (p. 259)
5 or 11
4
4
Solution to Exercise 4.6.23 (p. 259)
9 or 41
2
2
Solution to Exercise 4.6.25 (p. 259)
4
13
Solution to Exercise 4.6.27 (p. 259)
7
23
Solution to Exercise 4.6.29 (p. 259)
1Solution to Exercise 4.6.31 (p. 259)
5
8
Solution to Exercise 4.6.33 (p. 260)
3
10
Solution to Exercise 4.6.35 (p. 260)
225
196 or 1 29
196
Solution to Exercise 4.6.37 (p. 260)
3
5
Solution to Exercise 4.6.39 (p. 260)
1Solution to Exercise 4.6.41 (p. 260)
1Solution to Exercise 4.6.43 (p. 260)
49
100
Solution to Exercise 4.6.45 (p. 260)
3
5
Solution to Exercise 4.6.47 (p. 260)
6
7
Solution to Exercise 4.6.49 (p. 260)
85 or 141
6
6
Solution to Exercise 4.6.51 (p. 260)
28
18 = 14 or 1 5
9
9
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 4.6.53 (p. 260)
10
Solution to Exercise 4.6.55 (p. 261)
10 or 31
3
3
Solution to Exercise 4.6.57 (p. 261)
4
21
Solution to Exercise 4.6.59 (p. 261)
3 or 11
2
2
Solution to Exercise 4.6.61 (p. 261)
4
5
Solution to Exercise 4.6.63 (p. 261)
3Solution to Exercise 4.6.65 (p. 261)
1Solution to Exercise 4.6.67 (p. 261)
321,600
Solution to Exercise 4.6.69 (p. 261)
144
Solution to Exercise 4.7.1 (p. 263)
2
5
Solution to Exercise 4.7.2 (p. 263)
3
4
Solution to Exercise 4.7.3 (p. 263)
1
6
Solution to Exercise 4.7.4 (p. 265)
3
4
Solution to Exercise 4.7.5 (p. 265)
16
27
Solution to Exercise 4.7.6 (p. 265)
1 12
Solution to Exercise 4.7.7 (p. 265)
1 12
Solution to Exercise 4.7.8 (p. 265)
1
2
Solution to Exercise 4.7.10 (p. 265)
1
3
Solution to Exercise 4.7.12 (p. 265)
9 or 11
8
8
Solution to Exercise 4.7.14 (p. 265)
1
16
Solution to Exercise 4.7.16 (p. 265)
3
4
Solution to Exercise 4.7.18 (p. 265)
1
1,000
Solution to Exercise 4.7.20 (p. 265)
10
27
Solution to Exercise 4.7.22 (p. 265)
1
2
Solution to Exercise 4.7.24 (p. 266)
2
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
Solution to Exercise 4.7.26 (p. 266)
1
6
Solution to Exercise 4.7.28 (p. 266)
2
3
Solution to Exercise 4.7.30 (p. 266)
1Solution to Exercise 4.7.32 (p. 266)
1Solution to Exercise 4.7.34 (p. 266)
3 or 12
2
3
Solution to Exercise 4.7.36 (p. 266)
3Solution to Exercise 4.7.38 (p. 266)
5 or 12
3
3
Solution to Exercise 4.7.40 (p. 266)
27
40
Solution to Exercise 4.7.42 (p. 266)
1
15
Solution to Exercise 4.7.44 (p. 266)
3
8
Solution to Exercise 4.7.46 (p. 267)
9
10
Solution to Exercise 4.7.48 (p. 267)
9 = 4 1
2
2
Solution to Exercise 4.7.50 (p. 267)
16
11 or 1 5
11
Solution to Exercise 4.7.52 (p. 267)
30
77
Solution to Exercise 4.7.54 (p. 267)
no
Solution to Exercise 4.7.56 (p. 267)
41
12
Solution to Exercise 4.9.1 (p. 270)
2 or 1
6
3
Solution to Exercise 4.9.3 (p. 270)
numerator, 4; denominator, 5
Solution to Exercise 4.9.5 (p. 271)
numerator, 1; denominator, 3
Solution to Exercise 4.9.7 (p. 271)
8
11
Solution to Exercise 4.9.9 (p. 271)
200
6,000
Solution to Exercise 4.9.11 (p. 271)
ten seventeenths
Solution to Exercise 4.9.13 (p. 271)
six hundred six, one thousand four hundred thirty-rsts
Solution to Exercise 4.9.15 (p. 271)
one sixteenth
Solution to Exercise 4.9.17 (p. 271)
numerator, 56; denominator, 14,190
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
291
Solution to Exercise 4.9.19 (p. 271)
Solution to Exercise 4.9.21 (p. 272)
2 34
Solution to Exercise 4.9.23 (p. 272)
6 38
Solution to Exercise 4.9.25 (p. 272)
11823
Solution to Exercise 4.9.27 (p. 272)
1 14
Solution to Exercise 4.9.29 (p. 272)
3Solution to Exercise 4.9.31 (p. 272)
129
8
Solution to Exercise 4.9.33 (p. 272)
16
5
Solution to Exercise 4.9.35 (p. 272)
377
21
Solution to Exercise 4.9.37 (p. 272)
3
2
Solution to Exercise 4.9.39 (p. 273)
62
7
Solution to Exercise 4.9.41 (p. 273)
because the whole number part is zero
Solution to Exercise 4.9.43 (p. 273)
equivalent
Solution to Exercise 4.9.45 (p. 273)
not equivalent
Solution to Exercise 4.9.47 (p. 273)
not equivalent
Solution to Exercise 4.9.49 (p. 273)
8
11
Solution to Exercise 4.9.51 (p. 273)
5
11
Solution to Exercise 4.9.53 (p. 273)
3
5
Solution to Exercise 4.9.55 (p. 273)
9
17
Solution to Exercise 4.9.57 (p. 273)
35
68
Solution to Exercise 4.9.59 (p. 274)
65
162
Solution to Exercise 4.9.61 (p. 274)
15
Solution to Exercise 4.9.63 (p. 274)
6Solution to Exercise 4.9.65 (p. 274)
27
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
292
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
Solution to Exercise 4.9.67 (p. 274)
42
Solution to Exercise 4.9.69 (p. 274)
168
Solution to Exercise 4.9.71 (p. 274)
192
Solution to Exercise 4.9.73 (p. 274)
3
4
Solution to Exercise 4.9.75 (p. 274)
1
24
Solution to Exercise 4.9.77 (p. 274)
5
36
Solution to Exercise 4.9.79 (p. 275)
1Solution to Exercise 4.9.81 (p. 275)
1
48
Solution to Exercise 4.9.83 (p. 275)
4
35
Solution to Exercise 4.9.85 (p. 275)
50 = 71
7
7
Solution to Exercise 4.9.87 (p. 275)
2Solution to Exercise 4.9.89 (p. 275)
3Solution to Exercise 4.9.91 (p. 275)
1
2
Solution to Exercise 4.9.93 (p. 275)
90
Solution to Exercise 4.9.95 (p. 275)
1Solution to Exercise 4.9.97 (p. 276)
7 or 31
2
2
Solution to Exercise 4.9.99 (p. 276)
4Solution to Exercise 4.9.101 (p. 276)
12
13
Solution to Exercise 4.9.103 (p. 276)
4Solution to Exercise 4.9.105 (p. 276)
11
12
Solution to Exercise 4.10.1 (p. 276)
Solution to Exercise 4.10.2 (p. 276)
Numerator, 5; denominator, 9
Solution to Exercise 4.10.3 (p. 276)
5
11
Solution to Exercise 4.10.4 (p. 276)
Four fths
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 4.10.5 (p. 276)
5
12
Solution to Exercise 4.10.6 (p. 276)
25
7
Solution to Exercise 4.10.7 (p. 276)
3 15
Solution to Exercise 4.10.8 (p. 277)
yes
Solution to Exercise 4.10.9 (p. 277)
3
5
Solution to Exercise 4.10.10 (p. 277)
5
17
Solution to Exercise 4.10.11 (p. 277)
13
60
Solution to Exercise 4.10.12 (p. 277)
20
Solution to Exercise 4.10.13 (p. 277)
24
Solution to Exercise 4.10.14 (p. 277)
3
20
Solution to Exercise 4.10.15 (p. 277)
55
Solution to Exercise 4.10.16 (p. 277)
5
6
Solution to Exercise 4.10.17 (p. 277)
3
4
Solution to Exercise 4.10.18 (p. 277)
1
2
Solution to Exercise 4.10.19 (p. 277)
1
30
Solution to Exercise 4.10.20 (p. 277)
1
11
Solution to Exercise 4.10.21 (p. 277)
36
25 = 1 11
25
Solution to Exercise 4.10.22 (p. 277)
2
5
Solution to Exercise 4.10.23 (p. 277)
1
4
Solution to Exercise 4.10.24 (p. 277)
9 = 1 4
5
5
Solution to Exercise 4.10.25 (p. 277)
4
or 11
3
3
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Addition and Subtraction of Fractions,
Comparing Fractions, and Complex
Fractions
5.1 Objectives1
After completing this chapter, you should
Addition and Subtraction of Fractions with Like Denominators (Section 5.2)
• be able to add and subtract fractions with like denominators
Addition and Subtraction of Fractions with Unlike Denominators (Section 5.3)
• be able to add and subtract fractions with unlike denominators
Addition and Subtraction of Mixed Numbers (Section 5.4)
• be able to add and subtract mixed numbers
Comparing Fractions (Section 5.5)
• understand ordering of numbers and be familiar with grouping symbols
• be able to compare two or more fractions
Complex Fractions (Section 5.6)
• be able to distinguish between simple and complex fractions
• be able to convert a complex fraction to a simple fraction
Combinations of Operations with Fractions (Section 5.7)
• gain a further understanding of the order of operations
1This content is available online at <http://cnx.org/content/m18893/1.3/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4> 295
296
CHAPTER 5. ADDITION AND SUBTRACTION OF FRACTIONS,
COMPARING FRACTIONS, AND COMPLEX FRACTIONS
5.2 Addition and Subtraction of Fractions with Like Denominators2
5.2.1 Section Overview
• Addition of Fraction With Like Denominators
• Subtraction of Fractions With Like Denominators
5.2.2 Addition of Fraction With Like Denominators
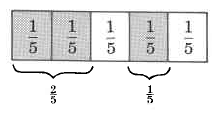
Let’s examine the following diagram.
2 one-fths and 1 one fth is shaded.
It is shown in the shaded regions of the diagram that
(2 one-fths) + (1 one-fth) = (3 one-fths)
That is,
2 + 1 = 3
5
5
5
From this observation, we can suggest the following rule.
Method of Adding Fractions Having Like Denominators
To add two or more fractions that have the same denominators, add the numerators and place the resulting sum over the common denominator. Reduce, if necessary.
5.2.2.1 Sample Set A
Find the following sums.
Example 5.1
3 + 2 . The denominators are the same. Add the numerators and place that sum over 7.
7
7
3 + 2 = 3+2 = 5
7
7
7
7
Example 5.2
1 + 3 . The denominators are the same. Add the numerators and place the sum over 8. Reduce.
8
8
1 + 3 = 1+3 = 4 = 1
8
8
8
8
2
Example 5.3
4 + 5 . The denominators are the same. Add the numerators and place the sum over 9.
9
9
4 + 5 = 4+5 = 9 = 1
9
9
9
9
Example 5.4
7 + 5 . The denominators are the same. Add the numerators and place the sum over 8.
8
8
7 + 5 = 7+5 = 12 = 3
8
8
8
8
2
2This content is available online at <http://cnx.org/content/m34934/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
297
Example 5.5
To see what happens if we mistakenly add the denominators as well as the numerators, let’s add 1 + 1
2
2
Adding the numerators and mistakenly adding the denominators produces
1 + 1 = 1+1 = 2 = 1
2
2
2+2
4
2
This means that two 1’s is the same as one 1. Preposterous! We do not add denominators.
2
2
5.2.2.2 Practice Set A
Find the following sums.
Exercise 5.2.1
(Solution on p. 329.)
1
10 + 3
10
Exercise 5.2.2
(Solution on p. 329.)
1 + 1
4
4
Exercise 5.2.3
(Solution on p. 329.)
7
11 + 4
11
Exercise 5.2.4
(Solution on p. 329.)
3 + 1
5
5
Exercise 5.2.5
(Solution on p. 329.)
Show why adding both the numerators and denominators is preposterous by adding 3 and 3 and 4
4
examining the result.
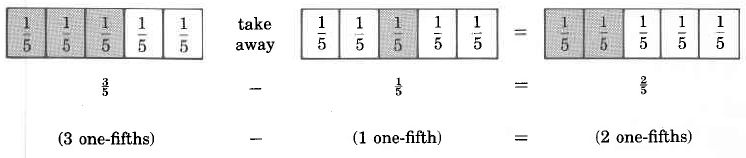
5.2.3 Subtraction of Fractions With Like Denominators
We can picture the concept of subtraction of fractions in much the same way we pictured addition.
From this observation, we can suggest the following rule for subtracting fractions having like denominators: Subtraction of Fractions with Like Denominators
To subtract two fractions that have like denominators, subtract the numerators and place the resulting dierence over the common denominator. Reduce, if possible.
5.2.3.1 Sample Set B
Find the following dierences.
Example 5.6
3 − 1 . The denominators are the same. Subtract the numerators. Place the dierence over 5.
5
5
3 − 1 = 3−1 = 2
5
5
5
5
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 5. ADDITION AND SUBTRACTION OF FRACTIONS,
COMPARING FRACTIONS, AND COMPLEX FRACTIONS
Example 5.7
8 − 2 . The denominators are the same. Subtract the numerators. Place the dierence over 6.
6
6
8 − 2 = 8−2 = 6 = 1
6
6
6
6
Example 5.8
16 − 2. The denominators are the same. Subtract numerators and place the dierence over 9.
9
9
16 − 2 = 16−2 = 14
9
9
9
9
Example 5.9
To see what happens if we mistakenly subtract the denominators, let’s consider 7
15 − 4
15 = 7−4
15−15 = 30
We get division by zero, which is undened. We do not subtract denominators.
5.2.3.2 Practice Set B
Find the following dierences.
Exercise 5.2.6
(Solution on p. 329.)
10
13 − 8
13
Exercise 5.2.7
(Solution on p. 329.)
5
12 − 1
12
Exercise 5.2.8
(Solution on p. 329.)
1 − 1
2
2
Exercise 5.2.9
(Solution on p. 329.)
26
10 − 14
10
Exercise 5.2.10
(Solution on p. 329.)
Show why subtracting both the numerators and the denominators is in error by performing the subtraction 5 − 2.
9
9
5.2.4 Exercises
For the following problems, nd the sums and dierences. Be sure to reduce.
Exercise 5.2.11
(Solution on p. 329.)
3 + 2
8
8
Exercise 5.2.12
1 + 2
6
6
Exercise 5.2.13
(Solution on p. 329.)
9
10 + 1
10
Exercise 5.2.14
3
11 + 4
11
Exercise 5.2.15
(Solution on p. 329.)
9
15 + 4
15
Exercise 5.2.16
3
10 + 2
10
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 5.2.17
(Solution on p. 329.)
5
12 + 7
12
Exercise 5.2.18
11
16 − 2
16
Exercise 5.2.19
(Solution on p. 329.)
3
16 − 3
16
Exercise 5.2.20
15
23 − 2
23
Exercise 5.2.21
(Solution on p. 329.)
1 − 1
6
6
Exercise 5.2.22
1 + 1 + 1
4
4
4
Exercise 5.2.23
(Solution on p. 329.)
3
11 + 1
11 + 5
11
Exercise 5.2.24
16
20 + 1
20 + 2
20
Exercise 5.2.25
(Solution on p. 329.)
12 + 2 + 1
8
8
8
Exercise 5.2.26
1
15 + 8
15 + 6
15
Exercise 5.2.27
(Solution on p. 329.)
3 + 2
8
8 − 18
Exercise 5.2.28
11
16 + 9
16 − 5
16
Exercise 5.2.29
(Solution on p. 329.)
4
20 − 1
20 + 9
20
Exercise 5.2.30
7
10 − 3
10 + 11
10
Exercise 5.2.31
(Solution on p. 329.)
16 − 1 − 2
5
5
5
Exercise 5.2.32
21
35 − 17
35 + 31
35
Exercise 5.2.33
(Solution on p. 329.)
5 + 16 − 1
2
2
2
Exercise 5.2.34
1
18 + 3
18 + 1
18 + 4
18 − 5
18
Exercise 5.2.35
(Solution on p. 329.)
6
22 − 2
22 + 4
22 − 1
22 + 11
22
The following rule for addition and subtraction of two fractions is preposterous. Show why by performing the operations using the rule for the following two problems.
Preposterous Rule
To add or subtract two fractions, simply add or subtract the numerators and place this result over the sum or dierence of the denominators.
Exercise 5.2.36
3
10 − 3
10
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
300
CHAPTER 5. ADDITION AND SUBTRACTION OF FRACTIONS,
COMPARING FRACTIONS, AND COMPLEX FRACTIONS
Exercise 5.2.37
(Solution on p. 329.)
8
15 + 8
15
Exercise 5.2.38
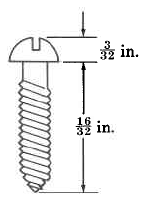
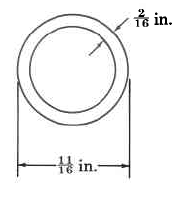
Find the total length of the screw.
Exercise 5.2.39
(Solution on p. 329.)
Two months ago, a woman paid o 324 of a loan. One month ago, she paid o 524 of the total loan.
This month she will again pay o 524 of the total loan. At the end of the month, how much of her total loan will she have paid o?
Exercise 5.2.40
Find the inside diameter of the pipe.
5.2.4.1 Exercises for Review
Exercise 5.2.41
(Solution on p. 329.)
(Section 1.4) Round 2,650 to the nearest hundred.
Exercise 5.2.42
(Section 2.6) Use the numbers 2, 4, and 8 to illustrate the associative property of addition.
Exercise 5.2.43
(Solution on p. 330.)
(Section 3.4) Find the prime factors of 495.
Exercise 5.2.44
(Section 4.5) Find the value of 3 · 16
.
4
25 · 59
Exercise 5.2.45
(Solution on p. 330.)
(Section 4.7) 8 of what number is 17?
3
9
5.3 Addition and Subtraction of Fractions with Unlike Denominators3
5.3.1 Section Overview
• A Basic Rule
• Addition and Subtraction of Fractions
3This content is available online at <http://cnx.org/content/m34935/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
5.3.2 A Basic Rule
There is a basic rule that must be followed when adding or subtracting fractions.
A Basic Rule
Fractions can only be added or subtracted conveniently if they have like denominators.
To see why this rule makes sense, let’s consider the problem of adding a quarter and a dime.
1 quarter + 1 dime = 35 cents
Now,
1 quarter = 25
100 } same denominations
1 dime = 10
100
35, = 35
100
25
100 + 10
100 = 25+10
100 = 35
100
In order to combine a quarter and a dime to produce 35¢, we convert them to quantities of the same denomination.
Same denomination → same denominator
5.3.3 Addition and Subtraction of Fractions
Least Common Multiple (LCM) and Least Common Denominator (LCD)
In Section 3.6, we examined the least common multiple (LCM) of a collection of numbers. If these numbers are used as denominators of fractions, we call the least common multiple, the least common denominator (LCD).
Method of Adding or Subtracting Fractions with Unlike Denominators
To add or subtract fractions having unlike denominators, convert each fraction to an equivalent fraction having as a denominator the least common denominator ( LCD) of the original denominators.
5.3.3.1 Sample Set A
Find the following sums and dierences.
Example 5.10
1 + 3 . The denominators are not the same. Find the LCD of 6 and 4.
6
4
6 = 2 ·3}The LCD = 22 · 3 = 4 · 3 = 12
4 = 22
Write each of the original fractions as a new, equivalent fraction having the common denominator 12.
1 + 3 =
6
4
12 + 12
To nd a new numerator, we divide the original denominator into the LCD. Since the original denominator is being multiplied by this quotient, we must multiply the original numerator by this quotient.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

302
CHAPTER 5. ADDITION AND SUBTRACTION OF FRACTIONS,
COMPARING FRACTIONS, AND COMPLEX FRACTIONS
12 ÷ 6 = 2
12 ÷ 4 = 3
1 + 3
=
1·2
6
4
12 + 3·3
12
=
2
12 + 9
12
Now the denominators are the same.
=
2+9
12
Add the numerators and place the sum over the common denominator.
=
11
12
Example 5.11
1 + 2 . The denominators are not the same. Find the LCD of 2 and 3.
2
3
LCD = 2 · 3 = 6
Write each of the original fractions as a new, equivalent fraction having the common denominator 6.
1 + 2 =
+
2
3
6
6
To nd a new numerator, we divide the original denominator into the LCD. Since the original denominator is being multiplied by this quotient, we must multiply the original numerator by this quotient.
6 ÷ 2 = 3 Multiply the numerator 1 by 3.
6 ÷ 2 = 3 Multiply the numerator 2 by 2.
1 + 2
=
1·3 + 2·3
2
3
6
6
=
3 + 4
6
6
=
3+4
6
=
7 or 11
6
6
Example 5.12
5 − 5
9
12 . The denominators are not the same. Find the LCD of 9 and 12.
9 = 3 · 3 = 32
}
LCD = 22 · 32 = 4 · 9 = 36
12 = 2 · 6 = 2 · 2 · 3 = 22 · 3
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
5 − 5
9
12 = 36 − 36
36 ÷ 9 = 4 Multiply the numerator 5 by 4.
36 ÷ 12 = 3 Multiply the numerator 5 by 3.
5 − 5
9
12
=
5·4
36 − 5·3
36
=
20
36 − 15
36
=
20−15
36
=
5
36
Example 5.13
5 − 1 + 7
6
8
16 The denominators are not the same. Find the LCD of 6, 8, and 16
6
=
2 · 3
8
=
2 · 4 = 2 · 2 · 2 = 23
} The LCD is 24 · 3 = 48
16 = 2 · 8 = 2 · 2 · 4 = 2 · 2 · 2 · 2 = 24
5 − 1 + 7
6
8
16 = 48 − 48 + 48
48 ÷ 6 = 8 Multiply the numerator 5 by 8
48 ÷ 8 = 6 Multiply the numerator 1 by 6
48 ÷ 16 = 3 Multiply the numerator 7 by 3
5 − 1 + 7
6
8
16
=
5·8
48 − 1·6
48 + 7·3
48
=
40
48 − 6
48 + 21
48
=
40−6+21
48
=
55
48 or 1 7
48
5.3.3.2 Practice Set A
Find the following sums and dierences.
Exercise 5.3.1
(Solution on p. 330.)
3 + 1
4
12
Exercise 5.3.2
(Solution on p. 330.)
1 − 3
2
7
Exercise 5.3.3
(Solution on p. 330.)
7
10 − 58
Exercise 5.3.4
(Solution on p. 330.)
15
16 + 1 − 3
2
4
Exercise 5.3.5
(Solution on p. 330.)
1
32 − 1
48
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 5. ADDITION AND SUBTRACTION OF FRACTIONS,
COMPARING FRACTIONS, AND COMPLEX FRACTIONS
5.3.4 Exercises
Exercise 5.3.6
(Solution on p. 330.)
A most basic rule of arithmetic states that two fractions may be added or subtracted conveniently only if they have
.
For the following problems, nd the sums and dierences.
Exercise 5.3.7
1 + 1
2
6
Exercise 5.3.8
(Solution on p. 330.)
1 + 1
8
2
Exercise 5.3.9
3 + 1
4
3
Exercise 5.3.10
(Solution on p. 330.)
5 + 2
8
3
Exercise 5.3.11
1
12 + 13
Exercise 5.3.12
(Solution on p. 330.)
6 − 1
7
4
Exercise 5.3.13
9
10 − 25
Exercise 5.3.14
(Solution on p. 330.)
7 − 1
9
4
Exercise 5.3.15
8
15 − 3
10
Exercise 5.3.16
(Solution on p. 330.)
8
13 − 5
39
Exercise 5.3.17
11
12 − 25
Exercise 5.3.18
(Solution on p. 330.)
1
15 + 5
12
Exercise 5.3.19
13
88 − 14
Exercise 5.3.20
(Solution on p. 330.)
1 − 1
9
81
Exercise 5.3.21
19
40 + 5
12
Exercise 5.3.22
(Solution on p. 330.)
25
26 − 7
10
Exercise 5.3.23
9
28 − 4
45
Exercise 5.3.24
(Solution on p. 330.)
22
45 − 16
35
Exercise 5.3.25
56
63 + 22
33
Exercise 5.3.26
(Solution on p. 330.)
1
16 + 3 − 3
4
8
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 5.3.27
5
12 − 1
120 + 19
20
Exercise 5.3.28
(Solution on p. 330.)
8 − 1 + 7
3
4
36
Exercise 5.3.29
11 − 1 + 16
9
7
63
Exercise 5.3.30
(Solution on p. 330.)
12 − 2 + 17
5
3
10
Exercise 5.3.31
4 + 13
9
21 − 9
14
Exercise 5.3.32
(Solution on p. 330.)
3 − 3
4
22 + 5
24
Exercise 5.3.33
25
48 − 7
88 + 5
24
Exercise 5.3.34
(Solution on p. 330.)
27
40 + 47
48 − 119
126
Exercise 5.3.35
41
44 − 5
99 − 11
175
Exercise 5.3.36
(Solution on p. 330.)
5
12 + 1
18 + 1
24
Exercise 5.3.37
5 + 1 + 7
9
6
15
Exercise 5.3.38
(Solution on p. 330.)
21
25 + 1 + 7
6
15
Exercise 5.3.39
5
18 − 1
36 + 79
Exercise 5.3.40
(Solution on p. 330.)
11
14 − 1
36 − 1
32
Exercise 5.3.41
21
33 + 12
22 + 15
55
Exercise 5.3.42
(Solution on p. 331.)
5
51 + 2
34 + 11
68
Exercise 5.3.43
8 − 16
7
14 + 19
21
Exercise 5.3.44
(Solution on p. 331.)
7
15 + 3
10 − 34
60
Exercise 5.3.45
14
15 − 3
10 − 6
25 + 7
20
Exercise 5.3.46
(Solution on p. 331.)
11 − 5
6
12 + 17
30 + 25
18
Exercise 5.3.47
1 + 22
9
21 − 5
18 − 1
45
Exercise 5.3.48
(Solution on p. 331.)
7
26 + 28
65 − 51
104 + 0
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 5. ADDITION AND SUBTRACTION OF FRACTIONS,
COMPARING FRACTIONS, AND COMPLEX FRACTIONS
Exercise 5.3.49
A morning trip from San Francisco to Los Angeles took 13
12 hours. The return trip took 57
60 hours.
How much longer did the morning trip take?
Exercise 5.3.50
(Solution on p. 331.)
At the beginning of the week, Starlight Publishing Company’s stock was selling for 115 dollars per 8
share. At the end of the week, analysts had noted that the stock had gone up 11 dollars per share.
4
What was the price of the stock, per share, at the end of the week?
Exercise 5.3.51
A recipe for fruit punch calls for 23 cups of pineapple juice, 1 cup of lemon juice, 15 cups of orange 3
4
2
juice, 2 cups of sugar, 6 cups of water, and 8 cups of carbonated non-cola soft drink. How many cups of ingredients will be in the nal mixture?
Exercise 5.3.52
(Solution on p. 331.)
The side of a particular type of box measures 83 inches in length. Is it possible to place three such 4
boxes next to each other on a shelf that is 261 inches in length? Why or why not?
5
Exercise 5.3.53
Four resistors, 3 ohm, 1 ohm, 3 ohm, and 7 ohm, are connected in series in an electrical circuit.
8
4
5
8
What is the total resistance in the circuit due to these resistors? (“In series” implies addition.) Exercise 5.3.54
(Solution on p. 331.)
A copper pipe has an inside diameter of 2 316 inches and an outside diameter of 2 534 inches. How thick is the pipe?
Exercise 5.3.55
The probability of an event was originally thought to be 15
32 . Additional information decreased the
probability by 314. What is the updated probability?
5.3.4.1 Exercises for Review
Exercise 5.3.56
(Solution on p. 331.)
(Section 1.6) Find the dierence between 867 and 418.
Exercise 5.3.57
(Section 2.5) Is 81,147 divisible by 3?
Exercise 5.3.58
(Solution on p. 331.)
(Section 3.6) Find the LCM of 11, 15, and 20.
Exercise 5.3.59
(Section 4.5) Find 3 of 42.
4
9
Exercise 5.3.60
(Solution on p. 331.)
(Section 5.2) Find the value of 815 − 315 + 215.
5.4 Addition and Subtraction of Mixed Numbers4
5.4.1 Section Overview
• The Method of Converting to Improper Fractions
To add or subtract mixed numbers, convert each mixed number to an improper fraction, then add or subtract the resulting improper fractions.
4This content is available online at <http://cnx.org/content/m34936/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
5.4.1.1 Sample Set A
Find the following sums and dierences.
Example 5.14
8 3 + 5 1 . Convert each mixed number to an improper fraction.
5
4
8 3 = 5·8+3 = 40+3 = 43
5
5
5
5
5 1 = 4·5+1 = 20+1 = 21 Now add the improper fractions 43 and 21 .
4
4
4
4
5
4
43 + 21 The LCD = 20.
5
4
43 + 21 = 43·4
5
4
20 + 21·5
20
=
172
20 + 105
20
=
172+105
20
=
277
20
Convert this improper fraction to a mixed number.
=
1317
20
Thus, 83 + 51 = 1317
5
4
20 .
Example 5.15
3 1 − 5 . Convert the mixed number to an improper fraction.
8
6
3 1 = 3·8+1 = 24+1 = 25
8
8
8
8
25 − 5 The LCD = 24.
8
6
25 − 5 = 25·3
8
6
24 − 5·4
24
=
75
24 − 20
24
=
75−20
24
=
55
24
Convert his improper fraction to a mixed number.
=
2 7
24
Thus, 31 − 5 = 2 7
8
6
24 .
5.4.1.2 Practice Set A
Find the following sums and dierences.
Exercise 5.4.1
(Solution on p. 331.)
1 5 + 3 2
9
9
Exercise 5.4.2
(Solution on p. 331.)
103 − 21
4
2
Exercise 5.4.3
(Solution on p. 331.)
2 7 + 5 1
8
4
Exercise 5.4.4
(Solution on p. 331.)
8 3 − 3
5
10
Exercise 5.4.5
(Solution on p. 331.)
16 + 2 916
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 5. ADDITION AND SUBTRACTION OF FRACTIONS,
COMPARING FRACTIONS, AND COMPLEX FRACTIONS
5.4.2 Exercises
For the following problems, perform each indicated operation.
Exercise 5.4.6
(Solution on p. 331.)
3 1 + 4 3
8
8
Exercise 5.4.7
5 1 + 6 1
3
3
Exercise 5.4.8
(Solution on p. 331.)
10 512 + 2 112
Exercise 5.4.9
151 − 113
5
5
Exercise 5.4.10
(Solution on p. 331.)
9 3
11 + 12 3
11
Exercise 5.4.11
1 1 + 3 2 + 8 1
6
6
6
Exercise 5.4.12
(Solution on p. 331.)
5 3 + 1 1 − 2 5
8
8
8
Exercise 5.4.13
3 + 5 1
5
5
Exercise 5.4.14
(Solution on p. 331.)
2 2 − 5
9
9
Exercise 5.4.15
6 + 11 23
Exercise 5.4.16
(Solution on p. 331.)
17 − 8 314
Exercise 5.4.17
5 1 + 2 1
3
4
Exercise 5.4.18
(Solution on p. 331.)
6 2 − 1 1
7
3
Exercise 5.4.19
8 2 + 4 1
5
10
Exercise 5.4.20
(Solution on p. 331.)
1 1 + 12 3
3
8
Exercise 5.4.21
3 1 + 1 1 − 2 1
4
3
2
Exercise 5.4.22
(Solution on p. 331.)
4 3 − 3 5 + 1 2
4
6
3
Exercise 5.4.23
3 1
12 + 4 1 + 1 1
3
4
Exercise 5.4.24
(Solution on p. 331.)
5 1
15 + 8 3
10 − 5 45
Exercise 5.4.25
7 1 + 8 5 − 2 1
3
6
4
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 5.4.26
(Solution on p. 332.)
1920
21 + 42 6 − 5
7
14 + 12 17
Exercise 5.4.27
1
16 + 4 3 + 10 3 − 9
4
8
Exercise 5.4.28
(Solution on p. 332.)
11 − 2 + 101 − 2 − 51 + 6 1
9
3
3
6
18
Exercise 5.4.29
5 + 2 1 + 111 − 11
2
6
3
6
Exercise 5.4.30
(Solution on p. 332.)
1 1 + 9 − 1
8
4
16 − 1
32 + 19
8
Exercise 5.4.31
223 − 161
8
7
Exercise 5.4.32
(Solution on p. 332.)
154 + 4 9
9
16
Exercise 5.4.33
4 17
88 + 5 9
110
Exercise 5.4.34
(Solution on p. 332.)
6 11
12 + 23
Exercise 5.4.35
8 9
16 − 79
Exercise 5.4.36
(Solution on p. 332.)
5 2
11 − 1
12
Exercise 5.4.37
1815
16 − 33
34
Exercise 5.4.38
(Solution on p. 332.)
1 89
112 − 21
56
Exercise 5.4.39
1111
24 − 7 13
18
Exercise 5.4.40
(Solution on p. 332.)
5 27
84 − 3 5
42 + 1 1
21
Exercise 5.4.41
16 148 − 16 196 + 1
144
Exercise 5.4.42
(Solution on p. 332.)
A man pours 25 gallons of paint from a bucket into a tray. After he nishes pouring, there are 11
8
4
gallons of paint left in his bucket. How much paint did the man pour into the tray?
Hint: Think about the wording.
Exercise 5.4.43
A particular computer stock opened at 373 and closed at 381 . What was the net gain for this 8
4
stock?
Exercise 5.4.44
(Solution on p. 332.)
A particular diet program claims that 4 316 pounds can be lost the rst month, 31 pounds can be 4
lost the second month, and 11 pounds can be lost the third month. How many pounds does this 2
diet program claim a person can lose over a 3-month period?
Exercise 5.4.45
If a person who weighs 1453 pounds goes on the diet program described in the problem above, 4
how much would he weigh at the end of 3 months?
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
310
CHAPTER 5. ADDITION AND SUBTRACTION OF FRACTIONS,
COMPARING FRACTIONS, AND COMPLEX FRACTIONS
Exercise 5.4.46
(Solution on p. 332.)
If the diet program described in the problem above makes the additional claim that from the fourth month on, a person will lose 11 pounds a month, how much will a person who begins the program 8
weighing 2083 pounds weight after 8 months?
4
5.4.2.1 Exercises for Review
Exercise 5.4.47
(Section 3.2) Use exponents to write 4 · 4 · 4.
Exercise 5.4.48
(Solution on p. 332.)
(Section 3.5) Find the greatest common factor of 14 and 20.
Exercise 5.4.49
(Section 4.3) Convert 16 to a mixed number.
5
Exercise 5.4.50
(Solution on p. 332.)
(Section 5.2) Find the sum. 4 + 1 + 2.
9
9
9
Exercise 5.4.51
(Section 5.3) Find the dierence. 15
26 − 3
10 .
5.5 Comparing Fractions5
5.5.1 Section Overview
• Order and the Inequality Symbols
• Comparing Fractions
5.5.2 Order and the Inequality Symbols
Our number system is called an ordered number system because the numbers in the system can be placed in order from smaller to larger. This is easily seen on the number line.
On the number line, a number that appears to the right of another number is larger than that other number.
For example, 5 is greater than 2 because 5 is located to the right of 2 on the number line. We may also say that 2 is less than 5.
To make the inequality phrases “greater than” and “less than” more brief, mathematicians represent them with the symbols > and <, respectively.
Symbols for Greater Than > and Less Than <
> represents the phrase “greater than.”
< represents the phrase “less than.”
5 > 2 represents “5 is greater than 2.”
2 < 5 represents “2 is less than 5.”
5This content is available online at <http://cnx.org/content/m34937/1.3/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
5.5.3 Comparing Fractions
Recall that the fraction 4 indicates that we have 4 of 5 parts of some whole quantity, and the fraction 3
5
5
indicates that we have 3 of 5 parts. Since 4 of 5 parts is more than 3 of 5 parts, 4 is greater than 3; that is, 5
5
4 > 3
5
5
We have just observed that when two fractions have the same denominator, we can determine which is larger by comparing the numerators.
Comparing Fractions
If two fractions have the same denominators, the fraction with the larger numerator is the larger fraction.
Thus, to compare the sizes of two or more fractions, we need only convert each of them to equivalent fractions that have a common denominator. We then compare the numerators. It is convenient if the common denominator is the LCD. The fraction with the larger numerator is the larger fraction.
5.5.3.1 Sample Set A
Example 5.16
Compare 8 and 14
9
15 .
Convert each fraction to an equivalent fraction with the LCD as the denominator. Find the LCD.
9
=
32
} The LCD = 32 · 5 = 9 · 5 = 45
15 = 3 · 5
8 = 8·5
9
45 = 40
45
14
15 = 14·3
45 = 42
45
Since 40 < 42,
40
45 < 42
45
Thus 8 < 14
9
15 .
Example 5.17
Write 5, 7
6
10 , and 13
15 in order from smallest to largest.
Convert each fraction to an equivalent fraction with the LCD as the denominator.
Find the LCD.
6 = 2 · 3
10 = 2 · 5 }The LCD = 2 · 3 · 5 = 30
15 = 3 · 5
5 = 5·5
6
30 = 25
30
7
10 = 7·3
30 = 21
30
13
15 = 13·2
30 = 26
30
Since 21 < 25 < 26,
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 5. ADDITION AND SUBTRACTION OF FRACTIONS,
COMPARING FRACTIONS, AND COMPLEX FRACTIONS
21
30 < 25
30 < 26
30
7
10 < 5 < 13
6
15
Writing these numbers in order from smallest to largest, we get 710, 5, 13
6
15 .
Example 5.18
Compare 86 and 63.
7
4
To compare mixed numbers that have dierent whole number parts, we need only compare whole number parts. Since 6 < 8,
6 3 < 8 6
4
7
Example 5.19
Compare 45 and 4 7
8
12
To compare mixed numbers that have the same whole number parts, we need only compare fractional parts.
8
=
23
}The LCD = 23 · 3 = 8 · 3 = 24
12 = 22 · 3
5 = 5·3
8
24 = 15
24
7
12 = 7·2
24 = 14
24
Since 14 < 15,
14
24 < 15
24
7
12 < 58
Hence, 4 712 < 458
5.5.3.2 Practice Set A
Exercise 5.5.1
(Solution on p. 332.)
Compare 3 and 4.
4
5
Exercise 5.5.2
(Solution on p. 332.)
Compare 910 and 13
15 .
Exercise 5.5.3
(Solution on p. 332.)
Write 13
16 , 17
20 , and 33
40 in order from smallest to largest.
Exercise 5.5.4
(Solution on p. 332.)
Compare 111 and 92.
6
5
Exercise 5.5.5
(Solution on p. 332.)
Compare 1 914 and 111
16 .
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
5.5.4 Exercises
Arrange each collection of numbers in order from smallest to largest.
Exercise 5.5.6
(Solution on p. 332.)
3 , 5
5
8
Exercise 5.5.7
1 , 2
6
7
Exercise 5.5.8
(Solution on p. 332.)
3 , 5
4
6
Exercise 5.5.9
7 , 11
9
12
Exercise 5.5.10
(Solution on p. 332.)
3 , 2
8
5
Exercise 5.5.11
1 , 5 ,
7
2
8
16
Exercise 5.5.12
(Solution on p. 332.)
1 , 3 , 4
2
5
7
Exercise 5.5.13
3 , 2 , 5
4
3
6
Exercise 5.5.14
(Solution on p. 332.)
3 , 7 , 5
4
9
4
Exercise 5.5.15
7 , 15
8
16 , 11
12
Exercise 5.5.16
(Solution on p. 332.)
3
14 , 2 , 3
7
4
Exercise 5.5.17
17
32 , 25
48 , 13
16
Exercise 5.5.18
(Solution on p. 332.)
5 3 , 5 4
5
7
Exercise 5.5.19
11 316, 11 112
Exercise 5.5.20
(Solution on p. 333.)
9 2 , 9 4
3
5
Exercise 5.5.21
7 2 , 8 5
3
6
Exercise 5.5.22
(Solution on p. 333.)
1 9
16 , 2 1
20
Exercise 5.5.23
2015
16 , 20 23
24
Exercise 5.5.24
(Solution on p. 333.)
2 2 , 2 3
9
7
Exercise 5.5.25
5 8
13 ,
5 9
20
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 5. ADDITION AND SUBTRACTION OF FRACTIONS,
COMPARING FRACTIONS, AND COMPLEX FRACTIONS
5.5.4.1 Exercises for Review
Exercise 5.5.26
(Solution on p. 333.)
(Section 1.4) Round 267,006,428 to the nearest ten million.
Exercise 5.5.27
(Section 2.5) Is the number 82,644 divisible by 2? by 3? by 4?
Exercise 5.5.28
(Solution on p. 333.)
(Section 4.3) Convert 32 to an improper fraction.
7
Exercise 5.5.29
(Section 5.3) Find the value of 5 + 3
6
10 − 25
Exercise 5.5.30
(Solution on p. 333.)
(Section 5.4) Find the value of 83 + 51.
8
4
5.6 Complex Fractions 6
5.6.1 Section Overview
• Simple Fractions and Complex Fractions
• Converting Complex Fractions to Simple Fractions
5.6.2 Simple Fractions and Complex Fractions
Simple Fraction
A simple fraction is any fraction in which the numerator is any whole number and the denominator is any nonzero whole number. Some examples are the following:
1
,
4
,
763
2
3
1,000
Complex Fraction
A complex fraction is any fraction in which the numerator and/or the denominator is a fraction; it is a fraction of fractions. Some examples of complex fractions are the following: 3
1
4+ 3
4
,
3
,
6
,
8
5
2
9
7− 5
6
10
6
5.6.3 Converting Complex Fractions to Simple Fractions
The goal here is to convert a complex fraction to a simple fraction. We can do so by employing the methods of adding, subtracting, multiplying, and dividing fractions. Recall from Section 4.2 that a fraction bar serves as a grouping symbol separating the fractional quantity into two individual groups. We proceed in simplifying a complex fraction to a simple fraction by simplifying the numerator and the denominator of the complex fraction separately. We will simplify the numerator and denominator completely before removing the fraction bar by dividing. This technique is illustrated in problems 3, 4, 5, and 6 of Section 5.6.3.1 (Sample Set A).
6This content is available online at <http://cnx.org/content/m34941/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
5.6.3.1 Sample Set A
Convert each of the following complex fractions to a simple fraction.
Example 5.20
3
8
15
16
Convert this complex fraction to a simple fraction by performing the indicated division.
3
8
15
=
3 ÷ 15
16
The divisor is15
16 .Invert 15
16 and multiply.
16
8
1
2
=
)3 · )16 = 1·2 = 2
)8
)15
1·5
5
1
5
Example 5.21
4
9
Write 6 as 6 and divide.
6
1
4
9
=
4 ÷ 6
6
9
1
1
2
=
)4 · 1 = 2·1 = 2
9
)6
9·3
27
3
Example 5.22
5+ 3
4
46
Simplify the numerator.
4·5+3
20+3
23
4
4
4
46
= 46 = 46 Write 46 as 46.
1
23
4
46
=
23 ÷ 46
4
1
1
1
=
)23 · 1 = 1·1 = 1
4
)46
4·2
8
2
Example 5.23
1 + 3
2 + 3
2+3
5
4
8
= 8 8 =
8
= 8 = 5 ÷ 25
1 + 13
12
12+13
25
8
24
2
24
24 + 13
24
24
24
1
3
5 ÷ 25
)5 · )24 = 1·3 = 3
8
24 = )8
)25
1·5
5
1
5
Example 5.24
4+ 5
4·6+5
29
6
=
6
= 6
=
29 ÷ 20
7− 1
7·3−1
20
6
3
3
3
3
1
=
29 · )3
)6
20 = 29
40
2
Example 5.25
11+ 3
11·10+3
110+3
113
10 =
10
=
10
= 10 = 113
4 4
4·5+4
20+4
24
10 ÷ 24
5
5
5
5
5
1
113
)5
10 ÷ 24 = 113 ·
5
)10
24 = 113·1
2·24 = 113
48 = 2 17
48
2
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 5. ADDITION AND SUBTRACTION OF FRACTIONS,
COMPARING FRACTIONS, AND COMPLEX FRACTIONS
5.6.3.2 Practice Set A
Convert each of the following complex fractions to a simple fraction.
Exercise 5.6.1
(Solution on p. 333.)
4
9
8
15
Exercise 5.6.2
(Solution on p. 333.)
7
10
28
Exercise 5.6.3
(Solution on p. 333.)
5+ 2
5
3+ 3
5
Exercise 5.6.4
(Solution on p. 333.)
1 + 7
8
8
6− 3
10
Exercise 5.6.5
(Solution on p. 333.)
1 + 5
6
8
5 − 1
9
4
Exercise 5.6.6
(Solution on p. 333.)
16−10 23
11 5 −7 7
6
6
5.6.4 Exercises
Simplify each fraction.
Exercise 5.6.7
(Solution on p. 333.)
3
5
9
15
Exercise 5.6.8
1
3
1
9
Exercise 5.6.9
(Solution on p. 333.)
1
4
5
12
Exercise 5.6.10
8
9
4
15
Exercise 5.6.11
(Solution on p. 333.)
6+ 1
4
11+ 14
Exercise 5.6.12
2+ 1
2
7+ 1
2
Exercise 5.6.13
(Solution on p. 333.)
5+ 1
3
2+ 2
15
Exercise 5.6.14
9+ 1
2
1+ 8
11
Exercise 5.6.15
(Solution on p. 333.)
4+ 10
13
12
39
Exercise 5.6.16
1 + 2
3
7
26
21
Exercise 5.6.17
(Solution on p. 333.)
5 − 1
6
4
1
12
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 5.6.18
3
10 + 4
12
19
90
Exercise 5.6.19
(Solution on p. 333.)
9
16 + 7
3
139
48
Exercise 5.6.20
1
288
8 − 3
9
16
Exercise 5.6.21
(Solution on p. 333.)
27
429
5 − 1
11
13
Exercise 5.6.22
1 + 2
3
5
3 + 17
5
45
Exercise 5.6.23
(Solution on p. 333.)
9
70 + 5
42
13
30 − 1
21
Exercise 5.6.24
1
16 + 1
14
2 − 13
3
60
Exercise 5.6.25
(Solution on p. 333.)
3
20 + 11
12
19 −1 11
7
35
Exercise 5.6.26
2 2 −1 1
3
2
1 +1 1
4
16
Exercise 5.6.27
(Solution on p. 333.)
3 1 +3 1
5
3
6 − 15
5
63
Exercise 5.6.28
1 1 +15
2
5 1 −3 5
4
12
8 1 −4 1
3
2
11 2 −5 11
3
12
Exercise 5.6.29
(Solution on p. 333.)
5 3 +3 1
4
5
2 1 +15 7
5
10
9 1 −4 1
2
6
1 +2 1
8
120
5.6.4.1 Exercises for Review
Exercise 5.6.30
(Section 3.4) Find the prime factorization of 882.
Exercise 5.6.31
(Solution on p. 333.)
(Section 4.3) Convert 62 to a mixed number.
7
Exercise 5.6.32
(Section 4.4) Reduce 114
342 to lowest terms.
Exercise 5.6.33
(Solution on p. 334.)
(Section 5.4) Find the value of 63 − 45.
8
6
Exercise 5.6.34
(Section 5.5) Arrange from smallest to largest: 1, 3, 4.
2
5
7
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 5. ADDITION AND SUBTRACTION OF FRACTIONS,
COMPARING FRACTIONS, AND COMPLEX FRACTIONS
5.7 Combinations of Operations with Fractions 7
5.7.1 Section Overview
• The Order of Operations
5.7.2 The Order of Operations
To determine the value of a quantity such as
1 + 5 · 2
2
8
15
where we have a combination of operations (more than one operation occurs), we must use the accepted order of operations.
The Order of Operations:
1. In the order (2), (3), (4) described below, perform all operations inside grouping symbols: ( ), [ ], (
),
. Work from the innermost set to the outermost set.
2. Perform exponential and root operations.
3. Perform all multiplications and divisions moving left to right.
4. Perform all additions and subtractions moving left to right.
5.7.2.1 Sample Set A
Determine the value of each of the following quantities.
Example 5.26
1 + 5 · 2
4
8
15
(a) Multiply rst.
1
1
1 + )5 · )2 = 1 + 1·1 = 1 + 1
4
)8
)15
4
4·3
4
12
4
3
(b) Now perform this addition. Find the LCD.
4 = 22} The LCD = 22 · 3 = 12.
12 = 22 · 3
1 + 1
4
12
=
1·3
12 + 1
12 = 3
12 + 1
12
=
3+1
12 = 4
12 = 13
Thus, 1 + 5 · 2
4
8
15 = 13
Example 5.27
3 + 9 5 − 1
5
44 9
4
(a) Operate within the parentheses rst, 5 − 1.
9
4
9 = 32} The LCD = 22 · 32 = 4 · 9 = 36.
4 = 22
7This content is available online at <http://cnx.org/content/m34942/1.3/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
5·4
36 − 1·9
36 = 20
36 − 9
36 = 20−9
36 = 11
36
Now we have
3 + 9 11
5
44 36
(b) Perform the multiplication.
1
1
3 + )9 · )11 = 3 + 1·1 = 3 + 1
5
)44
)36
5
4·4
5
16
4
4
(c) Now perform the addition. The LCD=80.
3 + 1
5
16 = 3·16
80 + 1·5
80 = 48
80 + 5
80 = 48+5
80 = 53
80
Thus, 3 + 9 5 − 1 = 53
5
44 9
4
80
Example 5.28
8 − 15
426 2 − 1 4
15
3 1 + 2 1
5
8
(a) Work within each set of parentheses individually.
2 − 1 4
15
=
2 1·15+4
15
= 2 − 19
15
=
30
15 − 19
15 = 30−19
15
= 11
15
3 1 + 2 1
=
3·5+1 + 2·8+1
5
8
5
8
=
16 + 17 LCD = 40
5
8
=
16·8
40 + 17·5
40
=
128
40 + 85
40
=
128+85
40
=
213
40
Now we have
8 − 15
11 213
426 15
40
(b) Now multiply.
1
1
8 − )15 · 11 · )213
)426
)15
40 = 8 − 1·11·1
2·1·40 = 8 − 11
80
2
1
(c) Now subtract.
8 − 11
80 = 80·8
80 − 11
80 = 640
80 − 11
80 = 640−11
80
= 629
80 or 7 69
80
Thus, 8 − 15 2 − 1 4 31 + 21 = 769
426
15
5
8
80
Example 5.29
3 2 · 8 − 5
4
9
12
(a) Square 3.
4
3 2 = 3 · 3 = 3·3 = 9
4
4
4
4·4
16
Now we have
9
16 · 8 − 5
9
12
(b) Perform the multiplication.
1
1
)9 · )8 − 5
− 5
− 5
)16
)9
12 = 1·1
2·1
12 = 12
12
2
1
(c) Now perform the subtraction.
1 − 5
2
12 = 6
12 − 5
12 = 6−5
12 = 1
12
Thus, 42 · 8 − 5
3
9
12 = 1
12
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 5. ADDITION AND SUBTRACTION OF FRACTIONS,
COMPARING FRACTIONS, AND COMPLEX FRACTIONS
Example 5.30
q
2 7 +
25
− 1 1
8
36 ÷ 2 12
3
(a) Begin by operating inside the parentheses.
2 1 − 1 1
=
2·2+1 − 1·3+1 = 5 − 4
2
3
2
3
2
3
=
15 − 8 = 15−8 = 7
6
6
6
6
(b) Now simplify the square root.
q 25
2
36 = 5 since 5
= 25
6
6
36
Now we have
2 7 + 5 ÷ 7
8
6
6
(c) Perform the division.
1
2 7 + 5 · )6 = 2 7 + 5·1 = 2 7 + 5
8
)6
7
8
1·7
8
7
1
(d) Now perform the addition.
2 7 + 5
=
2·8+7 + 5 = 23 + 5
LCD = 56.
8
7
8
7
8
7
=
23·7
56 + 5·8
56 = 161
56 + 40
56
=
161+40
56
= 201
56 or 3 33
56
q
Thus, 27 +
25
− 1 1 = 3 33
8
36 ÷ 2 12
3
56
5.7.2.2 Practice Set A
Find the value of each of the following quantities.
Exercise 5.7.1
(Solution on p. 334.)
5
16 · 1
10 − 1
32
Exercise 5.7.2
(Solution on p. 334.)
6 · 21
7
40 ÷ 9
10 + 5 13
Exercise 5.7.3
(Solution on p. 334.)
8 7
10 − 2 4 1 − 3 2
2
3
Exercise 5.7.4
(Solution on p. 334.)
17
1
18 − 58
30
− 3
1 − 13
4
32
29
Exercise 5.7.5
(Solution on p. 334.)
1
10 + 1 1 ÷ 1 4 − 1 6
2
5
25
Exercise 5.7.6
(Solution on p. 334.)
2 − 3 · 4
3
8
9
7
16 ·1 1 +1 1
3
4
Exercise 5.7.7
(Solution on p. 334.)
3 2 + 3 · 1
8
4
8
Exercise 5.7.8
(Solution on p. 334.)
q
2 · 2 1 −
4
3
4
25
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
5.7.3 Exercises
Find each value.
Exercise 5.7.9
(Solution on p. 334.)
4 − 1 · 1
3
6
2
Exercise 5.7.10
7 − 4 · 5
9
5
36
Exercise 5.7.11
(Solution on p. 334.)
2 2 + 5 ÷ 5
7
8
16
Exercise 5.7.12
3
16 ÷ 9
14 · 12
21 + 56
Exercise 5.7.13
(Solution on p. 334.)
4
25 ÷ 8
15 − 7
20 ÷ 2 1
10
Exercise 5.7.14
2 · 1
5
19 + 3
38
Exercise 5.7.15
(Solution on p. 334.)
3 · 3
7
10 − 1
15
Exercise 5.7.16
10
11 · 8 − 2 + 3
+ 1
9
5
25 · 53
4
Exercise 5.7.17
(Solution on p. 334.)
2 · 6 − 3 + 5 1 · 1 1 − 1
7
7
28
3
4
8
Exercise 5.7.18
( 6
11 − 1 )·( 1
3
21 +2 13
42 )
1 1 + 7
5
40
Exercise 5.7.19
(Solution on p. 334.)
1 2 + 1
2
8
Exercise 5.7.20
3 2 − 3
5
10
Exercise 5.7.21
(Solution on p. 334.)
q 36
81 + 1 · 2
3
9
Exercise 5.7.22
q 49
q 9
64 −
4
Exercise 5.7.23
(Solution on p. 334.)
q
q
2 ·
9 − 15 ·
16
3
4
4
225
Exercise 5.7.24
q
3 2 +
25
4
16
Exercise 5.7.25
(Solution on p. 334.)
q
1 2 ·
81
3
25 + 1
40 ÷ 18
Exercise 5.7.26
2
q
4
49
+ 3 ÷ 1 3
7
4
Exercise 5.7.27
(Solution on p. 334.)
2
q 100
121
+ 21
(11)2
Exercise 5.7.28
q 3 + 1
÷ 1 1
8
64 − 12
3
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 5. ADDITION AND SUBTRACTION OF FRACTIONS,
COMPARING FRACTIONS, AND COMPLEX FRACTIONS
Exercise 5.7.29
(Solution on p. 334.)
q
q
1 · 5 2 + 9
−
1
4
6
14 · 2 13
81
Exercise 5.7.30
q
q
1 ·
6 3 +2 5
8
8
9
16
+ 7 7
10
Exercise 5.7.31
(Solution on p. 334.)
3 3 + 4 ·( 1 )3
4
5
2
67
240 +( 1 )4·( 9
3
10 )
Exercise 5.7.32
rq 16
81 + 1 · 6
4
Exercise 5.7.33
(Solution on p. 334.)
rq 81
256 − 3
32 · 1 18
5.7.3.1 Exercises for Review
Exercise 5.7.34
(Section 1.2) True or false: Our number system, the Hindu-Arabic number system, is a positional number system with base ten.
Exercise 5.7.35
(Solution on p. 334.)
(Section 2.6) The fact that 1 times any whole number = that particular whole number illustrates which property of multiplication?
Exercise 5.7.36
(Section 4.3) Convert 86 to an improper fraction.
7
Exercise 5.7.37
(Solution on p. 334.)
(Section 5.3) Find the sum. 3 + 4 + 5.
8
5
6
Exercise 5.7.38
(Section 5.6) Simplify 6+18 .
6− 1
8
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
5.8 Summary of Key Concepts 8
5.8.1 Summary of Key Concepts
Addition and Subtraction of Fractions with Like Denominators (Section 5.2) To add or subtract two fractions that have the same denominators, add or subtract the numerators and place the resulting sum or dierence over the common denominator. Reduce, if necessary. Do not add or subtract the denominators.
1 + 5 = 1+5 = 6 = 3
8
8
8
8
4
Basic Rule for Adding and Subtracting Fractions (Section 5.3)
Fractions can be added or subtracted conveniently only if they have like denominators.
Addition and Subtraction of Fractions with Unlike Denominators (Section 5.3) To add or subtract fractions having unlike denominators, convert each fraction to an equivalent fraction having as denominator the LCD of the original denominators.
Addition and Subtraction of Mixed Numbers (Section 5.4)
1. To add or subtract mixed numbers, convert each mixed number to an improper fraction, then add or subtract the fractions.
Ordered Number System (Section 5.5)
Our number system is ordered because the numbers in the system can be placed in order from smaller to larger.
Inequality Symbols (Section 5.5)
> represents the phrase “greater than.”
< represents the phrase “less than.”
Comparing Fractions (Section 5.5)
If two fractions have the same denominators, the fraction with the larger numerator is the larger fraction.
5 > 3
8
8
Simple Fractions (Section 5.6)
A simple fraction is any fraction in which the numerator is any whole number and the denominator is any nonzero whole number.
Complex Fractions (Section 5.6)
A complex fraction is any fraction in which the numerator and/or the denominator is a fraction.
Complex fractions can be converted to simple fractions by employing the methods of adding, subtracting, multiplying, and dividing fractions.
5.9 Exercise Supplement 9
5.9.1 Exercise Supplement
5.9.1.1 Addition and Subtractions of Fractions with Like and Unlike Denominators, and Addition and Subtraction of Mixed Numbers (Section 5.2, Section 5.3, Section 5.4) For problems 1-53, perform each indicated operation and write the result in simplest form.
8This content is available online at <http://cnx.org/content/m34943/1.2/>.
9This content is available online at <http://cnx.org/content/m34944/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 5. ADDITION AND SUBTRACTION OF FRACTIONS,
COMPARING FRACTIONS, AND COMPLEX FRACTIONS
Exercise 5.9.1
(Solution on p. 334.)
3 + 5
4
8
Exercise 5.9.2
9
16 + 14
Exercise 5.9.3
(Solution on p. 335.)
1 + 3
8
8
Exercise 5.9.4
5 + 1
7
14 + 5
21
Exercise 5.9.5
(Solution on p. 335.)
5 + 1 + 5
6
3
21
Exercise 5.9.6
2 + 1
5
8
Exercise 5.9.7
(Solution on p. 335.)
1 + 1 + 1
4
8
4
Exercise 5.9.8
1
16 + 1
10
Exercise 5.9.9
(Solution on p. 335.)
2 + 1
7
3
Exercise 5.9.10
2 1 + 1
3
6
Exercise 5.9.11
(Solution on p. 335.)
3 11
16 + 34
Exercise 5.9.12
5 1
12 + 3 18
Exercise 5.9.13
(Solution on p. 335.)
162 + 81
5
4
Exercise 5.9.14
1 1 + 2 4
7
7
Exercise 5.9.15
(Solution on p. 335.)
1 3 + 0
8
Exercise 5.9.16
3 1
10 + 4
Exercise 5.9.17
(Solution on p. 335.)
182 + 6
3
Exercise 5.9.18
1 4 + 5 5
3
4
Exercise 5.9.19
(Solution on p. 335.)
21 + 2
4
3
Exercise 5.9.20
15
16 − 18
Exercise 5.9.21
(Solution on p. 335.)
9
11 − 5
22
Exercise 5.9.22
6 2
15 − 1 3
10
Exercise 5.9.23
(Solution on p. 335.)
5 2 + 8 1 − 2 1
3
5
4
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 5.9.24
8 3
10 − 4 5 − 3 1
6
15
Exercise 5.9.25
(Solution on p. 335.)
11
12 + 1 − 1
9
16
Exercise 5.9.26
7 2 − 5 5 − 1 1
9
6
3
Exercise 5.9.27
(Solution on p. 335.)
16 2 − 8 1 − 3 2
5
6
15
Exercise 5.9.28
4 1 + 0 − 32
8
8
Exercise 5.9.29
(Solution on p. 335.)
4 1 + 0 − 32
8
8
Exercise 5.9.30
8 − 2 13
Exercise 5.9.31
(Solution on p. 335.)
4 − 3 5
16
Exercise 5.9.32
6 3 + 4
7
Exercise 5.9.33
(Solution on p. 335.)
11 211 − 3
Exercise 5.9.34
215 − 5
8
8
Exercise 5.9.35
(Solution on p. 335.)
3 + 5
4
16 · 45
Exercise 5.9.36
11
12 + 15
16 ÷ 2 12
Exercise 5.9.37
(Solution on p. 335.)
1 3
10 + 2 2 ÷ 4
3
9
Exercise 5.9.38
8 3 − 1 1
5
14 · 37
Exercise 5.9.39
(Solution on p. 335.)
2 3 ÷ 3 9
8
16 − 19
Exercise 5.9.40
152 ÷ 50 − 1
5
10
5.9.1.2 Complex Fractions and Combinations of Operations with Fractions (Section 5.5,Section 5.6)
Exercise 5.9.41
(Solution on p. 335.)
9
16
21
32
Exercise 5.9.42
10
21
11
14
Exercise 5.9.43
(Solution on p. 335.)
1 7
9
1 5
27
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 5. ADDITION AND SUBTRACTION OF FRACTIONS,
COMPARING FRACTIONS, AND COMPLEX FRACTIONS
Exercise 5.9.44
15
17
50
51
Exercise 5.9.45
(Solution on p. 335.)
1 9
16
2 11
12
Exercise 5.9.46
8 4
15
3
Exercise 5.9.47
(Solution on p. 335.)
9 1
18
6
Exercise 5.9.48
3 1 +2 1
4
8
5 1
6
Exercise 5.9.49
(Solution on p. 335.)
3+2 1
2
1 + 5
4
6
Exercise 5.9.50
4+1 7
10
9−2 1
5
Exercise 5.9.51
(Solution on p. 335.)
1 2
5
9− 2
2
Exercise 5.9.52
1 2 ·( 1 + 1 )
3
4
5
1 1
2
Exercise 5.9.53
(Solution on p. 336.)
10
23 ·( 5 +2)
6
8
9
5.9.1.3 Comparing Fractions (Section 5.5)
For problems 54-65, place each collection in order from smallest to largest.
Exercise 5.9.54
1 , 3
8
16
Exercise 5.9.55
(Solution on p. 336.)
3
32 , 18
Exercise 5.9.56
5
16 , 3
24
Exercise 5.9.57
(Solution on p. 336.)
3
10 , 56
Exercise 5.9.58
2 , 1, 1
9
3
6
Exercise 5.9.59
(Solution on p. 336.)
3 , 8, 19
8
3
6
Exercise 5.9.60
3 , 2
5
10 , 7
20
Exercise 5.9.61
(Solution on p. 336.)
4 , 5
7
9
Exercise 5.9.62
4 , 5
5
7
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 5.9.63
(Solution on p. 336.)
5
12 , 4 , 7
9
15
Exercise 5.9.64
7
36 , 1
24 , 5
12
Exercise 5.9.65
(Solution on p. 336.)
5 , 13
8
16 , 34
5.10 Prociency Exam 10
5.10.1 Prociency Exam
For problems 1-12, perform each indicated operation and write the result in simplest form.
Exercise 5.10.1
(Solution on p. 336.)
(Section 5.3) 316 + 18
Exercise 5.10.2
(Solution on p. 336.)
(Section 5.4) 22 + 51
3
6
Exercise 5.10.3
(Solution on p. 336.)
(Section 5.7) 715 · 20
21 + 59
Exercise 5.10.4
(Solution on p. 336.)
(Section 5.2) 311 + 511
Exercise 5.10.5
(Solution on p. 336.)
(Section 5.7) 62 · 117
9
28 − 3 4
17 − 21
17
Exercise 5.10.6
(Solution on p. 336.)
(Section 5.4) 51 − 24
8
5
Exercise 5.10.7
(Solution on p. 336.)
(Section 5.6) 7128
21
Exercise 5.10.8
(Solution on p. 336.)
(Section 5.6) 1+3
8
4
1 7
8
Exercise 5.10.9
(Solution on p. 336.)
(Section 5.4) 4 516 + 11 − 2 5
3
24
Exercise 5.10.10
(Solution on p. 336.)
(Section 5.7) 5
18 · 15
16 − 38
Exercise 5.10.11
(Solution on p. 336.)
(Section 5.4) 4 + 213
Exercise 5.10.12
(Solution on p. 336.)
(Section 5.4) 83 − 5
7
For problems 13-15, specify the fractions that are equivalent.
Exercise 5.10.13
(Solution on p. 336.)
(Section 5.5) 4, 12
5
15
Exercise 5.10.14
(Solution on p. 336.)
(Section 5.5) 5, 24
8
40
Exercise 5.10.15
(Solution on p. 336.)
(Section 5.5) 512, 80
192
10This content is available online at <http://cnx.org/content/m34948/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 5. ADDITION AND SUBTRACTION OF FRACTIONS,
COMPARING FRACTIONS, AND COMPLEX FRACTIONS
For problems 16-20, place each collection of fractions in order from smallest to largest.
Exercise 5.10.16
(Solution on p. 336.)
(Section 5.5) 8, 6
9
7
Exercise 5.10.17
(Solution on p. 336.)
(Section 5.5) 5, 7
8
9
Exercise 5.10.18
(Solution on p. 336.)
(Section 5.5) 11 516, 11 512
Exercise 5.10.19
(Solution on p. 337.)
(Section 5.5) 215, 310, 16
Exercise 5.10.20
(Solution on p. 337.)
(Section 5.5) 19
32 , 9
16 , 58
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solutions to Exercises in Chapter 5
Solution to Exercise 5.2.1 (p. 297)
2
5
Solution to Exercise 5.2.2 (p. 297)
1
2
Solution to Exercise 5.2.3 (p. 297)
1Solution to Exercise 5.2.4 (p. 297)
4
5
Solution to Exercise 5.2.5 (p. 297)
3 + 3 = 3+3 = 6 = 3 , so two 3’s= one 3 which is preposterous.
4
4
4+4
8
4
4
4
Solution to Exercise 5.2.6 (p. 298)
2
13
Solution to Exercise 5.2.7 (p. 298)
1
3
Solution to Exercise 5.2.8 (p. 298)
0Solution to Exercise 5.2.9 (p. 298)
6
5
Solution to Exercise 5.2.10 (p. 298)
5 − 2 = 5−2 = 3 , which is undened
9
9
9−9
0
Solution to Exercise 5.2.11 (p. 298)
5
8
Solution to Exercise 5.2.13 (p. 298)
1Solution to Exercise 5.2.15 (p. 298)
13
15
Solution to Exercise 5.2.17 (p. 299)
1Solution to Exercise 5.2.19 (p. 299)
0Solution to Exercise 5.2.21 (p. 299)
0Solution to Exercise 5.2.23 (p. 299)
9
11
Solution to Exercise 5.2.25 (p. 299)
15
8
Solution to Exercise 5.2.27 (p. 299)
1
2
Solution to Exercise 5.2.29 (p. 299)
3
5
Solution to Exercise 5.2.31 (p. 299)
13
5
Solution to Exercise 5.2.33 (p. 299)
10
Solution to Exercise 5.2.35 (p. 299)
9
11
Solution to Exercise 5.2.37 (p. 300)
16
30 = 8 (using the preposterous rule)
5
Solution to Exercise 5.2.39 (p. 300)
13
24
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 5. ADDITION AND SUBTRACTION OF FRACTIONS,
COMPARING FRACTIONS, AND COMPLEX FRACTIONS
Solution to Exercise 5.2.41 (p. 300)
2700
Solution to Exercise 5.2.43 (p. 300)
32 · 5 · 11
Solution to Exercise 5.2.45 (p. 300)
2
3
Solution to Exercise 5.3.1 (p. 303)
5
6
Solution to Exercise 5.3.2 (p. 303)
1
14
Solution to Exercise 5.3.3 (p. 303)
3
40
Solution to Exercise 5.3.4 (p. 303)
11
16
Solution to Exercise 5.3.5 (p. 303)
1
96
Solution to Exercise 5.3.6 (p. 304)
The same denominator
Solution to Exercise 5.3.8 (p. 304)
5
8
Solution to Exercise 5.3.10 (p. 304)
31
24
Solution to Exercise 5.3.12 (p. 304)
17
28
Solution to Exercise 5.3.14 (p. 304)
19
36
Solution to Exercise 5.3.16 (p. 304)
19
39
Solution to Exercise 5.3.18 (p. 304)
29
60
Solution to Exercise 5.3.20 (p. 304)
8
81
Solution to Exercise 5.3.22 (p. 304)
17
65
Solution to Exercise 5.3.24 (p. 304)
2
63
Solution to Exercise 5.3.26 (p. 304)
7
16
Solution to Exercise 5.3.28 (p. 305)
47
18
Solution to Exercise 5.3.30 (p. 305)
103
30
Solution to Exercise 5.3.32 (p. 305)
217
264
Solution to Exercise 5.3.34 (p. 305)
511
720
Solution to Exercise 5.3.36 (p. 305)
37
72
Solution to Exercise 5.3.38 (p. 305)
221
150
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 5.3.40 (p. 305)
1,465
2,016
Solution to Exercise 5.3.42 (p. 305)
65
204
Solution to Exercise 5.3.44 (p. 305)
1
5
Solution to Exercise 5.3.46 (p. 305)
607
180
Solution to Exercise 5.3.48 (p. 305)
109
520
Solution to Exercise 5.3.50 (p. 306)
$ 137 or $17 1
8
8
Solution to Exercise 5.3.52 (p. 306)
No; 3 boxes add up to 26100 , which is larger than 25100 .
4
5
Solution to Exercise 5.3.54 (p. 306)
No pipe at all; inside diameter is greater than outside diameter
Solution to Exercise 5.3.56 (p. 306)
449
Solution to Exercise 5.3.58 (p. 306)
660
Solution to Exercise 5.3.60 (p. 306)
7
15
Solution to Exercise 5.4.1 (p. 307)
4 79
Solution to Exercise 5.4.2 (p. 307)
8 14
Solution to Exercise 5.4.3 (p. 307)
8 18
Solution to Exercise 5.4.4 (p. 307)
8 3
10
Solution to Exercise 5.4.5 (p. 307)
18 916
Solution to Exercise 5.4.6 (p. 308)
7 12
Solution to Exercise 5.4.8 (p. 308)
1212
Solution to Exercise 5.4.10 (p. 308)
21 611
Solution to Exercise 5.4.12 (p. 308)
3 78
Solution to Exercise 5.4.14 (p. 308)
1 23
Solution to Exercise 5.4.16 (p. 308)
8 11
14
Solution to Exercise 5.4.18 (p. 308)
4 20
21
Solution to Exercise 5.4.20 (p. 308)
1317
24
Solution to Exercise 5.4.22 (p. 308)
2 712
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 5. ADDITION AND SUBTRACTION OF FRACTIONS,
COMPARING FRACTIONS, AND COMPLEX FRACTIONS
Solution to Exercise 5.4.24 (p. 308)
7 17
30
Solution to Exercise 5.4.26 (p. 309)
7425
42
Solution to Exercise 5.4.28 (p. 309)
2113
Solution to Exercise 5.4.30 (p. 309)
5 21
32
Solution to Exercise 5.4.32 (p. 309)
20 1
144
Solution to Exercise 5.4.34 (p. 309)
7 7
12
Solution to Exercise 5.4.36 (p. 309)
5 13
132
Solution to Exercise 5.4.38 (p. 309)
1 47
212
Solution to Exercise 5.4.40 (p. 309)
3 14
Solution to Exercise 5.4.42 (p. 309)
2 5 gallons
8
Solution to Exercise 5.4.44 (p. 309)
8 15 pounds
16
Solution to Exercise 5.4.46 (p. 310)
194 3 pounds
16
Solution to Exercise 5.4.48 (p. 310)
2Solution to Exercise 5.4.50 (p. 310)
7
9
Solution to Exercise 5.5.1 (p. 312)
3 < 4
4
5
Solution to Exercise 5.5.2 (p. 312)
13
15 < 9
10
Solution to Exercise 5.5.3 (p. 312)
13
16 , 33
40 , 17
20
Solution to Exercise 5.5.4 (p. 312)
9 2 < 11 1
5
6
Solution to Exercise 5.5.5 (p. 312)
1 9
14 < 1 11
16
Solution to Exercise 5.5.6 (p. 313)
3 < 5
5
8
Solution to Exercise 5.5.8 (p. 313)
3 < 5
4
6
Solution to Exercise 5.5.10 (p. 313)
3 < 2
8
5
Solution to Exercise 5.5.12 (p. 313)
1 < 4 < 3
2
7
5
Solution to Exercise 5.5.14 (p. 313)
3 < 7 < 5
4
9
4
Solution to Exercise 5.5.16 (p. 313)
3
14 < 2 < 3
7
4
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 5.5.18 (p. 313)
5 4 < 5 3
7
5
Solution to Exercise 5.5.20 (p. 313)
9 2 < 9 4
3
5
Solution to Exercise 5.5.22 (p. 313)
1 9
16 < 2 1
20
Solution to Exercise 5.5.24 (p. 313)
2 2 < 2 3
9
7
Solution to Exercise 5.5.26 (p. 314)
270,000,000
Solution to Exercise 5.5.28 (p. 314)
23
7
Solution to Exercise 5.5.30 (p. 314)
135 or 109
8
8
Solution to Exercise 5.6.1 (p. 316)
5
6
Solution to Exercise 5.6.2 (p. 316)
1
40
Solution to Exercise 5.6.3 (p. 316)
3
2
Solution to Exercise 5.6.4 (p. 316)
10
57
Solution to Exercise 5.6.5 (p. 316)
2 13
22
Solution to Exercise 5.6.6 (p. 316)
1 5
11
Solution to Exercise 5.6.7 (p. 316)
1Solution to Exercise 5.6.9 (p. 316)
3
5
Solution to Exercise 5.6.11 (p. 316)
5
9
Solution to Exercise 5.6.13 (p. 316)
5
2
Solution to Exercise 5.6.15 (p. 316)
31
2
Solution to Exercise 5.6.17 (p. 316)
7
Solution to Exercise 5.6.19 (p. 317)
1Solution to Exercise 5.6.21 (p. 317)
1
6
Solution to Exercise 5.6.23 (p. 317)
52
81
Solution to Exercise 5.6.25 (p. 317)
16
21
Solution to Exercise 5.6.27 (p. 317)
686
101
Solution to Exercise 5.6.29 (p. 317)
1
3
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 5. ADDITION AND SUBTRACTION OF FRACTIONS,
COMPARING FRACTIONS, AND COMPLEX FRACTIONS
Solution to Exercise 5.6.31 (p. 317)
8 67
Solution to Exercise 5.6.33 (p. 317)
1 13
24 or 37
24
Solution to Exercise 5.7.1 (p. 320)
0Solution to Exercise 5.7.2 (p. 320)
35 or 55
6
6
Solution to Exercise 5.7.3 (p. 320)
211
30 or 7 1
30
Solution to Exercise 5.7.4 (p. 320)
7
9
Solution to Exercise 5.7.5 (p. 320)
2 67
Solution to Exercise 5.7.6 (p. 320)
3
11
Solution to Exercise 5.7.7 (p. 320)
15
64
Solution to Exercise 5.7.8 (p. 320)
11
10
Solution to Exercise 5.7.9 (p. 321)
5
4
Solution to Exercise 5.7.11 (p. 321)
4 27
Solution to Exercise 5.7.13 (p. 321)
2
15
Solution to Exercise 5.7.15 (p. 321)
1
10
Solution to Exercise 5.7.17 (p. 321)
6 3
14
Solution to Exercise 5.7.19 (p. 321)
3
8
Solution to Exercise 5.7.21 (p. 321)
20
27
Solution to Exercise 5.7.23 (p. 321)
0Solution to Exercise 5.7.25 (p. 321)
2
5
Solution to Exercise 5.7.27 (p. 321)
1Solution to Exercise 5.7.29 (p. 322)
125
72
Solution to Exercise 5.7.31 (p. 322)
252
19
Solution to Exercise 5.7.33 (p. 322)
165
256
Solution to Exercise 5.7.35 (p. 322)
multiplicative identity
Solution to Exercise 5.7.37 (p. 322)
241
120 or 2 1
120
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 5.9.1 (p. 324)
11 or 13
8
8
Solution to Exercise 5.9.3 (p. 324)
1
2
Solution to Exercise 5.9.5 (p. 324)
59
42 = 1 17
42
Solution to Exercise 5.9.7 (p. 324)
5
8
Solution to Exercise 5.9.9 (p. 324)
13
21
Solution to Exercise 5.9.11 (p. 324)
4 7
16
Solution to Exercise 5.9.13 (p. 324)
8 3
20
Solution to Exercise 5.9.15 (p. 324)
1 38
Solution to Exercise 5.9.17 (p. 324)
2423
Solution to Exercise 5.9.19 (p. 324)
71
12 = 5 11
12
Solution to Exercise 5.9.21 (p. 324)
13
22
Solution to Exercise 5.9.23 (p. 324)
1137
60
Solution to Exercise 5.9.25 (p. 325)
139
144
Solution to Exercise 5.9.27 (p. 325)
5 1
10
Solution to Exercise 5.9.29 (p. 325)
1
8
Solution to Exercise 5.9.31 (p. 325)
11
16
Solution to Exercise 5.9.33 (p. 325)
8 2
11
Solution to Exercise 5.9.35 (p. 325)
1Solution to Exercise 5.9.37 (p. 325)
7 3
10
Solution to Exercise 5.9.39 (p. 325)
5
9
Solution to Exercise 5.9.41 (p. 325)
6
7
Solution to Exercise 5.9.43 (p. 325)
3 or 11
2
2
Solution to Exercise 5.9.45 (p. 326)
15
28
Solution to Exercise 5.9.47 (p. 326)
163
108 or 1 55
108
Solution to Exercise 5.9.49 (p. 326)
66
13 or 5 1
13
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 5. ADDITION AND SUBTRACTION OF FRACTIONS,
COMPARING FRACTIONS, AND COMPLEX FRACTIONS
Solution to Exercise 5.9.51 (p. 326)
7
40
Solution to Exercise 5.9.53 (p. 326)
255
184 or 1 71
184
Solution to Exercise 5.9.55 (p. 326)
3
32 , 18
Solution to Exercise 5.9.57 (p. 326)
3
10 , 56
Solution to Exercise 5.9.59 (p. 326)
3 , 8, 19
8
3
6
Solution to Exercise 5.9.61 (p. 326)
5 , 4
9
7
Solution to Exercise 5.9.63 (p. 327)
5
12 , 4 , 7
9
15
Solution to Exercise 5.9.65 (p. 327)
5 , 3, 13
8
4
16
Solution to Exercise 5.10.1 (p. 327)
5
16
Solution to Exercise 5.10.2 (p. 327)
7 56
Solution to Exercise 5.10.3 (p. 327)
1
Solution to Exercise 5.10.4 (p. 327)
8
11
Solution to Exercise 5.10.5 (p. 327)
8Solution to Exercise 5.10.6 (p. 327)
2 13
40
Solution to Exercise 5.10.7 (p. 327)
49
32 or 17
32
Solution to Exercise 5.10.8 (p. 327)
7
15
Solution to Exercise 5.10.9 (p. 327)
3 7
16
Solution to Exercise 5.10.10 (p. 327)
5
32
Solution to Exercise 5.10.11 (p. 327)
6 1 or 19
3
3
Solution to Exercise 5.10.12 (p. 327)
3 37
Solution to Exercise 5.10.13 (p. 327)
equivalent
Solution to Exercise 5.10.14 (p. 327)
not equivalent
Solution to Exercise 5.10.15 (p. 327)
equivalent
Solution to Exercise 5.10.16 (p. 328)
6 , 8
7
9
Solution to Exercise 5.10.17 (p. 328)
5 , 7
8
9
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 5.10.18 (p. 328)
11 516, 11 512
Solution to Exercise 5.10.19 (p. 328)
2
15 , 1 , 3
6
10
Solution to Exercise 5.10.20 (p. 328)
9
16 , 19
32 , 58
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 5. ADDITION AND SUBTRACTION OF FRACTIONS,
COMPARING FRACTIONS, AND COMPLEX FRACTIONS
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Decimals
6.1 Objectives1
After completing this chapter, you should
Reading and Writing Decimals (Section 6.2)
• understand the meaning of digits occurring to the right of the ones position
• be familiar with the meaning of decimal fractions
• be able to read and write a decimal fraction
Converting a Decimal to a Fraction (Section 6.3)
• be able to convert an ordinary decimal and a complex decimal to a fraction Rounding Decimals (Section 6.4)
• be able to round a decimal number to a specied position
Addition and Subtraction of Decimals (Section 6.5)
• understand the method used for adding and subtracting decimals
• be able to add and subtract decimals
• be able to use the calculator to add and subtract decimals
Multiplication of Decimals (Section 6.6)
• understand the method used for multiplying decimals
• be able to multiply decimals
• be able to simplify a multiplication of a decimal by a power of 10
• understand how to use the word “of” in multiplication
Division of Decimals (Section 6.7)
• understand the method used for dividing decimals
• be able to divide a decimal number by a nonzero whole number and by another, nonzero, decimal number
• be able to simplify a division of a decimal by a power of 10
Nonterminating Divisions (Section 6.8)
1This content is available online at <http://cnx.org/content/m18894/1.3/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4> 339
340
CHAPTER 6. DECIMALS
• understand the meaning of a nonterminating division
• be able to recognize a nonterminating number by its notation
Converting a Fraction to a Decimal (Section 6.9)
• be able to convert a fraction to a decimal
Combinations of Operations with Decimals and Fractions (Section 6.10)
• be able to combine operations with decimals
6.2 Reading and Writing Decimals2
6.2.1 Section Overview
• Digits to the Right of the Ones Position
• Decimal Fractions
• Reading Decimal Fractions
• Writing Decimal Fractions
6.2.2 Digits to the Right of the Ones Position
We began our study of arithmetic (Section 1.2) by noting that our number system is called a positional number system with base ten. We also noted that each position has a particular value. We observed that each position has ten times the value of the position to its right.
This means that each position has 1 the value of the position to its left.
10
Thus, a digit written to the right of the units position must have a value of 110 of 1. Recalling that the word
“of” translates to multiplication (·), we can see that the value of the rst position to the right of the units digit is 110 of 1, or
1
10 · 1 = 1
10
The value of the second position to the right of the units digit is 110 of 110, or 1
10 · 1
10 = 1
10 = 1
2
100
2This content is available online at <http://cnx.org/content/m34957/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
341
The value of the third position to the right of the units digit is 110 of 1
100 , or
1
10 · 1
100 = 1
10 =
1
3
1000
This pattern continues.
We can now see that if we were to write digits in positions to the right of the units positions, those positions have values that are fractions. Not only do the positions have fractional values, but the fractional values are all powers of 10 10, 102, 103, . . . .
6.2.3 Decimal Fractions
Decimal Point, Decimal
If we are to write numbers with digits appearing to the right of the units digit, we must have a way of denoting where the whole number part ends and the fractional part begins. Mathematicians denote the separation point of the units digit and the tenths digit by writing a decimal point. The word decimal comes from the Latin prex “deci” which means ten, and we use it because we use a base ten number system. Numbers written in this form are called decimal fractions, or more simply, decimals.
Notice that decimal numbers have the sux “th.”
Decimal Fraction
A decimal fraction is a fraction in which the denominator is a power of 10.
The following numbers are examples of decimals.
1. 42.6
The 6 is in the tenths position.
42.6 = 42 610
2. 9.8014
The 8 is in the tenths position.
The 0 is in the hundredths position.
The 1 is in the thousandths position.
The 4 is in the ten thousandths position.
9.8014 = 9 8014
10,000
3. 0.93
The 9 is in the tenths position.
The 3 is in the hundredths position.
0.93 = 93
100
note: Quite often a zero is inserted in front of a decimal point (in the units position) of a decimal fraction that has a value less than one. This zero helps keep us from overlooking the decimal point.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

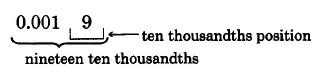
342
CHAPTER 6. DECIMALS
4. 0.7
The 7 is in the tenths position.
0.7 = 7
10
note: We can insert zeros to the right of the right-most digit in a decimal fraction without changing the value of the number.
7
10 = 0.7 = 0.70 = 70
100 = 7
10
6.2.4 Reading Decimal Fractions
Reading a Decimal Fraction
To read a decimal fraction,
1. Read the whole number part as usual. (If the whole number is less than 1, omit steps 1 and 2.) 2. Read the decimal point as the word “and.”
3. Read the number to the right of the decimal point as if it were a whole number.
4. Say the name of the position of the last digit.
6.2.4.1 Sample Set A
Read the following numbers.
Example 6.1
6.8
note: Some people read this as “six point eight.” This phrasing gets the message across, but technically, “six and eight tenths” is the correct phrasing.
Example 6.2
14.116
Example 6.3
0.0019
Example 6.4
81
Eighty-one
In this problem, the indication is that any whole number is a decimal fraction. Whole numbers are often called decimal numbers.
81 = 81.0
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
6.2.4.2 Practice Set A
Read the following decimal fractions.
Exercise 6.2.1
(Solution on p. 404.)
12.9
Exercise 6.2.2
(Solution on p. 404.)
4.86
Exercise 6.2.3
(Solution on p. 404.)
7.00002
Exercise 6.2.4
(Solution on p. 404.)
0.030405
6.2.5 Writing Decimal Fractions
Writing a Decimal Fraction
To write a decimal fraction,
1. Write the whole number part.
2. Write a decimal point for the word “and.”
3. Write the decimal part of the number so that the right-most digit appears in the position indicated in the word name. If necessary, insert zeros to the right of the decimal point in order that the right-most digit appears in the correct position.
6.2.5.1 Sample Set B
Write each number.
Example 6.5
Thirty-one and twelve hundredths.
The decimal position indicated is the hundredths position.
31.12
Example 6.6
Two and three hundred-thousandths.
The decimal position indicated is the hundred thousandths. We’ll need to insert enough zeros to the immediate right of the decimal point in order to locate the 3 in the correct position.
2.00003
Example 6.7
Six thousand twenty-seven and one hundred four millionths.
The decimal position indicated is the millionths position. We’ll need to insert enough zeros to the immediate right of the decimal point in order to locate the 4 in the correct position.
6,027.000104
Example 6.8
Seventeen hundredths.
The decimal position indicated is the hundredths position.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 6. DECIMALS
0.17
6.2.5.2 Practice Set B
Write each decimal fraction.
Exercise 6.2.5
(Solution on p. 404.)
Three hundred six and forty-nine hundredths.
Exercise 6.2.6
(Solution on p. 404.)
Nine and four thousandths.
Exercise 6.2.7
(Solution on p. 404.)
Sixty-one millionths.
6.2.6 Exercises
For the following three problems, give the decimal name of the position of the given number in each decimal fraction.
Exercise 6.2.8
(Solution on p. 404.)
1. 3.941
9 is in the
position.
4 is in the
position.
1 is in the
position.
Exercise 6.2.9
17.1085
1 is in the
position.
0 is in the
position.
8 is in the
position.
5 is in the
position.
Exercise 6.2.10
(Solution on p. 404.)
652.3561927
9 is in the
position.
7 is in the
position.
For the following 7 problems, read each decimal fraction by writing it.
Exercise 6.2.11
9.2
Exercise 6.2.12
(Solution on p. 404.)
8.1
Exercise 6.2.13
10.15
Exercise 6.2.14
(Solution on p. 404.)
55.06
Exercise 6.2.15
0.78
Exercise 6.2.16
(Solution on p. 404.)
1.904
Exercise 6.2.17
10.00011
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
For the following 10 problems, write each decimal fraction.
Exercise 6.2.18
(Solution on p. 404.)
Three and twenty one-hundredths.
Exercise 6.2.19
Fourteen and sixty seven-hundredths.
Exercise 6.2.20
(Solution on p. 404.)
One and eight tenths.
Exercise 6.2.21
Sixty-one and ve tenths.
Exercise 6.2.22
(Solution on p. 404.)
Five hundred eleven and four thousandths.
Exercise 6.2.23
Thirty-three and twelve ten-thousandths.
Exercise 6.2.24
(Solution on p. 404.)
Nine hundred forty-seven thousandths.
Exercise 6.2.25
Two millionths.
Exercise 6.2.26
(Solution on p. 404.)
Seventy-one hundred-thousandths.
Exercise 6.2.27
One and ten ten-millionths.
Calculator Problems
For the following 10 problems, perform each division using a calculator. Then write the resulting decimal using words.
Exercise 6.2.28
(Solution on p. 404.)
3 ÷ 4
Exercise 6.2.29
1 ÷ 8
Exercise 6.2.30
(Solution on p. 404.)
4 ÷ 10
Exercise 6.2.31
2 ÷ 5
Exercise 6.2.32
(Solution on p. 404.)
4 ÷ 25
Exercise 6.2.33
1 ÷ 50
Exercise 6.2.34
(Solution on p. 404.)
3 ÷ 16
Exercise 6.2.35
15 ÷ 8
Exercise 6.2.36
(Solution on p. 404.)
11 ÷ 20
Exercise 6.2.37
9 ÷ 40
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

346
CHAPTER 6. DECIMALS
6.2.6.1 Exercises for Review
Exercise 6.2.38
(Solution on p. 404.)
(Section 1.4) Round 2,614 to the nearest ten.
Exercise 6.2.39
(Section 2.5) Is 691,428,471 divisible by 3?
Exercise 6.2.40
(Solution on p. 404.)
(Section 4.4) Determine the missing numerator.
3 = ?
14
56
Exercise 6.2.41
(Section 4.7) Find 316 of 32
39
Exercise 6.2.42
(Solution on p. 404.)
q
(Section 5.7) Find the value of
25
2
81 + 2
+ 1
3
9
6.3 Converting a Decimal to a Fraction3
6.3.1 Section Overview
• Converting an Ordinary Decimal to a Fraction
• Converting a Complex Decimal to a Fraction
6.3.2 Converting an Ordinary Decimal to a Fraction
We can convert a decimal fraction to a fraction, essentially, by saying it in words, then writing what we say.
We may have to reduce that fraction.
6.3.2.1 Sample Set A
Convert each decimal fraction to a proper fraction or a mixed number.
Example 6.9
Reading: six tenths→ 6 .
10
Reduce: 3.
5
Example 6.10
Reading: nine hundred three thousands→ 903
1000 .
Example 6.11
3This content is available online at <http://cnx.org/content/m34958/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
347
Reading: eighteen and sixty-one hundredths→ 18 61
100 .
Example 6.12
Reading: ve hundred eight and ve ten thousandths→ 508 5
10,000 .
Reduce: 508 1
2,000 .
6.3.2.2 Practice Set A
Convert the following decimals to fractions or mixed numbers. Be sure to reduce.
Exercise 6.3.1
(Solution on p. 404.)
16.84
Exercise 6.3.2
(Solution on p. 405.)
0.513
Exercise 6.3.3
(Solution on p. 405.)
6,646.0107
Exercise 6.3.4
(Solution on p. 405.)
1.1
6.3.3 Converting A Complex Decimal to a Fraction
Complex Decimals
Numbers such as 0.112 are called complex decimals. We can also convert complex decimals to fractions.
3
6.3.3.1 Sample Set B
Convert the following complex decimals to fractions.
Example 6.13
0.11 23
The 2 appears to occur in the thousands position, but it is referring to 2 of a hundredth. So, we 3
3
read 0.112 as “eleven and two-thirds hundredths.”
3
11 2
11·3+2
0.11 2 =
3
3
3
100
=
100
35
=
3
100
1
=
35 ÷ 100
3
1
7
=
)35 · 1
3
)100
20
=
7
60
Example 6.14
4.006 14
Note that 4.0061 = 4 + .0061
4
4
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 6. DECIMALS
6 1
4 + .006 1
=
4 +
4
4
1000
25
=
4 +
4
1000
1
1
=
4 + )25 ·
1
4
)1000
40
=
4 + 1·1
4·40
=
4 + 1
160
=
4 1
160
6.3.3.2 Practice Set B
Convert each complex decimal to a fraction or mixed number. Be sure to reduce.
Exercise 6.3.5
(Solution on p. 405.)
0.8 34
Exercise 6.3.6
(Solution on p. 405.)
0.12 25
Exercise 6.3.7
(Solution on p. 405.)
6.005 56
Exercise 6.3.8
(Solution on p. 405.)
18.1 317
6.3.4 Exercises
For the following 20 problems, convert each decimal fraction to a proper fraction or a mixed number. Be sure to reduce.
Exercise 6.3.9
(Solution on p. 405.)
0.7
Exercise 6.3.10
0.1
Exercise 6.3.11
(Solution on p. 405.)
0.53
Exercise 6.3.12
0.71
Exercise 6.3.13
(Solution on p. 405.)