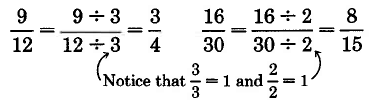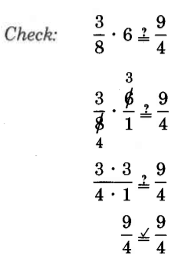125 Fundamentals of Mathematics: Part 7
Introduction to Fractions and
Multiplication and Division of Fractions
4.1 Objectives 1
After completing this chapter, you should
Fractions of Whole Numbers (Section 4.2)
• understand the concept of fractions of whole numbers
• be able to recognize the parts of a fraction
Proper Fractions, improper Fractions, and Mixed Numbers (Section 4.3)
• be able to distinguish between proper fractions, improper fractions, and mixed numbers
• be able to convert an improper fraction to a mixed number
• be able to convert a mixed number to an improper fraction
Equivalent Fractions, Reducing Fractions to Lowest Terms, and Raising Fractions to Higher Terms (Section 4.4)
• be able to recognize equivalent fractions
• be able to reduce a fraction to lowest terms
• be able to raise a fraction to higher terms
Multiplication of Fractions (Section 4.5)
• understand the concept of multiplication of fractions
• be able to multiply one fraction by another
• be able to multiply mixed numbers
• be able to nd powers and roots of various fractions
Division of Fractions (Section 4.6)
• be able to determine the reciprocal of a number
• be able to divide one fraction by another
Applications Involving Fractions (Section 4.7)
• be able to solve missing product statements
• be able to solve missing factor statements
1This content is available online at <http://cnx.org/content/m18892/1.3/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4> 213


214
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
4.2 Fractions of Whole Numbers 2
4.2.1 Section Overview
• More Numbers on the Number Line
• Fractions of Whole Numbers
• The Parts of a Fraction
• Reading and Writing Fractions
4.2.2 More Numbers on the Number Line
In Chapters Section 1.1, Section 2.1, and Section 3.1, we studied the whole numbers and methods of combining them. We noted that we could visually display the whole numbers by drawing a number line and placing closed circles at whole number locations.
By observing this number line, we can see that the whole numbers do not account for every point on the line. What numbers, if any, can be associated with these points? In this section we will see that many of the points on the number line, including the points already associated with whole numbers, can be associated with numbers called fractions.
4.2.3 Fractions of Whole Numbers
The Nature of the Positive Fractions
We can extend our collection of numbers, which now contains only the whole numbers, by including fractions of whole numbers. We can determine the nature of these fractions using the number line.
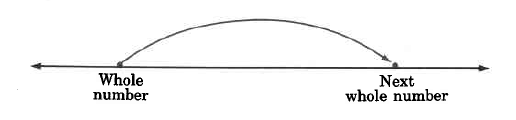
If we place a pencil at some whole number and proceed to travel to the right to the next whole number, we see that our journey can be broken into dierent types of equal parts as shown in the following examples.
a. 1 part.
b. 2 equal parts.
c. 3 equal parts.
2This content is available online at <http://cnx.org/content/m34908/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

215
d. 4 equal parts.
The Latin Word Fractio
Notice that the number of parts, 2, 3, and 4, that we are breaking the original quantity into is always a nonzero whole number. The idea of breaking up a whole quantity gives us the word fraction. The word fraction comes from the Latin word “fractio” which means a breaking, or fracture.
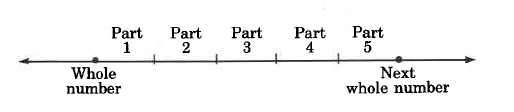
Suppose we break up the interval from some whole number to the next whole number into ve equal parts.
After starting to move from one whole number to the next, we decide to stop after covering only two parts.
We have covered 2 parts of 5 equal parts. This situation is described by writing 2.
5
Positive Fraction
A number such as 2 is called a positive fraction, or more simply, a fraction.
5
4.2.4 The Parts of a Fraction
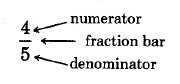
A fraction has three parts.
1. The fraction bar
.Fraction Bar
The fraction bar serves as a grouping symbol. It separates a quantity into individual groups. These groups have names, as noted in 2 and 3 below.
2. The nonzero number below the fraction bar.Denominator
This number is called the denominator of the fraction, and it indicates the number of parts the whole quantity has been divided into. Notice that the denominator must be a nonzero whole number since the least number of parts any quantity can have is one.
3. The number above the fraction bar. Numerator
This number is called the numerator of the fraction, and it indicates how many of the specied parts are being considered. Notice that the numerator can be any whole number (including zero) since any number of the specied parts can be considered.
whole number
nonzero whole number ↔ numerator
denominator
4.2.4.1 Sample Set A
The diagrams in the following problems are illustrations of fractions.
Example 4.1
Available for free at Connexions <http://cnx.org/content/col10615/1.4>




216
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
(a)
(b)
(c)
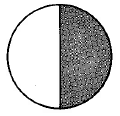
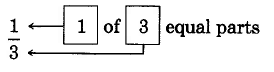
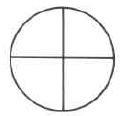
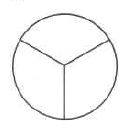
Diagrams 4.1: (a) A whole circle (b) The whole circle divided into 3 equal parts (c) 1 of the 3 equal parts
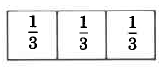
The fraction 1 is read as “one third.”
3
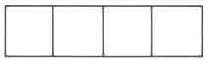
Example 4.2
(a)
(b)
(c)
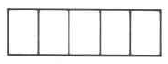
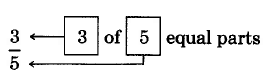
Figure 4.2: (a) A whole rectangle (b) The whole rectangle divided into 5 equal parts (c) 3 of the 5
equal parts
The fraction 3 “is read as “three fths.”
5
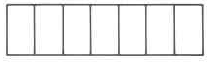
Example 4.3
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

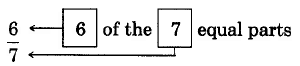

217
(a)
(b)
(c)
Figure 4.3: (a) The number line between 0 and 1 (b) The number line between 0 and 1 divided into 7 equal parts (c) 6 of the 7 equal parts
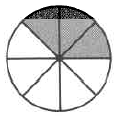
The fraction 6 is read as “six sevenths.”
7
Example 4.4
(a)
(b)
(c)
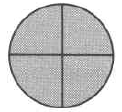
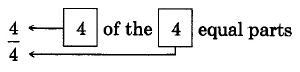
Figure 4.4: (a) A whole circle (b) The whole circle divided into 4 equal parts (c) 4 of the 4 equal parts When the numerator and denominator are equal, the fraction represents the entire quantity, and its value is 1.
nonzero whole number
same nonzero whole number = 1
4.2.4.2 Practice Set A
Specify the numerator and denominator of the following fractions.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
Exercise 4.2.1
(Solution on p. 278.)
4
7
Exercise 4.2.2
(Solution on p. 278.)
5
8
Exercise 4.2.3
(Solution on p. 278.)
10
15
Exercise 4.2.4
(Solution on p. 278.)
1
9
Exercise 4.2.5
(Solution on p. 278.)
0
2
4.2.5 Reading and Writing Fractions
In order to properly translate fractions from word form to number form, or from number form to word form, it is necessary to understand the use of the hyphen.
Use of the Hyphen
One of the main uses of the hyphen is to tell the reader that two words not ordinarily joined are to be taken in combination as a unit. Hyphens are always used for numbers between and including 21 and 99 (except those ending in zero).
4.2.5.1 Sample Set B
Write each fraction using whole numbers.
Example 4.5
Fifty three-hundredths.
The hyphen joins the words three and hundredths and tells us to
consider them as a single unit. Therefore,
fty three-hundredths translates as 50
300
Example 4.6
Fifty-three hundredths.
The hyphen joins the numbers fty and three and tells us to consider
them as a single unit. Therefore,
fty-three hundredths translates as 53
100
Example 4.7
Four hundred seven-thousandths.
The hyphen joins the words seven and thousandths and
tells us to consider them as a single unit. Therefore,
four hundred seven-thousandths translates as 400
7,000
Example 4.8
Four hundred seven thousandths.
The absence of hyphens indicates that the words seven and
thousandths are to be considered individually.
four hundred seven thousandths translates as 407
1000
Write each fraction using words.
Example 4.9
21
85 translates as twenty-one eighty-fths.
Example 4.10
200
3,000 translates as two hundred three-thousandths.
A hyphen is needed between the words
three and thousandths to tell the reader that these words are to be considered as a single unit.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
219
Example 4.11
203
1,000 translates as two hundred three thousandths.
4.2.5.2 Practice Set B
Write the following fractions using whole numbers.
Exercise 4.2.6
(Solution on p. 278.)
one tenth
Exercise 4.2.7
(Solution on p. 278.)
eleven fourteenths
Exercise 4.2.8
(Solution on p. 278.)
sixteen thirty-fths
Exercise 4.2.9
(Solution on p. 278.)
eight hundred seven-thousandths
Write the following using words.
Exercise 4.2.10
(Solution on p. 278.)
3
8
Exercise 4.2.11
(Solution on p. 278.)
1
10
Exercise 4.2.12
(Solution on p. 278.)
3
250
Exercise 4.2.13
(Solution on p. 278.)
114
3,190
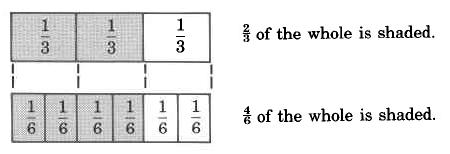
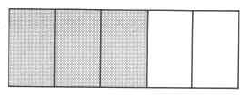
Name the fraction that describes each shaded portion.
Exercise 4.2.14
(Solution on p. 278.)
Exercise 4.2.15
(Solution on p. 278.)
In the following 2 problems, state the numerator and denominator, and write each fraction in words.
Exercise 4.2.16
(Solution on p. 278.)
The number 5 is used in converting from Fahrenheit to Celsius.
9
Exercise 4.2.17
(Solution on p. 278.)
A dime is 110 of a dollar.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
4.2.6 Exercises
For the following 10 problems, specify the numerator and denominator in each fraction.
Exercise 4.2.18
(Solution on p. 278.)
3
4
Exercise 4.2.19
9
10
Exercise 4.2.20
(Solution on p. 278.)
1
5
Exercise 4.2.21
5
6
Exercise 4.2.22
(Solution on p. 278.)
7
7
Exercise 4.2.23
4
6
Exercise 4.2.24
(Solution on p. 278.)
0
12
Exercise 4.2.25
25
25
Exercise 4.2.26
(Solution on p. 278.)
18
1
Exercise 4.2.27
0
16
For the following 10 problems, write the fractions using whole numbers.
Exercise 4.2.28
(Solution on p. 278.)
four fths
Exercise 4.2.29
two ninths
Exercise 4.2.30
(Solution on p. 278.)
fteen twentieths
Exercise 4.2.31
forty-seven eighty-thirds
Exercise 4.2.32
(Solution on p. 278.)
ninety-one one hundred sevenths
Exercise 4.2.33
twenty-two four hundred elevenths
Exercise 4.2.34
(Solution on p. 279.)
six hundred ve eight hundred thirty-fourths
Exercise 4.2.35
three thousand three forty-four ten-thousandths
Exercise 4.2.36
(Solution on p. 279.)
ninety-two one-millionths
Exercise 4.2.37
one three-billionths
For the following 10 problems, write the fractions using words.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

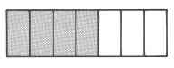
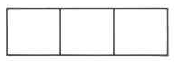
221
Exercise 4.2.38
(Solution on p. 279.)
5
9
Exercise 4.2.39
6
10
Exercise 4.2.40
(Solution on p. 279.)
8
15
Exercise 4.2.41
10
13
Exercise 4.2.42
(Solution on p. 279.)
75
100
Exercise 4.2.43
86
135
Exercise 4.2.44
(Solution on p. 279.)
916
1,014
Exercise 4.2.45
501
10,001
Exercise 4.2.46
(Solution on p. 279.)
18
31,608
Exercise 4.2.47
1
500,000
For the following 4 problems, name the fraction corresponding to the shaded portion.
Exercise 4.2.48
(Solution on p. 279.)
Exercise 4.2.49
Exercise 4.2.50
(Solution on p. 279.)
Exercise 4.2.51
For the following 4 problems, shade the portion corresponding to the given fraction on the given gure.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
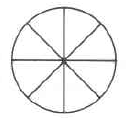
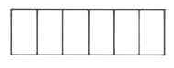
222
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
Exercise 4.2.52
(Solution on p. 279.)
3
5
Exercise 4.2.53
1
8
Exercise 4.2.54
(Solution on p. 279.)
6
6
Exercise 4.2.55
0
3
State the numerator and denominator and write in words each of the fractions appearing in the statements for the following 10 problems.
Exercise 4.2.56
(Solution on p. 279.)
A contractor is selling houses on 1 acre lots.
4
Exercise 4.2.57
The fraction 22 is sometimes used as an approximation to the number π. (The symbol is read 7
pi.”)
Exercise 4.2.58
(Solution on p. 279.)
The fraction 4 is used in nding the volume of a sphere.
3
Exercise 4.2.59
One inch is 112 of a foot.
Exercise 4.2.60
(Solution on p. 279.)
About 2 of the students in a college statistics class received a B in the course.
7
Exercise 4.2.61
The probability of randomly selecting a club when drawing one card from a standard deck of 52
cards is 13
52 .
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 4.2.62
(Solution on p. 279.)
In a box that contains eight computer chips, ve are known to be good and three are known to be defective. If three chips are selected at random, the probability that all three are defective is 156.
Exercise 4.2.63
In a room of 25 people, the probability that at least two people have the same birthdate (date and month, not year) is 569
1000 .
Exercise 4.2.64
(Solution on p. 279.)
The mean (average) of the numbers 21, 25, 43, and 36 is 125.
4
Exercise 4.2.65
If a rock falls from a height of 20 meters on Jupiter, the rock will be 32
25 meters high after 6 seconds.
5
4.2.6.1 Exercises For Review
Exercise 4.2.66
(Solution on p. 279.)
(Section 1.7) Use the numbers 3 and 11 to illustrate the commutative property of addition.
Exercise 4.2.67
(Section 2.4) Find the quotient. 676 ÷ 26
Exercise 4.2.68
(Solution on p. 279.)
(Section 3.2) Write 7 · 7 · 7 · 7 · 7 using exponents.
Exercise 4.2.69
(Section 3.3) Find the value of 8·(6+20) + 3·(6+16)
8
22
.
Exercise 4.2.70
(Solution on p. 279.)
(Section 3.6) Find the least common multiple of 12, 16, and 18.
4.3 Proper Fractions, Improper Fractions, and Mixed Numbers3
4.3.1 Section Overview
• Positive Proper Fractions
• Positive Improper Fractions
• Positive Mixed Numbers
• Relating Positive Improper Fractions and Positive Mixed Numbers
• Converting an Improper Fraction to a Mixed Number
• Converting a Mixed Number to an Improper Fraction
Now that we know what positive fractions are, we consider three types of positive fractions: proper fractions, improper fractions, and mixed numbers.
4.3.2 Positive Proper Fractions
Positive Proper Fraction
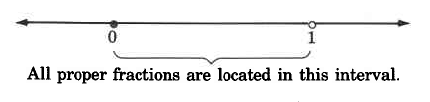
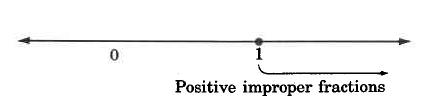
Fractions in which the whole number in the numerator is strictly less than the whole number in the denominator are called positive proper fractions. On the number line, proper fractions are located in the interval from 0 to 1. Positive proper fractions are always less than one.
3This content is available online at <http://cnx.org/content/m34912/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

224
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
The closed circle at 0 indicates that 0 is included, while the open circle at 1 indicates that 1 is not included.
Some examples of positive proper fractions are
1 , 3, 20
2
5
27 , and 106
255
Note that 1 < 2, 3 < 5, 20 < 27, and 106 < 225.
4.3.3 Positive Improper Fractions
Positive Improper Fractions
Fractions in which the whole number in the numerator is greater than or equal to the whole number in the denominator are called positive improper fractions. On the number line, improper fractions lie to the right of (and including) 1. Positive improper fractions are always greater than or equal to 1.
Some examples of positive improper fractions are
3 , 8, 4, and 105
2
5
4
16
Note that 3 ≥ 2, 8 ≥ 5, 4 ≥ 4, and 105 ≥ 16.
4.3.4 Positive Mixed Numbers
Positive Mixed Numbers
A number of the form
nonzero whole number + proper fraction
is called a positive mixed number. For example, 23 is a mixed number. On the number line, mixed 5
numbers are located in the interval to the right of (and including) 1. Mixed numbers are always greater than or equal to 1.
4.3.5 Relating Positive Improper Fractions and Positive Mixed Numbers
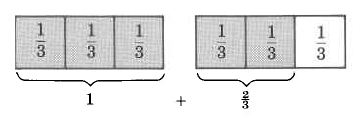
A relationship between improper fractions and mixed numbers is suggested by two facts. The rst is that improper fractions and mixed numbers are located in the same interval on the number line. The second fact, that mixed numbers are the sum of a natural number and a fraction, can be seen by making the following observations.
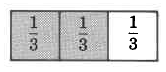
Divide a whole quantity into 3 equal parts.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>






225
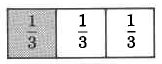
Now, consider the following examples by observing the respective shaded areas.
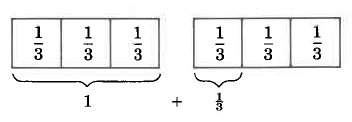
In the shaded region, there are 2 one thirds, or 2.
3
2 1 = 2
3
3
There are 3 one thirds, or 3, or 1.
3
3 1 = 3
or 1
3
3
Thus,
3 = 1
3
Improper fraction = whole number.
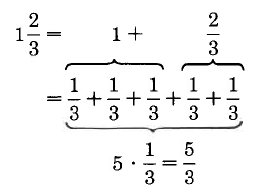
There are 4 one thirds, or 4, or 1 and 1.
3
3
4 1 = 4 or 1 and 1
3
3
3
The terms 1 and 1 can be represented as 1 + 1 or 11
3
3
3
Thus,
4 = 1 1 .
3
3
Improper fraction = mixed number.
There are 5 one thirds, or 5, or 1 and 2.
3
3
5 1 = 5
or 1 and 2
3
3
3
The terms 1 and 2 can be represented as 1 + 2 or 12.
3
3
3
Thus,
5 = 1 2 .
3
3
Improper fraction = mixed number.
There are 6 one thirds, or 6, or 2.
3
6 1 = 6 = 2
3
3
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
226
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
Thus,
6 = 2
3
Improper fraction = whole number.
The following important fact is illustrated in the preceding examples.
Mixed Number = Natural Number + Proper Fraction
Mixed numbers are the sum of a natural number and a proper fraction. Mixed number = (natural number)
+ (proper fraction)
For example 11 can be expressed as 1 + 1 The fraction 57 can be expressed as 5 + 7.
3
3
8
8
It is important to note that a number such as 5 + 7 does not indicate multiplication. To indicate multipli-8
cation, we would need to use a multiplication symbol (such as ·)
note: 57 means 5 + 7 and not 5 · 7, which means 5 times 7 or 5 multiplied by 7.
8
8
8
8
8
Thus, mixed numbers may be represented by improper fractions, and improper fractions may be represented by mixed numbers.
4.3.6 Converting Improper Fractions to Mixed Numbers
To understand how we might convert an improper fraction to a mixed number, let’s consider the fraction, 4.
3
1
1
1
4
=
+
+
+ 1
3
3
3
3
3
|
{z
}
1
=
1 + 13
=
1 13
Thus, 4 = 11.
3
3
We can illustrate a procedure for converting an improper fraction to a mixed number using this example.
However, the conversion is more easily accomplished by dividing the numerator by the denominator and using the result to write the mixed number.
Converting an Improper Fraction to a Mixed Number
To convert an improper fraction to a mixed number, divide the numerator by the denominator.
1. The whole number part of the mixed number is the quotient.
2. The fractional part of the mixed number is the remainder written over the divisor (the denominator of the improper fraction).
Available for free at Connexions <http://cnx.org/content/col10615/1.4>



227
4.3.6.1 Sample Set A
Convert each improper fraction to its corresponding mixed number.
Example 4.12
5 Divide 5 by 3.
3
The improper fraction 5 = 12.
3
3
Example 4.13
46 . Divide 46 by 9.
9
The improper fraction 46 = 51.
9
9
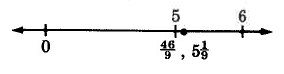
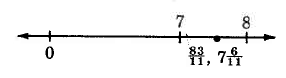
Example 4.14
83
11 . Divide 83 by 11.
The improper fraction 83
11 = 7 6
11 .
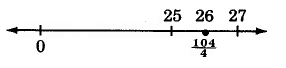
Example 4.15
104 Divide 104 by 4.
4
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
228
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
104 = 260 = 26
4
4
The improper fraction 104 = 26.
4
4.3.6.2 Practice Set A
Convert each improper fraction to its corresponding mixed number.
Exercise 4.3.1
(Solution on p. 279.)
9
2
Exercise 4.3.2
(Solution on p. 279.)
11
3
Exercise 4.3.3
(Solution on p. 279.)
14
11
Exercise 4.3.4
(Solution on p. 279.)
31
13
Exercise 4.3.5
(Solution on p. 280.)
79
4
Exercise 4.3.6
(Solution on p. 280.)
496
8
4.3.7 Converting Mixed Numbers to Improper Fractions
To understand how to convert a mixed number to an improper fraction, we’ll recall mixed number = (natural number) + (proper fraction)
and consider the following diagram.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
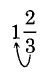

229
Recall that multiplication describes repeated addition.
Notice that 5 can be obtained from 12 using multiplication in the following way.
3
3
Multiply: 3 · 1 = 3
Add: 3 + 2 = 5. Place the 5 over the 3: 53
The procedure for converting a mixed number to an improper fraction is illustrated in this example.
Converting a Mixed Number to an Improper Fraction
To convert a mixed number to an improper fraction,
1. Multiply the denominator of the fractional part of the mixed number by the whole number part.
2. To this product, add the numerator of the fractional part.
3. Place this result over the denominator of the fractional part.
4.3.7.1 Sample Set B
Convert each mixed number to an improper fraction.
Example 4.16
5 78
1. Multiply: 8 · 5 = 40.
2. Add: 40 + 7 = 47.
3. Place 47 over 8: 47.
8
Thus, 57 = 47.
8
8
Example 4.17
1623
1. Multiply: 3 · 16 = 48.
2. Add: 48 + 2 = 50.
3. Place 50 over 3: 503
Thus, 162 = 50
3
3
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
4.3.7.2 Practice Set B
Convert each mixed number to its corresponding improper fraction.
Exercise 4.3.7
(Solution on p. 280.)
8 14
Exercise 4.3.8
(Solution on p. 280.)
5 35
Exercise 4.3.9
(Solution on p. 280.)
1 4
15
Exercise 4.3.10
(Solution on p. 280.)
1227
4.3.8 Exercises
For the following 15 problems, identify each expression as a proper fraction, an improper fraction, or a mixed number.
Exercise 4.3.11
(Solution on p. 280.)
3
2
Exercise 4.3.12
4
9
Exercise 4.3.13
(Solution on p. 280.)
5
7
Exercise 4.3.14
1
8
Exercise 4.3.15
(Solution on p. 280.)
6 14
Exercise 4.3.16
11
8
Exercise 4.3.17
(Solution on p. 280.)
1,001
12
Exercise 4.3.18
19145
Exercise 4.3.19
(Solution on p. 280.)
1 9
13
Exercise 4.3.20
3167
Exercise 4.3.21
(Solution on p. 280.)
3 1
40
Exercise 4.3.22
55
12
Exercise 4.3.23
(Solution on p. 280.)
0
9
Exercise 4.3.24
8
9
Exercise 4.3.25
(Solution on p. 280.)
101 111
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
For the following 15 problems, convert each of the improper fractions to its corresponding mixed number.
Exercise 4.3.26
11
6
Exercise 4.3.27
(Solution on p. 280.)
14
3
Exercise 4.3.28
25
4
Exercise 4.3.29
(Solution on p. 280.)
35
4
Exercise 4.3.30
71
8
Exercise 4.3.31
(Solution on p. 280.)
63
7
Exercise 4.3.32
121
11
Exercise 4.3.33
(Solution on p. 280.)
165
12
Exercise 4.3.34
346
15
Exercise 4.3.35
(Solution on p. 280.)
5,000
9
Exercise 4.3.36
23
5
Exercise 4.3.37
(Solution on p. 280.)
73
2
Exercise 4.3.38
19
2
Exercise 4.3.39
(Solution on p. 280.)
316
41
Exercise 4.3.40
800
3
For the following 15 problems, convert each of the mixed numbers to its corresponding improper fraction.
Exercise 4.3.41
(Solution on p. 280.)
4 18
Exercise 4.3.42
1 5
12
Exercise 4.3.43
(Solution on p. 280.)
6 79
Exercise 4.3.44
1514
Exercise 4.3.45
(Solution on p. 280.)
10 511
Exercise 4.3.46
15 310
Exercise 4.3.47
(Solution on p. 280.)
8 23
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
Exercise 4.3.48
4 34
Exercise 4.3.49
(Solution on p. 281.)
2125
Exercise 4.3.50
17 910
Exercise 4.3.51
(Solution on p. 281.)
9 20
21
Exercise 4.3.52
5 1
16
Exercise 4.3.53
(Solution on p. 281.)
90 1
100
Exercise 4.3.54
300 43
1,000
Exercise 4.3.55
(Solution on p. 281.)
1978
Exercise 4.3.56
Why does 04 not qualify as a mixed number?
7
Hint: See the denition of a mixed number.
Exercise 4.3.57
(Solution on p. 281.)
Why does 5 qualify as a mixed number?
note: See the denition of a mixed number.
Calculator Problems
For the following 8 problems, use a calculator to convert each mixed number to its corresponding improper fraction.
Exercise 4.3.58
3511
12
Exercise 4.3.59
(Solution on p. 281.)
27 561
Exercise 4.3.60
8340
41
Exercise 4.3.61
(Solution on p. 281.)
10521
23
Exercise 4.3.62
72605
606
Exercise 4.3.63
(Solution on p. 281.)
81619
25
Exercise 4.3.64
70842
51
Exercise 4.3.65
(Solution on p. 281.)
6, 012 4,216
8,117
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
233
4.3.8.1 Exercises For Review
Exercise 4.3.66
(Section 1.4) Round 2,614,000 to the nearest thousand.
Exercise 4.3.67
(Solution on p. 281.)
(Section 2.2) Find the product. 1,004 · 1,005.
Exercise 4.3.68
(Section 2.5) Determine if 41,826 is divisible by 2 and 3.
Exercise 4.3.69
(Solution on p. 281.)
(Section 3.6) Find the least common multiple of 28 and 36.
Exercise 4.3.70
(Section 4.2) Specify the numerator and denominator of the fraction 12
19 .
4.4 Equivalent Fractions, Reducing Fractions to Lowest Terms, and
Raising Fractions to Higher Terms 4
4.4.1 Section Overview
• Equivalent Fractions
• Reducing Fractions to Lowest Terms
• Raising Fractions to Higher Terms
4.4.2 Equivalent Fractions
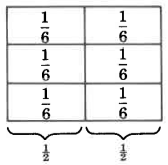
Let’s examine the following two diagrams.
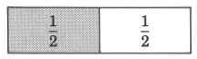
Notice that both 2 and 4 represent the same part of the whole, that is, they represent the same number.
3
6
Equivalent Fractions
Fractions that have the same value are called equivalent fractions. Equivalent fractions may look dierent, but they are still the same point on the number line.
There is an interesting property that equivalent fractions satisfy.
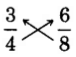
A Test for Equivalent Fractions Using the Cross Product
These pairs of products are called cross products.
4This content is available online at <http://cnx.org/content/m34927/1.3/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

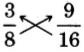
234
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
If the cross products are equal, the fractions are equivalent. If the cross products are not equal, the fractions are not equivalent.
Thus, 2 and 4 are equivalent, that is, 2 = 4.
3
6
3
6
4.4.2.1 Sample Set A
Determine if the following pairs of fractions are equivalent.
Example 4.18
3 and 6. Test for equality of the cross products.
4
8
The cross products are equals.
The fractions 3 and 6 are equivalent, so 3 = 6.
4
8
4
8
Example 4.19
3 and 9
8
16 . Test for equality of the cross products.
The cross products are not equal.
The fractions 3 and 9
8
16 are not equivalent.
4.4.2.2 Practice Set A
Determine if the pairs of fractions are equivalent.
Exercise 4.4.1
(Solution on p. 281.)
1 , 3
2
6
Exercise 4.4.2
(Solution on p. 281.)
4 , 12
5
15
Exercise 4.4.3
(Solution on p. 281.)
2 , 8
3
15
Exercise 4.4.4
(Solution on p. 281.)
1 , 5
8
40
Exercise 4.4.5
(Solution on p. 281.)
3
12 , 14
4.4.3 Reducing Fractions to Lowest Terms
It is often very useful to convert one fraction to an equivalent fraction that has reduced values in the numerator and denominator. We can suggest a method for doing so by considering the equivalent fractions 9
15 and 3 . First, divide both the numerator and denominator of 9
are
5
15 by 3. The fractions 9
15 and 35
equivalent.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
235
(Can you prove this?) So, 915 = 3. We wish to convert 9
. Now divide the numerator and denominator
5
15 to 35
of 915 by 3, and see what happens.
9÷3
15
= 3
÷3
5
The fraction 915 is converted to 3.
5
A natural question is “Why did we choose to divide by 3?” Notice that 9
15 = 3·3
5·3
We can see that the factor 3 is common to both the numerator and denominator.
Reducing a Fraction
From these observations we can suggest the following method for converting one fraction to an equivalent fraction that has reduced values in the numerator and denominator. The method is called reducing a fraction.
A fraction can be reduced by dividing both the numerator and denominator by the same nonzero whole number.
Consider the collection of equivalent fractions
5
20 , 4
16 , 3
12 , 2 , 1
8
4
Reduced to Lowest Terms
Notice that each of the rst four fractions can be reduced to the last fraction, 1, by dividing both the 4
numerator and denominator by, respectively, 5, 4, 3, and 2. When a fraction is converted to the fraction that has the smallest numerator and denominator in its collection of equivalent fractions, it is said to be reduced to lowest terms. The fractions 1, 3, 2, and 7
4
8
5
10 are all reduced to lowest terms.
Observe a very important property of a fraction that has been reduced to lowest terms. The only whole number that divides both the numerator and denominator without a remainder is the number 1. When 1 is the only whole number that divides two whole numbers, the two whole numbers are said to be relatively prime.
Relatively Prime
A fraction is reduced to lowest terms if its numerator and denominator are relatively prime.
4.4.3.1 Methods of Reducing Fractions to Lowest Terms
Method 1: Dividing Out Common Primes
1. Write the numerator and denominator as a product of primes.
2. Divide the numerator and denominator by each of the common prime factors. We often indicate this division by drawing a slanted line through each divided out factor. This process is also called cancelling common factors.
3. The product of the remaining factors in the numerator and the product of remaining factors of the denominator are relatively prime, and this fraction is reduced to lowest terms.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
4.4.3.1.1 Sample Set B
Reduce each fraction to lowest terms.
Example 4.20
1
1
6
)2·)3
18 =
= 1 1 and 3 are relatively prime.
)2·)3·3
3
1
1
Example 4.21
1
1
16
)2·)2·2·2
20 =
= 4 4 and 5 are relatively prime.
)2·)2·5
5
1
1
Example 4.22
1
1
1
56
)2·)2·)2·7
104 =
= 7
)2·)2·)2·13
13 7 and 13 are relatively prime (and also truly prime)
1
1
1
Example 4.23
1
1
315
)3·3·5·)7
336 =
= 15
2·2·2·2·)3·)7·
16
15 and 16 are relatively prime.
1
1
Example 4.24
8
15 = 2·2·2 No common prime factors, so 8 and 15 are relatively prime.
3·5
The fraction 815 is reduced to lowest terms.
4.4.3.1.2 Practice Set B
Reduce each fraction to lowest terms.
Exercise 4.4.6
(Solution on p. 281.)
4
8
Exercise 4.4.7
(Solution on p. 281.)
6
15
Exercise 4.4.8
(Solution on p. 281.)
6
48
Exercise 4.4.9
(Solution on p. 281.)
21
48
Exercise 4.4.10
(Solution on p. 281.)
72
42
Exercise 4.4.11
(Solution on p. 281.)
135
243
Method 2: Dividing Out Common Factors
1. Mentally divide the numerator and the denominator by a factor that is common to each. Write the quotient above the original number.
2. Continue this process until the numerator and denominator are relatively prime.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
4.4.3.1.3 Sample Set C
Reduce each fraction to lowest terms.
Example 4.25
25
30 . 5 divides into both 25 and 30.
5
)25 = 5 5 and 6 are relatively prime.
)30
6
6
Example 4.26
18
24 . Both numbers are even so we can divide by 2.
9
)18 Now, both 9 and 12 are divisible by 3.
)24
12
3
)9
)18 = 3 3 and 4 are relatively prime.
)24
4
)12
4
Example 4.27
7
)21
)210 = 7 . 7 and 5 are relatively prime.
)150
5
)15
5
Example 4.28
36
96 = 18
48 = 9
24 = 3 . 3 and 8 are relatively prime.
8
4.4.3.1.4 Practice Set C
Reduce each fraction to lowest terms.
Exercise 4.4.12
(Solution on p. 281.)
12
16
Exercise 4.4.13
(Solution on p. 281.)
9
24
Exercise 4.4.14
(Solution on p. 281.)
21
84
Exercise 4.4.15
(Solution on p. 282.)
48
64
Exercise 4.4.16
(Solution on p. 282.)
63
81
Exercise 4.4.17
(Solution on p. 282.)
150
240
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
238
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
4.4.4 Raising Fractions to Higher Terms
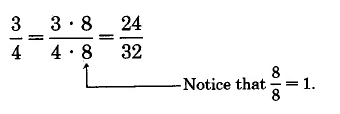
Equally as important as reducing fractions is raising fractions to higher terms. Raising a fraction to higher terms is the process of constructing an equivalent fraction that has higher values in the numerator and denominator than the original fraction.
The fractions 3 and 9
= 9
5
15 are equivalent, that is, 35
15 . Notice also,
3·3 = 9
5·3
15
Notice that 3 = 1 and that 3 · 1 = 3. We are not changing the value of 3.
3
5
5
5
From these observations we can suggest the following method for converting one fraction to an equivalent fraction that has higher values in the numerator and denominator. This method is called raising a fraction to higher terms.
Raising a Fraction to Higher Terms
A fraction can be raised to an equivalent fraction that has higher terms in the numerator and denominator by multiplying both the numerator and denominator by the same nonzero whole number.
The fraction 3 can be raised to 24
4
32 by multiplying both the numerator and denominator by 8.
Most often, we will want to convert a given fraction to an equivalent fraction with a higher specied denominator. For example, we may wish to convert 5 to an equivalent fraction that has denominator 32, that 8
is,
5 = ?
8
32
This is possible to do because we know the process. We must multiply both the numerator and denominator of 5 by the same nonzero whole number in order to 8 obtain an equivalent fraction.
8
We have some information. The denominator 8 was raised to 32 by multiplying it by some nonzero whole number. Division will give us the proper factor. Divide the original denominator into the new denominator.
32 ÷ 8 = 4
Now, multiply the numerator 5 by 4.
5 · 4 = 20
Thus,
5 = 5·4 = 20
8
8·4
32
So,
5 = 20
8
32
4.4.4.1 Sample Set D
Determine the missing numerator or denominator.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Example 4.29
3 = ?
7
35 . Divide the original denominator into the new denominator.
35 ÷ 7 = 5 The quotient is 5. Multiply the original numerator by 5.
3 = 3·5 = 15
7
7·5
35 The missing numerator is 15.
Example 4.30
5 = 45 . Divide the original numerator into the new numerator.
6
?
45 ÷ 5 = 9 The quotient is 9. Multiply the original denominator by 9.
5 = 5·9 = 45
6
6·9
54 The missing denominator is 45.
4.4.4.2 Practice Set D
Determine the missing numerator or denominator.
Exercise 4.4.18
(Solution on p. 282.)
4 = ?
5
40
Exercise 4.4.19
(Solution on p. 282.)
3 = ?
7
28
Exercise 4.4.20
(Solution on p. 282.)
1 = ?
6
24
Exercise 4.4.21
(Solution on p. 282.)
3
10 = 45
?
Exercise 4.4.22
(Solution on p. 282.)
8
15 = ?
165
4.4.5 Exercises
For the following problems, determine if the pairs of fractions are equivalent.
Exercise 4.4.23
(Solution on p. 282.)
1 , 5
2
10
Exercise 4.4.24
2 , 8
3
12
Exercise 4.4.25
(Solution on p. 282.)
5
12 , 10
24
Exercise 4.4.26
1 , 3
2
6
Exercise 4.4.27
(Solution on p. 282.)
3 , 12
5
15
Exercise 4.4.28
1 , 7
6
42
Exercise 4.4.29
(Solution on p. 282.)
16
25 , 49
75
Exercise 4.4.30
5
28 , 20
112
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
Exercise 4.4.31
(Solution on p. 282.)
3
10 , 36
110
Exercise 4.4.32
6
10 , 18
32
Exercise 4.4.33
(Solution on p. 282.)
5 , 15
8
24
Exercise 4.4.34
10
16 , 15
24
Exercise 4.4.35
(Solution on p. 282.)
4 , 3
5
4
Exercise 4.4.36
5 , 15
7
21
Exercise 4.4.37
(Solution on p. 282.)
9
11 , 11
9
For the following problems, determine the missing numerator or denominator.
Exercise 4.4.38
1 = ?
3
12
Exercise 4.4.39
(Solution on p. 282.)
1 = ?
5
30
Exercise 4.4.40
2 = ?
3
9
Exercise 4.4.41
(Solution on p. 282.)
1 = ?
5
30
Exercise 4.4.42
2 = ?
3
9
Exercise 4.4.43
(Solution on p. 282.)
3 = ?
4
16
Exercise 4.4.44
5 = ?
6
18
Exercise 4.4.45
(Solution on p. 282.)
4 = ?
5
25
Exercise 4.4.46
1 = 4
2
?
Exercise 4.4.47
(Solution on p. 282.)
9
25 = 27
?
Exercise 4.4.48
3 = 18
2
?
Exercise 4.4.49
(Solution on p. 282.)
5 = 80
3
?
Exercise 4.4.50
1 = 3
8
?
Exercise 4.4.51
(Solution on p. 282.)
4 = ?
5
100
Exercise 4.4.52
1 = 25
2
?
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 4.4.53
(Solution on p. 282.)
3
16 = ?
96
Exercise 4.4.54
15
16 = 225
?
Exercise 4.4.55
(Solution on p. 282.)
11
12 = ?
168
Exercise 4.4.56
9
13 = ?
286
Exercise 4.4.57
(Solution on p. 283.)
32
33 =
?
1518
Exercise 4.4.58
19
20 = 1045
?
Exercise 4.4.59
(Solution on p. 283.)
37
50 = 1369
?
For the following problems, reduce, if possible, each of the fractions to lowest terms.
Exercise 4.4.60
6
8
Exercise 4.4.61
(Solution on p. 283.)
8
10
Exercise 4.4.62
5
10
Exercise 4.4.63
(Solution on p. 283.)
6
14
Exercise 4.4.64
3
12
Exercise 4.4.65
(Solution on p. 283.)
4
14
Exercise 4.4.66
1
6
Exercise 4.4.67
(Solution on p. 283.)
4
6
Exercise 4.4.68
18
14
Exercise 4.4.69
(Solution on p. 283.)
20
8
Exercise 4.4.70
4
6
Exercise 4.4.71
(Solution on p. 283.)
10
6
Exercise 4.4.72
6
14
Exercise 4.4.73
(Solution on p. 283.)
14
6
Exercise 4.4.74
10
12
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
Exercise 4.4.75
(Solution on p. 283.)
16
70
Exercise 4.4.76
40
60
Exercise 4.4.77
(Solution on p. 283.)
20
12
Exercise 4.4.78
32
28
Exercise 4.4.79
(Solution on p. 283.)
36
10
Exercise 4.4.80
36
60
Exercise 4.4.81
(Solution on p. 283.)
12
18
Exercise 4.4.82
18
27
Exercise 4.4.83
(Solution on p. 283.)
18
24
Exercise 4.4.84
32
40
Exercise 4.4.85
(Solution on p. 283.)
11
22
Exercise 4.4.86
27
81
Exercise 4.4.87
(Solution on p. 283.)
17
51
Exercise 4.4.88
16
42
Exercise 4.4.89
(Solution on p. 283.)
39
13
Exercise 4.4.90
44
11
Exercise 4.4.91
(Solution on p. 283.)
66
33
Exercise 4.4.92
15
1
Exercise 4.4.93
(Solution on p. 283.)
15
16
Exercise 4.4.94
15
40
Exercise 4.4.95
(Solution on p. 283.)
36
100
Exercise 4.4.96
45
32
Exercise 4.4.97
(Solution on p. 283.)
30
75
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 4.4.98
121
132
Exercise 4.4.99
(Solution on p. 283.)
72
64
Exercise 4.4.100
30
105
Exercise 4.4.101
(Solution on p. 283.)
46
60
Exercise 4.4.102
75
45
Exercise 4.4.103
(Solution on p. 283.)
40
18
Exercise 4.4.104
108
76
Exercise 4.4.105
(Solution on p. 283.)
7
21
Exercise 4.4.106
6
51
Exercise 4.4.107
(Solution on p. 284.)
51
12
Exercise 4.4.108
8
100
Exercise 4.4.109
(Solution on p. 284.)
51
54
Exercise 4.4.110
A ream of paper contains 500 sheets. What fraction of a ream of paper is 200 sheets? Be sure to reduce.
Exercise 4.4.111
(Solution on p. 284.)
There are 24 hours in a day. What fraction of a day is 14 hours?
Exercise 4.4.112
A full box contains 80 calculators. How many calculators are in 1 of a box?
4
Exercise 4.4.113
(Solution on p. 284.)
There are 48 plants per at. How many plants are there in 1 of a at?
3
Exercise 4.4.114
A person making $18,000 per year must pay $3,960 in income tax. What fraction of this person’s yearly salary goes to the IRS?
For the following problems, nd the mistake.
Exercise 4.4.115
(Solution on p. 284.)
3
24 = )3 = 0 = 0
)3·8
8
Exercise 4.4.116
8
10 = )2+6 = 6 = 3
)2+8
8
4
Exercise 4.4.117
(Solution on p. 284.)
7
15 = )7 = 1
)7+8
8
Exercise 4.4.118
6 = )5+1 = 1
7
)5+2
2
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
244
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
Exercise 4.4.119
(Solution on p. 284.)
)9 = 0 = 0
)9
0
4.4.5.1 Exercises for Review
Exercise 4.4.120
(Section 1.4) Round 816 to the nearest thousand.
Exercise 4.4.121
(Solution on p. 284.)
(Section 2.3) Perform the division: 0 ÷ 6.
Exercise 4.4.122
(Section 3.4) Find all the factors of 24.
Exercise 4.4.123
(Solution on p. 284.)
(Section 3.5) Find the greatest common factor of 12 and 18.
Exercise 4.4.124
(Section 4.3) Convert 15 to a mixed number.
8
4.5 Multiplication of Fractions5
4.5.1 Section Overview
• Fractions of Fractions
• Multiplication of Fractions
• Multiplication of Fractions by Dividing Out Common Factors
• Multiplication of Mixed Numbers
• Powers and Roots of Fractions
4.5.2 Fractions of Fractions
We know that a fraction represents a part of a whole quantity. For example, two fths of one unit can be represented by
2 of the whole is shaded.
5
A natural question is, what is a fractional part of a fractional quantity, or, what is a fraction of a fraction?
For example, what 2 of 1?
3
2
We can suggest an answer to this question by using a picture to examine 2 of 1.
3
2
First, let’s represent 1.
2
1 of the whole is shaded.
2
Then divide each of the 1 parts into 3 equal parts.
2
5This content is available online at <http://cnx.org/content/m34928/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

245
Each part is 1 of the whole.
6
Now we’ll take 2 of the 1 unit.
3
2
2 of 1 is 2, which reduces to 1.
3
2
6
3
4.5.3 Multiplication of Fractions
Now we ask, what arithmetic operation (+, , ×, ÷) will produce 2 from 2 of 1?
6
3
2
Notice that, if in the fractions 2 and 1, we multiply the numerators together and the denominators together, 3
2
we get precisely 2.
6
2·1 = 2
3·2
6
This reduces to 1 as before.
3
Using this observation, we can suggest the following:
1. The word “of” translates to the arithmetic operation “times.”
2. To multiply two or more fractions, multiply the numerators together and then multiply the denominators together. Reduce if necessary.
numerator 1
denominator 1 · numerator 2
denominator 2 = numerator 1
denominator 1 · numerator 2
denominator 2
4.5.3.1 Sample Set A
Perform the following multiplications.
Example 4.31
3 · 1 = 3·1
= 3
4
6
4·6
24
Now, reduce.
1
= )3 = 1
)24
8
8
Thus
3 · 1 = 1
4
6
8
This means that 3 of 1 is 1, that is, 3 of 1 of a unit is 1 of the original unit.
4
6
8
4
6
8
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
Example 4.32
3 · 4. Write 4 as a fraction by writing 4
8
1
3
3 · 4 = 3·4 = 12 = )12 = 3
8
1
8·1
8
)8
2
2
3 · 4 = 3
8
2
This means that 3 of 4 whole units is 3 of one whole unit.
8
2
Example 4.33
1
2 · 5 · 1 = 2·5·1 = )10 = 1
5
8
4
5·8·4
)160
16
16
This means that 2 of 5 of 1 of a whole unit is 1
5
8
4
16 of the original unit.
4.5.3.2 Practice Set A
Perform the following multiplications.
Exercise 4.5.1
(Solution on p. 284.)
2 · 1
5
6
Exercise 4.5.2
(Solution on p. 284.)
1 · 8
4
9
Exercise 4.5.3
(Solution on p. 284.)
4 · 15
9
16
Exercise 4.5.4
(Solution on p. 284.)
2
2
3
3
Exercise 4.5.5
(Solution on p. 284.)
7
8
4
5
Exercise 4.5.6
(Solution on p. 284.)
5 · 7
6
8
Exercise 4.5.7
(Solution on p. 284.)
2 · 5
3
Exercise 4.5.8
(Solution on p. 284.)
3 (10)
4
Exercise 4.5.9
(Solution on p. 284.)
3 · 8 · 5
4
9
12
4.5.4 Multiplying Fractions by Dividing Out Common Factors
We have seen that to multiply two fractions together, we multiply numerators together, then denominators together, then reduce to lowest terms, if necessary. The reduction can be tedious if the numbers in the fractions are large. For example,
9
16 · 10
21 = 9·10
16·21 = 90
336 = 45
168 = 15
28
We avoid the process of reducing if we divide out common factors before we multiply.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
3
5
9
)9
)10
16 · 10
21 =
·
= 3·5 = 15
)16
)21
8·7
56
8
7
Divide 3 into 9 and 21, and divide 2 into 10 and 16. The product is a fraction that is reduced to lowest terms.
The Process of Multiplication by Dividing Out Common Factors
To multiply fractions by dividing out common factors, divide out factors that are common to both a numerator and a denominator. The factor being divided out can appear in any numerator and any denominator.
4.5.4.1 Sample Set B
Perform the following multiplications.
Example 4.34
4 · 5
5
6
2
1
)4 · )5 = 2·1 = 2
)5
)6
1·3
3
1
3
Divide 4 and 6 by 2
Divide 5 and 5 by 5
Example 4.35
8
12 · 8
10
4
2
)8 · )8 = 4·2 = 8
)12
)10
3·5
15
3
5
Divide 8 and 10 by 2.
Divide 8 and 12 by 4.
Example 4.36
2
8 · 5
)8
12 =
· 5 = 2·5 = 10
1
)12
1·3
3
3
Example 4.37
35
18 · 63
105
1
)7
7
)35 )63 = 1·7 = 7
)18 )105
2·3
6
2
)21
3
Example 4.38
13 · 6
9
39 · 1
12
1
1
)2
)13 · )6 · 1 = 1·1·1 = 1
9
)39
)12
9·1·6
54
)3
6
1
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
4.5.4.2 Practice Set B
Perform the following multiplications.
Exercise 4.5.10
(Solution on p. 284.)
2 · 7
3
8
Exercise 4.5.11
(Solution on p. 284.)
25
12 · 10
45
Exercise 4.5.12
(Solution on p. 284.)
40
48 · 72
90
Exercise 4.5.13
(Solution on p. 284.)
7 · 2
49
Exercise 4.5.14
(Solution on p. 284.)
12 · 38
Exercise 4.5.15
(Solution on p. 284.)
13 14
7
26
Exercise 4.5.16
(Solution on p. 284.)
16
10 · 22 · 21
6
44
4.5.5 Multiplication of Mixed Numbers
Multiplying Mixed Numbers
To perform a multiplication in which there are mixed numbers, it is convenient to rst convert each mixed number to an improper fraction, then multiply.
4.5.5.1 Sample Set C
Perform the following multiplications. Convert improper fractions to mixed numbers.
Example 4.39
1 1 · 4 2
8
3
Convert each mixed number to an improper fraction.
1 1 = 8·1+1 = 9
8
8
8
4 2 = 4·3+2 = 14
3
3
3
3
7
)9 · )14 = 3·7 = 21 = 5 1
)8
)3
4·1
4
4
4
1
Example 4.40
16 · 815
Convert 81 to an improper fraction.
5
8 1 = 5·8+1 = 41
5
5
5
16 · 41 .
1
5
There are no common factors to divide out.
16 · 41 = 16·41 = 656 = 1311
1
5
1·5
5
5
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Example 4.41
9 1 · 12 3
6
5
Convert to improper fractions.
9 1 = 6·9+1 = 55
6
6
6
123 = 5·12+3 = 63
5
5
5
11
21
)55 · )63 = 11·21 = 231 = 1151
)6
)5
2·1
2
2
2
1
Example 4.42
3
5
11 · 4 1 · 3 1
=
11 · )9 · )10
8
2
8
8
)2
)3
1
1
=
11·3·5 = 165 = 20 5
8·1·1
8
8
4.5.5.2 Practice Set C
Perform the following multiplications. Convert improper fractions to mixed numbers.
Exercise 4.5.17
(Solution on p. 285.)
2 2 · 2 1
3
4
Exercise 4.5.18
(Solution on p. 285.)
6 2 · 3 3
3
10
Exercise 4.5.19
(Solution on p. 285.)
7 1 · 12
8
Exercise 4.5.20
(Solution on p. 285.)
2 2 · 3 3 · 3 1
5
4
3
4.5.6 Powers and Roots of Fractions
4.5.6.1 Sample Set D
Find the value of each of the following.
Example 4.43
1 2 = 1 · 1 = 1·1 = 1
6
6
6
6·6
36
Example 4.44
q
9
100 . We’re looking for a number, call it ?, such that when it is squared, 9
100 is produced.
(?)2 = 9
100
We know that
32 = 9 and 102 = 100
We’ll try 310. Since
3 2
10
= 3
10 · 3
10 = 3·3
10·10 = 9
100
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
250
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
q
9
100 = 3
10
Example 4.45
q
4 2 ·
100
5
121
2
2
)22 · )10 = 2·2 = 4 = 4
)5
)11
1·1
1
1
1
q
4 2 ·
100
5
121 = 4
4.5.6.2 Practice Set D
Find the value of each of the following.
Exercise 4.5.21
(Solution on p. 285.)
1 2
8
Exercise 4.5.22
(Solution on p. 285.)
3 2
10
Exercise 4.5.23
(Solution on p. 285.)
q 4
9
Exercise 4.5.24
(Solution on p. 285.)
q 1
4
Exercise 4.5.25
(Solution on p. 285.)
q
3 ·
1
8
9
Exercise 4.5.26
(Solution on p. 285.)
q
9 1 ·
81
3
100
Exercise 4.5.27
(Solution on p. 285.)
q
2 8
169
13 ·
16
4.5.7 Exercises
For the following six problems, use the diagrams to nd each of the following parts. Use multiplication to verify your result.
Exercise 4.5.28
(Solution on p. 285.)
3 of 1
4
3
Exercise 4.5.29
2 of 3
3
5
Available for free at Connexions <http://cnx.org/content/col10615/1.4>



251
Exercise 4.5.30
(Solution on p. 285.)
2 of 7
7
8
Exercise 4.5.31
5 of 3
6
4
Exercise 4.5.32
(Solution on p. 285.)
1 of 1
8
8
Exercise 4.5.33
7
12 of 67
For the following problems, nd each part without using a diagram.
Exercise 4.5.34
(Solution on p. 285.)
1 of 4
2
5
Exercise 4.5.35
3 of 5
5
12
Exercise 4.5.36
(Solution on p. 285.)
1 of 8
4
9
Exercise 4.5.37
3
16 of 12
15
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
Exercise 4.5.38
(Solution on p. 286.)
2 of 6
9
5
Exercise 4.5.39
1 of 3
8
8
Exercise 4.5.40
(Solution on p. 286.)
2 of 9
3
10
Exercise 4.5.41
18
19 of 38
54
Exercise 4.5.42
(Solution on p. 286.)
5 of 22
6
5
Exercise 4.5.43
3 of 33
4
5
Exercise 4.5.44
(Solution on p. 286.)
3 of 22
2
9
Exercise 4.5.45
15 of 44
4
5
Exercise 4.5.46
(Solution on p. 286.)
5 1 of 9 3
3
4
Exercise 4.5.47
1 13
15 of 8 34
Exercise 4.5.48
(Solution on p. 286.)
8 of 3 of 2
9
4
3
Exercise 4.5.49
1 of 12
6
13 of 26
36
Exercise 4.5.50
(Solution on p. 286.)
1 of 1 of 1
2
3
4
Exercise 4.5.51
1 3 of 5 1 of 8 1
7
5
3
Exercise 4.5.52
(Solution on p. 286.)
2 4 of 5 5 of 7 5
5
6
7
For the following problems, nd the products. Be sure to reduce.
Exercise 4.5.53
1 · 2
3
3
Exercise 4.5.54
(Solution on p. 286.)
1 · 1
2
2
Exercise 4.5.55
3 · 3
4
8
Exercise 4.5.56
(Solution on p. 286.)
2 · 5
5
6
Exercise 4.5.57
3 · 8
8
9
Exercise 4.5.58
(Solution on p. 286.)
5 · 14
6
15
Exercise 4.5.59
4 · 7
7
4
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 4.5.60
(Solution on p. 286.)
3
11 · 11
3
Exercise 4.5.61
9
16 · 20
27
Exercise 4.5.62
(Solution on p. 286.)
35
36 · 48
55
Exercise 4.5.63
21
25 · 15
14
Exercise 4.5.64
(Solution on p. 286.)
76
99 · 66
38
Exercise 4.5.65
3 · 14
7
18 · 62
Exercise 4.5.66
(Solution on p. 286.)
4
15 · 10 · 27
3
2
Exercise 4.5.67
14
15 · 21
28 · 45
7
Exercise 4.5.68
(Solution on p. 286.)
8 · 15 · 16
3
4
21
Exercise 4.5.69
18
14 · 21
35 · 36
7
Exercise 4.5.70
(Solution on p. 286.)
3 · 20
5
Exercise 4.5.71
8 · 18
9
Exercise 4.5.72
(Solution on p. 286.)
6
11 · 33
Exercise 4.5.73
18
19 · 38
Exercise 4.5.74
(Solution on p. 286.)
5 · 10
6
Exercise 4.5.75
1 · 3
9
Exercise 4.5.76
(Solution on p. 286.)
5 · 38
Exercise 4.5.77
16 · 14
Exercise 4.5.78
(Solution on p. 286.)
2 · 12 · 3
3
4
Exercise 4.5.79
3 · 24 · 2
8
3
Exercise 4.5.80
(Solution on p. 286.)
5
18 · 10 · 25
Exercise 4.5.81
16
15 · 50 · 3
10
Exercise 4.5.82
(Solution on p. 286.)
5 1 · 27
3
32
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
Exercise 4.5.83
2 6 · 5 3
7
5
Exercise 4.5.84
(Solution on p. 286.)
6 1 · 2 4
4
15
Exercise 4.5.85
9 1 · 9
3
16 · 1 13
Exercise 4.5.86
(Solution on p. 286.)
3 5 · 1 13
9
14 · 10 12
Exercise 4.5.87
201 · 82 · 164
4
3
5
Exercise 4.5.88
(Solution on p. 287.)
2 2
3
Exercise 4.5.89
3 2
8
Exercise 4.5.90
(Solution on p. 287.)
2 2
11
Exercise 4.5.91
8 2
9
Exercise 4.5.92
(Solution on p. 287.)
1 2
2
Exercise 4.5.93
3 2 · 20
5
3
Exercise 4.5.94
(Solution on p. 287.)
1 2 · 16
4
15
Exercise 4.5.95
1 2 · 8
2
9
Exercise 4.5.96
(Solution on p. 287.)
1 2 · 2 2
2
5
Exercise 4.5.97
3 2 · 1 2
7
9
For the following problems, nd each value. Reduce answers to lowest terms or convert to mixed numbers.
Exercise 4.5.98
(Solution on p. 287.)
q 4
9
Exercise 4.5.99
q 16
25
Exercise 4.5.100
(Solution on p. 287.)
q 81
121
Exercise 4.5.101
q 36
49
Exercise 4.5.102
(Solution on p. 287.)
q 144
25
Exercise 4.5.103
q
2 ·
9
3
16
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 4.5.104
(Solution on p. 287.)
q
3 ·
25
5
81
Exercise 4.5.105
q
8 2 ·
25
5
64
Exercise 4.5.106
(Solution on p. 287.)
q
1 3 2 ·
4
4
49
Exercise 4.5.107
q
q
2 2 2 ·
36
64
3
49 ·
81
4.5.7.1 Exercises for Review
Exercise 4.5.108
(Solution on p. 287.)
(Section 1.2) How many thousands in 342,810?
Exercise 4.5.109
(Section 1.5) Find the sum of 22, 42, and 101.
Exercise 4.5.110
(Solution on p. 287.)
(Section 2.5) Is 634,281 divisible by 3?
Exercise 4.5.111
(Section 3.4) Is the whole number 51 prime or composite?
Exercise 4.5.112
(Solution on p. 287.)
(Section 4.4) Reduce 36
150 to lowest terms.
4.6 Division of Fractions6
4.6.1 Section Overview
• Reciprocals
• Dividing Fractions
4.6.2 Reciprocals
Reciprocals
Two numbers whose product is 1 are called reciprocals of each other.
4.6.2.1 Sample Set A
The following pairs of numbers are reciprocals.
Example 4.46
3 and4
4
3
|
{z
}
3 · 4 = 1
4
3
6This content is available online at <http://cnx.org/content/m34929/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
256
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
Example 4.47
7 and16
16
7
|
{z
}
7 · 16 = 1
16
7
Example 4.48
1 and6
6
1
|
{z
}
1 · 6 = 1
6
1
Notice that we can nd the reciprocal of a nonzero number in fractional form by inverting it (exchanging positions of the numerator and denominator).
4.6.2.2 Practice Set A
Find the reciprocal of each number.
Exercise 4.6.1
(Solution on p. 287.)
3
10
Exercise 4.6.2
(Solution on p. 287.)
2
3
Exercise 4.6.3
(Solution on p. 287.)
7
8
Exercise 4.6.4
(Solution on p. 287.)
1
5
Exercise 4.6.5
(Solution on p. 287.)
2 27
Hint: Write this number as an improper fraction rst.
Exercise 4.6.6
(Solution on p. 287.)
5 14
Exercise 4.6.7
(Solution on p. 287.)
10 316
4.6.3 Dividing Fractions
Our concept of division is that it indicates how many times one quantity is contained in another quantity.
For example, using the diagram we can see that there are 6 one-thirds in 2.
There are 6 one-thirds in 2.
Since 2 contains six 1’s we express this as
3
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
257
Using these observations, we can suggest the following method for dividing a number by a fraction.
Dividing One Fraction by Another Fraction
To divide a rst fraction by a second, nonzero fraction, multiply the rst traction by the reciprocal of the second fraction.
Invert and Multiply
This method is commonly referred to as “invert the divisor and multiply.”
4.6.3.1 Sample Set B
Perform the following divisions.
Example 4.49
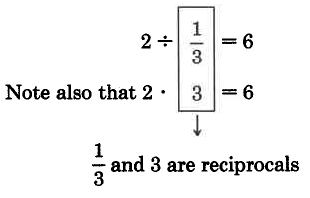
1 ÷ 3 . The divisor is 3. Its reciprocal is 4. Multiply 1 by 4.
3
4
4
3
3
3
1 · 4 = 1·4 = 4
3
3
3·3
9
1 ÷ 3 = 4
3
4
9
Example 4.50
3 ÷ 5 The divisor is 5. Its reciprocal is 4. Multiply 3 by 4.
8
4
4
5
8
5
1
3 · )4 = 3·1 = 3
)3
5
2·5
10
2
3 ÷ 5 = 3
8
4
10
Example 4.51
5 ÷ 5
. Multiply 5 by 12.
6
12 . The divisor is 5
12 . Its reciprocal is 12
5
6
5
1
2
)5 · )12 = 1·2 = 2 = 2
)6
)5
1·1
1
1
1
5 ÷ 5 = 2
6
12
Example 4.52
2 2 ÷ 3 1 . Convert each mixed number to an improper fraction.
9
3
2 2 = 9·2+2 = 20 .
9
9
9
3 1 = 3·3+1 = 10 .
3
3
3
20 ÷ 10 The divisor is 10. Its reciprocal is 3
by 3
9
3
3
10 . Multiply 20
9
10 .
2
1
)20 · )3 = 2·1 = 2
)9
)10
3·1
3
3
1
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
2 2 ÷ 3 1 = 2
9
3
3
Example 4.53
12
11 ÷ 8. First conveniently write 8 as 8 .
1
12
11 ÷ 8 The divisor is 8 . Its reciprocal is 1 . Multiply 12
.
1
1
8
11 by 18
3
)12
11 · 1 = 3·1 = 3
)8
11·2
22
2
12
11 ÷ 8 = 3
22
Example 4.54
7 ÷ 21
8
20 · 3
35 . The divisor is 21
20 . Its reciprocal is 20
21 .
1
1
)5
1
)7 · )20 )3 = 1·1·1 = 1
)8
)21 )35
2·1·7
14
2
)3
7
1
7 ÷ 21
8
20 · 3
25 = 1
14
Example 4.55
How many 23-inch-wide packages can be placed in a box 19 inches wide?
8
The problem is to determine how many two and three eighths are contained in 19, that is, what is 19 ÷ 23?
8
2 3 = 19 Convert the divisor 2 3 to an improper fraction.
8
8
8
19 = 19 Write the dividend 19 as 19.
1
1
19 ÷ 19 The divisor is 19. Its reciprocal is 8
1
8
8
19 .
1
)19 · 8 = 1·8 = 8 = 8
1
)19
1·1
1
1
Thus, 8 packages will t into the box.
4.6.3.2 Practice Set B
Perform the following divisions.
Exercise 4.6.8
(Solution on p. 287.)
1 ÷ 9
2
8
Exercise 4.6.9
(Solution on p. 287.)
3 ÷ 9
8
24
Exercise 4.6.10
(Solution on p. 287.)
7
15 ÷ 14
15
Exercise 4.6.11
(Solution on p. 287.)
8 ÷ 8
15
Exercise 4.6.12
(Solution on p. 287.)
6 1 ÷ 5
4
12
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 4.6.13
(Solution on p. 288.)
3 1 ÷ 1 2
3
3
Exercise 4.6.14
(Solution on p. 288.)
5 ÷ 2 · 8
6
3
25
Exercise 4.6.15
(Solution on p. 288.)
A container will hold 106 ounces of grape juice. How many 65-ounce glasses of grape juice can 8
be served from this container?
Determine each of the following quotients and then write a rule for this type of division.
Exercise 4.6.16
(Solution on p. 288.)
1 ÷ 23
Exercise 4.6.17
(Solution on p. 288.)
1 ÷ 38
Exercise 4.6.18
(Solution on p. 288.)
1 ÷ 34
Exercise 4.6.19
(Solution on p. 288.)
1 ÷ 52
Exercise 4.6.20
(Solution on p. 288.)
When dividing 1 by a fraction, the quotient is the
.
4.6.4 Exercises
For the following problems, nd the reciprocal of each number.
Exercise 4.6.21
(Solution on p. 288.)
4
5
Exercise 4.6.22
8
11
Exercise 4.6.23
(Solution on p. 288.)
2
9
Exercise 4.6.24
1
5
Exercise 4.6.25
(Solution on p. 288.)
3 14
Exercise 4.6.26
8 14
Exercise 4.6.27
(Solution on p. 288.)
3 27
Exercise 4.6.28
5 34
Exercise 4.6.29
(Solution on p. 288.)
1
Exercise 4.6.30
4
For the following problems, nd each value.
Exercise 4.6.31
(Solution on p. 288.)
3 ÷ 3
8
5
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
Exercise 4.6.32
5 ÷ 5
9
6
Exercise 4.6.33
(Solution on p. 288.)
9
16 ÷ 15
8
Exercise 4.6.34
4 ÷ 6
9
15
Exercise 4.6.35
(Solution on p. 288.)
25
49 ÷ 49
Exercise 4.6.36
15 ÷ 27
4
8
Exercise 4.6.37
(Solution on p. 288.)
24
75 ÷ 8
15
Exercise 4.6.38
5 ÷ 0
7
Exercise 4.6.39
(Solution on p. 288.)
7 ÷ 7
8
8
Exercise 4.6.40
0 ÷ 35
Exercise 4.6.41
(Solution on p. 288.)
4
11 ÷ 4
11
Exercise 4.6.42
2 ÷ 2
3
3
Exercise 4.6.43
(Solution on p. 288.)
7
10 ÷ 10
7
Exercise 4.6.44
3 ÷ 6
4
Exercise 4.6.45
(Solution on p. 288.)
9 ÷ 3
5
Exercise 4.6.46
4 1 ÷ 3 1
6
3
Exercise 4.6.47
(Solution on p. 288.)
7 1 ÷ 8 1
7
3
Exercise 4.6.48
1 1 ÷ 1 1
2
5
Exercise 4.6.49
(Solution on p. 288.)
3 2 ÷ 6
5
25
Exercise 4.6.50
5 1 ÷ 31
6
6
Exercise 4.6.51
(Solution on p. 288.)
35 ÷ 33
6
4
Exercise 4.6.52
5 1 ÷ 1
9
18
Exercise 4.6.53
(Solution on p. 288.)
8 3 ÷ 7
4
8
Exercise 4.6.54
12 ÷ 11
8
2
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 4.6.55
(Solution on p. 289.)
3 1 ÷ 15
8
16
Exercise 4.6.56
1111
12 ÷ 9 58
Exercise 4.6.57
(Solution on p. 289.)
2 2 ÷ 11 2
9
3
Exercise 4.6.58
16 ÷ 62
3
5
Exercise 4.6.59
(Solution on p. 289.)
4 3
25 ÷ 2 56
75
Exercise 4.6.60
1
1000 ÷ 1
100
Exercise 4.6.61
(Solution on p. 289.)
3 ÷ 9
8
16 · 65
Exercise 4.6.62
3
16 · 9 · 6
8
5
Exercise 4.6.63
(Solution on p. 289.)
4
15 ÷ 2
25 · 9
10
Exercise 4.6.64
21
30 · 1 1 ÷ 9
4
10
Exercise 4.6.65
(Solution on p. 289.)
8 1 · 36
3
75 ÷ 4
4.6.4.1 Exercises for Review
Exercise 4.6.66
(Section 1.2) What is the value of 5 in the number 504,216?
Exercise 4.6.67
(Solution on p. 289.)
(Section 2.2) Find the product of 2,010 and 160.
Exercise 4.6.68
(Section 2.6) Use the numbers 8 and 5 to illustrate the commutative property of multiplication.
Exercise 4.6.69
(Solution on p. 289.)
(Section 3.6) Find the least common multiple of 6, 16, and 72.
Exercise 4.6.70
(Section 4.5) Find 8 of 63.
9
4
4.7 Applications Involving Fractions 7
4.7.1 Section Overview
• Multiplication Statements
• Missing Product Statements
• Missing Factor Statements
7This content is available online at <http://cnx.org/content/m34930/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
262
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
4.7.2 Multiplication Statements
Statement, Multiplication Statement
A statement is a sentence that is either true or false. A mathematical statement of the form product = (factor 1) · (factor 2)
is a multiplication statement. Depending on the numbers that are used, it can be either true or false.
Omitting exactly one of the three numbers in the statement will produce exactly one of the following three problems. For convenience, we’ll represent the omitted (or missing) number with the letter M (M for Missing).
1. M = (factor 1) · (factor 2) Missing product statement.
2. M · (factor 2) = product Missing factor statement.
3. (factor 1) · M = product Missing factor statement.
We are interested in developing and working with methods to determine the missing number that makes the statement true. Fundamental to these methods is the ability to translate two words to mathematical symbols. The word
of translates to times
is translates to equals
4.7.3 Missing Products Statements
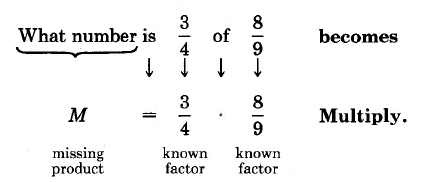
The equation M = 8 · 4 is a missing product statement. We can nd the value of M that makes this statement true by multiplying the known factors.
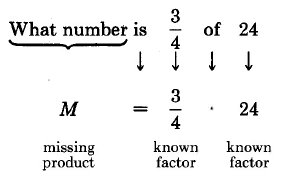
Missing product statements can be used to determine the answer to a question such as, “What number is fraction 1 of fraction 2?
4.7.3.1 Sample Set A
Find 3 of 8. We are being asked the question, “What number is 3 of 8?” We must translate from words to 4
9
4
9
mathematical symbols.
1
2
M = )3 · )8 = 1·2 = 2
)4
)9
1·3
3
1
3
Thus, 3 of 8 is 2.
4
9
3
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

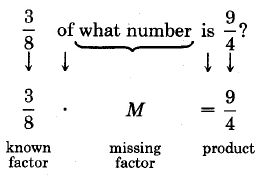
263
6
M = 3 · )24 = 3·6 = 18 = 18
)4
1
1·1
1
1
Thus, 18 is 3 of 24.
4
4.7.3.2 Practice Set A
Exercise 4.7.1
(Solution on p. 289.)
Find 3 of 16
8
15 .
Exercise 4.7.2
(Solution on p. 289.)
What number is 910 of 5 ?
6
Exercise 4.7.3
(Solution on p. 289.)
11
16 of 8
33 is what number?
4.7.4 Missing Factor Statements
The equation 8 · M = 32 is a missing factor statement. We can nd the value of M that makes this statement true by dividing (since we know that 32 ÷ 8 = 4).
Finding the Missing Factor
To nd the missing factor in a missing factor statement, divide the product by the known factor.
missing factor = (product) ÷ (known factor)
Missing factor statements can be used to answer such questions as
1. 3 of what number is 9?
8
4
2. What part of 12 is 113
7
14 ?
4.7.4.1 Sample Set B
Now, using
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
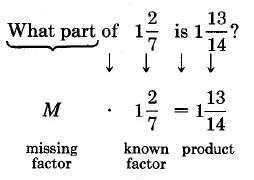

264
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
missing factor = (product) ÷ (known factor)
We get
3
2
M = 9 ÷ 3 = 9 · 8
=
)9 · )8
4
8
4
3
)4
)3
1
1
=
3·2
1·1
=
6
Thus, 3 of 6 is 9.
8
4
For convenience, let’s convert the mixed numbers to improper fractions.
M · 9 = 27
7
14
Now, using
missing factor = (product)÷(known factor)
we get
3
1
M = 27
)27
)7
14 ÷ 9 = 27
=
·
7
14 · 79
)14
)9
2
1
= 3·1
2·1
= 32
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Thus, 3 of 12 is 113
2
7
14 .
4.7.4.2 Practice Set B
Exercise 4.7.4
(Solution on p. 289.)
3 of what number is 9
5
20 ?
Exercise 4.7.5
(Solution on p. 289.)
3 3 of what number is 2 2 ?
4
9
Exercise 4.7.6
(Solution on p. 289.)
What part of 3 is 9
5
10 ?
Exercise 4.7.7
(Solution on p. 289.)
What part of 11 is 17?
4
8
4.7.5 Exercises
Exercise 4.7.8
(Solution on p. 289.)
Find 2 of 3.
3
4
Exercise 4.7.9
Find 5 of 1
8
10 .
Exercise 4.7.10
(Solution on p. 289.)
Find 12
13 of 13
36 .
Exercise 4.7.11
Find 1 of 4.
4
7
Exercise 4.7.12
(Solution on p. 289.)
3
10 of 15 is what number?
4
Exercise 4.7.13
14
15 of 20
21 is what number?
Exercise 4.7.14
(Solution on p. 289.)
3
44 of 11
12 is what number?
Exercise 4.7.15
1 of 2 is what number?
3
Exercise 4.7.16
(Solution on p. 289.)
1 of 3 is what number?
4
Exercise 4.7.17
1
10 of 1
100 is what number?
Exercise 4.7.18
(Solution on p. 289.)
1
100 of 1
10 is what number?
Exercise 4.7.19
1 5 of 2 4 is what number?
9
7
Exercise 4.7.20
(Solution on p. 289.)
1 7
18 of 4
15 is what number?
Exercise 4.7.21
1 1 of 1 11
8
16 is what number?
Exercise 4.7.22
(Solution on p. 289.)
Find 2 of 1 of 9.
3
6
2
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
Exercise 4.7.23
Find 5 of 9
.
8
20 of 49
Exercise 4.7.24
(Solution on p. 289.)
5
12 of what number is 5 ?
6
Exercise 4.7.25
3
14 of what number is 6 ?
7
Exercise 4.7.26
(Solution on p. 289.)
10 of what number is 5?
3
9
Exercise 4.7.27
15 of what number is 20
7
21 ?
Exercise 4.7.28
(Solution on p. 290.)
8 of what number is 17?
3
9
Exercise 4.7.29
1 of what number is 1?
3
3
Exercise 4.7.30
(Solution on p. 290.)
1 of what number is 1?
6
6
Exercise 4.7.31
3 of what number is 3?
4
4
Exercise 4.7.32
(Solution on p. 290.)
8
11 of what number is 8
11 ?
Exercise 4.7.33
3 of what number is 0?
8
Exercise 4.7.34
(Solution on p. 290.)
2 of what number is 1?
3
Exercise 4.7.35
3 1 of what number is 1?
5
Exercise 4.7.36
(Solution on p. 290.)
1 9
12 of what number is 5 1 ?
4
Exercise 4.7.37
3 1
25 of what number is 2 8
15 ?
Exercise 4.7.38
(Solution on p. 290.)
What part of 2 is 11?
3
9
Exercise 4.7.39
What part of 910 is 33?
5
Exercise 4.7.40
(Solution on p. 290.)
What part of 8 is 3?
9
5
Exercise 4.7.41
What part of 14
15 is 7
30 ?
Exercise 4.7.42
(Solution on p. 290.)
What part of 3 is 1?
5
Exercise 4.7.43
What part of 8 is 2?
3
Exercise 4.7.44
(Solution on p. 290.)
What part of 24 is 9?
Exercise 4.7.45
What part of 42 is 26?
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 4.7.46
(Solution on p. 290.)
Find 12
13 of 39
40 .
Exercise 4.7.47
14
15 of 12
21 is what number?
Exercise 4.7.48
(Solution on p. 290.)
8
15 of what number is 2 2 ?
5
Exercise 4.7.49
11
15 of what number is 22
35 ?
Exercise 4.7.50
(Solution on p. 290.)
11
16 of what number is 1?
Exercise 4.7.51
What part of 23
40 is 3 9
20 ?
Exercise 4.7.52
(Solution on p. 290.)
4
35 of 3 9
22 is what number?
4.7.5.1 Exercises for Review
Exercise 4.7.53
(Section 1.7) Use the numbers 2 and 7 to illustrate the commutative property of addition.
Exercise 4.7.54
(Solution on p. 290.)
(Section 2.3) Is 4 divisible by 0?
Exercise 4.7.55
(Section 3.5) Expand 37. Do not nd the actual value.
Exercise 4.7.56
(Solution on p. 290.)
(Section 4.3) Convert 3 512 to an improper fraction.
Exercise 4.7.57
(Section 4.4) Find the value of 3 ÷ 9
.
8
16 · 65
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
268
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
4.8 Summary of Key Concepts 8
4.8.1 Summary of Key Concepts
Fraction (Section 4.2)
The idea of breaking up a whole quantity into equal parts gives us the word fraction.
Fraction Bar, Denominator, Numerator (Section 4.2)
A fraction has three parts:
1. The fraction bar
2. The nonzero whole number below the fraction bar is the denominator.
3. The whole number above the fraction bar is the numerator.
Proper Fraction (Section 4.3)
Proper fractions are fractions in which the numerator is strictly less than the denominator.
4 is a proper fraction
5
Improper Fraction (Section 4.3)
Improper fractions are fractions in which the numerator is greater than or equal to the denominator.
Also, any nonzero number placed over 1 is an improper fraction.
5 , 5, and 5 are improper fractions
4
5
1
Mixed Number (Section 4.3)
A mixed number is a number that is the sum of a whole number and a proper fraction.
1 1 is a mixed number 1 1 = 1 + 1
5
5
5
Correspondence Between Improper Fractions and Mixed Numbers (Section 4.3) Each improper fraction corresponds to a particular mixed number, and each mixed number corresponds to a particular improper fraction.
Converting an Improper Fraction to a Mixed Number (Section 4.3)
A method, based on division, converts an improper fraction to an equivalent mixed number.
5 can be converted to 11
4
4
Converting a Mixed Number to an Improper Fraction (Section 4.3)
A method, based on multiplication, converts a mixed number to an equivalent improper fraction.
5 7 can be converted to 47
8
8
Equivalent Fractions (Section 4.4)
Fractions that represent the same quantity are equivalent fractions.
3 and 6 are equivalent fractions
4
8
8This content is available online at <http://cnx.org/content/m34931/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
269
Test for Equivalent Fractions (Section 4.4)
If the cross products of two fractions are equal, then the two fractions are equivalent.
Thus, 3 and 6 are equivalent.
4
8
Relatively Prime (Section 4.4)
Two whole numbers are relatively prime when 1 is the only number that divides both of them.
3 and 4 are relatively prime
Reduced to Lowest Terms (Section 4.4)
A fraction is reduced to lowest terms if its numerator and denominator are relatively prime.
The number 3 is reduced to lowest terms, since 3 and 4 are relatively prime.
4
The number 6 is not reduced to lowest terms since 6 and 8 are not relatively prime.
8
Reducing Fractions to Lowest Terms (Section 4.4)
Two methods, one based on dividing out common primes and one based on dividing out any common factors, are available for reducing a fraction to lowest terms.
Raising Fractions to Higher Terms (Section 4.4)
A fraction can be raised to higher terms by multiplying both the numerator and denominator by the same nonzero number.
3 = 3·2 = 6
4
4·2
8
The Word OF Means Multiplication (Section 4.5)
In many mathematical applications, the word “of” means multiplication.
Multiplication of Fractions (Section 4.5)
To multiply two or more fractions, multiply the numerators together and multiply the denominators together.
Reduce if possible.
5 · 4
8
15 = 5·4
8·15 = 20
120 = 16
Multiplying Fractions by Dividing Out Common Factors (Section 4.5)
Two or more fractions can be multiplied by rst dividing out common factors and then using the rule for multiplying fractions.
1
1
)5 · )4 = 1·1 = 1
)8
)15
2·3
6
2
3
Multiplication of Mixed Numbers (Section 4.5)
To perform a multiplication in which there are mixed numbers, rst convert each mixed number to an improper fraction, then multiply. This idea also applies to division of mixed numbers.
Reciprocals (Section 4.6)
Two numbers whose product is 1 are reciprocals.
7 and 1 are reciprocals
7
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

270
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
Division of Fractions (Section 4.6)
To divide one fraction by another fraction, multiply the dividend by the reciprocal of the divisor.
4 ÷ 2
· 15
5
15 = 45
2
Dividing 1 by a Fraction (Section 4.6)
When dividing 1 by a fraction, the quotient is the reciprocal of the fraction.
1 = 7
3
3
7
Multiplication Statements (Section 4.7)
A mathematical statement of the form
product = (factor 1) (factor 2)
is a multiplication statement.
By omitting one of the three numbers, one of three following problems result: 1. M = (factor 1) · (factor 2) Missing product statement.
2. product = (factor 1) · M Missing factor statement.
3. product = M · (factor 2) Missing factor statement.
Missing products are determined by simply multiplying the known factors. Missing factors are determined by
missing factor = (product) ÷ (known factor)
4.9 Exercise Supplement 9
4.9.1 Exercise Supplement
4.9.1.1 Fractions of Whole Numbers (Section 4.2)
For Problems 1 and 2, name the suggested fraction.
Exercise 4.9.1
(Solution on p. 290.)
Exercise 4.9.2
For problems 3-5, specify the numerator and denominator.
Exercise 4.9.3
(Solution on p. 290.)
4
5
9This content is available online at <http://cnx.org/content/m34932/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
271
Exercise 4.9.4
5
12
Exercise 4.9.5
(Solution on p. 290.)
1
3
For problems 6-10, write each fraction using digits.
Exercise 4.9.6
Three fths
Exercise 4.9.7
(Solution on p. 290.)
Eight elevenths
Exercise 4.9.8
Sixty-one forty rsts
Exercise 4.9.9
(Solution on p. 290.)
Two hundred six-thousandths
Exercise 4.9.10
zero tenths
For problems 11-15, write each fraction using words.
Exercise 4.9.11
(Solution on p. 290.)
10
17
Exercise 4.9.12
21
38
Exercise 4.9.13
(Solution on p. 290.)
606
1431
Exercise 4.9.14
0
8
Exercise 4.9.15
(Solution on p. 290.)
1
16
For problems 16-18, state each numerator and denominator and write each fraction using digits.
Exercise 4.9.16
One minute is one sixtieth of an hour.
Exercise 4.9.17
(Solution on p. 290.)
In a box that contains forty-ve electronic components, eight are known to be defective. If three components are chosen at random from the box, the probability that all three are defective is fty-six fourteen thousand one hundred ninetieths.
Exercise 4.9.18
About three fths of the students in a college algebra class received a B in the course.
For problems 19 and 20, shade the region corresponding to the given fraction.
Exercise 4.9.19
(Solution on p. 290.)
1
4
Exercise 4.9.20
3
7
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
272
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
4.9.1.2 Proper Fraction, Improper Fraction, and Mixed Numbers (Section 4.3) For problems 21-29, convert each improper fraction to a mixed number.
Exercise 4.9.21
(Solution on p. 291.)
11
4
Exercise 4.9.22
15
2
Exercise 4.9.23
(Solution on p. 291.)
51
8
Exercise 4.9.24
121
15
Exercise 4.9.25
(Solution on p. 291.)
356
3
Exercise 4.9.26
3
2
Exercise 4.9.27
(Solution on p. 291.)
5
4
Exercise 4.9.28
20
5
Exercise 4.9.29
(Solution on p. 291.)
9
3
For problems 30-40, convert each mixed number to an improper fraction.
Exercise 4.9.30
5 23
Exercise 4.9.31
(Solution on p. 291.)
1618
Exercise 4.9.32
1813
Exercise 4.9.33
(Solution on p. 291.)
3 15
Exercise 4.9.34
2 9
16
Exercise 4.9.35
(Solution on p. 291.)
1720
21
Exercise 4.9.36
1 78
Exercise 4.9.37
(Solution on p. 291.)
1 12
Exercise 4.9.38
2 12
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 4.9.39
(Solution on p. 291.)
8 67
Exercise 4.9.40
2 92
Exercise 4.9.41
(Solution on p. 291.)
Why does 0 112 not qualify as a mixed number?
Exercise 4.9.42
Why does 8 qualify as a mixed number?
4.9.1.3 Equivalent Fractions, Reducing Fractions to Lowest Terms, and Raising Fractions to Higher Term (Section 4.4)
For problems 43-47, determine if the pairs of fractions are equivalent.
Exercise 4.9.43
(Solution on p. 291.)
1 , 15
2
30
Exercise 4.9.44
8 , 32
9
36
Exercise 4.9.45
(Solution on p. 291.)
3
14 , 24
110
Exercise 4.9.46
2 3 , 38
8
16
Exercise 4.9.47
(Solution on p. 291.)
108
77 , 1 5
13
For problems 48-60, reduce, if possible, each fraction.
Exercise 4.9.48
10
25
Exercise 4.9.49
(Solution on p. 291.)
32
44
Exercise 4.9.50
102
266
Exercise 4.9.51
(Solution on p. 291.)
15
33
Exercise 4.9.52
18
25
Exercise 4.9.53
(Solution on p. 291.)
21
35
Exercise 4.9.54
9
16
Exercise 4.9.55
(Solution on p. 291.)
45
85
Exercise 4.9.56
24
42
Exercise 4.9.57
(Solution on p. 291.)
70
136
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
Exercise 4.9.58
182
580
Exercise 4.9.59
(Solution on p. 291.)
325
810
Exercise 4.9.60
250
1000
For problems 61-72, determine the missing numerator or denominator.
Exercise 4.9.61
(Solution on p. 291.)
3 = ?
7
35
Exercise 4.9.62
4
11 = ?
99
Exercise 4.9.63
(Solution on p. 291.)
1
12 = ?
72
Exercise 4.9.64
5 = 25
8
?
Exercise 4.9.65
(Solution on p. 291.)
11 = 33
9
?
Exercise 4.9.66
4
15 = 24
?
Exercise 4.9.67
(Solution on p. 291.)
14
15 = ?
45
Exercise 4.9.68
0 = ?
5
20
Exercise 4.9.69
(Solution on p. 292.)
12
21 = 96
?
Exercise 4.9.70
14
23 = ?
253
Exercise 4.9.71
(Solution on p. 292.)
15
16 = 180
?
Exercise 4.9.72
21
22 = 336
?
4.9.1.4 Multiplication and Division of Fractions (Section 4.5, Section 4.6) For problems 73-95, perform each multiplication and division.
Exercise 4.9.73
(Solution on p. 292.)
4 · 15
5
16
Exercise 4.9.74
8 · 3
9
24
Exercise 4.9.75
(Solution on p. 292.)
1
10 · 5
12
Exercise 4.9.76
14
15 · 75
Exercise 4.9.77
(Solution on p. 292.)
5 · 13
6
22 · 11
39
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 4.9.78
2 ÷ 15 · 5
3
7
6
Exercise 4.9.79
(Solution on p. 292.)
3 1 ÷ 7
2
2
Exercise 4.9.80
2 4 ÷ 11
9
45
Exercise 4.9.81
(Solution on p. 292.)
8
15 · 3
16 · 5
24
Exercise 4.9.82
8
15 ÷ 3 3 · 9
5
16
Exercise 4.9.83
(Solution on p. 292.)
14
15 ÷ 3 8 · 10
9
21
Exercise 4.9.84
18 · 534
Exercise 4.9.85
(Solution on p. 292.)
3 3 · 2 1
7
12
Exercise 4.9.86
4 1 ÷ 2 4
2
7
Exercise 4.9.87
(Solution on p. 292.)
6 1 ÷ 3 1
2
4
Exercise 4.9.88
3 5
16 ÷ 2 7
18
Exercise 4.9.89
(Solution on p. 292.)
7 ÷ 2 13
Exercise 4.9.90
17 ÷ 414
Exercise 4.9.91
(Solution on p. 292.)
5 ÷ 1 1
8
4
Exercise 4.9.92
2 2 · 3 3
3
4
Exercise 4.9.93
(Solution on p. 292.)
20 · 184
Exercise 4.9.94
0 ÷ 4 18
Exercise 4.9.95
(Solution on p. 292.)
1 ÷ 6 1 · 25
4
4
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
276
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
4.9.1.5 Applications Involving Fractions (Section 4.7)
Exercise 4.9.96
Find 8 of 27.
9
2
Exercise 4.9.97
(Solution on p. 292.)
What part of 3 is 21
8
16 ?
Exercise 4.9.98
What part of 31 is 1 7
5
25 ?
Exercise 4.9.99
(Solution on p. 292.)
Find 62 of 9
3
15 .
Exercise 4.9.100
7
20 of what number is 14
35 ?
Exercise 4.9.101
(Solution on p. 292.)
What part of 4 116 is 33?
4
Exercise 4.9.102
Find 8 310 of 162.
3
Exercise 4.9.103
(Solution on p. 292.)
3
20 of what number is 18
30 ?
Exercise 4.9.104
Find 1 of 0.
3
Exercise 4.9.105
(Solution on p. 292.)
Find 11
12 of 1.
4.10 Prociency Exam10
4.10.1 Prociency Exam
Exercise 4.10.1
(Solution on p. 292.)
(Section 4.2) Shade a portion that corresponds to the fraction 5.
8
Exercise 4.10.2
(Solution on p. 292.)
(Section 4.2) Specify the numerator and denominator of the fraction 5.
9
Exercise 4.10.3
(Solution on p. 292.)
(Section 4.2) Write the fraction ve elevenths.
Exercise 4.10.4
(Solution on p. 292.)
(Section 4.2) Write, in words, 4.
5
Exercise 4.10.5
(Solution on p. 292.)
(Section 4.3) Which of the fractions is a proper fraction? 4 112, 512, 125
Exercise 4.10.6
(Solution on p. 293.)
(Section 4.3) Convert 34 to an improper fraction.
7
Exercise 4.10.7
(Solution on p. 293.)
(Section 4.3) Convert 16 to a mixed number.
5
10This content is available online at <http://cnx.org/content/m34933/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 4.10.8
(Solution on p. 293.)
(Section 4.4) Determine if 512 and 20
48 are equivalent fractions.
For problems 9-11, reduce, if possible, each fraction to lowest terms.
Exercise 4.10.9
(Solution on p. 293.)
(Section 4.4) 21
35
Exercise 4.10.10
(Solution on p. 293.)
(Section 4.4) 15
51
Exercise 4.10.11
(Solution on p. 293.)
(Section 4.4) 104
480
For problems 12 and 13, determine the missing numerator or denominator.
Exercise 4.10.12
(Solution on p. 293.)
(Section 4.4) 5 = ?
9
36
Exercise 4.10.13
(Solution on p. 293.)
(Section 4.4) 4 = 32
3
?
For problems 14-25, nd each value.
Exercise 4.10.14
(Solution on p. 293.)
(Section 4.5) 15
16 · 4
25
Exercise 4.10.15
(Solution on p. 293.)
(Section 4.5) 33 · 22 · 63
4
9
5
Exercise 4.10.16
(Solution on p. 293.)
q
(Section 4.5)
25
36
Exercise 4.10.17
(Solution on p. 293.)
q
q
(Section 4.5)
4 ·
81
9
64
Exercise 4.10.18
(Solution on p. 293.)
q
(Section 4.5) 11
225
30 ·
121
Exercise 4.10.19
(Solution on p. 293.)
(Section 4.6) 415 ÷ 8
Exercise 4.10.20
(Solution on p. 293.)
(Section 4.6) 815 · 512 ÷ 249
Exercise 4.10.21
(Solution on p. 293.)
q
(Section 4.6) 63 ÷ 111
5
25
Exercise 4.10.22
(Solution on p. 293.)
(Section 4.7) Find 512 of 24
25 .
Exercise 4.10.23
(Solution on p. 293.)
(Section 4.7) 2 of what number is 1
9
18 ?
Exercise 4.10.24
(Solution on p. 293.)
(Section 4.7) 15 of 21
7
20 is what number?
Exercise 4.10.25
(Solution on p. 293.)
(Section 4.7) What part of 914 is 6?
7
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
Solutions to Exercises in Chapter 4
Solution to Exercise 4.2.1 (p. 217)
4, 7
Solution to Exercise 4.2.2 (p. 218)
5, 8
Solution to Exercise 4.2.3 (p. 218)
10, 15
Solution to Exercise 4.2.4 (p. 218)
1, 9
Solution to Exercise 4.2.5 (p. 218)
0, 2
Solution to Exercise 4.2.6 (p. 219)
1
10
Solution to Exercise 4.2.7 (p. 219)
11
14
Solution to Exercise 4.2.8 (p. 219)
16
35
Solution to Exercise 4.2.9 (p. 219)
800
7,000
Solution to Exercise 4.2.10 (p. 219)
three eighths
Solution to Exercise 4.2.11 (p. 219)
one tenth
Solution to Exercise 4.2.12 (p. 219)
three two hundred ftieths
Solution to Exercise 4.2.13 (p. 219)
one hundred fourteen three thousand one hundred ninetieths
Solution to Exercise 4.2.14 (p. 219)
3
8
Solution to Exercise 4.2.15 (p. 219)
1
16
Solution to Exercise 4.2.16 (p. 219)
5, 9, ve ninths
Solution to Exercise 4.2.17 (p. 219)
1, 10, one tenth
Solution to Exercise 4.2.18 (p. 220)
numerator, 3; denominator, 4
Solution to Exercise 4.2.20 (p. 220)
numerator, 1; denominator, 5
Solution to Exercise 4.2.22 (p. 220)
numerator, 7; denominator, 7
Solution to Exercise 4.2.24 (p. 220)
numerator, 0; denominator, 12
Solution to Exercise 4.2.26 (p. 220)
numerator, 18; denominator, 1
Solution to Exercise 4.2.28 (p. 220)
4
5
Solution to Exercise 4.2.30 (p. 220)
15
20
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

279
Solution to Exercise 4.2.32 (p. 220)
91
107
Solution to Exercise 4.2.34 (p. 220)
605
834
Solution to Exercise 4.2.36 (p. 220)
92
1,000,000
Solution to Exercise 4.2.38 (p. 220)
ve ninths
Solution to Exercise 4.2.40 (p. 221)
eight fteenths
Solution to Exercise 4.2.42 (p. 221)
seventy-ve one hundredths
Solution to Exercise 4.2.44 (p. 221)
nine hundred sixteen one thousand fourteenths
Solution to Exercise 4.2.46 (p. 221)
eighteen thirty-one thousand six hundred eighths
Solution to Exercise 4.2.48 (p. 221)
1
2
Solution to Exercise 4.2.50 (p. 221)
4
7
Solution to Exercise 4.2.52 (p. 221)
Solution to Exercise 4.2.54 (p. 222)
Solution to Exercise 4.2.56 (p. 222)
Numerator, 1; denominator, 4; one fourth
Solution to Exercise 4.2.58 (p. 222)
Numerator, 4; denominator, 3; four thirds
Solution to Exercise 4.2.60 (p. 222)
Numerator, 2; denominator, 7; two sevenths
Solution to Exercise 4.2.62 (p. 223)
Numerator, 1; denominator, 56; one fty-sixth
Solution to Exercise 4.2.64 (p. 223)
Numerator, 125; denominator, 4; one hundred twenty-ve fourths
Solution to Exercise 4.2.66 (p. 223)
3 + 11 = 11 + 3 = 14
Solution to Exercise 4.2.68 (p. 223)
75
Solution to Exercise 4.2.70 (p. 223)
144
Solution to Exercise 4.3.1 (p. 228)
4 12
Solution to Exercise 4.3.2 (p. 228)
3 23
Solution to Exercise 4.3.3 (p. 228)
1 3
11
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
Solution to Exercise 4.3.4 (p. 228)
2 5
13
Solution to Exercise 4.3.5 (p. 228)
1934
Solution to Exercise 4.3.6 (p. 228)
62
Solution to Exercise 4.3.7 (p. 230)
33
4
Solution to Exercise 4.3.8 (p. 230)
28
5
Solution to Exercise 4.3.9 (p. 230)
19
15
Solution to Exercise 4.3.10 (p. 230)
86
7
Solution to Exercise 4.3.11 (p. 230)
improper fraction
Solution to Exercise 4.3.13 (p. 230)
proper fraction
Solution to Exercise 4.3.15 (p. 230)
mixed number
Solution to Exercise 4.3.17 (p. 230)
improper fraction
Solution to Exercise 4.3.19 (p. 230)
mixed number
Solution to Exercise 4.3.21 (p. 230)
mixed number
Solution to Exercise 4.3.23 (p. 230)
proper fraction
Solution to Exercise 4.3.25 (p. 230)
mixed number
Solution to Exercise 4.3.27 (p. 231)
4 23
Solution to Exercise 4.3.29 (p. 231)
8 34
Solution to Exercise 4.3.31 (p. 231)
9
Solution to Exercise 4.3.33 (p. 231)
13 912 or 1334
Solution to Exercise 4.3.35 (p. 231)
55559
Solution to Exercise 4.3.37 (p. 231)
3612
Solution to Exercise 4.3.39 (p. 231)
7 29
41
Solution to Exercise 4.3.41 (p. 231)
33
8
Solution to Exercise 4.3.43 (p. 231)
61
9
Solution to Exercise 4.3.45 (p. 231)
115
11
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
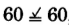
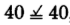
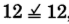
281
Solution to Exercise 4.3.47 (p. 231)
26
3
Solution to Exercise 4.3.49 (p. 232)
107
5
Solution to Exercise 4.3.51 (p. 232)
209
21
Solution to Exercise 4.3.53 (p. 232)
9001
100
Solution to Exercise 4.3.55 (p. 232)
159
8
Solution to Exercise 4.3.57 (p. 232)
. . . because it may be written as 5 0 , where n is any positive whole number.
n
Solution to Exercise 4.3.59 (p. 232)
1,652
61
Solution to Exercise 4.3.61 (p. 232)
2,436
23
Solution to Exercise 4.3.63 (p. 232)
20,419
25
Solution to Exercise 4.3.65 (p. 232)
48,803,620
8,117
Solution to Exercise 4.3.67 (p. 233)
1,009,020
Solution to Exercise 4.3.69 (p. 233)
252
Solution to Exercise 4.4.1 (p. 234)
, yes
Solution to Exercise 4.4.2 (p. 234)
, yes
Solution to Exercise 4.4.3 (p. 234)
30 6= 24, no
Solution to Exercise 4.4.4 (p. 234)
, yes
Solution to Exercise 4.4.5 (p. 234)
, yes
Solution to Exercise 4.4.6 (p. 236)
1
2
Solution to Exercise 4.4.7 (p. 236)
2
5
Solution to Exercise 4.4.8 (p. 236)
1
8
Solution to Exercise 4.4.9 (p. 236)
7
16
Solution to Exercise 4.4.10 (p. 236)
12
7
Solution to Exercise 4.4.11 (p. 236)
5
9
Solution to Exercise 4.4.12 (p. 237)
3
4
Solution to Exercise 4.4.13 (p. 237)
3
8
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
Solution to Exercise 4.4.14 (p. 237)
1
4
Solution to Exercise 4.4.15 (p. 237)
3
4
Solution to Exercise 4.4.16 (p. 237)
7
9
Solution to Exercise 4.4.17 (p. 237)
5
8
Solution to Exercise 4.4.18 (p. 239)
32
Solution to Exercise 4.4.19 (p. 239)
12
Solution to Exercise 4.4.20 (p. 239)
4Solution to Exercise 4.4.21 (p. 239)
150
Solution to Exercise 4.4.22 (p. 239)
88
Solution to Exercise 4.4.23 (p. 239)
equivalent
Solution to Exercise 4.4.25 (p. 239)
equivalent
Solution to Exercise 4.4.27 (p. 239)
not equivalent
Solution to Exercise 4.4.29 (p. 239)
not equivalent
Solution to Exercise 4.4.31 (p. 240)
not equivalent
Solution to Exercise 4.4.33 (p. 240)
equivalent
Solution to Exercise 4.4.35 (p. 240)
not equivalent
Solution to Exercise 4.4.37 (p. 240)
not equivalent
Solution to Exercise 4.4.39 (p. 240)
6Solution to Exercise 4.4.41 (p. 240)
12
Solution to Exercise 4.4.43 (p. 240)
12
Solution to Exercise 4.4.45 (p. 240)
20
Solution to Exercise 4.4.47 (p. 240)
75
Solution to Exercise 4.4.49 (p. 240)
48
Solution to Exercise 4.4.51 (p. 240)
80
Solution to Exercise 4.4.53 (p. 241)
18
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 4.4.55 (p. 241)
154
Solution to Exercise 4.4.57 (p. 241)
1,472
Solution to Exercise 4.4.59 (p. 241)
1,850
Solution to Exercise 4.4.61 (p. 241)
4
5
Solution to Exercise 4.4.63 (p. 241)
3
7
Solution to Exercise 4.4.65 (p. 241)
2
7
Solution to Exercise 4.4.67 (p. 241)
2
3
Solution to Exercise 4.4.69 (p. 241)
5
2
Solution to Exercise 4.4.71 (p. 241)
5
3
Solution to Exercise 4.4.73 (p. 241)
7
3
Solution to Exercise 4.4.75 (p. 242)
8
35
Solution to Exercise 4.4.77 (p. 242)
5
3
Solution to Exercise 4.4.79 (p. 242)
18
5
Solution to Exercise 4.4.81 (p. 242)
2
3
Solution to Exercise 4.4.83 (p. 242)
3
4
Solution to Exercise 4.4.85 (p. 242)
1
2
Solution to Exercise 4.4.87 (p. 242)
1
3
Solution to Exercise 4.4.89 (p. 242)
3Solution to Exercise 4.4.91 (p. 242)
2Solution to Exercise 4.4.93 (p. 242)
already reduced
Solution to Exercise 4.4.95 (p. 242)
9
25
Solution to Exercise 4.4.97 (p. 242)
2
5
Solution to Exercise 4.4.99 (p. 243)
9
8
Solution to Exercise 4.4.101 (p. 243)
23
30
Solution to Exercise 4.4.103 (p. 243)
20
9
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 4. INTRODUCTION TO FRACTIONS AND MULTIPLICATION
AND DIVISION OF FRACTIONS
Solution to Exercise 4.4.105 (p. 243)
1
3
Solution to Exercise 4.4.107 (p. 243)
17
4
Solution to Exercise 4.4.109 (p. 243)
17
18
Solution to Exercise 4.4.111 (p. 243)
7
12
Solution to Exercise 4.4.113 (p. 243)
16
Solution to Exercise 4.4.115 (p. 243)
Should be 1; the cancellation is division, so the numerator should be 1.
8
Solution to Exercise 4.4.117 (p. 243)
Cancel factors only, not addends; 715 is already reduced.
Solution to Exercise 4.4.119 (p. 244)
Same as Exercise 4.4.115; answer is 1 or 1.
1
Solution to Exercise 4.4.121 (p. 244)
0Solution to Exercise 4.4.123 (p. 244)
6Solution to Exercise 4.5.1 (p. 246)
1
15
Solution to Exercise 4.5.2 (p. 246)
2
9
Solution to Exercise 4.5.3 (p. 246)
5
12
Solution to Exercise 4.5.4 (p. 246)
4
9
Solution to Exercise 4.5.5 (p. 246)
14
5
Solution to Exercise 4.5.6 (p. 246)
35
48
Solution to Exercise 4.5.7 (p. 246)
10
3
Solution to Exercise 4.5.8 (p. 246)
15