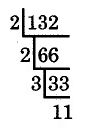124 Fundamentals of Mathematics: Part 6
32
Exercise 3.2.31
(Solution on p. 200.)
42
Exercise 3.2.32
12
Exercise 3.2.33
(Solution on p. 200.)
102
Exercise 3.2.34
112
Exercise 3.2.35
(Solution on p. 200.)
122
Exercise 3.2.36
132
Exercise 3.2.37
(Solution on p. 200.)
152
Exercise 3.2.38
14
Exercise 3.2.39
(Solution on p. 201.)
34
Exercise 3.2.40
73
Exercise 3.2.41
(Solution on p. 201.)
103
Exercise 3.2.42
1002
Exercise 3.2.43
(Solution on p. 201.)
83
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 3. EXPONENTS, ROOTS, AND FACTORIZATION OF WHOLE
NUMBERS
Exercise 3.2.44
55
Exercise 3.2.45
(Solution on p. 201.)
93
Exercise 3.2.46
62
Exercise 3.2.47
(Solution on p. 201.)
71
Exercise 3.2.48
128
Exercise 3.2.49
(Solution on p. 201.)
27
Exercise 3.2.50
05
Exercise 3.2.51
(Solution on p. 201.)
84
Exercise 3.2.52
58
Exercise 3.2.53
(Solution on p. 201.)
69
Exercise 3.2.54
253
Exercise 3.2.55
(Solution on p. 201.)
422
Exercise 3.2.56
313
Exercise 3.2.57
(Solution on p. 201.)
155
Exercise 3.2.58
220
Exercise 3.2.59
(Solution on p. 201.)
8162
For the following problems, nd the roots (using your knowledge of multiplication). Use a calculator to check each result.
Exercise 3.2.60
√9
Exercise 3.2.61
(Solution on p. 201.)
√16
Exercise 3.2.62
√36
Exercise 3.2.63
(Solution on p. 201.)
√64
Exercise 3.2.64
√121
Exercise 3.2.65
(Solution on p. 201.)
√144
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 3.2.66
√169
Exercise 3.2.67
(Solution on p. 201.)
√225
Exercise 3.2.68
√
3 27
Exercise 3.2.69
(Solution on p. 201.)
√
5 32
Exercise 3.2.70
√
4 256
Exercise 3.2.71
(Solution on p. 201.)
√
3 216
Exercise 3.2.72
√
7 1
Exercise 3.2.73
(Solution on p. 201.)
√400
Exercise 3.2.74
√900
Exercise 3.2.75
(Solution on p. 201.)
√10,000
Exercise 3.2.76
√324
Exercise 3.2.77
(Solution on p. 201.)
√3,600
√
For the following problems, use a calculator with the keys x, yx, and 1/x to nd each of the values.
Exercise 3.2.78
√676
Exercise 3.2.79
(Solution on p. 201.)
√1,156
Exercise 3.2.80
√46,225
Exercise 3.2.81
(Solution on p. 201.)
√17,288,964
Exercise 3.2.82
√
3 3, 375
Exercise 3.2.83
(Solution on p. 201.)
√
4 331, 776
Exercise 3.2.84
√
8 5, 764, 801
Exercise 3.2.85
(Solution on p. 201.)
√
12 16, 777, 216
Exercise 3.2.86
√
8 16, 777, 216
Exercise 3.2.87
(Solution on p. 201.)
√
10 9, 765, 625
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 3. EXPONENTS, ROOTS, AND FACTORIZATION OF WHOLE
NUMBERS
Exercise 3.2.88
√
4 160, 000
Exercise 3.2.89
(Solution on p. 202.)
√
3 531, 441
3.2.7.1 Exercises for Review
Exercise 3.2.90
(Section 1.7) Use the numbers 3, 8, and 9 to illustrate the associative property of addition.
Exercise 3.2.91
(Solution on p. 202.)
(Section 2.2) In the multiplication 8 · 4 = 32, specify the name given to the numbers 8 and 4.
Exercise 3.2.92
(Section 2.3) Does the quotient 15 ÷ 0 exist? If so, what is it?
Exercise 3.2.93
(Solution on p. 202.)
(Section 2.3) Does the quotient 0 ÷ 15exist? If so, what is it?
Exercise 3.2.94
(Section 2.6) Use the numbers 4 and 7 to illustrate the commutative property of multiplication.
3.3 Grouping Symbols and the Order of Operations 3
3.3.1 Section Overview
• Grouping Symbols
• Multiple Grouping Symbols
• The Order of Operations
• Calculators
3.3.2 Grouping Symbols
Grouping symbols are used to indicate that a particular collection of numbers and meaningful operations are to be grouped together and considered as one number. The grouping symbols commonly used in mathematics are the following:
( ), [ ], { },
Parentheses: ( )
Brackets: [ ]
Braces: { }
Bar:
In a computation in which more than one operation is involved, grouping symbols indicate which operation to perform rst. If possible, we perform operations inside grouping symbols rst.
3This content is available online at <http://cnx.org/content/m34872/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
3.3.2.1 Sample Set A
If possible, determine the value of each of the following.
Example 3.9
9 + (3 · 8)
Since 3 and 8 are within parentheses, they are to be combined rst.
9 + (3 · 8)
= 9 + 24
= 33
Thus,
9 + (3 · 8) = 33
Example 3.10
(10 ÷ 0) · 6
Since 10 ÷ 0 is undened, this operation is meaningless, and we attach no value to it. We write,
“undened.”
3.3.2.2 Practice Set A
If possible, determine the value of each of the following.
Exercise 3.3.1
(Solution on p. 202.)
16 − (3 · 2)
Exercise 3.3.2
(Solution on p. 202.)
5 + (7 · 9)
Exercise 3.3.3
(Solution on p. 202.)
(4 + 8) · 2
Exercise 3.3.4
(Solution on p. 202.)
28 ÷ (18 − 11)
Exercise 3.3.5
(Solution on p. 202.)
(33 ÷ 3) − 11
Exercise 3.3.6
(Solution on p. 202.)
4 + (0 ÷ 0)
3.3.3 Multiple Grouping Symbols
When a set of grouping symbols occurs inside another set of grouping symbols, we perform the operations within the innermost set rst.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 3. EXPONENTS, ROOTS, AND FACTORIZATION OF WHOLE
NUMBERS
3.3.3.1 Sample Set B
Determine the value of each of the following.
Example 3.11
2 + (8 · 3) − (5 + 6)
Combine 8 and 3 rst, then combine 5 and 6.
2 + 24 − 11
Now combine left to right.
26 − 11
15
Example 3.12
10 + [30 − (2 · 9)]
Combine 2 and 9 since they occur in the innermost set of parentheses.
10 + [30 − 18]
Now combine 30 and 18.
10 + 12
22
3.3.3.2 Practice Set B
Determine the value of each of the following.
Exercise 3.3.7
(Solution on p. 202.)
(17 + 8) + (9 + 20)
Exercise 3.3.8
(Solution on p. 202.)
(55 − 6) − (13 · 2)
Exercise 3.3.9
(Solution on p. 202.)
23 + (12 ÷ 4) − (11 · 2)
Exercise 3.3.10
(Solution on p. 202.)
86 + [14 ÷ (10 − 8)]
Exercise 3.3.11
(Solution on p. 202.)
31 + {9 + [1 + (35 − 2)]}
Exercise 3.3.12
(Solution on p. 202.)
{6 − [24 ÷ (4 · 2)]}3
3.3.4 The Order of Operations
Sometimes there are no grouping symbols indicating which operations to perform rst. For example, suppose we wish to nd the value of 3 + 5 · 2. We could do either of two things: Add 3 and 5, then multiply this sum by 2.
3 + 5 · 2
= 8 · 2
= 16
Multiply 5 and 2, then add 3 to this product.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
3 + 5 · 2
= 3 + 10
= 13
We now have two values for one number. To determine the correct value, we must use the accepted order of operations.
Order of Operations
1. Perform all operations inside grouping symbols, beginning with the innermost set, in the order 2, 3, 4
described below,
2. Perform all exponential and root operations.
3. Perform all multiplications and divisions, moving left to right.
4. Perform all additions and subtractions, moving left to right.
3.3.4.1 Sample Set C
Determine the value of each of the following.
Example 3.13
21 + 3 · 12
Multiply rst.
21 + 36
Add.
57
Example 3.14
(15 − 8) + 5 · (6 + 4) .
Simplify inside parentheses rst.
7 + 5 · 10
Multiply.
7 + 50
Add.
57
Example 3.15
63 − (4 + 6 · 3) + 76 − 4
Simplify rst within the parenthesis by multiplying, then adding.
63 − (4 + 18) + 76 − 4
63 − 22 + 76 − 4
Now perform the additions and subtractions, moving left to right.
41 + 76 − 4
Add 41 and 76: 41 + 76 = 117.
117 − 4
Subtract 4 from 117:
117 − 4 = 113.
113
Example 3.16
7 · 6 − 42 + 15
Evaluate the exponential forms, moving left to right.
7 · 6 − 16 + 1
Multiply 7 and 6: 7 · 6 = 42
42 − 16 + 1
Subtract 16 from 42: 42 − 16 = 26
26 + 1
Add 26 and 1: 26 + 1 = 27
27
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 3. EXPONENTS, ROOTS, AND FACTORIZATION OF WHOLE
NUMBERS
Example 3.17
6 · 32 + 22 + 42
Evaluate the exponential forms in the parentheses: 32 = 9 and 22 = 4
6 · (9 + 4) + 42
Add the 9 and 4 in the parentheses: 9 + 4 = 13
6 · (13) + 42
Evaluate the exponential form: 42 = 16
6 · (13) + 16
Multiply 6 and 13: 6 · 13 = 78
78 + 16
Add 78 and 16: 78 + 16 = 94
94
Example 3.18
Recall that the bar is a grouping symbol.
62+22
+ 13+82
42+6·22
102−19·5
The fraction 62+22 is equivalent to 62 + 22 ÷ 42 + 6 · 22
42+6·22
36+4
16
+
1+64
+6·4
100−19·5
36+4
16+24 + 1+64
100−95
40
40 + 65
5
1 + 13
14
3.3.4.2 Practice Set C
Determine the value of each of the following.
Exercise 3.3.13
(Solution on p. 202.)
8 + (32 − 7)
Exercise 3.3.14
(Solution on p. 202.)
(34 + 18 − 2 · 3) + 11
Exercise 3.3.15
(Solution on p. 202.)
8 (10) + 4 (2 + 3) − (20 + 3 · 15 + 40 − 5)
Exercise 3.3.16
(Solution on p. 202.)
5 · 8 + 42 − 22
Exercise 3.3.17
(Solution on p. 202.)
4 62 − 33 ÷ 42 − 4
Exercise 3.3.18
(Solution on p. 202.)
(8 + 9 · 3) ÷ 7 + 5 · (8 ÷ 4 + 7 + 3 · 5)
Exercise 3.3.19
(Solution on p. 202.)
33+23
82+24
÷ 8·3+18
62−29 + 5
72−32
23−3
3.3.5 Calculators
Using a calculator is helpful for simplifying computations that involve large numbers.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
3.3.5.1 Sample Set D
Use a calculator to determine each value.
Example 3.19
9, 842 + 56 · 85
Key
Display Reads
Perform the multiplication rst. Type 56
56
Press ×
56
Type 85
85
Now perform the addition.
Press +
4760
Type 9842 9842
Press =
14602
Table 3.3
The display now reads 14,602.
Example 3.20
42 (27 + 18) + 105 (810 ÷ 18)
Key
Display Reads
Operate inside the parentheses Type 27 27
Press +
27
Type 18 18
Press =
45
Multiply by 42.
Press ×
45
Type 42 42
Press =
1890
Table 3.4
Place this result into memory by pressing the memory key.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 3. EXPONENTS, ROOTS, AND FACTORIZATION OF WHOLE
NUMBERS
Key
Display Reads
Now operate in the other parentheses.
Type 810 810
Press ÷
810
Type 18
18
Press =
45
Now multiply by 105.
Press ×
45
Type 105 105
Press =
4725
We are now ready to add these two quantities together. Press +
4725
Press the memory recall key.
1890
Press =
6615
Table 3.5
Thus, 42 (27 + 18) + 105 (810 ÷ 18) = 6, 615
Example 3.21
164 + 373
Nonscientic Calculators
Key
Display Reads
Type
16 16
Press
×
16
Type
16 16
Press
×
256
Type
16 16
Press
×
4096
Type
16 16
Press
=
65536
Press the memory key
Type
37 37
Press
×
37
Type
37 37
Press
×
1396
Type
37 37
Press
×
50653
Press
+
50653
Press memory recall key
65536
Press
=
116189
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Table 3.6
Calculators with yx Key
Key
Display Reads
Type 16 16
Press yx 16
Type 4
4
Press =
4096
Press +
4096
Type 37 37
Press yx 37
Type 3
3
Press =
116189
Table 3.7
Thus, 164 + 373 = 116, 189
We can certainly see that the more powerful calculator simplies computations.
Example 3.22
Nonscientic calculators are unable to handle calculations involving very large numbers.
85612 · 21065
Key
Display Reads
Type 85612 85612
Press ×
85612
Type 21065 21065
Press =
Table 3.8
This number is too big for the display of some calculators and we’ll probably get some kind of error message. On some scientic calculators such large numbers are coped with by placing them in a form called “scientic notation.” Others can do the multiplication directly. (1803416780) 3.3.5.2 Practice Set D
Use a calculator to nd each value.
Exercise 3.3.20
(Solution on p. 202.)
9, 285 + 86 (49)
Exercise 3.3.21
(Solution on p. 202.)
55 (84 − 26) + 120 (512 − 488)
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 3. EXPONENTS, ROOTS, AND FACTORIZATION OF WHOLE
NUMBERS
Exercise 3.3.22
(Solution on p. 202.)
1063 − 174
Exercise 3.3.23
(Solution on p. 203.)
6, 0533
3.3.6 Exercises
For the following problems, nd each value. Check each result with a calculator.
Exercise 3.3.24
(Solution on p. 203.)
2 + 3 · (8)
Exercise 3.3.25
18 + 7 · (4 − 1)
Exercise 3.3.26
(Solution on p. 203.)
3 + 8 · (6 − 2) + 11
Exercise 3.3.27
1 − 5 · (8 − 8)
Exercise 3.3.28
(Solution on p. 203.)
37 − 1 · 62
Exercise 3.3.29
98 ÷ 2 ÷ 72
Exercise 3.3.30
(Solution on p. 203.)
42 − 2 · 4 − 23
Exercise 3.3.31
√9 + 14
Exercise 3.3.32
(Solution on p. 203.)
√
√
100 + 81 − 42
Exercise 3.3.33
√
3 8 + 8 − 2 · 5
Exercise 3.3.34
(Solution on p. 203.)
√
4 16 − 1 + 52
Exercise 3.3.35
61 − 22 + 4 [3 · (10) + 11]
Exercise 3.3.36
(Solution on p. 203.)
121 − 4 · [(4) · (5) − 12] + 162
Exercise 3.3.37
(1+16)−3 + 5 · (12)
7
Exercise 3.3.38
(Solution on p. 203.)
8·(6+20) + 3·(6+16)
8
22
Exercise 3.3.39
10 · [8 + 2 · (6 + 7)]
Exercise 3.3.40
(Solution on p. 203.)
21 ÷ 7 ÷ 3
Exercise 3.3.41
102 · 3 ÷ 52 · 3 − 2 · 3
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 3.3.42
(Solution on p. 203.)
85 ÷ 5 · 5 − 85
Exercise 3.3.43
51
17 + 7 − 2 · 5 · 12
3
Exercise 3.3.44
(Solution on p. 203.)
22 · 3 + 23 · (6 − 2) − (3 + 17) + 11 (6)
Exercise 3.3.45
26 − 2 · {6+20
13 }
Exercise 3.3.46
(Solution on p. 203.)
2 · {(7 + 7) + 6 · [4 · (8 + 2)]}
Exercise 3.3.47
0 + 10 (0) + 15 · {4 · 3 + 1}
Exercise 3.3.48
(Solution on p. 203.)
18 + 7+2
9
Exercise 3.3.49
(4 + 7) · (8 − 3)
Exercise 3.3.50
(Solution on p. 203.)
(6 + 8) · (5 + 2 − 4)
Exercise 3.3.51
(21 − 3) · (6 − 1) · (7) + 4 (6 + 3)
Exercise 3.3.52
(Solution on p. 203.)
(10 + 5) · (10 + 5) − 4 · (60 − 4)
Exercise 3.3.53
6 · {2 · 8 + 3} − (5) · (2) + 8 + (1 + 8) · (1 + 11)
4
Exercise 3.3.54
(Solution on p. 203.)
25 + 3 · (8 + 1)
Exercise 3.3.55
34 + 24 · (1 + 5)
Exercise 3.3.56
(Solution on p. 203.)
16 + 08 + 52 · (2 + 8)3
Exercise 3.3.57
(7) · (16) − 34 + 22 · 17 + 32
Exercise 3.3.58
(Solution on p. 203.)
23−7
52
Exercise 3.3.59
(1+6)2+2
3·6+1
Exercise 3.3.60
(Solution on p. 203.)
62−1 + 43+2·3
23−3
2·5
Exercise 3.3.61
5(82−9·6) + 72−42
25−7
24−5
Exercise 3.3.62
(Solution on p. 203.)
(2+1)3+23+110 − 152−[2·5]2
62
5·52
Exercise 3.3.63
63−2·102
18(23+72)
+
22
2(19)−33
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 3. EXPONENTS, ROOTS, AND FACTORIZATION OF WHOLE
NUMBERS
Exercise 3.3.64
(Solution on p. 203.)
√
2 · {6 + 102 − 6 25}
Exercise 3.3.65
√
√
181 − 3 · 2 36 + 3 3 64
Exercise 3.3.66
(Solution on p. 203.)
√
√
2·( 81− 3 125)
42−10+22
3.3.6.1 Exercises for Review
Exercise 3.3.67
(Section 1.7) The fact that 0 + any whole number = that particular whole number is an example of which property of addition?
Exercise 3.3.68
(Solution on p. 203.)
(Section 2.2) Find the product. 4, 271 × 630.
Exercise 3.3.69
(Section 2.3) In the statement 27 ÷ 3 = 9, what name is given to the result 9?
Exercise 3.3.70
(Solution on p. 203.)
(Section 2.7) What number is the multiplicative identity?
Exercise 3.3.71
(Section 2.7) Find the value of 24.
3.4 Prime Factorization of Natural Numbers4
3.4.1 Section Overview
• Factors
• Determining the Factors of a Whole Number
• Prime and Composite Numbers
• The Fundamental Principle of Arithmetic
• The Prime Factorization of a Natural Number
3.4.2 Factors
From observations made in the process of multiplication, we have seen that (factor) · (factor) = product
Factors, Product
The two numbers being multiplied are the factors and the result of the multiplication is the product. Now, using our knowledge of division, we can see that a rst number is a factor of a second number if the rst number divides into the second number a whole number of times (without a remainder).
One Number as a Factor of Another
A rst number is a factor of a second number if the rst number divides into the second number a whole number of times (without a remainder).
4This content is available online at <http://cnx.org/content/m34873/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
We show this in the following examples:
Example 3.23
3 is a factor of 27, since 27 ÷ 3 = 9, or 3 · 9 = 27.
Example 3.24
7 is a factor of 56, since 56 ÷ 7 = 8, or 7 · 8 = 56.
Example 3.25
4 is not a factor of 10, since 10 ÷ 4 = 2R2. (There is a remainder.)
3.4.3 Determining the Factors of a Whole Number
We can use the tests for divisibility from Section 2.5 to determine all the factors of a whole number.
3.4.3.1 Sample Set A
Example 3.26
Find all the factors of 24.
Try 1:
24 ÷ 1 = 24
1 and 24 are factors
Try 2:
24 is even, so 24 is divisible by 2.
24 ÷ 2 = 12
2 and 12 are factors
Try 3: 2 + 4 = 6 and 6 is divisible by 3, so 24 is divisible by 3.
24 ÷ 3 = 8
3 and 8 are factors
Try 4:
24 ÷ 4 = 6
4 and 6 are factors
Try 5:
24 ÷ 5 = 4R4
5 is not a factor.
The next number to try is 6, but we already have that 6 is a factor. Once we come upon a factor that we already have discovered, we can stop.
All the whole number factors of 24 are 1, 2, 3, 4, 6, 8, 12, and 24.
3.4.3.2 Practice Set A
Find all the factors of each of the following numbers.
Exercise 3.4.1
(Solution on p. 204.)
6
Exercise 3.4.2
(Solution on p. 204.)
12
Exercise 3.4.3
(Solution on p. 204.)
18
Exercise 3.4.4
(Solution on p. 204.)
5
Exercise 3.4.5
(Solution on p. 204.)
10
Exercise 3.4.6
(Solution on p. 204.)
33
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 3. EXPONENTS, ROOTS, AND FACTORIZATION OF WHOLE
NUMBERS
Exercise 3.4.7
(Solution on p. 204.)
19
3.4.4 Prime and Composite Numbers
Notice that the only factors of 7 are 1 and 7 itself, and that the only factors of 3 are 1 and 3 itself. However, the number 8 has the factors 1, 2, 4, and 8, and the number 10 has the factors 1, 2, 5, and 10. Thus, we can see that a whole number can have only two factors (itself and 1) and another whole number can have several factors.
We can use this observation to make a useful classication for whole numbers: prime numbers and composite numbers.
Prime Number
A whole number (greater than one) whose only factors are itself and 1 is called a prime number.
The Number 1 is Not a Prime Number
The rst seven prime numbers are 2, 3, 5, 7, 11, 13, and 17. Notice that the whole number 1 is not considered to be a prime number, and the whole number 2 is the rst prime and the only even prime number.
Composite Number
A whole number composed of factors other than itself and 1 is called a composite number. Composite numbers are not prime numbers.
Some composite numbers are 4, 6, 8, 9, 10, 12, and 15.
3.4.4.1 Sample Set B
Determine which whole numbers are prime and which are composite.
Example 3.27
39. Since 3 divides into 39, the number 39 is composite: 39 ÷ 3 = 13
Example 3.28
47. A few division trials will assure us that 47 is only divisible by 1 and 47. Therefore, 47 is prime.
3.4.4.2 Practice Set B
Determine which of the following whole numbers are prime and which are composite.
Exercise 3.4.8
(Solution on p. 204.)
3
Exercise 3.4.9
(Solution on p. 204.)
16
Exercise 3.4.10
(Solution on p. 204.)
21
Exercise 3.4.11
(Solution on p. 204.)
35
Exercise 3.4.12
(Solution on p. 204.)
47
Exercise 3.4.13
(Solution on p. 204.)
29
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 3.4.14
(Solution on p. 204.)
101
Exercise 3.4.15
(Solution on p. 204.)
51
3.4.5 The Fundamental Principle of Arithmetic
Prime numbers are very useful in the study of mathematics. We will see how they are used in subsequent sections. We now state the Fundamental Principle of Arithmetic.
Fundamental Principle of Arithmetic
Except for the order of the factors, every natural number other than 1 can be factored in one and only one way as a product of prime numbers.
Prime Factorization
When a number is factored so that all its factors are prime numbers. the factorization is called the prime factorization of the number.
The technique of prime factorization is illustrated in the following three examples.
1. 10 = 5 · 2. Both 2 and 5 are primes. Therefore, 2 · 5 is the prime factorization of 10.
2. 11. The number 11 is a prime number. Prime factorization applies only to composite numbers. Thus, 11 has no prime factorization.
3. 60 = 2 · 30. The number 30 is not prime: 30 = 2 · 15.
60 = 2 · 2 · 15
The number 15 is not prime: 15 = 3 · 5
60 = 2 · 2 · 3 · 5
We’ll use exponents.
60 = 22 · 3 · 5
The numbers 2, 3, and 5 are each prime. Therefore, 22 · 3 · 5 is the prime factorization of 60.
3.4.6 The Prime Factorization of a Natural Number
The following method provides a way of nding the prime factorization of a natural number.
The Method of Finding the Prime Factorization of a Natural Number
1. Divide the number repeatedly by the smallest prime number that will divide into it a whole number of times (without a remainder).
2. When the prime number used in step 1 no longer divides into the given number without a remainder, repeat the division process with the next largest prime that divides the given number.
3. Continue this process until the quotient is smaller than the divisor.
4. The prime factorization of the given number is the product of all these prime divisors. If the number has no prime divisors, it is a prime number.
We may be able to use some of the tests for divisibility we studied in Section 2.5 to help nd the primes that divide the given number.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
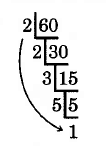
176
CHAPTER 3. EXPONENTS, ROOTS, AND FACTORIZATION OF WHOLE
NUMBERS
3.4.6.1 Sample Set C
Example 3.29
Find the prime factorization of 60.
Since the last digit of 60 is 0, which is even, 60 is divisible by 2. We will repeatedly divide by 2
until we no longer can. We shall divide as follows:
30 is divisible by 2 again.
15 is not divisible by 2, but it is divisible by 3, the next prime.
5 is not divisble by 3, but it is divisible by 5, the next prime.
The quotient 1 is nally smaller than the divisor 5, and the prime factorization of 60 is the product of these prime divisors.
60 = 2 · 2 · 3 · 5
We use exponents when possible.
60 = 22 · 3 · 5
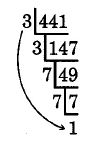
Example 3.30
Find the prime factorization of 441.
441 is not divisible by 2 since its last digit is not divisible by 2.
441 is divisible by 3 since 4 + 4 + 1 = 9 and 9 is divisible by 3.
147 is divisible by 3 (1 + 4 + 7 = 12) .
49 is not divisible by 3, nor is it divisible by 5. It is divisible by 7.
The quotient 1 is nally smaller than the divisor 7, and the prime factorization of 441 is the product of these prime divisors.
441 = 3 · 3 · 7 · 7
Use exponents.
441 = 32 · 72
Example 3.31
Find the prime factorization of 31.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
31 is not divisible by 2
Its last digit is not even
31 ÷ 2 = 15R1
The quotient, 15, is larger than the divisor, 3. Continue.
31 is not divisible by 3
The digits 3 + 1 = 4, and 4 is not divisible by 3.
31 ÷ 3 = 10R1
The quotient, 10, is larger than the divisor, 3. Continue.
31 is not divisible by 5
The last digit of 31 is not 0 or 5.
31 ÷ 5 = 6R1
The quotient, 6, is larger than the divisor, 5. Continue.
31 is not divisible by 7.
Divide by 7.
31 ÷ 7 = 4R1
The quotient, 4, is smaller than the divisor, 7.
We can stop the process and conclude that 31 is a prime number.
The number 31 is a prime number
3.4.6.2 Practice Set C
Find the prime factorization of each whole number.
Exercise 3.4.16
(Solution on p. 204.)
22
Exercise 3.4.17
(Solution on p. 204.)
40
Exercise 3.4.18
(Solution on p. 204.)
48
Exercise 3.4.19
(Solution on p. 204.)
63
Exercise 3.4.20
(Solution on p. 204.)
945
Exercise 3.4.21
(Solution on p. 204.)
1,617
Exercise 3.4.22
(Solution on p. 204.)
17
Exercise 3.4.23
(Solution on p. 204.)
61
3.4.7 Exercises
For the following problems, determine the missing factor(s).
Exercise 3.4.24
(Solution on p. 204.)
14=7·
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 3. EXPONENTS, ROOTS, AND FACTORIZATION OF WHOLE
NUMBERS
Exercise 3.4.25
20=4·
Exercise 3.4.26
(Solution on p. 204.)
36=9·
Exercise 3.4.27
42 = 21·
Exercise 3.4.28
(Solution on p. 205.)
44=4·
Exercise 3.4.29
38=2·
Exercise 3.4.30
(Solution on p. 205.)
18=3·
·
Exercise 3.4.31
28=2·
·
Exercise 3.4.32
(Solution on p. 205.)
300=2·5·
·
Exercise 3.4.33
840=2·
·
·
For the following problems, nd all the factors of each of the numbers.
Exercise 3.4.34
(Solution on p. 205.)
16
Exercise 3.4.35
22
Exercise 3.4.36
(Solution on p. 205.)
56
Exercise 3.4.37
105
Exercise 3.4.38
(Solution on p. 205.)
220
Exercise 3.4.39
15
Exercise 3.4.40
(Solution on p. 205.)
32
Exercise 3.4.41
80
Exercise 3.4.42
(Solution on p. 205.)
142
Exercise 3.4.43
218
For the following problems, determine which of the whole numbers are prime and which are composite.
Exercise 3.4.44
(Solution on p. 205.)
23
Exercise 3.4.45
25
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 3.4.46
(Solution on p. 205.)
27
Exercise 3.4.47
2
Exercise 3.4.48
(Solution on p. 205.)
3
Exercise 3.4.49
5
Exercise 3.4.50
(Solution on p. 205.)
7
Exercise 3.4.51
9
Exercise 3.4.52
(Solution on p. 205.)
11
Exercise 3.4.53
34
Exercise 3.4.54
(Solution on p. 205.)
55
Exercise 3.4.55
63
Exercise 3.4.56
(Solution on p. 205.)
1,044
Exercise 3.4.57
924
Exercise 3.4.58
(Solution on p. 205.)
339
Exercise 3.4.59
103
Exercise 3.4.60
(Solution on p. 205.)
209
Exercise 3.4.61
667
Exercise 3.4.62
(Solution on p. 205.)
4,575
Exercise 3.4.63
119
For the following problems, nd the prime factorization of each of the whole numbers.
Exercise 3.4.64
(Solution on p. 205.)
26
Exercise 3.4.65
38
Exercise 3.4.66
(Solution on p. 205.)
54
Exercise 3.4.67
62
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 3. EXPONENTS, ROOTS, AND FACTORIZATION OF WHOLE
NUMBERS
Exercise 3.4.68
(Solution on p. 205.)
56
Exercise 3.4.69
176
Exercise 3.4.70
(Solution on p. 205.)
480
Exercise 3.4.71
819
Exercise 3.4.72
(Solution on p. 205.)
2,025
Exercise 3.4.73
148,225
3.4.7.1 Exercises For Review
Exercise 3.4.74
(Solution on p. 205.)
(Section 1.4) Round 26,584 to the nearest ten.
Exercise 3.4.75
(Section 1.6) How much bigger is 106 than 79?
Exercise 3.4.76
(Solution on p. 205.)
(Section 2.3) True or false? Zero divided by any nonzero whole number is zero.
Exercise 3.4.77
(Section 2.4) Find the quotient. 10, 584 ÷ 126.
Exercise 3.4.78
(Solution on p. 206.)
√
√
(Section 3.3) Find the value of 121 − 81 + 62 ÷ 3.
3.5 The Greatest Common Factor 5
3.5.1 Section Overview
• The Greatest Common Factor (GCF)
• A Method for Determining the Greatest Common Factor
3.5.2 The Greatest Common Factor (GCF)
Using the method we studied in Section 3.4, we could obtain the prime factorizations of 30 and 42.
30 = 2 · 3 · 5
42 = 2 · 3 · 7
Common Factor
We notice that 2 appears as a factor in both numbers, that is, 2 is a common factor of 30 and 42. We also notice that 3 appears as a factor in both numbers. Three is also a common factor of 30 and 42.
5This content is available online at <http://cnx.org/content/m34874/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Greatest Common Factor (GCF)
When considering two or more numbers, it is often useful to know if there is a largest common factor of the numbers, and if so, what that number is. The largest common factor of two or more whole numbers is called the greatest common factor, and is abbreviated by GCF. The greatest common factor of a collection of whole numbers is useful in working with fractions (which we will do in Section 4.1).
3.5.3 A Method for Determining the Greatest Common Factor
A straightforward method for determining the GCF of two or more whole numbers makes use of both the prime factorization of the numbers and exponents.
Finding the GCF
To nd the greatest common factor (GCF) of two or more whole numbers:
1. Write the prime factorization of each number, using exponents on repeated factors.
2. Write each base that is common to each of the numbers.
3. To each base listed in step 2, attach the smallest exponent that appears on it in either of the prime factorizations.
4. The GCF is the product of the numbers found in step 3.
3.5.3.1 Sample Set A
Find the GCF of the following numbers.
Example 3.32
12 and 18
12 = 2 · 6 = 2 · 2 · 3 = 22 · 3
1. 18 = 2·9 = 2·3·3 = 2·32
2. The common bases are 2 and 3.
3. The smallest exponents appearing on 2 and 3 in the prime factorizations are, respectively, 1
and 1 ( 21and 31), or 2 and 3.
4. The GCF is the product of these numbers. 2 · 3 = 6
The GCF of 30 and 42 is 6 because 6 is the largest number that divides both 30 and 42 without a remainder.
Example 3.33
18, 60, and 72
18 = 2 · 9 = 2 · 3 · 3 = 2 · 32
1.
60 = 2 · 30 = 2 · 2 · 15 = 2 · 2 · 3 · 5 = 22 · 3 · 5
72 = 2 · 36 = 2 · 2 · 18 = 2 · 2 · 2 · 9 = 2 · 2 · 2 · 3 · 3 = 23 · 32
2. The common bases are 2 and 3.
3. The smallest exponents appearing on 2 and 3 in the prime factorizations are, respectively, 1
and 1:
21 from 18
31 from 60
4. The GCF is the product of these numbers.
GCF is 2 · 3 = 6
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 3. EXPONENTS, ROOTS, AND FACTORIZATION OF WHOLE
NUMBERS
Thus, 6 is the largest number that divides 18, 60, and 72 without a remainder.
Example 3.34
700, 1,880, and 6,160
700
=
2 · 350
=
2 · 2 · 175
=
2 · 2 · 5 · 35
=
2 · 2 · 5 · 5 · 7
=
22 · 52 · 7
1, 880
=
2 · 940
=
2 · 2 · 470
=
2 · 2 · 2 · 235
=
2 · 2 · 2 · 5 · 47
1.
=
23 · 5 · 47
6, 160
=
2 · 3, 080
=
2 · 2 · 1, 540
=
2 · 2 · 2 · 770
=
2 · 2 · 2 · 2 · 385
=
2 · 2 · 2 · 2 · 5 · 77
=
2 · 2 · 2 · 2 · 5 · 7 · 11
=
24 · 5 · 7 · 11
2. The common bases are 2 and 5
3. The smallest exponents appearing on 2 and 5 in the prime factorizations are, respectively, 2
and 1.
22 from 700.
51 from either 1,880 or 6,160.
4. The GCF is the product of these numbers.
GCF is 22 · 5 = 4 · 5 = 20
Thus, 20 is the largest number that divides 700, 1,880, and 6,160 without a remainder.
3.5.3.2 Practice Set A
Find the GCF of the following numbers.
Exercise 3.5.1
(Solution on p. 206.)
24 and 36
Exercise 3.5.2
(Solution on p. 206.)
48 and 72
Exercise 3.5.3
(Solution on p. 206.)
50 and 140
Exercise 3.5.4
(Solution on p. 206.)
21 and 225
Exercise 3.5.5
(Solution on p. 206.)
450, 600, and 540
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
3.5.4 Exercises
For the following problems, nd the greatest common factor (GCF) of the numbers.
Exercise 3.5.6
(Solution on p. 206.)
6 and 8
Exercise 3.5.7
5 and 10
Exercise 3.5.8
(Solution on p. 206.)
8 and 12
Exercise 3.5.9
9 and 12
Exercise 3.5.10
(Solution on p. 206.)
20 and 24
Exercise 3.5.11
35 and 175
Exercise 3.5.12
(Solution on p. 206.)
25 and 45
Exercise 3.5.13
45 and 189
Exercise 3.5.14
(Solution on p. 206.)
66 and 165
Exercise 3.5.15
264 and 132
Exercise 3.5.16
(Solution on p. 206.)
99 and 135
Exercise 3.5.17
65 and 15
Exercise 3.5.18
(Solution on p. 206.)
33 and 77
Exercise 3.5.19
245 and 80
Exercise 3.5.20
(Solution on p. 206.)
351 and 165
Exercise 3.5.21
60, 140, and 100
Exercise 3.5.22
(Solution on p. 206.)
147, 343, and 231
Exercise 3.5.23
24, 30, and 45
Exercise 3.5.24
(Solution on p. 206.)
175, 225, and 400
Exercise 3.5.25
210, 630, and 182
Exercise 3.5.26
(Solution on p. 206.)
14, 44, and 616
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 3. EXPONENTS, ROOTS, AND FACTORIZATION OF WHOLE
NUMBERS
Exercise 3.5.27
1,617, 735, and 429
Exercise 3.5.28
(Solution on p. 206.)
1,573, 4,862, and 3,553
Exercise 3.5.29
3,672, 68, and 920
Exercise 3.5.30
(Solution on p. 206.)
7, 2,401, 343, 16, and 807
Exercise 3.5.31
500, 77, and 39
Exercise 3.5.32
(Solution on p. 206.)
441, 275, and 221
3.5.4.1 Exercises for Review
Exercise 3.5.33
(Section 2.2) Find the product. 2, 753 × 4, 006.
Exercise 3.5.34
(Solution on p. 206.)
(Section 2.4) Find the quotient. 954 ÷ 18.
Exercise 3.5.35
(Section 2.5) Specify which of the digits 2, 3, or 4 divide into 9,462.
Exercise 3.5.36
(Solution on p. 206.)
(Section 3.2) Write 8 × 8 × 8 × 8 × 8 × 8 using exponents.
Exercise 3.5.37
(Section 3.4) Find the prime factorization of 378.
3.6 The Least Common Multiple6
3.6.1 Section Overview
• Multiples
• Common Multiples
• The Least Common Multiple (LCM)
• Finding the Least Common Multiple
3.6.2 Multiples
When a whole number is multiplied by other whole numbers, with the exception of zero, the resulting products are called multiples of the given whole number. Note that any whole number is a multiple of itself.
6This content is available online at <http://cnx.org/content/m34876/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
185
3.6.2.1 Sample Set A
Multiples of 2 Multiples of 3 Multiples of 8 Multiples of 10
2 × 1 = 2
3 × 1 = 3
8 × 1 = 8
10 × 1 = 10
2 × 2 = 4
3 × 2 = 6
8 × 2 = 16
10 × 2 = 20
2 × 3 = 6
3 × 3 = 9
8 × 3 = 24
10 × 3 = 30
2 × 4 = 8
3 × 4 = 12
8 × 4 = 32
10 × 4 = 40
2 × 5 = 10
3 × 5 = 15
8 × 5 = 40
10 × 5 = 50
..
.
.
.
.
..
..
..
Table 3.9
3.6.2.2 Practice Set A
Find the rst ve multiples of the following numbers.
Exercise 3.6.1
(Solution on p. 206.)
4
Exercise 3.6.2
(Solution on p. 206.)
5
Exercise 3.6.3
(Solution on p. 206.)
6
Exercise 3.6.4
(Solution on p. 207.)
7
Exercise 3.6.5
(Solution on p. 207.)
9
3.6.3 Common Multiples
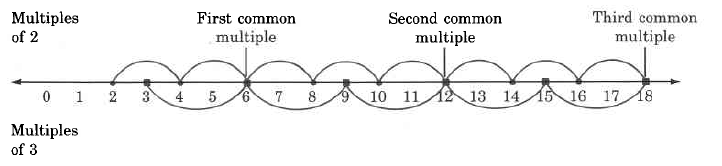
There will be times when we are given two or more whole numbers and we will need to know if there are any multiples that are common to each of them. If there are, we will need to know what they are. For example, some of the multiples that are common to 2 and 3 are 6, 12, and 18.
3.6.3.1 Sample Set B
Example 3.35
We can visualize common multiples using the number line.
Notice that the common multiples can be divided by both whole numbers.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 3. EXPONENTS, ROOTS, AND FACTORIZATION OF WHOLE
NUMBERS
3.6.3.2 Practice Set B
Find the rst ve common multiples of the following numbers.
Exercise 3.6.6
(Solution on p. 207.)
2 and 4
Exercise 3.6.7
(Solution on p. 207.)
3 and 4
Exercise 3.6.8
(Solution on p. 207.)
2 and 5
Exercise 3.6.9
(Solution on p. 207.)
3 and 6
Exercise 3.6.10
(Solution on p. 207.)
4 and 5
3.6.4 The Least Common Multiple (LCM)
Notice that in our number line visualization of common multiples (above), the rst common multiple is also the smallest, or least common multiple, abbreviated by LCM.
Least Common Multiple
The least common multiple, LCM, of two or more whole numbers is the smallest whole number that each of the given numbers will divide into without a remainder.
The least common multiple will be extremely useful in working with fractions (Section 4.1).
3.6.5 Finding the Least Common Multiple
Finding the LCM
To nd the LCM of two or more numbers:
1. Write the prime factorization of each number, using exponents on repeated factors.
2. Write each base that appears in each of the prime factorizations.
3. To each base, attach the largest exponent that appears on it in the prime factorizations.
4. The LCM is the product of the numbers found in step 3.
There are some major dierences between using the processes for obtaining the GCF and the LCM that we must note carefully:
The Dierence Between the Processes for Obtaining the GCF and the LCM
1. Notice the dierence between step 2 for the LCM and step 2 for the GCF. For the GCF, we use only the bases that are common in the prime factorizations, whereas for the LCM, we use each base that appears in the prime factorizations.
2. Notice the dierence between step 3 for the LCM and step 3 for the GCF. For the GCF, we attach the smallest exponents to the common bases, whereas for the LCM, we attach the largest exponents to the bases.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
3.6.5.1 Sample Set C
Find the LCM of the following numbers.
Example 3.36
9 and 12
9 = 3 · 3 = 32
1. 12 = 2·6 = 2·2·3 = 22 ·3
2. The bases that appear in the prime factorizations are 2 and 3.
3. The largest exponents appearing on 2 and 3 in the prime factorizations are, respectively, 2
and 2: 22 from 12.
32 from 9.
4. The LCM is the product of these numbers. LCM = 22 · 32 = 4 · 9 = 36
Thus, 36 is the smallest number that both 9 and 12 divide into without remainders.
Example 3.37
90 and 630
90
=
2 · 45 = 2 · 3 · 15 = 2 · 3 · 3 · 5 = 2 · 32 · 5
1. 630 =
2 · 315 = 2 · 3 · 105 = 2 · 3 · 3 · 35
= 2 · 3 · 3 · 5 · 7
= 2 · 32 · 5 · 7
2. The bases that appear in the prime factorizations are 2, 3, 5, and 7.
3. The largest exponents that appear on 2, 3, 5, and 7 are, respectively, 1, 2, 1, and 1: 21 from either 90 or 630.
32 from either 90 or 630.
51 from either 90 or 630.
71 from 630.
4. The LCM is the product of these numbers. LCM = 2 · 32 · 5 · 7 = 2 · 9 · 5 · 7 = 630
Thus, 630 is the smallest number that both 90 and 630 divide into with no remainders.
Example 3.38
33, 110, and 484
33
=
3 · 11
1. 110 =
2 · 55 = 2 · 5 · 11
484
=
2 · 242 = 2 · 2 · 121 = 2 · 2 · 11 · 11 = 22 · 112.
2. The bases that appear in the prime factorizations are 2, 3, 5, and 11.
3. The largest exponents that appear on 2, 3, 5, and 11 are, respectively, 2, 1, 1, and 2: 22 from 484.
31 from 33.
51 from 110
112 from 484.
LCM = 22 · 3 · 5 · 112
4. The LCM is the product of these numbers.
=
4 · 3 · 5 · 121
=
7260
Thus, 7260 is the smallest number that 33, 110, and 484 divide into without remainders.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 3. EXPONENTS, ROOTS, AND FACTORIZATION OF WHOLE
NUMBERS
3.6.5.2 Practice Set C
Find the LCM of the following numbers.
Exercise 3.6.11
(Solution on p. 207.)
20 and 54
Exercise 3.6.12
(Solution on p. 207.)
14 and 28
Exercise 3.6.13
(Solution on p. 207.)
6 and 63
Exercise 3.6.14
(Solution on p. 207.)
28, 40, and 98
Exercise 3.6.15
(Solution on p. 207.)
16, 27, 125, and 363
3.6.6 Exercises
For the following problems, nd the least common multiple of the numbers.
Exercise 3.6.16
(Solution on p. 207.)
8 and 12
Exercise 3.6.17
6 and 15
Exercise 3.6.18
(Solution on p. 207.)
8 and 10
Exercise 3.6.19
10 and 14
Exercise 3.6.20
(Solution on p. 207.)
4 and 6
Exercise 3.6.21
6 and 12
Exercise 3.6.22
(Solution on p. 207.)
9 and 18
Exercise 3.6.23
6 and 8
Exercise 3.6.24
(Solution on p. 207.)
5 and 6
Exercise 3.6.25
7 and 8
Exercise 3.6.26
(Solution on p. 207.)
3 and 4
Exercise 3.6.27
2 and 9
Exercise 3.6.28
(Solution on p. 207.)
7 and 9
Exercise 3.6.29
28 and 36
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 3.6.30
(Solution on p. 207.)
24 and 36
Exercise 3.6.31
28 and 42
Exercise 3.6.32
(Solution on p. 207.)
240 and 360
Exercise 3.6.33
162 and 270
Exercise 3.6.34
(Solution on p. 207.)
20 and 24
Exercise 3.6.35
25 and 30
Exercise 3.6.36
(Solution on p. 207.)
24 and 54
Exercise 3.6.37
16 and 24
Exercise 3.6.38
(Solution on p. 207.)
36 and 48
Exercise 3.6.39
24 and 40
Exercise 3.6.40
(Solution on p. 207.)
15 and 21
Exercise 3.6.41
50 and 140
Exercise 3.6.42
(Solution on p. 208.)
7, 11, and 33
Exercise 3.6.43
8, 10, and 15
Exercise 3.6.44
(Solution on p. 208.)
18, 21, and 42
Exercise 3.6.45
4, 5, and 21
Exercise 3.6.46
(Solution on p. 208.)
45, 63, and 98
Exercise 3.6.47
15, 25, and 40
Exercise 3.6.48
(Solution on p. 208.)
12, 16, and 20
Exercise 3.6.49
84 and 96
Exercise 3.6.50
(Solution on p. 208.)
48 and 54
Exercise 3.6.51
12, 16, and 24
Exercise 3.6.52
(Solution on p. 208.)
12, 16, 24, and 36
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 3. EXPONENTS, ROOTS, AND FACTORIZATION OF WHOLE
NUMBERS
Exercise 3.6.53
6, 9, 12, and 18
Exercise 3.6.54
(Solution on p. 208.)
8, 14, 28, and 32
Exercise 3.6.55
18, 80, 108, and 490
Exercise 3.6.56
(Solution on p. 208.)
22, 27, 130, and 225
Exercise 3.6.57
38, 92, 115, and 189
Exercise 3.6.58
(Solution on p. 208.)
8 and 8
Exercise 3.6.59
12, 12, and 12
Exercise 3.6.60
(Solution on p. 208.)
3, 9, 12, and 3
3.6.6.1 Exercises for Review
Exercise 3.6.61
(Section 1.4) Round 434,892 to the nearest ten thousand.
Exercise 3.6.62
(Solution on p. 208.)
(Section 1.6) How much bigger is 14,061 than 7,509?
Exercise 3.6.63
(Section 2.4) Find the quotient. 22, 428 ÷ 14.
Exercise 3.6.64
(Solution on p. 208.)
(Section 3.2) Expand 843. Do not nd the value.
Exercise 3.6.65
(Section 3.5) Find the greatest common factor of 48 and 72.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
3.7 Summary of Key Concepts7
3.7.1 Summary of Key Concepts
Exponential Notation (Section 3.2)
Exponential notation is a description of repeated multiplication.
Exponent (Section 3.2)
An exponent records the number of identical factors repeated in a multiplication.
In a number such as 73,
Base (Section 3.2)
7 is called the base.
Exponent (Section 3.2)
3 is called the exponent, or power.
Power (Section 3.2)
73 is read “seven to the third power,” or “seven cubed.”
Squared, Cubed (Section 3.2)
A number raised to the second power is often called squared. A number raised to the third power is often called cubed.
Root (Section 3.2)
In mathematics, the word root is used to indicate that, through repeated multiplication, one number is the source of another number.
The Radical Sign √ (Section 3.2)
The symbol √ is called a radical sign and indicates the square root of a number. The symbol √
n
represents the nth root.
Radical, Index, Radicand (Section 3.2)
√
An expression such as 4 16 is called a radical and 4 is called the index. The number 16 is called the radicand.
Grouping Symbols (Section 3.3)
Grouping symbols are used to indicate that a particular collection of numbers and meaningful operations are to be grouped together and considered as one number. The grouping symbols commonly used in mathematics are
Parentheses: ( )
Brackets: [ ]
Braces: { }
Bar:
Order of Operations (Section 3.3)
1. Perform all operations inside grouping symbols, beginning with the innermost set, in the order of 2, 3, and 4 below.
2. Perform all exponential and root operations, moving left to right.
3. Perform all multiplications and division, moving left to right.
7This content is available online at <http://cnx.org/content/m34877/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
192
CHAPTER 3. EXPONENTS, ROOTS, AND FACTORIZATION OF WHOLE
NUMBERS
4. Perform all additions and subtractions, moving left to right.
One Number as the Factor of Another (Section 3.4)
A rst number is a factor of a second number if the rst number divides into the second number a whole number of times.
Prime Number (Section 3.4)
A whole number greater than one whose only factors are itself and 1 is called a prime number. The whole number 1 is not a prime number. The whole number 2 is the rst prime number and the only even prime number.
Composite Number (Section 3.4)
A whole number greater than one that is composed of factors other than itself and 1 is called a composite number.
Fundamental Principle of Arithmetic (Section 3.4)
Except for the order of factors, every whole number other than 1 can be written in one and only one way as a product of prime numbers.
Prime Factorization (Section 3.4)
The prime factorization of 45 is 3 · 3 · 5. The numbers that occur in this factorization of 45 are each prime.
Determining the Prime Factorization of a Whole Number (Section 3.4)
There is a simple method, based on division by prime numbers, that produces the prime factorization of a whole number. For example, we determine the prime factorization of 132 as follows.
The prime factorization of 132 is 2 · 2 · 3 · 11 = 22 · 3 · 11.
Common Factor (Section 3.5)
A factor that occurs in each number of a group of numbers is called a common factor. 3 is a common factor to the group 18, 6, and 45
Greatest Common Factor (GCF) (Section 3.5)
The largest common factor of a group of whole numbers is called the greatest common factor. For example, to nd the greatest common factor of 12 and 20,
12
=
2 · 2 · 3 = 22 · 3
1. Write the prime factorization of each number. 60 = 2 · 2 · 3 · 5 = 22 · 3 · 5
2. Write each base that is common to each of the numbers: 2 and 3
3. The smallest exponent appearing on 2 is 2.
The smallest exponent appearing on 3 is 1.
4. The GCF of 12 and 60 is the product of the numbers 22 and 3. 22 · 3 = 4 · 3 = 12
Thus, 12 is the largest number that divides both 12 and 60 without a remainder.
Finding the GCF (Section 3.5)
There is a simple method, based on prime factorization, that determines the GCF of a group of whole numbers.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Multiple (Section 3.6)
When a whole number is multiplied by all other whole numbers, with the exception of zero, the resulting individual products are called multiples of that whole number. Some multiples of 7 are 7, 14, 21, and 28.
Common Multiples (Section 3.6)
Multiples that are common to a group of whole numbers are called common multiples. Some common multiples of 6 and 9 are 18, 36, and 54.
The LCM (Section 3.6)
The least common multiple (LCM) of a group of whole numbers is the smallest whole number that each of the given whole numbers divides into without a remainder. The least common multiple of 9 and 6 is 18.
Finding the LCM (Section 3.6)
There is a simple method, based on prime factorization, that determines the LCM of a group of whole numbers. For example, the least common multiple of 28 and 72 is found in the following way.
28
=
2 · 2 · 7 = 22 · 7
1. Write the prime factorization of each number 72 = 2 · 2 · 2 · 3 · 3 = 23 · 32
2. Write each base that appears in each of the prime factorizations, 2, 3, and 7.
3. To each of the bases listed in step 2, attach the largest exponent that appears on it in the prime factorization. 23, 32, and 7
4. The LCM is the product of the numbers found in step 3. 23 · 32 · 7 = 8 · 9 · 7 = 504
Thus, 504 is the smallest number that both 28 and 72 will divide into without a remainder.
The Dierence Between the GCF and the LCM (Section 3.6)
The GCF of two or more whole numbers is the largest number that divides into each of the given whole numbers. The LCM of two or more whole numbers is the smallest whole number that each of the given numbers divides into without a remainder.
3.8 Exercise Supplement 8
3.8.1 Exercise Supplement
3.8.1.1 Exponents and Roots (Section 3.2)
For problems 1 -25, determine the value of each power and root.
Exercise 3.8.1
(Solution on p. 208.)
33
Exercise 3.8.2
43
Exercise 3.8.3
(Solution on p. 208.)
05
Exercise 3.8.4
14
Exercise 3.8.5
(Solution on p. 208.)
122
Exercise 3.8.6
72
8This content is available online at <http://cnx.org/content/m34878/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 3. EXPONENTS, ROOTS, AND FACTORIZATION OF WHOLE
NUMBERS
Exercise 3.8.7
(Solution on p. 208.)
82
Exercise 3.8.8
112
Exercise 3.8.9
(Solution on p. 208.)
25
Exercise 3.8.10
34
Exercise 3.8.11
(Solution on p. 208.)
152
Exercise 3.8.12
202
Exercise 3.8.13
(Solution on p. 208.)
252
Exercise 3.8.14
√36
Exercise 3.8.15
(Solution on p. 208.)
√225
Exercise 3.8.16
√
3 64
Exercise 3.8.17
(Solution on p. 208.)
√
4 16
Exercise 3.8.18
√0
Exercise 3.8.19
(Solution on p. 208.)
√
3 1
Exercise 3.8.20
√
3 216
Exercise 3.8.21
(Solution on p. 208.)
√144
Exercise 3.8.22
√196
Exercise 3.8.23
(Solution on p. 208.)
√1
Exercise 3.8.24
√
4 0
Exercise 3.8.25
(Solution on p. 208.)
√
6 64
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
3.8.1.2 Section 3.2
For problems 26-45, use the order of operations to determine each value.
Exercise 3.8.26
23 − 2 · 4
Exercise 3.8.27
(Solution on p. 209.)
52 − 10 · 2 − 5
Exercise 3.8.28
√81 − 32 + 6 · 2
Exercise 3.8.29
(Solution on p. 209.)
152 + 52 · 22
Exercise 3.8.30
3 · 22 + 32
Exercise 3.8.31
(Solution on p. 209.)
64 · 32 − 23
Exercise 3.8.32
52+1
13 + 33+1
14
Exercise 3.8.33
(Solution on p. 209.)
62−1 − 49+7
5·7
2·7
Exercise 3.8.34
2·[3+5(22+1)]
5·23−32
Exercise 3.8.35
(Solution on p. 209.)
32·[25−14(23+25)]
2·52+5+2
Exercise 3.8.36
(52−23)−2·7
h
i
+ 5 · 32−3 + 1
22−1
2
Exercise 3.8.37
(Solution on p. 209.)
(8 − 3)2 + 2 + 322
Exercise 3.8.38
√
√
32 · 42 +
25 + 23 ·
81 − 32
Exercise 3.8.39
(Solution on p. 209.)
√16 + 9
Exercise 3.8.40
√
√
16 + 9
Exercise 3.8.41
(Solution on p. 209.)
Compare the results of problems 39 and 40. What might we conclude?
Exercise 3.8.42
√18 · 2
Exercise 3.8.43
(Solution on p. 209.)
√6 · 6
Exercise 3.8.44
√7 · 7
Exercise 3.8.45
(Solution on p. 209.)
√8 · 8
Exercise 3.8.46
An
records the number of identical factors that are repeated in a multiplication.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 3. EXPONENTS, ROOTS, AND FACTORIZATION OF WHOLE
NUMBERS
3.8.1.3 Prime Factorization of Natural Numbers (Section 3.4)
For problems 47- 53, nd all the factors of each number.
Exercise 3.8.47
(Solution on p. 209.)
18
Exercise 3.8.48
24
Exercise 3.8.49
(Solution on p. 209.)
11
Exercise 3.8.50
12
Exercise 3.8.51
(Solution on p. 209.)
51
Exercise 3.8.52
25
Exercise 3.8.53
(Solution on p. 209.)
2
Exercise 3.8.54
What number is the smallest prime number?
3.8.1.4 Grouping Symbol and the Order of Operations (Section 3.3)
For problems 55 -64, write each number as a product of prime factors.
Exercise 3.8.55
(Solution on p. 209.)
55
Exercise 3.8.56
20
Exercise 3.8.57
(Solution on p. 209.)
80
Exercise 3.8.58
284
Exercise 3.8.59
(Solution on p. 209.)
700
Exercise 3.8.60
845
Exercise 3.8.61
(Solution on p. 209.)
1,614
Exercise 3.8.62
921
Exercise 3.8.63
(Solution on p. 209.)
29
Exercise 3.8.64
37
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
3.8.1.5 The Greatest Common Factor (Section 3.5)
For problems 65 – 75, nd the greatest common factor of each collection of numbers.
Exercise 3.8.65
(Solution on p. 209.)
5 and 15
Exercise 3.8.66
6 and 14
Exercise 3.8.67
(Solution on p. 209.)
10 and 15
Exercise 3.8.68
6, 8, and 12
Exercise 3.8.69
(Solution on p. 209.)
18 and 24
Exercise 3.8.70
42 and 54
Exercise 3.8.71
(Solution on p. 209.)
40 and 60
Exercise 3.8.72
18, 48, and 72
Exercise 3.8.73
(Solution on p. 209.)
147, 189, and 315
Exercise 3.8.74
64, 72, and 108
Exercise 3.8.75
(Solution on p. 209.)
275, 297, and 539
3.8.1.6 The Least Common Multiple (Section 3.6)
For problems 76-86, nd the least common multiple of each collection of numbers.
Exercise 3.8.76
5 and 15
Exercise 3.8.77
(Solution on p. 210.)
6 and 14
Exercise 3.8.78
10 and 15
Exercise 3.8.79
(Solution on p. 210.)
36 and 90
Exercise 3.8.80
42 and 54
Exercise 3.8.81
(Solution on p. 210.)
8, 12, and 20
Exercise 3.8.82
40, 50, and 180
Exercise 3.8.83
(Solution on p. 210.)
135, 147, and 324
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 3. EXPONENTS, ROOTS, AND FACTORIZATION OF WHOLE
NUMBERS
Exercise 3.8.84
108, 144, and 324
Exercise 3.8.85
(Solution on p. 210.)
5, 18, 25, and 30
Exercise 3.8.86
12, 15, 18, and 20
Exercise 3.8.87
(Solution on p. 210.)
Find all divisors of 24.
Exercise 3.8.88
Find all factors of 24.
Exercise 3.8.89
(Solution on p. 210.)
Write all divisors of 23 · 52 · 7.
Exercise 3.8.90
Write all divisors of 6 · 82 · 103.
Exercise 3.8.91
(Solution on p. 210.)
Does 7 divide 53 · 64 · 72 · 85?
Exercise 3.8.92
Does 13 divide 83 · 102 · 114 · 132 · 15?
3.9 Prociency Exam 9
3.9.1 Prociency Exam
Exercise 3.9.1
(Solution on p. 210.)
(Section 3.2) In the number 85, write the names used for the number 8 and the number 5.
Exercise 3.9.2
(Solution on p. 210.)
(Section 3.2) Write using exponents. 12 × 12 × 12 × 12 × 12 × 12 × 12
Exercise 3.9.3
(Solution on p. 210.)
(Section 3.2) Expand 94.
For problems 4-15, determine the value of each expression.
Exercise 3.9.4
(Solution on p. 210.)
(Section 3.3) 43
Exercise 3.9.5
(Solution on p. 210.)
(Section 3.3) 15
Exercise 3.9.6
(Solution on p. 210.)
(Section 3.3) 03
Exercise 3.9.7
(Solution on p. 210.)
(Section 3.3) 26
Exercise 3.9.8
(Solution on p. 210.)
√
(Section 3.3) 49
Exercise 3.9.9
(Solution on p. 210.)
√
(Section 3.3) 3 27
Exercise 3.9.10
(Solution on p. 210.)
√
(Section 3.3) 8 1
9This content is available online at <http://cnx.org/content/m34879/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 3.9.11
(Solution on p. 210.)
(Section 3.3) 16 + 2 · (8 − 6)
Exercise 3.9.12
(Solution on p. 210.)
√
(Section 3.3) 53 − 100 + 8 · 2 − 20 ÷ 5
Exercise 3.9.13
(Solution on p. 210.)
(Section 3.3) 3 · 82−2·32 · 63−4·52
52−2
29
Exercise 3.9.14
(Solution on p. 210.)
√
(Section 3.3) 20+24 · 5·7− 81
23·2−5·2
7+3·2
Exercise 3.9.15
(Solution on p. 210.)
√
(Section 3.3) h
i
(8 − 3)2 + 33 − 4 49 − 2 10 − 32 + 9 − 5
For problems 16-20, nd the prime factorization of each whole number. If the number is prime, write “prime.”
Exercise 3.9.16
(Solution on p. 210.)
(Section 3.4) 18
Exercise 3.9.17
(Solution on p. 210.)
(Section 3.4) 68
Exercise 3.9.18
(Solution on p. 211.)
(Section 3.4) 142
Exercise 3.9.19
(Solution on p. 211.)
(Section 3.4) 151
Exercise 3.9.20
(Solution on p. 211.)
(Section 3.4) 468
For problems 21 and 22, nd the greatest common factor.
Exercise 3.9.21
(Solution on p. 211.)
(Section 3.5) 200 and 36
Exercise 3.9.22
(Solution on p. 211.)
(Section 3.5) 900 and 135
Exercise 3.9.23
(Solution on p. 211.)
(Section 3.5) Write all the factors of 36.
Exercise 3.9.24
(Solution on p. 211.)
(Section 3.5) Write all the divisors of 18.
Exercise 3.9.25
(Solution on p. 211.)
(Section 3.5) Does 7 divide into 52 · 63 · 74 · 8? Explain.
Exercise 3.9.26
(Solution on p. 211.)
(Section 3.5) Is 3 a factor of 26 · 32 · 53 · 46? Explain.
Exercise 3.9.27
(Solution on p. 211.)
(Section 3.5) Does 13 divide into 113 · 124 · 152? Explain.
For problems 28 and 29, nd the least common multiple.
Exercise 3.9.28
(Solution on p. 211.)
(Section 3.6) 432 and 180
Exercise 3.9.29
(Solution on p. 211.)
(Section 3.6) 28, 40, and 95
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 3. EXPONENTS, ROOTS, AND FACTORIZATION OF WHOLE
NUMBERS
Solutions to Exercises in Chapter 3
Solution to Exercise 3.2.1 (p. 155)
372
Solution to Exercise 3.2.2 (p. 155)
165
Solution to Exercise 3.2.3 (p. 155)
910
Solution to Exercise 3.2.4 (p. 155)
85 · 85 · 85
Solution to Exercise 3.2.5 (p. 155)
4 · 4 · 4 · 4 · 4 · 4 · 4
Solution to Exercise 3.2.6 (p. 155)
1, 739 · 1, 739
Solution to Exercise 3.2.7 (p. 157)
8Solution to Exercise 3.2.8 (p. 157)
10
Solution to Exercise 3.2.9 (p. 157)
4Solution to Exercise 3.2.10 (p. 157)
2Solution to Exercise 3.2.11 (p. 158)
9Solution to Exercise 3.2.12 (p. 158)
54
Solution to Exercise 3.2.13 (p. 158)
231
Solution to Exercise 3.2.14 (p. 158)
4Solution to Exercise 3.2.15 (p. 158)
42
Solution to Exercise 3.2.17 (p. 158)
94
Solution to Exercise 3.2.19 (p. 158)
8263
Solution to Exercise 3.2.21 (p. 158)
685
Solution to Exercise 3.2.23 (p. 159)
13008
Solution to Exercise 3.2.25 (p. 159)
7 · 7 · 7 · 7
Solution to Exercise 3.2.27 (p. 159)
117 · 117 · 117 · 117 · 117
Solution to Exercise 3.2.29 (p. 159)
30 · 30
Solution to Exercise 3.2.31 (p. 159)
4 · 4 = 16
Solution to Exercise 3.2.33 (p. 159)
10 · 10 = 100
Solution to Exercise 3.2.35 (p. 159)
12 · 12 = 144
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 3.2.37 (p. 159)
15 · 15 = 225
Solution to Exercise 3.2.39 (p. 159)
3 · 3 · 3 · 3 = 81
Solution to Exercise 3.2.41 (p. 159)
10 · 10 · 10 = 1, 000
Solution to Exercise 3.2.43 (p. 159)
8 · 8 · 8 = 512
Solution to Exercise 3.2.45 (p. 160)
9 · 9 · 9 = 729
Solution to Exercise 3.2.47 (p. 160)
71 = 7
Solution to Exercise 3.2.49 (p. 160)
2 · 2 · 2 · 2 · 2 · 2 · 2 = 128
Solution to Exercise 3.2.51 (p. 160)
8 · 8 · 8 · 8 = 4, 096
Solution to Exercise 3.2.53 (p. 160)
6 · 6 · 6 · 6 · 6 · 6 · 6 · 6 · 6 = 10, 077, 696
Solution to Exercise 3.2.55 (p. 160)
42 · 42 = 1, 764
Solution to Exercise 3.2.57 (p. 160)
15 · 15 · 15 · 15 · 15 = 759, 375
Solution to Exercise 3.2.59 (p. 160)
816 · 816 = 665, 856
Solution to Exercise 3.2.61 (p. 160)
4Solution to Exercise 3.2.63 (p. 160)
8Solution to Exercise 3.2.65 (p. 160)
12
Solution to Exercise 3.2.67 (p. 161)
15
Solution to Exercise 3.2.69 (p. 161)
2Solution to Exercise 3.2.71 (p. 161)
6Solution to Exercise 3.2.73 (p. 161)
20
Solution to Exercise 3.2.75 (p. 161)
100
Solution to Exercise 3.2.77 (p. 161)
60
Solution to Exercise 3.2.79 (p. 161)
34
Solution to Exercise 3.2.81 (p. 161)
4,158
Solution to Exercise 3.2.83 (p. 161)
24
Solution to Exercise 3.2.85 (p. 161)
4
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 3. EXPONENTS, ROOTS, AND FACTORIZATION OF WHOLE
NUMBERS
Solution to Exercise 3.2.87 (p. 161)
5Solution to Exercise 3.2.89 (p. 162)
81
Solution to Exercise 3.2.91 (p. 162)
8 is the multiplier; 4 is the multiplicand
Solution to Exercise 3.2.93 (p. 162)
Yes; 0
Solution to Exercise 3.3.1 (p. 163)
10
Solution to Exercise 3.3.2 (p. 163)
68
Solution to Exercise 3.3.3 (p. 163)
24
Solution to Exercise 3.3.4 (p. 163)
4Solution to Exercise 3.3.5 (p. 163)
0Solution to Exercise 3.3.6 (p. 163)
not possible (indeterminant)
Solution to Exercise 3.3.7 (p. 164)
54
Solution to Exercise 3.3.8 (p. 164)
23
Solution to Exercise 3.3.9 (p. 164)
4Solution to Exercise 3.3.10 (p. 164)
93
Solution to Exercise 3.3.11 (p. 164)
74
Solution to Exercise 3.3.12 (p. 164)
27
Solution to Exercise 3.3.13 (p. 166)
33
Solution to Exercise 3.3.14 (p. 166)
57
Solution to Exercise 3.3.15 (p. 166)
0Solution to Exercise 3.3.16 (p. 166)
52
Solution to Exercise 3.3.17 (p. 166)
3Solution to Exercise 3.3.18 (p. 166)
125
Solution to Exercise 3.3.19 (p. 166)
7Solution to Exercise 3.3.20 (p. 169)
13,499
Solution to Exercise 3.3.21 (p. 169)
6,070
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 3.3.22 (p. 170)
1,107,495
Solution to Exercise 3.3.23 (p. 170)
This number is too big for a nonscientic calculator. A scientic calculator will probably give you 2.217747109 × 1011
Solution to Exercise 3.3.24 (p. 170)
26
Solution to Exercise 3.3.26 (p. 170)
46
Solution to Exercise 3.3.28 (p. 170)
1Solution to Exercise 3.3.30 (p. 170)
0Solution to Exercise 3.3.32 (p. 170)
3Solution to Exercise 3.3.34 (p. 170)
26
Solution to Exercise 3.3.36 (p. 170)
97
Solution to Exercise 3.3.38 (p. 170)
29
Solution to Exercise 3.3.40 (p. 170)
1Solution to Exercise 3.3.42 (p. 171)
0Solution to Exercise 3.3.44 (p. 171)
90
Solution to Exercise 3.3.46 (p. 171)
508
Solution to Exercise 3.3.48 (p. 171)
19
Solution to Exercise 3.3.50 (p. 171)
144
Solution to Exercise 3.3.52 (p. 171)
1
Solution to Exercise 3.3.54 (p. 171)
52
Solution to Exercise 3.3.56 (p. 171)
25,001
Solution to Exercise 3.3.58 (p. 171)
1
25
Solution to Exercise 3.3.60 (p. 171)
14
Solution to Exercise 3.3.62 (p. 171)
0
Solution to Exercise 3.3.64 (p. 172)
152
Solution to Exercise 3.3.66 (p. 172)
4
5
Solution to Exercise 3.3.68 (p. 172)
2,690,730
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 3. EXPONENTS, ROOTS, AND FACTORIZATION OF WHOLE
NUMBERS
Solution to Exercise 3.3.70 (p. 172)
1Solution to Exercise 3.4.1 (p. 173)
1, 2, 3, 6
Solution to Exercise 3.4.2 (p. 173)
1, 2, 3, 4, 6, 12
Solution to Exercise 3.4.3 (p. 173)
1, 2, 3, 6, 9, 18
Solution to Exercise 3.4.4 (p. 173)
1, 5
Solution to Exercise 3.4.5 (p. 173)
1, 2, 5, 10
Solution to Exercise 3.4.6 (p. 173)
1, 3, 11, 33
Solution to Exercise 3.4.7 (p. 174)
1, 19
Solution to Exercise 3.4.8 (p. 174)
prime
Solution to Exercise 3.4.9 (p. 174)
composite
Solution to Exercise 3.4.10 (p. 174)
composite
Solution to Exercise 3.4.11 (p. 174)
composite
Solution to Exercise 3.4.12 (p. 174)
prime
Solution to Exercise 3.4.13 (p. 174)
prime
Solution to Exercise 3.4.14 (p. 175)
prime
Solution to Exercise 3.4.15 (p. 175)
composite
Solution to Exercise 3.4.16 (p. 177)
22 = 2 · 11
Solution to Exercise 3.4.17 (p. 177)
40 = 23 · 5
Solution to Exercise 3.4.18 (p. 177)
48 = 24 · 3
Solution to Exercise 3.4.19 (p. 177)
63 = 32 · 7
Solution to Exercise 3.4.20 (p. 177)
945 = 33 · 5 · 7
Solution to Exercise 3.4.21 (p. 177)
1617 = 3 · 72 · 11
Solution to Exercise 3.4.22 (p. 177)
17 is prime
Solution to Exercise 3.4.23 (p. 177)
61 is prime
Solution to Exercise 3.4.24 (p. 177)
2
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 3.4.26 (p. 178)
4Solution to Exercise 3.4.28 (p. 178)
11
Solution to Exercise 3.4.30 (p. 178)
3 · 2
Solution to Exercise 3.4.32 (p. 178)
2 · 3 · 5
Solution to Exercise 3.4.34 (p. 178)
1, 2, 4, 8, 16
Solution to Exercise 3.4.36 (p. 178)
1, 2, 4, 7, 8, 14, 28, 56
Solution to Exercise 3.4.38 (p. 178)
1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110, 220
Solution to Exercise 3.4.40 (p. 178)
1, 2, 4, 8, 16, 32
Solution to Exercise 3.4.42 (p. 178)
1, 2, 71, 142
Solution to Exercise 3.4.44 (p. 178)
prime
Solution to Exercise 3.4.46 (p. 179)
composite
Solution to Exercise 3.4.48 (p. 179)
prime
Solution to Exercise 3.4.50 (p. 179)
prime
Solution to Exercise 3.4.52 (p. 179)
prime
Solution to Exercise 3.4.54 (p. 179)
composite ( 5 · 11)
Solution to Exercise 3.4.56 (p. 179)
composite
Solution to Exercise 3.4.58 (p. 179)
composite
Solution to Exercise 3.4.60 (p. 179)
composite ( 11 · 19)
Solution to Exercise 3.4.62 (p. 179)
composite
Solution to Exercise 3.4.64 (p. 179)
2 · 13
Solution to Exercise 3.4.66 (p. 179)
2 · 33
Solution to Exercise 3.4.68 (p. 180)
23 · 7
Solution to Exercise 3.4.70 (p. 180)
25 · 3 · 5
Solution to Exercise 3.4.72 (p. 180)
34 · 52
Solution to Exercise 3.4.74 (p. 180)
26,580
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 3. EXPONENTS, ROOTS, AND FACTORIZATION OF WHOLE
NUMBERS
Solution to Exercise 3.4.76 (p. 180)
true
Solution to Exercise 3.4.78 (p. 180)
14
Solution to Exercise 3.5.1 (p. 182)
12
Solution to Exercise 3.5.2 (p. 182)
24
Solution to Exercise 3.5.3 (p. 182)
10
Solution to Exercise 3.5.4 (p. 182)
3Solution to Exercise 3.5.5 (p. 182)
30
Solution to Exercise 3.5.6 (p. 183)
2Solution to Exercise 3.5.8 (p. 183)
4Solution to Exercise 3.5.10 (p. 183)
4Solution to Exercise 3.5.12 (p. 183)
5Solution to Exercise 3.5.14 (p. 183)
33
Solution to Exercise 3.5.16 (p. 183)
9Solution to Exercise 3.5.18 (p. 183)
11
Solution to Exercise 3.5.20 (p. 183)
3Solution to Exercise 3.5.22 (p. 183)
7Solution to Exercise 3.5.24 (p. 183)
25
Solution to Exercise 3.5.26 (p. 183)
2Solution to Exercise 3.5.28 (p. 184)
11
Solution to Exercise 3.5.30 (p. 184)
1Solution to Exercise 3.5.32 (p. 184)
1Solution to Exercise 3.5.34 (p. 184)
53
Solution to Exercise 3.5.36 (p. 184)
86 = 262, 144
Solution to Exercise 3.6.1 (p. 185)
4, 8, 12, 16, 20
Solution to Exercise 3.6.2 (p. 185)
5, 10, 15, 20, 25
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 3.6.3 (p. 185)
6, 12, 18, 24, 30
Solution to Exercise 3.6.4 (p. 185)
7, 14, 21, 28, 35
Solution to Exercise 3.6.5 (p. 185)
9, 18, 27, 36, 45
Solution to Exercise 3.6.6 (p. 186)
4, 8, 12, 16, 20
Solution to Exercise 3.6.7 (p. 186)
12, 24, 36, 48, 60
Solution to Exercise 3.6.8 (p. 186)
10, 20, 30, 40, 50
Solution to Exercise 3.6.9 (p. 186)
6, 12, 18, 24, 30
Solution to Exercise 3.6.10 (p. 186)
20, 40, 60, 80, 100
Solution to Exercise 3.6.11 (p. 188)
540
Solution to Exercise 3.6.12 (p. 188)
28
Solution to Exercise 3.6.13 (p. 188)
126
Solution to Exercise 3.6.14 (p. 188)
1,960
Solution to Exercise 3.6.15 (p. 188)
6,534,000
Solution to Exercise 3.6.16 (p. 188)
24
Solution to Exercise 3.6.18 (p. 188)
40
Solution to Exercise 3.6.20 (p. 188)
12
Solution to Exercise 3.6.22 (p. 188)
18
Solution to Exercise 3.6.24 (p. 188)
30
Solution to Exercise 3.6.26 (p. 188)
12
Solution to Exercise 3.6.28 (p. 188)
63
Solution to Exercise 3.6.30 (p. 189)
72
Solution to Exercise 3.6.32 (p. 189)
720
Solution to Exercise 3.6.34 (p. 189)
120
Solution to Exercise 3.6.36 (p. 189)
216
Solution to Exercise 3.6.38 (p. 189)
144
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 3. EXPONENTS, ROOTS, AND FACTORIZATION OF WHOLE
NUMBERS
Solution to Exercise 3.6.40 (p. 189)
105
Solution to Exercise 3.6.42 (p. 189)
231
Solution to Exercise 3.6.44 (p. 189)
126
Solution to Exercise 3.6.46 (p. 189)
4,410
Solution to Exercise 3.6.48 (p. 189)
240
Solution to Exercise 3.6.50 (p. 189)
432
Solution to Exercise 3.6.52 (p. 189)
144
Solution to Exercise 3.6.54 (p. 190)
224
Solution to Exercise 3.6.56 (p. 190)
193,050
Solution to Exercise 3.6.58 (p. 190)
8Solution to Exercise 3.6.60 (p. 190)
36
Solution to Exercise 3.6.62 (p. 190)
6,552
Solution to Exercise 3.6.64 (p. 190)
84 · 84 · 84
Solution to Exercise 3.8.1 (p. 193)
27
Solution to Exercise 3.8.3 (p. 193)
0Solution to Exercise 3.8.5 (p. 193)
144
Solution to Exercise 3.8.7 (p. 194)
64
Solution to Exercise 3.8.9 (p. 194)
32
Solution to Exercise 3.8.11 (p. 194)
225
Solution to Exercise 3.8.13 (p. 194)
625
Solution to Exercise 3.8.15 (p. 194)
15
Solution to Exercise 3.8.17 (p. 194)
2Solution to Exercise 3.8.19 (p. 194)
1Solution to Exercise 3.8.21 (p. 194)
12
Solution to Exercise 3.8.23 (p. 194)
1
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 3.8.25 (p. 194)
2Solution to Exercise 3.8.27 (p. 195)
0Solution to Exercise 3.8.29 (p. 195)
325
Solution to Exercise 3.8.31 (p. 195)
64
Solution to Exercise 3.8.33 (p. 195)
-3
Solution to Exercise 3.8.35 (p. 195)
− 9
57
Solution to Exercise 3.8.37 (p. 195)
146
Solution to Exercise 3.8.39 (p. 195)
5Solution to Exercise 3.8.41 (p. 195)
The sum of square roots is not necessarily equal to the square root of the sum.
Solution to Exercise 3.8.43 (p. 195)
6Solution to Exercise 3.8.45 (p. 195)
8Solution to Exercise 3.8.47 (p. 196)
1, 2, 3, 6, 9, 18
Solution to Exercise 3.8.49 (p. 196)
1, 11
Solution to Exercise 3.8.51 (p. 196)
1, 3, 17, 51,
Solution to Exercise 3.8.53 (p. 196)
1, 2
Solution to Exercise 3.8.55 (p. 196)
5 · 11
Solution to Exercise 3.8.57 (p. 196)
24 · 5
Solution to Exercise 3.8.59 (p. 196)
22 · 52 · 7
Solution to Exercise 3.8.61 (p. 196)
2 · 3 · 269
Solution to Exercise 3.8.63 (p. 196)
29 is a prime number
Solution to Exercise 3.8.65 (p. 197)
5Solution to Exercise 3.8.67 (p. 197)
5Solution to Exercise 3.8.69 (p. 197)
6Solution to Exercise 3.8.71 (p. 197)
20
Solution to Exercise 3.8.73 (p. 197)
21
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 3. EXPONENTS, ROOTS, AND FACTORIZATION OF WHOLE
NUMBERS
Solution to Exercise 3.8.75 (p. 197)
11
Solution to Exercise 3.8.77 (p. 197)
42
Solution to Exercise 3.8.79 (p. 197)
180
Solution to Exercise 3.8.81 (p. 197)
120
Solution to Exercise 3.8.83 (p. 197)
79, 380
Solution to Exercise 3.8.85 (p. 198)
450
Solution to Exercise 3.8.87 (p. 198)
1, 2, 3, 4, 6, 8, 12, 24
Solution to Exercise 3.8.89 (p. 198)
1, 2, 4, 5, 7, 8, 10, 14, 20, 25, 35, 40, 50, 56, 70, 100, 140, 175, 200, 280, 700, 1,400
Solution to Exercise 3.8.91 (p. 198)
yes
Solution to Exercise 3.9.1 (p. 198)
base; exponent
Solution to Exercise 3.9.2 (p. 198)
127
Solution to Exercise 3.9.3 (p. 198)
94 = 9 · 9 · 9 · 9 = 6, 561
Solution to Exercise 3.9.4 (p. 198)
64
Solution to Exercise 3.9.5 (p. 198)
1Solution to Exercise 3.9.6 (p. 198)
0Solution to Exercise 3.9.7 (p. 198)
64
Solution to Exercise 3.9.8 (p. 198)
7Solution to Exercise 3.9.9 (p. 198)
3Solution to Exercise 3.9.10 (p. 198)
1Solution to Exercise 3.9.11 (p. 199)
20
Solution to Exercise 3.9.12 (p. 199)
127
Solution to Exercise 3.9.13 (p. 199)
24
Solution to Exercise 3.9.14 (p. 199)
8Solution to Exercise 3.9.15 (p. 199)
5Solution to Exercise 3.9.16 (p. 199)
32 · 2
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 3.9.17 (p. 199)
22 · 17
Solution to Exercise 3.9.18 (p. 199)
2 · 71
Solution to Exercise 3.9.19 (p. 199)
prime
Solution to Exercise 3.9.20 (p. 199)
22 · 32 · 13
Solution to Exercise 3.9.21 (p. 199)
4Solution to Exercise 3.9.22 (p. 199)
45
Solution to Exercise 3.9.23 (p. 199)
1, 2, 3, 4, 6, 9, 12, 18, 36
Solution to Exercise 3.9.24 (p. 199)
1, 2, 3, 6, 9, 18
Solution to Exercise 3.9.25 (p. 199)
Yes, because one of the (prime) factors of the number is 7.
Solution to Exercise 3.9.26 (p. 199)
Yes, because it is one of the factors of the number.
Solution to Exercise 3.9.27 (p. 199)
No, because the prime 13 is not a factor any of the listed factors of the number.
Solution to Exercise 3.9.28 (p. 199)
2,160
Solution to Exercise 3.9.29 (p. 199)
5,320
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 3. EXPONENTS, ROOTS, AND FACTORIZATION OF WHOLE
NUMBERS
Available for free at Connexions <http://cnx.org/content/col10615/1.4>