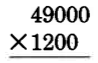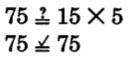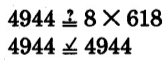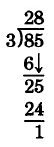123 Fundamentals of Mathematics: Part 5
Part 3:
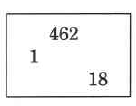
The product is 310,648
2.2.4.2 Practice Set C
Exercise 2.2.10
(Solution on p. 142.)
Multiply 73 by 14.
Exercise 2.2.11
(Solution on p. 142.)
Multiply 86 by 52.
Exercise 2.2.12
(Solution on p. 142.)
Multiply 419 by 85.
Exercise 2.2.13
(Solution on p. 142.)
Multiply 2,376 by 613.
Exercise 2.2.14
(Solution on p. 142.)
Multiply 8,107 by 304.
Exercise 2.2.15
(Solution on p. 142.)
Multiply 66,260 by 1,008.
Exercise 2.2.16
(Solution on p. 142.)
Multiply 209 by 501.
Exercise 2.2.17
(Solution on p. 142.)
Multiply 24 by 10.
Exercise 2.2.18
(Solution on p. 142.)
Multiply 3,809 by 1,000.
Exercise 2.2.19
(Solution on p. 142.)
Multiply 813 by 10,000.
2.2.5 Multiplications With Numbers Ending in Zero
Often, when performing a multiplication, one or both of the factors will end in zeros. Such multiplications can be done quickly by aligning the numbers so that the rightmost nonzero digits are in the same column.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
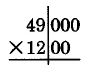

98
CHAPTER 2. MULTIPLICATION AND DIVISION OF WHOLE NUMBERS
2.2.5.1 Sample Set D
Perform the multiplication (49, 000) (1, 200).
(49,000)(1,200) =
49000
×
1200
Since 9 and 2 are the rightmost nonzero digits, put them in the same column.
Draw (perhaps mentally) a vertical line to separate the zeros from the nonzeros.
Multiply the numbers to the left of the vertical line as usual, then attach to the right end of this product the total number of zeros.
The product is 58,800,000
2.2.5.2 Practice Set D
Exercise 2.2.20
(Solution on p. 142.)
Multiply 1,800 by 90.
Exercise 2.2.21
(Solution on p. 142.)
Multiply 420,000 by 300.
Exercise 2.2.22
(Solution on p. 142.)
Multiply 20,500,000 by 140,000.
2.2.6 Calculators
Most multiplications are performed using a calculator.
2.2.6.1 Sample Set E
Example 2.9
Multiply 75,891 by 263.
Display Reads
Type 75891
75891
Press ×
75891
Type 263
263
Press =
19959333
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Table 2.1
The product is 19,959,333.
Example 2.10
Multiply 4,510,000,000,000 by 1,700.
Display Reads
Type 451
451
Press ×
451
Type 17
17
Press =
7667
Table 2.2
The display now reads 7667. We’ll have to add the zeros ourselves. There are a total of 12 zeros.
Attaching 12 zeros to 7667, we get 7,667,000,000,000,000.
The product is 7,667,000,000,000,000.
Example 2.11
Multiply 57,847,298 by 38,976.
Display Reads
Type 57847298
57847298
Press ×
57847298
Type 38976
38976
Press =
2.2546563 12
Table 2.3
The display now reads 2.2546563 12. What kind of number is this? This is an example of a whole number written in scientic notation. We’ll study this concept when we get to decimal numbers.
2.2.6.2 Practice Set E
Use a calculator to perform each multiplication.
Exercise 2.2.23
(Solution on p. 142.)
52 × 27
Exercise 2.2.24
(Solution on p. 142.)
1, 448 × 6, 155
Exercise 2.2.25
(Solution on p. 142.)
8, 940, 000 × 205, 000
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 2. MULTIPLICATION AND DIVISION OF WHOLE NUMBERS
2.2.7 Exercises
For the following problems, perform the multiplications. You may check each product with a calculator.
Exercise 2.2.26
(Solution on p. 142.)
8
×3
Exercise 2.2.27
3
×5
Exercise 2.2.28
(Solution on p. 143.)
8
×6
Exercise 2.2.29
5
×7
Exercise 2.2.30
(Solution on p. 143.)
6 × 1
Exercise 2.2.31
4 × 5
Exercise 2.2.32
(Solution on p. 143.)
75 × 3
Exercise 2.2.33
35 × 5
Exercise 2.2.34
(Solution on p. 143.)
45
× 6
Exercise 2.2.35
31
× 7
Exercise 2.2.36
(Solution on p. 143.)
97
× 6
Exercise 2.2.37
75
×57
Exercise 2.2.38
(Solution on p. 143.)
64
×15
Exercise 2.2.39
73
×15
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 2.2.40
(Solution on p. 143.)
81
×95
Exercise 2.2.41
31
×33
Exercise 2.2.42
(Solution on p. 143.)
57 × 64
Exercise 2.2.43
76 × 42
Exercise 2.2.44
(Solution on p. 143.)
894 × 52
Exercise 2.2.45
684 × 38
Exercise 2.2.46
(Solution on p. 143.)
115
× 22
Exercise 2.2.47
706
× 81
Exercise 2.2.48
(Solution on p. 143.)
328
× 21
Exercise 2.2.49
550
× 94
Exercise 2.2.50
(Solution on p. 143.)
930 × 26
Exercise 2.2.51
318 × 63
Exercise 2.2.52
(Solution on p. 143.)
582
×127
Exercise 2.2.53
247
×116
Exercise 2.2.54
(Solution on p. 143.)
305
×225
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 2. MULTIPLICATION AND DIVISION OF WHOLE NUMBERS
Exercise 2.2.55
782
×547
Exercise 2.2.56
(Solution on p. 143.)
771
×663
Exercise 2.2.57
638
×516
Exercise 2.2.58
(Solution on p. 143.)
1,905 × 710
Exercise 2.2.59
5,757 × 5,010
Exercise 2.2.60
(Solution on p. 143.)
3, 106
×1, 752
Exercise 2.2.61
9, 300
×1, 130
Exercise 2.2.62
(Solution on p. 143.)
7, 057
×5, 229
Exercise 2.2.63
8, 051
×5, 580
Exercise 2.2.64
(Solution on p. 143.)
5, 804
×4, 300
Exercise 2.2.65
357
×16
Exercise 2.2.66
(Solution on p. 143.)
724
×
0
Exercise 2.2.67
2, 649
×
41
Exercise 2.2.68
(Solution on p. 143.)
5, 173
×
8
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 2.2.69
1, 999
×
0
Exercise 2.2.70
(Solution on p. 143.)
1, 666
×
0
Exercise 2.2.71
51, 730
×
142
Exercise 2.2.72
(Solution on p. 143.)
387
×190
Exercise 2.2.73
3, 400
×
70
Exercise 2.2.74
(Solution on p. 143.)
460, 000
× 14, 000
Exercise 2.2.75
558, 000, 000
×
81, 000
Exercise 2.2.76
(Solution on p. 143.)
37, 000
×
120
Exercise 2.2.77
498, 000
×
0
Exercise 2.2.78
(Solution on p. 144.)
4, 585, 000
×
140
Exercise 2.2.79
30, 700, 000
×
180
Exercise 2.2.80
(Solution on p. 144.)
8, 000
×
10
Exercise 2.2.81
Suppose a theater holds 426 people. If the theater charges $4 per ticket and sells every seat, how much money would they take in?
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 2. MULTIPLICATION AND DIVISION OF WHOLE NUMBERS
Exercise 2.2.82
(Solution on p. 144.)
In an English class, a student is expected to read 12 novels during the semester and prepare a report on each one of them. If there are 32 students in the class, how many reports will be prepared?
Exercise 2.2.83
In a mathematics class, a nal exam consists of 65 problems. If this exam is given to 28 people, how many problems must the instructor grade?
Exercise 2.2.84
(Solution on p. 144.)
A business law instructor gives a 45 problem exam to two of her classes. If each class has 37 people in it, how many problems will the instructor have to grade?
Exercise 2.2.85
An algebra instructor gives an exam that consists of 43 problems to four of his classes. If the classes have 25, 28, 31, and 35 students in them, how many problems will the instructor have to grade?
Exercise 2.2.86
(Solution on p. 144.)
In statistics, the term “standard deviation” refers to a number that is calculated from certain data.
If the data indicate that one standard deviation is 38 units, how many units is three standard deviations?
Exercise 2.2.87
Soft drinks come in cases of 24 cans. If a supermarket sells 857 cases during one week, how many individual cans were sold?
Exercise 2.2.88
(Solution on p. 144.)
There are 60 seconds in 1 minute and 60 minutes in 1 hour. How many seconds are there in 1 hour?
Exercise 2.2.89
There are 60 seconds in 1 minute, 60 minutes in one hour, 24 hours in one day, and 365 days in one year. How many seconds are there in 1 year?
Exercise 2.2.90
(Solution on p. 144.)
Light travels 186,000 miles in one second. How many miles does light travel in one year? (Hint: Can you use the result of the previous problem?)
Exercise 2.2.91
An elementary school cafeteria sells 328 lunches every day. Each lunch costs $1. How much money does the cafeteria bring in in 2 weeks?
Exercise 2.2.92
(Solution on p. 144.)
A computer company is selling stock for $23 a share. If 87 people each buy 55 shares, how much money would be brought in?
2.2.7.1 Exercises for Review
Exercise 2.2.93
(Section 1.2) In the number 421,998, how may ten thousands are there?
Exercise 2.2.94
(Solution on p. 144.)
(Section 1.4) Round 448,062,187 to the nearest hundred thousand.
Exercise 2.2.95
(Section 1.5) Find the sum. 22,451 + 18,976.
Exercise 2.2.96
(Solution on p. 144.)
(Section 1.6) Subtract 2,289 from 3,001.
Exercise 2.2.97
(Section 1.7) Specify which property of addition justies the fact that (a rst whole number + a second whole number) = (the second whole number + the rst whole number) Available for free at Connexions <http://cnx.org/content/col10615/1.4>
2.3 Concepts of Division of Whole Numbers3
2.3.1 Section Overview
• Division
• Division into Zero (Zero As a Dividend: 0 , a 6= 0)
a
• Division by Zero (Zero As a Divisor: 0 , a 6= 0)
a
• Division by and into Zero (Zero As a Dividend and Divisor: 0 )
0
• Calculators
2.3.2 Division
Division is a description of repeated subtraction.
In the process of division, the concern is how many times one number is contained in another number. For example, we might be interested in how many 5’s are contained in 15. The word times is signicant because it implies a relationship between division and multiplication.
There are several notations used to indicate division. Suppose Q records the number of times 5 is contained in 15. We can indicate this by writing
Q
15 = Q
5)15
5
|
{z
}
|
{z
}
15 divided by 5
5 into 15
15/5 = Q
15 ÷ 5 = Q
|
{z
}
|
{z
}
15 divided by 5
15 divided by 5
Each of these division notations describes the same number, represented here by the symbol Q. Each notation also converts to the same multiplication form. It is 15 = 5 × Q
In division,
Dividend
the number being divided into is called the dividend.
Divisor
the number dividing into the dividend is the divisor.
Quotient
the result of the division is called the quotient.
quotient
divisor)dividend
dividend
divisor = quotient
dividend/divisor = quotient dividend ÷ divisor = quotient
3This content is available online at <http://cnx.org/content/m34864/1.3/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 2. MULTIPLICATION AND DIVISION OF WHOLE NUMBERS
2.3.2.1 Sample Set A
Find the following quotients using multiplication facts.
Example 2.12
18 ÷ 6
Since 6 × 3 = 18,
18 ÷ 6 = 3
Notice also that
18
−6
12
−6 }Repeated subtraction
6
−6
0
Thus, 6 is contained in 18 three times.
Example 2.13
24
3
Since 3 × 8 = 24,
24 = 8
3
Notice also that 3 could be subtracted exactly 8 times from 24. This implies that 3 is contained in 24 eight times.
Example 2.14
36
6
Since 6 × 6 = 36,
36 = 6
6
Thus, there are 6 sixes in 36.
Example 2.15
9)72
Since 9 × 8 = 72,
8
9)72
Thus, there are 8 nines in 72.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
2.3.2.2 Practice Set A
Use multiplication facts to determine the following quotients.
Exercise 2.3.1
(Solution on p. 144.)
32 ÷ 8
Exercise 2.3.2
(Solution on p. 144.)
18 ÷ 9
Exercise 2.3.3
(Solution on p. 144.)
25
5
Exercise 2.3.4
(Solution on p. 144.)
48
8
Exercise 2.3.5
(Solution on p. 144.)
28
7
Exercise 2.3.6
(Solution on p. 144.)
4)36
2.3.3 Division into Zero (Zero as a Dividend: 0 , a 6= 0)
a
Let’s look at what happens when the dividend (the number being divided into) is zero, and the divisor (the number doing the dividing) is any whole number except zero. The question is What number, if any, is
0
any nonzero whole number ?
Let’s represent this unknown quotient by Q. Then,
0
any nonzero whole number = Q
Converting this division problem to its corresponding multiplication problem, we get 0 = Q × (any nonzero whole number)
From our knowledge of multiplication, we can understand that if the product of two whole numbers is zero, then one or both of the whole numbers must be zero. Since any nonzero whole number is certainly not zero, Q must represent zero. Then,
0
any nonzero whole number = 0
Zero Divided By Any Nonzero Whole Number Is Zero
Zero divided any nonzero whole number is zero.
2.3.4 Division by Zero (Zero as a Divisor:a , a 6= 0)
0
Now we ask,
What number, if any, is any nonzero whole number ?
0
Letting Q represent a possible quotient, we get
any nonzero whole number = Q
0
Converting to the corresponding multiplication form, we have
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 2. MULTIPLICATION AND DIVISION OF WHOLE NUMBERS
(any nonzero whole number) = Q × 0
Since Q × 0 = 0, (any nonzero whole number) = 0. But this is absurd. This would mean that 6 = 0, or 37 = 0. A nonzero whole number cannot equal 0! Thus,
any nonzero whole number does not name a number
0
Division by Zero is Undened
Division by zero does not name a number. It is, therefore, undened.
2.3.5 Division by and Into Zero (Zero as a Dividend and Divisor:0)
0
We are now curious about zero divided by zero 0. If we let Q represent a potential quotient, we get 0
0 = Q
0
Converting to the multiplication form,
0 = Q × 0
This results in
0 = 0
This is a statement that is true regardless of the number used in place of Q. For example, 0 = 5, since 0 = 5 × 0.
0
0 = 31, since 0 = 31 × 0.
0
0 = 286, since 0 = 286 × 0.
0
A unique quotient cannot be determined.
Indeterminant
Since the result of the division is inconclusive, we say that 0 is indeterminant.
0
0 is Indeterminant
0
The division 0 is indeterminant.
0
2.3.5.1 Sample Set B
Perform, if possible, each division.
Example 2.16
19 . Since division by 0 does not name a whole number, no quotient exists, and we state 19 is 0
0
undened
Example 2.17
0)14 . Since division by 0 does not name a dened number, no quotient exists, and we state 0)14 is undened
Example 2.18
0
9)0 . Since division into 0 by any nonzero whole number results in 0, we have 9)0
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Example 2.19
0 . Since division into 0 by any nonzero whole number results in 0, we have 0 = 0
7
7
2.3.5.2 Practice Set B
Perform, if possible, the following divisions.
Exercise 2.3.7
(Solution on p. 144.)
5
0
Exercise 2.3.8
(Solution on p. 144.)
0
4
Exercise 2.3.9
(Solution on p. 144.)
0)0
Exercise 2.3.10
(Solution on p. 144.)
0)8
Exercise 2.3.11
(Solution on p. 144.)
9
0
Exercise 2.3.12
(Solution on p. 144.)
0
1
2.3.6 Calculators
Divisions can also be performed using a calculator.
2.3.6.1 Sample Set C
Example 2.20
Divide 24 by 3.
Display Reads
Type 24 24
Press ÷
24
Type 3
3
Press =
8
Table 2.4
The display now reads 8, and we conclude that 24 ÷ 3 = 8.
Example 2.21
Divide 0 by 7.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 2. MULTIPLICATION AND DIVISION OF WHOLE NUMBERS
Display Reads
Type 0
0
Press ÷ 0
Type 7
7
Press = 0
Table 2.5
The display now reads 0, and we conclude that 0 ÷ 7 = 0.
Example 2.22
Divide 7 by 0.
Since division by zero is undened, the calculator should register some kind of error message.
Display Reads
Type 7
7
Press ÷ 7
Type 0
0
Press = Error
Table 2.6
The error message indicates an undened operation was attempted, in this case, division by zero.
2.3.6.2 Practice Set C
Use a calculator to perform each division.
Exercise 2.3.13
(Solution on p. 144.)
35 ÷ 7
Exercise 2.3.14
(Solution on p. 144.)
56 ÷ 8
Exercise 2.3.15
(Solution on p. 144.)
0 ÷ 6
Exercise 2.3.16
(Solution on p. 145.)
3 ÷ 0
Exercise 2.3.17
(Solution on p. 145.)
0 ÷ 0
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
2.3.7 Exercises
For the following problems, determine the quotients (if possible). You may use a calculator to check the result.
Exercise 2.3.18
(Solution on p. 145.)
4)32
Exercise 2.3.19
7)42
Exercise 2.3.20
(Solution on p. 145.)
6)18
Exercise 2.3.21
2)14
Exercise 2.3.22
(Solution on p. 145.)
3)27
Exercise 2.3.23
1)6
Exercise 2.3.24
(Solution on p. 145.)
4)28
Exercise 2.3.25
30
5
Exercise 2.3.26
(Solution on p. 145.)
16
4
Exercise 2.3.27
24 ÷ 8
Exercise 2.3.28
(Solution on p. 145.)
10 ÷ 2
Exercise 2.3.29
21 ÷ 7
Exercise 2.3.30
(Solution on p. 145.)
21 ÷ 3
Exercise 2.3.31
0 ÷ 6
Exercise 2.3.32
(Solution on p. 145.)
8 ÷ 0
Exercise 2.3.33
12 ÷ 4
Exercise 2.3.34
(Solution on p. 145.)
3)9
Exercise 2.3.35
0)0
Exercise 2.3.36
(Solution on p. 145.)
7)0
Exercise 2.3.37
6)48
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 2. MULTIPLICATION AND DIVISION OF WHOLE NUMBERS
Exercise 2.3.38
(Solution on p. 145.)
15
3
Exercise 2.3.39
35
0
Exercise 2.3.40
(Solution on p. 145.)
56 ÷ 7
Exercise 2.3.41
0
9
Exercise 2.3.42
(Solution on p. 145.)
72 ÷ 8
Exercise 2.3.43
Write 16 = 8 using three dierent notations.
2
Exercise 2.3.44
(Solution on p. 145.)
Write 27 = 3 using three dierent notations.
9
Exercise 2.3.45
4
In the statement 6)24
6 is called the
.
24 is called the
.
4 is called the
.
Exercise 2.3.46
(Solution on p. 145.)
In the statement 56 ÷ 8 = 7,
7 is called the
.
8 is called the
.
56 is called the
.
2.3.7.1 Exercises for Review
Exercise 2.3.47
(Section 1.2) What is the largest digit?
Exercise 2.3.48
(Solution on p. 145.)
8, 006
(Section 1.5) Find the sum. +4,118
Exercise 2.3.49
631
(Section 1.6) Find the dierence. −589
Exercise 2.3.50
(Solution on p. 145.)
(Section 1.7) Use the numbers 2, 3, and 7 to illustrate the associative property of addition.
Exercise 2.3.51
86
(Section 2.2) Find the product. × 12
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
2.4 Division of Whole Numbers 4
2.4.1 Section Overview
• Division with a Single Digit Divisor
• Division with a Multiple Digit Divisor
• Division with a Remainder
• Calculators
2.4.2 Division with a Single Digit Divisor
Our experience with multiplication of whole numbers allows us to perform such divisions as 75÷5. We perform the division by performing the corresponding multiplication, 5 × Q = 75. Each division we considered in Section 2.3 had a one-digit quotient. Now we will consider divisions in which the quotient may consist of two or more digits. For example, 75 ÷ 5.
Let’s examine the division 75 ÷ 5. We are asked to determine how many 5’s are contained in 75. We’ll approach the problem in the following way.
1. Make an educated guess based on experience with multiplication.
2. Find how close the estimate is by multiplying the estimate by 5.
3. If the product obtained in step 2 is less than 75, nd out how much less by subtracting it from 75.
4. If the product obtained in step 2 is greater than 75, decrease the estimate until the product is less than 75. Decreasing the estimate makes sense because we do not wish to exceed 75.
We can suggest from this discussion that the process of division consists of The Four Steps in Division
1. an educated guess
2. a multiplication
3. a subtraction
4. bringing down the next digit (if necessary)
The educated guess can be made by determining how many times the divisor is contained in the dividend by using only one or two digits of the dividend.
2.4.2.1 Sample Set A
Example 2.23
Find 75 ÷ 5.
5)75 Rewrite the problem using a division bracket.
10
5)75
Make an educated guess by noting that one 5 is contained in 75 at most 10 times.
Since 7 is the tens digit, we estimate that 5 goes into 75 at most 10 times.
4This content is available online at <http://cnx.org/content/m34865/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
114
CHAPTER 2. MULTIPLICATION AND DIVISION OF WHOLE NUMBERS
10
5)75
−50
25
Now determine how close the estimate is.
10 ves is 10 × 5 = 50. Subtract 50 from 75.
Estimate the number of 5’s in 25.
There are exactly 5 ves in 25.
5
10 ves + 5 ves = 15 ves.
}
10
There are 15 ves contained in 75.
5)75
−50
25
−25
0
Check:
Thus, 75 ÷ 5 = 15.
The notation in this division can be shortened by writing.
15
5)75
−5 ↓
25
−25
0
Divide:
5 goes into 7 at most 1 time.
Divide:
5 goes into 25 exactly 5 times.
{ Multiply: 1 × 5 = 5. Write 5 below 7. { Multiply: 5 × 5 = 25. Write 25 below 25.
Subtract: 7 – 5 = 2. Bring down the 5.
Subtract:
25 – 25 = 0.
Example 2.24
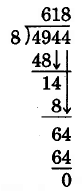
Find 4, 944 ÷ 8.
8)4944
Rewrite the problem using a division bracket.
600
8)4944
−4800
144
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
115
8 goes into 49 at most 6 times, and 9 is in the hundreds column. We’ll guess 600.
Then, 8 × 600 = 4800.
10
600
8)4944
−4800
144
− 80
64
8 goes into 14 at most 1 time, and 4 is in the tens column. We’ll guess 10.
8
10
600
8)4944
−4800
144
− 80
64
−64
0
8 goes into 64 exactly 8 times.
600 eights + 10 eights + 8 eights = 618 eights.
Check:
Thus, 4, 944 ÷ 8 = 618.
As in the rst problem, the notation in this division can be shortened by eliminating the subtraction signs and the zeros in each educated guess.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 2. MULTIPLICATION AND DIVISION OF WHOLE NUMBERS
Divide:
8 goes into 49 at most 6 times.
Divide:
8 goes into 14 at most 1 time.
{ Multiply: 6 × 8 = 48. Write 48 below 49.
{ Multiply: 1 × 8 = 8. Write 8 below 14.
Subtract: 49 – 48 = 1. Bring down the 4.
Subtract: 14 – 8 = 6. Bring down the 4.
Divide:
8 goes into 64 exactly 8 times.
{ Multiply: 8 × 8 = 64. Write 64 below 64.
Subtract:
64 – 64 = 0.
note: Not all divisions end in zero. We will examine such divisions in a subsequent subsection.
2.4.2.2 Practice Set A
Perform the following divisions.
Exercise 2.4.1
(Solution on p. 145.)
126 ÷ 7
Exercise 2.4.2
(Solution on p. 145.)
324 ÷ 4
Exercise 2.4.3
(Solution on p. 145.)
2, 559 ÷ 3
Exercise 2.4.4
(Solution on p. 145.)
5, 645 ÷ 5
Exercise 2.4.5
(Solution on p. 145.)
757, 125 ÷ 9
2.4.3 Division with a Multiple Digit Divisor
The process of division also works when the divisor consists of two or more digits. We now make educated guesses using the rst digit of the divisor and one or two digits of the dividend.
2.4.3.1 Sample Set B
Example 2.25
Find 2, 232 ÷ 36.
36)2232
Use the rst digit of the divisor and the rst two digits of the dividend to make the educated guess.
3 goes into 22 at most 7 times.
Try 7: 7 × 36 = 252 which is greater than 223. Reduce the estimate.
Try 6: 6 × 36 = 216 which is less than 223.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
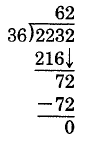

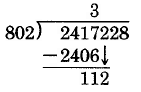
117
Multiply: 6 × 36 = 216. Write 216 below 223.
Subtract:
223 – 216 = 7. Bring down the 2.
Divide 3 into 7 to estimate the number of times 36 goes into 72. The 3 goes into 7 at most 2 times.
Try 2: 2 × 36 = 72.
Check:
Thus, 2, 232 ÷ 36 = 62.
Example 2.26
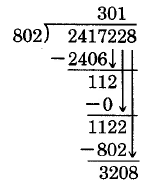
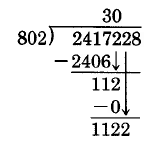
Find 2, 417, 228 ÷ 802.
802)2417228
First, the educated guess: 24 ÷ 8 = 3. Then 3 × 802 = 2406, which is less than 2417. Use 3 as the guess. Since 3 × 802 = 2406, and 2406 has four digits, place the 3 above the fourth digit of the dividend.
Subtract: 2417 – 2406 = 11.
Bring down the 2.
The divisor 802 goes into 112 at most 0 times. Use 0.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
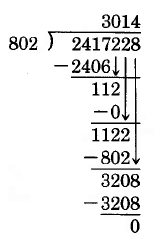
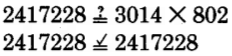
118
CHAPTER 2. MULTIPLICATION AND DIVISION OF WHOLE NUMBERS
Multiply:
0 × 802 = 0.
Subtract:
112 – 0 = 112.
Bring down the 2.
The 8 goes into 11 at most 1 time, and 1 × 802 = 802, which is less than 1122. Try 1.
Subtract 1122 − 802 = 320
Bring down the 8.
8 goes into 32 at most 4 times.
4 × 802 = 3208.
Use 4.
Check:
Thus, 2, 417, 228 ÷ 802 = 3, 014.
2.4.3.2 Practice Set B
Perform the following divisions.
Exercise 2.4.6
(Solution on p. 146.)
1, 376 ÷ 32
Exercise 2.4.7
(Solution on p. 146.)
6, 160 ÷ 55
Exercise 2.4.8
(Solution on p. 146.)
18, 605 ÷ 61
Exercise 2.4.9
(Solution on p. 146.)
144, 768 ÷ 48
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
119
2.4.4 Division with a Remainder
We might wonder how many times 4 is contained in 10. Repeated subtraction yields 10
− 4
6
−4
2
Since the remainder is less than 4, we stop the subtraction. Thus, 4 goes into 10 two times with 2 remaining.
We can write this as a division as follows.
2
4)10
− 8
2
Divide:
4 goes into 10 at most 2 times.
Multiply:
2 × 4 = 8. Write 8 below 0.
Subtract:
10 – 8 = 2.
Since 4 does not divide into 2 (the remainder is less than the divisor) and there are no digits to bring down to continue the process, we are done. We write
2 R2
4) 10 or 10 ÷ 4 =
2R2
−8
|{z}
2 with remainder 2
2
2.4.4.1 Sample Set C
Example 2.27
Find 85 ÷ 3.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
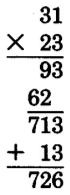
120
CHAPTER 2. MULTIPLICATION AND DIVISION OF WHOLE NUMBERS
Divide:
3 goes into 8 at most 2 times.
Divide:
3 goes into 25 at most 8 times.
{ Multiply:
2 × 3 = 6. Write 6 below 8. { Multiply: 3 × 8 = 24. Write 24 below 25.
Subtract: 8 – 6 = 2. Bring down the 5.
Subtract:
25 – 24 = 1.
There are no more digits to bring down to continue the process. We are done. One is the remainder.
Check: Multiply 28 and 3, then add 1.
28
× 3
84
+ 1
85
Thus, 85 ÷ 3 = 28R1.
Example 2.28
Find 726 ÷ 23.
Check: Multiply 31 by 23, then add 13.
Thus, 726 ÷ 23 = 31R13.
2.4.4.2 Practice Set C
Perform the following divisions.
Exercise 2.4.10
(Solution on p. 146.)
75 ÷ 4
Exercise 2.4.11
(Solution on p. 146.)
346 ÷ 8
Exercise 2.4.12
(Solution on p. 146.)
489 ÷ 21
Exercise 2.4.13
(Solution on p. 146.)
5, 016 ÷ 82
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 2.4.14
(Solution on p. 146.)
41, 196 ÷ 67
2.4.5 Calculators
The calculator can be useful for nding quotients with single and multiple digit divisors. If, however, the division should result in a remainder, the calculator is unable to provide us with the particular value of the remainder. Also, some calculators (most nonscientic) are unable to perform divisions in which one of the numbers has more than eight digits.
2.4.5.1 Sample Set D
Use a calculator to perform each division.
Example 2.29
328 ÷ 8
Type 328
Press ÷
Type 8
Press =
Table 2.7
The display now reads 41.
Example 2.30
53, 136 ÷ 82
Type 53136
Press ÷
Type 82
Press =
Table 2.8
The display now reads 648.
Example 2.31
730, 019, 001 ÷ 326
We rst try to enter 730,019,001 but nd that we can only enter 73001900. If our calculator has only an eight-digit display (as most nonscientic calculators do), we will be unable to use the calculator to perform this division.
Example 2.32
3727 ÷ 49
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 2. MULTIPLICATION AND DIVISION OF WHOLE NUMBERS
Type 3727
Press ÷
Type 49
Press =
Table 2.9
The display now reads 76.061224.
This number is an example of a decimal number (see Section 6.1). When a decimal number results in a calculator division, we can conclude that the division produces a remainder.
2.4.5.2 Practice Set D
Use a calculator to perform each division.
Exercise 2.4.15
(Solution on p. 146.)
3, 330 ÷ 74
Exercise 2.4.16
(Solution on p. 146.)
63, 365 ÷ 115
Exercise 2.4.17
(Solution on p. 146.)
21, 996, 385, 287 ÷ 53
Exercise 2.4.18
(Solution on p. 146.)
4, 558 ÷ 67
2.4.6 Exercises
For the following problems, perform the divisions.
The rst 38 problems can be checked with a calculator by multiplying the divisor and quotient then adding the remainder.
Exercise 2.4.19
(Solution on p. 146.)
52 ÷ 4
Exercise 2.4.20
776 ÷ 8
Exercise 2.4.21
(Solution on p. 146.)
603 ÷ 9
Exercise 2.4.22
240 ÷ 8
Exercise 2.4.23
(Solution on p. 146.)
208 ÷ 4
Exercise 2.4.24
576 ÷ 6
Exercise 2.4.25
(Solution on p. 146.)
21 ÷ 7
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 2.4.26
0 ÷ 0
Exercise 2.4.27
(Solution on p. 146.)
140 ÷ 2
Exercise 2.4.28
528 ÷ 8
Exercise 2.4.29
(Solution on p. 146.)
244 ÷ 4
Exercise 2.4.30
0 ÷ 7
Exercise 2.4.31
(Solution on p. 146.)
177 ÷ 3
Exercise 2.4.32
96 ÷ 8
Exercise 2.4.33
(Solution on p. 146.)
67 ÷ 1
Exercise 2.4.34
896 ÷ 56
Exercise 2.4.35
(Solution on p. 146.)
1, 044 ÷ 12
Exercise 2.4.36
988 ÷ 19
Exercise 2.4.37
(Solution on p. 146.)
5, 238 ÷ 97
Exercise 2.4.38
2, 530 ÷ 55
Exercise 2.4.39
(Solution on p. 146.)
4, 264 ÷ 82
Exercise 2.4.40
637 ÷ 13
Exercise 2.4.41
(Solution on p. 147.)
3, 420 ÷ 90
Exercise 2.4.42
5, 655 ÷ 87
Exercise 2.4.43
(Solution on p. 147.)
2, 115 ÷ 47
Exercise 2.4.44
9, 328 ÷ 22
Exercise 2.4.45
(Solution on p. 147.)
55, 167 ÷ 71
Exercise 2.4.46
68, 356 ÷ 92
Exercise 2.4.47
(Solution on p. 147.)
27, 702 ÷ 81
Exercise 2.4.48
6, 510 ÷ 31
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 2. MULTIPLICATION AND DIVISION OF WHOLE NUMBERS
Exercise 2.4.49
(Solution on p. 147.)
60, 536 ÷ 94
Exercise 2.4.50
31, 844 ÷ 38
Exercise 2.4.51
(Solution on p. 147.)
23, 985 ÷ 45
Exercise 2.4.52
60, 606 ÷ 74
Exercise 2.4.53
(Solution on p. 147.)
2, 975, 400 ÷ 285
Exercise 2.4.54
1, 389, 660 ÷ 795
Exercise 2.4.55
(Solution on p. 147.)
7, 162, 060 ÷ 879
Exercise 2.4.56
7, 561, 060 ÷ 909
Exercise 2.4.57
(Solution on p. 147.)
38 ÷ 9
Exercise 2.4.58
97 ÷ 4
Exercise 2.4.59
(Solution on p. 147.)
199 ÷ 3
Exercise 2.4.60
573 ÷ 6
Exercise 2.4.61
(Solution on p. 147.)
10, 701 ÷ 13
Exercise 2.4.62
13, 521 ÷ 53
Exercise 2.4.63
(Solution on p. 147.)
3, 628 ÷ 90
Exercise 2.4.64
10, 592 ÷ 43
Exercise 2.4.65
(Solution on p. 147.)
19, 965 ÷ 30
Exercise 2.4.66
8, 320 ÷ 21
Exercise 2.4.67
(Solution on p. 147.)
61, 282 ÷ 64
Exercise 2.4.68
1, 030 ÷ 28
Exercise 2.4.69
(Solution on p. 147.)
7, 319 ÷ 11
Exercise 2.4.70
3, 628 ÷ 90
Exercise 2.4.71
(Solution on p. 147.)
35, 279 ÷ 77
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 2.4.72
52, 196 ÷ 55
Exercise 2.4.73
(Solution on p. 147.)
67, 751 ÷ 68
For the following 5 problems, use a calculator to nd the quotients.
Exercise 2.4.74
4, 346 ÷ 53
Exercise 2.4.75
(Solution on p. 147.)
3, 234 ÷ 77
Exercise 2.4.76
6, 771 ÷ 37
Exercise 2.4.77
(Solution on p. 147.)
4, 272, 320 ÷ 520
Exercise 2.4.78
7, 558, 110 ÷ 651
Exercise 2.4.79
(Solution on p. 147.)
A mathematics instructor at a high school is paid $17,775 for 9 months. How much money does this instructor make each month?
Exercise 2.4.80
A couple pays $4,380 a year for a one-bedroom apartment. How much does this couple pay each month for this apartment?
Exercise 2.4.81
(Solution on p. 147.)
Thirty-six people invest a total of $17,460 in a particular stock. If they each invested the same amount, how much did each person invest?
Exercise 2.4.82
Each of the 28 students in a mathematics class buys a textbook. If the bookstore sells $644 worth of books, what is the price of each book?
Exercise 2.4.83
(Solution on p. 147.)
A certain brand of refrigerator has an automatic ice cube maker that makes 336 ice cubes in one day. If the ice machine makes ice cubes at a constant rate, how many ice cubes does it make each hour?
Exercise 2.4.84
A beer manufacturer bottles 52,380 ounces of beer each hour. If each bottle contains the same number of ounces of beer, and the manufacturer lls 4,365 bottles per hour, how many ounces of beer does each bottle contain?
Exercise 2.4.85
(Solution on p. 147.)
A computer program consists of 68,112 bits. 68,112 bits equals 8,514 bytes. How many bits in one byte?
Exercise 2.4.86
A 26-story building in San Francisco has a total of 416 oces. If each oor has the same number of oces, how many oors does this building have?
Exercise 2.4.87
(Solution on p. 147.)
A college has 67 classrooms and a total of 2,546 desks. How many desks are in each classroom if each classroom has the same number of desks?
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 2. MULTIPLICATION AND DIVISION OF WHOLE NUMBERS
2.4.6.1 Exercises for Review
Exercise 2.4.88
(Section 1.2) What is the value of 4 in the number 124,621?
Exercise 2.4.89
(Solution on p. 147.)
(Section 1.4) Round 604,092 to the nearest hundred thousand.
Exercise 2.4.90
(Section 1.7) What whole number is the additive identity?
Exercise 2.4.91
(Solution on p. 148.)
(Section 2.2) Find the product. 6, 256 × 100.
Exercise 2.4.92
(Section 2.3) Find the quotient. 0 ÷ 11.
2.5 Some Interesting Facts about Division 5
2.5.1 Section Overview
• Division by 2, 3, 4, and 5
• Division by 6, 8, 9, and 10
Quite often, we are able to determine if a whole number is divisible by another whole number just by observing some simple facts about the number. Some of these facts are listed in this section.
2.5.2 Division by 2, 3, 4, and 5
Division by 2
A whole number is divisible by 2 if its last digit is 0, 2, 4, 6, or 8.
The numbers 80, 112, 64, 326, and 1,008 are all divisible by 2 since the last digit of each is 0, 2, 4, 6, or 8, respectively.
The numbers 85 and 731 are not divisible by 2.
Division by 3
A whole number is divisible by 3 if the sum of its digits is divisible by 3.
The number 432 is divisible by 3 since 4 + 3 + 2 = 9 and 9 is divisible by 3.
432 ÷ 3 = 144
The number 25 is not divisible by 3 since 2 + 5 = 7, and 7 is not divisible by 3.
Division by 4
A whole number is divisible by 4 if its last two digits form a number that is divisible by 4.
The number 31,048 is divisible by 4 since the last two digits, 4 and 8, form a number, 48, that is divisible by 4.
31048 ÷ 4 = 7262
5This content is available online at <http://cnx.org/content/m34866/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
The number 137 is not divisible by 4 since 37 is not divisible by 4.
Division by 5
A whole number is divisible by 5 if its last digit is 0 or 5.
2.5.2.1 Sample Set A
Example 2.33
The numbers 65, 110, 8,030, and 16,955 are each divisible by 5 since the last digit of each is 0 or 5.
2.5.2.2 Practice Set A
State which of the following whole numbers are divisible by 2, 3, 4, or 5. A number may be divisible by more than one number.
Exercise 2.5.1
(Solution on p. 148.)
26
Exercise 2.5.2
(Solution on p. 148.)
81
Exercise 2.5.3
(Solution on p. 148.)
51
Exercise 2.5.4
(Solution on p. 148.)
385
Exercise 2.5.5
(Solution on p. 148.)
6,112
Exercise 2.5.6
(Solution on p. 148.)
470
Exercise 2.5.7
(Solution on p. 148.)
113,154
2.5.3 Division by 6, 8, 9, 10
Division by 6
A number is divisible by 6 if it is divisible by both 2 and 3.
The number 234 is divisible by 2 since its last digit is 4. It is also divisible by 3 since 2 + 3 + 4 = 9 and 9 is divisible by 3. Therefore, 234 is divisible by 6.
The number 6,532 is not divisible by 6. Although its last digit is 2, making it divisible by 2, the sum of its digits, 6 + 5 + 3 + 2 = 16, and 16 is not divisible by 3.
Division by 8
A whole number is divisible by 8 if its last three digits form a number that is divisible by 8.
The number 4,000 is divisible by 8 since 000 is divisible by 8.
The number 13,128 is divisible by 8 since 128 is divisible by 8.
The number 1,170 is not divisible by 8 since 170 is not divisible by 8.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 2. MULTIPLICATION AND DIVISION OF WHOLE NUMBERS
Division by 9
A whole number is divisible by 9 if the sum of its digits is divisible by 9.
The number 702 is divisible by 9 since 7 + 0 + 2 is divisible by 9.
The number 6588 is divisible by 9 since 6 + 5 + 8 + 8 = 27 is divisible by 9.
The number 14,123 is not divisible by 9 since 1 + 4 + 1 + 2 + 3 = 11 is not divisible by 9.
Division by 10
A Whole number is divisible by 10 if its last digit is 0.
2.5.3.1 Sample Set B
Example 2.34
The numbers 30, 170, 16,240, and 865,000 are all divisible by 10.
2.5.3.2 Practice Set B
State which of the following whole numbers are divisible 6, 8, 9, or 10. Some numbers may be divisible by more than one number.
Exercise 2.5.8
(Solution on p. 148.)
900
Exercise 2.5.9
(Solution on p. 148.)
6,402
Exercise 2.5.10
(Solution on p. 148.)
6,660
Exercise 2.5.11
(Solution on p. 148.)
55,116
2.5.4 Exercises
For the following 30 problems, specify if the whole number is divisible by 2, 3, 4, 5, 6, 8, 9, or 10. Write
“none” if the number is not divisible by any digit other than 1. Some numbers may be divisible by more than one number.
Exercise 2.5.12
(Solution on p. 148.)
48
Exercise 2.5.13
85
Exercise 2.5.14
(Solution on p. 148.)
30
Exercise 2.5.15
83
Exercise 2.5.16
(Solution on p. 148.)
98
Exercise 2.5.17
972
Exercise 2.5.18
(Solution on p. 148.)
892
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 2.5.19
676
Exercise 2.5.20
(Solution on p. 148.)
903
Exercise 2.5.21
800
Exercise 2.5.22
(Solution on p. 148.)
223
Exercise 2.5.23
836
Exercise 2.5.24
(Solution on p. 148.)
665
Exercise 2.5.25
4,381
Exercise 2.5.26
(Solution on p. 148.)
2,195
Exercise 2.5.27
2,544
Exercise 2.5.28
(Solution on p. 148.)
5,172
Exercise 2.5.29
1,307
Exercise 2.5.30
(Solution on p. 148.)
1,050
Exercise 2.5.31
3,898
Exercise 2.5.32
(Solution on p. 148.)
1,621
Exercise 2.5.33
27,808
Exercise 2.5.34
(Solution on p. 148.)
45,764
Exercise 2.5.35
49,198
Exercise 2.5.36
(Solution on p. 148.)
296,122
Exercise 2.5.37
178,656
Exercise 2.5.38
(Solution on p. 149.)
5,102,417
Exercise 2.5.39
16,990,792
Exercise 2.5.40
(Solution on p. 149.)
620,157,659
Exercise 2.5.41
457,687,705
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
130
CHAPTER 2. MULTIPLICATION AND DIVISION OF WHOLE NUMBERS
2.5.4.1 Exercises for Review
Exercise 2.5.42
(Solution on p. 149.)
(Section 1.2) In the number 412, how many tens are there?
Exercise 2.5.43
(Section 1.6) Subtract 613 from 810.
Exercise 2.5.44
(Solution on p. 149.)
(Section 1.7) Add 35, 16, and 7 in two dierent ways.
Exercise 2.5.45
(Section 2.3) Find the quotient 35 ÷ 0, if it exists.
Exercise 2.5.46
(Solution on p. 149.)
(Section 2.4) Find the quotient. 3654 ÷ 42.
2.6 Properties of Multiplication 6
2.6.1 Section Overview
• The Commutative Property of Multiplication
• The Associative Property of Multiplication
• The Multiplicative Identity
We will now examine three simple but very important properties of multiplication.
2.6.2 The Commutative Property of Multiplication
Commutative Property of Multiplication
The product of two whole numbers is the same regardless of the order of the factors.
2.6.2.1 Sample Set A
Example 2.35
Multiply the two whole numbers.
6 · 7 = 42
7 · 6 = 42
The numbers 6 and 7 can be multiplied in any order. Regardless of the order they are multiplied, the product is 42.
6This content is available online at <http://cnx.org/content/m34867/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

131
2.6.2.2 Practice Set A
Use the commutative property of multiplication to nd the products in two ways.
Exercise 2.6.1
(Solution on p. 149.)
Exercise 2.6.2
(Solution on p. 149.)
2.6.3 The Associative Property of Multiplication
Associative Property of Multiplication
If three whole numbers are multiplied, the product will be the same if the rst two are multiplied rst and then that product is multiplied by the third, or if the second two are multiplied rst and that product is multiplied by the rst. Note that the order of the factors is maintained.
It is a common mathematical practice to use parentheses to show which pair of numbers is to be combined rst.
2.6.3.1 Sample Set B
Example 2.36
Multiply the whole numbers.
(8 · 3) · 14 = 24 · 14 = 336
8 · (3 · 14) = 8 · 42 = 336
2.6.3.2 Practice Set B
Use the associative property of multiplication to nd the products in two ways.
Exercise 2.6.3
(Solution on p. 149.)
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
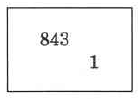
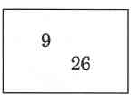
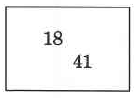
132
CHAPTER 2. MULTIPLICATION AND DIVISION OF WHOLE NUMBERS
Exercise 2.6.4
(Solution on p. 149.)
2.6.4 The Multiplicative Identity
The Multiplicative Identity is 1
The whole number 1 is called the multiplicative identity, since any whole number multiplied by 1 is not changed.
2.6.4.1 Sample Set C
Example 2.37
Multiply the whole numbers.
12 · 1 = 12
1 · 12 = 12
2.6.4.2 Practice Set C
Multiply the whole numbers.
Exercise 2.6.5
(Solution on p. 149.)
2.6.5 Exercises
For the following problems, multiply the numbers.
Exercise 2.6.6
(Solution on p. 149.)
Exercise 2.6.7
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
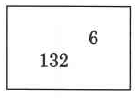



133
Exercise 2.6.8
(Solution on p. 149.)
Exercise 2.6.9
Exercise 2.6.10
(Solution on p. 149.)
Exercise 2.6.11
Exercise 2.6.12
(Solution on p. 149.)
Exercise 2.6.13
Exercise 2.6.14
(Solution on p. 149.)
Exercise 2.6.15
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

134
CHAPTER 2. MULTIPLICATION AND DIVISION OF WHOLE NUMBERS
Exercise 2.6.16
(Solution on p. 149.)
Exercise 2.6.17
For the following 4 problems, show that the quantities yield the same products by performing the multiplications.
Exercise 2.6.18
(Solution on p. 149.)
(4 · 8) · 2 and 4 · (8 · 2)
Exercise 2.6.19
(100 · 62) · 4 and 100 · (62 · 4)
Exercise 2.6.20
(Solution on p. 149.)
23 · (11 · 106) and (23 · 11) · 106
Exercise 2.6.21
1 · (5 · 2) and (1 · 5) · 2
Exercise 2.6.22
(Solution on p. 149.)
The fact that (a rst number · a second number) · a third number
=
a rst number ·
(a second number · a third number)is an example of the
property of multiplication.
Exercise 2.6.23
The fact that 1 · any number = that particular numberis an example of the property of
multiplication.
Exercise 2.6.24
(Solution on p. 149.)
Use the numbers 7 and 9 to illustrate the commutative property of multiplication.
Exercise 2.6.25
Use the numbers 6, 4, and 7 to illustrate the associative property of multiplication.
2.6.5.1 Exercises for Review
Exercise 2.6.26
(Solution on p. 149.)
(Section 1.2) In the number 84,526,098,441, how many millions are there?
Exercise 2.6.27
85
(Section 1.5) Replace the letter m with the whole number that makes the addition true. + m 97
Exercise 2.6.28
(Solution on p. 149.)
(Section 1.7) Use the numbers 4 and 15 to illustrate the commutative property of addition.
Exercise 2.6.29
(Section 2.3) Find the product. 8, 000, 000 × 1, 000.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 2.6.30
(Solution on p. 149.)
(Section 2.5) Specify which of the digits 2, 3, 4, 5, 6, 8,10 are divisors of the number 2,244.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 2. MULTIPLICATION AND DIVISION OF WHOLE NUMBERS
2.7 Summary of Key Concepts 7
2.7.1 Summary of Key Concepts
Multiplication (Section 2.2)
Multiplication is a description of repeated addition.
7 + 7 + 7 + 7
|
{z
}
7 appears 4 times
This expression is described by writing 4 X 7.
Multiplicand/Multiplier/Product (Section 2.2)
In a multiplication of whole numbers, the repeated addend is called the multiplicand, and the number that records the number of times the multiplicand is used is the multiplier. The result of the multiplication is the product.
Factors (Section 2.2)
In a multiplication, the numbers being multiplied are also called factors. Thus, the multiplicand and the multiplier can be called factors.
Division (Section 2.3)
Division is a description of repeated subtraction.
Dividend/Divisor/Quotient (Section 2.3)
In a division, the number divided into is called the dividend, and the number dividing into the dividend is called the divisor. The result of the division is called the quotient.
quotient
divisor)dividend
Division into Zero (Section 2.3)
Zero divided by any nonzero whole number is zero.
Division by Zero (Section 2.3)
Division by zero does not name a whole number. It is, therefore, undened. The quotient 0 is indeterminant.
0
Division by 2, 3, 4, 5, 6, 8, 9, 10 (Section 2.5)
Division by the whole numbers 2, 3, 4, 5, 6, 8, 9, and 10 can be determined by noting some certain properties of the particular whole number.
Commutative Property of Multiplication (Section 2.6)
The product of two whole numbers is the same regardless of the order of the factors. 3 × 5 = 5 × 3
Associative Property of Multiplication (Section 2.6)
If three whole numbers are to be multiplied, the product will be the same if the rst two are multiplied rst and then that product is multiplied by the third, or if the second two are multiplied rst and then that product is multiplied by the rst.
(3 × 5) × 2 = 3 × (5 × 2)
Note that the order of the factors is maintained.
Multiplicative Identity (Section 2.6)
The whole number 1 is called the multiplicative identity since any whole number multiplied by 1 is not changed.
7This content is available online at <http://cnx.org/content/m34868/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
4 × 1 = 4
1 × 4 = 4
2.8 Exercise Supplement 8
2.8.1 Exercise Supplement
2.8.1.1 Multiplication of Whole Numbers (Section 2.2)
Exercise 2.8.1
(Solution on p. 149.)
In the multiplication 5 × 9 = 45, 5 and 9 are called
and 45 is called the
.
Exercise 2.8.2
In the multiplication 4 × 8 = 32, 4 and 8 are called
and 32 is called the
.
2.8.1.2 Concepts of Division of Whole Numbers (Section 2.3)
Exercise 2.8.3
(Solution on p. 150.)
In the division 24 ÷ 6 = 4, 6 is called the
, and 4 is called the
.
Exercise 2.8.4
In the division 36 ÷ 2 = 18, 2 is called the
, and 18 is called the
.
2.8.1.3 Some Interesting Facts about Division (Section 2.5)
Exercise 2.8.5
(Solution on p. 150.)
A number is divisible by 2 only if its last digit is
.
Exercise 2.8.6
A number is divisible by 3 only if
of its digits is divisible by 3.
Exercise 2.8.7
(Solution on p. 150.)
A number is divisible by 4 only if the rightmost two digits form a number that is
.
2.8.1.4 Multiplication and Division of Whole Numbers (Section 2.2,Section 2.4) Find each product or quotient.
Exercise 2.8.8
24
× 3
Exercise 2.8.9
(Solution on p. 150.)
14
× 8
Exercise 2.8.10
21 ÷ 7
Exercise 2.8.11
(Solution on p. 150.)
35 ÷ 5
8This content is available online at <http://cnx.org/content/m34869/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 2. MULTIPLICATION AND DIVISION OF WHOLE NUMBERS
Exercise 2.8.12
36
×22
Exercise 2.8.13
(Solution on p. 150.)
87
×35
Exercise 2.8.14
117
×42
Exercise 2.8.15
(Solution on p. 150.)
208 ÷ 52
Exercise 2.8.16
521
× 87
Exercise 2.8.17
(Solution on p. 150.)
1005
×
15
Exercise 2.8.18
1338 ÷ 446
Exercise 2.8.19
(Solution on p. 150.)
2814 ÷ 201
Exercise 2.8.20
5521
×8
Exercise 2.8.21
(Solution on p. 150.)
6016
×
7
Exercise 2.8.22
576 ÷ 24
Exercise 2.8.23
(Solution on p. 150.)
3969 ÷ 63
Exercise 2.8.24
5482
× 322
Exercise 2.8.25
(Solution on p. 150.)
9104
× 115
Exercise 2.8.26
6102
×1000
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 2.8.27
(Solution on p. 150.)
10101
×10000
Exercise 2.8.28
162, 006 ÷ 31
Exercise 2.8.29
(Solution on p. 150.)
0 ÷ 25
Exercise 2.8.30
25 ÷ 0
Exercise 2.8.31
(Solution on p. 150.)
4280 ÷ 10
Exercise 2.8.32
2126000 ÷ 100
Exercise 2.8.33
(Solution on p. 150.)
84 ÷ 15
Exercise 2.8.34
126 ÷ 4
Exercise 2.8.35
(Solution on p. 150.)
424 ÷ 0
Exercise 2.8.36
1198 ÷ 46
Exercise 2.8.37
(Solution on p. 150.)
995 ÷ 31
Exercise 2.8.38
0 ÷ 18
Exercise 2.8.39
(Solution on p. 150.)
2162
×1421
Exercise 2.8.40
0 × 0
Exercise 2.8.41
(Solution on p. 150.)
5 × 0
Exercise 2.8.42
64 × 1
Exercise 2.8.43
(Solution on p. 150.)
1 × 0
Exercise 2.8.44
0 ÷ 3
Exercise 2.8.45
(Solution on p. 150.)
14 ÷ 0
Exercise 2.8.46
35 ÷ 1
Exercise 2.8.47
(Solution on p. 150.)
1 ÷ 1
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 2. MULTIPLICATION AND DIVISION OF WHOLE NUMBERS
2.8.1.5 Properties of Multiplication (Section 2.6)
Exercise 2.8.48
Use the commutative property of multiplication to rewrite 36 × 128.
Exercise 2.8.49
(Solution on p. 150.)
Use the commutative property of multiplication to rewrite 114 × 226.
Exercise 2.8.50
Use the associative property of multiplication to rewrite (5 · 4) · 8.
Exercise 2.8.51
(Solution on p. 150.)
Use the associative property of multiplication to rewrite 16 · (14 · 0).
2.8.1.6 Multiplication and Division of Whole Numbers (Section 2.2,Section 2.4) Exercise 2.8.52
A computer store is selling diskettes for $4 each. At this price, how much would 15 diskettes cost?
Exercise 2.8.53
(Solution on p. 151.)
Light travels 186,000 miles in one second. How far does light travel in 23 seconds?
Exercise 2.8.54
A dinner bill for eight people comes to exactly $112. How much should each person pay if they all agree to split the bill equally?
Exercise 2.8.55
(Solution on p. 151.)
Each of the 33 students in a math class buys a textbook. If the bookstore sells $1089 worth of books, what is the price of each book?
2.9 Prociency Exam 9
2.9.1 Prociency Exam
Exercise 2.9.1
(Solution on p. 151.)
(Section 2.2) In the multiplication of 8 × 7 = 56, what are the names given to the 8 and 7 and the 56?
Exercise 2.9.2
(Solution on p. 151.)
(Section 2.2) Multiplication is a description of what repeated process?
Exercise 2.9.3
(Solution on p. 151.)
(Section 2.3) In the division 12 ÷ 3 = 4, what are the names given to the 3 and the 4?
Exercise 2.9.4
(Solution on p. 151.)
(Section 2.5) Name the digits that a number must end in to be divisible by 2.
Exercise 2.9.5
(Solution on p. 151.)
(Section 2.6) Name the property of multiplication that states that the order of the factors in a multiplication can be changed without changing the product.
Exercise 2.9.6
(Solution on p. 151.)
(Section 2.6) Which number is called the multiplicative identity?
For problems 7-17, nd the product or quotient.
Exercise 2.9.7
(Solution on p. 151.)
(Section 2.2) 14 × 6
9This content is available online at <http://cnx.org/content/m34870/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 2.9.8
(Solution on p. 151.)
(Section 2.2) 37 × 0
Exercise 2.9.9
(Solution on p. 151.)
(Section 2.2) 352 × 1000
Exercise 2.9.10
(Solution on p. 151.)
(Section 2.2) 5986 × 70
Exercise 2.9.11
(Solution on p. 151.)
(Section 2.2) 12 × 12
Exercise 2.9.12
(Solution on p. 151.)
(Section 2.3) 856 ÷ 0
Exercise 2.9.13
(Solution on p. 151.)
(Section 2.3) 0 ÷ 8
Exercise 2.9.14
(Solution on p. 151.)
(Section 2.4) 136 ÷ 8
Exercise 2.9.15
(Solution on p. 151.)
(Section 2.4) 432 ÷ 24
Exercise 2.9.16
(Solution on p. 151.)
(Section 2.4) 5286 ÷ 37
Exercise 2.9.17
(Solution on p. 151.)
(Section 2.6) 211 × 1
For problems 18-20, use the numbers 216, 1,005, and 640.
Exercise 2.9.18
(Solution on p. 151.)
(Section 2.5) Which numbers are divisible by 3?
Exercise 2.9.19
(Solution on p. 151.)
(Section 2.5) Which number is divisible by 4?
Exercise 2.9.20
(Solution on p. 151.)
(Section 2.5) Which number(s) is divisible by 5?
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 2. MULTIPLICATION AND DIVISION OF WHOLE NUMBERS
Solutions to Exercises in Chapter 2
Solution to Exercise 2.2.1 (p. 93)
4 × 12. Multiplier is 4. Multiplicand is 12.
Solution to Exercise 2.2.2 (p. 93)
8 × 36. Multiplier is 8. Multiplicand is 36.
Solution to Exercise 2.2.3 (p. 93)
5 × 0. Multiplier is 5. Multiplicand is 0.
Solution to Exercise 2.2.4 (p. 93)
12, 000 × 1, 847. Multiplier is 12,000. Multiplicand is 1,847.
Solution to Exercise 2.2.5 (p. 94)
185
Solution to Exercise 2.2.6 (p. 94)
624
Solution to Exercise 2.2.7 (p. 95)
3,752
Solution to Exercise 2.2.8 (p. 95)
320,152
Solution to Exercise 2.2.9 (p. 95)
904,797
Solution to Exercise 2.2.10 (p. 97)
1,022
Solution to Exercise 2.2.11 (p. 97)
4,472
Solution to Exercise 2.2.12 (p. 97)
35,615
Solution to Exercise 2.2.13 (p. 97)
1,456,488
Solution to Exercise 2.2.14 (p. 97)
2,464,528
Solution to Exercise 2.2.15 (p. 97)
66,790,080
Solution to Exercise 2.2.16 (p. 97)
104,709
Solution to Exercise 2.2.17 (p. 97)
240
Solution to Exercise 2.2.18 (p. 97)
3,809,000
Solution to Exercise 2.2.19 (p. 97)
8,130,000
Solution to Exercise 2.2.20 (p. 98)
162,000
Solution to Exercise 2.2.21 (p. 98)
126,000,000
Solution to Exercise 2.2.22 (p. 98)
2,870,000,000,000
Solution to Exercise 2.2.23 (p. 99)
1,404
Solution to Exercise 2.2.24 (p. 99)
8,912,440
Solution to Exercise 2.2.25 (p. 99)
1,832,700,000,000
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 2.2.26 (p. 100)
24
Solution to Exercise 2.2.28 (p. 100)
48
Solution to Exercise 2.2.30 (p. 100)
6Solution to Exercise 2.2.32 (p. 100)
225
Solution to Exercise 2.2.34 (p. 100)
270
Solution to Exercise 2.2.36 (p. 100)
582
Solution to Exercise 2.2.38 (p. 100)
960
Solution to Exercise 2.2.40 (p. 100)
7,695
Solution to Exercise 2.2.42 (p. 101)
3,648
Solution to Exercise 2.2.44 (p. 101)
46,488
Solution to Exercise 2.2.46 (p. 101)
2,530
Solution to Exercise 2.2.48 (p. 101)
6,888
Solution to Exercise 2.2.50 (p. 101)
24,180
Solution to Exercise 2.2.52 (p. 101)
73,914
Solution to Exercise 2.2.54 (p. 101)
68,625
Solution to Exercise 2.2.56 (p. 102)
511,173
Solution to Exercise 2.2.58 (p. 102)
1,352,550
Solution to Exercise 2.2.60 (p. 102)
5,441,712
Solution to Exercise 2.2.62 (p. 102)
36,901,053
Solution to Exercise 2.2.64 (p. 102)
24,957,200
Solution to Exercise 2.2.66 (p. 102)
0Solution to Exercise 2.2.68 (p. 102)
41,384
Solution to Exercise 2.2.70 (p. 103)
0Solution to Exercise 2.2.72 (p. 103)
73,530
Solution to Exercise 2.2.74 (p. 103)
6,440,000,000
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 2. MULTIPLICATION AND DIVISION OF WHOLE NUMBERS
Solution to Exercise 2.2.76 (p. 103)
4,440,000
Solution to Exercise 2.2.78 (p. 103)
641,900,000
Solution to Exercise 2.2.80 (p. 103)
80,000
Solution to Exercise 2.2.82 (p. 104)
384 reports
Solution to Exercise 2.2.84 (p. 104)
3,330 problems
Solution to Exercise 2.2.86 (p. 104)
114 units
Solution to Exercise 2.2.88 (p. 104)
3,600 seconds
Solution to Exercise 2.2.90 (p. 104)
5,865,696,000,000 miles per year
Solution to Exercise 2.2.92 (p. 104)
$110,055
Solution to Exercise 2.2.94 (p. 104)
448,100,000
Solution to Exercise 2.2.96 (p. 104)
712
Solution to Exercise 2.3.1 (p. 107)
4
Solution to Exercise 2.3.2 (p. 107)
2
Solution to Exercise 2.3.3 (p. 107)
5
Solution to Exercise 2.3.4 (p. 107)
6
Solution to Exercise 2.3.5 (p. 107)
4Solution to Exercise 2.3.6 (p. 107)
9
Solution to Exercise 2.3.7 (p. 109)
undened
Solution to Exercise 2.3.8 (p. 109)
0
Solution to Exercise 2.3.9 (p. 109)
indeterminant
Solution to Exercise 2.3.10 (p. 109)
undened
Solution to Exercise 2.3.11 (p. 109)
undened
Solution to Exercise 2.3.12 (p. 109)
0
Solution to Exercise 2.3.13 (p. 110)
5
Solution to Exercise 2.3.14 (p. 110)
7
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 2.3.15 (p. 110)
0
Solution to Exercise 2.3.16 (p. 110)
An error message tells us that this operation is undened. The particular message depends on the calculator.
Solution to Exercise 2.3.17 (p. 110)
An error message tells us that this operation cannot be performed. Some calculators actually set 0 ÷ 0 equal to 1. We know better! 0 ÷ 0 is indeterminant.
Solution to Exercise 2.3.18 (p. 111)
8
Solution to Exercise 2.3.20 (p. 111)
3
Solution to Exercise 2.3.22 (p. 111)
9
Solution to Exercise 2.3.24 (p. 111)
7
Solution to Exercise 2.3.26 (p. 111)
4
Solution to Exercise 2.3.28 (p. 111)
5
Solution to Exercise 2.3.30 (p. 111)
7
Solution to Exercise 2.3.32 (p. 111)
not dened
Solution to Exercise 2.3.34 (p. 111)
3
Solution to Exercise 2.3.36 (p. 111)
0
Solution to Exercise 2.3.38 (p. 111)
5
Solution to Exercise 2.3.40 (p. 112)
8
Solution to Exercise 2.3.42 (p. 112)
9
Solution to Exercise 2.3.44 (p. 112)
27 ÷ 9 = 3; 9)27 = 3 ; 27 = 3
9
Solution to Exercise 2.3.46 (p. 112)
7 is quotient; 8 is divisor; 56 is dividend
Solution to Exercise 2.3.48 (p. 112)
12,124
Solution to Exercise 2.3.50 (p. 112)
(2 + 3) + 7 = 2 + (3 + 7) = 12
5+7=2+10=12
Solution to Exercise 2.4.1 (p. 116)
18
Solution to Exercise 2.4.2 (p. 116)
81
Solution to Exercise 2.4.3 (p. 116)
853
Solution to Exercise 2.4.4 (p. 116)
1,129
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 2. MULTIPLICATION AND DIVISION OF WHOLE NUMBERS
Solution to Exercise 2.4.5 (p. 116)
84,125
Solution to Exercise 2.4.6 (p. 118)
43
Solution to Exercise 2.4.7 (p. 118)
112
Solution to Exercise 2.4.8 (p. 118)
305
Solution to Exercise 2.4.9 (p. 118)
3,016
Solution to Exercise 2.4.10 (p. 120)
18 R3
Solution to Exercise 2.4.11 (p. 120)
43 R2
Solution to Exercise 2.4.12 (p. 120)
23 R6
Solution to Exercise 2.4.13 (p. 120)
61 R14
Solution to Exercise 2.4.14 (p. 121)
614 R58
Solution to Exercise 2.4.15 (p. 122)
45
Solution to Exercise 2.4.16 (p. 122)
551
Solution to Exercise 2.4.17 (p. 122)
Since the dividend has more than eight digits, this division cannot be performed on most nonscientic calculators. On others, the answer is 415,026,137.4
Solution to Exercise 2.4.18 (p. 122)
This division results in 68.02985075, a decimal number, and therefore, we cannot, at this time, nd the value of the remainder. Later, we will discuss decimal numbers.
Solution to Exercise 2.4.19 (p. 122)
13
Solution to Exercise 2.4.21 (p. 122)
67
Solution to Exercise 2.4.23 (p. 122)
52
Solution to Exercise 2.4.25 (p. 122)
3Solution to Exercise 2.4.27 (p. 123)
70
Solution to Exercise 2.4.29 (p. 123)
61
Solution to Exercise 2.4.31 (p. 123)
59
Solution to Exercise 2.4.33 (p. 123)
67
Solution to Exercise 2.4.35 (p. 123)
87
Solution to Exercise 2.4.37 (p. 123)
54
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 2.4.39 (p. 123)
52
Solution to Exercise 2.4.41 (p. 123)
38
Solution to Exercise 2.4.43 (p. 123)
45
Solution to Exercise 2.4.45 (p. 123)
777
Solution to Exercise 2.4.47 (p. 123)
342
Solution to Exercise 2.4.49 (p. 124)
644
Solution to Exercise 2.4.51 (p. 124)
533
Solution to Exercise 2.4.53 (p. 124)
10,440
Solution to Exercise 2.4.55 (p. 124)
8,147 remainder 847
Solution to Exercise 2.4.57 (p. 124)
4 remainder 2
Solution to Exercise 2.4.59 (p. 124)
66 remainder 1
Solution to Exercise 2.4.61 (p. 124)
823 remainder 2
Solution to Exercise 2.4.63 (p. 124)
40 remainder 28
Solution to Exercise 2.4.65 (p. 124)
665 remainder 15
Solution to Exercise 2.4.67 (p. 124)
957 remainder 34
Solution to Exercise 2.4.69 (p. 124)
665 remainder 4
Solution to Exercise 2.4.71 (p. 124)
458 remainder 13
Solution to Exercise 2.4.73 (p. 125)
996 remainder 23
Solution to Exercise 2.4.75 (p. 125)
42
Solution to Exercise 2.4.77 (p. 125)
8,216
Solution to Exercise 2.4.79 (p. 125)
$1,975 per month
Solution to Exercise 2.4.81 (p. 125)
$485 each person invested
Solution to Exercise 2.4.83 (p. 125)
14 cubes per hour
Solution to Exercise 2.4.85 (p. 125)
8 bits in each byte
Solution to Exercise 2.4.87 (p. 125)
38
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 2. MULTIPLICATION AND DIVISION OF WHOLE NUMBERS
Solution to Exercise 2.4.89 (p. 126)
600,000
Solution to Exercise 2.4.91 (p. 126)
625,600
Solution to Exercise 2.5.1 (p. 127)
2Solution to Exercise 2.5.2 (p. 127)
3Solution to Exercise 2.5.3 (p. 127)
3Solution to Exercise 2.5.4 (p. 127)
5Solution to Exercise 2.5.5 (p. 127)
2, 4
Solution to Exercise 2.5.6 (p. 127)
2, 5
Solution to Exercise 2.5.7 (p. 127)
2, 3
Solution to Exercise 2.5.8 (p. 128)
6, 9, 10
Solution to Exercise 2.5.9 (p. 128)
6Solution to Exercise 2.5.10 (p. 128)
6, 9, 10
Solution to Exercise 2.5.11 (p. 128)
6, 9
Solution to Exercise 2.5.12 (p. 128)
2, 3, 4, 6, 8
Solution to Exercise 2.5.14 (p. 128)
2, 3, 5, 6, 10
Solution to Exercise 2.5.16 (p. 128)
2Solution to Exercise 2.5.18 (p. 128)
2, 4
Solution to Exercise 2.5.20 (p. 129)
3Solution to Exercise 2.5.22 (p. 129)
none
Solution to Exercise 2.5.24 (p. 129)
5Solution to Exercise 2.5.26 (p. 129)
5Solution to Exercise 2.5.28 (p. 129)
2, 3, 4, 6
Solution to Exercise 2.5.30 (p. 129)
2, 3, 5, 6, 10
Solution to Exercise 2.5.32 (p. 129)
none
Solution to Exercise 2.5.34 (p. 129)
2, 4
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 2.5.36 (p. 129)
2Solution to Exercise 2.5.38 (p. 129)
none
Solution to Exercise 2.5.40 (p. 129)
none
Solution to Exercise 2.5.42 (p. 130)
1Solution to Exercise 2.5.44 (p. 130)
(35 + 16) + 7 = 51 + 7 = 58
35 + (16 + 7) = 35 + 23 = 58
Solution to Exercise 2.5.46 (p. 130)
87
Solution to Exercise 2.6.1 (p. 131)
15 · 6 = 90 and 6 · 15 = 90
Solution to Exercise 2.6.2 (p. 131)
432 · 428 = 184, 896 and 428 · 432 = 184, 896
Solution to Exercise 2.6.3 (p. 131)
168
Solution to Exercise 2.6.4 (p. 132)
165,564
Solution to Exercise 2.6.5 (p. 132)
843
Solution to Exercise 2.6.6 (p. 132)
234
Solution to Exercise 2.6.8 (p. 133)
4,032
Solution to Exercise 2.6.10 (p. 133)
326,000
Solution to Exercise 2.6.12 (p. 133)
252
Solution to Exercise 2.6.14 (p. 133)
21,340
Solution to Exercise 2.6.16 (p. 134)
8,316
Solution to Exercise 2.6.18 (p. 134)
32 · 2 = 64 = 4 · 16
Solution to Exercise 2.6.20 (p. 134)
23 · 1, 166 = 26, 818 = 253 · 106
Solution to Exercise 2.6.22 (p. 134)
associative
Solution to Exercise 2.6.24 (p. 134)
7 · 9 = 63 = 9 · 7
Solution to Exercise 2.6.26 (p. 134)
6Solution to Exercise 2.6.28 (p. 134)
4 + 15 = 19
15 + 4 = 19
Solution to Exercise 2.6.30 (p. 135)
2, 3, 4, 6
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 2. MULTIPLICATION AND DIVISION OF WHOLE NUMBERS
Solution to Exercise 2.8.1 (p. 137)
factors; product
Solution to Exercise 2.8.3 (p. 137)
divisor; quotient
Solution to Exercise 2.8.5 (p. 137)
an even digit (0, 2, 4, 6, or 8)
Solution to Exercise 2.8.7 (p. 137)
divisible by 4
Solution to Exercise 2.8.9 (p. 137)
112
Solution to Exercise 2.8.11 (p. 137)
7Solution to Exercise 2.8.13 (p. 138)
3,045
Solution to Exercise 2.8.15 (p. 138)
4Solution to Exercise 2.8.17 (p. 138)
15,075
Solution to Exercise 2.8.19 (p. 138)
14
Solution to Exercise 2.8.21 (p. 138)
42,112
Solution to Exercise 2.8.23 (p. 138)
63
Solution to Exercise 2.8.25 (p. 138)
1,046,960
Solution to Exercise 2.8.27 (p. 138)
101,010,000
Solution to Exercise 2.8.29 (p. 139)
0Solution to Exercise 2.8.31 (p. 139)
428
Solution to Exercise 2.8.33 (p. 139)
5 remainder 9
Solution to Exercise 2.8.35 (p. 139)
not dened
Solution to Exercise 2.8.37 (p. 139)
32 remainder 3
Solution to Exercise 2.8.39 (p. 139)
3,072,202
Solution to Exercise 2.8.41 (p. 139)
0Solution to Exercise 2.8.43 (p. 139)
0Solution to Exercise 2.8.45 (p. 139)
not dened
Solution to Exercise 2.8.47 (p. 139)
1Solution to Exercise 2.8.49 (p. 140)
226 · 114
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 2.8.51 (p. 140)
(16 · 14) · 0
Solution to Exercise 2.8.53 (p. 140)
4,278,000
Solution to Exercise 2.8.55 (p. 140)
$33
Solution to Exercise 2.9.1 (p. 140)
8 and 7 are factors; 56 is the product
Solution to Exercise 2.9.2 (p. 140)
Addition
Solution to Exercise 2.9.3 (p. 140)
3 is the divisor; 4 is the quotient
Solution to Exercise 2.9.4 (p. 140)
0, 2, 4, 6, or 8
Solution to Exercise 2.9.5 (p. 140)
commutative
Solution to Exercise 2.9.6 (p. 140)
1Solution to Exercise 2.9.7 (p. 140)
84
Solution to Exercise 2.9.8 (p. 141)
0Solution to Exercise 2.9.9 (p. 141)
352,000
Solution to Exercise 2.9.10 (p. 141)
419,020
Solution to Exercise 2.9.11 (p. 141)
252
Solution to Exercise 2.9.12 (p. 141)
not dened
Solution to Exercise 2.9.13 (p. 141)
0Solution to Exercise 2.9.14 (p. 141)
17
Solution to Exercise 2.9.15 (p. 141)
18
Solution to Exercise 2.9.16 (p. 141)
142 remainder 32
Solution to Exercise 2.9.17 (p. 141)
211
Solution to Exercise 2.9.18 (p. 141)
216; 1,005
Solution to Exercise 2.9.19 (p. 141)
216; 640
Solution to Exercise 2.9.20 (p. 141)
1,005; 640
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 2. MULTIPLICATION AND DIVISION OF WHOLE NUMBERS
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exponents, Roots, and Factorization of
Whole Numbers
3.1 Objectives1
After completing this chapter, you should
Exponents and Roots (Section 3.2)
• understand and be able to read exponential notation
• understand the concept of root and be able to read root notation
• be able to use a calculator having the yx key to determine a root
Grouping Symbols and the Order of Operations (Section 3.3)
• understand the use of grouping symbols
• understand and be able to use the order of operations
• use the calculator to determine the value of a numerical expression
Prime Factorization of Natural Numbers (Section 3.4)
• be able to determine the factors of a whole number
• be able to distinguish between prime and composite numbers
• be familiar with the fundamental principle of arithmetic
• be able to nd the prime factorization of a whole number
The Greatest Common Factor (Section 3.5)
• be able to nd the greatest common factor of two or more whole numbers The Least Common Multiple (Section 3.6)
• be able to nd the least common multiple of two or more whole numbers
1This content is available online at <http://cnx.org/content/m18890/1.4/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4> 153
CHAPTER 3. EXPONENTS, ROOTS, AND FACTORIZATION OF WHOLE
NUMBERS
3.2 Exponents and Roots 2
3.2.1 Section Overview
• Exponential Notation
• Reading Exponential Notation
• Roots
• Reading Root Notation
• Calculators
3.2.2 Exponential Notation
Exponential Notation
We have noted that multiplication is a description of repeated addition. Exponential notation is a description of repeated multiplication.
Suppose we have the repeated multiplication
8 · 8 · 8 · 8 · 8
Exponent
The factor 8 is repeated 5 times. Exponential notation uses a superscript for the number of times the factor is repeated. The superscript is placed on the repeated factor, 85, in this case. The superscript is called an exponent.
The Function of an Exponent
An exponent records the number of identical factors that are repeated in a multiplication.
3.2.2.1 Sample Set A
Write the following multiplication using exponents.
Example 3.1
3 · 3. Since the factor 3 appears 2 times, we record this as
32
Example 3.2
62 · 62 · 62 · 62 · 62 · 62 · 62 · 62 · 62. Since the factor 62 appears 9 times, we record this as 629
Expand (write without exponents) each number.
Example 3.3
124. The exponent 4 is recording 4 factors of 12 in a multiplication. Thus, 124 = 12 · 12 · 12 · 12
Example 3.4
7063. The exponent 3 is recording 3 factors of 706 in a multiplication. Thus, 7063 = 706 · 706 · 706
2This content is available online at <http://cnx.org/content/m34871/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
3.2.2.2 Practice Set A
Write the following using exponents.
Exercise 3.2.1
(Solution on p. 200.)
37 · 37
Exercise 3.2.2
(Solution on p. 200.)
16 · 16 · 16 · 16 · 16
Exercise 3.2.3
(Solution on p. 200.)
9 · 9 · 9 · 9 · 9 · 9 · 9 · 9 · 9 · 9
Write each number without exponents.
Exercise 3.2.4
(Solution on p. 200.)
853
Exercise 3.2.5
(Solution on p. 200.)
47
Exercise 3.2.6
(Solution on p. 200.)
1, 7392
3.2.3 Reading Exponential Notation
In a number such as 85,
Base
8 is called the base.
Exponent, Power
5 is called the exponent, or power. 85 is read as “eight to the fth power,” or more simply as “eight to the fth,” or “the fth power of eight.”
Squared
When a whole number is raised to the second power, it is said to be squared. The number 52 can be read as
5 to the second power, or
5 to the second, or
5 squared.
Cubed
When a whole number is raised to the third power, it is said to be cubed. The number 53 can be read as 5 to the third power, or
5 to the third, or
5 cubed.
When a whole number is raised to the power of 4 or higher, we simply say that that number is raised to that particular power. The number 58 can be read as
5 to the eighth power, or just
5 to the eighth.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 3. EXPONENTS, ROOTS, AND FACTORIZATION OF WHOLE
NUMBERS
3.2.4 Roots
In the English language, the word “root” can mean a source of something. In mathematical terms, the word
“root” is used to indicate that one number is the source of another number through repeated multiplication.
Square Root
We know that 49 = 72, that is, 49 = 7 · 7. Through repeated multiplication, 7 is the source of 49. Thus, 7 is a root of 49. Since two 7’s must be multiplied together to produce 49, the 7 is called the second or square root of 49.
Cube Root
We know that 8 = 23, that is, 8 = 2 · 2 · 2. Through repeated multiplication, 2 is the source of 8. Thus, 2 is a root of 8. Since three 2’s must be multiplied together to produce 8, 2 is called the third or cube root of 8.
We can continue this way to see such roots as fourth roots, fth roots, sixth roots, and so on.
3.2.5 Reading Root Notation
There is a symbol used to indicate roots of a number. It is called the radical sign √
n
The Radical Sign √
n
The symbol √
n
is called a radical sign and indicates the nth root of a number.
We discuss particular roots using the radical sign as follows:
Square Root
√
2 number indicates the square root of the number under the radical sign. It is customary to drop the 2 in the radical sign when discussing square roots. The symbol√
is understood to be the square root radical
sign.
√49 = 7 since 7 · 7 = 72 = 49
Cube Root
√
3 number indicates the cube root of the number under the radical sign.
√
3 8 = 2 since 2 · 2 · 2 = 23 = 8
Fourth Root
√
4 number indicates the fourth root of the number under the radical sign.
√
4 81 = 3 since 3 · 3 · 3 · 3 = 34 = 81
√
In an expression such as 5 32
Radical Sign
√
is called the radical sign.
Index
5 is called the index. (The index describes the indicated root.)
Radicand
32 is called the radicand.
Radical
√
5 32 is called a radical (or radical expression).
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
3.2.5.1 Sample Set B
Find each root.
Example 3.5
√25 To determine the square root of 25, we ask, “What whole number squared equals 25?” From our experience with multiplication, we know this number to be 5. Thus,
√25 = 5
Check: 5 · 5 = 52 = 25
Example 3.6
√
5 32 To determine the fth root of 32, we ask, “What whole number raised to the fth power equals 32?” This number is 2.
√
5 32 = 2
Check: 2 · 2 · 2 · 2 · 2 = 25 = 32
3.2.5.2 Practice Set B
Find the following roots using only a knowledge of multiplication.
Exercise 3.2.7
(Solution on p. 200.)
√64
Exercise 3.2.8
(Solution on p. 200.)
√100
Exercise 3.2.9
(Solution on p. 200.)
√
3 64
Exercise 3.2.10
(Solution on p. 200.)
√
6 64
3.2.6 Calculators√
Calculators with the x, yx, and 1/x keys can be used to nd or approximate roots.
3.2.6.1 Sample Set C
Example 3.7
√
Use the calculator to nd 121
Display Reads
Type 121 121
√
Press
x
11
Table 3.1
Example 3.8
√
Find 7 2187.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 3. EXPONENTS, ROOTS, AND FACTORIZATION OF WHOLE
NUMBERS
Display Reads
Type 2187 2187
Press yx
2187
Type 7
7
Press 1/x
.14285714
Press =
3
Table 3.2
√
7 2187 = 3 (Which means that 37 = 2187 .)
3.2.6.2 Practice Set C
Use a calculator to nd the following roots.
Exercise 3.2.11
(Solution on p. 200.)
√
3 729
Exercise 3.2.12
(Solution on p. 200.)
√
4 8503056
Exercise 3.2.13
(Solution on p. 200.)
√53361
Exercise 3.2.14
(Solution on p. 200.)
√
12 16777216
3.2.7 Exercises
For the following problems, write the expressions using exponential notation.
Exercise 3.2.15
(Solution on p. 200.)
4 · 4
Exercise 3.2.16
12 · 12
Exercise 3.2.17
(Solution on p. 200.)
9 · 9 · 9 · 9
Exercise 3.2.18
10 · 10 · 10 · 10 · 10 · 10
Exercise 3.2.19
(Solution on p. 200.)
826 · 826 · 826
Exercise 3.2.20
3, 021 · 3, 021 · 3, 021 · 3, 021 · 3, 021
Exercise 3.2.21
(Solution on p. 200.)
6 · 6 · · · · · 6
|
{z
}
85 factors of 6
Exercise 3.2.22
2 · 2 · · · · · 2
|
{z
}
112 factors of 2
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 3.2.23
(Solution on p. 200.)
1 · 1 · · · · · 1
|
{z
}
3,008 factors of 1
For the following problems, expand the terms. (Do not nd the actual value.) Exercise 3.2.24
53
Exercise 3.2.25
(Solution on p. 200.)
74
Exercise 3.2.26
152
Exercise 3.2.27
(Solution on p. 200.)
1175
Exercise 3.2.28
616
Exercise 3.2.29
(Solution on p. 200.)
302
For the following problems, determine the value of each of the powers. Use a calculator to check each result.
Exercise 3.2.30