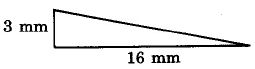134 Fundamentals of Mathematics: Part 16
Volume
Exercise 9.8.54
Exact area
Exercise 9.8.55
(Solution on p. 575.)
Approximate area
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
564
CHAPTER 9. MEASUREMENT AND GEOMETRY
Exercise 9.8.56
Exact area
Exercise 9.8.57
(Solution on p. 575.)
Approximate area
Exercise 9.8.58
Approximate area
9.9 Prociency Exam9
9.9.1 Prociency Exam
Exercise 9.9.1
(Solution on p. 575.)
(Section 9.2) The process of determining, by comparison to some standard, the size of something is called
.
9This content is available online at <http://cnx.org/content/m35026/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
565
For problems 2-9, make each conversion.
Exercise 9.9.2
(Solution on p. 575.)
(Section 9.2) 14 yards to feet
Exercise 9.9.3
(Solution on p. 575.)
(Section 9.2) 51 feet to inches
Exercise 9.9.4
(Solution on p. 575.)
(Section 9.2) 1 yard to feet
3
Exercise 9.9.5
(Solution on p. 575.)
(Section 9.2) 21 minutes to seconds
4
Exercise 9.9.6
(Solution on p. 575.)
(Section 9.3) 8,500 mg to cg
Exercise 9.9.7
(Solution on p. 575.)
(Section 9.3) 5.8623 L to kL
Exercise 9.9.8
(Solution on p. 575.)
(Section 9.3) 213.1062 mm to m
Exercise 9.9.9
(Solution on p. 575.)
(Section 9.3) 100,001 kL to mL
For problems 10-13, simplify each number.
Exercise 9.9.10
(Solution on p. 575.)
(Section 9.4) 23 da
Exercise 9.9.11
(Solution on p. 575.)
(Section 9.4) 88 ft
Exercise 9.9.12
(Solution on p. 575.)
(Section 9.4) 4216 lb
Exercise 9.9.13
(Solution on p. 575.)
(Section 9.4) 7 qt
For problems 14-18, perform the indicated operations. Simplify answers if possible.
Exercise 9.9.14
(Solution on p. 575.)
(Section 9.4) Add 6 wk 3 da to 2 wk 2 da.
Exercise 9.9.15
(Solution on p. 575.)
(Section 9.4) Add 9 gal 3 qt to 4 gal 3 qt.
Exercise 9.9.16
(Solution on p. 575.)
(Section 9.4) Subtract 3 yd 2 ft 5 in. from 5 yd 8 ft 2 in.
Exercise 9.9.17
(Solution on p. 575.)
(Section 9.4) Subtract 2 hr 50 min 12 sec from 3 hr 20 min 8 sec.
Exercise 9.9.18
(Solution on p. 575.)
(Section 9.4) Subtract the sum of 3 wk 6 da and 2 wk 3 da from 10 wk.
For problems 19-30, nd either the perimeter, circumference, area, or volume.
Exercise 9.9.19
(Solution on p. 575.)
(Section 9.5) Perimeter
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

566
CHAPTER 9. MEASUREMENT AND GEOMETRY
Exercise 9.9.20
(Solution on p. 575.)
(Section 9.5) Perimeter
Exercise 9.9.21
(Solution on p. 575.)
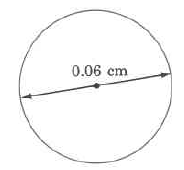
(Section 9.5) Approximate circumference
Exercise 9.9.22
(Solution on p. 576.)
(Section 9.5) Approximate perimeter
Exercise 9.9.23
(Solution on p. 576.)
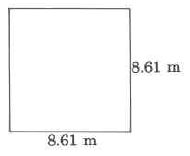
(Section 9.6) Area
Exercise 9.9.24
(Solution on p. 576.)
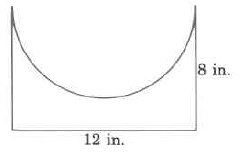
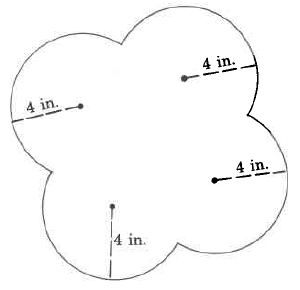
(Section 9.6) Approximate area
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
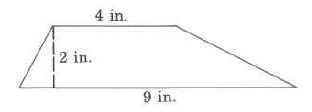
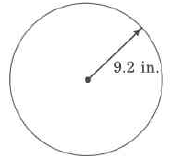


567
Exercise 9.9.25
(Solution on p. 576.)
(Section 9.6) Approximate area
Exercise 9.9.26
(Solution on p. 576.)
(Section 9.6) Area
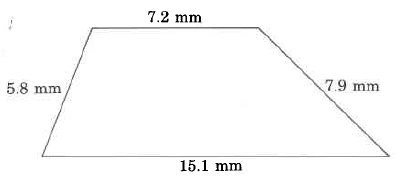
Exercise 9.9.27
(Solution on p. 576.)
(Section 9.6) Exact area
Exercise 9.9.28
(Solution on p. 576.)
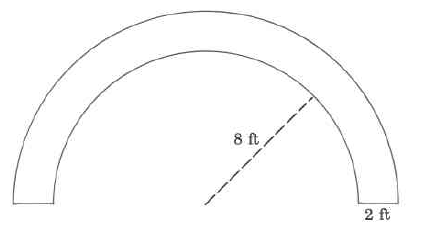
(Section 9.6) Approximate volume
Exercise 9.9.29
(Solution on p. 576.)
(Section 9.6) Exact volume
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
568
CHAPTER 9. MEASUREMENT AND GEOMETRY
Exercise 9.9.30
(Solution on p. 576.)
(Section 9.6) Approximate volume
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solutions to Exercises in Chapter 9
Solution to Exercise 9.2.1 (p. 516)
6 yd
Solution to Exercise 9.2.2 (p. 517)
10,560 ft
Solution to Exercise 9.2.3 (p. 517)
8.67 yd
Solution to Exercise 9.2.4 (p. 517)
18 pt
Solution to Exercise 9.2.5 (p. 517)
0.87 hr
Solution to Exercise 9.2.6 (p. 517)
2.45 wk
Solution to Exercise 9.2.7 (p. 517)
42 feet
Solution to Exercise 9.2.9 (p. 517)
506,880 inches
Solution to Exercise 9.2.11 (p. 517)
1.5 feet
Solution to Exercise 9.2.13 (p. 517)
0.14 yard
Solution to Exercise 9.2.15 (p. 517)
0.00 miles (to two decimal places)
Solution to Exercise 9.2.17 (p. 517)
6 pints
Solution to Exercise 9.2.19 (p. 517)
192,000 ounces
Solution to Exercise 9.2.21 (p. 517)
937.5 pounds
Solution to Exercise 9.2.23 (p. 518)
27 teaspoons
Solution to Exercise 9.2.25 (p. 518)
80 uid ounces
Solution to Exercise 9.2.27 (p. 518)
0.16 quart
Solution to Exercise 9.2.29 (p. 518)
480 teaspoons
Solution to Exercise 9.2.31 (p. 518)
1,080 seconds
Solution to Exercise 9.2.33 (p. 518)
1 = 0.125 day
8
Solution to Exercise 9.2.35 (p. 518)
1
14 = 0.0714 week
Solution to Exercise 9.2.37 (p. 518)
1,2,4,5,8
Solution to Exercise 9.2.39 (p. 518)
11
30
Solution to Exercise 9.2.41 (p. 518)
60 (50 − 4) = 3, 000 − 240 = 2, 760
Solution to Exercise 9.3.1 (p. 522)
411,000 g
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 9. MEASUREMENT AND GEOMETRY
Solution to Exercise 9.3.2 (p. 522)
562.6 cL
Solution to Exercise 9.3.3 (p. 522)
0.00008 kL
Solution to Exercise 9.3.4 (p. 522)
15 cg
Solution to Exercise 9.3.5 (p. 522)
0.025 m
Solution to Exercise 9.3.6 (p. 523)
8,700 cm
Solution to Exercise 9.3.8 (p. 523)
16.005 g
Solution to Exercise 9.3.10 (p. 523)
11,161 L
Solution to Exercise 9.3.12 (p. 523)
126 dg
Solution to Exercise 9.3.14 (p. 523)
5.1 daL
Solution to Exercise 9.3.16 (p. 523)
0.5 dm
Solution to Exercise 9.3.18 (p. 523)
81,060 cg
Solution to Exercise 9.3.20 (p. 523)
0.03 m
Solution to Exercise 9.3.22 (p. 523)
4,000 mg
Solution to Exercise 9.3.24 (p. 523)
6,000,000 mg
Solution to Exercise 9.3.26 (p. 524)
25
24 = 1 1
24
Solution to Exercise 9.3.28 (p. 524)
12,300 (12,344)
Solution to Exercise 9.3.30 (p. 524)
0.083 yard
Solution to Exercise 9.4.1 (p. 525)
1 ft 6 in.
Solution to Exercise 9.4.2 (p. 525)
10 gal 1 qt
Solution to Exercise 9.4.3 (p. 526)
6 hr 20 min
Solution to Exercise 9.4.4 (p. 526)
9 wk 4 da
Solution to Exercise 9.4.5 (p. 526)
12 wk 2 da
Solution to Exercise 9.4.6 (p. 527)
6 gal 1 qt
Solution to Exercise 9.4.7 (p. 527)
14 hr 14 min
Solution to Exercise 9.4.8 (p. 527)
6 ft 2in.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 9.4.9 (p. 527)
12 km 340 m
Solution to Exercise 9.4.10 (p. 527)
3 min 35 sec
Solution to Exercise 9.4.11 (p. 527)
14 yd 2 ft 3 in
Solution to Exercise 9.4.12 (p. 527)
13 min 13 sec
Solution to Exercise 9.4.13 (p. 529)
20 min
Solution to Exercise 9.4.14 (p. 529)
15 qt = 3 gal 3 qt
Solution to Exercise 9.4.15 (p. 529)
20 ft 32 in. = 7 yd 1 ft 8 in.
Solution to Exercise 9.4.16 (p. 529)
20 hr 150 min 400 sec = 22 hr 36 min 40 sec
Solution to Exercise 9.4.17 (p. 530)
2 hr 4 min
Solution to Exercise 9.4.18 (p. 530)
4 hr 16 min
Solution to Exercise 9.4.19 (p. 530)
2 yd 1 ft 11 in
Solution to Exercise 9.4.20 (p. 530)
15 gal 3 qt 1 pt
Solution to Exercise 9.4.21 (p. 530)
1 foot 4 inches
Solution to Exercise 9.4.23 (p. 530)
1 hour 25 minutes
Solution to Exercise 9.4.25 (p. 530)
2 weeks 3 days
Solution to Exercise 9.4.27 (p. 530)
15 pounds
Solution to Exercise 9.4.29 (p. 530)
6 gallons 2 quarts
Solution to Exercise 9.4.31 (p. 530)
8 pounds 7 ounces
Solution to Exercise 9.4.33 (p. 530)
2 gallons 1 quart
Solution to Exercise 9.4.35 (p. 530)
16 liters 300 milliliters (or 1daL 6 L 3dL)
Solution to Exercise 9.4.37 (p. 531)
15 days 11 hours
Solution to Exercise 9.4.39 (p. 531)
59 pounds 9 ounces
Solution to Exercise 9.4.41 (p. 531)
1 foot 10 inches
Solution to Exercise 9.4.43 (p. 531)
1 hour 18 minutes
Solution to Exercise 9.4.45 (p. 531)
5 days 16 hours 5 minutes
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 9. MEASUREMENT AND GEOMETRY
Solution to Exercise 9.4.47 (p. 531)
1 ton 1,100 pounds (or 1T 1,100 lb)
Solution to Exercise 9.4.49 (p. 531)
2 weeks 23 hours 29 minutes 53 seconds
Solution to Exercise 9.4.51 (p. 531)
1
Solution to Exercise 9.4.53 (p. 531)
2 14
275
Solution to Exercise 9.4.55 (p. 531)
126,000 g
Solution to Exercise 9.5.1 (p. 534)
20 ft
Solution to Exercise 9.5.2 (p. 534)
26.8 m
Solution to Exercise 9.5.3 (p. 534)
49.89 mi
Solution to Exercise 9.5.4 (p. 537)
9.1π in.
Solution to Exercise 9.5.5 (p. 537)
5.652 mm
Solution to Exercise 9.5.6 (p. 537)
126.228 m
Solution to Exercise 9.5.7 (p. 537)
41.634 mm
Solution to Exercise 9.5.8 (p. 538)
21.8 cm
Solution to Exercise 9.5.10 (p. 538)
38.14 inches
Solution to Exercise 9.5.12 (p. 538)
0.86 m
Solution to Exercise 9.5.14 (p. 539)
87.92 m
Solution to Exercise 9.5.16 (p. 539)
16.328 cm
Solution to Exercise 9.5.18 (p. 539)
0.0771 cm
Solution to Exercise 9.5.20 (p. 540)
120.78 m
Solution to Exercise 9.5.22 (p. 540)
21.71 inches
Solution to Exercise 9.5.24 (p. 541)
43.7 mm
Solution to Exercise 9.5.26 (p. 541)
45.68 cm
Solution to Exercise 9.5.28 (p. 542)
8.5 or 17 or 81
2
2
Solution to Exercise 9.5.30 (p. 542)
0.875
Solution to Exercise 9.5.32 (p. 542)
1 hour 36 minutes 6 seconds
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 9.6.1 (p. 546)
36 sq cm
Solution to Exercise 9.6.2 (p. 546)
37.503 sq mm
Solution to Exercise 9.6.3 (p. 546)
13.26 sq in.
Solution to Exercise 9.6.4 (p. 546)
367.5 sq mi
Solution to Exercise 9.6.5 (p. 546)
452.16 sq ft
Solution to Exercise 9.6.6 (p. 547)
44.28 sq cm
Solution to Exercise 9.6.7 (p. 551)
21 cu in.
Solution to Exercise 9.6.8 (p. 551)
904.32 cu ft
Solution to Exercise 9.6.9 (p. 551)
157 cu m
Solution to Exercise 9.6.10 (p. 551)
0.00942 cu in.
Solution to Exercise 9.6.11 (p. 551)
16 sq m
Solution to Exercise 9.6.13 (p. 552)
1.21 sq mm
Solution to Exercise 9.6.15 (p. 552)
18 sq in.
Solution to Exercise 9.6.17 (p. 552)
(60.5π + 132) sq ft
Solution to Exercise 9.6.19 (p. 553)
40.8 sq in.
Solution to Exercise 9.6.21 (p. 553)
31.0132 sq in.
Solution to Exercise 9.6.23 (p. 553)
158.2874 sq mm
Solution to Exercise 9.6.25 (p. 554)
64.2668 sq in.
Solution to Exercise 9.6.27 (p. 554)
43.96 sq ft
Solution to Exercise 9.6.29 (p. 554)
512 cu cm
Solution to Exercise 9.6.31 (p. 555)
11.49 cu cm
Solution to Exercise 9.6.33 (p. 555)
1024 π cu ft
3
Solution to Exercise 9.6.35 (p. 556)
22.08 cu in.
Solution to Exercise 9.6.37 (p. 556)
4
Solution to Exercise 9.6.39 (p. 556)
31
12 = 2 7
12 = 2.58
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 9. MEASUREMENT AND GEOMETRY
Solution to Exercise 9.6.41 (p. 556)
27.9m
Solution to Exercise 9.8.1 (p. 559)
Measurement is comparison to a standard (unit of measure).
Solution to Exercise 9.8.3 (p. 559)
2 pounds
Solution to Exercise 9.8.5 (p. 559)
6 tons
Solution to Exercise 9.8.7 (p. 559)
69 feet
Solution to Exercise 9.8.9 (p. 559)
2 = 0.666 feet
3
Solution to Exercise 9.8.11 (p. 559)
6 pints
Solution to Exercise 9.8.13 (p. 559)
80 tablespoons
Solution to Exercise 9.8.15 (p. 559)
210 seconds
Solution to Exercise 9.8.17 (p. 560)
1 = 0.25L
4
Solution to Exercise 9.8.19 (p. 560)
19,610 mg
Solution to Exercise 9.8.21 (p. 560)
540.06 g
Solution to Exercise 9.8.23 (p. 560)
3,500,000 mL
Solution to Exercise 9.8.25 (p. 560)
6 weeks 1 day
Solution to Exercise 9.8.27 (p. 560)
5 gallons 2 quarts 1 pint
Solution to Exercise 9.8.29 (p. 560)
7 T 1,850 pounds
Solution to Exercise 9.8.31 (p. 560)
7 days, 11 hours, 56 minutes, 7 seconds
Solution to Exercise 9.8.33 (p. 560)
1 yard 1 foot
Solution to Exercise 9.8.35 (p. 560)
1 ton 1,100 pounds
Solution to Exercise 9.8.37 (p. 561)
1 tablespoon 1 teaspoon
Solution to Exercise 9.8.39 (p. 561)
3 quarts 1 pint
Solution to Exercise 9.8.41 (p. 561)
2.3 meters
Solution to Exercise 9.8.43 (p. 561)
1.05 km
Solution to Exercise 9.8.45 (p. 561)
5.652 sq cm
Solution to Exercise 9.8.47 (p. 562)
104.28568 cu ft
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 9.8.49 (p. 562)
0.18π sq in.
Solution to Exercise 9.8.51 (p. 563)
267.94667 cu mm
Solution to Exercise 9.8.53 (p. 563)
32 cu cm
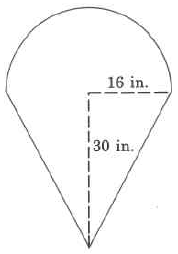
Solution to Exercise 9.8.55 (p. 563)
39.48 sq in.
Solution to Exercise 9.8.57 (p. 564)
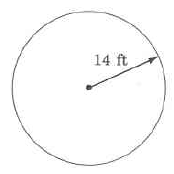
56.52 sq ft
Solution to Exercise 9.9.1 (p. 564)
measurement
Solution to Exercise 9.9.2 (p. 565)
42 feet
Solution to Exercise 9.9.3 (p. 565)
612 inches
Solution to Exercise 9.9.4 (p. 565)
1 foot
Solution to Exercise 9.9.5 (p. 565)
135 seconds
Solution to Exercise 9.9.6 (p. 565)
850 cg
Solution to Exercise 9.9.7 (p. 565)
0.0058623 kL
Solution to Exercise 9.9.8 (p. 565)
0.2132062 m
Solution to Exercise 9.9.9 (p. 565)
100,001,000,000 mL
Solution to Exercise 9.9.10 (p. 565)
3 weeks 2 days
Solution to Exercise 9.9.11 (p. 565)
29 yards 1 foot
Solution to Exercise 9.9.12 (p. 565)
2 tons 216 pounds
Solution to Exercise 9.9.13 (p. 565)
1 gallon 3 quarts
Solution to Exercise 9.9.14 (p. 565)
8 weeks 5 days
Solution to Exercise 9.9.15 (p. 565)
14 gallons 2 quarts
Solution to Exercise 9.9.16 (p. 565)
2 yards 5 feet 9 inches
Solution to Exercise 9.9.17 (p. 565)
29 minutes 56 seconds
Solution to Exercise 9.9.18 (p. 565)
3 weeks 5 days
Solution to Exercise 9.9.19 (p. 565)
34.44 m
Solution to Exercise 9.9.20 (p. 566)
36 mm
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 9. MEASUREMENT AND GEOMETRY
Solution to Exercise 9.9.21 (p. 566)
87.92 feet
Solution to Exercise 9.9.22 (p. 566)
55.14 miles
Solution to Exercise 9.9.23 (p. 566)
3.75 sq in.
Solution to Exercise 9.9.24 (p. 566)
6.002826 sq cm
Solution to Exercise 9.9.25 (p. 567)
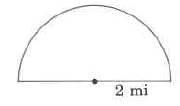
6.28 sq miles
Solution to Exercise 9.9.26 (p. 567)
13 sq in.
Solution to Exercise 9.9.27 (p. 567)
84.64π sq in.
Solution to Exercise 9.9.28 (p. 567)
25.12 cu mm
Solution to Exercise 9.9.29 (p. 567)
4.608π cu ft
Solution to Exercise 9.9.30 (p. 568)
340.48 cu mm
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Signed Numbers
10.1 Objectives1
After completing this chapter, you should
Variables, Constants, and Real Numbers (Section 10.2)
• be able to distinguish between variables and constants
• be able to recognize a real number and particular subsets of the real numbers
• understand the ordering of the real numbers
Signed Numbers (Section 10.3)
• be able to distinguish between positive and negative real numbers
• be able to read signed numbers
• understand the origin and use of the double-negative product property Absolute Value (Section 10.4)
• understand the geometric and algebraic denitions of absolute value
Addition of Signed Numbers (Section 10.5)
• be able to add numbers with like signs and with unlike signs
• be able to use the calculator for addition of signed numbers
Subtraction of Signed Numbers (Section 10.6)
• understand the denition of subtraction
• be able to subtract signed numbers
• be able to use a calculator to subtract signed numbers
Multiplication and Division of Signed Numbers (Section 10.7)
• be able to multiply and divide signed numbers
• be able to multiply and divide signed numbers using a calculator
1This content is available online at <http://cnx.org/content/m18898/1.3/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4> 577
CHAPTER 10. SIGNED NUMBERS
10.2 Variables, Constants, and Real Numbers 2
10.2.1 Section Overview
• Variables and Constants
• Real Numbers
• Subsets of Real Numbers
• Ordering Real Numbers
10.2.2 Variables and Constants
A basic distinction between algebra and arithmetic is the use of symbols (usually letters) in algebra to represent numbers. So, algebra is a generalization of arithmetic. Let us look at two examples of situations in which letters are substituted for numbers:
1. Suppose that a student is taking four college classes, and each class can have at most 1 exam per week.
In any 1-week period, the student may have 0, 1, 2, 3, or 4 exams. In algebra, we can let the letter x represent the number of exams this student may have in a 1-week period. The letter x may assume any of the various values 0, 1, 2, 3, 4.
2. Suppose that in writing a term paper for a biology class a student needs to specify the average lifetime, in days, of a male housey. If she does not know this number o the top of her head, she might represent it (at least temporarily) on her paper with the letter t (which reminds her of time). Later, she could look up the average time in a reference book and nd it to be 17 days. The letter t can assume only the one value, 17, and no other values. The value t is constant.
Variable, Constant
1. A letter or symbol that represents any member of a collection of two or more numbers is called a variable.
2. A letter or symbol that represents one specic number, known or unknown, is called a constant.
In example 1, the letter x is a variable since it can represent any of the numbers 0, 1, 2, 3, 4. The letter t example 2 is a constant since it can only have the value 17.
10.2.3 Real Numbers
Real Number Line
The study of mathematics requires the use of several collections of numbers. The real number line allows us to visually display (graph) the numbers in which we are interested.
A line is composed of innitely many points. To each point we can associate a unique number, and with each number, we can associate a particular point.
Coordinate
The number associated with a point on the number line is called the coordinate of the point.
Graph
The point on a number line that is associated with a particular number is called the graph of that number.
Constructing a Real Number Line
We construct a real number line as follows:
2This content is available online at <http://cnx.org/content/m35027/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>




579
1. Draw a horizontal line.
2. Origin
Choose any point on the line and label it 0. This point is called the origin.
3. Choose a convenient length. Starting at 0, mark this length o in both directions, being careful to have the lengths look like they are about the same.
We now dene a real number.
Real Number
A real number is any number that is the coordinate of a point on the real number line.
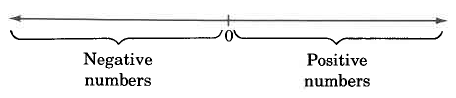
Positive Numbers, Negative Numbers
Real numbers whose graphs are to the right of 0 are called positive real numbers, or more simply, positive numbers. Real numbers whose graphs appear to the left of 0 are called negative real numbers, or more simply, negative numbers.
The number 0 is neither positive nor negative.
10.2.4 Subsets of Real Numbers
The set of real numbers has many subsets. Some of the subsets that are of interest in the study of algebra are listed below along with their notations and graphs.
Natural Numbers, Counting Numbers
The natural or counting numbers (N): 1, 2, 3, 4, . . . Read and so on.
Whole Numbers
The whole numbers (W ): 0, 1, 2, 3, 4, . . .
Notice that every natural number is a whole number.
Integers
The integers (Z): . . . -3, -2, -1, 0, 1, 2, 3, . . .
Notice that every whole number is an integer.
Rational Numbers (Fractions)
The rational numbers (Q): Rational numbers are sometimes called fractions. They are numbers that can be written as the quotient of two integers. They have decimal representations that either terminate or do not terminate but contain a repeating block of digits. Some examples are
−3
11
= −0.75
8
= 8.407407407…
4
27
|
{z
}
|
{z
}
Terminating
Nonterminating, but repeating
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
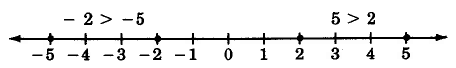
580
CHAPTER 10. SIGNED NUMBERS
Some rational numbers are graphed below.
Notice that every integer is a rational number.
Notice that there are still a great many points on the number line that have not yet been assigned a type of number. We will not examine these other types of numbers in this text. They are examined in detail in algebra. An example of these numbers is the number π, whose decimal representation does not terminate nor contain a repeating block of digits. An approximation for π is 3.14.
10.2.4.1 Sample Set A
Example 10.1
Is every whole number a natural number?
No. The number 0 is a whole number but it is not a natural number.
Example 10.2
Is there an integer that is not a natural number?
Yes. Some examples are 0, -1, -2, -3, and -4.
Example 10.3
Is there an integer that is a whole number?
Yes. In fact, every whole number is an integer.
10.2.4.2 Practice Set A
Exercise 10.2.1
(Solution on p. 620.)
Is every natural number a whole number?
Exercise 10.2.2
(Solution on p. 620.)
Is every whole number an integer?
Exercise 10.2.3
(Solution on p. 620.)
Is every integer a real number?
Exercise 10.2.4
(Solution on p. 620.)
Is there an integer that is a whole number?
Exercise 10.2.5
(Solution on p. 620.)
Is there an integer that is not a natural number?
10.2.5 Ordering Real Numbers
Ordering Real Numbers
A real number b is said to be greater than a real number a, denoted b > a, if b is to the right of a on the number line. Thus, as we would expect, 5 > 2 since 5 is to the right of 2 on the number line. Also, −2 > − 5
since -2 is to the right of -5 on the number line.
If we let a and b represent two numbers, then a and b are related in exactly one of three ways: Either Available for free at Connexions <http://cnx.org/content/col10615/1.4>


581
Equality Symbol
a = b
a and b are equal (8 = 8)
Inequality Symbols
a > b
a is greater than b
(8 > 5)
a < b
a is less than b
(5 < 8)
Some variations of these symbols are
{
a 6= b
a is not equal to b
(8 6= 5)
a ≥ b
a is greater than or equal to b
(a ≥ 8)
a ≤ b
a is less than or equal to b
(a ≤ 8)
10.2.5.1 Sample Set B
Example 10.4
What integers can replace x so that the following statement is true?
−3 ≤ x < 2
The integers are -3, -2, -1, 0, 1.
Example 10.5
Draw a number line that extends from -3 to 5. Place points at all whole numbers between and including -1 and 3.
-1 is not a whole number
10.2.5.2 Practice Set B
Exercise 10.2.6
(Solution on p. 620.)
What integers can replace x so that the following statement is true? −5 ≤ x < 2
Exercise 10.2.7
(Solution on p. 620.)
Draw a number line that extends from -4 to 3. Place points at all natural numbers between, but not including, -2 to 2.
10.2.6 Exercises
For the following 8problems, next to each real number, note all collections to which it belongs by writing N
for natural number, W for whole number, or Z for integer. Some numbers may belong to more than one collection.
Exercise 10.2.8
(Solution on p. 620.)
6
Exercise 10.2.9
12
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 10. SIGNED NUMBERS
Exercise 10.2.10
(Solution on p. 620.)
0
Exercise 10.2.11
1
Exercise 10.2.12
(Solution on p. 620.)
-3
Exercise 10.2.13
-7
Exercise 10.2.14
(Solution on p. 620.)
-805
Exercise 10.2.15
-900
Exercise 10.2.16
(Solution on p. 620.)
Is the number 0 a positive number, a negative number, neither, or both?
Exercise 10.2.17
An integer is an even integer if it is evenly divisible by 2. Draw a number line that extends from
-5 to 5 and place points at all negative even integers and all positive odd integers.
Exercise 10.2.18
(Solution on p. 620.)
Draw a number line that extends from -5 to 5. Place points at all integers that satisfy −3 ≤ x < 4.
Exercise 10.2.19
Is there a largest two digit number? If so, what is it?
Exercise 10.2.20
(Solution on p. 620.)
Is there a smallest two digit number? If so, what is it?
For the pairs of real numbers in the following 5 problems, write the appropriate symbol (<, >, =) in place of the .
Exercise 10.2.21
-7 -2
Exercise 10.2.22
(Solution on p. 620.)
-5 0
Exercise 10.2.23
-1 4
Exercise 10.2.24
(Solution on p. 620.)
6 -1
Exercise 10.2.25
10 10
For the following 5 problems, what numbers can replace m so that the following statements are true?
Exercise 10.2.26
(Solution on p. 620.)
−1 ≤ m ≤ −5, m an integer.
Exercise 10.2.27
−7 < m < − 1, m an integer.
Exercise 10.2.28
(Solution on p. 620.)
−3 ≤ m < 2, m a natural number.
Exercise 10.2.29
−15 < m ≤ −1, m a natural number.
Exercise 10.2.30
(Solution on p. 620.)
−5 ≤ m < 5, m a whole number.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
583
For the following 10 problems, on the number line, how many units are there between the given pair of numbers?
Exercise 10.2.31
0 and 3
Exercise 10.2.32
(Solution on p. 620.)
-4 and 0
Exercise 10.2.33
-1 and 6
Exercise 10.2.34
(Solution on p. 620.)
-6 and 2
Exercise 10.2.35
-3 and 3
Exercise 10.2.36
(Solution on p. 620.)
Are all positive numbers greater than zero?
Exercise 10.2.37
Are all positive numbers greater than all negative numbers?
Exercise 10.2.38
(Solution on p. 620.)
Is 0 greater than all negative number?
Exercise 10.2.39
Is there a largest natural number?
Exercise 10.2.40
(Solution on p. 620.)
Is there a largest negative integer?
10.2.6.1 Exercises for Review
Exercise 10.2.41
(Section 4.3) Convert 65 to an improper fraction.
8
Exercise 10.2.42
(Solution on p. 621.)
(Section 4.5) Find the value: 311 of 33.
5
Exercise 10.2.43
(Section 5.3) Find the sum of 4 + 3.
5
8
Exercise 10.2.44
(Solution on p. 621.)
(Section 9.3) Convert 30.06 cm to m.
Exercise 10.2.45
(Section 9.6) Find the area of the triangle.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 10. SIGNED NUMBERS
10.3 Signed Numbers 3
10.3.1 Section Overview
• Positive and Negative Numbers
• Reading Signed Numbers
• Opposites
• The Double-Negative Property
10.3.2 Positive and Negative Numbers
Positive and Negative Numbers
Each real number other than zero has a sign associated with it. A real number is said to be a positive number if it is to the right of 0 on the number line and negative if it is to the left of 0 on the number line.
note: + and − Notation
A number is denoted as positive if it is directly preceded by a plus sign or no sign at all.
A number is denoted as negative if it is directly preceded by a minus sign.
10.3.3 Reading Signed Numbers
The plus and minus signs now have two meanings:
The plus sign can denote the operation of addition or a positive number.
The minus sign can denote the operation of subtraction or a negative number.
To avoid any confusion between “sign” and “operation,” it is preferable to read the sign of a number as
“positive” or “negative.” When “+” is used as an operation sign, it is read as “plus.” When “−” is used as an operation sign, it is read as “minus.”
10.3.3.1 Sample Set A
Read each expression so as to avoid confusion between “operation” and “sign.”
Example 10.6
−8 should be read as “negative eight” rather than “minus eight.”
Example 10.7
4 + (−2) should be read as “four plus negative two” rather than “four plus minus two.”
Example 10.8
−6 + (−3)should be read as “negative six plus negative three” rather than “minus six plus minus three.”
Example 10.9
−15 − (−6)should be read as “negative fteen minus negative six” rather than “minus fteen minus minus six.”
Example 10.10
−5 + 7 should be read as “negative ve plus seven” rather than “minus ve plus seven.”
Example 10.11
0 − 2 should be read as “zero minus two.”
3This content is available online at <http://cnx.org/content/m35029/1.3/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
585
10.3.3.2 Practice Set A
Write each expression in words.
Exercise 10.3.1
(Solution on p. 621.)
6 + 1
Exercise 10.3.2
(Solution on p. 621.)
2 + (−8)
Exercise 10.3.3
(Solution on p. 621.)
−7 + 5
Exercise 10.3.4
(Solution on p. 621.)
−10 − (+3)
Exercise 10.3.5
(Solution on p. 621.)
−1 − (−8)
Exercise 10.3.6
(Solution on p. 621.)
0 + (−11)
10.3.4 Opposites
Opposites
On the number line, each real number, other than zero, has an image on the opposite side of 0. For this reason, we say that each real number has an opposite. Opposites are the same distance from zero but have opposite signs.
The opposite of a real number is denoted by placing a negative sign directly in front of the number. Thus, if a is any real number, then −a is its opposite.
note: The letter “a” is a variable. Thus, “a” need not be positive, and “−a” need not be negative.
If a is any real number, −a is opposite a on the number line.
10.3.5 The Double-Negative Property
The number a is opposite −a on the number line. Therefore, − (−a) is opposite −a on the number line.
This means that
− (−a) = a
From this property of opposites, we can suggest the double-negative property for real numbers.
Double-Negative Property: − (−a) = a
If a is a real number, then
− (−a) = a
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

586
CHAPTER 10. SIGNED NUMBERS
10.3.5.1 Sample Set B
Find the opposite of each number.
Example 10.12
If a = 2, then −a = −2. Also, − (−a) = − (−2) = 2.
Example 10.13
If a = −4, then −a = − (−4) = 4. Also, − (−a) = a = − 4.
10.3.5.2 Practice Set B
Find the opposite of each number.
Exercise 10.3.7
(Solution on p. 621.)
8
Exercise 10.3.8
(Solution on p. 621.)
17
Exercise 10.3.9
(Solution on p. 621.)
-6
Exercise 10.3.10
(Solution on p. 621.)
-15
Exercise 10.3.11
(Solution on p. 621.)
-(-1)
Exercise 10.3.12
(Solution on p. 621.)
− [− (−7)]
Exercise 10.3.13
(Solution on p. 621.)
Suppose a is a positive number. Is −a positive or negative?
Exercise 10.3.14
(Solution on p. 621.)
Suppose a is a negative number. Is −a positive or negative?
Exercise 10.3.15
(Solution on p. 621.)
Suppose we do not know the sign of the number k. Is −k positive, negative, or do we not know?
10.3.6 Exercises
Exercise 10.3.16
(Solution on p. 621.)
A number is denoted as positive if it is directly preceded by
.
Exercise 10.3.17
A number is denoted as negative if it is directly preceded by
.
How should the number in the following 6 problems be read? (Write in words.) Exercise 10.3.18
(Solution on p. 621.)
−7
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 10.3.19
−5
Exercise 10.3.20
(Solution on p. 621.)
15
Exercise 10.3.21
11
Exercise 10.3.22
(Solution on p. 621.)
− (−1)
Exercise 10.3.23
− (−5)
For the following 6 problems, write each expression in words.
Exercise 10.3.24
(Solution on p. 621.)
5 + 3
Exercise 10.3.25
3 + 8
Exercise 10.3.26
(Solution on p. 621.)
15 + (−3)
Exercise 10.3.27
1 + (−9)
Exercise 10.3.28
(Solution on p. 621.)
−7 − (−2)
Exercise 10.3.29
0 − (−12)
For the following 6 problems, rewrite each number in simpler form.
Exercise 10.3.30
(Solution on p. 621.)
− (−2)
Exercise 10.3.31
− (−16)
Exercise 10.3.32
(Solution on p. 622.)
− [− (−8)]
Exercise 10.3.33
− [− (−20)]
Exercise 10.3.34
(Solution on p. 622.)
7 − (−3)
Exercise 10.3.35
6 − (−4)
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

588
CHAPTER 10. SIGNED NUMBERS
10.3.6.1 Exercises for Review
Exercise 10.3.36
(Solution on p. 622.)
(Section 6.7) Find the quotient; 8 ÷ 27.
Exercise 10.3.37
(Section 7.3) Solve the proportion: 5 = 60
9
x
Exercise 10.3.38
(Solution on p. 622.)
(Section 8.2) Use the method of rounding to estimate the sum: 5829 + 8767
Exercise 10.3.39
(Section 9.2) Use a unit fraction to convert 4 yd to feet.
Exercise 10.3.40
(Solution on p. 622.)
(Section 9.3) Convert 25 cm to hm.
10.4 Absolute Value4
10.4.1 Section Overview
• Geometric Denition of Absolute Value
• Algebraic Denition of Absolute Value
10.4.2 Geometric Denition of Absolute Value
Absolute Value-Geometric Approach
Geometric denition of absolute value:
The absolute value of a number a, denoted | a |, is the distance from a to 0 on the number line.
Absolute value answers the question of “how far,” and not “which way.” The phrase “how far” implies
“length” and length is always a nonnegative quantity. Thus, the absolute value of a number is a nonnegative number.
10.4.2.1 Sample Set A
Determine each value.
Example 10.14
| 4 |= 4
Example 10.15
| −4 |= 4
Example 10.16
| 0 |= 0
4This content is available online at <http://cnx.org/content/m35030/1.3/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Example 10.17
− | 5 |= −5. The quantity on the left side of the equal sign is read as “negative the absolute value of 5.” The absolute value of 5 is 5. Hence, negative the absolute value of 5 is -5.
Example 10.18
− | −3 |= −3. The quantity on the left side of the equal sign is read as “negative the absolute value of -3.” The absolute value of -3 is 3. Hence, negative the absolute value of -3 is − (3) = −3.
10.4.2.2 Practice Set A
By reasoning geometrically, determine each absolute value.
Exercise 10.4.1
(Solution on p. 622.)
| 7 |
Exercise 10.4.2
(Solution on p. 622.)
| −3 |
Exercise 10.4.3
(Solution on p. 622.)
| 12 |
Exercise 10.4.4
(Solution on p. 622.)
| 0 |
Exercise 10.4.5
(Solution on p. 622.)
− | 9 |
Exercise 10.4.6
(Solution on p. 622.)
− | −6 |
10.4.3 Algebraic Denition of Absolute Value
From the problems in Section 10.4.2.1 (Sample Set A), we can suggest the following algebraic denition of absolute value. Note that the denition has two parts.
Absolute ValueAlgebraic Approach
Algebraic denition of absolute value
The absolute value of a number a is
a,
if a ≥ 0
|a| = { −a, if < 0
The algebraic denition takes into account the fact that the number a could be either positive or zero (a ≥ 0) or negative (a < 0).
1. If the number a is positive or zero (a ≥ 0), the upper part of the denition applies. The upper part of the denition tells us that if the number enclosed in the absolute value bars is a nonnegative number, the absolute value of the number is the number itself.
2. The lower part of the denition tells us that if the number enclosed within the absolute value bars is a negative number, the absolute value of the number is the opposite of the number. The opposite of a negative number is a positive number.
note: The denition says that the vertical absolute value lines may be eliminated only if we know whether the number inside is positive or negative.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 10. SIGNED NUMBERS
10.4.3.1 Sample Set B
Use the algebraic denition of absolute value to nd the following values.
Example 10.19
| 8 |. The number enclosed within the absolute value bars is a nonnegative number, so the upper part of the denition applies. This part says that the absolute value of 8 is 8 itself.
| 8 |= 8
Example 10.20
| −3 |. The number enclosed within absolute value bars is a negative number, so the lower part of the denition applies. This part says that the absolute value of -3 is the opposite of -3, which is
− (−3). By the denition of absolute value and the double-negative property,
| −3 |= − (−3) = 3
10.4.3.2 Practice Set B
Use the algebraic denition of absolute value to nd the following values.
Exercise 10.4.7
(Solution on p. 622.)
| 7 |
Exercise 10.4.8
(Solution on p. 622.)
| 9 |
Exercise 10.4.9
(Solution on p. 622.)
| −12 |
Exercise 10.4.10
(Solution on p. 622.)
| −5 |
Exercise 10.4.11
(Solution on p. 622.)
− | 8 |
Exercise 10.4.12
(Solution on p. 622.)
− | 1 |
Exercise 10.4.13
(Solution on p. 622.)
− | −52 |
Exercise 10.4.14
(Solution on p. 622.)
− | −31 |
10.4.4 Exercises
Determine each of the values.
Exercise 10.4.15
(Solution on p. 622.)
| 5 |
Exercise 10.4.16
| 3 |
Exercise 10.4.17
(Solution on p. 622.)
| 6 |
Exercise 10.4.18
| −9 |
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 10.4.19
(Solution on p. 622.)
| −1 |
Exercise 10.4.20
| −4 |
Exercise 10.4.21
(Solution on p. 622.)
− | 3 |
Exercise 10.4.22
− | 7 |
Exercise 10.4.23
(Solution on p. 622.)
− | −14 |
Exercise 10.4.24
| 0 |
Exercise 10.4.25
(Solution on p. 622.)
| −26 |
Exercise 10.4.26
− | −26 |
Exercise 10.4.27
(Solution on p. 623.)
− (− | 4 |)
Exercise 10.4.28
− (− | 2 |)
Exercise 10.4.29
(Solution on p. 623.)
− (− | −6 |)
Exercise 10.4.30
− (− | −42 |)
Exercise 10.4.31
(Solution on p. 623.)
| 5 | − | −2 |
Exercise 10.4.32
| −2 |3
Exercise 10.4.33
(Solution on p. 623.)
| − (2 · 3) |
Exercise 10.4.34
| −2 | − | −9 |
Exercise 10.4.35
(Solution on p. 623.)
(| −6 | + | 4 |)2
Exercise 10.4.36
(| −1 | − | 1 |)3
Exercise 10.4.37
(Solution on p. 623.)
(| 4 | + | −6 |)2 − (| −2 |)3
Exercise 10.4.38
−[|−10| − 6]2
Exercise 10.4.39
(Solution on p. 623.)
2
−{−[− | −4 | + | −3 |]3}
Exercise 10.4.40
A Mission Control Ocer at Cape Canaveral makes the statement lift-o, T minus 50 seconds.
How long is it before lift-o?
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
592
CHAPTER 10. SIGNED NUMBERS
Exercise 10.4.41
(Solution on p. 623.)
Due to a slowdown in the industry, a Silicon Valley computer company nds itself in debt $2,400,000. Use absolute value notation to describe this company’s debt.
Exercise 10.4.42
A particular machine is set correctly if upon action its meter reads 0. One particular machine has a meter reading of −1.6 upon action. How far is this machine o its correct setting?
10.4.4.1 Exercises for Review
Exercise 10.4.43
(Solution on p. 623.)
(Section 5.3) Find the sum: 970 + 521 + 815.
Exercise 10.4.44
(Section 5.6) Find the value of 310+ 412
19
.
20
Exercise 10.4.45
(Solution on p. 623.)
(Section 6.3) Convert 3.23 to a fraction.
5
Exercise 10.4.46
(Section 7.3) The ratio of acid to water in a solution is 3. How many mL of acid are there in a 8
solution that contain 112 mL of water?
Exercise 10.4.47
(Solution on p. 623.)
(Section 10.3) Find the value of −6 − (−8).
10.5 Addition of Signed Numbers5
10.5.1 Section Overview
• Addition of Numbers with Like Signs
• Addition with Zero
• Addition of Numbers with Unlike Signs
• Calculators
10.5.2 Addition of Numbers with Like Signs
The addition of the two positive numbers 2 and 3 is performed on the number line as follows.
Begin at 0, the origin.
Since 2 is positive, move 2 units to the right.
Since 3 is positive, move 3 more units to the right.
We are now located at 5.
Thus, 2 + 3 = 5.
Summarizing, we have
5This content is available online at <http://cnx.org/content/m35031/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
593
(2 positive units) + (3 positive units) = (5 positive units)
The addition of the two negative numbers -2 and -3 is performed on the number line as follows.
Begin at 0, the origin.
Since -2 is negative, move 2 units to the left.
Since -3 is negative, move 3 more units to the left.
We are now located at -5.
Thus, (−2) + (−3) = −5.
Summarizing, we have
(2 negative units) + (3 negative units) = (5 negative units)
Observing these two examples, we can suggest these relationships:
(positive number) + (positive number) = (positive number)
(negative number) + (negative number) = (negative number)
Adding Numbers with the Same Sign
Addition of numbers with like sign:
To add two real numbers that have the same sign, add the absolute values of the numbers and associate with the sum the common sign.
10.5.2.1 Sample Set A
Find the sums.
Example 10.21
3 + 7
|3|
=
3 } Add these absolute values.
|7|
=
7
3 + 7 = 10
The common sign is +.
Thus, 3 + 7 = +10, or 3 + 7 = 10.
Example 10.22
(−4) + (−9)
| − 4|
=
4 } Add these absolute values.
| − 9|
=
9
4 + 9 = 13
The common sign is −.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
594
CHAPTER 10. SIGNED NUMBERS
Thus, (−4) + (−9) = −13.
10.5.2.2 Practice Set A
Find the sums.
Exercise 10.5.1
(Solution on p. 623.)
8 + 6
Exercise 10.5.2
(Solution on p. 623.)
41 + 11
Exercise 10.5.3
(Solution on p. 623.)
(−4) + (−8)
Exercise 10.5.4
(Solution on p. 623.)
(−36) + (−9)
Exercise 10.5.5
(Solution on p. 623.)
−14 + (−20)
Exercise 10.5.6
(Solution on p. 623.)
− 2 + − 5
3
3
Exercise 10.5.7
(Solution on p. 623.)
−2.8 + (−4.6)
Exercise 10.5.8
(Solution on p. 623.)
0 + (−16)
10.5.3 Addition With Zero
Addition with Zero
Notice that
(0) + (a positive number) = (that same positive number).
(0) + (a negative number) = (that same negative number).
The Additive Identity Is Zero
Since adding zero to a real number leaves that number unchanged, zero is called the additive identity.
10.5.4 Addition of Numbers with Unlike Signs
The addition 2 + (−6), two numbers with unlike signs, can also be illustrated using the number line.
Begin at 0, the origin.
Since 2 is positive, move 2 units to the right.
Since -6 is negative, move, from 2, 6 units to the left.
We are now located at -4.
We can suggest a rule for adding two numbers that have unlike signs by noting that if the signs are disregarded, 4 can be obtained by subtracting 2 from 6. But 2 and 6 are precisely the absolute values of 2 and Available for free at Connexions <http://cnx.org/content/col10615/1.4>
-6. Also, notice that the sign of the number with the larger absolute value is negative and that the sign of the resulting sum is negative.
Adding Numbers with Unlike Signs
Addition of numbers with unlike signs: To add two real numbers that have unlike signs, subtract the smaller absolute value from the larger absolute value and associate with this dierence the sign of the number with the larger absolute value.
10.5.4.1 Sample Set B
Find the following sums.
Example 10.23
7 + (−2)
|7| = 7
| − 2| = 2
|
{z
}
|
{z
}
Larger absolute
Smaller absolute
value. Sign is positive.
value.
Subtract absolute values: 7 − 2 = 5.
Attach the proper sign: “+.”
Thus, 7 + (−2) = +5 or 7 + (−2) = 5.
Example 10.24
3 + (−11)
|3| = 3
| − 11| = 11
|
{z
}
|
{z
}
Smaller absolute
Larger absolute
value.
value. Sign is negative.
Subtract absolute values: 11 − 3 = 8.
Attach the proper sign: “−.”
Thus, 3 + (−11) = −8.
Example 10.25
The morning temperature on a winter’s day in Lake Tahoe was -12 degrees. The afternoon temperature was 25 degrees warmer. What was the afternoon temperature?
We need to nd −12 + 25.
| − 12| = 12
|25| = 25
|
{z
}
|
{z
}
Smaller absolute
Larger absolute
value.
value. Sign is positive.
Subtract absolute values: 25 − 12 = 16.
Attach the proper sign: “+.”
Thus, −12 + 25 = 13.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
596
CHAPTER 10. SIGNED NUMBERS
10.5.4.2 Practice Set B
Find the sums.
Exercise 10.5.9
(Solution on p. 623.)
4 + (−3)
Exercise 10.5.10
(Solution on p. 623.)
−3 + 5
Exercise 10.5.11
(Solution on p. 623.)
15 + (−18)
Exercise 10.5.12
(Solution on p. 623.)
0 + (−6)
Exercise 10.5.13
(Solution on p. 623.)
−26 + 12
Exercise 10.5.14
(Solution on p. 623.)
35 + (−78)
Exercise 10.5.15
(Solution on p. 624.)
15 + (−10)
Exercise 10.5.16
(Solution on p. 624.)
1.5 + (−2)
Exercise 10.5.17
(Solution on p. 624.)
−8 + 0
Exercise 10.5.18
(Solution on p. 624.)
0 + (0.57)
Exercise 10.5.19
(Solution on p. 624.)
−879 + 454
10.5.5 Calculators
Calculators having the
key can be used for nding sums of signed numbers.
10.5.5.1 Sample Set C
Use a calculator to nd the sum of -147 and 84.
Display Reads
Type 147
147
Press
-147
This key changes the sign of a number. It is dierent than −.
Press +
-147
Type 84
84
Press =
-63
Table 10.1
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
10.5.5.2 Practice Set C
Use a calculator to nd each sum.
Exercise 10.5.20
(Solution on p. 624.)
673 + (−721)
Exercise 10.5.21
(Solution on p. 624.)
−8, 261 + 2,206
Exercise 10.5.22
(Solution on p. 624.)
−1, 345.6 + (−6, 648.1)
10.5.6 Exercises
Find the sums in the following 27 problems. If possible, use a calculator to check each result.
Exercise 10.5.23
(Solution on p. 624.)
4 + 12
Exercise 10.5.24
8 + 6
Exercise 10.5.25
(Solution on p. 624.)
(−3) + (−12)
Exercise 10.5.26
(−6) + (−20)
Exercise 10.5.27
(Solution on p. 624.)
10 + (−2)
Exercise 10.5.28
8 + (−15)
Exercise 10.5.29
(Solution on p. 624.)
−16 + (−9)
Exercise 10.5.30
−22 + (−1)
Exercise 10.5.31
(Solution on p. 624.)
0 + (−12)
Exercise 10.5.32
0 + (−4)
Exercise 10.5.33
(Solution on p. 624.)
0 + (24)
Exercise 10.5.34
−6 + 1 + (−7)
Exercise 10.5.35
(Solution on p. 624.)
−5 + (−12) + (−4)
Exercise 10.5.36
−5 + 5
Exercise 10.5.37
(Solution on p. 624.)
−7 + 7
Exercise 10.5.38
−14 + 14
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 10. SIGNED NUMBERS
Exercise 10.5.39
(Solution on p. 624.)
4 + (−4)
Exercise 10.5.40
9 + (−9)
Exercise 10.5.41
(Solution on p. 624.)
84 + (−61)
Exercise 10.5.42
13 + (−56)
Exercise 10.5.43
(Solution on p. 624.)
452 + (−124)
Exercise 10.5.44
636 + (−989)
Exercise 10.5.45
(Solution on p. 624.)
1, 811 + (−935)
Exercise 10.5.46
−373 + (−14)
Exercise 10.5.47
(Solution on p. 624.)
−1, 211 + (−44)
Exercise 10.5.48
−47.03 + (−22.71)
Exercise 10.5.49
(Solution on p. 624.)
−1.998 + (−4.086)
Exercise 10.5.50
In order for a small business to break even on a project, it must have sales of $21,000. If the amount of sales was $15,000, by how much money did this company fall short?
Exercise 10.5.51
(Solution on p. 624.)
Suppose a person has $56 in his checking account. He deposits $100 into his checking account by using the automatic teller machine. He then writes a check for $84.50. If an error causes the deposit not to be listed into this person’s account, what is this person’s checking balance?
Exercise 10.5.52
A person borrows $7 on Monday and then $12 on Tuesday. How much has this person borrowed?
Exercise 10.5.53
(Solution on p. 624.)
A person borrows $11 on Monday and then pays back $8 on Tuesday. How much does this person owe?
10.5.6.1 Exercises for Review
Exercise 10.5.54
(Section 4.6) Find the reciprocal of 85.
6
Exercise 10.5.55
(Solution on p. 624.)
(Section 5.3) Find the value of 512 + 718 − 1.
3
Exercise 10.5.56
(Section 6.4) Round 0.01628 to the nearest tenth.
Exercise 10.5.57
(Solution on p. 625.)
(Section 7.5) Convert 62% to a fraction.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
599
Exercise 10.5.58
(Section 10.4) Find the value of | −12 |.
10.6 Subtraction of Signed Numbers6
10.6.1 Section Overview
• Denition of Subtraction
• The Process of Subtraction
• Calculators
10.6.2 Denition of Subtraction
We know from experience with arithmetic that the subtraction 5 − 2 produces 3, that is 5 − 2 = 3. We can suggest a rule for subtracting signed numbers by illustrating this process on the number line.
Begin at 0, the origin.
Since 5 is positive, move 5 units to the right.
Then, move 2 units to the left to get to 6. (This reminds us of addition with a negative number.) From this illustration we can see that 5 − 2 is the same as 5 + (−2). This leads us directly to the denition of subtraction.
Denition of Subtraction
If a and b are real numbers, a − b is the same as a + (−b), where −b is the opposite of b.
10.6.3 The Process of Subtraction
From this denition, we suggest the following rule for subtracting signed numbers.
Subtraction of Signed Numbers
To perform the subtraction a − b, add the opposite of b to a, that is, change the sign of b and add.
10.6.3.1 Sample Set A
Perform the indicated subtractions.
Example 10.26
5 − 3 = 5 + (−3) = 2
Example 10.27
4 − 9 = 4 + (−9) = −5
Example 10.28
−4 − 6 = −4 + (−6) = −10
Example 10.29
−3 − (−12) = −3 + 12 = 9
6This content is available online at <http://cnx.org/content/m35032/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 10. SIGNED NUMBERS
Example 10.30
0 − (−15) = 0 + 15 = 15
Example 10.31
The high temperature today in Lake Tahoe was 26 ◦F. The low temperature tonight is expected to be -7 ◦F. How many degrees is the temperature expected to drop?
We need to nd the dierence between 26 and -7.
26 − (−7) = 26 + 7 = 33
Thus, the expected temperature drop is 33 ◦F.
Example 10.32
−6 − (−5) − 10
=
−6 + 5 + (−10)
=
(−6 + 5) + (−10)
=
−1 + (−10)
=
−11
10.6.3.2 Practice Set A
Perform the indicated subtractions.
Exercise 10.6.1
(Solution on p. 625.)
9 − 6
Exercise 10.6.2
(Solution on p. 625.)
6 − 9
Exercise 10.6.3
(Solution on p. 625.)
0 − 7
Exercise 10.6.4
(Solution on p. 625.)
1 − 14
Exercise 10.6.5
(Solution on p. 625.)
−8 − 12
Exercise 10.6.6
(Solution on p. 625.)
−21 − 6
Exercise 10.6.7
(Solution on p. 625.)
−6 − (−4)
Exercise 10.6.8
(Solution on p. 625.)
8 − (−10)
Exercise 10.6.9
(Solution on p. 625.)
1 − (−12)
Exercise 10.6.10
(Solution on p. 625.)
86 − (−32)
Exercise 10.6.11
(Solution on p. 625.)
0 − 16
Exercise 10.6.12
(Solution on p. 625.)
0 − (−16)
Exercise 10.6.13
(Solution on p. 625.)
0 − (8)
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
601
Exercise 10.6.14
(Solution on p. 625.)
5 − (−5)
Exercise 10.6.15
(Solution on p. 625.)
24 − [− (−24)]
10.6.4 Calculators
Calculators can be used for subtraction of signed numbers. The most ecient calculators are those with a key.
10.6.4.1 Sample Set B
Use a calculator to nd each dierence.
Example 10.33
3, 187 − 8, 719
Display Reads
Type 3187 3187
Press –
3187
Type 8719 8719
Press =
-5532
Table 10.2
Thus, 3, 187 − 8, 719 = −5, 532.
Example 10.34
−156 − (−211)
Method A:
Display Reads
Type 156
156
Press
-156
Type –
-156
Press 211
211
Type
-211
Press =
55
Table 10.3
Thus, −156 − (−211) = 55.
Method B:
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
602
CHAPTER 10. SIGNED NUMBERS
We manually change the subtraction to an addition and change the sign of the number to be subtracted.
−156 − (−211) becomes −156 + 211
Display Reads
Type 156
156
Press
-156
Press +
-156
Type 211
211
Press =
55
Table 10.4
10.6.4.2 Practice Set B
Use a calculator to nd each dierence.
Exercise 10.6.16
(Solution on p. 625.)
44 − 315
Exercise 10.6.17
(Solution on p. 625.)
12.756 − 15.003
Exercise 10.6.18
(Solution on p. 625.)
−31.89 − 44.17
Exercise 10.6.19
(Solution on p. 625.)
−0.797 − (−0.615)
10.6.5 Exercises
For the following 18 problems, perform each subtraction. Use a calculator to check each result.
Exercise 10.6.20
(Solution on p. 625.)
8 − 3
Exercise 10.6.21
12 − 7
Exercise 10.6.22
(Solution on p. 625.)
5 − 6
Exercise 10.6.23
14 − 30
Exercise 10.6.24
(Solution on p. 625.)
−6 − 8
Exercise 10.6.25
−1 − 12
Exercise 10.6.26
(Solution on p. 625.)
−5 − (−3)
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 10.6.27
−11 − (−8)
Exercise 10.6.28
(Solution on p. 625.)
0 − 6
Exercise 10.6.29
0 − 15
Exercise 10.6.30
(Solution on p. 626.)
0 − (−7)
Exercise 10.6.31
0 − (−10)
Exercise 10.6.32
(Solution on p. 626.)
67 − 38
Exercise 10.6.33
142 − 85
Exercise 10.6.34
(Solution on p. 626.)
816 − 1140
Exercise 10.6.35
105 − 421
Exercise 10.6.36
(Solution on p. 626.)
−550 − (−121)
Exercise 10.6.37
−15.016 − (4.001)
For the following 4 problems, perform the indicated operations.
Exercise 10.6.38
(Solution on p. 626.)
−26 + 7 − 52
Exercise 10.6.39
−15 − 21 − (−2)
Exercise 10.6.40
(Solution on p. 626.)
−104 − (−216) − (−52)
Exercise 10.6.41
−0.012 − (−0.111) − (0.035)
Exercise 10.6.42
(Solution on p. 626.)
When a particular machine is operating properly, its meter will read 34. If a broken bearing in the machine causes the meter reading to drop by 45 units, what is the meter reading?
Exercise 10.6.43
The low temperature today in Denver was −4 ◦F and the high was −42 ◦F. What is the temperature dierence?
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 10. SIGNED NUMBERS
10.6.5.1 Exercises for Review
Exercise 10.6.44
(Solution on p. 626.)
(Section 6.3) Convert 16.021 to a decimal.
5
Exercise 10.6.45
(Section 6.6) Find 4.01 of 6.2.
Exercise 10.6.46
(Solution on p. 626.)
(Section 7.5) Convert 516 to a percent.
Exercise 10.6.47
(Section 8.4) Use the distributive property to compute the product: 15 · 82.
Exercise 10.6.48
(Solution on p. 626.)
(Section 10.5) Find the sum: 16 + (−21).
10.7 Multiplication and Division of Signed Numbers7
10.7.1 Section Overview
• Multiplication of Signed Numbers
• Division of Signed Numbers
• Calculators
10.7.2 Multiplication of Signed Numbers
Let us consider rst, the product of two positive numbers. Multiply: 3 · 5.
3 · 5 means 5 + 5 + 5 = 15
This suggests8 that
(positive number) · (positive number) = (positive number)
More briey,
(+) (+) = (+)
Now consider the product of a positive number and a negative number. Multiply: (3) (−5).
(3) (−5) means (−5) + (−5) + (−5) = −15
This suggests that
(positive number) · (negative number) = (negative number)
More briey,
(+) (−) = (−)
By the commutative property of multiplication, we get
7This content is available online at <http://cnx.org/content/m35033/1.2/>.
8In later mathematics courses, the word “suggests” turns into the word “proof.” One example does not prove a claim.
Mathematical proofs are constructed to validate a claim for all possible cases.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
605
(negative number) · (positive number) = (negative number)
More briey,
(−) (+) = (−)
The sign of the product of two negative numbers can be suggested after observing the following illustration.
Multiply -2 by, respectively, 4, 3, 2, 1, 0, -1, -2, -3, -4.
We have the following rules for multiplying signed numbers.
Rules for Multiplying Signed Numbers
Multiplying signed numbers:
1. To multiply two real numbers that have the same sign, multiply their absolute values. The product is positive.
(+) (+) = (+)
(−) (−) = (+)
2. To multiply two real numbers that have opposite signs, multiply their absolute values. The product is negative.
(+) (−) = (−)
(−) (+) = (−)
10.7.2.1 Sample Set A
Find the following products.
Example 10.35
8 · 6
|8|
=
8 } Multiply these absolute values.
|6|
=
6
8 · 6 = 48
Since the numbers have the same sign, the product is positive.
Thus, 8 · 6=+48, or 8 · 6 = 48.
Example 10.36
(−8) (−6)
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 10. SIGNED NUMBERS
| − 8|
=
8 } Multiply these absolute values.
| − 6|
=
6
8 · 6 = 48
Since the numbers have the same sign, the product is positive.
Thus, (−8) (−6) =+48, or (−8) (−6) = 48.
Example 10.37
(−4) (7)
| − 4|
=
4 } Multiply these absolute values.
|7|
=
7
4 · 7 = 28
Since the numbers have opposite signs, the product is negative.
Thus, (−4) (7) = −28.
Example 10.38
6 (−3)
|6|
=
6 } Multiply these absolute values.
| − 3|
=
3
6 · 3 = 18
Since the numbers have opposite signs, the product is negative.
Thus, 6 (−3) = −18.
10.7.2.2 Practice Set A
Find the following products.
Exercise 10.7.1
(Solution on p. 626.)
3 (−8)
Exercise 10.7.2
(Solution on p. 626.)
4 (16)
Exercise 10.7.3
(Solution on p. 626.)
(−6) (−5)
Exercise 10.7.4
(Solution on p. 626.)
(−7) (−2)
Exercise 10.7.5
(Solution on p. 626.)
(−1) (4)
Exercise 10.7.6
(Solution on p. 626.)
(−7) 7
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
10.7.3 Division of Signed Numbers
To determine the signs in a division problem, recall that
12 = 4 since 12 = 3 · 4
3
This suggests that
(+) = (+)
(+)
(+) = (+) since (+) = (+) (+)
(+)
What is 12 ?
−3
−12 = (−3) (−4) suggests that 12 = −4. That is,
−3
(+) = (−)
(−)
(+) = (−) (−) suggests that (+) = (−)
(−)
What is −12?
3
−12 = (3) (−4) suggests that −12 = −4. That is,
3
(−) = (−)
(+)
(−) = (+) (−) suggests that (−) = (−)
(+)
What is −12?
−3
−12 = (−3) (4) suggests that −12 = 4. That is,
−3
(−) = (+)
(−)
(−) = (−) (+) suggests that (−) = (+)
(−)
We have the following rules for dividing signed numbers.
Rules for Dividing Signed Numbers
Dividing signed numbers:
1. To divide two real numbers that have the same sign, divide their absolute values. The quotient is positive.
(+) = (+) (−) = (+)
(+)
(−)
2. To divide two real numbers that have opposite signs, divide their absolute values. The quotient is negative.
(−) = (−) (+) = (−)
(+)
(−)
10.7.3.1 Sample Set B
Find the following quotients.
Example 10.39
−10
2
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 10. SIGNED NUMBERS
| − 10|
=
10 } Divide these absolute values.
|2|
=
2
10 = 5
2
Since the numbers have opposite signs, the quotient is negative.
Thus −10 = −5.
2
Example 10.40
−35
−7
| − 35|
=
35 } Divide these absolute values.
| − 7|
=
7
35 = 5
7
Since the numbers have the same signs, the quotient is positive.
Thus, −35 = 5.
−7
Example 10.41
18
−9
|18|
=
18 } Divide these absolute values.
| − 9|
=
9
18 = 2
9
Since the numbers have opposite signs, the quotient is negative.
Thus, 18 = 2.
−9
10.7.3.2 Practice Set B
Find the following quotients.
Exercise 10.7.7
(Solution on p. 626.)
−24
−6
Exercise 10.7.8
(Solution on p. 626.)
30
−5
Exercise 10.7.9
(Solution on p. 626.)
−54
27
Exercise 10.7.10
(Solution on p. 626.)
51
17
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
609
10.7.3.3 Sample Set C
Example 10.42
Find the value of −6(4−7)−2(8−9).
−(4+1)+1
Using the order of operations and what we know about signed numbers, we get,
−6(4−7)−2(8−9)
=
−6(−3)−2(−1)
−(4+1)+1
−(5)+1
=
18+2
−5+1
=
20
−
=
−5
10.7.3.4 Practice Set C
Exercise 10.7.11
(Solution on p. 626.)
Find the value of −5(2−6)−4(−8−1).
2(3−10)−9(−2)
10.7.4 Calculators
Calculators with the
key can be used for multiplying and dividing signed numbers.
10.7.4.1 Sample Set D
Use a calculator to nd each quotient or product.
Example 10.43
(−186) · (−43)
Since this product involves a (negative)·(negative), we know the result should be a positive number.
We’ll illustrate this on the calculator.
Display Reads
Type 186
186
Press
-186
Press ×
-186
Type 43
43
Press
-43
Press =
7998
Table 10.5
Thus, (−186) · (−43) = 7, 998.
Example 10.44
158.64 . Round to one decimal place.
−54.3
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
610
CHAPTER 10. SIGNED NUMBERS
Display Reads
Type 158.64 158.64
Press ÷
158.64
Type 54.3
54.3
Press
-54.3
Press =
-2.921546961
Table 10.6
Rounding to one decimal place we get -2.9.
10.7.4.2 Practice Set D
Use a calculator to nd each value.
Exercise 10.7.12
(Solution on p. 626.)
(−51.3) · (−21.6)
Exercise 10.7.13
(Solution on p. 626.)
−2.5746 ÷ −2.1
Exercise 10.7.14
(Solution on p. 626.)
(0.006) · (−0.241). Round to three decimal places.
10.7.5 Exercises
Find the value of each of the following. Use a calculator to check each result.
Exercise 10.7.15
(Solution on p. 626.)
(−2) (−8)
Exercise 10.7.16
(−3) (−9)
Exercise 10.7.17
(Solution on p. 627.)
(−4) (−8)
Exercise 10.7.18
(−5) (−2)
Exercise 10.7.19
(Solution on p. 627.)
(3) (−12)
Exercise 10.7.20
(4) (−18)
Exercise 10.7.21
(Solution on p. 627.)
(10) (−6)
Exercise 10.7.22
(−6) (4)
Exercise 10.7.23
(Solution on p. 627.)
(−2) (6)
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 10.7.24
(−8) (7)
Exercise 10.7.25
(Solution on p. 627.)
21
7
Exercise 10.7.26
42
6
Exercise 10.7.27
(Solution on p. 627.)
−39
3
Exercise 10.7.28
−20
10
Exercise 10.7.29
(Solution on p. 627.)
−45
−5
Exercise 10.7.30
−16
−8
Exercise 10.7.31
(Solution on p. 627.)
25
−5
Exercise 10.7.32
36
−4
Exercise 10.7.33
(Solution on p. 627.)
8 − (−3)
Exercise 10.7.34
14 − (−20)
Exercise 10.7.35
(Solution on p. 627.)
20 − (−8)
Exercise 10.7.36
−4 − (−1)
Exercise 10.7.37
(Solution on p. 627.)
0 − 4
Exercise 10.7.38
0 − (−1)
Exercise 10.7.39
(Solution on p. 627.)
−6 + 1 − 7
Exercise 10.7.40
15 − 12 − 20
Exercise 10.7.41
(Solution on p. 627.)
1 − 6 − 7 + 8
Exercise 10.7.42
2 + 7 − 10 + 2
Exercise 10.7.43
(Solution on p. 627.)
3 (4 − 6)
Exercise 10.7.44
8 (5 − 12)
Exercise 10.7.45
(Solution on p. 627.)
−3 (1 − 6)
Exercise 10.7.46
−8 (4 − 12) + 2
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 10. SIGNED NUMBERS
Exercise 10.7.47
(Solution on p. 627.)
−4 (1 − 8) + 3 (10 − 3)
Exercise 10.7.48
−9 (0 − 2) + 4 (8 − 9) + 0 (−3)
Exercise 10.7.49
(Solution on p. 627.)
6 (−2 − 9) − 6 (2 + 9) + 4 (−1 − 1)
Exercise 10.7.50
3(4+1)−2(5)
−2
Exercise 10.7.51
(Solution on p. 627.)
4(8+1)−3(−2)
−4−2
Exercise 10.7.52
−1(3+2)+5
−1
Exercise 10.7.53
(Solution on p. 627.)
−3(4−2)+(−3)(−6)
−4
Exercise 10.7.54
−1 (4 + 2)
Exercise 10.7.55
(Solution on p. 627.)
−1 (6 − 1)
Exercise 10.7.56
− (8 + 21)
Exercise 10.7.57
(Solution on p. 627.)
− (8 − 21)
10.7.5.1 Exercises for Review
Exercise 10.7.58
(Section 3.3) Use the order of operations to simplify 52 + 32 + 2 ÷ 22.
Exercise 10.7.59
(Solution on p. 627.)
(Section 4.7) Find 3 of 32.
8
9
Exercise 10.7.60
(Section 6.2) Write this number in decimal form using digits: fty-two three-thousandths Exercise 10.7.61
(Solution on p. 627.)
(Section 7.4) The ratio of chlorine to water in a solution is 2 to 7. How many mL of water are in a solution that contains 15 mL of chlorine?
Exercise 10.7.62
(Section 10.6) Perform the subtraction −8 − (−20)
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
613
10.8 Summary of Key Concepts9
10.8.1 Summary of Key Concepts
Variables and Constants (Section 10.2)
A variable is a letter or symbol that represents any member of a set of two or more numbers. A constant is a letter or symbol that represents a specic number. For example, the Greek letter π (pi) represents the constant 3.14159 . . . .
The Real Number Line (Section 10.2)
The real number line allows us to visually display some of the numbers in which we are interested.
Coordinate and Graph (Section 10.2)
The number associated with a point on the number line is called the coordinate of the point. The point associated with a number is called the graph of the number.
Real Number (Section 10.2)
A real number is any number that is the coordinate of a point on the real number line.
Types of Real Numbers (Section 10.2)
The set of real numbers has many subsets. The ones of most interest to us are: The natural numbers: {1, 2, 3, 4, . . .}
The whole numbers: {0, 1, 2, 3, 4, . . .}
The integers: {. . . ,-3,-2,-1,0, 1, 2, 3, . . .}
The rational numbers: {All numbers that can be expressed as the quotient of two integers.}
Positive and Negative Numbers (Section 10.3)
A number is denoted as positive if it is directly preceded by a plus sign (+) or no sign at all. A number is denoted as negative if it is directly preceded by a minus sign ().
Opposites (Section 10.3)
Opposites are numbers that are the same distance from zero on the number line but have opposite signs.
The numbers a and −a are opposites.
Double-Negative Property (Section 10.3)
− (−a) = a
Absolute Value (Geometric) (Section 10.4)
The absolute value of a number a, denoted | a |, is the distance from a to 0 on the number line.
Absolute Value (Algebraic) (Section 10.4)
a,
if a ≥ 0
|a| = { −a, if a < 0
Addition of Signed Numbers (Section 10.5)
To add two numbers with
1. like signs, add the absolute values of the numbers and associate with the sum the common sign.
2. unlike signs, subtract the smaller absolute value from the larger absolute value and associate with the dierence the sign of the larger absolute value.
9This content is available online at <http://cnx.org/content/m35034/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 10. SIGNED NUMBERS
Addition with Zero (Section 10.5)
0 + (any number) = that particular number.
Additive Identity (Section 10.5)
Since adding 0 to any real number leaves that number unchanged, 0 is called the additive identity.
Denition of Subtraction (Section 10.6)
a − b = a + (−b)
Subtraction of Signed Numbers (Section 10.6)
To perform the subtraction a − b, add the opposite of b to a, that is, change the sign of b and follow the addition rules (Section 10.5).
Multiplication and Division of Signed Numbers (Section 10.7)
(+) (+) = (+) (+) = (+) (+) = (−)
(+)
(−)
(−) (−) = (+)
(+) (−) = (−) (−) = (+) (−) = (−)
(−)
(+)
(−) (+) = (−)
10.9 Exercise Supplement 10
10.9.1 Exercise Supplement
10.9.1.1 Variables, Constants, and Real Numbers (Section 10.2)
For problems 1-5, next to each real number, note all subsets of the real numbers to which it belongs by writing N for natural numbers, W for whole numbers, or Z for integers. Some numbers may belong to more than one subset.
Exercise 10.9.1
(Solution on p. 627.)
61
Exercise 10.9.2
−14
Exercise 10.9.3
(Solution on p. 627.)
0
Exercise 10.9.4
1
Exercise 10.9.5
(Solution on p. 628.)
Write all the integers that are strictly between −4 and 3
Exercise 10.9.6
Write all the integers that are between and including −6 and −1
For each pair of numbers in problems 7-10, write the appropriate symbol (<, >, =) in place of the .
Exercise 10.9.7
(Solution on p. 628.)
-5 -1
Exercise 10.9.8
0 2
Exercise 10.9.9
(Solution on p. 628.)
-7 0
10This content is available online at <http://cnx.org/content/m35035/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 10.9.10
-1 0
For problems 11-15, what numbers can replace x so that each statement is true?
Exercise 10.9.11
(Solution on p. 628.)
−5 ≤ x ≤ −1, x is an integer
Exercise 10.9.12
−10 < x ≤ 0, x is a whole number.
Exercise 10.9.13
(Solution on p. 628.)
0 ≤ x < 5, x is a natural number.
Exercise 10.9.14
−3 < x < 3, x is a natural number
Exercise 10.9.15
(Solution on p. 628.)
−8 < x ≤ −2, x is a whole number.
For problems 16-20, how many units are there between the given pair of numbers?
Exercise 10.9.16
0 and 4
Exercise 10.9.17
(Solution on p. 628.)
−1 and 3
Exercise 10.9.18
−7 and −4
Exercise 10.9.19
(Solution on p. 628.)
−6 and 0
Exercise 10.9.20
−1 and 1
Exercise 10.9.21
(Solution on p. 628.)
A number is positive if it is directly preceded by a
sign or no sign at all.
Exercise 10.9.22
A number is negative if it is directly preceded by a
sign.
10.9.1.2 Signed Numbers (Section 10.3)
For problems 23-26, how should each number be read?
Exercise 10.9.23
(Solution on p. 628.)
−8
Exercise 10.9.24
− (−4)
Exercise 10.9.25
(Solution on p. 628.)
− (−1)
Exercise 10.9.26
−2
For problems 27-31, write each expression in words.
Exercise 10.9.27
(Solution on p. 628.)
1 + (−7)
Exercise 10.9.28
−2 − (−6)
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 10. SIGNED NUMBERS
Exercise 10.9.29
(Solution on p. 628.)
−1 − (+4)
Exercise 10.9.30
− (− (−3))
Exercise 10.9.31
(Solution on p. 628.)
0 − (−11)
For problems 32-36, rewrite each expression in simpler form.
Exercise 10.9.32
− (−4)
Exercise 10.9.33
(Solution on p. 628.)
− (−15)
Exercise 10.9.34
− [− (−7)]
Exercise 10.9.35
(Solution on p. 628.)
1 − (−18)
Exercise 10.9.36
0 − (−1)
10.9.1.3 Absolute Value (Section 10.4)
For problems 37-52, determine each value.
Exercise 10.9.37
(Solution on p. 628.)
| 9 |
Exercise 10.9.38
| 16 |
Exercise 10.9.39
(Solution on p. 628.)
| −5 |
Exercise 10.9.40
| −8 |
Exercise 10.9.41
(Solution on p. 628.)
− | −2 |
Exercise 10.9.42
− | −1 |
Exercise 10.9.43
(Solution on p. 628.)
− (− | 12 |)
Exercise 10.9.44
− (− | 90 |)
Exercise 10.9.45
(Solution on p. 628.)
− (− | −16 |)
Exercise 10.9.46
− (− | 0 |)
Exercise 10.9.47
(Solution on p. 628.)
| −4 |2
Exercise 10.9.48
| −5 |2
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 10.9.49
(Solution on p. 628.)
| −2 |3
Exercise 10.9.50
| − (3 · 4) |
Exercise 10.9.51
(Solution on p. 628.)
| −5 | + | −2 |
Exercise 10.9.52
| −7 | − | −10 |
10.9.1.4 Addition, Subtraction, Multiplication and Division of Signed Numbers (Section 10.5,Section 10.6,Section 10.7)
For problems 53-71, perform each operation.
Exercise 10.9.53
(Solution on p. 628.)
−6 + 4
Exercise 10.9.54
−10 + 8
Exercise 10.9.55
(Solution on p. 629.)
−1 − 6
Exercise 10.9.56
8 − 12
Exercise 10.9.57
(Solution on p. 629.)
0 − 14
Exercise 10.9.58
5 · (−2)
Exercise 10.9.59
(Solution on p. 629.)
−8 · (−6)
Exercise 10.9.60
(−3) · (−9)
Exercise 10.9.61
(Solution on p. 629.)
14 · (−3)
Exercise 10.9.62
5 · (−70)
Exercise 10.9.63
(Solution on p. 629.)
−18 ÷ −6
Exercise 10.9.64
72 ÷ −12
Exercise 10.9.65
(Solution on p. 629.)
−16 ÷ −16
Exercise 10.9.66
0÷ − 8
Exercise 10.9.67
(Solution on p. 629.)
−5 ÷ 0
Exercise 10.9.68
−15
−3
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 10. SIGNED NUMBERS
Exercise 10.9.69
(Solution on p. 629.)
−28
7
Exercise 10.9.70
−120
−|2|
Exercise 10.9.71
(Solution on p. 629.)
|−66|
−|−3|
10.10 Prociency Exam11
10.10.1 Prociency Exam
Exercise 10.10.1
(Solution on p. 629.)
(Section 10.2) Write all integers that are strictly between 8 and 3.
Exercise 10.10.2
(Solution on p. 629.)
(Section 10.2) Write all integers that are between and including 2 and 1.
For problems 3-5, write the appropriate symbol (<, >, =) in place of the for each pair of numbers.
Exercise 10.10.3
(Solution on p. 629.)
(Section 10.2) 1 1
Exercise 10.10.4
(Solution on p. 629.)
(Section 10.2) 0 3
Exercise 10.10.5
(Solution on p. 629.)
(Section 10.2) 1 2
For problems 6 and 7, what numbers can replace x so that the statement is true?
Exercise 10.10.6
(Solution on p. 629.)
(Section 10.2) −3 ≤ x < 0, x is an integer.
Exercise 10.10.7
(Solution on p. 629.)
(Section 10.2) −4 ≤ x ≤ 0, x is a natural number.
Exercise 10.10.8
(Solution on p. 629.)
(Section 10.2) How many units are there between 3 and 2?
For problems 9-20, nd each value.
Exercise 10.10.9
(Solution on p. 629.)
(Section 10.4) | −16 |
Exercise 10.10.10
(Solution on p. 629.)
(Section 10.4) − | −2 |
Exercise 10.10.11
(Solution on p. 629.)
(Section 10.4)
− −| −4 |2
Exercise 10.10.12
(Solution on p. 629.)
(Section 10.4) | −5 | + | −10 |
Exercise 10.10.13
(Solution on p. 629.)
(Section 10.5) −8 + 6
Exercise 10.10.14
(Solution on p. 629.)
(Section 10.5) −3 + (−8)
11This content is available online at <http://cnx.org/content/m35036/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 10.10.15
(Solution on p. 629.)
(Section 10.6) 0 − 16
Exercise 10.10.16
(Solution on p. 629.)
(Section 10.7) (−14) · (−3)
Exercise 10.10.17
(Solution on p. 630.)
(Section 10.7) (−5 − 6)2
Exercise 10.10.18
(Solution on p. 630.)
(Section 10.7) (−51) ÷ (−7)
Exercise 10.10.19
(Solution on p. 630.)
(Section 10.7) −42
−7
Exercise 10.10.20
(Solution on p. 630.)
(Section 10.7) | −32 − −15−5 |
8
5
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
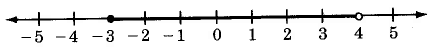
620
CHAPTER 10. SIGNED NUMBERS
Solutions to Exercises in Chapter 10
Solution to Exercise 10.2.1 (p. 580)
yes
Solution to Exercise 10.2.2 (p. 580)
yes
Solution to Exercise 10.2.3 (p. 580)
yes
Solution to Exercise 10.2.4 (p. 580)
yes
Solution to Exercise 10.2.5 (p. 580)
yes
Solution to Exercise 10.2.6 (p. 581)
-5, -4, -3, -2, -1, 0
Solution to Exercise 10.2.7 (p. 581)
Solution to Exercise 10.2.8 (p. 581)
N, W, Z
Solution to Exercise 10.2.10 (p. 582)
W, Z
Solution to Exercise 10.2.12 (p. 582)
ZSolution to Exercise 10.2.14 (p. 582)
ZSolution to Exercise 10.2.16 (p. 582)
Neither
Solution to Exercise 10.2.18 (p. 582)
Solution to Exercise 10.2.20 (p. 582)
Yes, 10
Solution to Exercise 10.2.22 (p. 582)
<
Solution to Exercise 10.2.24 (p. 582)
>
Solution to Exercise 10.2.26 (p. 582)
{-1, 0, 1, 2, 3, 4, 5}
Solution to Exercise 10.2.28 (p. 582)
{1}
Solution to Exercise 10.2.30 (p. 582)
{0, 1, 2, 3, 4}
Solution to Exercise 10.2.32 (p. 583)
4Solution to Exercise 10.2.34 (p. 583)
8
Solution to Exercise 10.2.36 (p. 583)
yes
Solution to Exercise 10.2.38 (p. 583)
yes
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 10.2.40 (p. 583)
yes, -1
Solution to Exercise 10.2.42 (p. 583)
9 or 14 or 1.8
5
5
Solution to Exercise 10.2.44 (p. 583)
0.3006 m
Solution to Exercise 10.3.1 (p. 585)
six plus one
Solution to Exercise 10.3.2 (p. 585)
two plus negative eight
Solution to Exercise 10.3.3 (p. 585)
negative seven plus ve
Solution to Exercise 10.3.4 (p. 585)
negative ten minus three
Solution to Exercise 10.3.5 (p. 585)
negative one minus negative eight
Solution to Exercise 10.3.6 (p. 585)
zero plus negative eleven
Solution to Exercise 10.3.7 (p. 586)
-8
Solution to Exercise 10.3.8 (p. 586)
-17
Solution to Exercise 10.3.9 (p. 586)
6
Solution to Exercise 10.3.10 (p. 586)
15
Solution to Exercise 10.3.11 (p. 586)
-1
Solution to Exercise 10.3.12 (p. 586)
7
Solution to Exercise 10.3.13 (p. 586)
−a is negative
Solution to Exercise 10.3.14 (p. 586)
−a is positive
Solution to Exercise 10.3.15 (p. 586)
We must say that we do not know.
Solution to Exercise 10.3.16 (p. 586)
+ (or no sign)
Solution to Exercise 10.3.18 (p. 586)
negative seven
Solution to Exercise 10.3.20 (p. 587)
fteen
Solution to Exercise 10.3.22 (p. 587)
negative negative one, or opposite negative one
Solution to Exercise 10.3.24 (p. 587)
ve plus three
Solution to Exercise 10.3.26 (p. 587)
fteen plus negative three
Solution to Exercise 10.3.28 (p. 587)
negative seven minus negative two
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 10. SIGNED NUMBERS
Solution to Exercise 10.3.30 (p. 587)
2
Solution to Exercise 10.3.32 (p. 587)
-8
Solution to Exercise 10.3.34 (p. 587)
7 + 3 = 10
Solution to Exercise 10.3.36 (p. 588)
0.296
Solution to Exercise 10.3.38 (p. 588)
6, 000 + 9, 000 = 15, 000 (5, 829 + 8, 767 = 14, 596) or 5,800 + 8, 800 = 14, 600
Solution to Exercise 10.3.40 (p. 588)
0.0025 hm
Solution to Exercise 10.4.1 (p. 589)
7Solution to Exercise 10.4.2 (p. 589)
3Solution to Exercise 10.4.3 (p. 589)
12
Solution to Exercise 10.4.4 (p. 589)
0Solution to Exercise 10.4.5 (p. 589)
-9
Solution to Exercise 10.4.6 (p. 589)
-6
Solution to Exercise 10.4.7 (p. 590)
7Solution to Exercise 10.4.8 (p. 590)
9Solution to Exercise 10.4.9 (p. 590)
12
Solution to Exercise 10.4.10 (p. 590)
5Solution to Exercise 10.4.11 (p. 590)
-8
Solution to Exercise 10.4.12 (p. 590)
-1
Solution to Exercise 10.4.13 (p. 590)
-52
Solution to Exercise 10.4.14 (p. 590)
-31
Solution to Exercise 10.4.15 (p. 590)
5Solution to Exercise 10.4.17 (p. 590)
6
Solution to Exercise 10.4.19 (p. 591)
1Solution to Exercise 10.4.21 (p. 591)
-3
Solution to Exercise 10.4.23 (p. 591)
-14
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 10.4.25 (p. 591)
26
Solution to Exercise 10.4.27 (p. 591)
4Solution to Exercise 10.4.29 (p. 591)
6Solution to Exercise 10.4.31 (p. 591)
3
Solution to Exercise 10.4.33 (p. 591)
6
Solution to Exercise 10.4.35 (p. 591)
100
Solution to Exercise 10.4.37 (p. 591)
92
Solution to Exercise 10.4.39 (p. 591)
-1
Solution to Exercise 10.4.41 (p. 592)
−$ | −2, 400, 000 |
Solution to Exercise 10.4.43 (p. 592)
9
10
Solution to Exercise 10.4.45 (p. 592)
3 13
50 or 163
50
Solution to Exercise 10.4.47 (p. 592)
2
Solution to Exercise 10.5.1 (p. 594)
14
Solution to Exercise 10.5.2 (p. 594)
52
Solution to Exercise 10.5.3 (p. 594)
-12
Solution to Exercise 10.5.4 (p. 594)
-45
Solution to Exercise 10.5.5 (p. 594)
-34
Solution to Exercise 10.5.6 (p. 594)
− 73
Solution to Exercise 10.5.7 (p. 594)
−7.4
Solution to Exercise 10.5.8 (p. 594)
−16
Solution to Exercise 10.5.9 (p. 596)
1Solution to Exercise 10.5.10 (p. 596)
2Solution to Exercise 10.5.11 (p. 596)
-3
Solution to Exercise 10.5.12 (p. 596)
-6
Solution to Exercise 10.5.13 (p. 596)
-14
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 10. SIGNED NUMBERS
Solution to Exercise 10.5.14 (p. 596)
-43
Solution to Exercise 10.5.15 (p. 596)
5Solution to Exercise 10.5.16 (p. 596)
-0.5
Solution to Exercise 10.5.17 (p. 596)
-8
Solution to Exercise 10.5.18 (p. 596)
0.57
Solution to Exercise 10.5.19 (p. 596)
-425
Solution to Exercise 10.5.20 (p. 597)
-48
Solution to Exercise 10.5.21 (p. 597)
-6,085
Solution to Exercise 10.5.22 (p. 597)
-7,993.7
Solution to Exercise 10.5.23 (p. 597)
16
Solution to Exercise 10.5.25 (p. 597)
-15
Solution to Exercise 10.5.27 (p. 597)
8
Solution to Exercise 10.5.29 (p. 597)
-25
Solution to Exercise 10.5.31 (p. 597)
-12
Solution to Exercise 10.5.33 (p. 597)
24
Solution to Exercise 10.5.35 (p. 597)
-21
Solution to Exercise 10.5.37 (p. 597)
0
Solution to Exercise 10.5.39 (p. 598)
0
Solution to Exercise 10.5.41 (p. 598)
23
Solution to Exercise 10.5.43 (p. 598)
328
Solution to Exercise 10.5.45 (p. 598)
876
Solution to Exercise 10.5.47 (p. 598)
-1,255
Solution to Exercise 10.5.49 (p. 598)
-6.084
Solution to Exercise 10.5.51 (p. 598)
-$28.50
Solution to Exercise 10.5.53 (p. 598)
$3.00
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 10.5.55 (p. 598)
17
36
Solution to Exercise 10.5.57 (p. 598)
62
100 = 31
50
Solution to Exercise 10.6.1 (p. 600)
3Solution to Exercise 10.6.2 (p. 600)
-3
Solution to Exercise 10.6.3 (p. 600)
-7
Solution to Exercise 10.6.4 (p. 600)
-13
Solution to Exercise 10.6.5 (p. 600)
-20
Solution to Exercise 10.6.6 (p. 600)
-27
Solution to Exercise 10.6.7 (p. 600)
-2
Solution to Exercise 10.6.8 (p. 600)
18
Solution to Exercise 10.6.9 (p. 600)
13
Solution to Exercise 10.6.10 (p. 600)
118
Solution to Exercise 10.6.11 (p. 600)
-16
Solution to Exercise 10.6.12 (p. 600)
16
Solution to Exercise 10.6.13 (p. 600)
-8
Solution to Exercise 10.6.14 (p. 601)
10
Solution to Exercise 10.6.15 (p. 601)
0Solution to Exercise 10.6.16 (p. 602)
-271
Solution to Exercise 10.6.17 (p. 602)
-2.247
Solution to Exercise 10.6.18 (p. 602)
-76.06
Solution to Exercise 10.6.19 (p. 602)
-0.182
Solution to Exercise 10.6.20 (p. 602)
5
Solution to Exercise 10.6.22 (p. 602)
-1
Solution to Exercise 10.6.24 (p. 602)
-14
Solution to Exercise 10.6.26 (p. 602)
-2
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 10. SIGNED NUMBERS
Solution to Exercise 10.6.28 (p. 603)
-6
Solution to Exercise 10.6.30 (p. 603)
7
Solution to Exercise 10.6.32 (p. 603)
29
Solution to Exercise 10.6.34 (p. 603)
-324
Solution to Exercise 10.6.36 (p. 603)
-429
Solution to Exercise 10.6.38 (p. 603)
-71
Solution to Exercise 10.6.40 (p. 603)
164
Solution to Exercise 10.6.42 (p. 603)
-11
Solution to Exercise 10.6.44 (p. 604)
16.022
Solution to Exercise 10.6.46 (p. 604)
31.25%
Solution to Exercise 10.6.48 (p. 604)
-5
Solution to Exercise 10.7.1 (p. 606)
-24
Solution to Exercise 10.7.2 (p. 606)
64
Solution to Exercise 10.7.3 (p. 606)
30
Solution to Exercise 10.7.4 (p. 606)
14
Solution to Exercise 10.7.5 (p. 606)
-4
Solution to Exercise 10.7.6 (p. 606)
-49
Solution to Exercise 10.7.7 (p. 608)
4
Solution to Exercise 10.7.8 (p. 608)
-6
Solution to Exercise 10.7.9 (p. 608)
-2
Solution to Exercise 10.7.10 (p. 608)
3Solution to Exercise 10.7.11 (p. 609)
14
Solution to Exercise 10.7.12 (p. 610)
1,108.08
Solution to Exercise 10.7.13 (p. 610)
1.226
Solution to Exercise 10.7.14 (p. 610)
-0.001
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 10.7.15 (p. 610)
16
Solution to Exercise 10.7.17 (p. 610)
32
Solution to Exercise 10.7.19 (p. 610)
-36
Solution to Exercise 10.7.21 (p. 610)
-60
Solution to Exercise 10.7.23 (p. 610)
-12
Solution to Exercise 10.7.25 (p. 611)
3Solution to Exercise 10.7.27 (p. 611)
-13
Solution to Exercise 10.7.29 (p. 611)
9Solution to Exercise 10.7.31 (p. 611)
-5
Solution to Exercise 10.7.33 (p. 611)
11
Solution to Exercise 10.7.35 (p. 611)
28
Solution to Exercise 10.7.37 (p. 611)
-4
Solution to Exercise 10.7.39 (p. 611)
-12
Solution to Exercise 10.7.41 (p. 611)
-4
Solution to Exercise 10.7.43 (p. 611)
-6
Solution to Exercise 10.7.45 (p. 611)
15
Solution to Exercise 10.7.47 (p. 612)
49
Solution to Exercise 10.7.49 (p. 612)
-140
Solution to Exercise 10.7.51 (p. 612)
-7
Solution to Exercise 10.7.53 (p. 612)
-3
Solution to Exercise 10.7.55 (p. 612)
-5
Solution to Exercise 10.7.57 (p. 612)
13
Solution to Exercise 10.7.59 (p. 612)
4 = 1 1
3
3
Solution to Exercise 10.7.61 (p. 612)
5212
Solution to Exercise 10.9.1 (p. 614)
N, W, Z
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 10. SIGNED NUMBERS
Solution to Exercise 10.9.3 (p. 614)
W, Z
Solution to Exercise 10.9.5 (p. 614)
{−3, −2, −1, 0, 1, 2}
Solution to Exercise 10.9.7 (p. 614)
<
Solution to Exercise 10.9.9 (p. 614)
<
Solution to Exercise 10.9.11 (p. 615)
{−5, −4, −3, −2, −1}
Solution to Exercise 10.9.13 (p. 615)
{1, 2, 3, 4}
Solution to Exercise 10.9.15 (p. 615)
none
Solution to Exercise 10.9.17 (p. 615)
4Solution to Exercise 10.9.19 (p. 615)
6Solution to Exercise 10.9.21 (p. 615)
+ (plus)
Solution to Exercise 10.9.23 (p. 615)
negative eight
Solution to Exercise 10.9.25 (p. 615)
negative negative one or opposite negative one
Solution to Exercise 10.9.27 (p. 615)
one plus negative seven
Solution to Exercise 10.9.29 (p. 616)
negative one minus four
Solution to Exercise 10.9.31 (p. 616)
zero minus negative eleven
Solution to Exercise 10.9.33 (p. 616)
15
Solution to Exercise 10.9.35 (p. 616)
19 or 1 + 18
Solution to Exercise 10.9.37 (p. 616)
9
Solution to Exercise 10.9.39 (p. 616)
5
Solution to Exercise 10.9.41 (p. 616)
−2
Solution to Exercise 10.9.43 (p. 616)
12
Solution to Exercise 10.9.45 (p. 616)
16
Solution to Exercise 10.9.47 (p. 616)
16
Solution to Exercise 10.9.49 (p. 617)
8
Solution to Exercise 10.9.51 (p. 617)
7
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 10.9.53 (p. 617)
−2
Solution to Exercise 10.9.55 (p. 617)
−7
Solution to Exercise 10.9.57 (p. 617)
−14
Solution to Exercise 10.9.59 (p. 617)
48
Solution to Exercise 10.9.61 (p. 617)
−42
Solution to Exercise 10.9.63 (p. 617)
3
Solution to Exercise 10.9.65 (p. 617)
1
Solution to Exercise 10.9.67 (p. 617)
not dened
Solution to Exercise 10.9.69 (p. 618)
−4
Solution to Exercise 10.9.71 (p. 618)
−22
Solution to Exercise 10.10.1 (p. 618)
{−7, −6, −5, −4}
Solution to Exercise 10.10.2 (p. 618)
{−2, −1, 0, 1}
Solution to Exercise 10.10.3 (p. 618)
=
Solution to Exercise 10.10.4 (p. 618)
<
Solution to Exercise 10.10.5 (p. 618)
>
Solution to Exercise 10.10.6 (p. 618)
{−3, −2, −1}
Solution to Exercise 10.10.7 (p. 618)
{1, 2}
Solution to Exercise 10.10.8 (p. 618)
5
Solution to Exercise 10.10.9 (p. 618)
16
Solution to Exercise 10.10.10 (p. 618)
−2
Solution to Exercise 10.10.11 (p. 618)
16
Solution to Exercise 10.10.12 (p. 618)
15
Solution to Exercise 10.10.13 (p. 618)
−2
Solution to Exercise 10.10.14 (p. 618)
−11
Solution to Exercise 10.10.15 (p. 619)
−16
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 10. SIGNED NUMBERS
Solution to Exercise 10.10.16 (p. 619)
42
Solution to Exercise 10.10.17 (p. 619)
121
Solution to Exercise 10.10.18 (p. 619)
51 or 72
7
7
Solution to Exercise 10.10.19 (p. 619)
6
Solution to Exercise 10.10.20 (p. 619)
0
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Algebraic Expressions and Equations
11.1 Objectives1
After completing this chapter, you should
Algebraic Expressions (Section 11.2)
• be able to recognize an algebraic expression
• be able to distinguish between terms and factors
• understand the meaning and function of coecients
• be able to perform numerical evaluation
Combining Like Terms Using Addition and Subtraction (Section 11.3)
• be able to combine like terms in an algebraic expression
Solving Equations of the Form x + a = b and x − a = b (Section 11.4)
• understand the meaning and function of an equation
• understand what is meant by the solution to an equation
• be able to solve equations of the form x + a = b and x − a = b
Solving Equations of the Form ax = b and x = b (Section 11.5)
a
• be familiar with the multiplication/division property of equality
• be able to solve equations of the form ax = b and x = b
a
• be able to use combined techniques to solve equations
Applications I: Translating Words to Mathematical Symbols (Section 11.6)
• be able to translate phrases and statements to mathematical expressions and equations Applications II: Solving Problems (Section 11.7)
• be more familiar with the ve-step method for solving applied problems
• be able to use the ve-step method to solve number problems and geometry problems 1This content is available online at <http://cnx.org/content/m18899/1.3/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4> 631
CHAPTER 11. ALGEBRAIC EXPRESSIONS AND EQUATIONS
11.2 Algebraic Expressions2
11.2.1 Section Overview
• Algebraic Expressions
• Terms and Factors
• Coecients
• Numerical Evaluation
11.2.2 Algebraic Expressions
Numerical Expression
In arithmetic, a numerical expression results when numbers are connected by arithmetic operation signs (+, -, · , ÷). For example, 8 + 5, 4 − 9, 3 · 8, and 9 ÷ 7 are numerical expressions.
Algebraic Expression
In algebra, letters are used to represent numbers, and an algebraic expression results when an arithmetic operation sign associates a letter with a number or a letter with a letter. For example, x + 8, 4 − y , 3 · x , x ÷ 7 , and x · y are algebraic expressions.
Expressions
Numerical expressions and algebraic expressions are often referred to simply as expressions.
11.2.3 Terms and Factors
In algebra, it is extremely important to be able to distinguish between terms and factors.
Distinction Between Terms and Factors
Terms are parts of sums and are therefore connected by + signs.
Factors are parts of products and are therefore separated by · signs.
note: While making the distinction between sums and products, we must remember that subtraction and division are functions of these operations.
1. In some expressions it will appear that terms are separated by minus signs. We must keep in mind that subtraction is addition of the opposite, that is,
x − y = x + (−y)
2. In some expressions it will appear that factors are separated by division signs. We must keep in mind that
x = x · 1 = x · 1
y
1
y
y
11.2.3.1 Sample Set A
State the number of terms in each expression and name them.
Example 11.1
x + 4. In this expression, x and 4 are connected by a “+” sign. Therefore, they are terms. This expression consists of two terms.
Example 11.2
y − 8. The expression y − 8 can be expressed as y + (−8). We can now see that this expression consists of the two terms y and −8.
2This content is available online at <http://cnx.org/content/m35038/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Rather than rewriting the expression when a subtraction occurs, we can identify terms more quickly by associating the + or – sign with the individual quantity.
Example 11.3
a + 7 − b − m. Associating the sign with the individual quantities, we see that this expression consists of the four terms a, 7, −b, −m.
Example 11.4
5m − 8n. This expression consists of the two terms, 5m and −8n. Notice that the term 5m is composed of the two factors 5 and m. The term −8n is composed of the two factors −8 and n.
Example 11.5
3x. This expression consists of one term. Notice that 3x can be expressed as 3x + 0 or 3x ·
1 (indicating the connecting signs of arithmetic). Note that no operation sign is necessary for multiplication.
11.2.3.2 Practice Set A
Specify the terms in each expression.
Exercise 11.2.1
(Solution on p. 682.)
x + 7
Exercise 11.2.2
(Solution on p. 682.)
3m − 6n
Exercise 11.2.3
(Solution on p. 682.)
5y
Exercise 11.2.4
(Solution on p. 682.)
a + 2b − c
Exercise 11.2.5
(Solution on p. 682.)
−3x − 5
11.2.4 Coecients
We know that multiplication is a description of repeated addition. For example, 5 · 7 describes 7 + 7 + 7 + 7 + 7
Suppose some quantity is represented by the letter x. The multiplication 5x describes x + x + x + x + x. It is now easy to see that 5x species 5 of the quantities represented by x. In the expression 5x, 5 is called the numerical coecient, or more simply, the coecient of x.
Coecient
The coecient of a quantity records how many of that quantity there are.
Since constants alone do not record the number of some quantity, they are not usually considered as numerical coecients. For example, in the expression 7x + 2y − 8z + 12, the coecient of 7x is 7. (There are 7 x’s.)
2y is 2. (There are 2 y ‘s.)
−8z is −8. (There are −8z ‘s.)
The constant 12 is not considered a numerical coecient.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 11. ALGEBRAIC EXPRESSIONS AND EQUATIONS
1x = x
When the numerical coecient of a variable is 1, we write only the variable and not the coecient. For example, we write x rather than 1x. It is clear just by looking at x that there is only one.
11.2.5 Numerical Evaluation
We know that a variable represents an unknown quantity. Therefore, any expression that contains a variable represents an unknown quantity. For example, if the value of x is unknown, then the value of 3x + 5 is unknown. The value of 3x + 5 depends on the value of x.
Numerical Evaluation
Numerical evaluation is the process of determining the numerical value of an algebraic expression by replacing the variables in the expression with specied numbers.
11.2.5.1 Sample Set B
Find the value of each expression.
Example 11.6
2x + 7y, if x = −4 and y = 2
Replace x with 4 and y with 2.
2x + 7y
=
2 (−4) + 7 (2)
=
−8 + 14
=
6
Thus, when x = − − 4 and y = 2, 2x + 7y = 6.
Example 11.7
5a + 8b , if a = 6 and b = −3.
b
12
Replace a with 6 and b with 3.
5a + 8b
=
5(6) + 8(−3)
b
12
−3
12
=
30 + −
−
24
=
−10 + (−2)
=
−12
Thus, when a = 6 and b = 3, 5a + 8b
b
12 = −12.
Example 11.8
6 (2a − 15b), if a = −5 and b = −1
Replace a with 5 and b with 1.
6 (2a − 15b)
=
6 (2 (−5) − 15 (−1))
=
6 (−10 + 15)
=
6 (5)
=
30
Thus, when a = − − 5 and b = − − 1, 6 (2a − 15b) = 30.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Example 11.9
3×2 − 2x + 1, if x = 4
Replace x with 4.
3×2 − 2x + 1
=
3(4)2 − 2 (4) + 1
=
3 · 16 − 2 (4) + 1
=
48 − 8 + 1
=
41
Thus, when x = 4, 3×2 − 2x + 1 = 41.
Example 11.10
−x2 − 4, if x = 3
Replace x with 3.
−x2 − 4
=
−3 − 4
Be careful to square only the 3. The exponent 2 is connected only to 3, not -3
=
−9 − 4
=
−13
Example 11.11
(−x)2 − 4, if x = 3.
Replace x with 3.
(−x)2 − 4
=
(−3)2 − 4
The exponent is connected to -3, not 3 as in problem 5 above.
=
9 − 4
=
−5
The exponent is connected to 3, not 3 as in the problem above.
11.2.5.2 Practice Set B
Find the value of each expression.
Exercise 11.2.6
(Solution on p. 682.)
9m − 2n, if m = −2 and n = 5
Exercise 11.2.7
(Solution on p. 682.)
−3x − 5y + 2z, if x = −4, y = 3, z = 0
Exercise 11.2.8
(Solution on p. 682.)
10a + 4b, if a = −6, and b = 2
3b
2
Exercise 11.2.9
(Solution on p. 682.)
8 (3m − 5n), if m = −4 and n = −5
Exercise 11.2.10
(Solution on p. 682.)
3 [−40 − 2 (4a − 3b)], if a = −6 and b = 0
Exercise 11.2.11
(Solution on p. 682.)
5y2 + 6y − 11, if y = −1
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 11. ALGEBRAIC EXPRESSIONS AND EQUATIONS
Exercise 11.2.12
(Solution on p. 682.)
−x2 + 2x + 7, if x = 4
Exercise 11.2.13
(Solution on p. 682.)
(−x)2 + 2x + 7, if x = 4
11.2.6 Exercises
Exercise 11.2.14
(Solution on p. 682.)
In an algebraic expression, terms are separated by
signs and factors are separated
by
signs.
For the following 8 problems, specify each term.
Exercise 11.2.15
3m + 7n
Exercise 11.2.16
(Solution on p. 682.)
5x + 18y
Exercise 11.2.17
4a − 6b + c
Exercise 11.2.18
(Solution on p. 682.)
8s + 2r − 7t
Exercise 11.2.19
m − 3n − 4a + 7b
Exercise 11.2.20
(Solution on p. 682.)
7a − 2b − 3c − 4d
Exercise 11.2.21
−6a − 5b
Exercise 11.2.22
(Solution on p. 682.)
−x − y
Exercise 11.2.23
What is the function of a numerical coecient?
Exercise 11.2.24
(Solution on p. 682.)
Write 1m in a simpler way.
Exercise 11.2.25
Write 1s in a simpler way.
Exercise 11.2.26
(Solution on p. 682.)
In the expression 5a, how many a’s are indicated?
Exercise 11.2.27
In the expression 7c, how many c’s are indicated?
Find the value of each expression.
Exercise 11.2.28
(Solution on p. 682.)
2m − 6n, if m = −3 and n = 4
Exercise 11.2.29
5a + 6b, if a = −6 and b = 5
Exercise 11.2.30
(Solution on p. 682.)
2x − 3y + 4z, if x = 1, y = −1, and z = −2
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 11.2.31
9a + 6b − 8x + 4y, if a = −2, b = −1, x = −2, and y = 0
Exercise 11.2.32
(Solution on p. 682.)
8x + 18y , if x = 9 and y = −2
3y
2x
Exercise 11.2.33
−3m − −6n , if m = −6 and n = 3
2n
m
Exercise 11.2.34
(Solution on p. 682.)
4 (3r + 2s), if r = 4 and s = 1
Exercise 11.2.35
3 (9a − 6b), if a = −1 and b = −2
Exercise 11.2.36
(Solution on p. 682.)
−8 (5m + 8n), if m = 0 and n = −1
Exercise 11.2.37
−2 (−6x + y − 2z), if x = 1, y = 1, and z = 2
Exercise 11.2.38
(Solution on p. 682.)
− (10x − 2y + 5z) if x = 2, y = 8, and z = −1
Exercise 11.2.39
− (a − 3b + 2c − d), if a = −5, b = 2, c = 0, and d = −1
Exercise 11.2.40
(Solution on p. 683.)
3 [16 − 3 (a + 3b)], if a = 3 and b = −2
Exercise 11.2.41
−2 [5a + 2b (b − 6)], if a = −2 and b = 3
Exercise 11.2.42
(Solution on p. 683.)
−{6x + 3y [−2 (x + 4y)]}, if x = 0 and y = 1
Exercise 11.2.43
−2{19 − 6 [4 − 2 (a − b − 7)]}, if a = 10 and b = 3
Exercise 11.2.44
(Solution on p. 683.)
x2 + 3x − 1, if x = 5
Exercise 11.2.45
m2 − 2m + 6, if m = 3
Exercise 11.2.46
(Solution on p. 683.)
6a2 + 2a − 15, if a = −2
Exercise 11.2.47
5s2 + 6s + 10, if x = −1
Exercise 11.2.48
(Solution on p. 683.)
16×2 + 8x − 7, if x = 0
Exercise 11.2.49
−8y2 + 6y + 11, if y = 0
Exercise 11.2.50
(Solution on p. 683.)
(y − 6)2 + 3 (y − 5) + 4, if y = 5
Exercise 11.2.51
(x + 8)2 + 4 (x + 9) + 1, if x = −6
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 11. ALGEBRAIC EXPRESSIONS AND EQUATIONS
11.2.6.1 Exercises for Review
Exercise 11.2.52
(Solution on p. 683.)
(Section 5.3) Perform the addition: 53 + 21.
8
6
Exercise 11.2.53
(Section 5.5) Arrange the numbers in order from smallest to largest: 11
32 , 15
48 , and 7
16
Exercise 11.2.54
(Solution on p. 683.)
(Section 5.7) Find the value of 22 + 8
3
27
Exercise 11.2.55
(Section 7.3) Write the proportion in fractional form: 9 is to 8 as x is to 7.
Exercise 11.2.56
(Solution on p. 683.)
(Section 10.7) Find the value of −3 (2 − 6) − 12
11.3 Combining Like Terms Using Addition and Subtraction3
11.3.1 Section Overview
• Combining Like Terms
11.3.2 Combining Like Terms
From our examination of terms in Section 11.2, we know that like terms are terms in which the variable parts are identical. Like terms is an appropriate name since terms with identical variable parts and dierent numerical coecients represent dierent amounts of the same quantity. When we are dealing with quantities of the same type, we may combine them using addition and subtraction.
Simplifying an Algebraic Expression
An algebraic expression may be simplied by combining like terms.
This concept is illustrated in the following examples.
1. 8 records + 5 records = 13 records.
Eight and 5 of the same type give 13 of that type. We have combined quantities of the same type.
2. 8 records + 5 records + 3 tapes = 13 records + 3 tapes. Eight and 5 of the same type give 13 of that type. Thus, we have 13 of one type and 3 of another type. We have combined only quantities of the same type.
3. Suppose we let the letter x represent “record.” Then, 8x + 5x = 13x. The terms 8x and 5x are like terms. So, 8 and 5 of the same type give 13 of that type. We have combined like terms.
4. Suppose we let the letter x represent “record” and y represent “tape.” Then, 8x + 5x + 3y = 13x + 5y We have combined only the like terms.
After observing the problems in these examples, we can suggest a method for simplifying an algebraic expression by combining like terms.
Combining Like Terms
Like terms may be combined by adding or subtracting their coecients and axing the result to the common variable.
3This content is available online at <http://cnx.org/content/m35039/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
639
11.3.2.1 Sample Set A
Simplify each expression by combining like terms.
Example 11.12
2m + 6m − 4m. All three terms are alike. Combine their coecients and ax this result to m: 2 + 6 − 4 = 4.
Thus, 2m + 6m − 4m = 4m .
Example 11.13
5x + 2y − 9y. The terms 2y and −9y are like terms. Combine their coecients: 2 − 9 = −7.
Thus, 5x + 2y − 9y = 5x − 7y .
Example 11.14
−3a + 2b − 5a + a + 6b. The like terms are
−3a,
− 5a, a 2b, 6b
|
{z
} |
{z
}
−3−5+1=−7
2+6=8
−7a
8b
Thus, −3a + 2b − 5a + a + 6b= − 7a + 8b.
Example 11.15
r − 2s + 7s + 3r − 4r − 5s . The like terms are
Thus, r − 2s + 7s + 3r − 4r − 5s = 0 .
11.3.2.2 Practice Set A
Simplify each expression by combining like terms.
Exercise 11.3.1
(Solution on p. 683.)
4x + 3x + 6x
Exercise 11.3.2
(Solution on p. 683.)
5a + 8b + 6a − 2b
Exercise 11.3.3
(Solution on p. 683.)
10m − 6n − 2n − m + n
Exercise 11.3.4
(Solution on p. 683.)
16a + 6m + 2r − 3r − 18a + m − 7m
Exercise 11.3.5
(Solution on p. 683.)
5h − 8k + 2h − 7h + 3k + 5k
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 11. ALGEBRAIC EXPRESSIONS AND EQUATIONS
11.3.3 Exercises
Simplify each expression by combining like terms.
Exercise 11.3.6
(Solution on p. 683.)
4a + 7a
Exercise 11.3.7
3m + 5m
Exercise 11.3.8
(Solution on p. 683.)
6h − 2h
Exercise 11.3.9
11k − 8k
Exercise 11.3.10
(Solution on p. 683.)
5m + 3n − 2m
Exercise 11.3.11
7x − 6x + 3y
Exercise 11.3.12
(Solution on p. 683.)
14s + 3s − 8r + 7r
Exercise 11.3.13
−5m − 3n + 2m + 6n
Exercise 11.3.14
(Solution on p. 683.)
7h + 3a − 10k + 6a − 2h − 5k − 3k
Exercise 11.3.15
4x − 8y − 3z + x − y − z − 3y − 2z
Exercise 11.3.16
(Solution on p. 683.)
11w + 3x − 6w − 5w + 8x − 11x
Exercise 11.3.17
15r − 6s + 2r + 8s − 6r − 7s − s − 2r
Exercise 11.3.18
(Solution on p. 683.)
| −7 | m+ | 6 | m+ | −3 | m
Exercise 11.3.19
| −2 | x+ | −8 | x+ | 10 | x
Exercise 11.3.20
(Solution on p. 683.)
(−4 + 1) k + (6 − 3) k + (12 − 4) h + (5 + 2) k
Exercise 11.3.21
(−5 + 3) a − (2 + 5) b − (3 + 8) b
Exercise 11.3.22
(Solution on p. 683.)
5 ? +2∆ + 3∆ − 8?
Exercise 11.3.23
9 +10 −11 −12
Exercise 11.3.24
(Solution on p. 683.)
16x − 12y + 5x + 7 − 5x − 16 − 3y
Exercise 11.3.25
−3y + 4z − 11 − 3z − 2y + 5 − 4 (8 − 3)
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
11.3.3.1 Exercises for Review
Exercise 11.3.26
(Solution on p. 683.)
(Section 4.3) Convert 24
11 to a mixed number
Exercise 11.3.27
(Section 4.4) Determine the missing numerator: 3 = ?
8
64 .
Exercise 11.3.28
(Solution on p. 684.)
(Section 5.6) Simplify 5−1
6
4 .
1
12
Exercise 11.3.29
(Section 7.5) Convert 516 to a percent.
Exercise 11.3.30
(Solution on p. 684.)
(Section 11.2) In the expression 6k, how many k’s are there?
11.4 Solving Equations of the Form x+a=b and x-a=b4
11.4.1 Section Overview
• Equations
• Solutions and Equivalent Equations
• Solving Equations
11.4.2 Equations
Equation
An equation is a statement that two algebraic expressions are equal.
The following are examples of equations:
x + 6
=
10
x − 4
=
−11
3y − 5 = −2 + 2y
[U+FE38]
|{z}
| {z }
|{z}
|
{z
}
|
{z
}
This
This
This
This
This
This
expression = expression expression = expression expression = expression Notice that x+6, x−4, and 3y −5 are not equations. They are expressions. They are not equations because there is no statement that each of these expressions is equal to another expression.
11.4.3 Solutions and Equivalent Equations
Conditional Equations
The truth of some equations is conditional upon the value chosen for the variable. Such equations are called conditional equations. There are two additional types of equations. They are examined in courses in algebra, so we will not consider them now.
Solutions and Solving an Equation
The set of values that, when substituted for the variables, make the equation true, are called the solutions of the equation.
An equation has been solved when all its solutions have been found.
4This content is available online at <http://cnx.org/content/m35044/1.3/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 11. ALGEBRAIC EXPRESSIONS AND EQUATIONS
11.4.3.1 Sample Set A
Example 11.16
Verify that 3 is a solution to x + 7 = 10.
When x = 3,
x + 7
=
10
becomes 3 + 7 = 10
which is a true statement, verifying that
10
=
10
3 is a solution to x + 7 = 10
Example 11.17
Verify that −6 is a solution to 5y + 8 = −22
When y = −6,
5y + 8
=
−22
becomes 5 (−6) + 8 = −22
−30 + 8
=
−22
which is a true statement, verifying that
−22
=
−22
−6 is a solution to 5y + 8 = −22
Example 11.18
Verify that 5 is not a solution to a − 1 = 2a + 3.
When a = 5,
a − 1
=
2a + 3
becomes 5 − 1 = 2 · 5 + 3
5 − 1
=
10 + 3
a false statement, verifying that 5
4
=
13
is not a solution to a − 1 = 2a + 3
Example 11.19
Verify that -2 is a solution to 3m − 2 = −4m − 16.
When m = −2,
3m − 2
=
−4m − 16
becomes 3 (−2) − 2 = −4 (−2) − 16
−6 − 2
=
8 − 16
which is a true statement, verifying that
−8
=
−8
−2
is a solution to 3m − 2 = −4m − 16
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
11.4.3.2 Practice Set A
Exercise 11.4.1
(Solution on p. 684.)
Verify that 5 is a solution to m + 6 = 11.
Exercise 11.4.2
(Solution on p. 684.)
Verify that −5 is a solution to 2m − 4 = −14.
Exercise 11.4.3
(Solution on p. 684.)
Verify that 0 is a solution to 5x + 1 = 1.
Exercise 11.4.4
(Solution on p. 684.)
Verify that 3 is not a solution to −3y + 1 = 4y + 5.
Exercise 11.4.5
(Solution on p. 684.)
Verify that -1 is a solution to 6m − 5 + 2m = 7m − 6.
Equivalent Equations
Some equations have precisely the same collection of solutions. Such equations are called equivalent equations. For example, x − 5 = −1, x + 7 = 11, and x = 4 are all equivalent equations since the only solution to each is x = 4. (Can you verify this?)
11.4.4 Solving Equations
We know that the equal sign of an equation indicates that the number represented by the expression on the left side is the same as the number represented by the expression on the right side.
This number is the same as this number
↓
↓
↓
x
=
4
x + 7
=
11
x − 5
=
-1
Table 11.1
Addition/Subtraction Property of Equality
From this, we can suggest the addition/subtraction property of equality.
Given any equation,
1. We can obtain an equivalent equation by adding the same number to both sides of the equation.
2. We can obtain an equivalent equation by subtracting the same number from both sides of the equation.
The Idea Behind Equation Solving
The idea behind equation solving is to isolate the variable on one side of the equation. Signs of operation (+, -, ·,÷) are used to associate two numbers. For example, in the expression 5 + 3, the numbers 5 and 3 are associated by addition. An association can be undone by performing the opposite operation. The addition/subtraction property of equality can be used to undo an association that is made by addition or subtraction.
Subtraction is used to undo an addition.
Addition is used to undo a subtraction.
The procedure is illustrated in the problems of .
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
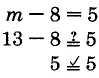
644
CHAPTER 11. ALGEBRAIC EXPRESSIONS AND EQUATIONS
11.4.4.1 Sample Set B
Use the addition/subtraction property of equality to solve each equation.
Example 11.20
x + 4 = 6.
4 is associated with x by addition. Undo the association by subtracting 4 from both sides.
x + 4 − 4 = 6 − 4
x + 0 = 2
x = 2
Check: When x = 2, x + 4 becomes
The solution to x + 4 = 6 is x = 2.
Example 11.21
m − 8 = 5. 8 is associated with m by subtraction. Undo the association by adding 8 to both sides.
m − 8 + 8 = 5 + 8
m + 0 = 13
m = 13
Check: When m = 13,
becomes
a true statement.
The solution to m − 8 = 5 is m = 13.
Example 11.22
−3 − 5 = y − 2 + 8. Before we use the addition/subtraction property, we should simplify as much as possible.
−3 − 5 = y − 2 + 8
−8 = y + 6
6 is associated with y by addition. Undo the association by subtracting 6 from both sides.
−8 − 6 = y + 6 − 6
−14 = y + 0
−14 = y
This is equivalent to y = −14.
Check: When y = −14,
−3 − 5 = y − 2 + 8
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
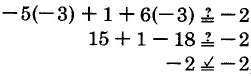
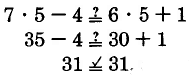
645
becomes
,
a true statement.
The solution to −3 − 5 = y − 2 + 8 is y = −14.
Example 11.23
−5a + 1 + 6a = −2. Begin by simplifying the left side of the equation.
−5a + 1 + 6a = −2
|
{z
}
−5+6=1
a + 1 = −2 1 is associated with a by addition. Undo the association by subtracting 1 from both sides.
a + 1 − 1 = −2 − 1
a + 0 = −3
a = −3
Check: When a = −3,
−5a + 1 + 6a = −2
becomes
,
a true statement.
The solution to −5a + 1 + 6a = −2 is a = −3.
Example 11.24
7k − 4 = 6k + 1. In this equation, the variable appears on both sides. We need to isolate it on one side. Although we can choose either side, it will be more convenient to choose the side with the larger coecient. Since 8 is greater than 6, we’ll isolate k on the left side.
7k − 4 = 6k + 1 Since 6k represents +6k, subtract 6k from each side.
7k − 4 − 6k = 6k + 1 − 6k
|
{z
}
|
{z
}
7−6=1
6−6=0
k − 4 = 1 4 is associated with k by subtraction. Undo the association by adding 4 to both sides.
k − 4 + 4 = 1 + 4
k = 5
Check: When k = 5,
7k − 4 = 6k + 1
becomes
a true statement.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
646
CHAPTER 11. ALGEBRAIC EXPRESSIONS AND EQUATIONS
The solution to 7k − 4 = 6k + 1 is k = 5.
Example 11.25
−8 + x = 5. -8 is associated with x by addition. Undo the by subtracting -8 from both sides.
Subtracting -8 we get − (−8) =+8. We actually add 8 to both sides.
−8 + x + 8 = 5 + 8
x = 13
Check: When x = 13
−8 + x = 5
becomes
,
a true statement.
The solution to −8 + x = 5 is x = 13.
11.4.4.2 Practice Set B
Exercise 11.4.6
(Solution on p. 684.)
y + 9 = 4
Exercise 11.4.7
(Solution on p. 684.)
a − 4 = 11
Exercise 11.4.8
(Solution on p. 684.)
−1 + 7 = x + 3
Exercise 11.4.9
(Solution on p. 684.)
8m + 4 − 7m = (−2) (−3)
Exercise 11.4.10
(Solution on p. 684.)
12k − 4 = 9k − 6 + 2k
Exercise 11.4.11
(Solution on p. 684.)
−3 + a = −4
11.4.5 Exercises
For the following 10 problems, verify that each given value is a solution to the given equation.
Exercise 11.4.12
(Solution on p. 684.)
x − 11 = 5, x = 16
Exercise 11.4.13
y − 4 = −6, y = −2
Exercise 11.4.14
(Solution on p. 684.)
2m − 1 = 1, m = 1
Exercise 11.4.15
5y + 6 = −14, y = −4
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 11.4.16
(Solution on p. 685.)
3x + 2 − 7x = −5x − 6, x = −8
Exercise 11.4.17
−6a + 3 + 3a = 4a + 7 − 3a, a = −1
Exercise 11.4.18