133 Fundamentals of Mathematics: Part 15
Volume
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

555
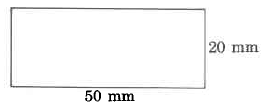
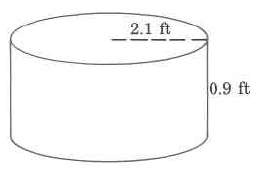
Exercise 9.6.30
Exact volume
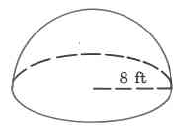
Exercise 9.6.31
(Solution on p. 573.)
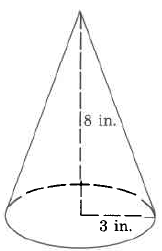
Approximate volume
Exercise 9.6.32
Approximate volume
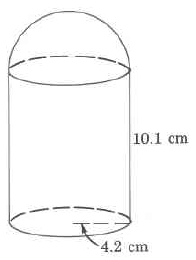
Exercise 9.6.33
(Solution on p. 573.)
Exact volume
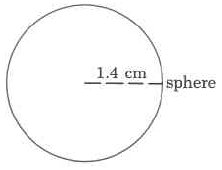
Exercise 9.6.34
Approximate volume
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

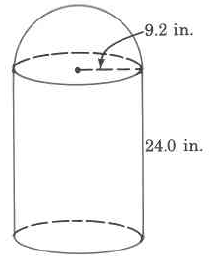
556
CHAPTER 9. MEASUREMENT AND GEOMETRY
Exercise 9.6.35
(Solution on p. 573.)
Approximate volume
Exercise 9.6.36
Approximate volume
9.6.8.1 Exercises for Review
Exercise 9.6.37
(Solution on p. 573.)
(Section 1.2) In the number 23,426, how many hundreds are there?
Exercise 9.6.38
(Section 3.4) List all the factors of 32.
Exercise 9.6.39
(Solution on p. 573.)
(Section 5.4) Find the value of 43 − 35 + 12.
4
6
3
Exercise 9.6.40
(Section 5.6) Find the value of 5+13 .
2+ 2
15
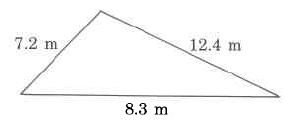
Exercise 9.6.41
(Solution on p. 573.)
(Section 9.5) Find the perimeter.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
9.7 Summary of Key Concepts7
9.7.1 Summary of Key Concepts
Measurement (Section 9.2)
Measurement is comparison to some standard.
Standard Unit of Measure (Section 9.2)
A quantity that is used for comparison is called a standard unit of measure.
Two Types of Measurement Systems (Section 9.2)
There are two major types of measurement systems in use today. They are the United States system and the metric system.
Unit Fraction (Section 9.2)
A unit fraction is a fraction that has a value of 1. Unit fractions can be used to convert from one unit of measure to another.
Meter, Liter, Gram, and associated prexes (Section 9.3)
Common units of measure in the metric system are the meter (m), for length, the liter (L), for volume, and the gram (g), for mass. To each of these units, a prex can be attached.
kilo thousand
deci tenth
hecto hundred
centi hundredth
deka ten
milli thousandth
Metric Conversions (Section 9.3)
To convert from one metric unit to another:
1. Determine the location of the original number on the metric scale.
2. Move the decimal point of the original number in the same direction and the same number of places as is necessary to move to the metric unit you wish to convert to.
Denominate Numbers (Section 9.4)
Numbers that have units of measure associated with them are denominate numbers. The number 25 mg is a denominate number since the mg unit is associated with the pure number 25. The number 82 is not a denominate number since it has no unit of measure associated with it.
Simplied Denominate Number (Section 9.4)
A denominate number is simplied when the number of standard units of measure associated with it does not exceed the next higher type of unit. 55 min is simplied, whereas 65 min is not simplied Addition and Subtraction of Denominate Numbers (Section 9.4)
Denominate numbers can be added or subtracted by
1. writing the numbers vertically so that the like units appear in the same column.
2. adding or subtracting the number parts, carrying along the unit.
3. simplifying the sum or dierence.
7This content is available online at <http://cnx.org/content/m35024/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 9. MEASUREMENT AND GEOMETRY
Multiplying a Denominate Number by a Whole Number (Section 9.4)
To multiply a denominate number by a whole number, multiply the number part of each unit by the whole number and ax the unit to the product.
Dividing a Denominate Number by a Whole Number (Section 9.4)
To divide a denominate number by a whole number, divide the number part of each unit by the whole number beginning with the largest unit. Ax the unit to this quotient. Carry the remainder to the next unit.
Polygon (Section 9.5)
A polygon is a closed plane (at) gure whose sides are line segments (portions of straight lines).
Perimeter (Section 9.5)
The perimeter of a polygon is the distance around the polygon.
Circumference, Diameter, Radius (Section 9.5)
The circumference of a circle is the distance around the circle. The diameter of a circle is any line segment that passes through the center of the circle and has its endpoints on the circle. The radius of a circle is one half the diameter of the circle.
The number π (Section 9.5)
The symbol π, read “pi,” represents the nonterminating, nonrepeating decimal number 3.14159… . For computational purposes, π is often approximated by the number 3.14.
Formula (Section 9.5)
A formula is a rule for performing a task. In mathematics, a formula is a rule that directs us in computations.
Circumference Formulas (Section 9.5)
C = π · d
C ≈ (3.14) d
C = 2 · π · r
C ≈ 2 (3.14) r
Area (Section 9.6)
The area of a surface is the amount of square length units contained in the surface.
Volume (Section 9.6)
The volume of an object is a measure of the amount of cubic length units contained in the object.
Area Formulas (Section 9.6)
Triangle: A = 1 · b · h
2
Rectangle: A = l · w
Parallelogram: A = b · h
Trapezoid: A = 1 · (b
2
1 + b2) · h
Circle: A = π · r2
Volume Formulas (Section 9.6)
Rectangle solid: V = l · w · h
Sphere: V = 4 · π · r3
3
Cylinder: V = π · r2 · h
Cone: V = 1 · π · r2 · h
3
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
9.8 Exercise Supplement8
9.8.1 Exercise Supplement
9.8.1.1 Measurement and the United States System (Section 9.2)
Exercise 9.8.1
(Solution on p. 574.)
What is measurement?
For problems 2-6, make each conversion. Use the conversion table given in Section 9.1.
Exercise 9.8.2
9 ft=
yd
Exercise 9.8.3
(Solution on p. 574.)
32 oz=
lb
Exercise 9.8.4
1,500 mg =
g
Exercise 9.8.5
(Solution on p. 574.)
12,000 lb =
T
Exercise 9.8.6
5,280 ft=
mi
For problems 7-23, make each conversion.
Exercise 9.8.7
(Solution on p. 574.)
23 yd to ft
Exercise 9.8.8
2 1 mi to yd
2
Exercise 9.8.9
(Solution on p. 574.)
8 in. to ft
Exercise 9.8.10
51 in. to mi
Exercise 9.8.11
(Solution on p. 574.)
3 qt to pt
Exercise 9.8.12
8 lb to oz
Exercise 9.8.13
(Solution on p. 574.)
5 cups to tbsp
Exercise 9.8.14
9 da to hr
Exercise 9.8.15
(Solution on p. 574.)
3 1 min to sec
2
Exercise 9.8.16
3 wk to min
4
8This content is available online at <http://cnx.org/content/m35025/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 9. MEASUREMENT AND GEOMETRY
9.8.1.2 The Metric System of Measurement (Section 9.3)
Exercise 9.8.17
(Solution on p. 574.)
250 mL to L
Exercise 9.8.18
18.57 cm to m
Exercise 9.8.19
(Solution on p. 574.)
0.01961 kg to mg
Exercise 9.8.20
52,211 mg to kg
Exercise 9.8.21
(Solution on p. 574.)
54.006 dag to g
Exercise 9.8.22
1.181 hg to mg
Exercise 9.8.23
(Solution on p. 574.)
3.5 kL to mL
9.8.1.3 Simplication of Denominate Numbers (Section 9.4)
For problems 24-31, perform the indicated operations. Simplify, if possible.
Exercise 9.8.24
Add 8 min 50 sec to 5 min 25 sec.
Exercise 9.8.25
(Solution on p. 574.)
Add 3 wk 3 da to 2 wk 5 da
Exercise 9.8.26
Subtract 4 gal 3 qt from 5 gal 2 qt.
Exercise 9.8.27
(Solution on p. 574.)
Subtract 2 gal 3 qt 1pt from 8 gal 2 qt.
Exercise 9.8.28
Subtract 5 wk 4 da 21 hr from 12 wk 3 da 14 hr.
Exercise 9.8.29
(Solution on p. 574.)
Subtract 2 T 1,850 lb from 10 T 1,700 lb.
Exercise 9.8.30
Subtract the sum of 2 wk 3 da 15 hr and 5 wk 2 da 9 hr from 10 wk.
Exercise 9.8.31
(Solution on p. 574.)
Subtract the sum of 20 hr 15 min and 18 hr 18 min from the sum of 8 da 1 hr 16 min 5 sec.
For problems 32-43, simplify, if necessary.
Exercise 9.8.32
18 in.
Exercise 9.8.33
(Solution on p. 574.)
4 ft
Exercise 9.8.34
23 da
Exercise 9.8.35
(Solution on p. 574.)
3,100 lb
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
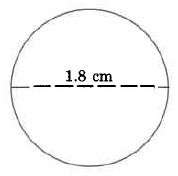
561
Exercise 9.8.36
135 min
Exercise 9.8.37
(Solution on p. 574.)
4 tsp
Exercise 9.8.38
10 oz
Exercise 9.8.39
(Solution on p. 574.)
7 pt
Exercise 9.8.40
9 qt
Exercise 9.8.41
(Solution on p. 574.)
2,300 mm
Exercise 9.8.42
14,780 mL
Exercise 9.8.43
(Solution on p. 574.)
1,050 m
9.8.1.4 Perimeter, Circumference, Area and Volume of Geometric Figures and Objects (Section 9.5,Section 9.6)
For problems 44-58, nd the perimeter, circumference, area or volume.
Exercise 9.8.44
Perimeter, area
Exercise 9.8.45
(Solution on p. 574.)
Approximate circumference
Exercise 9.8.46
Approximate volume
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
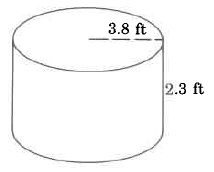

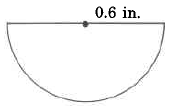
562
CHAPTER 9. MEASUREMENT AND GEOMETRY
Exercise 9.8.47
(Solution on p. 574.)
Approximate volume
Exercise 9.8.48
Exact area
Exercise 9.8.49
(Solution on p. 574.)
Exact area
Exercise 9.8.50
Exact volume
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

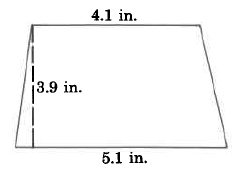
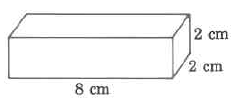

563
Exercise 9.8.51
(Solution on p. 575.)
Approximate volume
Exercise 9.8.52
Area
Exercise 9.8.53
(Solution on p. 575.)