131 Fundamentals of Mathematics: Part 13
Volume Formula
Statement
V
Rectangular solid
R
=
l · w · h
The volume of a rectan-
=
(area of base) · (height)
gular solid is the length
times the width times
the height.
Sphere
VS = 4 · π · r3
The volume of a sphere
3
is 4 times π times the
3
cube of the radius.
continued on next page
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

549
V
Cylinder
Cyl
=
π · r2 · h
The volume of a cylin-
=
(area of base) · (height)
der is π times the square
of the radius times the
height.
V
· π · r2 · h
Cone
c
=
1
3
The volume of a cone
=
(area of base) · (height)
is 1 times π times the
3
square of the radius
times the height.
Table 9.6
9.6.7 Finding Volumes of Some Common Geometric Objects
9.6.7.1 Sample Set B
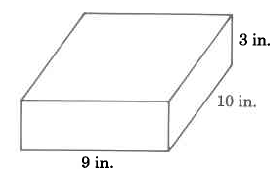
Example 9.32
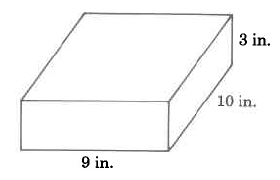
Find the volume of the rectangular solid.
VR
=
l · w · h
=
9 in. · 10 in. · 3 in.
=
270 cu in.
=
270 in.3
The volume of this rectangular solid is 270 cu in.
Example 9.33
Find the approximate volume of the sphere.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
550
CHAPTER 9. MEASUREMENT AND GEOMETRY
VS
=
4 · π · r3
3
≈
4 · (3.14) · (6 cm)3
3
≈
4 · (3.14) · (216 cu cm)
3
≈
904.32 cu cm
The approximate volume of this sphere is 904.32 cu cm, which is often written as 904.32 cm3.
Example 9.34
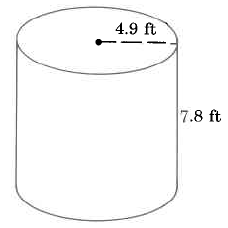
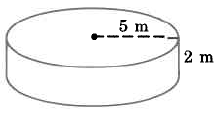
Find the approximate volume of the cylinder.
VCyl
=
π · r2 · h
≈
(3.14) · (4.9 ft)2 · (7.8 ft)
≈
(3.14) · (24.01 sq ft) · (7.8 ft)
≈
(3.14) · (187.278 cu ft)
≈
588.05292 cu ft
The volume of this cylinder is approximately 588.05292 cu ft. The volume is approximate because we approximated π with 3.14.
Example 9.35
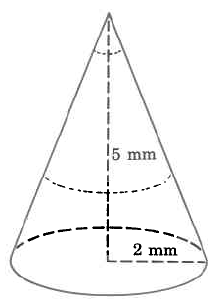
Find the approximate volume of the cone. Round to two decimal places.
Vc
=
1 · π · r2 · h
3
≈
1 · (3.14) · (2 mm)2 · (5 mm)
3
≈
1 · (3.14) · (4 sq mm) · (5 mm)
3
≈
1 · (3.14) · (20 cu mm)
3
≈
20.93 cu mm
≈
20.93 cu mm
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

551
The volume of this cone is approximately 20.93 cu mm. The volume is approximate because we approximated π with 3.14.
9.6.7.2 Practice Set B
Find the volume of each geometric object. If π is required, approximate it with 3.14 and nd the approximate volume.
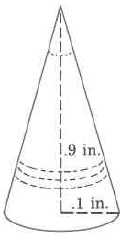
Exercise 9.6.7
(Solution on p. 573.)
Exercise 9.6.8
(Solution on p. 573.)
Sphere
Exercise 9.6.9
(Solution on p. 573.)
Exercise 9.6.10
(Solution on p. 573.)
9.6.8 Exercises
Find each indicated measurement.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
552
CHAPTER 9. MEASUREMENT AND GEOMETRY
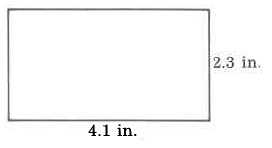
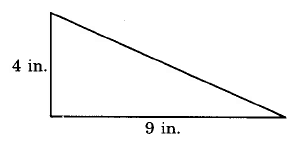
Exercise 9.6.11
(Solution on p. 573.)
Area
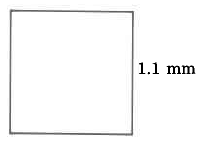
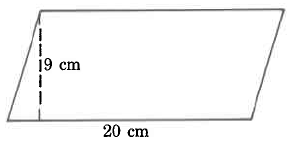
Exercise 9.6.12
Area
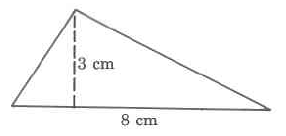
Exercise 9.6.13
(Solution on p. 573.)
Area
Exercise 9.6.14
Area
Exercise 9.6.15
(Solution on p. 573.)
Area
Exercise 9.6.16
Area
Exercise 9.6.17
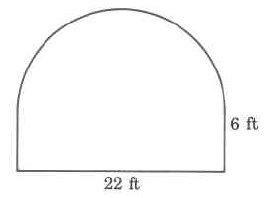
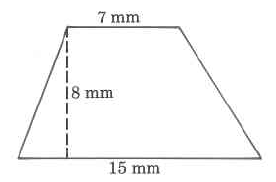
(Solution on p. 573.)
Exact area
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

553
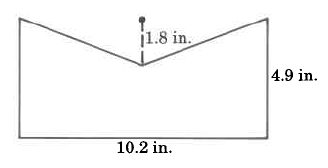
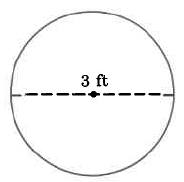
Exercise 9.6.18
Approximate area
Exercise 9.6.19
(Solution on p. 573.)
Area
Exercise 9.6.20
Area
Exercise 9.6.21
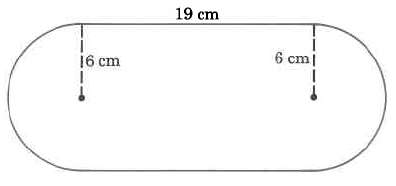
(Solution on p. 573.)
Approximate area
Exercise 9.6.22
Exact area
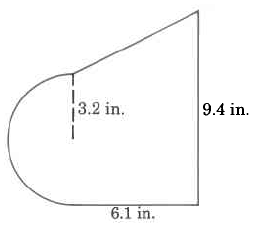
Exercise 9.6.23
(Solution on p. 573.)
Approximate area
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

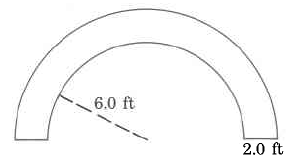
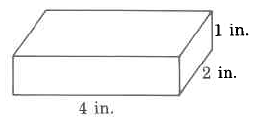
554
CHAPTER 9. MEASUREMENT AND GEOMETRY
Exercise 9.6.24
Exact area
Exercise 9.6.25
(Solution on p. 573.)
Approximate area
Exercise 9.6.26
Area
Exercise 9.6.27
(Solution on p. 573.)
Approximate area
Exercise 9.6.28