129 Fundamentals of Mathematics: Part 11
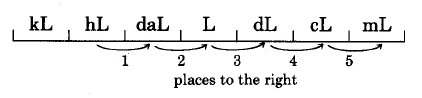
Volume
1 dekaliter (daL) = 10 liters
10 × 1 L
1 liter (L)
1 × 1 L
1 deciliter (dL) = 110 liter
.1 × 1 L
1 centiliter (cL) = 1
100 liter
.01 × 1 L
1 milliliter (mL) = 1
1,000
liter
.001 × 1 L
Time
Same as the United States system
Table 9.4
Distinction Between Mass and Weight
There is a distinction between mass and weight. The weight of a body is related to gravity whereas the mass of a body is not. For example, your weight on the earth is dierent than it is on the moon, but your mass is the same in both places. Mass is a measure of a body’s resistance to motion. The more massive a body, the more resistant it is to motion. Also, more massive bodies weigh more than less massive bodies.
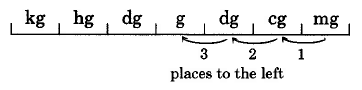
Converting Metric Units
To convert from one metric unit to another metric unit:
1. Determine the location of the original number on the metric scale (pictured in each of the following examples).
2. Move the decimal point of the original number in the same direction and same number of places as is necessary to move to the metric unit you wish to go to.
We can also convert from one metric unit to another using unit fractions. Both methods are shown in Example 9.4 of Section 9.3.5.1 (Sample Set A).
9.3.5.1 Sample Set A
Example 9.4
Convert 3 kilograms to grams.
(a) 3 kg can be written as 3.0 kg. Then,
Thus, 3kg = 3,000 g.
(b) We can also use unit fractions to make this conversion. Since we are converting to grams, and 1, 000
g = 1 kg, we choose the unit fraction 1,000 g
1 kg
since grams is in the numerator.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
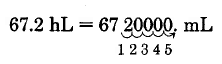
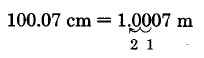
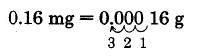
522
CHAPTER 9. MEASUREMENT AND GEOMETRY
3 kg =
3 kg · 1,000 g
1 kg
=
3 ) kg · 1,000 g
1 )kg
=
3 · 1, 000 g
=
3,000 g
Example 9.5
Convert 67.2 hectoliters to milliliters.
Thus, 67.2 hL = 6,720,000 mL.
Example 9.6
Convert 100.07 centimeters to meters.
Thus, 100.07 cm = 1.0007 m.
Example 9.7
Convert 0.16 milligrams to grams.
Thus, 0.16 mg = 0.00016 g.
9.3.5.2 Practice Set A
Exercise 9.3.1
(Solution on p. 569.)
Convert 411 kilograms to grams.
Exercise 9.3.2
(Solution on p. 569.)
Convert 5.626 liters to centiliters.
Exercise 9.3.3
(Solution on p. 570.)
Convert 80 milliliters to kiloliters.
Exercise 9.3.4
(Solution on p. 570.)
Convert 150 milligrams to centigrams.
Exercise 9.3.5
(Solution on p. 570.)
Convert 2.5 centimeters to meters.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
9.3.6 Exercises
Make each conversion.
Exercise 9.3.6
(Solution on p. 570.)
87 m to cm
Exercise 9.3.7
905 L to mL
Exercise 9.3.8
(Solution on p. 570.)
16,005 mg to g
Exercise 9.3.9
48.66 L to dL
Exercise 9.3.10
(Solution on p. 570.)
11.161 kL to L
Exercise 9.3.11
521.85 cm to mm
Exercise 9.3.12
(Solution on p. 570.)
1.26 dag to dg
Exercise 9.3.13
99.04 dam to cm
Exercise 9.3.14
(Solution on p. 570.)
0.51 kL to daL
Exercise 9.3.15
0.17 kL to daL
Exercise 9.3.16
(Solution on p. 570.)
0.05 m to dm
Exercise 9.3.17
0.001 km to mm
Exercise 9.3.18
(Solution on p. 570.)
8.106 hg to cg
Exercise 9.3.19
17.0186 kL to mL
Exercise 9.3.20
(Solution on p. 570.)
3 cm to m
Exercise 9.3.21
9 mm to m
Exercise 9.3.22
(Solution on p. 570.)
4 g to mg
Exercise 9.3.23
2 L to kL
Exercise 9.3.24
(Solution on p. 570.)
6 kg to mg
Exercise 9.3.25
7 daL to mL
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 9. MEASUREMENT AND GEOMETRY
9.3.6.1 Exercises for Review
Exercise 9.3.26
(Solution on p. 570.)
(Section 5.3) Find the value of 5 − 1 + 3.
8
3
4
Exercise 9.3.27
(Section 7.3) Solve the proportion: 9 = 27
x
60 .
Exercise 9.3.28
(Solution on p. 570.)
(Section 8.2) Use the method of rounding to estimate the sum: 8, 226 + 4, 118.
Exercise 9.3.29
(Section 8.3) Use the clustering method to estimate the sum: 87 + 121 + 118 + 91 + 92.
Exercise 9.3.30
(Solution on p. 570.)
(Section 9.2) Convert 3 in. to yd.
9.4 Simplication of Denominate Numbers4
9.4.1 Section Overview
• Converting to Multiple Units
• Adding and Subtracting Denominate Numbers
• Multiplying a Denominate Number by a Whole Number
• Dividing a Denominate Number by a Whole Number
9.4.2 Converting to Multiple Units
Denominate Numbers
Numbers that have units of measure associated with them are called denominate numbers. It is often convenient, or even necessary, to simplify a denominate number.
Simplied Denominate Number
A denominate number is simplied when the number of standard units of measure associated With it does not exceed the next higher type of unit.
The denominate number 55 min is simplied since it is smaller than the next higher type of unit, 1 hr. The denominate number 65 min is not simplied since it is not smaller than the next higher type of unit, 1 hr.
The denominate number 65 min can be simplied to 1 hr 5 min. The denominate number 1 hr 5 min is simplied since the next higher type of unit is day, and 1 hr does not exceed 1 day.
9.4.2.1 Sample Set A
Example 9.8
Simplify 19 in.
Since 12 in. = 1 ft, and 19 = 12 + 7,
19 in. = 12 in. + 7 in.
=
1 ft + 7 in.
=
1 ft 7 in.
4This content is available online at <http://cnx.org/content/m35021/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Example 9.9
Simplify 4 gal 5 qt.
Since 4 qt = 1 gal, and 5 = 4 + 1,
4 gal 5 qt =
4 gal + 4 qt + 1qt
=
4 gal + 1 gal + 1 qt
=
5 gal + 1 qt
=
5 gal 1 qt
Example 9.10
Simplify 2 hr 75 min.
Since 60 min = 1 hr, and 75 = 60 + 15,
2 hr 75 min = 2 hr + 60 min + 15 min
=
2 hr + 1 hr + 15 min
=
3 hr + 15 min
=
3 hr 15 min
Example 9.11
Simplify 43 oz.
Since 8 oz = 1 c (1 cup), and 43 ÷ 8 = 5 R3,
43 oz =
40 oz + 3 oz
=
5 · 8 oz + 3 oz
=
5 · 1 c + 3 oz
=
5 c + 3 oz
But, 2 c = 1 pt and 5 ÷ 2 = 2 R1. So,
5 c + 3 oz =
2 · 2 c + 1 c + 3 oz
=
2 · 1 pt + 1 c + 3 oz
=
2 pt + 1 c + 3 oz
But, 2 pt = 1 qt, so
2 pt + 1 c + 3 oz = 1 qt 1 c 3 oz
9.4.2.2 Practice Set A
Simplify each denominate number. Refer to the conversion tables given in Section 9.2, if necessary.
Exercise 9.4.1
(Solution on p. 570.)
18 in.
Exercise 9.4.2
(Solution on p. 570.)
8 gal 9 qt
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 9. MEASUREMENT AND GEOMETRY
Exercise 9.4.3
(Solution on p. 570.)
5 hr 80 min
Exercise 9.4.4
(Solution on p. 570.)
8 wk 11 da
Exercise 9.4.5
(Solution on p. 570.)
86 da
9.4.3 Adding and Subtracting Denominate Numbers
Adding and Subtracting Denominate Numbers
Denominate numbers can be added or subtracted by:
1. writing the numbers vertically so that the like units appear in the same column.
2. adding or subtracting the number parts, carrying along the unit.
3. simplifying the sum or dierence.
9.4.3.1 Sample Set B
Example 9.12
Add 6 ft 8 in. to 2 ft 9 in.
6 ft 8 in.
+2 ft 9 in.
8 ft 17 in. Simplify this denominate number.
Since 12 in. = 1 ft,
8 ft + 12 in. + 5 in. = 8 ft + 1 ft + 5 in.
=
9 ft + 5 in.
=
9 ft 5 in.
Example 9.13
Subtract 5 da 3 hr from 8 da 11 hr.
8 da 11 hr
−5 da 3 hr
3 da 8 hr
Example 9.14
Subtract 3 lb 14 oz from 5 lb 3 oz.
5 lb 3 oz
−3 lb 14 oz
We cannot directly subtract 14 oz from 3 oz, so we must borrow 16 oz from the pounds.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
5 lb 3 oz =
5 lb + 3 oz
=
4 lb + 1 lb + 3 oz
=
4 lb + 16 oz + 3 oz
(Since 1 lb = 16 oz.)
=
4 lb + 19 oz
=
4 lb 19 oz
4 lb 19 oz
−3 lb 14 oz
1 lb 5 oz
Example 9.15
Subtract 4 da 9 hr 21 min from 7 da 10 min.
7 da 0 hr 10 min Borrow 1 da from the 7 da.
−4 da 9 hr 21 min
6 da 24 hr 10 min Borrow 1 hr from the 24 hr.
−4 da 9 hr 21 min
6 da 23 hr 70 min
−4 da 9 hr 21 min
2 da 14 hr 49 min
9.4.3.2 Practice Set B
Perform each operation. Simplify when possible.
Exercise 9.4.6
(Solution on p. 570.)
Add 4 gal 3 qt to 1 gal 2 qt.
Exercise 9.4.7
(Solution on p. 570.)
Add 9 hr 48 min to 4 hr 26 min.
Exercise 9.4.8
(Solution on p. 570.)
Subtract 2 ft 5 in. from 8 ft 7 in.
Exercise 9.4.9
(Solution on p. 570.)
Subtract 15 km 460 m from 27 km 800 m.
Exercise 9.4.10
(Solution on p. 571.)
Subtract 8 min 35 sec from 12 min 10 sec.
Exercise 9.4.11
(Solution on p. 571.)
Add 4 yd 2 ft 7 in. to 9 yd 2 ft 8 in.
Exercise 9.4.12
(Solution on p. 571.)
Subtract 11 min 55 sec from 25 min 8 sec.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 9. MEASUREMENT AND GEOMETRY
9.4.4 Multiplying a Denominate Number by a Whole Number
Let’s examine the repeated sum
4 ft 9 in. + 4 ft 9 in. + 4 ft 9 in. = 12 ft 27 in.
|
{z
}
3 times
Recalling that multiplication is a description of repeated addition, by the distributive property we have 3 (4 ft 9 in.) =
3 (4 ft + 9 in.)
=
3 · 4 ft + 3 · 9 in.
=
12 ft + 27 in.
Now, 27 in. = 2 ft 3 in.
=
12 ft + 2 ft + 3 in.
=
14 ft + 3 in.
=
14 ft 3 in.
From these observations, we can suggest the following rule.
Multiplying a Denominate Number by a Whole Number
To multiply a denominate number by a whole number, multiply the number part of each unit by the whole number and ax the unit to this product.
9.4.4.1 Sample Set C
Perform the following multiplications. Simplify if necessary.
Example 9.16
6 · (2 ft 4 in.) = 6 · 2 ft + 6 · 4 in.
=
12 ft + 24 in.
Since 3 ft = 1 yd and 12 in. = 1 ft,
12 ft + 24 in. = 4 yd + 2 ft
=
4 yd 2 ft
Example 9.17
8 · (5 hr 21 min 55 sec) =
8 · 5 hr + 8 · 21 min + 8 · 55 sec
=
40 hr + 168 min + 440sec
=
40 hr + 168 min + 7 min + 20 sec
=
40 hr + 175 min + 20 sec
=
40 hr + 2 hr + 55 min + 20 sec
=
42 hr + 55 min + 20 sec
=
24hr + 18hr + 55 min + 20 sec
=
1 da + 18 hr + 55 min + 20 sec
=
1 da 18 hr 55 min 20 sec
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
529
9.4.4.2 Practice Set C
Perform the following multiplications. Simplify.
Exercise 9.4.13
(Solution on p. 571.)
2 · (10 min)
Exercise 9.4.14
(Solution on p. 571.)
5 · (3 qt)
Exercise 9.4.15
(Solution on p. 571.)
4 · (5 ft 8 in.)
Exercise 9.4.16
(Solution on p. 571.)
10 · (2 hr 15 min 40 sec)
9.4.5 Dividing a Denominate Number by a Whole Number
Dividing a Denominate Number by a Whole Number
To divide a denominate number by a whole number, divide the number part of each unit by the whole number beginning with the largest unit. Ax the unit to this quotient. Carry any remainder to the next unit.
9.4.5.1 Sample Set D
Perform the following divisions. Simplify if necessary.
Example 9.18
(12 min 40 sec) ÷ 4
Thus (12 min 40 sec) ÷ 4 = 3 min 10 sec
Example 9.19
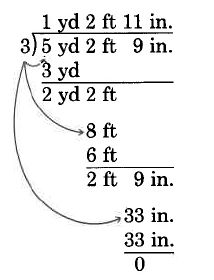
(5 yd 2 ft 9 in.) ÷ 3
Convert to feet: 2 yd 2 ft = 8 ft .
Convert to inches: 2 ft 9 in . = 33 in .
Thus (5 yd 2 ft 9 in.) ÷ 3 = 1 yd 2 ft 11 in.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 9. MEASUREMENT AND GEOMETRY
9.4.5.2 Practice Set D
Perform the following divisions. Simplify if necessary.
Exercise 9.4.17
(Solution on p. 571.)
(18 hr 36 min) ÷ 9
Exercise 9.4.18
(Solution on p. 571.)
(34 hr 8 min.) ÷ 8
Exercise 9.4.19
(Solution on p. 571.)
(13 yd 7 in.) ÷ 5
Exercise 9.4.20
(Solution on p. 571.)
(47 gal 2 qt 1 pt) ÷ 3
9.4.6 Exercises
For the following 15 problems, simplify the denominate numbers.
Exercise 9.4.21
(Solution on p. 571.)
16 in.
Exercise 9.4.22
19 ft
Exercise 9.4.23
(Solution on p. 571.)
85 min
Exercise 9.4.24
90 min
Exercise 9.4.25
(Solution on p. 571.)
17 da
Exercise 9.4.26
25 oz
Exercise 9.4.27
(Solution on p. 571.)
240 oz
Exercise 9.4.28
3,500 lb
Exercise 9.4.29
(Solution on p. 571.)
26 qt
Exercise 9.4.30
300 sec
Exercise 9.4.31
(Solution on p. 571.)
135 oz
Exercise 9.4.32
14 tsp
Exercise 9.4.33
(Solution on p. 571.)
18 pt
Exercise 9.4.34
3,500 m
Exercise 9.4.35
(Solution on p. 571.)
16,300 mL
For the following 15 problems, perform the indicated operations and simplify the answers if possible.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 9.4.36
Add 6 min 12 sec to 5 min 15 sec.
Exercise 9.4.37
(Solution on p. 571.)
Add 14 da 6 hr to 1 da 5 hr.
Exercise 9.4.38
Add 9 gal 3 qt to 2 gal 3 qt.
Exercise 9.4.39
(Solution on p. 571.)
Add 16 lb 10 oz to 42 lb 15 oz.
Exercise 9.4.40
Subtract 3 gal 1 qt from 8 gal 3 qt.
Exercise 9.4.41
(Solution on p. 571.)
Subtract 3 ft 10 in. from 5 ft 8 in.
Exercise 9.4.42
Subtract 5 lb 9 oz from 12 lb 5 oz.
Exercise 9.4.43
(Solution on p. 571.)
Subtract 10 hr 10 min from 11 hr 28 min.
Exercise 9.4.44
Add 3 oz 1 tbsp 2 tsp to 5 oz 1 tbsp 2 tsp.
Exercise 9.4.45
(Solution on p. 571.)
Add 4 da 7 hr 12 min to 1 da 8 hr 53 min.
Exercise 9.4.46
Subtract 5 hr 21 sec from 11 hr 2 min 14 sec.
Exercise 9.4.47
(Solution on p. 571.)
Subtract 6 T 1,300 lb 10 oz from 8 T 400 lb 10 oz.
Exercise 9.4.48
Subtract 15 mi 10 in. from 27 mi 800 ft 7 in.
Exercise 9.4.49
(Solution on p. 572.)
Subtract 3 wk 5 da 50 min 12 sec from 5 wk 6 da 20 min 5 sec.
Exercise 9.4.50
Subtract 3 gal 3 qt 1 pt 1 oz from 10 gal 2 qt 2 oz.
9.4.6.1 Exercises for Review
Exercise 9.4.51
(Solution on p. 572.)
(Section 4.6) Find the value: 52 + 39
8
64 .
Exercise 9.4.52
(Section 5.4) Find the sum: 8 + 63.
5
Exercise 9.4.53
(Solution on p. 572.)
(Section 6.3) Convert 2.05 111 to a fraction.
Exercise 9.4.54
(Section 7.4) An acid solution is composed of 3 parts acid to 7 parts water. How many parts of acid are there in a solution that contains 126 parts water?
Exercise 9.4.55
(Solution on p. 572.)
(Section 9.3) Convert 126 kg to grams.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>


532
CHAPTER 9. MEASUREMENT AND GEOMETRY
9.5 Perimeter and Circumference of Geometric Figures5
9.5.1 Section Overview
• Polygons
• Perimeter
• Circumference/Diameter/Radius
• The Number π
• Formulas
9.5.2 Polygons
We can make use of conversion skills with denominate numbers to make measurements of geometric gures such as rectangles, triangles, and circles. To make these measurements we need to be familiar with several denitions.
Polygon
A polygon is a closed plane (at) gure whose sides are line segments (portions of straight lines).
Polygons
Not polygons
9.5.3 Perimeter
Perimeter
The perimeter of a polygon is the distance around the polygon.
To nd the perimeter of a polygon, we simply add up the lengths of all the sides.
9.5.3.1 Sample Set A
Find the perimeter of each polygon.
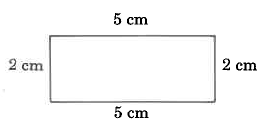
Example 9.20
5This content is available online at <http://cnx.org/content/m35022/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
533
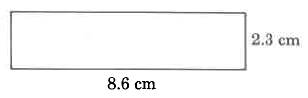
Perimeter = 2 cm + 5 cm + 2 cm + 5 cm
=
14 cm
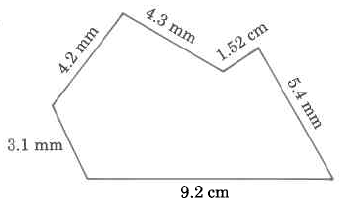
Example 9.21
Perimeter =
3.1 mm
4.2 mm
4.3 mm
1.52 mm
5.4 mm
+9.2 mm
27.72 mm
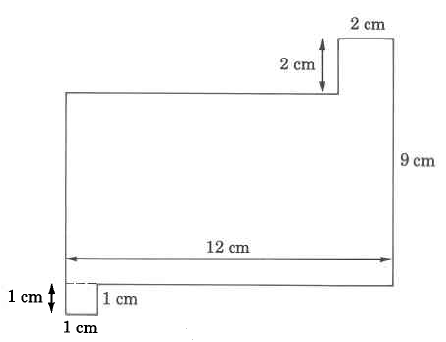
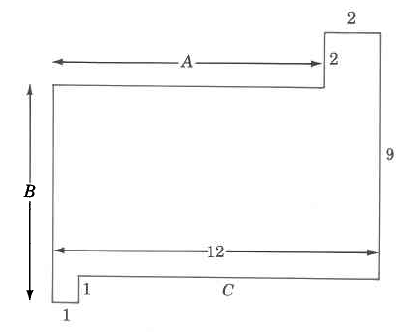
Example 9.22
Our rst observation is that three of the dimensions are missing. However, we can determine the missing measurements using the following process. Let A, B, and C represent the missing measurements. Visualize
A = 12m − 2m = 10m
B = 9m + 1m − 2m = 8m
C = 12m − 1m = 11m
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
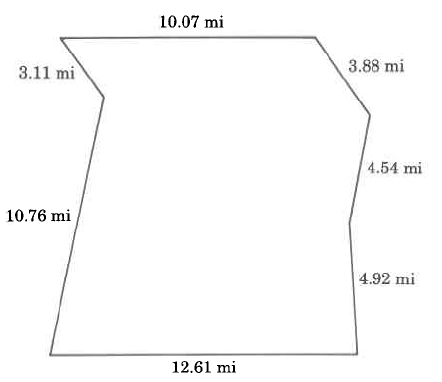
534
CHAPTER 9. MEASUREMENT AND GEOMETRY
Perimeter =
8 m
10 m
2 m
2 m
9 m
11 m
1 m
+ 1 m
44 m
9.5.3.2 Practice Set A
Find the perimeter of each polygon.
Exercise 9.5.1
(Solution on p. 572.)
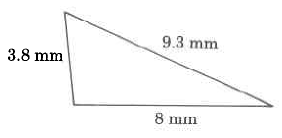
Exercise 9.5.2
(Solution on p. 572.)
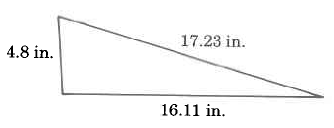
Exercise 9.5.3
(Solution on p. 572.)
9.5.4 Circumference/Diameter/Radius
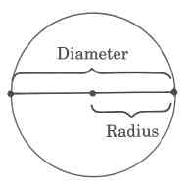
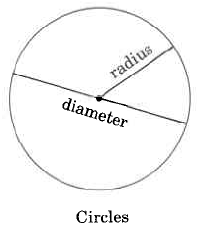
Circumference
The circumference of a circle is the distance around the circle.
Diameter
A diameter of a circle is any line segment that passes through the center of the circle and has its endpoints on the circle.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
535
Radius
A radius of a circle is any line segment having as its endpoints the center of the circle and a point on the circle.
The radius is one half the diameter.
9.5.5 The Number π
The symbol π, read “pi,” represents the nonterminating, nonrepeating decimal number 3.14159 . . . . This number has been computed to millions of decimal places without the appearance of a repeating block of digits.
For computational purposes, π is often approximated as 3.14. We will write π ≈ 3.14 to denote that π is approximately equal to 3.14. The symbol “≈” means “approximately equal to.”
9.5.6 Formulas
To nd the circumference of a circle, we need only know its diameter or radius. We then use a formula for computing the circumference of the circle.
Formula
A formula is a rule or method for performing a task. In mathematics, a formula is a rule that directs us in computations.
Formulas are usually composed of letters that represent important, but possibly unknown, quantities.
If C, d, and r represent, respectively, the circumference, diameter, and radius of a circle, then the following two formulas give us directions for computing the circumference of the circle.
Circumference Formulas
1. C = πd or C ≈ (3.14) d
2. C = 2πr or C ≈ 2 (3.14) r
9.5.6.1 Sample Set B
Example 9.23
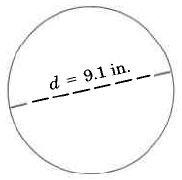
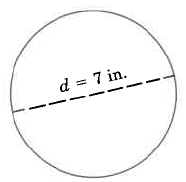
Find the exact circumference of the circle.
Use the formula C = πd.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
536
CHAPTER 9. MEASUREMENT AND GEOMETRY
C = π · 7in.
By commutativity of multiplication,
C = 7in. · π
C = 7πin., exactly
This result is exact since π has not been approximated.
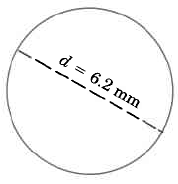
Example 9.24
Find the approximate circumference of the circle.
Use the formula C = πd.
C ≈ (3.14) (6.2)
C ≈ 19.648 mm
This result is approximate since π has been approximated by 3.14.
Example 9.25
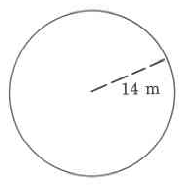
Find the approximate circumference of a circle with radius 18 inches.
Since we’re given that the radius, r, is 18 in., we’ll use the formula C = 2πr.
C ≈ (2) (3.14) (18 in.)
C ≈ 113.04 in.
Example 9.26
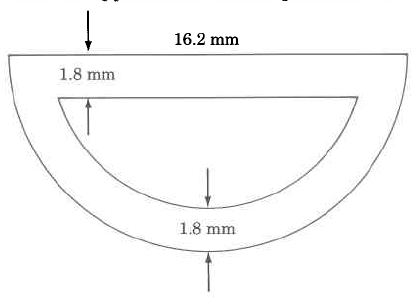
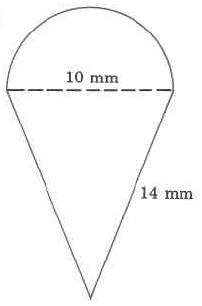
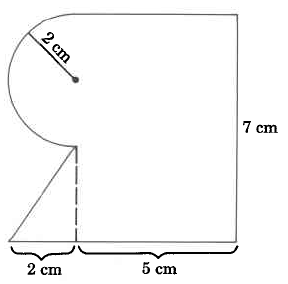
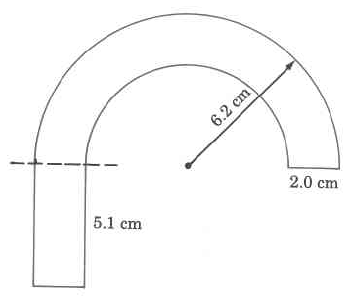
Find the approximate perimeter of the gure.
We notice that we have two semicircles (half circles).
The larger radius is 6.2 cm.
The smaller radius is 6.2 cm – 2.0 cm = 4.2 cm.
The width of the bottom part of the rectangle is 2.0 cm.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
537
Perimeter
=
2.0 cm
5.1 cm
2.0 cm
5.1 cm
(0.5) · (2) · (3.14) · (6.2 cm)
Circumference of outer semicircle.
+
(0.5) · (2) · (3.14) · (4.2 cm)
Circumference of inner semicircle
6.2 cm − 2.0 cm = 4.2 cm
The 0.5 appears because we want the
perimeter of only half a circle.
Perimeter ≈
2.0
cm
5.1
cm
2.0
cm
5.1
cm
19.468 cm
+13.188 cm
48.856 cm
9.5.6.2 Practice Set B
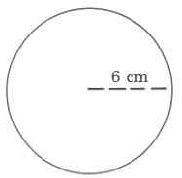
Exercise 9.5.4
(Solution on p. 572.)
Find the exact circumference of the circle.
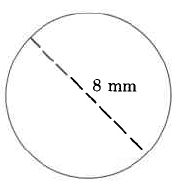
Exercise 9.5.5
(Solution on p. 572.)
Find the approximate circumference of the circle.
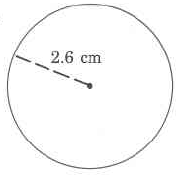
Exercise 9.5.6
(Solution on p. 572.)
Find the approximate circumference of the circle with radius 20.1 m.
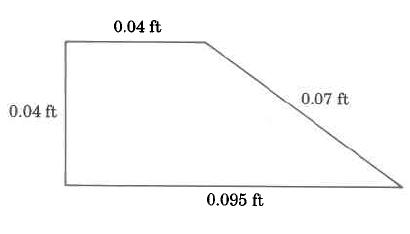
Exercise 9.5.7
(Solution on p. 572.)
Find the approximate outside perimeter of
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
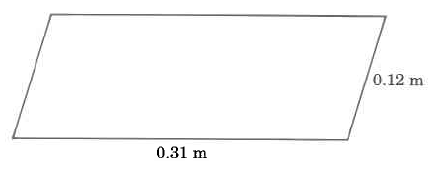
538
CHAPTER 9. MEASUREMENT AND GEOMETRY
9.5.7 Exercises
Find each perimeter or approximate circumference. Use π = 3.14.
Exercise 9.5.8
(Solution on p. 572.)
Exercise 9.5.9
Exercise 9.5.10
(Solution on p. 572.)
Exercise 9.5.11
Exercise 9.5.12
(Solution on p. 572.)
Exercise 9.5.13
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
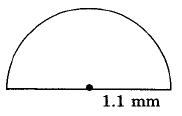
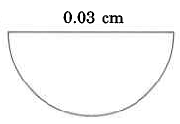
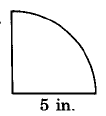
539
Exercise 9.5.14
(Solution on p. 572.)
Exercise 9.5.15
Exercise 9.5.16
(Solution on p. 572.)
Exercise 9.5.17
Exercise 9.5.18
(Solution on p. 572.)
Exercise 9.5.19
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
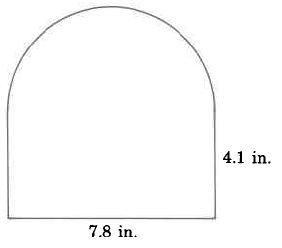

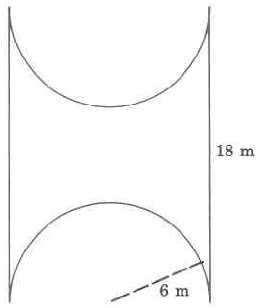
540
CHAPTER 9. MEASUREMENT AND GEOMETRY
Exercise 9.5.20
(Solution on p. 572.)
Exercise 9.5.21
Exercise 9.5.22
(Solution on p. 572.)
Exercise 9.5.23
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
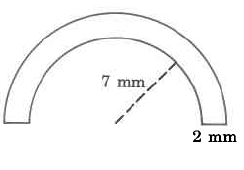
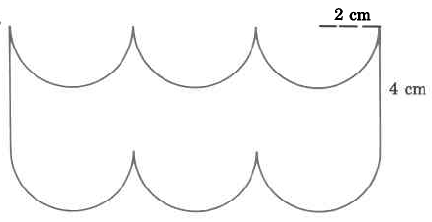
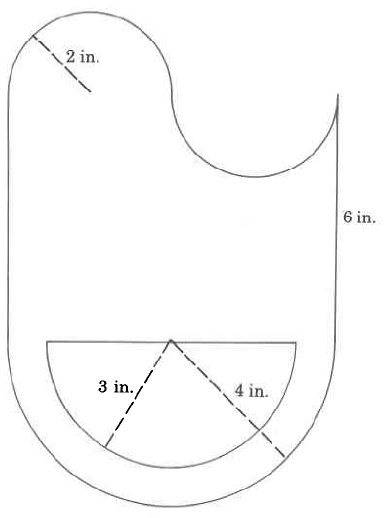
541
Exercise 9.5.24
(Solution on p. 572.)
Exercise 9.5.25
Exercise 9.5.26
(Solution on p. 572.)
Exercise 9.5.27
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 9. MEASUREMENT AND GEOMETRY
9.5.7.1 Exercises for Review
Exercise 9.5.28
(Solution on p. 572.)
q
(Section 4.5) Find the value of 2 813 · 10 916.
Exercise 9.5.29
(Section 5.3) Find the value of 815 + 710 + 21
60 .
Exercise 9.5.30
(Solution on p. 572.)
(Section 6.9) Convert 7 to a decimal.
8
Exercise 9.5.31
(Section 9.2) What is the name given to a quantity that is used as a comparison to determine the measure of another quantity?
Exercise 9.5.32
(Solution on p. 572.)
(Section 9.4) Add 42 min 26 sec to 53 min 40 sec and simplify the result.
9.6 Area and Volume of Geometric Figures and Objects6
9.6.1 Section Overview
• The Meaning and Notation for Area
• Area Formulas
• Finding Areas of Some Common Geometric Figures
• The Meaning and Notation for Volume
• Volume Formulas
• Finding Volumes of Some Common Geometric Objects
Quite often it is necessary to multiply one denominate number by another. To do so, we multiply the number parts together and the unit parts together. For example,
8 in. · 8 in. = 8 · 8 · in. · in.
=
64 in.2
4 mm · 4 mm · 4 mm = 4 · 4 · 4 · mm · mm · mm
=
64 mm3
Sometimes the product of units has a physical meaning. In this section, we will examine the meaning of the products (length unit)2 and (length unit)3.
9.6.2 The Meaning and Notation for Area
The product (length unit) · (length unit) = (length unit)2, or, square length unit (sq length unit), can be interpreted physically as the area of a surface.
Area
The area of a surface is the amount of square length units contained in the surface.
For example, 3 sq in. means that 3 squares, 1 inch on each side, can be placed precisely on some surface.
(The squares may have to be cut and rearranged so they match the shape of the surface.) 6This content is available online at <http://cnx.org/content/m35023/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

543
We will examine the area of the following geometric gures.
9.6.3 Area Formulas
We can determine the areas of these geometric gures using the following formulas.
Figure
Area Formula
Statement
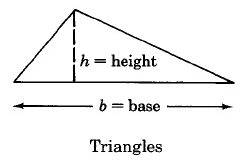
Triangle
AT = 1 · b · h
Area of a triangle is one
2
half the base times the
height.
Rectangle
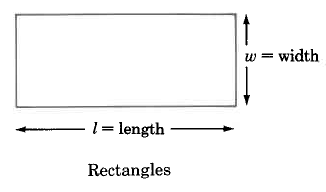
AR = l · w
Area of a rectangle is
the length times the
width.
continued on next page
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

544
CHAPTER 9. MEASUREMENT AND GEOMETRY
Parallelogram
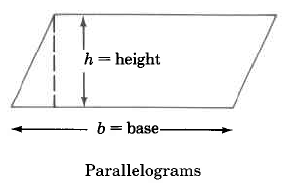
AP = b · h
Area of a parallelogram
is base times the height.
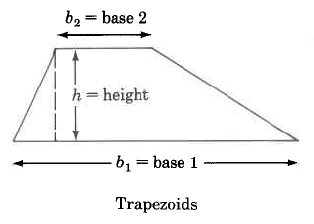
Trapezoid
ATrap = 1 · (b
2
1 + b2) · h
Area of a trapezoid is
one half the sum of
the two bases times the
height.
Circle
AC = πr2
Area of a circle is π
times the square of the
radius.
Table 9.5
9.6.4 Finding Areas of Some Common Geometric Figures
9.6.4.1 Sample Set A
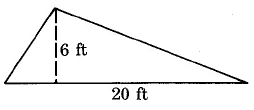
Example 9.27
Find the area of the triangle.
AT
=
1 · b · h
2
=
1 · 20 · 6 sq ft
2
=
10 · 6 sq ft
=
60 sq ft
=
60 ft2
The area of this triangle is 60 sq ft, which is often written as 60 ft2.
Example 9.28
Find the area of the rectangle.
Let’s rst convert 4 ft 2 in. to inches. Since we wish to convert to inches, we’ll use the unit fraction 12 in.
1 ft since it has inches in the numerator. Then,
4 ft
=
4 ft · 12 in.
1
1 ft
=
4) ft · 12 in.
1
1) ft
=
48 in.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>


545
Thus, 4 ft 2 in. = 48 in. + 2 in. = 50 in.
AR
=
l · w
=
50 in. · 8 in.
=
400 sq in.
The area of this rectangle is 400 sq in.
Example 9.29
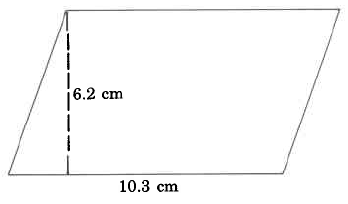
Find the area of the parallelogram.
AP
=
b · h
=
10.3 cm · 6.2 cm
=
63.86 sq cm
The area of this parallelogram is 63.86 sq cm.
Example 9.30
Find the area of the trapezoid.
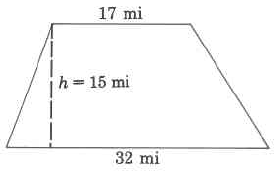
ATrap =
1 · (b
2
1 + b2) · h
=
1 · (14.5 mm, +, 20.4 mm) · (4.1 mm)
2
=
1 · (34.9 mm) · (4.1 mm)
2
=
1 · (143.09 sq mm)
2
=
71.545 sq mm
The area of this trapezoid is 71.545 sq mm.
Example 9.31
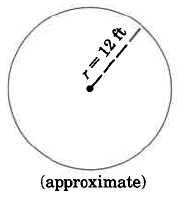
Find the approximate area of the circle.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>


546
CHAPTER 9. MEASUREMENT AND GEOMETRY
Ac
=
π · r2
≈
(3.14) · (16.8 ft)2
≈
(3.14) · (282.24 sq ft)
≈
888.23 sq ft
The area of this circle is approximately 886.23 sq ft.
9.6.4.2 Practice Set A
Find the area of each of the following geometric gures.
Exercise 9.6.1
(Solution on p. 572.)
Exercise 9.6.2
(Solution on p. 573.)
Exercise 9.6.3
(Solution on p. 573.)
Exercise 9.6.4
(Solution on p. 573.)
Exercise 9.6.5
(Solution on p. 573.)
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
547
Exercise 9.6.6
(Solution on p. 573.)
9.6.5 The Meaning and Notation for Volume
The product (length unit) (length unit) (length unit) = (length unit)3, or cubic length unit (cu length unit), can be interpreted physically as the volume of a three-dimensional object.