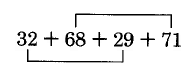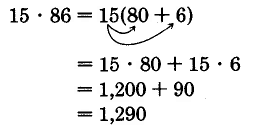128 Fundamentals of Mathematics: Part 10
Exercise 7.5.24
(Solution on p. 470.)
15%
Exercise 7.5.25
43%
Exercise 7.5.26
(Solution on p. 470.)
16.2%
Exercise 7.5.27
53.8%
Exercise 7.5.28
(Solution on p. 470.)
5.05%
Exercise 7.5.29
6.11%
Exercise 7.5.30
(Solution on p. 470.)
0.78%
Exercise 7.5.31
0.88%
Exercise 7.5.32
(Solution on p. 470.)
0.09%
Exercise 7.5.33
0.001%
For the following 14 problems, convert each fraction to a percent.
Exercise 7.5.34
(Solution on p. 470.)
1
5
Exercise 7.5.35
3
5
Exercise 7.5.36
(Solution on p. 470.)
5
8
Exercise 7.5.37
1
16
Exercise 7.5.38
(Solution on p. 470.)
7
25
Exercise 7.5.39
16
45
Exercise 7.5.40
(Solution on p. 470.)
27
55
Exercise 7.5.41
15
8
Exercise 7.5.42
(Solution on p. 470.)
41
25
Exercise 7.5.43
6 45
Exercise 7.5.44
(Solution on p. 470.)
9 9
20
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 7.5.45
1
200
Exercise 7.5.46
(Solution on p. 470.)
6
11
Exercise 7.5.47
35
27
For the following 14 problems, convert each percent to a fraction.
Exercise 7.5.48
(Solution on p. 470.)
80%
Exercise 7.5.49
60%
Exercise 7.5.50
(Solution on p. 470.)
25%
Exercise 7.5.51
75%
Exercise 7.5.52
(Solution on p. 470.)
65%
Exercise 7.5.53
18%
Exercise 7.5.54
(Solution on p. 470.)
12.5%
Exercise 7.5.55
37.5%
Exercise 7.5.56
(Solution on p. 470.)
512.5%
Exercise 7.5.57
937.5%
Exercise 7.5.58
(Solution on p. 470.)
_
9. 9 %
Exercise 7.5.59
_
55. 5 %
Exercise 7.5.60
(Solution on p. 470.)
_
22. 2 %
Exercise 7.5.61
_
63. 6 %
7.5.4.1 Exercises for Review
Exercise 7.5.62
(Solution on p. 470.)
(Section 4.6) Find the quotient. 40
54 ÷ 8 7
21 .
Exercise 7.5.63
(Section 4.7) 3 of what number is 22?
8
3
Exercise 7.5.64
(Solution on p. 470.)
(Section 5.3) Find the value of 28
15 + 7
10 − 5
12 .
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 7. RATIOS AND RATES
Exercise 7.5.65
(Section 6.4) Round 6.99997 to the nearest ten thousandths.
Exercise 7.5.66
(Solution on p. 470.)
(Section 7.4) On a map, 3 inches represent 40 miles. How many inches represent 480 miles?
7.6 Fractions of One Percent6
7.6.1 Section Overview
• Conversions Involving Fractions of One Percent
• Conversions Involving Nonterminating Fractions
7.6.2 Conversions Involving Fractions of One Percent
Percents such as 1%, 3 %, 5 %, and 7
2
5
8
11 %, where 1% has not been attained, are fractions of 1%. This implies that
1 % = 1 of 1%
2
2
3 % = 3 of 1%
5
5
5 % = 5 of 1%
8
8
7
11 % = 7
11 of 1%
Since “percent” means “for each hundred,” and “of” means “times,” we have 1 % = 1 of 1% = 1 · 1
2
2
2
100 = 1
200
3 % = 3 of 1% = 3 · 1
5
5
5
100 = 3
500
5 % = 5 of 1% = 5 · 1
8
8
8
100 = 5
800
7
11 % = 7
11 of 1% = 7
11 · 1
100 =
7
1100
7.6.2.1 Sample Set A
Example 7.31
Convert 2% to a fraction.
3
1
2 % = 2 of 1% = )2 · 1
3
3
3
)100
50
=
1·1
3·50
=
1
150
Example 7.32
Convert 5 % to a decimal.
8
6This content is available online at <http://cnx.org/content/m34997/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
5 % = 5 of 1% =
5 · 1
8
8
8
100
=
0.625 · 0.01
=
0.00625
7.6.2.2 Practice Set A
Exercise 7.6.1
(Solution on p. 470.)
Convert 1 % to a fraction.
4
Exercise 7.6.2
(Solution on p. 471.)
Convert 3 % to a fraction.
8
Exercise 7.6.3
(Solution on p. 471.)
Convert 31 % to a fraction.
3
7.6.3 Conversions Involving Nonterminating Fractions
We must be careful when changing a fraction of 1% to a decimal. The number 2, as we know, has a 3
nonterminating decimal representation. Therefore, it cannot be expressed exactly as a decimal.
When converting nonterminating fractions of 1% to decimals, it is customary to express the fraction as a rounded decimal with at least three decimal places.
Converting a Nonterminating Fraction to a Decimal
To convert a nonterminating fraction of 1% to a decimal:
1. Convert the fraction as a rounded decimal.
2. Move the decimal point two digits to the left and remove the percent sign.
7.6.3.1 Sample Set B
Example 7.33
Convert 2 % to a three-place decimal.
3
1. Convert 2 to a decimal.
3
Since we wish the resulting decimal to have three decimal digits, and removing the percent sign will account for two of them, we need to round 2 to one place (2 + 1 = 3).
3
2 % = 0.7% to one decimal place. 2 = 0.6666 . . .
3
3
2. Move the decimal point two digits to the left and remove the % sign. We’ll need to add zeros to locate the decimal point in the correct location.
2 % = 0.007 to 3 decimal places
3
Example 7.34
Convert 5 411% to a four-place decimal.
1. Since we wish the resulting decimal to have four decimal places, and removing the percent sign will account for two, we to round 411 to two places.
5 4
11 % = 5.36% to two decimal places.
4
11 = 0.3636 . . .
2. Move the decimal point two places to the left and drop the percent sign. 5 411% = 0.0536 to four decimal places.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 7. RATIOS AND RATES
Example 7.35
Convert 285% to a decimal rounded to ten thousandths.
9
1. Since we wish the resulting decimal to be rounded to ten thousandths (four decimal places), and removing the percent sign will account for two, we need to round 5 to two places.
9
285% = 28.56% to two decimal places. 5 = 0.5555 . . .
9
9
2. Move the decimal point to the left two places and drop the percent sign.
285% = 0.2856 correct to ten thousandths.
9
7.6.3.2 Practice Set B
Exercise 7.6.4
(Solution on p. 471.)
Convert 7% to a three-place decimal.
9
Exercise 7.6.5
(Solution on p. 471.)
Convert 51 5 % to a decimal rounded to ten thousandths.
11
7.6.4 Exercises
Make the conversions as indicated.
Exercise 7.6.6
(Solution on p. 471.)
Convert 3 % to a fraction.
4
Exercise 7.6.7
Convert 5% to a fraction.
6
Exercise 7.6.8
(Solution on p. 471.)
Convert 1% to a fraction.
9
Exercise 7.6.9
Convert 15
19 % to a fraction.
Exercise 7.6.10
(Solution on p. 471.)
Convert 5 % to a fraction.
4
Exercise 7.6.11
Convert 7% to a fraction.
3
Exercise 7.6.12
(Solution on p. 471.)
Convert 16% to a fraction.
7
Exercise 7.6.13
Convert 2 516% to a fraction.
Exercise 7.6.14
(Solution on p. 471.)
Convert 251% to a fraction.
4
Exercise 7.6.15
Convert 501% to a fraction.
2
Exercise 7.6.16
(Solution on p. 471.)
Convert 723% to a fraction.
5
Exercise 7.6.17
Convert 991% to a fraction.
8
Exercise 7.6.18
(Solution on p. 471.)
Convert 1362% to a fraction.
3
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 7.6.19
Convert 5213% to a fraction.
4
Exercise 7.6.20
(Solution on p. 471.)
Convert 101% to a decimal.
5
Exercise 7.6.21
Convert 123% to a decimal.
4
Exercise 7.6.22
(Solution on p. 471.)
Convert 37% to a decimal.
8
Exercise 7.6.23
Convert 7 116% to a decimal.
Exercise 7.6.24
(Solution on p. 471.)
Convert 3% to a three-place decimal.
7
Exercise 7.6.25
Convert 1% to a three-place decimal.
9
Exercise 7.6.26
(Solution on p. 471.)
Convert 6 311% to a four-place decimal.
Exercise 7.6.27
Convert 92% to a four-place decimal.
7
Exercise 7.6.28
(Solution on p. 471.)
Convert 24 521% to a three-place decimal.
Exercise 7.6.29
Convert 45 827% to a three-place decimal.
Exercise 7.6.30
(Solution on p. 471.)
Convert 1116
17 % to a four-place decimal.
Exercise 7.6.31
Convert 51% to a three-place decimal.
7
7.6.4.1 Exercises for Review
Exercise 7.6.32
(Solution on p. 471.)
(Section 3.2) Write 8 · 8 · 8 · 8 · 8 using exponents.
Exercise 7.6.33
(Section 4.3) Convert 47 to an improper fraction.
8
Exercise 7.6.34
(Solution on p. 471.)
(Section 5.4) Find the sum. 710 + 221 + 1.
7
Exercise 7.6.35
(Section 6.6) Find the product. (4.21) (0.006).
Exercise 7.6.36
(Solution on p. 471.)
(Section 7.5) Convert 8.062 to a percent.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 7. RATIOS AND RATES
7.7 Applications of Percents7
7.7.1 Section Overview
• Base, Percent, and Percentage
• Finding the Percentage
• Finding the Percent
• Finding the Base
7.7.2 Base, Percent, and Percentage
There are three basic types of percent problems. Each type involves a base, a percent, and a percentage, and when they are translated from words to mathematical symbols each becomes a multiplication statement.
Examples of these types of problems are the following:
1. What number is 30% of 50? (Missing product statement.)
2. 15 is what percent of 50? (Missing factor statement.)
3. 15 is 30% of what number? (Missing factor statement.)
In problem 1 (list, p. 448), the product is missing. To solve the problem, we represent the missing product with P .
P = 30% · 50
Percentage
The missing product P is called the percentage. Percentage means part, or portion. In P = 30% · 50, P
represents a particular part of 50.
In problem 2 (list, p. 448), one of the factors is missing. Here we represent the missing factor with Q.
15 = Q · 50
Percent
The missing factor is the percent. Percent, we know, means per 100, or part of 100. In 15 = Q · 50, Q
indicates what part of 50 is being taken or considered. Specically, 15 = Q · 50 means that if 50 was to be divided into 100 equal parts, then Q indicates 15 are being considered.
In problem 3 (list, p. 448), one of the factors is missing. Represent the missing factor with B.
15 = 30% · B
Base
The missing factor is the base. Some meanings of base are a source of supply, or a starting place. In 15 = 30% · B, B indicates the amount of supply. Specically, 15 = 30% · B indicates that 15 represents 30% of the total supply.
Each of these three types of problems is of the form
(percentage) = (percent) · (base)
We can determine any one of the three values given the other two using the methods discussed in Section 4.7.
7This content is available online at <http://cnx.org/content/m35007/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
7.7.3 Finding the Percentage
7.7.3.1 Sample Set A
Example 7.36
What number is
30%
of
50?
Missing product statement.
|
{z
}
↓
↓
↓
↓
(percentage)
= (percent) · (base)
↓
↓
↓
↓
↓
P
=
30%
·
50
Convert 30% to a decimal.
P
=
.30
·
50
Multiply.
P
=
15
Thus, 15 is 30% of 50.
Do Section 7.7.3.2 (Practice Set A), Exercise 7.7.1.
Example 7.37
What number is
36%
of
95?
Missing product statement.
|
{z
}
↓
↓
↓
↓
(percentage)
= (percent) · (base)
↓
↓
↓
↓
↓
P
=
36%
·
95
Convert 36% to a decimal.
P
=
.36
·
95
Multiply
P
=
34.2
Thus, 34.2 is 36% of 95.
Do Section 7.7.3.2 (Practice Set A), Exercise 7.7.1.
Example 7.38
A salesperson, who gets a commission of 12% of each sale she makes, makes a sale of $8,400.00.
How much is her commission?
We need to determine what part of $8,400.00 is to be taken. What part indicates percentage.
What number is
12%
of 8, 400.00? Missing product statement.
|
{z
}
↓
↓
↓
↓
(percentage)
= (percent) ·
(base)
↓
↓
↓
↓
↓
P
=
12%
·
8, 400.00
Convert to decimals.
P
=
.12
·
8, 400.00
Multiply.
P
=
1008.00
Thus, the salesperson’s commission is $1,008.00.
Do Section 7.7.3.2 (Practice Set A), Exercise 7.7.2.
Example 7.39
A girl, by practicing typing on her home computer, has been able to increase her typing speed by 110%. If she originally typed 16 words per minute, by how many words per minute was she able to increase her speed?
We need to determine what part of 16 has been taken. What part indicates percentage.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 7. RATIOS AND RATES
What number is
110%
of
16?
Missing product statement.
|
{z
}
↓
↓
↓
↓
(percentage)
= (percent) · (base)
↓
↓
↓
↓
↓
P
=
110%
·
16
Convert to decimals.
P
=
1.10
·
16
Multiply.
P
=
17.6
Thus, the girl has increased her typing speed by 17.6 words per minute. Her new speed is 16 + 17.6 =
33.6 words per minute.
Do Section 7.7.3.2 (Practice Set A), Exercise 7.7.3.
Example 7.40
A student who makes $125 a month working part-time receives a 4% salary raise. What is the student’s new monthly salary?
With a 4% raise, this student will make 100% of the original salary + 4% of the original salary.
This means the new salary will be 104% of the original salary. We need to determine what part of $125 is to be taken. What part indicates percentage.
What number is
104%
of
125
Missing product statement.
|
{z
}
↓
↓
↓
↓
(percentage)
= (percent) · (base)
↓
↓
↓
↓
↓
P
=
104%
·
125
Convert to decimals.
P
=
1.04
·
125
Multiply.
P
=
130
Thus, this student’s new monthly salary is $130.
Do Section 7.7.3.2 (Practice Set A), Exercise 7.7.4.
Example 7.41
An article of clothing is on sale at 15% o the marked price. If the marked price is $24.95, what is the sale price?
Since the item is discounted 15%, the new price will be 100% − 15% = 85% of the marked price.
We need to determine what part of 24.95 is to be taken. What part indicates percentage.
What number is
85%
of $24.95.
Missing product statement.
|
{z
}
↓
↓
↓
↓
(percentage)
= (percent) ·
(base)
↓
↓
↓
↓
↓
P
=
85%
·
24.95
Convert to decimals.
P
=
.85
·
24.95
Multiply.
Since this number represents money,
P
=
21.2075
we’ll round to 2 decimal places
P
=
21.21
Thus, the sale price of the item is $21.21.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
7.7.3.2 Practice Set A
Exercise 7.7.1
(Solution on p. 471.)
What number is 42% of 85?
Exercise 7.7.2
(Solution on p. 471.)
A sales person makes a commission of 16% on each sale he makes. How much is his commission if he makes a sale of $8,500?
Exercise 7.7.3
(Solution on p. 471.)
An assembly line worker can assemble 14 parts of a product in one hour. If he can increase his assembly speed by 35%, by how many parts per hour would he increase his assembly of products?
Exercise 7.7.4
(Solution on p. 471.)
A computer scientist in the Silicon Valley makes $42,000 annually. What would this scientist’s new annual salary be if she were to receive an 8% raise?
7.7.4 Finding the Percent
7.7.4.1 Sample Set B
Example 7.42
15
is what percent of
50?
Missing factor statement.
↓
↓
↓
↓
|
{z
}
(percentage) =
(percent)
·
(base) [(product) = (factor) · (factor)]
↓
↓
↓
↓
↓
15
=
Q
·
50
Recall that (missing factor) = (product) ÷ (known factor).
Q
=
15 ÷ 50
Divide.
Q
=
0.3
Convert to a percent.
Q
=
30%
Thus, 15 is 30% of 50.
Do Section 7.7.4.2 (Practice Set B), Exercise 7.7.5.
Example 7.43
4.32
is what percent of
72?
Missing factor statement.
↓
↓
↓
↓
|
{z
}
(percentage) =
(percent)
·
(base) [(product) = (factor) · (factor)]
↓
↓
↓
↓
↓
4.32
=
Q
·
72
Q
=
4.32 ÷ 72
Divide.
Q
=
0.06
Convert to a percent.
Q
=
6%
Thus, 4.32 is 6% of 72.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 7. RATIOS AND RATES
Do Section 7.7.4.2 (Practice Set B), Exercise 7.7.5.
Example 7.44
On a 160 question exam, a student got 125 correct answers. What percent is this? Round the result to two decimal places.
We need to determine the percent.
125
is what percent of
160?
Missing factor statement.
↓
↓
↓
↓
|
{z
}
(percentage) =
(percent)
·
(base) [(product) = (factor) · (factor)]
↓
↓
↓
↓
↓
125
=
Q
·
160
Q
=
125 ÷ 160
Divide.
Q
=
0.78125
Round to two decimal places.
Q
=
.78
Thus, this student received a 78% on the exam.
Do Section 7.7.4.2 (Practice Set B), Exercise 7.7.6.
Example 7.45
A bottle contains 80 milliliters of hydrochloric acid (HCl) and 30 milliliters of water. What percent of HCl does the bottle contain? Round the result to two decimal places.
We need to determine the percent. The total amount of liquid in the bottle is 80 milliliters + 30 milliliters = 110 milliliters.
80
is what percent of
110?
Missing factor statement.
↓
↓
↓
↓
|
{z
}
(percentage) =
(percent)
·
(base) [(product) = (factor) · (factor)]
↓
↓
↓
↓
↓
80
=
Q
·
110
Q
=
80 ÷ 110
Divide.
Q
=
0.727272. . .
Round to two decimal places.
Q
≈
73%
The symbol “≈” is read as “approximately.”
Thus, this bottle contains approximately 73% HCl.
Do Section 7.7.4.2 (Practice Set B), Exercise 7.7.7.
Example 7.46
Five years ago a woman had an annual income of $19,200. She presently earns $42,000 annually.
By what percent has her salary increased? Round the result to two decimal places.
We need to determine the percent.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
42, 000
is what percent of 19, 200? Missing factor statement.
↓
↓
↓
|
{z
}
↓
(percentage) =
(percent)
·
(base)
↓
↓
↓
↓
↓
42, 000
=
Q
·
19, 200
Q
=
42, 000 ÷ 19, 200
Divide.
Q
=
2.1875
Round to two decimal places.
Q
=
2.19
Convert to a percent.
Q
=
219%
Convert to a percent.
Thus, this woman’s annual salary has increased 219%.
7.7.4.2 Practice Set B
Exercise 7.7.5
(Solution on p. 471.)
99.13 is what percent of 431?
Exercise 7.7.6
(Solution on p. 472.)
On an 80 question exam, a student got 72 correct answers. What percent did the student get on the exam?
Exercise 7.7.7
(Solution on p. 472.)
A bottle contains 45 milliliters of sugar and 67 milliliters of water. What fraction of sugar does the bottle contain? Round the result to two decimal places (then express as a percent).
7.7.5 Finding the Base
7.7.5.1 Sample Set C
Example 7.47
15
is
30%
of what number?
Missing factor statement.
↓
↓
↓
↓
|
{z
}
(percentage) = (percent) ·
(base)
[(percentage) = (factor) · (factor)]
↓
↓
↓
↓
↓
15
=
30%
·
B
Convert to decimals.
15
=
.30
·
B
[(missing factor) = (product) ÷ (known factor)]
B
=
15 ÷ .30
B
=
50
Thus, 15 is 30% of 50.
Try Exercise 7.7.8 in Section 7.7.5.2 (Practice Set C).
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 7. RATIOS AND RATES
Example 7.48
56.43
is
33%
of what number? Missing factor statement.
↓
↓
↓
↓
|
{z
}
(percentage) = (percent) ·
(base)
↓
↓
↓
↓
↓
56.43
=
33%
·
B
Convert to decimals.
56.43
=
.33
·
B
Divide.
B
=
56.43 ÷ .33
B
=
171
Thus, 56.43 is 33% of 171.
Try Exercise 7.7.8 in Section 7.7.5.2 (Practice Set C).
Example 7.49
Fifteen milliliters of water represents 2% of a hydrochloric acid (HCl) solution. How many milliliters of solution are there?
We need to determine the total supply. The word supply indicates base.
15
is
2%
of what number? Missing factor statement.
↓
↓
↓
↓
|
{z
}
(percentage) = (percent) ·
(base)
↓
↓
↓
↓
↓
15
=
2%
·
B
Convert to decimals.
15
=
.02
·
B
Divide.
B
=
15 ÷ .02
B
=
750
Thus, there are 750 milliliters of solution in the bottle.
Try Exercise 7.7.9 in Section 7.7.5.2 (Practice Set C).
Example 7.50
In a particular city, a sales tax of 61% is charged on items purchased in local stores. If the tax on 2
an item is $2.99, what is the price of the item?
We need to determine the price of the item. We can think of price as the starting place. Starting place indicates base. We need to determine the base.
2.99
is
6 1 %
of what number?
Missing factor statement.
↓
↓
2
↓
↓
|
{z
}
(percentage) = (percent) ·
(base)
↓
↓
↓
↓
↓
2.99
=
6 1 %
·
B
Convert to decimals.
2
2.99
=
6.5%
·
B
2.99
=
.065
·
B
[(missing factor) = (product) ÷ (known factor)]
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
B
=
2.99 ÷ .065
Divide.
B
=
46
Thus, the price of the item is $46.00.
Try Exercise 7.7.10 in Section 7.7.5.2 (Practice Set C).
Example 7.51
A clothing item is priced at $20.40. This marked price includes a 15% discount. What is the original price?
We need to determine the original price. We can think of the original price as the starting place.
Starting place indicates base. We need to determine the base. The new price, $20.40, represents 100% − 15% = 85% of the original price.
20.40
is
85%
of what number?
Missing factor statement.
↓
↓
↓
↓
|
{z
}
(percentage) = (percent) ·
(base)
↓
↓
↓
↓
↓
20.40
=
85%
·
B
Convert to decimals.
20.40
=
.85
·
B
[(missing factor) = (product) ÷ (known factor)]
B
=
20.40 ÷ .85
Divide.
B
=
24
Thus, the original price of the item is $24.00.
Try Exercise 7.7.11 in Section 7.7.5.2 (Practice Set C).
7.7.5.2 Practice Set C
Exercise 7.7.8
(Solution on p. 472.)
1.98 is 2% of what number?
Exercise 7.7.9
(Solution on p. 472.)
3.3 milliliters of HCl represents 25% of an HCl solution. How many milliliters of solution are there?
Exercise 7.7.10
(Solution on p. 472.)
A salesman, who makes a commission of 181% on each sale, makes a commission of $152.39 on a 4
particular sale. Rounded to the nearest dollar, what is the amount of the sale?
Exercise 7.7.11
(Solution on p. 472.)
At “super-long play,” 21hours of play of a video cassette recorder represents 31.25% of the total 2
playing time. What is the total playing time?
7.7.6 Exercises
For the following 25 problems, nd each indicated quantity.
Exercise 7.7.12
(Solution on p. 472.)
What is 21% of 104?
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 7. RATIOS AND RATES
Exercise 7.7.13
What is 8% of 36?
Exercise 7.7.14
(Solution on p. 472.)
What is 98% of 545?
Exercise 7.7.15
What is 143% of 33?
Exercise 7.7.16
(Solution on p. 472.)
What is 101% of 20?
2
Exercise 7.7.17
3.25 is what percent of 88?
Exercise 7.7.18
(Solution on p. 472.)
22.44 is what percent of 44?
Exercise 7.7.19
0.0036 is what percent of 0.03?
Exercise 7.7.20
(Solution on p. 472.)
31.2 is what percent of 26?
Exercise 7.7.21
266.4 is what percent of 74?
Exercise 7.7.22
(Solution on p. 472.)
0.0101 is what percent of 0.0505?
Exercise 7.7.23
2.4 is 24% of what number?
Exercise 7.7.24
(Solution on p. 472.)
24.19 is 41% of what number?
Exercise 7.7.25
61.12 is 16% of what number?
Exercise 7.7.26
(Solution on p. 472.)
82.81 is 91% of what number?
Exercise 7.7.27
115.5 is 20% of what number?
Exercise 7.7.28
(Solution on p. 472.)
43.92 is 480% of what number?
Exercise 7.7.29
What is 85% of 62?
Exercise 7.7.30
(Solution on p. 472.)
29.14 is what percent of 5.13?
Exercise 7.7.31
0.6156 is what percent of 5.13?
Exercise 7.7.32
(Solution on p. 472.)
What is 0.41% of 291.1?
Exercise 7.7.33
26.136 is 121% of what number?
Exercise 7.7.34
(Solution on p. 472.)
1,937.5 is what percent of 775?
Exercise 7.7.35
1 is what percent of 2,000?
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 7.7.36
(Solution on p. 472.)
0 is what percent of 59?
Exercise 7.7.37
An item of clothing is on sale for 10% o the marked price. If the marked price is $14.95, what is the sale price? (Round to two decimal places.)
Exercise 7.7.38
(Solution on p. 472.)
A grocery clerk, who makes $365 per month, receives a 7% raise. How much is her new monthly salary?
Exercise 7.7.39
An item of clothing which originally sells for $55.00 is marked down to $46.75. What percent has it been marked down?
Exercise 7.7.40
(Solution on p. 472.)
On a 25 question exam, a student gets 21 correct. What percent is this?
Exercise 7.7.41
On a 45 question exam, a student gets 40%. How many questions did this student get correct?
Exercise 7.7.42
(Solution on p. 472.)
A vitamin tablet, which weighs 250 milligrams, contains 35 milligrams of vitamin C. What percent of the weight of this tablet is vitamin C?
Exercise 7.7.43
Five years ago a secretary made $11,200 annually. The secretary now makes $17,920 annually. By what percent has this secretary’s salary been increased?
Exercise 7.7.44
(Solution on p. 472.)
A baseball team wins 483% of all their games. If they won 78 games, how many games did they 4
play?
Exercise 7.7.45
A typist was able to increase his speed by 120% to 42 words per minute. What was his original typing speed?
Exercise 7.7.46
(Solution on p. 472.)
A salesperson makes a commission of 12% on the total amount of each sale. If, in one month, she makes a total of $8,520 in sales, how much has she made in commission?
Exercise 7.7.47
A salesperson receives a salary of $850 per month plus a commission of 81% of her sales. If, in a 2
particular month, she sells $22,800 worth of merchandise, what will be her monthly earnings?
Exercise 7.7.48
(Solution on p. 472.)
A man borrows $1150.00 from a loan company. If he makes 12 equal monthly payments of $130.60, what percent of the loan is he paying in interest?
Exercise 7.7.49
The distance from the sun to the earth is approximately 93,000,000 miles. The distance from the sun to Pluto is approximately 860.2% of the distance from the sun to the Earth. Approximately, how many miles is Pluto from the sun?
Exercise 7.7.50
(Solution on p. 473.)
The number of people on food stamps in Maine in 1975 was 151,000. By 1980, the number had decreased to 59,200. By what percent did the number of people on food stamps decrease? (Round the result to the nearest percent.)
Exercise 7.7.51
In Nebraska, in 1960, there were 734,000 motor-vehicle registrations. By 1979, the total had increased by about 165.6%. About how many motor-vehicle registrations were there in Nebraska in 1979?
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 7. RATIOS AND RATES
Exercise 7.7.52
(Solution on p. 473.)
From 1973 to 1979, in the United States, there was an increase of 166.6% of Ph.D. social scientists to 52,000. How many were there in 1973?
Exercise 7.7.53
In 1950, in the United States, there were 1,894 daily newspapers. That number decreased to 1,747
by 1981. What percent did the number of daily newspapers decrease?
Exercise 7.7.54
(Solution on p. 473.)
A particular alloy is 27% copper. How many pounds of copper are there in 55 pounds of the alloy?
Exercise 7.7.55
A bottle containing a solution of hydrochloric acid (HCl) is marked 15% (meaning that 15% of the HCl solution is acid). If a bottle contains 65 milliliters of solution, how many milliliters of water does it contain?
Exercise 7.7.56
(Solution on p. 473.)
A bottle containing a solution of HCl is marked 45%. A test shows that 36 of the 80 milliliters contained in the bottle are hydrochloric acid. Is the bottle marked correctly? If not, how should it be remarked?
7.7.6.1 Exercises For Review
Exercise 7.7.57
(Section 2.6) Use the numbers 4 and 7 to illustrate the commutative property of multiplication.
Exercise 7.7.58
(Solution on p. 473.)
(Section 4.3) Convert 14 to a mixed number.
5
Exercise 7.7.59
(Section 5.5) Arrange the numbers 712, 5 and 4 in increasing order.
9
7
Exercise 7.7.60
(Solution on p. 473.)
(Section 6.3) Convert 4.006 to a mixed number.
Exercise 7.7.61
(Section 7.6) Convert 7 % to a fraction.
8
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
7.8 Summary of Key Concepts8
7.8.1 Summary of Key Concepts
Denominate Numbers (Section 7.2)
Numbers that appear along with units are denominate numbers. The amounts 6 dollars and 4 pints are examples of denominate numbers.
Like and Unlike Denominate Numbers (Section 7.2)
Like denominate numbers are denominate numbers with like units. If the units are not the same, the numbers are unlike denominate numbers.
Pure Numbers (Section 7.2)
Numbers appearing without a unit are pure numbers.
Comparing Numbers by Subtraction and Division (Section 7.2)
Comparison of two numbers by subtraction indicates how much more one number is than another. Comparison by division indicates how many times larger or smaller one number is than another.
Comparing Pure or Like Denominate Numbers by Subtraction (Section 7.2)
Numbers can be compared by subtraction if and only if they are pure numbers or like denominate numbers.
Ratio Rate (Section 7.2)
A comparison, by division, of two like denominate numbers is a ratio. A comparison, by division, of two unlike denominate numbers is a rate.
Proportion (Section 7.3)
A proportion is a statement that two ratios or rates are equal.
3 people
2 jobs
= 6 people
4 jobs
is a proportion.
Solving a Proportion (Section 7.3)
To solve a proportion that contains three known numbers and a letter that represents an unknown quantity, perform the cross multiplication, then divide the product of the two numbers by the number that multiplies the letter.
Proportions Involving Rates (Section 7.3)
When writing a proportion involving rates it is very important to write it so that the same type of units appears on the same side of either the equal sign or the fraction bar.
unit type 1
unit type 2 = unit type 1
unit type 2 or unit type 1
unit type 1 = unit type 2
unit type 2
Five-Step Method for Solving Proportions (Section 7.4)
1. By careful reading, determine what the unknown quantity is and represent it with some letter. There will be only one unknown in a problem.
2. Identify the three specied numbers.
3. Determine which comparisons are to be made and set up the proportion.
4. Solve the proportion.
5. Interpret and write a conclusion.
When solving applied problems, ALWAYS begin by determining the unknown quantity and representing it with a letter.
8This content is available online at <http://cnx.org/content/m35008/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 7. RATIOS AND RATES
Percents (Section 7.5)
A ratio in which one number is compared to 100 is a percent. Percent means “for each hundred.”
Conversion of Fractions, Decimals, and Percents (Section 7.5)
It is possible to convert decimals to percents, fractions to percents, percents to decimals, and percents to fractions.
Applications of Percents:
The three basic types of percent problems involve a base, a percentage, and a percent.
Base (Section 7.7)
The base is the number used for comparison.
Percentage (Section 7.7)
The percentage is the number being compared to the base.
Percent (Section 7.7)
By its denition, percent means part of.
Solving Problems (Section 7.7)
Percentage = (percent) × (base)
Percent = percentage
base
Base = percentage
percent
7.9 Exercise Supplement9
7.9.1 Exercise Supplement
7.9.1.1 Ratios and Rates (Section 7.2)
Exercise 7.9.1
(Solution on p. 473.)
Compare 250 watts to 100 watts by subtraction.
Exercise 7.9.2
Compare 126 and 48 by subtraction.
Exercise 7.9.3
(Solution on p. 473.)
Compare 98 radishes to 41 radishes by division.
Exercise 7.9.4
Compare 144 to 9 by division.
Exercise 7.9.5
(Solution on p. 473.)
Compare 100 tents to 5 tents by division.
Exercise 7.9.6
Compare 28 feet to 7 feet by division.
Exercise 7.9.7
(Solution on p. 473.)
Comparison, by division, of two pure numbers or two like denominate numbers is called a
.
Exercise 7.9.8
A comparison, by division, of two unlike denominate numbers is called a
.
For problems 9-12, express each ratio or rate as a fraction.
9This content is available online at <http://cnx.org/content/m35009/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 7.9.9
(Solution on p. 473.)
15 to 5
Exercise 7.9.10
72 to 12
Exercise 7.9.11
(Solution on p. 473.)
8 millimeters to 5 milliliters
Exercise 7.9.12
106 tablets to 52 tablets
For problems 13-16, write each ratio in the form “a to b”.
Exercise 7.9.13
(Solution on p. 473.)
9
16
Exercise 7.9.14
5
11
Exercise 7.9.15
(Solution on p. 473.)
1 diskette
8 diskettes
Exercise 7.9.16
5 papers
3 pens
For problems 17-21, write each ratio or rate using words.
Exercise 7.9.17
(Solution on p. 473.)
9 = 18
16
32
Exercise 7.9.18
1 = 12
4
48
Exercise 7.9.19
(Solution on p. 473.)
8 items
4 dollars = 2 items
1 dollar
Exercise 7.9.20
150 milligrams of niacin is to 2 tablets as 300 milligrams of niacin is to 4 tablets.
Exercise 7.9.21
(Solution on p. 473.)
20 people is to 4 seats as 5 people is to 1 seat.
7.9.1.2 Proportions (Section 7.3)
For problems 22-27, determine the missing number in each proportion.
Exercise 7.9.22
x = 24
3
9
Exercise 7.9.23
(Solution on p. 473.)
15 = 60
7
x
Exercise 7.9.24
1 = x
1
44
Exercise 7.9.25
(Solution on p. 473.)
3 = 15
x
50
Exercise 7.9.26
15 bats
16 balls =
x bats
128 balls
Exercise 7.9.27
(Solution on p. 473.)
36 rooms
29 fans
= 504 rooms
x fans
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 7. RATIOS AND RATES
7.9.1.3 Applications of Proportions (Section 7.4)
Exercise 7.9.28
On a map, 3 inches represents 20 miles. How many miles does 27 inches represent?
Exercise 7.9.29
(Solution on p. 473.)
A salt solution is composed of 8 parts of salt to 5 parts of water. How many parts of salt are there in a solution that contains 50 parts of water?
Exercise 7.9.30
A model is built to 4 scale. If a particular part of the model measures 8 inches in length, how long 15
is the actual structure?
Exercise 7.9.31
(Solution on p. 473.)
The ratio of ammonia to air in a container is 3 How many milliliters of air should be in a container 40
that contains 8 milliliters of ammonia?
Exercise 7.9.32
A 4-foot girl casts a 9-foot shadow at a particular time of the day. How tall is a pole that casts a 144-foot shadow at the same time of the day?
Exercise 7.9.33
(Solution on p. 473.)
The odds that a particular event will occur are 11 to 2. If this event occurs 55 times, how many times would you predict it does not occur?
Exercise 7.9.34
Every 1 3 teaspoon of a multiple vitamin, in granular form, contains 0.85 the minimum daily 4
requirement of vitamin A. How many teaspoons of this vitamin are required to supply 2.25 the minimum daily requirement?
7.9.1.4 Percent and Fractions of One Percent (Section 7.5,Section 7.6)
For problems 35-39, convert each decimal to a percent.
Exercise 7.9.35
(Solution on p. 473.)
0.16
Exercise 7.9.36
0.818
Exercise 7.9.37
(Solution on p. 473.)
5.3536
Exercise 7.9.38
0.50
Exercise 7.9.39
(Solution on p. 474.)
3
For problems 40-48, convert each percent to a decimal.
Exercise 7.9.40
62%
Exercise 7.9.41
(Solution on p. 474.)
1.58%
Exercise 7.9.42
9.15%
Exercise 7.9.43
(Solution on p. 474.)
0.06%
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 7.9.44
0.003%
Exercise 7.9.45
(Solution on p. 474.)
5 3 % to a three-place decimal
11
Exercise 7.9.46
9
% to a three-place decimal
13
Exercise 7.9.47
(Solution on p. 474.)
82 25 % to a four-place decimal
29
Exercise 7.9.48
18 1 % to a four-place decimal
7
For problems 49-55, convert each fraction or mixed number to a percent.
Exercise 7.9.49
(Solution on p. 474.)
3
5
Exercise 7.9.50
2
10
Exercise 7.9.51
(Solution on p. 474.)
5
16
Exercise 7.9.52
35
8
Exercise 7.9.53
(Solution on p. 474.)
105
16
Exercise 7.9.54
45 111
Exercise 7.9.55
(Solution on p. 474.)
6 278
9
For problems 56-64, convert each percent to a fraction or mixed number.
Exercise 7.9.56
95%
Exercise 7.9.57
(Solution on p. 474.)
12%
Exercise 7.9.58
83%
Exercise 7.9.59
(Solution on p. 474.)
38.125%
Exercise 7.9.60
_
61. 2 %
Exercise 7.9.61
(Solution on p. 474.)
5 %
8
Exercise 7.9.62
6 9 %
20
Exercise 7.9.63
(Solution on p. 474.)
15 3 %
22
Exercise 7.9.64
106 19 %
45
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 7. RATIOS AND RATES
7.9.1.5 Applications of Percents (Section 7.7)
For problems 65-72, nd each solution.
Exercise 7.9.65
(Solution on p. 474.)
What is 16% of 40?
Exercise 7.9.66
29.4 is what percent of 105?
Exercise 7.9.67
(Solution on p. 474.)
3 21 is 547.2% of what number?
50
Exercise 7.9.68
0.09378 is what percent of 52.1?
Exercise 7.9.69
(Solution on p. 474.)
What is 680% of 1.41?
Exercise 7.9.70
A kitchen knife is on sale for 15% o the marked price. If the marked price is $ 39.50, what is the sale price?
Exercise 7.9.71
(Solution on p. 474.)
On an 80 question geology exam, a student gets 68 correct. What percent is correct?
Exercise 7.9.72
A salesperson makes a commission of 18% of her monthly sales total. She also receives a monthly salary of $1,600.00. If, in a particular month, she sells $4,000.00 worth of merchandise, how much will she make that month?
7.10 Prociency Exam10
7.10.1 Prociency Exam
Exercise 7.10.1
(Solution on p. 474.)
(Section 7.2) Compare 4 cassette tapes to 7 dollars.
Exercise 7.10.2
(Solution on p. 474.)
(Section 7.2) What do we call a comparison, by division, of two unlike denominate numbers?
For problems 3 and 4, express each ratio or rate as a fraction.
Exercise 7.10.3
(Solution on p. 474.)
(Section 7.2) 11 to 9
Exercise 7.10.4
(Solution on p. 474.)
(Section 7.2) 5 televisions to 2 radios
For problems 5 and 6, write each ratio or rate in the form “a to b.”
Exercise 7.10.5
(Solution on p. 474.)
(Section 7.2) 8 maps
3 people
Exercise 7.10.6
(Solution on p. 474.)
(Section 7.2) 2 psychologists
75 people
For problems 7-9, solve each proportion.
Exercise 7.10.7
(Solution on p. 474.)
(Section 7.3) 8 = 48
x
90
10This content is available online at <http://cnx.org/content/m35010/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 7.10.8
(Solution on p. 474.)
(Section 7.3) x = 4
7
28
Exercise 7.10.9
(Solution on p. 475.)
(Section 7.3) 3 computers
8 students = 24 computers
x students
Exercise 7.10.10
(Solution on p. 475.)
(Section 7.4) On a map, 4 inches represents 50 miles. How many miles does 3 inches represent?
Exercise 7.10.11
(Solution on p. 475.)
(Section 7.4) An acid solution is composed of 6 milliliters of acid to 10 milliliters of water. How many milliliters of acid are there in an acid solution that is composed of 3 milliliters of water?
Exercise 7.10.12
(Solution on p. 475.)
(Section 7.4) The odds that a particular event will occur are 9 to 7. If the event occurs 27 times, how many times would you predict it will it not occur?
For problems 13 and 14, convert each decimal to a percent.
Exercise 7.10.13
(Solution on p. 475.)
(Section 7.5) 0.82
Exercise 7.10.14
(Solution on p. 475.)
_
(Section 7.5) 3. 7
For problems 15 and 16, convert each percent to a decimal.
Exercise 7.10.15
(Solution on p. 475.)
(Section 7.5) 2.813%
Exercise 7.10.16
(Solution on p. 475.)
(Section 7.5) 0.006%
For problems 17-19, convert each fraction to a percent.
Exercise 7.10.17
(Solution on p. 475.)
(Section 7.5) 425
Exercise 7.10.18
(Solution on p. 475.)
(Section 7.5) 18
Exercise 7.10.19
(Solution on p. 475.)
(Section 7.5) 800
80
For problems 20 and 21, convert each percent to a fraction.
Exercise 7.10.20
(Solution on p. 475.)
(Section 7.5) 15%
Exercise 7.10.21
(Solution on p. 475.)
(Section 7.5) 427 %
For problems 22-25, nd each indicated quantity.
Exercise 7.10.22
(Solution on p. 475.)
(Section 7.7) What is 18% of 26?
Exercise 7.10.23
(Solution on p. 475.)
(Section 7.7) 0.618 is what percent of 0.3?
Exercise 7.10.24
(Solution on p. 475.)
(Section 7.7) 0.1 is 1.1% of what number?
Exercise 7.10.25
(Solution on p. 475.)
(Section 7.7) A salesperson makes a monthly salary of $1,000.00. He also gets a commission of 12% of his total monthly sales. If, in a particular month, he sells $5,500.00 worth of merchandise, what is his income that month?
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 7. RATIOS AND RATES
Solutions to Exercises in Chapter 7
Solution to Exercise 7.2.1 (p. 421)
(a) 8 diskettes; 10 diskettes is 8 diskettes more than 2 diskettes.
(b) 5; 10 diskettes is 5 times as many diskettes as 2 diskettes.
Solution to Exercise 7.2.2 (p. 421)
(a) Comparison by subtraction makes no sense.
(b) 16 bananas
2 bags
= 8 bananas
bag
, 8 bananas per bag.
Solution to Exercise 7.2.3 (p. 422)
3
2
Solution to Exercise 7.2.4 (p. 422)
1
9
Solution to Exercise 7.2.5 (p. 422)
5 books
4 people
Solution to Exercise 7.2.6 (p. 422)
60 miles
1 hour
Solution to Exercise 7.2.7 (p. 422)
8
3
Solution to Exercise 7.2.8 (p. 422)
9 to 5
Solution to Exercise 7.2.9 (p. 422)
1 to 3
Solution to Exercise 7.2.10 (p. 422)
25 miles to 2 gallons
Solution to Exercise 7.2.11 (p. 423)
1 mechanic to 2 wrenches
Solution to Exercise 7.2.12 (p. 423)
5 to 6
Solution to Exercise 7.2.13 (p. 423)
They are pure numbers or like denominate numbers.
Solution to Exercise 7.2.15 (p. 423)
rate
Solution to Exercise 7.2.17 (p. 423)
ratio
Solution to Exercise 7.2.19 (p. 423)
rate
Solution to Exercise 7.2.21 (p. 423)
ratio
Solution to Exercise 7.2.23 (p. 423)
two to ve
Solution to Exercise 7.2.25 (p. 423)
29 mile per 2 gallons or 141 miles per 1 gallon
2
Solution to Exercise 7.2.27 (p. 423)
5 to 2
Solution to Exercise 7.2.29 (p. 423)
12
5
Solution to Exercise 7.2.31 (p. 424)
42 plants
5 homes
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 7.2.33 (p. 424)
16 pints
1 quart
Solution to Exercise 7.2.35 (p. 424)
2.54 cm
1 inch
Solution to Exercise 7.2.37 (p. 424)
5
2
Solution to Exercise 7.2.39 (p. 424)
1 hit
3 at bats
Solution to Exercise 7.2.41 (p. 424)
1,042 characters
1 page
Solution to Exercise 7.2.43 (p. 424)
5 13
Solution to Exercise 7.2.45 (p. 424)
299
1260
Solution to Exercise 7.2.47 (p. 424)
3.3875
Solution to Exercise 7.3.1 (p. 426)
3 is to 8 as 6 is to 16
Solution to Exercise 7.3.2 (p. 426)
2 people are to 1 window as 10 people are to 5 windows
Solution to Exercise 7.3.3 (p. 426)
15 = 75
4
20
Solution to Exercise 7.3.4 (p. 426)
2 plates
1 tray = 20 plates
10 trays
Solution to Exercise 7.3.5 (p. 427)
x = 3
Solution to Exercise 7.3.6 (p. 428)
x = 5
Solution to Exercise 7.3.7 (p. 428)
x = 45
Solution to Exercise 7.3.8 (p. 428)
x = 48
Solution to Exercise 7.3.9 (p. 429)
rates, proportion
Solution to Exercise 7.3.11 (p. 429)
1
11 = 3
33
Solution to Exercise 7.3.13 (p. 429)
6
90 = 3
45
Solution to Exercise 7.3.15 (p. 429)
18 gr cobalt
10 gr silver = 36 gr cobalt
20 gr silver
Solution to Exercise 7.3.17 (p. 429)
3 people absent
31 people present = 15 people absent
155 people present
Solution to Exercise 7.3.19 (p. 429)
3 is to 4 as 15 is to 20
Solution to Exercise 7.3.21 (p. 429)
3 joggers are to 100 feet as 6 joggers are to 200 feet
Solution to Exercise 7.3.23 (p. 430)
40 miles are to 80 miles as 2 gallons are to 4 gallons
Solution to Exercise 7.3.25 (p. 430)
1 person is to 1 job as 8 people are to 8 jobs
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 7. RATIOS AND RATES
Solution to Exercise 7.3.27 (p. 430)
2,000 pounds are to 1 ton as 60,000 pounds are to 30 tons
Solution to Exercise 7.3.29 (p. 430)
x = 2
Solution to Exercise 7.3.31 (p. 430)
x = 8
Solution to Exercise 7.3.33 (p. 430)
x = 8
Solution to Exercise 7.3.35 (p. 430)
x = 27
Solution to Exercise 7.3.37 (p. 430)
x = 40
Solution to Exercise 7.3.39 (p. 430)
x = 30
Solution to Exercise 7.3.41 (p. 430)
x = 35
Solution to Exercise 7.3.43 (p. 430)
x = 30
Solution to Exercise 7.3.45 (p. 431)
true
Solution to Exercise 7.3.47 (p. 431)
false
Solution to Exercise 7.3.49 (p. 431)
true
Solution to Exercise 7.3.51 (p. 431)
true
Solution to Exercise 7.3.53 (p. 431)
5+7=12
7+5=12
Solution to Exercise 7.3.55 (p. 431)
17
77
Solution to Exercise 7.3.57 (p. 431)
8 sentences
1 paragraph
Solution to Exercise 7.4.1 (p. 434)
500 miles
Solution to Exercise 7.4.2 (p. 435)
24 parts of alcohol
Solution to Exercise 7.4.3 (p. 435)
3 9
11 feet
Solution to Exercise 7.4.4 (p. 435)
864 outside plants
Solution to Exercise 7.4.5 (p. 435)
The event occurs 99 times.
Solution to Exercise 7.4.6 (p. 435)
6 failing grades
Solution to Exercise 7.4.7 (p. 436)
24
Solution to Exercise 7.4.9 (p. 436)
45 inches
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 7.4.11 (p. 436)
33 parts
Solution to Exercise 7.4.13 (p. 436)
2328.75
Solution to Exercise 7.4.15 (p. 436)
21
22 feet
Solution to Exercise 7.4.17 (p. 436)
12,250
Solution to Exercise 7.4.19 (p. 436)
12
Solution to Exercise 7.4.21 (p. 436)
1 56
Solution to Exercise 7.4.23 (p. 437)
1 78
Solution to Exercise 7.4.25 (p. 437)
3114
Solution to Exercise 7.4.27 (p. 437)
0Solution to Exercise 7.4.29 (p. 437)
2
3
Solution to Exercise 7.4.31 (p. 437)
5Solution to Exercise 7.5.1 (p. 438)
16%
Solution to Exercise 7.5.2 (p. 438)
195%
Solution to Exercise 7.5.3 (p. 438)
83
100
Solution to Exercise 7.5.4 (p. 438)
362
100 or 181
50
Solution to Exercise 7.5.5 (p. 441)
0.21
Solution to Exercise 7.5.6 (p. 441)
4.61
Solution to Exercise 7.5.7 (p. 441)
55%
Solution to Exercise 7.5.8 (p. 441)
564%
Solution to Exercise 7.5.9 (p. 441)
15%
Solution to Exercise 7.5.10 (p. 441)
137.5%
Solution to Exercise 7.5.11 (p. 441)
27.27%
Solution to Exercise 7.5.12 (p. 441)
25%
Solution to Exercise 7.5.14 (p. 441)
48%
Solution to Exercise 7.5.16 (p. 441)
77.1%
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 7. RATIOS AND RATES
Solution to Exercise 7.5.18 (p. 441)
258%
Solution to Exercise 7.5.20 (p. 441)
1,618.14%
Solution to Exercise 7.5.22 (p. 441)
200%
Solution to Exercise 7.5.24 (p. 442)
0.15
Solution to Exercise 7.5.26 (p. 442)
0.162
Solution to Exercise 7.5.28 (p. 442)
0.0505
Solution to Exercise 7.5.30 (p. 442)
0.0078
Solution to Exercise 7.5.32 (p. 442)
0.0009
Solution to Exercise 7.5.34 (p. 442)
20%
Solution to Exercise 7.5.36 (p. 442)
62.5%
Solution to Exercise 7.5.38 (p. 442)
28%
Solution to Exercise 7.5.40 (p. 442)
49.09%
Solution to Exercise 7.5.42 (p. 442)
164%
Solution to Exercise 7.5.44 (p. 442)
945%
Solution to Exercise 7.5.46 (p. 443)
54.54%
Solution to Exercise 7.5.48 (p. 443)
4
5
Solution to Exercise 7.5.50 (p. 443)
1
4
Solution to Exercise 7.5.52 (p. 443)
13
20
Solution to Exercise 7.5.54 (p. 443)
1
8
Solution to Exercise 7.5.56 (p. 443)
41 or 51
8
8
Solution to Exercise 7.5.58 (p. 443)
1
10
Solution to Exercise 7.5.60 (p. 443)
2
9
Solution to Exercise 7.5.62 (p. 443)
4
45
Solution to Exercise 7.5.64 (p. 443)
129
60 or 2 9
60 = 2 3
20
Solution to Exercise 7.5.66 (p. 444)
36 inches
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 7.6.1 (p. 445)
1
400
Solution to Exercise 7.6.2 (p. 445)
3
800
Solution to Exercise 7.6.3 (p. 445)
1
30
Solution to Exercise 7.6.4 (p. 446)
0.008
Solution to Exercise 7.6.5 (p. 446)
0.5145
Solution to Exercise 7.6.6 (p. 446)
3
400
Solution to Exercise 7.6.8 (p. 446)
1
900
Solution to Exercise 7.6.10 (p. 446)
5
400 or 1
80
Solution to Exercise 7.6.12 (p. 446)
13
700
Solution to Exercise 7.6.14 (p. 446)
101
400
Solution to Exercise 7.6.16 (p. 446)
363
500
Solution to Exercise 7.6.18 (p. 446)
41
30
Solution to Exercise 7.6.20 (p. 447)
51
500 = 0.102
Solution to Exercise 7.6.22 (p. 447)
31
800 = 0.03875
Solution to Exercise 7.6.24 (p. 447)
0.004
Solution to Exercise 7.6.26 (p. 447)
0.0627
Solution to Exercise 7.6.28 (p. 447)
0.242
Solution to Exercise 7.6.30 (p. 447)
0.1194
Solution to Exercise 7.6.32 (p. 447)
85
Solution to Exercise 7.6.34 (p. 447)
197
210
Solution to Exercise 7.6.36 (p. 447)
806.2%
Solution to Exercise 7.7.1 (p. 451)
35.7
Solution to Exercise 7.7.2 (p. 451)
$1,360
Solution to Exercise 7.7.3 (p. 451)
4.9
Solution to Exercise 7.7.4 (p. 451)
$45,360
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 7. RATIOS AND RATES
Solution to Exercise 7.7.5 (p. 453)
23%
Solution to Exercise 7.7.6 (p. 453)
90%
Solution to Exercise 7.7.7 (p. 453)
40%
Solution to Exercise 7.7.8 (p. 455)
99
Solution to Exercise 7.7.9 (p. 455)
13.2ml
Solution to Exercise 7.7.10 (p. 455)
$835
Solution to Exercise 7.7.11 (p. 455)
8 hours
Solution to Exercise 7.7.12 (p. 455)
21.84
Solution to Exercise 7.7.14 (p. 456)
534.1
Solution to Exercise 7.7.16 (p. 456)
2.1
Solution to Exercise 7.7.18 (p. 456)
51
Solution to Exercise 7.7.20 (p. 456)
120
Solution to Exercise 7.7.22 (p. 456)
20
Solution to Exercise 7.7.24 (p. 456)
59
Solution to Exercise 7.7.26 (p. 456)
91
Solution to Exercise 7.7.28 (p. 456)
9.15
Solution to Exercise 7.7.30 (p. 456)
568
Solution to Exercise 7.7.32 (p. 456)
1.19351
Solution to Exercise 7.7.34 (p. 456)
250
Solution to Exercise 7.7.36 (p. 457)
0Solution to Exercise 7.7.38 (p. 457)
390.55
Solution to Exercise 7.7.40 (p. 457)
84
Solution to Exercise 7.7.42 (p. 457)
14
Solution to Exercise 7.7.44 (p. 457)
160
Solution to Exercise 7.7.46 (p. 457)
$1,022.40
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 7.7.48 (p. 457)
36.28%
Solution to Exercise 7.7.50 (p. 457)
61
Solution to Exercise 7.7.52 (p. 458)
19,500
Solution to Exercise 7.7.54 (p. 458)
14.85
Solution to Exercise 7.7.56 (p. 458)
Marked correctly
Solution to Exercise 7.7.58 (p. 458)
2 45
Solution to Exercise 7.7.60 (p. 458)
4 3
500
Solution to Exercise 7.9.1 (p. 460)
250 watts are 150 watts more than 100 watts
Solution to Exercise 7.9.3 (p. 460)
98 radishes are 2.39 times as many radishes as 41 radishes
Solution to Exercise 7.9.5 (p. 460)
100 tents are 20 times as many tents as 5 tents
Solution to Exercise 7.9.7 (p. 460)
ratio
Solution to Exercise 7.9.9 (p. 460)
3
1
Solution to Exercise 7.9.11 (p. 461)
8ml
5ml
Solution to Exercise 7.9.13 (p. 461)
9 to 16
Solution to Exercise 7.9.15 (p. 461)
1 diskette to 8 diskettes
Solution to Exercise 7.9.17 (p. 461)
9 is to 16 as 18 is to 32
Solution to Exercise 7.9.19 (p. 461)
8 items are to 4 dollars as 2 items are to 1 dollar
Solution to Exercise 7.9.21 (p. 461)
20 = 5
4
1
20 people are to 4 seats as 5 people are to 1 seat
Solution to Exercise 7.9.23 (p. 461)
28
Solution to Exercise 7.9.25 (p. 461)
10
Solution to Exercise 7.9.27 (p. 461)
406
Solution to Exercise 7.9.29 (p. 462)
80
Solution to Exercise 7.9.31 (p. 462)
320 or 1062
3
3
Solution to Exercise 7.9.33 (p. 462)
10
Solution to Exercise 7.9.35 (p. 462)
16%
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 7. RATIOS AND RATES
Solution to Exercise 7.9.37 (p. 462)
535.36%
Solution to Exercise 7.9.39 (p. 462)
300%
Solution to Exercise 7.9.41 (p. 462)
0.0158
Solution to Exercise 7.9.43 (p. 462)
0.0006
Solution to Exercise 7.9.45 (p. 463)
0.053
Solution to Exercise 7.9.47 (p. 463)
0.8286
Solution to Exercise 7.9.49 (p. 463)
60%
Solution to Exercise 7.9.51 (p. 463)
31.25%
Solution to Exercise 7.9.53 (p. 463)
656.25%
Solution to Exercise 7.9.55 (p. 463)
_
3688. 8 %
Solution to Exercise 7.9.57 (p. 463)
3
25
Solution to Exercise 7.9.59 (p. 463)
61
160
Solution to Exercise 7.9.61 (p. 463)
1
160
Solution to Exercise 7.9.63 (p. 463)
2977
19800
Solution to Exercise 7.9.65 (p. 464)
6.4
Solution to Exercise 7.9.67 (p. 464)
0.625 or 58
Solution to Exercise 7.9.69 (p. 464)
9.588
Solution to Exercise 7.9.71 (p. 464)
85
Solution to Exercise 7.10.1 (p. 464)
4 cassette tapes
7 dollars
Solution to Exercise 7.10.2 (p. 464)
Rate
Solution to Exercise 7.10.3 (p. 464)
11
9
Solution to Exercise 7.10.4 (p. 464)
5 televisions
2 radios
Solution to Exercise 7.10.5 (p. 464)
8 maps to 3 people
Solution to Exercise 7.10.6 (p. 464)
two psychologists to seventy-ve people
Solution to Exercise 7.10.7 (p. 464)
15
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 7.10.8 (p. 465)
1Solution to Exercise 7.10.9 (p. 465)
64
Solution to Exercise 7.10.10 (p. 465)
3712
Solution to Exercise 7.10.11 (p. 465)
1.8
Solution to Exercise 7.10.12 (p. 465)
21
Solution to Exercise 7.10.13 (p. 465)
82%
Solution to Exercise 7.10.14 (p. 465)
3777%
9
Solution to Exercise 7.10.15 (p. 465)
0.02813
Solution to Exercise 7.10.16 (p. 465)
0.00006
Solution to Exercise 7.10.17 (p. 465)
840%
Solution to Exercise 7.10.18 (p. 465)
12.5%
Solution to Exercise 7.10.19 (p. 465)
1,000%
Solution to Exercise 7.10.20 (p. 465)
3
20
Solution to Exercise 7.10.21 (p. 465)
4
2,700 or 1
675
Solution to Exercise 7.10.22 (p. 465)
4.68
Solution to Exercise 7.10.23 (p. 465)
206
Solution to Exercise 7.10.24 (p. 465)
9.09
Solution to Exercise 7.10.25 (p. 465)
$1,660
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 7. RATIOS AND RATES
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Techniques of Estimation
8.1 Objectives1
After completing this chapter, you should
Estimation by Rounding (Section 8.2)
• understand the reason for estimation
• be able to estimate the result of an addition, multiplication, subtraction, or division using the rounding technique
Estimation by Clustering (Section 8.3)
• understand the concept of clustering
• be able to estimate the result of adding more than two numbers when clustering occurs using the clustering technique
Mental ArithmeticUsing the Distributive Property (Section 8.4)
• understand the distributive property
• be able to obtain the exact result of a multiplication using the distributive property Estimation by Rounding Fractions (Section 8.5)
• be able to estimate the sum of two or more fractions using the technique of rounding fractions 8.2 Estimation by Rounding2
8.2.1 Section Overview
• Estimation By Rounding
When beginning a computation, it is valuable to have an idea of what value to expect for the result. When a computation is completed, it is valuable to know if the result is reasonable.
In the rounding process, it is important to note two facts:
1This content is available online at <http://cnx.org/content/m18896/1.3/>.
2This content is available online at <http://cnx.org/content/m35011/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4> 477
CHAPTER 8. TECHNIQUES OF ESTIMATION
1. The rounding that is done in estimation does not always follow the rules of rounding discussed in Section 1.4 (Rounding Whole Numbers). Since estimation is concerned with the expected value of a computation, rounding is done using convenience as the guide rather than using hard-and-fast rounding rules. For example, if we wish to estimate the result of the division 80 ÷ 26, we might round 26 to 20
rather than to 30 since 80 is more conveniently divided by 20 than by 30.
2. Since rounding may occur out of convenience, and dierent people have dierent ideas of what may be convenient, results of an estimation done by rounding may vary. For a particular computation, dierent people may get dierent estimated results. Results may vary.
Estimation
Estimation is the process of determining an expected value of a computation.
Common words used in estimation are about, near, and between.
8.2.2 Estimation by Rounding
The rounding technique estimates the result of a computation by rounding the numbers involved in the computation to one or two nonzero digits.
8.2.2.1 Sample Set A
Example 8.1
Estimate the sum: 2,357 + 6,106.
Notice that 2,357 is near 2, 400, and that 6,106 is near 6, 100.
|
{z
}
|
{z
}
two nonzero
two nonzero
digits
digits
The sum can be estimated by 2,400 + 6,100 = 8,500. (It is quick and easy to add 24 and 61.) Thus, 2,357 + 6,106 is about 8,400. In fact, 2,357 + 6,106 = 8,463.
8.2.2.2 Practice Set A
Exercise 8.2.1
(Solution on p. 505.)
Estimate the sum: 4,216 + 3,942.
Exercise 8.2.2
(Solution on p. 505.)
Estimate the sum: 812 + 514.
Exercise 8.2.3
(Solution on p. 505.)
Estimate the sum: 43,892 + 92,106.
8.2.2.3 Sample Set B
Example 8.2
Estimate the dierence: 5, 203 − 3, 015.
Notice that 5,203 is near 5, 200, and that 3,015 is near 3, 000.
|
{z
}
|
{z
}
two nonzero
one nonzero
digits
digit
The dierence can be estimated by 5, 200 − 3, 000 = 2,200.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Thus, 5, 203 − 3, 015 is about 2,200. In fact, 5, 203 − 3, 015 = 2,188.
We could make a less accurate estimation by observing that 5,203 is near 5,000. The number 5,000
has only one nonzero digit rather than two (as does 5,200). This fact makes the estimation quicker (but a little less accurate). We then estimate the dierence by 5, 000−3, 000 = 2,000, and conclude that 5, 203 − 3, 015 is about 2,000. This is why we say “answers may vary.”
8.2.2.4 Practice Set B
Exercise 8.2.4
(Solution on p. 505.)
Estimate the dierence: 628 − 413.
Exercise 8.2.5
(Solution on p. 505.)
Estimate the dierence: 7, 842 − 5, 209.
Exercise 8.2.6
(Solution on p. 505.)
Estimate the dierence: 73, 812 − 28, 492.
8.2.2.5 Sample Set C
Example 8.3
Estimate the product: 73 · 46.
Notice that 73 is near
70,
and that 46 is near
50.
|{z}
|{z}
one nonzero
one nonzero
digit
digit
The product can be estimated by 70 · 50 = 3,500. (Recall that to multiply numbers ending in zeros, we multiply the nonzero digits and ax to this product the total number of ending zeros in the factors. See Section 2.2 for a review of this technique.)
Thus, 73 · 46 is about 3,500. In fact, 73 · 46 = 3,358.
Example 8.4
Estimate the product: 87 · 4,316.
Notice that 87 is close to
90,
and that 4,316 is close to 4, 000.
|{z}
|
{z
}
one nonzero
one nonzero
digit
digit
The product can be estimated by 90 · 4,000 = 360,000.
Thus, 87 · 4,316 is about 360,000. In fact, 87 · 4,316 = 375,492.
8.2.2.6 Practice Set C
Exercise 8.2.7
(Solution on p. 505.)
Estimate the product: 31 · 87.
Exercise 8.2.8
(Solution on p. 505.)
Estimate the product: 18 · 42.
Exercise 8.2.9
(Solution on p. 505.)
Estimate the product: 16 · 94.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 8. TECHNIQUES OF ESTIMATION
8.2.2.7 Sample Set D
Example 8.5
Estimate the quotient: 153 ÷ 17.
Notice that 153 is close to
150,
and that 17 is close to
15.
|{z}
|{z}
two nonzero
two nonzero
digits
digits
The quotient can be estimated by 150 ÷ 15 = 10.
Thus, 153 ÷ 17 is about 10. In fact, 153 ÷ 17 = 9.
Example 8.6
Estimate the quotient: 742,000 ÷ 2,400.
Notice that 742,000 is close to 700, 000 , and that 2,400 is close to 2, 000.
|
{z
}
|
{z
}
one nonzero
one nonzero
digit
digit
The quotient can be estimated by 700,000 ÷ 2,000 = 350.
Thus, 742,000 ÷ 2,400 is about 350. In fact, 742,000 ÷ 2,400 = 309.16.
8.2.2.8 Practice Set D
Exercise 8.2.10
(Solution on p. 505.)
Estimate the quotient: 221 ÷ 18.
Exercise 8.2.11
(Solution on p. 505.)
Estimate the quotient: 4,079 ÷ 381.
Exercise 8.2.12
(Solution on p. 505.)
Estimate the quotient: 609,000 ÷ 16,000.
8.2.2.9 Sample Set E
Example 8.7
Estimate the sum: 53.82 + 41.6.
Notice that 53.82 is close to
54,
and that 41.6 is close to
42.
|{z}
|{z}
two nonzero
two nonzero
digits
digits
The sum can be estimated by 54 + 42 = 96.
Thus, 53.82 + 41.6 is about 96. In fact, 53.82 + 41.6 = 95.42.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
8.2.2.10 Practice Set E
Exercise 8.2.13
(Solution on p. 505.)
Estimate the sum: 61.02 + 26.8.
Exercise 8.2.14
(Solution on p. 505.)
Estimate the sum: 109.12 + 137.88.
8.2.2.11 Sample Set F
Example 8.8
Estimate the product: (31.28) (14.2).
Notice that 31.28 is close to
30,
and that 14.2 is close to
15.
|{z}
|{z}
one nonzero
two nonzero
digit
digits
The product can be estimated by 30 · 15 = 450. ( 3 · 15 = 45, then ax one zero.) Thus, (31.28) (14.2) is about 450. In fact, (31.28) (14.2) = 444.176.
Example 8.9
Estimate 21% of 5.42.
Notice that 21% = .21 as a decimal, and that .21 is close to
.2.
|{z}
one nonzero
digit
Notice also that 5.42 is close to
5.
|{z}
one nonzero
digit
Then, 21% of 5.42 can be estimated by (.2) (5) = 1.
Thus, 21% of 5.42 is about 1. In fact, 21% of 5.42 is 1.1382.
8.2.2.12 Practice Set F
Exercise 8.2.15
(Solution on p. 505.)
Estimate the product: (47.8) (21.1).
Exercise 8.2.16
(Solution on p. 505.)
Estimate 32% of 14.88.
8.2.3 Exercises
Estimate each calculation using the method of rounding. After you have made an estimate, nd the exact value and compare this to the estimated result to see if your estimated value is reasonable. Results may vary.
Exercise 8.2.17
(Solution on p. 505.)
1, 402 + 2, 198
Exercise 8.2.18
3,481 + 4,216
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 8. TECHNIQUES OF ESTIMATION
Exercise 8.2.19
(Solution on p. 505.)
921 + 796
Exercise 8.2.20
611 + 806
Exercise 8.2.21
(Solution on p. 505.)
4, 681 + 9, 325
Exercise 8.2.22
6, 476 + 7, 814
Exercise 8.2.23
(Solution on p. 505.)
7, 805 − 4, 266
Exercise 8.2.24
8, 427 − 5, 342
Exercise 8.2.25
(Solution on p. 505.)
14, 106 − 8, 412
Exercise 8.2.26
26, 486 − 18, 931
Exercise 8.2.27
(Solution on p. 505.)
32 · 53
Exercise 8.2.28
67 · 42
Exercise 8.2.29
(Solution on p. 505.)
628 · 891
Exercise 8.2.30
426 · 741
Exercise 8.2.31
(Solution on p. 505.)
18, 012 · 32, 416
Exercise 8.2.32
22, 481 · 51, 076
Exercise 8.2.33
(Solution on p. 505.)
287 ÷ 19
Exercise 8.2.34
884 ÷ 33
Exercise 8.2.35
(Solution on p. 506.)
1, 254 ÷ 57
Exercise 8.2.36
2, 189 ÷ 42
Exercise 8.2.37
(Solution on p. 506.)
8, 092 ÷ 239
Exercise 8.2.38
2, 688 ÷ 48
Exercise 8.2.39
(Solution on p. 506.)
72.14 + 21.08
Exercise 8.2.40
43.016 + 47.58
Exercise 8.2.41
(Solution on p. 506.)
96.53 − 26.91
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 8.2.42
115.0012 − 25.018
Exercise 8.2.43
(Solution on p. 506.)
206.19 + 142.38
Exercise 8.2.44
592.131 + 211.6
Exercise 8.2.45
(Solution on p. 506.)
(32.12) (48.7)
Exercise 8.2.46
(87.013) (21.07)
Exercise 8.2.47
(Solution on p. 506.)
(3.003) (16.52)
Exercise 8.2.48
(6.032) (14.091)
Exercise 8.2.49
(Solution on p. 506.)
(114.06) (384.3)
Exercise 8.2.50
(5, 137.118) (263.56)
Exercise 8.2.51
(Solution on p. 506.)
(6.92) (0.88)
Exercise 8.2.52
(83.04) (1.03)
Exercise 8.2.53
(Solution on p. 506.)
(17.31) (.003)
Exercise 8.2.54
(14.016) (.016)
Exercise 8.2.55
(Solution on p. 506.)
93% of 7.01
Exercise 8.2.56
107% of 12.6
Exercise 8.2.57
(Solution on p. 506.)
32% of 15.3
Exercise 8.2.58
74% of 21.93
Exercise 8.2.59
(Solution on p. 506.)
18% of 4.118
Exercise 8.2.60
4% of .863
Exercise 8.2.61
(Solution on p. 506.)
2% of .0039
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
484
CHAPTER 8. TECHNIQUES OF ESTIMATION
8.2.3.1 Exercises for Review
Exercise 8.2.62
(Section 5.3) Find the dierence: 710 − 516.
Exercise 8.2.63
(Solution on p. 506.)
(Section 5.6) Find the value 6−14 .
6+ 1
4
Exercise 8.2.64
(Section 6.3) Convert the complex decimal 1.111 to a decimal.
4
Exercise 8.2.65
(Solution on p. 506.)
(Section 7.4) A woman 5 foot tall casts an 8-foot shadow at a particular time of the day. How tall is a tree that casts a 96-foot shadow at the same time of the day?
Exercise 8.2.66
(Section 7.7) 11.62 is 83% of what number?
8.3 Estimation by Clustering3
8.3.1 Section Overview
• Estimation by Clustering
Cluster
When more than two numbers are to be added, the sum may be estimated using the clustering technique.
The rounding technique could also be used, but if several of the numbers are seen to cluster (are seen to be close to) one particular number, the clustering technique provides a quicker estimate. Consider a sum such as
32 + 68 + 29 + 73
Notice two things:
1. There are more than two numbers to be added.
2. Clustering occurs.
(a) Both 68 and 73 cluster around 70, so 68 + 73 is close to 80 + 70 = 2 (70) = 140.
(b) Both 32 and 29 cluster around 30, so 32 + 29 is close to 30 + 30 = 2 (30) = 60.
The sum may be estimated by
(2 · 30) + (2 · 70) = 6 + 140
=
200
In fact, 32 + 68 + 29 + 73 = 202.
3This content is available online at <http://cnx.org/content/m35012/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
8.3.1.1 Sample Set A
Estimate each sum. Results may vary.
Example 8.10
27 + 48 + 31 + 52.
27 and 31 cluster near 30. Their sum is about 2 · 30 = 60.
48 and 52 cluster near 50. Their sum is about 2 · 50 = 100.
(2 · 30) + (2 · 50)
=
60 + 100
Thus, 27 + 48 + 31 + 52 is about
=
160
In fact, 27 + 48 + 31 + 52 = 158.
Example 8.11
88 + 21 + 19 + 91.
88 and 91 cluster near 90. Their sum is about 2 · 90 = 180.
21 and 19 cluster near 20. Their sum is about 2 · 20 = 40.
(2 · 90) + (2 · 20)
=
180 + 40
Thus, 88 + 21 + 19 + 91 is about
=
220
In fact, 88 + 21 + 19 + 91 = 219.
Example 8.12
17 + 21 + 48 + 18.
17, 21, and 18 cluster near 20. Their sum is about 3 · 20 = 60.
48 is about 50.
(3 · 20) + 50
=
60 + 50
Thus, 17 + 21 + 48 + 18 is about
=
110
In fact, 17 + 21 + 48 + 18 = 104.
Example 8.13
61 + 48 + 49 + 57 + 52.
61 and 57 cluster near 60. Their sum is about 2 · 60 = 120.
48, 49, and 52 cluster near 50. Their sum is about 3 · 50 = 150.
(2 · 60) + (3 · 50)
=
120 + 150
Thus, 61 + 48 + 49 + 57 + 52 is about
=
270
In fact, 61 + 48 + 49 + 57 + 52 = 267.
Example 8.14
706 + 321 + 293 + 684.
706 and 684 cluster near 700. Their sum is about 2 · 700 = 1,400.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 8. TECHNIQUES OF ESTIMATION
321 and 293 cluster near 300. Their sum is about 2 · 300 = 600.
(2 · 700) + (2 · 300)
=
1, 400 + 600
Thus, 706 + 321 + 293 + 684 is about
=
2, 000
In fact, 706 + 321 + 293 + 684 = 2,004.
8.3.1.2 Practice Set A
Use the clustering method to estimate each sum.
Exercise 8.3.1
(Solution on p. 506.)
28 + 51 + 31 + 47
Exercise 8.3.2
(Solution on p. 506.)
42 + 39 + 68 + 41
Exercise 8.3.3
(Solution on p. 506.)
37 + 39 + 83 + 42 + 79
Exercise 8.3.4
(Solution on p. 506.)
612 + 585 + 830 + 794
8.3.2 Exercises
Use the clustering method to estimate each sum. Results may vary.
Exercise 8.3.5
(Solution on p. 506.)
28 + 51 + 31 + 47
Exercise 8.3.6
42 + 19 + 39 + 23
Exercise 8.3.7
(Solution on p. 506.)
88 + 62 + 59 + 90
Exercise 8.3.8
76 + 29 + 33 + 82
Exercise 8.3.9
(Solution on p. 506.)
19 + 23 + 87 + 21
Exercise 8.3.10
41 + 28 + 42 + 37
Exercise 8.3.11
(Solution on p. 506.)
89 + 32 + 89 + 93
Exercise 8.3.12
73 + 72 + 27 + 71
Exercise 8.3.13
(Solution on p. 506.)
43 + 62 + 61 + 55
Exercise 8.3.14
31 + 77 + 31 + 27
Exercise 8.3.15
(Solution on p. 507.)
57 + 34 + 28 + 61 + 62
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 8.3.16
94 + 18 + 23 + 91 + 19
Exercise 8.3.17
(Solution on p. 507.)
103 + 72 + 66 + 97 + 99
Exercise 8.3.18
42 + 121 + 119 + 124 + 41
Exercise 8.3.19
(Solution on p. 507.)
19 + 24 + 87 + 23 + 91 + 93
Exercise 8.3.20
108 + 61 + 63 + 96 + 57 + 99
Exercise 8.3.21
(Solution on p. 507.)
518 + 721 + 493 + 689
Exercise 8.3.22
981 + 1208 + 1214 + 1006
Exercise 8.3.23
(Solution on p. 507.)
23 + 81 + 77 + 79 + 19 + 81
Exercise 8.3.24
94 + 68 + 66 + 101 + 106 + 71 + 110
8.3.2.1 Exercises for Review
Exercise 8.3.25
(Solution on p. 507.)
(Section 1.2) Specify all the digits greater than 6.
Exercise 8.3.26
(Section 4.5) Find the product: 2 · 9
3
14 · 7
12 .
Exercise 8.3.27
(Solution on p. 507.)
(Section 6.3) Convert 0.06 to a fraction.
Exercise 8.3.28
(Section 7.3) Write the proportion in fractional form: “5 is to 8 as 25 is to 40.”
Exercise 8.3.29
(Solution on p. 507.)
(Section 8.2) Estimate the sum using the method of rounding: 4,882 + 2,704.
8.4 Mental Arithmetic-Using the Distributive Property4
8.4.1 Section Overview
• The Distributive Property
• Estimation Using the Distributive Property
4This content is available online at <http://cnx.org/content/m35013/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
488
CHAPTER 8. TECHNIQUES OF ESTIMATION
8.4.2 The Distributive Property
Distributive Property
The distributive property is a characteristic of numbers that involves both addition and multiplication.
It is used often in algebra, and we can use it now to obtain exact results for a multiplication.
Suppose we wish to compute 3 (2 + 5). We can proceed in either of two ways, one way which is known to us already (the order of operations), and a new way (the distributive property).
1. Compute 3 (2 + 5) using the order of operations.
3 (2 + 5)
Operate inside the parentheses rst: 2 + 5 = 7.
3 (2 + 5) = 3 · 7
Now multiply 3 and 7.
3 (2 + 5) = 3 · 7 = 21
Thus, 3 (2 + 5) = 21.
2. Compute 3 (2 + 5) using the distributive property.
We know that multiplication describes repeated addition. Thus,
3 (2 + 5)
=
2 + 5 + 2 + 5 + 2 + 5
|
{z
}
2 + 5 appears 3 times
=
2 + 2 + 2 + 5 + 5 + 5
(by the commutative property of addition)
=
3 · 2 + 3 · 5
(since multiplication describes repeated addition)
=
6 + 15
=
21
Thus, 3 (2 + 5) = 21.
Let’s look again at this use of the distributive property.
3 (2 + 5)
=
2 + 5 + 2 + 5 + 2 + 5
|
{z
}
2 + 5 appears 3 times
3 (2 + 5)
=
2 + 2 + 2
+
5 + 5 + 5
|
{z
}
|
{z
}
2 appears 3 times
5 appears 3 times
The 3 has been distributed to the 2 and 5.
This is the distributive property. We distribute the factor to each addend in the parentheses. The distributive property works for both sums and dierences.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
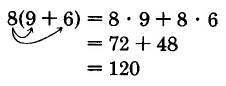
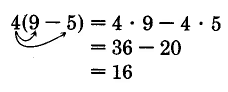
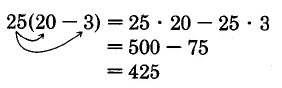
489
8.4.2.1 Sample Set A
Example 8.15
Using the order of operations, we get
4 (6 + 2)
=
4 · 8
=
32
Example 8.16
Using the order of operations, we get
8 (9 + 6)
=
8 · 15
=
120
Example 8.17
Example 8.18
8.4.2.2 Practice Set A
Use the distributive property to compute each value.
Exercise 8.4.1
(Solution on p. 507.)
6 (8 + 4)
Exercise 8.4.2
(Solution on p. 507.)
4 (4 + 7)
Exercise 8.4.3
(Solution on p. 507.)
8 (2 + 9)
Exercise 8.4.4
(Solution on p. 507.)
12 (10 + 3)
Exercise 8.4.5
(Solution on p. 507.)
6 (11 − 3)
Exercise 8.4.6
(Solution on p. 507.)
8 (9 − 7)
Exercise 8.4.7
(Solution on p. 507.)
15 (30 − 8)
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
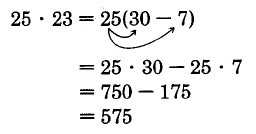
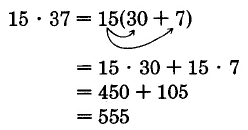
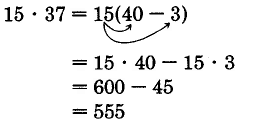
490
CHAPTER 8. TECHNIQUES OF ESTIMATION
8.4.3 Estimation Using the Distributive Property
We can use the distributive property to obtain exact results for products such as 25 · 23. The distributive property works best for products when one of the factors ends in 0 or 5. We shall restrict our attention to only such products.
8.4.3.1 Sample Set B
Use the distributive property to compute each value.
Example 8.19
25 · 23
Notice that 23 = 20 + 3. We now write
Thus, 25 · 23 = 575
We could have proceeded by writing 23 as 30 − 7.
Example 8.20
15 · 37
Notice that 37 = 30 + 7. We now write
Thus, 15 · 37 = 555
We could have proceeded by writing 37 as 40 − 3.
Example 8.21
15 · 86
Notice that 86 = 80 + 6. We now write
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
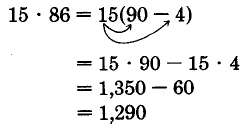
491
We could have proceeded by writing 86 as 90 − 4.
8.4.3.2 Practice Set B
Use the distributive property to compute each value.
Exercise 8.4.8
(Solution on p. 507.)
25 · 12
Exercise 8.4.9
(Solution on p. 507.)
35 · 14
Exercise 8.4.10
(Solution on p. 507.)
80 · 58
Exercise 8.4.11
(Solution on p. 507.)
65 · 62
8.4.4 Exercises
Use the distributive property to compute each product.
Exercise 8.4.12
(Solution on p. 507.)
15 · 13
Exercise 8.4.13
15 · 14
Exercise 8.4.14
(Solution on p. 507.)
25 · 11
Exercise 8.4.15
25 · 16
Exercise 8.4.16
(Solution on p. 507.)
15 · 16
Exercise 8.4.17
35 · 12
Exercise 8.4.18
(Solution on p. 507.)
45 · 83
Exercise 8.4.19
45 · 38
Exercise 8.4.20
(Solution on p. 507.)
25 · 38
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 8. TECHNIQUES OF ESTIMATION
Exercise 8.4.21
25 · 96
Exercise 8.4.22
(Solution on p. 507.)
75 · 14
Exercise 8.4.23
85 · 34
Exercise 8.4.24
(Solution on p. 508.)
65 · 26
Exercise 8.4.25
55 · 51
Exercise 8.4.26
(Solution on p. 508.)
15 · 107
Exercise 8.4.27
25 · 208
Exercise 8.4.28
(Solution on p. 508.)
35 · 402
Exercise 8.4.29
85 · 110
Exercise 8.4.30
(Solution on p. 508.)
95 · 12
Exercise 8.4.31
65 · 40
Exercise 8.4.32
(Solution on p. 508.)
80 · 32
Exercise 8.4.33
30 · 47
Exercise 8.4.34
(Solution on p. 508.)
50 · 63
Exercise 8.4.35
90 · 78
Exercise 8.4.36
(Solution on p. 508.)
40 · 89
8.4.4.1 Exercises for Review
Exercise 8.4.37
(Section 3.5) Find the greatest common factor of 360 and 3,780.
Exercise 8.4.38
(Solution on p. 508.)
(Section 4.5) Reduce 594
5,148 to lowest terms.
Exercise 8.4.39
(Section 4.7) 15 of 24 is what number?
9
7
Exercise 8.4.40
(Solution on p. 508.)
(Section 7.3) Solve the proportion: 715 = x90.
Exercise 8.4.41
(Section 8.3) Use the clustering method to estimate the sum: 88 + 106 + 91 + 114.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
8.5 Estimation by Rounding Fractions5
8.5.1 Section Overview
• Estimation by Rounding Fractions
Estimation by rounding fractions is a useful technique for estimating the result of a computation involving fractions. Fractions are commonly rounded to 1, 1, 3, 0, and 1. Remember that rounding may cause 4
2
4
estimates to vary.
8.5.1.1 Sample Set A
Make each estimate remembering that results may vary.
Example 8.22
Estimate 3 + 5
5
12 .
Notice that 3 is about 1, and that 5
.
5
2
12 is about 12
Thus, 3 + 5
+ 1 = 1. In fact, 3 + 5
5
12 is about 12
2
5
12 = 61
60 , a little more than 1.
Example 8.23
Estimate 53 + 4 9
.
8
10 + 11 15
Adding the whole number parts, we get 20. Notice that 3 is close to 1, 9
is
8
4
10 is close to 1, and 15
close to 1. Then 3 + 9
is close to 1 + 1 + 1 = 11.
4
8
10 + 15
4
4
2
Thus, 53 + 4 9
is close to 20 + 11 = 211.
8
10 + 11 15
2
2
In fact, 53 + 4 9
= 21 19
.
8
10 + 11 15
40 , a little less than 21 12
8.5.1.2 Practice Set A
Use the method of rounding fractions to estimate the result of each computation. Results may vary.
Exercise 8.5.1
(Solution on p. 508.)
5 + 5
8
12
Exercise 8.5.2
(Solution on p. 508.)
7 + 3
9
5
Exercise 8.5.3
(Solution on p. 508.)
8 4
15 + 3 7
10
Exercise 8.5.4
(Solution on p. 508.)
16 1 + 47
20
8
5This content is available online at <http://cnx.org/content/m35014/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 8. TECHNIQUES OF ESTIMATION
8.5.2 Exercises
Estimate each sum or dierence using the method of rounding. After you have made an estimate, nd the exact value of the sum or dierence and compare this result to the estimated value. Result may vary.
Exercise 8.5.5
(Solution on p. 508.)
5 + 7
6
8
Exercise 8.5.6
3 + 11
8
12
Exercise 8.5.7
(Solution on p. 508.)
9
10 + 35
Exercise 8.5.8
13
15 + 1
20
Exercise 8.5.9
(Solution on p. 508.)
3
20 + 6
25
Exercise 8.5.10
1
12 + 45
Exercise 8.5.11
(Solution on p. 508.)
15
16 + 1
12
Exercise 8.5.12
29
30 + 11
20
Exercise 8.5.13
(Solution on p. 508.)
5
12 + 6 4
11
Exercise 8.5.14
3 + 8 4
7
15
Exercise 8.5.15
(Solution on p. 508.)
9
10 + 2 38
Exercise 8.5.16
19
20 + 15 59
Exercise 8.5.17
(Solution on p. 508.)
8 3 + 4 1
5
20
Exercise 8.5.18
5 3
20 + 2 8
15
Exercise 8.5.19
(Solution on p. 508.)
9 1
15 + 6 45
Exercise 8.5.20
7 5
12 + 10 1
16
Exercise 8.5.21
(Solution on p. 508.)
3 11
20 + 2 13
25 + 1 78
Exercise 8.5.22
6 1
12 + 1 1
10 + 5 56
Exercise 8.5.23
(Solution on p. 508.)
15
16 − 78
Exercise 8.5.24
12
25 − 9
20
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
8.5.2.1 Exercises for Review
Exercise 8.5.25
(Solution on p. 508.)
(Section 2.6) The fact that
(a rst number · a second number)
·
a third number
=
a rst number
·
(a second number · a third number)
is an example of which property of multiplication?
Exercise 8.5.26
(Section 4.6) Find the quotient: 14
15 ÷ 4
45 .
Exercise 8.5.27
(Solution on p. 508.)
(Section 5.4) Find the dierence: 35 − 22.
9
3
Exercise 8.5.28
(Section 6.8) Find the quotient: 4.6 ÷ 0.11.
Exercise 8.5.29
(Solution on p. 509.)
(Section 8.4) Use the distributive property to compute the product: 25 · 37.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 8. TECHNIQUES OF ESTIMATION
8.6 Summary of Key Concepts6
8.6.1 Summary of Key Concepts
Estimation (Section 8.2)
Estimation is the process of determining an expected value of a computation.
Estimation By Rounding (Section 8.2)
The rounding technique estimates the result of a computation by rounding the numbers involved in the computation to one or two nonzero digits. For example, 512 + 896 can be estimated by 500 + 900 = 1,400.
Cluster (Section 8.3)
When several numbers are close to one particular number, they are said to cluster near that particular number.
Estimation By Clustering (Section 8.3)
The clustering technique of estimation can be used when
1. there are more than two numbers to be added, and
2. clustering occurs.
For example, 31 + 62 + 28 + 59 can be estimated by
(2 · 30) + (2 · 60) = 60 + 120 = 180
Distributive Property (Section 8.4)
The distributive property is a characteristic of numbers that involves both addition and multiplication.
For example,
3 (4 + 6) = 3 · 4 + 3 · 6 = 12 + 18 = 30
Estimation Using the Distributive Property (Section 8.4)
The distributive property can be used to obtain exact results for a multiplication.
For example,
15 · 23 = 15 · (20 + 3) = 15 · 20 + 15 · 3 = 300 + 45 = 345
Estimation by Rounding Fractions (Section 8.5)
Estimation by rounding fractions commonly rounds fractions to 1, 1, 3, 0, and 1.
4
2
4
For example,
5
12 + 5
16 can be estimated by 1 + 1 = 3
2
4
4
8.7 Exercise Supplement7
8.7.1 Exercise Supplement
8.7.1.1 Estimation by Rounding (Section 8.2)
For problems 1-70, estimate each value using the method of rounding. After you have made an estimate, nd the exact value. Compare the exact and estimated values. Results may vary.
Exercise 8.7.1
(Solution on p. 509.)
286 + 312
Exercise 8.7.2
419 + 582
6This content is available online at <http://cnx.org/content/m35015/1.2/>.
7This content is available online at <http://cnx.org/content/m35016/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 8.7.3
(Solution on p. 509.)
689 + 511
Exercise 8.7.4
926 + 1, 105
Exercise 8.7.5
(Solution on p. 509.)
1, 927 + 3, 017
Exercise 8.7.6
5, 026 + 2, 814
Exercise 8.7.7
(Solution on p. 509.)
1, 408 + 2, 352
Exercise 8.7.8
1, 186 + 4, 228
Exercise 8.7.9
(Solution on p. 509.)
5, 771 + 246
Exercise 8.7.10
8, 305 + 484
Exercise 8.7.11
(Solution on p. 509.)
3, 812 + 2, 906
Exercise 8.7.12
5, 293 + 8, 007
Exercise 8.7.13
(Solution on p. 509.)
28, 481 + 32, 856
Exercise 8.7.14
92, 512 + 26, 071
Exercise 8.7.15
(Solution on p. 509.)
87, 612 + 2, 106
Exercise 8.7.16
42, 612 + 4, 861
Exercise 8.7.17
(Solution on p. 509.)
212, 413 + 609
Exercise 8.7.18
487, 235 + 494
Exercise 8.7.19
(Solution on p. 509.)
2, 409 + 1, 526
Exercise 8.7.20
3, 704 + 4, 704
Exercise 8.7.21
(Solution on p. 509.)
41 · 63
Exercise 8.7.22
38 · 81
Exercise 8.7.23
(Solution on p. 509.)
18 · 28
Exercise 8.7.24
52 · 21
Exercise 8.7.25
(Solution on p. 509.)
307 · 489
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 8. TECHNIQUES OF ESTIMATION
Exercise 8.7.26
412 · 807
Exercise 8.7.27
(Solution on p. 509.)
77 · 614
Exercise 8.7.28
62 · 596
Exercise 8.7.29
(Solution on p. 509.)
27 · 473
Exercise 8.7.30
92 · 336
Exercise 8.7.31
(Solution on p. 509.)
12 · 814
Exercise 8.7.32
8 · 2, 106
Exercise 8.7.33
(Solution on p. 509.)
192 · 452
Exercise 8.7.34
374 · 816
Exercise 8.7.35
(Solution on p. 509.)
88 · 4, 392
Exercise 8.7.36
126 · 2, 834
Exercise 8.7.37
(Solution on p. 509.)
3, 896 · 413
Exercise 8.7.38
5, 794 · 837
Exercise 8.7.39
(Solution on p. 509.)
6, 311 · 3, 512
Exercise 8.7.40
7, 471 · 5, 782
Exercise 8.7.41
(Solution on p. 509.)
180 ÷ 12
Exercise 8.7.42
309 ÷ 16
Exercise 8.7.43
(Solution on p. 509.)
286 ÷ 22
Exercise 8.7.44
527 ÷ 17
Exercise 8.7.45
(Solution on p. 509.)
1, 007 ÷ 19
Exercise 8.7.46
1, 728 ÷ 36
Exercise 8.7.47
(Solution on p. 509.)
2, 703 ÷ 53
Exercise 8.7.48
2, 562 ÷ 61
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 8.7.49
(Solution on p. 510.)
1, 260 ÷ 12
Exercise 8.7.50
3, 618 ÷ 18
Exercise 8.7.51
(Solution on p. 510.)
3, 344 ÷ 76
Exercise 8.7.52
7, 476 ÷ 356
Exercise 8.7.53
(Solution on p. 510.)
20, 984 ÷ 488
Exercise 8.7.54
43, 776 ÷ 608
Exercise 8.7.55
(Solution on p. 510.)
7, 196 ÷ 514
Exercise 8.7.56
51, 492 ÷ 514
Exercise 8.7.57
(Solution on p. 510.)
26, 962 ÷ 442
Exercise 8.7.58
33, 712 ÷ 112
Exercise 8.7.59
(Solution on p. 510.)
105, 152 ÷ 106
Exercise 8.7.60
176, 978 ÷ 214
Exercise 8.7.61
(Solution on p. 510.)
48.06 + 23.11
Exercise 8.7.62
73.73 + 72.9
Exercise 8.7.63
(Solution on p. 510.)
62.91 + 56.4
Exercise 8.7.64
87.865 + 46.772
Exercise 8.7.65
(Solution on p. 510.)
174.6 + 97.2
Exercise 8.7.66
(48.3) (29.6)
Exercise 8.7.67
(Solution on p. 510.)
(87.11) (23.2)
Exercise 8.7.68
(107.02) (48.7)
Exercise 8.7.69
(Solution on p. 510.)
(0.76) (5.21)
Exercise 8.7.70
(1.07) (13.89)
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 8. TECHNIQUES OF ESTIMATION
8.7.1.2 Estimation by Clustering (Section 8.3)
For problems 71-90, estimate each value using the method of clustering. After you have made an estimate, nd the exact value. Compare the exact and estimated values. Results may vary.
Exercise 8.7.71
(Solution on p. 510.)
38 + 51 + 41 + 48
Exercise 8.7.72
19 + 73 + 23 + 71
Exercise 8.7.73
(Solution on p. 510.)
27 + 62 + 59 + 31
Exercise 8.7.74
18 + 73 + 69 + 19
Exercise 8.7.75
(Solution on p. 510.)
83 + 49 + 79 + 52
Exercise 8.7.76
67 + 71 + 84 + 81
Exercise 8.7.77
(Solution on p. 510.)
16 + 13 + 24 + 26
Exercise 8.7.78
34 + 56 + 36 + 55
Exercise 8.7.79
(Solution on p. 510.)
14 + 17 + 83 + 87
Exercise 8.7.80
93 + 108 + 96 + 111
Exercise 8.7.81
(Solution on p. 510.)
18 + 20 + 31 + 29 + 24 + 38
Exercise 8.7.82
32 + 27 + 48 + 51 + 72 + 69
Exercise 8.7.83
(Solution on p. 510.)
64 + 17 + 27 + 59 + 31 + 21
Exercise 8.7.84
81 + 41 + 92 + 38 + 88 + 80
Exercise 8.7.85
(Solution on p. 510.)
87 + 22 + 91
Exercise 8.7.86
44 + 38 + 87
Exercise 8.7.87
(Solution on p. 510.)
19 + 18 + 39 + 22 + 42
Exercise 8.7.88
31 + 28 + 49 + 29
Exercise 8.7.89
(Solution on p. 510.)
88 + 86 + 27 + 91 + 29
Exercise 8.7.90
57 + 62 + 18 + 23 + 61 + 21
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
8.7.1.3 Mental Arithmetic- Using the Distributive Property (Section 8.4) For problems 91-110, compute each product using the distributive property.
Exercise 8.7.91
(Solution on p. 510.)
15 · 33
Exercise 8.7.92
15 · 42
Exercise 8.7.93
(Solution on p. 510.)
35 · 36
Exercise 8.7.94
35 · 28
Exercise 8.7.95
(Solution on p. 510.)
85 · 23
Exercise 8.7.96
95 · 11
Exercise 8.7.97
(Solution on p. 510.)
30 · 14
Exercise 8.7.98
60 · 18
Exercise 8.7.99
(Solution on p. 511.)
75 · 23
Exercise 8.7.100
65 · 31
Exercise 8.7.101
(Solution on p. 511.)
17 · 15
Exercise 8.7.102
38 · 25
Exercise 8.7.103
(Solution on p. 511.)
14 · 65
Exercise 8.7.104
19 · 85
Exercise 8.7.105
(Solution on p. 511.)
42 · 60
Exercise 8.7.106
81 · 40
Exercise 8.7.107
(Solution on p. 511.)
15 · 105
Exercise 8.7.108
35 · 202
Exercise 8.7.109
(Solution on p. 511.)
45 · 306
Exercise 8.7.110
85 · 97
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 8. TECHNIQUES OF ESTIMATION
8.7.1.4 Estimation by Rounding Fractions (Section 8.5)
For problems 111-125, estimate each sum using the method of rounding fractions. After you have made an estimate, nd the exact value. Compare the exact and estimated values. Results may vary.
Exercise 8.7.111
(Solution on p. 511.)
3 + 5
8
6
Exercise 8.7.112
7
16 + 1
24
Exercise 8.7.113
(Solution on p. 511.)
7
15 + 13
30
Exercise 8.7.114
14
15 + 19
20
Exercise 8.7.115
(Solution on p. 511.)
13
25 + 7
30
Exercise 8.7.116
11
12 + 78
Exercise 8.7.117
(Solution on p. 511.)
9
32 + 15
16
Exercise 8.7.118
5 + 1
8
32
Exercise 8.7.119
(Solution on p. 511.)
2 3 + 6 3
4
5
Exercise 8.7.120
4 5 + 8 1
9
27
Exercise 8.7.121
(Solution on p. 511.)
11 518 + 722
45
Exercise 8.7.122
1419
36 + 2 7
18
Exercise 8.7.123
(Solution on p. 511.)
6 1
20 + 2 1
10 + 8 13
60
Exercise 8.7.124
5 7 + 1 1 + 12 5
8
4
12
Exercise 8.7.125
(Solution on p. 511.)
101 + 615
2
16 + 8 19
80
8.8 Prociency Exam8
8.8.1 Prociency Exam
For problems 1 – 16, estimate each value. After you have made an estimate, nd the exact value. Results may vary.
Exercise 8.8.1
(Solution on p. 511.)
(Section 8.2) 3,716 + 6,789
Exercise 8.8.2
(Solution on p. 511.)
(Section 8.2) 8,821 + 9,217
8This content is available online at <http://cnx.org/content/m35017/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 8.8.3
(Solution on p. 511.)
(Section 8.2) 7, 316 − 2, 305
Exercise 8.8.4
(Solution on p. 511.)
(Section 8.2) 110, 812 − 83, 406
Exercise 8.8.5
(Solution on p. 511.)
(Section 8.2) 82 · 38
Exercise 8.8.6
(Solution on p. 511.)
(Section 8.2) 51 · 92
Exercise 8.8.7
(Solution on p. 511.)
(Section 8.2) 48 · 6,012
Exercise 8.8.8
(Solution on p. 511.)
(Section 8.2) 238 ÷ 17
Exercise 8.8.9
(Solution on p. 511.)
(Section 8.2) 2,660 ÷ 28
Exercise 8.8.10
(Solution on p. 511.)
(Section 8.2) 43.06 + 37.94
Exercise 8.8.11
(Solution on p. 511.)
(Section 8.2) 307.006 + 198.0005
Exercise 8.8.12
(Solution on p. 512.)
(Section 8.2) (47.2) (92.8)
Exercise 8.8.13
(Solution on p. 512.)
(Section 8.3) 58 + 91 + 61 + 88
Exercise 8.8.14
(Solution on p. 512.)
(Section 8.3) 43 + 39 + 89 + 92
Exercise 8.8.15
(Solution on p. 512.)
(Section 8.3) 81 + 78 + 27 + 79
Exercise 8.8.16
(Solution on p. 512.)
(Section 8.3) 804 + 612 + 801 + 795 + 606
For problems 17-21, use the distributive property to obtain the exact result.
Exercise 8.8.17
(Solution on p. 512.)
(Section 8.4) 25 · 14
Exercise 8.8.18
(Solution on p. 512.)
(Section 8.4) 15 · 83
Exercise 8.8.19
(Solution on p. 512.)
(Section 8.4) 65 · 98
Exercise 8.8.20
(Solution on p. 512.)
(Section 8.4) 80 · 107
Exercise 8.8.21
(Solution on p. 512.)
(Section 8.4) 400 · 215
For problems 22-25, estimate each value. After you have made an estimate, nd the exact value. Results may vary.
Exercise 8.8.22
(Solution on p. 512.)
(Section 8.5) 15
16 + 58
Exercise 8.8.23
(Solution on p. 512.)
(Section 8.5 ) 125 + 11
20 + 17
30
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 8. TECHNIQUES OF ESTIMATION
Exercise 8.8.24
(Solution on p. 512.)
(Section 8.5) 8 916 + 14 112
Exercise 8.8.25
(Solution on p. 512.)
(Section 8.5) 54 + 117
9
36 + 6 5
12
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solutions to Exercises in Chapter 8
Solution to Exercise 8.2.1 (p. 478)
4, 216 + 3, 942 : 4, 200 + 3, 900. About 8,100. In fact, 8,158.
Solution to Exercise 8.2.2 (p. 478)
812 + 514 : 800 + 500. About 1,300. In fact, 1,326.
Solution to Exercise 8.2.3 (p. 478)
43, 892 + 92, 106 : 44, 000 + 92, 000. About 136,000. In fact, 135,998.
Solution to Exercise 8.2.4 (p. 479)
628 − 413 : 600 − 400. About 200. In fact, 215.
Solution to Exercise 8.2.5 (p. 479)
7, 842 − 5, 209 : 7, 800 − 5, 200. About 2,600. In fact, 2,633.
Solution to Exercise 8.2.6 (p. 479)
73, 812 − 28, 492 : 74, 000 − 28, 000. About 46,000. In fact, 45,320.
Solution to Exercise 8.2.7 (p. 479)
31 · 87 : 30 · 90. About 2,700. In fact, 2,697.
Solution to Exercise 8.2.8 (p. 479)
18 · 42 : 20 · 40. About 800. In fact, 756.
Solution to Exercise 8.2.9 (p. 479)
16 · 94 : 15 · 100. About 1,500. In fact, 1,504.
Solution to Exercise 8.2.10 (p. 480)
221 ÷ 18 : 200 ÷ 20. About 10. In fact, 12.27.
Solution to Exercise 8.2.11 (p. 480)
4, 079 ÷ 381 : 4, 000 ÷ 400. About 10. In fact, 10.70603675…
Solution to Exercise 8.2.12 (p. 480)
609, 000 ÷ 16, 000 : 600, 000 ÷ 15, 000. About 40. In fact, 38.0625.
Solution to Exercise 8.2.13 (p. 481)
61.02 + 26.8 : 61 + 27. About 88. In fact, 87.82.
Solution to Exercise 8.2.14 (p. 481)
109.12 + 137.88 : 110 + 138. About 248. In fact, 247. We could have estimated 137.88 with 140. Then 110 + 140 is an easy mental addition. We would conclude then that 109.12 + 137.88 is about 250.
Solution to Exercise 8.2.15 (p. 481)
(47.8) (21.1) : (50) (20). About 1,000. In fact, 1,008.58.
Solution to Exercise 8.2.16 (p. 481)
32% of 14.88 : (.3) (15). About 4.5. In fact, 4.7616.
Solution to Exercise 8.2.17 (p. 481)
about 3,600; in fact 3,600
Solution to Exercise 8.2.19 (p. 482)
about 1,700; in fact 1,717
Solution to Exercise 8.2.21 (p. 482)
about 14,000; in fact 14,006
Solution to Exercise 8.2.23 (p. 482)
about 3,500; in fact 3,539
Solution to Exercise 8.2.25 (p. 482)
about 5,700; in fact 5,694
Solution to Exercise 8.2.27 (p. 482)
about 1,500; in fact 1,696
Solution to Exercise 8.2.29 (p. 482)
about 540,000; in fact 559,548
Solution to Exercise 8.2.31 (p. 482)
about 583,200,000; in fact 583,876,992
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 8. TECHNIQUES OF ESTIMATION
Solution to Exercise 8.2.33 (p. 482)
about 15; in fact 15.11
Solution to Exercise 8.2.35 (p. 482)
about 20; in fact 22
Solution to Exercise 8.2.37 (p. 482)
about 33; in fact 33.86
Solution to Exercise 8.2.39 (p. 482)
about 93.2; in fact 93.22
Solution to Exercise 8.2.41 (p. 482)
about 70; in fact 69.62
Solution to Exercise 8.2.43 (p. 483)
about 348.6; in fact 348.57
Solution to Exercise 8.2.45 (p. 483)
about 1,568.0; in fact 1,564.244
Solution to Exercise 8.2.47 (p. 483)
about 49.5; in fact 49.60956
Solution to Exercise 8.2.49 (p. 483)
about 43,776; in fact 43,833.258
Solution to Exercise 8.2.51 (p. 483)
about 6.21; in fact 6.0896
Solution to Exercise 8.2.53 (p. 483)
about 0.0519; in fact 0.05193
Solution to Exercise 8.2.55 (p. 483)
about 6.3; in fact 6.5193
Solution to Exercise 8.2.57 (p. 483)
about 4.5; in fact 4.896
Solution to Exercise 8.2.59 (p. 483)
about 0.8; in fact 0.74124
Solution to Exercise 8.2.61 (p. 483)
about 0.00008; in fact 0.000078
Solution to Exercise 8.2.63 (p. 484)
23
25
Solution to Exercise 8.2.65 (p. 484)
60 feet tall
Solution to Exercise 8.3.1 (p. 486)
(2 · 30) + (2 · 50) = 60 + 100 = 160
Solution to Exercise 8.3.2 (p. 486)
(3 · 40) + 70 = 120 + 70 = 190
Solution to Exercise 8.3.3 (p. 486)
(3 · 40) + (2 · 80) = 120 + 160 = 280
Solution to Exercise 8.3.4 (p. 486)
(2 · 600) + (2 · 800) = 1, 200 + 1, 600 = 2, 800
Solution to Exercise 8.3.5 (p. 486)
2 (30) + 2 (50) = 160 (157)
Solution to Exercise 8.3.7 (p. 486)
2 (90) + 2 (60) = 300 (299)
Solution to Exercise 8.3.9 (p. 486)
3 (20) + 90 = 150 (150)
Solution to Exercise 8.3.11 (p. 486)
3 (90) + 30 = 300 (303)
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 8.3.13 (p. 486)
40 + 3 (60) = 220 (221)
Solution to Exercise 8.3.15 (p. 486)
3 (60) + 2 (30) = 240 (242)
Solution to Exercise 8.3.17 (p. 487)
3 (100) + 2 (70) = 440 (437)
Solution to Exercise 8.3.19 (p. 487)
3 (20) + 3 (90) = 330 (337)
Solution to Exercise 8.3.21 (p. 487)
2 (500) + 2 (700) = 2, 400 (2, 421)
Solution to Exercise 8.3.23 (p. 487)
2 (20) + 4 (80) = 360 (360)
Solution to Exercise 8.3.25 (p. 487)
7, 8, 9
Solution to Exercise 8.3.27 (p. 487)
3
50
Solution to Exercise 8.3.29 (p. 487)
4, 900 + 2, 700 = 7, 600 (7, 586)
Solution to Exercise 8.4.1 (p. 489)
6 · 8 + 6 · 4 = 48 + 24 = 72
Solution to Exercise 8.4.2 (p. 489)
4 · 4 + 4 · 7 = 16 + 28 = 44
Solution to Exercise 8.4.3 (p. 489)
8 · 2 + 8 · 9 = 16 + 72 = 88
Solution to Exercise 8.4.4 (p. 489)
12 · 10 + 12 · 3 = 120 + 36 = 156
Solution to Exercise 8.4.5 (p. 489)
6 · 11 − 6 · 3 = 66 − 18 = 48
Solution to Exercise 8.4.6 (p. 489)
8 · 9 − −8 · 7 = 72 − −56 = 16
Solution to Exercise 8.4.7 (p. 489)
15 · 30 − 15 · 8 = 450 − 120 = 330
Solution to Exercise 8.4.8 (p. 491)
25 (10 + 2) = 25 · 10 + 25 · 2 = 250 + 50 = 300
Solution to Exercise 8.4.9 (p. 491)
35 (10 + 4) = 35 · 10 + 35 · 4 = 350 + 140 = 490
Solution to Exercise 8.4.10 (p. 491)
80 (50 + 8) = 80 · 50 + 80 · 8 = 4, 000 + 640 = 4, 640
Solution to Exercise 8.4.11 (p. 491)
65 (60 + 2) = 65 · 60 + 65 · 2 = 3, 900 + 130 = 4, 030
Solution to Exercise 8.4.12 (p. 491)
15 (10 + 3) = 150 + 45 = 195
Solution to Exercise 8.4.14 (p. 491)
25 (10 + 1) = 250 + 25 = 275
Solution to Exercise 8.4.16 (p. 491)
15 (20 − 4) = 300 − 60 = 240
Solution to Exercise 8.4.18 (p. 491)
45 (80 + 3) = 3600 + 135 = 3735
Solution to Exercise 8.4.20 (p. 491)
25 (40 − 2) = 1, 000 − 50 = 950
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 8. TECHNIQUES OF ESTIMATION
Solution to Exercise 8.4.22 (p. 492)
75 (10 + 4) = 750 + 300 = 1, 050
Solution to Exercise 8.4.24 (p. 492)
65 (20 + 6) = 1, 300 + 390 = 1, 690 or 65 (30 − 4) = 1, 950 − 260 = 1, 690
Solution to Exercise 8.4.26 (p. 492)
15 (100 + 7) = 1, 500 + 105 = 1, 605
Solution to Exercise 8.4.28 (p. 492)
35 (400 + 2) = 14, 000 + 70 = 14, 070
Solution to Exercise 8.4.30 (p. 492)
95 (10 + 2) = 950 + 190 = 1, 140
Solution to Exercise 8.4.32 (p. 492)
80 (30 + 2) = 2, 400 + 160 = 2, 560
Solution to Exercise 8.4.34 (p. 492)
50 (60 + 3) = 3, 000 + 150 = 3, 150
Solution to Exercise 8.4.36 (p. 492)
40 (90 − 1) = 3, 600 − 40 = 3, 560
Solution to Exercise 8.4.38 (p. 492)
3
26
Solution to Exercise 8.4.40 (p. 492)
x = 42
Solution to Exercise 8.5.1 (p. 493)
Results may vary. 1 + 1 = 1. In fact, 5 + 5
2
2
8
12 = 25
24 = 1 1
24
Solution to Exercise 8.5.2 (p. 493)
Results may vary. 1 + 1 = 11. In fact, 7 + 3 = 117
2
2
9
5
45
Solution to Exercise 8.5.3 (p. 493)
Results may vary. 81 + 33 = 11 + 1 = 12. In fact, 8 4
4
4
15 + 3 7
10 = 11 29
30
Solution to Exercise 8.5.4 (p. 493)
Results may vary. (16 + 0) + (4 + 1) = 16 + 5 = 21. In fact, 16 120 + 47 = 2037
8
40
Solution to Exercise 8.5.5 (p. 494)
1 + 1 = 2
1 17
24
Solution to Exercise 8.5.7 (p. 494)
1 + 1 = 1 1 1 1
2
2
2
Solution to Exercise 8.5.9 (p. 494)
1 + 1 = 1 39
4
4
2
100
Solution to Exercise 8.5.11 (p. 494)
1 + 0 = 1 1 1
48
Solution to Exercise 8.5.13 (p. 494)
1 + 6 1 = 7 6 103
2
2
132
Solution to Exercise 8.5.15 (p. 494)
1 + 2 1 = 3 1 3 11
2
2
40
Solution to Exercise 8.5.17 (p. 494)
8 1 + 4 = 12 1 12 13
2
2
20
Solution to Exercise 8.5.19 (p. 494)
9 + 7 = 16
1513
15
Solution to Exercise 8.5.21 (p. 494)
3 1 + 2 1 + 2 = 8
7 189
2
2
200
Solution to Exercise 8.5.23 (p. 494)
1 − 1 = 0
1
16
Solution to Exercise 8.5.25 (p. 495)
associative
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 8.5.27 (p. 495)
8
9
Solution to Exercise 8.5.29 (p. 495)
25 (40 − 3) = 1000 − 75 = 925
Solution to Exercise 8.7.1 (p. 496)
600 (598)
Solution to Exercise 8.7.3 (p. 497)
(1,200)
Solution to Exercise 8.7.5 (p. 497)
4,900 (4,944)
Solution to Exercise 8.7.7 (p. 497)
3,800 (3,760)
Solution to Exercise 8.7.9 (p. 497)
6,050 (6,017)
Solution to Exercise 8.7.11 (p. 497)
6,700 (6,718)
Solution to Exercise 8.7.13 (p. 497)
61,400 (61,337)
Solution to Exercise 8.7.15 (p. 497)
89,700 (89,718)
Solution to Exercise 8.7.17 (p. 497)
213,000 (213,022)
Solution to Exercise 8.7.19 (p. 497)
3,900 (3,935)
Solution to Exercise 8.7.21 (p. 497)
2,400 (2,583)
Solution to Exercise 8.7.23 (p. 497)
600 (504)
Solution to Exercise 8.7.25 (p. 497)
150,123 147,000 (150,123)
Solution to Exercise 8.7.27 (p. 498)
47,278 48,000 (47,278)
Solution to Exercise 8.7.29 (p. 498)
12,771 14,100 (12,711)
Solution to Exercise 8.7.31 (p. 498)
8,100 (9,768)
Solution to Exercise 8.7.33 (p. 498)
90,000 (86,784)
Solution to Exercise 8.7.35 (p. 498)
396,000 (386,496)
Solution to Exercise 8.7.37 (p. 498)
1,609,048 1,560,000 (1,609,048)
Solution to Exercise 8.7.39 (p. 498)
22,050,000 (22,164,232)
Solution to Exercise 8.7.41 (p. 498)
18 (15)
Solution to Exercise 8.7.43 (p. 498)
141 (13)
2
Solution to Exercise 8.7.45 (p. 498)
50 (53)
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 8. TECHNIQUES OF ESTIMATION
Solution to Exercise 8.7.47 (p. 498)
54 (51)
Solution to Exercise 8.7.49 (p. 499)
130 (105)
Solution to Exercise 8.7.51 (p. 499)
41.25 (44)
Solution to Exercise 8.7.53 (p. 499)
42 (43)
Solution to Exercise 8.7.55 (p. 499)
14.4 (14)
Solution to Exercise 8.7.57 (p. 499)
60 (61)
Solution to Exercise 8.7.59 (p. 499)
1,000 (992)
Solution to Exercise 8.7.61 (p. 499)
71.1 (71.17)
Solution to Exercise 8.7.63 (p. 499)
119.4 (119.31)
Solution to Exercise 8.7.65 (p. 499)
272 (271.8)
Solution to Exercise 8.7.67 (p. 499)
2,001 (2,020.952)
Solution to Exercise 8.7.69 (p. 499)
4.16 (3.9596)
Solution to Exercise 8.7.71 (p. 500)
2 (40) + 2 (50) = 180 (178)
Solution to Exercise 8.7.73 (p. 500)
2 (30) + 2 (60) = 180 (179)
Solution to Exercise 8.7.75 (p. 500)
2 (80) + 2 (50) = 260 (263)
Solution to Exercise 8.7.77 (p. 500)
3 (20) + 1 (10) = 70 (79)
Solution to Exercise 8.7.79 (p. 500)
2 (15) + 2 (80) = 190 (201)
Solution to Exercise 8.7.81 (p. 500)
3 (20) + 2 (30) + 40 = 160 (160)
Solution to Exercise 8.7.83 (p. 500)
2 (60) + 2 (20) + 2 (30) = 220 (219)
Solution to Exercise 8.7.85 (p. 500)
2 (90) + 20 = 200 (200)
Solution to Exercise 8.7.87 (p. 500)
3 (20) + 2 (40) = 140 (140)
Solution to Exercise 8.7.89 (p. 500)
3 (90) + 2 (30) = 330 (321)
Solution to Exercise 8.7.91 (p. 501)
15 (30 + 3) = 450 + 45 = 495
Solution to Exercise 8.7.93 (p. 501)
35 (40 − 4) = 1400 − 140 = 1, 260
Solution to Exercise 8.7.95 (p. 501)
85 (20 + 3) = 1, 700 + 225 = 1, 955
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 8.7.97 (p. 501)
30 (10 + 4) = 300 + 120 = 420
Solution to Exercise 8.7.99 (p. 501)
75 (20 + 3) = 1, 500 + 225 = 1, 725
Solution to Exercise 8.7.101 (p. 501)
15 (20 − 3) = 300 − 45 = 255
Solution to Exercise 8.7.103 (p. 501)
65 (10 + 4) = 650 + 260 = 910
Solution to Exercise 8.7.105 (p. 501)
60 (40 + 2) = 2, 400 + 120 = 2, 520
Solution to Exercise 8.7.107 (p. 501)
15 (100 + 5) = 1, 500 + 75 = 1, 575
Solution to Exercise 8.7.109 (p. 501)
45 (300 + 6) = 13, 500 + 270 = 13, 770
Solution to Exercise 8.7.111 (p. 502)
1 + 1 = 1 1 1 5
2
2
24
Solution to Exercise 8.7.113 (p. 502)
1 + 1 = 1
27
2
2
30 or 9
10
Solution to Exercise 8.7.115 (p. 502)
1 + 1 = 3 113
2
4
4
150
Solution to Exercise 8.7.117 (p. 502)
1 + 1 = 1 1 39
4
4
32 or 1 7
32
Solution to Exercise 8.7.119 (p. 502)
2 3 + 6 1 = 9 1 9 7
4
2
4
20
Solution to Exercise 8.7.121 (p. 502)
111 + 71 = 183 1823
4
2
4
30
Solution to Exercise 8.7.123 (p. 502)
6 + 2 + 8 1 = 16 1 16 11
4
4
30
Solution to Exercise 8.7.125 (p. 502)
101 + 7 + 81 = 253 2527
2
4
4
40
Solution to Exercise 8.8.1 (p. 502)
10,500 (10,505)
Solution to Exercise 8.8.2 (p. 502)
18,000 (18,038)
Solution to Exercise 8.8.3 (p. 503)
5,000 (5,011)
Solution to Exercise 8.8.4 (p. 503)
28,000 (27,406)
Solution to Exercise 8.8.5 (p. 503)
3,200 (3,116)
Solution to Exercise 8.8.6 (p. 503)
4,500 (4,692)
Solution to Exercise 8.8.7 (p. 503)
300,000 (288,576)
Solution to Exercise 8.8.8 (p. 503)
12 (14)
Solution to Exercise 8.8.9 (p. 503)
90 (95)
Solution to Exercise 8.8.10 (p. 503)
81 (81.00)
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 8. TECHNIQUES OF ESTIMATION
Solution to Exercise 8.8.11 (p. 503)
505 (505.0065)
Solution to Exercise 8.8.12 (p. 503)
4,371 (4,380.16)
Solution to Exercise 8.8.13 (p. 503)
2 (60) + 2 (90) = 300 (298)
Solution to Exercise 8.8.14 (p. 503)
2 (40) + 2 (90) = 260 (263)
Solution to Exercise 8.8.15 (p. 503)
30 + 3 (80) = 270 (265)
Solution to Exercise 8.8.16 (p. 503)
3 (800) + 2 (600) = 3, 600 (3,618)
Solution to Exercise 8.8.17 (p. 503)
25 (10 + 4) = 250 + 100 = 350
Solution to Exercise 8.8.18 (p. 503)
15 (80 + 3) = 1, 200 + 45 = 1, 245
Solution to Exercise 8.8.19 (p. 503)
65 (100 − 2) = 6, 500 − 130 = 6, 370
Solution to Exercise 8.8.20 (p. 503)
80 (100 + 7) = 8, 000 + 560 = 8, 560
Solution to Exercise 8.8.21 (p. 503)
400 (200 + 15) = 80, 000 + 6, 000 = 86, 000
Solution to Exercise 8.8.22 (p. 503)
1 + 1 = 1 1 1 9
2
2
16
Solution to Exercise 8.8.23 (p. 503)
0 + 1 + 1 = 1 1 47
2
2
300
Solution to Exercise 8.8.24 (p. 504)
8 1 + 14 = 22 1 22 31
2
2
48
Solution to Exercise 8.8.25 (p. 504)
5 1 + 1 1 + 6 1 = 13 1 13 1
2
2
2
2
3
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Measurement and Geometry
9.1 Objectives1
After completing this chapter, you should
Measurement and the United States System (Section 9.2)
• know what the word measurement means
• be familiar with United States system of measurement
• be able to convert from one unit of measure in the United States system to another unit of measure The Metric System of Measurement (Section 9.3)
• be more familiar with some of the advantages of the base ten number system
• know the prexes of the metric measures
• be familiar with the metric system of measurement
• be able to convert from one unit of measure in the metric system to another unit of measure Simplication of Denominate Numbers (Section 9.4)
• be able to convert an unsimplied unit of measure to a simplied unit of measure
• be able to add and subtract denominate numbers
• be able to multiply and divide a denominate number by a whole number
Perimeter and Circumference of Geometric Figures (Section 9.5)
• know what a polygon is
• know what perimeter is and how to nd it
• know what the circumference, diameter, and radius of a circle is and how to nd each one
• know the meaning of the symbol π and its approximating value
• know what a formula is and four versions of the circumference formula of a circle Area and Volume of Geometric Figures and Objects (Section 9.6)
• know the meaning and notation for area
• know the area formulas for some common geometric gures
• be able to nd the areas of some common geometric gures
• know the meaning and notation for volume
• know the volume formulas for some common geometric objects
• be able to nd the volume of some common geometric objects
1This content is available online at <http://cnx.org/content/m18897/1.3/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4> 513
CHAPTER 9. MEASUREMENT AND GEOMETRY
9.2 Measurement and the United States System2
9.2.1 Section Overview
• Measurement
• The United States System of Measurement
• Conversions in the United States System
9.2.2 Measurement
There are two major systems of measurement in use today. They are the United States system and the metric system. Before we describe these systems, let’s gain a clear understanding of the concept of measurement.
Measurement
Measurement is comparison to some standard.
Standard Unit of Measure
The concept of measurement is based on the idea of direct comparison. This means that measurement is the result of the comparison of two quantities. The quantity that is used for comparison is called the standard unit of measure.
Over the years, standards have changed. Quite some time in the past, the standard unit of measure was determined by a king. For example,
1 inch was the distance between the tip of the thumb and the knuckle of the king.
1 inch was also the length of 16 barley grains placed end to end.
Today, standard units of measure rarely change. Standard units of measure are the responsibility of the Bureau of Standards in Washington D.C.
Some desirable properties of a standard are the following:
1. Accessibility. We should have access to the standard so we can make comparisons.
2. Invariance. We should be condent that the standard is not subject to change.
3. Reproducibility. We should be able to reproduce the standard so that measurements are convenient and accessible to many people.
9.2.3 The United States System of Measurement
Some of the common units (along with their abbreviations) for the United States system of measurement are listed in the following table.
Unit Conversion Table
Length
1 foot (ft) = 12 inches (in.)
1 yard (yd) = 3 feet (ft)
1 mile (mi) = 5,280 feet
continued on next page
2This content is available online at <http://cnx.org/content/m35018/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Weight
1 pound (lb) =16 ounces (oz)
1 ton (T) = 2,000 pounds
Liquid Volume
1 tablespoon (tbsp) = 3 teaspoons (tsp)
1 uid ounce ( oz) = 2 tablespoons
1 cup (c) = 8 uid ounces
1 pint (pt) = 2 cups
1 quart (qt) = 2 pints
1 gallon (gal) = 4 quarts
Time
1 minute (min) = 60 seconds (sec)
1 hour ( hr) = 60 minutes
1 day (da) = 24 hours
1 week (wk) = 7 days
Table 9.1
9.2.4 Conversions in the United States System
It is often convenient or necessary to convert from one unit of measure to another. For example, it may be convenient to convert a measurement of length that is given in feet to one that is given in inches. Such conversions can be made using unit fractions.
Unit Fraction
A unit fraction is a fraction with a value of 1.
Unit fractions are formed by using two equal measurements. One measurement is placed in the numerator of the fraction, and the other in the denominator. Placement depends on the desired conversion.
Placement of Units
Place the unit being converted to in the numerator.
Place the unit being converted from in the denominator.
For example,
Equal Measurements Unit Fraction
1ft = 12in.
1ft
12in. or 12in.
1ft
1pt = 16 oz
1pt
16 oz or 16 oz
1pt
1wk = 7da
7da
1wk or 1wk
7da
Table 9.2
9.2.4.1 Sample Set A
Make the following conversions. If a fraction occurs, convert it to a decimal rounded to two decimal places.
Example 9.1
Convert 11 yards to feet.
Looking in the unit conversion table under length, we see that 1 yd = 3 ft. There are two corresponding unit fractions, 1 yd
3 ft and 3 ft
1 yd . Which one should we use? Look to see which unit we wish
to convert to. Choose the unit fraction with this unit in the numerator. We will choose 3 ft 1 yd since
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 9. MEASUREMENT AND GEOMETRY
this unit fraction has feet in the numerator. Now, multiply 11 yd by the unit fraction. Notice that since the unit fraction has the value of 1, multiplying by it does not change the value of 11 yd.
11 yd =
11yd · 3ft
1
1yd
Divide out common units.
=
11)yd · 3ft
(Units can be added, subtracted, multiplied, and divided, just as numbers can.) 1
1)yd
=
11·3ft
1
=
33ft
Thus, 11 yd = 33ft.
Example 9.2
Convert 36 oz to pints.
Looking in the unit conversion table under liquid volume, we see that 1 pt = 16 oz. Since we are to convert to pints, we will construct a unit fraction with pints in the numerator.
36 oz =
36 oz · 1 pt
1
16 oz
Divide out common units.
=
36) oz · 1 pt
1
16) oz
=
36·1 pt
16
=
36 pt
Reduce.
16
=
9 pt
Convert to decimals: 9 = 2.25.
4
4
Thus, 36 oz = 2.25 pt.
Example 9.3
Convert 2,016 hr to weeks.
Looking in the unit conversion table under time, we see that 1wk = 7da and that 1 da = 24 hr.
To convert from hours to weeks, we must rst convert from hours to days and then from days to weeks. We need two unit fractions.
The unit fraction needed for converting from hours to days is 1 da
24 hr . The unit fraction needed for
converting from days to weeks is 1 wk
7 da .
2, 016 hr =
2,016 hr · 1 da
1
24 hr · 1 wk
7 da
Divide out common units.
=
2,016) hr · 1) da · 1 wk
1
24) hr
7) da
=
2,016·1wk
Reduce.
24·7
=
12wk
Thus, 2,016 hr = 12 wk.
9.2.4.2 Practice Set A
Make the following conversions. If a fraction occurs, convert it to a decimal rounded to two decimal places.
Exercise 9.2.1
(Solution on p. 569.)
Convert 18 ft to yards.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 9.2.2
(Solution on p. 569.)
Convert 2 mi to feet.
Exercise 9.2.3
(Solution on p. 569.)
Convert 26 ft to yards.
Exercise 9.2.4
(Solution on p. 569.)
Convert 9 qt to pints.
Exercise 9.2.5
(Solution on p. 569.)
Convert 52 min to hours.
Exercise 9.2.6
(Solution on p. 569.)
Convert 412 hr to weeks.
9.2.5 Exercises
Make each conversion using unit fractions. If fractions occur, convert them to decimals rounded to two decimal places.
Exercise 9.2.7
(Solution on p. 569.)
14 yd to feet
Exercise 9.2.8
3 mi to yards
Exercise 9.2.9
(Solution on p. 569.)
8 mi to inches
Exercise 9.2.10
2 mi to inches
Exercise 9.2.11
(Solution on p. 569.)
18 in. to feet
Exercise 9.2.12
84 in. to yards
Exercise 9.2.13
(Solution on p. 569.)
5 in. to yards
Exercise 9.2.14
106 ft to miles
Exercise 9.2.15
(Solution on p. 569.)
62 in. to miles
Exercise 9.2.16
0.4 in. to yards
Exercise 9.2.17
(Solution on p. 569.)
3 qt to pints
Exercise 9.2.18
5 lb to ounces
Exercise 9.2.19
(Solution on p. 569.)
6 T to ounces
Exercise 9.2.20
4 oz to pounds
Exercise 9.2.21
(Solution on p. 569.)
15,000 oz to pounds
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 9. MEASUREMENT AND GEOMETRY
Exercise 9.2.22
15,000 oz to tons
Exercise 9.2.23
(Solution on p. 569.)
9 tbsp to teaspoons
Exercise 9.2.24
3 c to tablespoons
Exercise 9.2.25
(Solution on p. 569.)
5 pt to uid ounces
Exercise 9.2.26
16 tsp to cups
Exercise 9.2.27
(Solution on p. 569.)
5 oz to quarts
Exercise 9.2.28
3 qt to gallons
Exercise 9.2.29
(Solution on p. 569.)
5 pt to teaspoons
Exercise 9.2.30
3 qt to tablespoons
Exercise 9.2.31
(Solution on p. 569.)
18 min to seconds
Exercise 9.2.32
4 days to hours
Exercise 9.2.33
(Solution on p. 569.)
3 hr to days
Exercise 9.2.34
1 hr to days
2
Exercise 9.2.35
(Solution on p. 569.)
1 da to weeks
2
Exercise 9.2.36
3 1 wk to seconds
7
9.2.5.1 Exercises for Review
Exercise 9.2.37
(Solution on p. 569.)
(Section 2.5) Specify the digits by which 23,840 is divisible.
Exercise 9.2.38
(Section 4.5) Find 24 of 55 of 75.
5
6
7
Exercise 9.2.39
(Solution on p. 569.)
() Convert 0.32 to a fraction.
3
Exercise 9.2.40
(Section 8.3) Use the clustering method to estimate the sum: 53 + 82 + 79 + 49.
Exercise 9.2.41
(Solution on p. 569.)
(Section 8.4) Use the distributive property to compute the product: 60 · 46.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
9.3 The Metric System of Measurement3
9.3.1 Section Overview
• The Advantages of the Base Ten Number System
• Prexes
• Conversion from One Unit to Another Unit
• Conversion Table
9.3.2 The Advantages of the Base Ten Number System
The metric system of measurement takes advantage of our base ten number system. The advantage of the metric system over the United States system is that in the metric system it is possible to convert from one unit of measure to another simply by multiplying or dividing the given number by a power of 10. This means we can make a conversion simply by moving the decimal point to the right or the left.
9.3.3 Prexes
Common units of measure in the metric system are the meter (for length), the liter (for volume), and the gram (for mass). To each of the units can be attached a prex. The metric prexes along with their meaning are listed below.
Metric Prexes
kilo thousand
deci tenth
hecto hundred
centi hundredth
deka ten
milli thousandth
For example, if length is being measured,
1 kilometer is equivalent to 1000 meters.
1 centimeter is equivalent to one hundredth of a meter.
1 millimeter is equivalent to one thousandth of a meter.
9.3.4 Conversion from One Unit to Another Unit
Let’s note three characteristics of the metric system that occur in the metric table of measurements.
1. In each category, the prexes are the same.
2. We can move from a larger to a smaller unit of measure by moving the decimal point to the right.
3. We can move from a smaller to a larger unit of measure by moving the decimal point to the left.
The following table provides a summary of the relationship between the basic unit of measure (meter, gram, liter) and each prex, and how many places the decimal point is moved and in what direction.
kilo hecto deka unit deci centi milli
3This content is available online at <http://cnx.org/content/m35019/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 9. MEASUREMENT AND GEOMETRY
Basic Unit to Prex
Move the Decimal Point
unit to deka
1 to 10
1 place to the left
unit to hector
1 to 100
2 places to the left
unit to kilo
1 to 1,000 3 places to the left
unit to deci
1 to 0.1
1 place to the right
unit to centi
1 to 0.01
2 places to the right
unit to milli
1 to 0.001 3 places to the right
Table 9.3
9.3.5 Conversion Table
Listed below, in the unit conversion table, are some of the common metric units of measure.
Unit Conversion Table
1
kilometer
(km)
=
1, 000 × 1 m
1,000 meters (m)
1 hectometer
(hm)
=
100 × 1 m
100 meters
Length
1 dekameter
(dam)
=
10 × 1m
10 meters
1 meter (m)
1 × 1 m
1 decimeter (dm) = 1
10 meter
.1 × 1 m
1 centimeter (cm) = 1
100 meter
.01 × 1 m
1 millimeter
(mm)
=
.001 × 1 m
1
1,000 meter
1 kilogram
(kg)
=
1, 000 × 1 g
1,000 grams (g)
1 hectogram (hg) = 100 grams
100 × 1 g
Mass
1 dekagram (dag) = 10 grams
10 × 1 g
1 gram (g)
1 × 1 g
1 decigram (dg) = 110 gram
.1 × 1 g
continued on next page
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
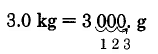
521
1 centigram (cg) = 1
100 gram
.01 × 1 g
1 milligram
(mg)
=
.001 × 1 g
1
1,000 gram
1 kiloliter
(kL)
=
1, 000 × 1 L
1, 000 liters (L)
1 hectoliter (hL) = 100 liters
100 × 1 L