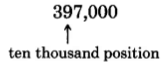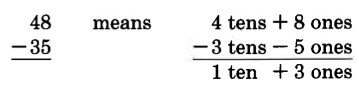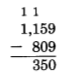119 Fundamentals of Mathematics 1
By:
Denny Burzynski
Wade Ellis
By:
Denny Burzynski
Wade Ellis
Online:
< http://cnx.org/content/col10615/1.4/ >
C O N N E X I O N S
Rice University, Houston, Texas
This selection and arrangement of content as a collection is copyrighted by Denny Burzynski, Wade Ellis. It is licensed under the Creative Commons Attribution 2.0 license (http://creativecommons.org/licenses/by/2.0/).
Collection structure revised: August 18, 2010
PDF generated: July 29, 2013
For copyright and attribution information for the modules contained in this collection, see p. 699.
Preface . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
Acknowledgements . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
1 Addition and Subtraction of Whole Numbers
1.1 Objectives . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
1.2 Whole Numbers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
1.3 Reading and Writing Whole Numbers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
1.4 Rounding Whole Numbers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . 21
1.5 Addition of Whole Numbers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
1.6 Subtraction of Whole Numbers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44
1.7 Properties of Addition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62
1.8 Summary of Key Concepts . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68
1.9 Exercise Supplement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
1.10 Prociency Exam . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74
Solutions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 76
2 Multiplication and Division of Whole Numbers
2.1 Objectives . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . 91
2.2 Multiplication of Whole Numbers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . 92
2.3 Concepts of Division of Whole Numbers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 105
2.4 Division of Whole Numbers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . 113
2.5 Some Interesting Facts about Division . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 126
2.6 Properties of Multiplication . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 130
2.7 Summary of Key Concepts . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 136
2.8 Exercise Supplement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 137
2.9 Prociency Exam . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . 140
Solutions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 142
3 Exponents, Roots, and Factorization of Whole Numbers
3.1 Objectives . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . 153
3.2 Exponents and Roots . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . 154
3.3 Grouping Symbols and the Order of Operations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 162
3.4 Prime Factorization of Natural Numbers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . 172
3.5 The Greatest Common Factor . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 180
3.6 The Least Common Multiple . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 184
3.7 Summary of Key Concepts . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 191
3.8 Exercise Supplement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 193
3.9 Prociency Exam . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . 198
Solutions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 200
4 Introduction to Fractions and Multiplication and Division of Fractions 4.1 Objectives . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . 213
4.2 Fractions of Whole Numbers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . 214
4.3 Proper Fractions, Improper Fractions, and Mixed Numbers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 223
4.4 Equivalent Fractions, Reducing Fractions to Lowest Terms, and Raising Fractions to Higher Terms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 233
4.5 Multiplication of Fractions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 244
4.6 Division of Fractions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 255
4.7 Applications Involving Fractions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . 261
4.8 Summary of Key Concepts . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 268
4.9 Exercise Supplement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 270
4.10 Prociency Exam . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 276
Solutions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 278
5 Addition and Subtraction of Fractions, Comparing Fractions, and Complex Fractions 5.1 Objectives . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . 295
5.2 Addition and Subtraction of Fractions with Like Denominators . . . . . . . . . . . . . . . . . . . . . . . . . . . . 296
5.3 Addition and Subtraction of Fractions with Unlike Denominators . . . . . . . . . . . . . . . . . . . . . . . . . . 300
5.4 Addition and Subtraction of Mixed Numbers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 306
5.5 Comparing Fractions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 310
5.6 Complex Fractions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 314
5.7 Combinations of Operations with Fractions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 318
5.8 Summary of Key Concepts . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 323
5.9 Exercise Supplement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 323
5.10 Prociency Exam . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 327
Solutions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 329
6 Decimals
6.1 Objectives . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . 339
6.2 Reading and Writing Decimals . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 340
6.3 Converting a Decimal to a Fraction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . 346
6.4 Rounding Decimals . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . 350
6.5 Addition and Subtraction of Decimals . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 354
6.6 Multiplication of Decimals . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . 360
6.7 Division of Decimals . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . 371
6.8 Nonterminating Divisions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . 383
6.9 Converting a Fraction to a Decimal . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . 388
6.10 Combinations of Operations with Decimals and Fractions . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . 394
6.11 Summary of Key Concepts . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 398
6.12 Exercise Supplement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 399
6.13 Prociency Exam . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 402
Solutions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 404
7 Ratios and Rates
7.1 Objectives . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . 419
7.2 Ratios and Rates . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 419
7.3 Proportions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 425
7.4 Applications of Proportions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . 431
7.5 Percent . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . 437
7.6 Fractions of One Percent . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 444
7.7 Applications of Percents . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . 448
7.8 Summary of Key Concepts . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 459
7.9 Exercise Supplement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 460
7.10 Prociency Exam . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 464
Solutions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 466
8 Techniques of Estimation
8.1 Objectives . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . 477
8.2 Estimation by Rounding . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . 477
8.3 Estimation by Clustering . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 484
8.4 Mental Arithmetic-Using the Distributive Property . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 487
8.5 Estimation by Rounding Fractions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . 493
8.6 Summary of Key Concepts . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 496
8.7 Exercise Supplement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 496
8.8 Prociency Exam . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . 502
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solutions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 505
9 Measurement and Geometry
9.1 Objectives . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . 513
9.2 Measurement and the United States System . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 514
9.3 The Metric System of Measurement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 519
9.4 Simplication of Denominate Numbers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 524
9.5 Perimeter and Circumference of Geometric Figures . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 532
9.6 Area and Volume of Geometric Figures and Objects . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 542
9.7 Summary of Key Concepts . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 557
9.8 Exercise Supplement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 559
9.9 Prociency Exam . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . 564
Solutions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 569
10 Signed Numbers
10.1 Objectives . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 577
10.2 Variables, Constants, and Real Numbers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 578
10.3 Signed Numbers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 584
10.4 Absolute Value . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . 588
10.5 Addition of Signed Numbers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 592
10.6 Subtraction of Signed Numbers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . 599
10.7 Multiplication and Division of Signed Numbers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . 604
10.8 Summary of Key Concepts . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 613
10.9 Exercise Supplement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 614
10.10 Prociency Exam . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 618
Solutions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 620
11 Algebraic Expressions and Equations
11.1 Objectives . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 631
11.2 Algebraic Expressions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 632
11.3 Combining Like Terms Using Addition and Subtraction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 638
11.4 Solving Equations of the Form x+a=b and x-a=b . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 641
11.5 Solving Equations of the Form ax=b and x/a=b . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 649
11.6 Applications I: Translating Words to Mathematical Symbols . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . 657
11.7 Applications II: Solving Problems . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 662
11.8 Summary of Key Concepts . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 672
11.9 Exercise Supplement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 674
11.10 Prociency Exam . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 680
Solutions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 682
Index . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 694
Attributions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .699
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
To the next generation of explorers: Kristi, BreAnne, Lindsey, Randi, Piper, Meghan, Wyatt, Lara, Mason, and Sheanna.
Fundamentals of Mathematics is a work text that covers the traditional topics studied in a modern prealgebra course, as well as the topics of estimation, elementary analytic geometry, and introductory algebra. It is intended for students who
1. have had a previous course in prealgebra,
2. wish to meet the prerequisite of a higher level course such as elementary algebra, and 3. need to review fundamental mathematical concepts and techniques.
This text will help the student develop the insight and intuition necessary to master arithmetic techniques and manipulative skills. It was written with the following main objectives: 1. to provide the student with an understandable and usable source of information, 2. to provide the student with the maximum opportunity to see that arithmetic concepts and techniques are logically based,
3. to instill in the student the understanding and intuitive skills necessary to know how and when to use particular arithmetic concepts in subsequent material, courses, and nonclassroom situations, and 4. to give the student the ability to correctly interpret arithmetically obtained results.
We have tried to meet these objectives by presenting material dynamically, much the way an instructor might present the material visually in a classroom. (See the development of the concept of addition and subtraction of fractions in Section 5.3, for example.) Intuition and understanding are some of the keys to creative thinking; we believe that the material presented in this text will help the student realize that mathematics is a creative subject.
This text can be used in standard lecture or self-paced classes. To help meet our objectives and to make the study of prealgebra a pleasant and rewarding experience, Fundamentals of Mathematics is organized as follows.
Pedagogical Features
The work text format gives the student space to practice mathematical skills with ready reference to sample problems. The chapters are divided into sections, and each section is a complete treatment of a particular topic, which includes the following features:
• Section Overview
• Sample Sets
• Practice Sets
1This content is available online at <http://cnx.org/content/m18884/1.4/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4> 1
• Section Exercises
• Exercises for Review
• Answers to Practice Sets
The chapters begin with Objectives and end with a Summary of Key Concepts, an Exercise Supplement, and a Prociency Exam.
Objectives
Each chapter begins with a set of objectives identifying the material to be covered. Each section begins with an overview that repeats the objectives for that particular section. Sections are divided into subsections that correspond to the section objectives, which makes for easier reading.
Sample Sets
Fundamentals of Mathematics contains examples that are set o in boxes for easy reference. The examples are referred to as Sample Sets for two reasons:
1. They serve as a representation to be imitated, which we believe will foster understanding of mathematical concepts and provide experience with mathematical techniques.
2. Sample Sets also serve as a preliminary representation of problem-solving techniques that may be used to solve more general and more complicated problems.
The examples have been carefully chosen to illustrate and develop concepts and techniques in the most instructive, easily remembered way. Concepts and techniques preceding the examples are introduced at a level below that normally used in similar texts and are thoroughly explained, assuming little previous knowledge.
Practice Sets
A parallel Practice Set follows each Sample Set, which reinforces the concepts just learned. There is adequate space for the student to work each problem directly on the page.
Answers to Practice Sets
The Answers to Practice Sets are given at the end of each section and can be easily located by referring to the page number, which appears after the last Practice Set in each section.
Section Exercises
The exercises at the end of each section are graded in terms of diculty, although they are not grouped into categories. There is an ample number of problems, and after working through the exercises, the student will be capable of solving a variety of challenging problems.
The problems are paired so that the odd-numbered problems are equivalent in kind and diculty to the even-numbered problems. Answers to the odd-numbered problems are provided at the back of the book.
Exercises for Review
This section consists of ve problems that form a cumulative review of the material covered in the preceding sections of the text and is not limited to material in that chapter. The exercises are keyed by section for easy reference. Since these exercises are intended for review only, no work space is provided.
Summary of Key Concepts
A summary of the important ideas and formulas used throughout the chapter is included at the end of each chapter. More than just a list of terms, the summary is a valuable tool that reinforces concepts in preparation for the Prociency Exam at the end of the chapter, as well as future exams. The summary keys each item to the section of the text where it is discussed.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise Supplement
In addition to numerous section exercises, each chapter includes approximately 100 supplemental problems, which are referenced by section. Answers to the odd-numbered problems are included in the back of the book.
Prociency Exam
Each chapter ends with a Prociency Exam that can serve as a chapter review or evaluation. The Prociency Exam is keyed to sections, which enables the student to refer back to the text for assistance. Answers to all the problems are included in the Answer Section at the end of the book.
Content
The writing style used in Fundamentals of Mathematics is informal and friendly, oering a straightforward approach to prealgebra mathematics. We have made a deliberate eort not to write another text that mini-mizes the use of words because we believe that students can best study arithmetic concepts and understand arithmetic techniques by using words and symbols rather than symbols alone. It has been our experience that students at the prealgebra level are not nearly experienced enough with mathematics to understand symbolic explanations alone; they need literal explanations to guide them through the symbols.
We have taken great care to present concepts and techniques so they are understandable and easily remembered. After concepts have been developed, students are warned about common pitfalls. We have tried to make the text an information source accessible to prealgebra students.
Addition and Subtraction of Whole Numbers
This chapter includes the study of whole numbers, including a discussion of the Hindu-Arabic numeration and the base ten number systems. Rounding whole numbers is also presented, as are the commutative and associative properties of addition.
Multiplication and Division of Whole Numbers
The operations of multiplication and division of whole numbers are explained in this chapter. Multiplication is described as repeated addition. Viewing multiplication in this way may provide students with a visualization of the meaning of algebraic terms such as 8x when they start learning algebra. The chapter also includes the commutative and associative properties of multiplication.
Exponents, Roots, and Factorizations of Whole Numbers
The concept and meaning of the word root is introduced in this chapter. A method of reading root notation and a method of determining some common roots, both mentally and by calculator, is then presented. We also present grouping symbols and the order of operations, prime factorization of whole numbers, and the greatest common factor and least common multiple of a collection of whole numbers.
Introduction to Fractions and Multiplication and Division of Fractions
We recognize that fractions constitute one of the foundations of problem solving. We have, therefore, given a detailed treatment of the operations of multiplication and division of fractions and the logic behind these operations. We believe that the logical treatment and many practice exercises will help students retain the information presented in this chapter and enable them to use it as a foundation for the study of rational expressions in an algebra course.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Addition and Subtraction of Fractions, Comparing Fractions, and Complex Fractions
A detailed treatment of the operations of addition and subtraction of fractions and the logic behind these operations is given in this chapter. Again, we believe that the logical treatment and many practice exercises will help students retain the information, thus enabling them to use it in the study of rational expressions in an algebra course. We have tried to make explanations dynamic. A method for comparing fractions is introduced, which gives the student another way of understanding the relationship between the words denominator and denomination. This method serves to show the student that it is sometimes possible to compare two dierent types of quantities. We also study a method of simplifying complex fractions and of combining operations with fractions.
Decimals
The student is introduced to decimals in terms of the base ten number system, fractions, and digits occurring to the right of the units position. A method of converting a fraction to a decimal is discussed. The logic behind the standard methods of operating on decimals is presented and many examples of how to apply the methods are given. The word of as related to the operation of multiplication is discussed. Nonterminating divisions are examined, as are combinations of operations with decimals and fractions.
Ratios and Rates
We begin by dening and distinguishing the terms ratio and rate. The meaning of proportion and some applications of proportion problems are described. Proportion problems are solved using the “Five-Step Method.” We hope that by using this method the student will discover the value of introducing a variable as a rst step in problem solving and the power of organization. The chapter concludes with discussions of percent, fractions of one percent, and some applications of percent.
Techniques of Estimation
One of the most powerful problem-solving tools is a knowledge of estimation techniques. We feel that estimation is so important that we devote an entire chapter to its study. We examine three estimation techniques: estimation by rounding, estimation by clustering, and estimation by rounding fractions. We also include a section on the distributive property, an important algebraic property.
Measurement and Geometry
This chapter presents some of the techniques of measurement in both the United States system and the metric system. Conversion from one unit to another (in a system) is examined in terms of unit fractions. A discussion of the simplication of denominate numbers is also included. This discussion helps the student understand more clearly the association between pure numbers and dimensions. The chapter concludes with a study of perimeter and circumference of geometric gures and area and volume of geometric gures and objects.
Signed Numbers
A look at algebraic concepts and techniques is begun in this chapter. Basic to the study of algebra is a working knowledge of signed numbers. Denitions of variables, constants, and real numbers are introduced. We then distinguish between positive and negative numbers, learn how to read signed numbers, and examine the origin and use of the double-negative property of real numbers. The concept of absolute value is presented both geometrically (using the number line) and algebraically. The algebraic denition is followed by an interpretation of its meaning and several detailed examples of its use. Addition, subtraction, multiplication, and division of signed numbers are presented rst using the number line, then with absolute value.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Algebraic Expressions and Equations
The student is introduced to some elementary algebraic concepts and techniques in this nal chapter. Algebraic expressions and the process of combining like terms are discussed in Section 11.2 and Section 11.3.
The method of combining like terms in an algebraic expression is explained by using the interpretation of multiplication as a description of repeated addition (as in Section 2.1).
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Many extraordinarily talented people are responsible for helping to create this text. We wish to acknowledge the eorts and skill of the following mathematicians. Their contributions have been invaluable.
Barbara Conway, Berkshire Community College
Bill Hajdukiewicz, Miami-Dade Community College
Virginia Hamilton, Shawnee State University
David Hares, El Centro College
Norman Lee, Ball State University
Ginger Y. Manchester, Hinds Junior College
John R. Martin, Tarrant County Junior College
Shelba Mormon, Northlake College
Lou Ann Pate, Pima Community College
Gus Pekara, Oklahoma City Community College
David Price, Tarrant County Junior College
David Schultz, Virginia Western Community College
Sue S. Watkins, Lorain County Community College
Elizabeth M. Wayt, Tennessee State University
Prentice E. Whitlock, Jersey City State College
Thomas E. Williamson, Montclair State College
Special thanks to the following individuals for their careful accuracy reviews of manuscript, galleys, and page proofs: Steve Blasberg, West Valley College; Wade Ellis, Sr., University of Michigan; John R. Martin, Tarrant County Junior College; and Jane Ellis. We would also like to thank Amy Miller and Guy Sanders, Branham High School.
Our sincere thanks to Debbie Wiedemann for her encouragement, suggestions concerning psychobiological examples, proofreading much of the manuscript, and typing many of the section exercises; Sandi Wiedemann for collating the annotated reviews, counting the examples and exercises, and untiring use of “white-out”; and Jane Ellis for solving and typing all of the exercise solutions.
We thank the following people for their excellent work on the various ancillary items that accompany Fundamentals of Mathematics: Steve Blasberg, West Valley College; Wade Ellis, Sr., University of Michigan; and Jane Ellis ( Instructor’s Manual); John R. Martin, Tarrant County Junior College (Student Solutions Manual and Study Guide); Virginia Hamilton, Shawnee State University (Computerized Test Bank); Pa-tricia Morgan, San Diego State University (Prepared Tests); and George W. Bergeman, Northern Virginia Community College (Maxis Interactive Software).
We also thank the talented people at Saunders College Publishing whose eorts made this text run smoothly and less painfully than we had imagined. Our particular thanks to Bob Stern, Mathematics Editor, Ellen Newman, Developmental Editor, and Janet Nuciforo, Project Editor. Their guidance, suggestions, open 2This content is available online at <http://cnx.org/content/m34775/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4> 7
minds to our suggestions and concerns, and encouragement have been extraordinarily helpful. Although there were times we thought we might be permanently damaged from rereading and rewriting, their eorts have improved this text immensely. It is a pleasure to work with such high-quality professionals.
Denny Burzynski
Wade Ellis, Jr.
San Jose, California
December 1988
I would like to thank Doug Campbell, Ed Lodi, and Guy Sanders for listening to my frustrations and encouraging me on. Thanks also go to my cousin, David Raety, who long ago in Sequoia National Forest told me what a dierential equation is.
Particular thanks go to each of my colleagues at West Valley College. Our everyday conversations regarding mathematics instruction have been of the utmost importance to the development of this text and to my teaching career.
D.B.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Addition and Subtraction of Whole
Numbers
1.1 Objectives1
After completing this chapter, you should
Whole Numbers (Section 1.2)
• know the dierence between numbers and numerals
• know why our number system is called the Hindu-Arabic numeration system
• understand the base ten positional number system
• be able to identify and graph whole numbers
Reading and Writing Whole Numbers (Section 1.3)
• be able to read and write a whole number
Rounding Whole Numbers (Section 1.4)
• understand that rounding is a method of approximation
• be able to round a whole number to a specied position
Addition of Whole Numbers (Section 1.5)
• understand the addition process
• be able to add whole numbers
• be able to use the calculator to add one whole number to another
Subtraction of Whole Numbers (Section 1.6)
• understand the subtraction process
• be able to subtract whole numbers
• be able to use a calculator to subtract one whole number from another whole number Properties of Addition (Section 1.7)
• understand the commutative and associative properties of addition
• understand why 0 is the additive identity
1This content is available online at <http://cnx.org/content/m18885/1.4/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4> 9
10
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
1.2 Whole Numbers2
1.2.1 Section Overview
• Numbers and Numerals
• The Hindu-Arabic Numeration System
• The Base Ten Positional Number System
• Whole Numbers
• Graphing Whole Numbers
1.2.2 Numbers and Numerals
We begin our study of introductory mathematics by examining its most basic building block, the number.
Number
A number is a concept. It exists only in the mind.
The earliest concept of a number was a thought that allowed people to mentally picture the size of some collection of objects. To write down the number being conceptualized, a numeral is used.
Numeral
A numeral is a symbol that represents a number.
In common usage today we do not distinguish between a number and a numeral. In our study of introductory mathematics, we will follow this common usage.
1.2.2.1 Sample Set A
The following are numerals. In each case, the rst represents the number four, the second represents the number one hundred twenty-three, and the third, the number one thousand ve. These numbers are represented in dierent ways.
• Hindu-Arabic numerals
4, 123, 1005
• Roman numerals
IV, CXXIII, MV
• Egyptian numerals
1.2.2.2 Practice Set A
Exercise 1.2.1
(Solution on p. 76.)
Do the phrases “four,” “one hundred twenty-three,” and “one thousand ve” qualify as numerals?
Yes or no?
2This content is available online at <http://cnx.org/content/m34795/1.5/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

11
1.2.3 The Hindu-Arabic Numeration System
Hindu-Arabic Numeration System
Our society uses the Hindu-Arabic numeration system. This system of numeration began shortly before the third century when the Hindus invented the numerals
0 1 2 3 4 5 6 7 8 9
Leonardo Fibonacci
About a thousand years later, in the thirteenth century, a mathematician named Leonardo Fibonacci of Pisa introduced the system into Europe. It was then popularized by the Arabs. Thus, the name, Hindu-Arabic numeration system.
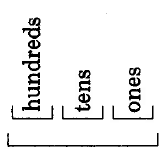
1.2.4 The Base Ten Positional Number System
Digits
The Hindu-Arabic numerals 0 1 2 3 4 5 6 7 8 9 are called digits. We can form any number in the number system by selecting one or more digits and placing them in certain positions. Each position has a particular value. The Hindu mathematician who devised the system about A.D. 500 stated that “from place to place each is ten times the preceding.”
Base Ten Positional Systems
It is for this reason that our number system is called a positional number system with base ten.
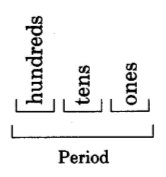
Commas
When numbers are composed of more than three digits, commas are sometimes used to separate the digits into groups of three.
Periods
These groups of three are called periods and they greatly simplify reading numbers.
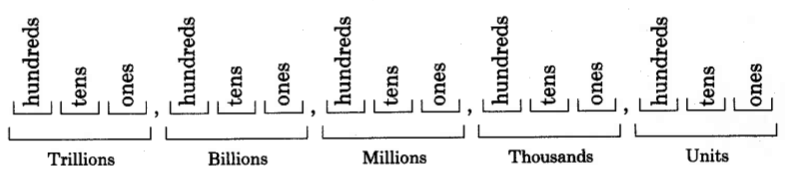
In the Hindu-Arabic numeration system, a period has a value assigned to each or its three positions, and the values are the same for each period. The position values are
Thus, each period contains a position for the values of one, ten, and hundred. Notice that, in looking from right to left, the value of each position is ten times the preceding. Each period has a particular name.
As we continue from right to left, there are more periods. The ve periods listed above are the most common, and in our study of introductory mathematics, they are sucient.
The following diagram illustrates our positional number system to trillions. (There are, to be sure, other periods.)
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
12
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
In our positional number system, the value of a digit is determined by its position in the number.
1.2.4.1 Sample Set B
Example 1.1
Find the value of 6 in the number 7,261.
Since 6 is in the tens position of the units period, its value is 6 tens.
6 tens = 60
Example 1.2
Find the value of 9 in the number 86,932,106,005.
Since 9 is in the hundreds position of the millions period, its value is 9 hundred millions.
9 hundred millions = 9 hundred million
Example 1.3
Find the value of 2 in the number 102,001.
Since 2 is in the ones position of the thousands period, its value is 2 one thousands.
2 one thousands = 2 thousand
1.2.4.2 Practice Set B
Exercise 1.2.2
(Solution on p. 76.)
Find the value of 5 in the number 65,000.
Exercise 1.2.3
(Solution on p. 76.)
Find the value of 4 in the number 439,997,007,010.
Exercise 1.2.4
(Solution on p. 76.)
Find the value of 0 in the number 108.
1.2.5 Whole Numbers
Whole Numbers
Numbers that are formed using only the digits
0 1 2 3 4 5 6 7 8 9
are called whole numbers. They are
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, . . .
The three dots at the end mean “and so on in this same pattern.”
Available for free at Connexions <http://cnx.org/content/col10615/1.4>



13
1.2.6 Graphing Whole Numbers
Number Line
Whole numbers may be visualized by constructing a number line. To construct a number line, we simply draw a straight line and choose any point on the line and label it 0.
Origin
This point is called the origin. We then choose some convenient length, and moving to the right, mark o consecutive intervals (parts) along the line starting at 0. We label each new interval endpoint with the next whole number.
Graphing
We can visually display a whole number by drawing a closed circle at the point labeled with that whole number. Another phrase for visually displaying a whole number is graphing the whole number. The word graph means to “visually display.”
1.2.6.1 Sample Set C
Example 1.4
Graph the following whole numbers: 3, 5, 9.
Example 1.5
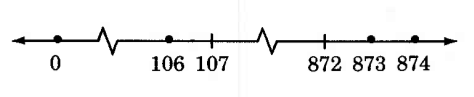
Specify the whole numbers that are graphed on the following number line. The break in the number line indicates that we are aware of the whole numbers between 0 and 106, and 107 and 872, but we are not listing them due to space limitations.
The numbers that have been graphed are
0, 106, 873, 874
1.2.6.2 Practice Set C
Exercise 1.2.5
(Solution on p. 76.)
Graph the following whole numbers: 46, 47, 48, 325, 327.
Exercise 1.2.6
(Solution on p. 76.)
Specify the whole numbers that are graphed on the following number line.
A line is composed of an endless number of points. Notice that we have labeled only some of them. As we proceed, we will discover new types of numbers and determine their location on the number line.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
1.2.7 Exercises
Exercise 1.2.7
(Solution on p. 76.)
What is a number?
Exercise 1.2.8
What is a numeral?
Exercise 1.2.9
(Solution on p. 76.)
Does the word “eleven” qualify as a numeral?
Exercise 1.2.10
How many dierent digits are there?
Exercise 1.2.11
(Solution on p. 76.)
Our number system, the Hindu-Arabic number system, is a
number system with
base
.
Exercise 1.2.12
Numbers composed of more than three digits are sometimes separated into groups of three by commas. These groups of three are called
.
Exercise 1.2.13
(Solution on p. 76.)
In our number system, each period has three values assigned to it. These values are the same for each period. From right to left, what are they?
Exercise 1.2.14
Each period has its own particular name. From right to left, what are the names of the rst four?
Exercise 1.2.15
(Solution on p. 76.)
In the number 841, how many tens are there?
Exercise 1.2.16
In the number 3,392, how many ones are there?
Exercise 1.2.17
(Solution on p. 76.)
In the number 10,046, how many thousands are there?
Exercise 1.2.18
In the number 779,844,205, how many ten millions are there?
Exercise 1.2.19
(Solution on p. 76.)
In the number 65,021, how many hundred thousands are there?
For following problems, give the value of the indicated digit in the given number.
Exercise 1.2.20
5 in 599
Exercise 1.2.21
(Solution on p. 76.)
1 in 310,406
Exercise 1.2.22
9 in 29,827
Exercise 1.2.23
(Solution on p. 76.)
6 in 52,561,001,100
Exercise 1.2.24
Write a two-digit number that has an eight in the tens position.
Exercise 1.2.25
(Solution on p. 76.)
Write a four-digit number that has a one in the thousands position and a zero in the ones position.
Exercise 1.2.26
How many two-digit whole numbers are there?
Available for free at Connexions <http://cnx.org/content/col10615/1.4>


15
Exercise 1.2.27
(Solution on p. 76.)
How many three-digit whole numbers are there?
Exercise 1.2.28
How many four-digit whole numbers are there?
Exercise 1.2.29
(Solution on p. 76.)
Is there a smallest whole number? If so, what is it?
Exercise 1.2.30
Is there a largest whole number? If so, what is it?
Exercise 1.2.31
(Solution on p. 76.)
Another term for “visually displaying” is
.
Exercise 1.2.32
The whole numbers can be visually displayed on a
.
Exercise 1.2.33
(Solution on p. 76.)
Graph (visually display) the following whole numbers on the number line below: 0, 1, 31, 34.
Exercise 1.2.34
Construct a number line in the space provided below and graph (visually display) the following whole numbers: 84, 85, 901, 1006, 1007.
Exercise 1.2.35
(Solution on p. 76.)
Specify, if any, the whole numbers that are graphed on the following number line.
Exercise 1.2.36
Specify, if any, the whole numbers that are graphed on the following number line.
1.3 Reading and Writing Whole Numbers3
1.3.1 Section Overview
• Reading Whole Numbers
• Writing Whole Numbers
Because our number system is a positional number system, reading and writing whole numbers is quite simple.
3This content is available online at <http://cnx.org/content/m34778/1.5/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
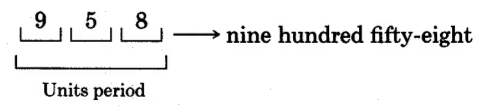



16
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
1.3.2 Reading Whole Numbers
To convert a number that is formed by digits into a verbal phrase, use the following method: 1. Beginning at the right and working right to left, separate the number into distinct periods by inserting commas every three digits.
2. Beginning at the left, read each period individually, saying the period name.
1.3.2.1 Sample Set A
Write the following numbers as words.
Example 1.6
Read 42958.
1. Beginning at the right, we can separate this number into distinct periods by inserting a comma between the 2 and 9.
42,958
2. Beginning at the left, we read each period individually:
Forty-two thousand, nine hundred fty-eight.
Example 1.7
Read 307991343.
1. Beginning at the right, we can separate this number into distinct periods by placing commas between the 1 and 3 and the 7 and 9.
307,991,343
2. Beginning at the left, we read each period individually.
Three hundred seven million, nine hundred ninety-one thousand, three hundred forty-three.
Example 1.8
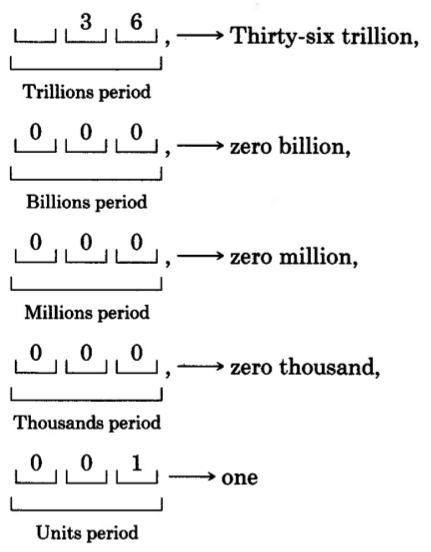
Read 36000000000001.
1. Beginning at the right, we can separate this number into distinct periods by placing commas.
36,000,000,001
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
17
2. Beginning at the left, we read each period individually.
Thirty-six trillion, one.
1.3.2.2 Practice Set A
Write each number in words.
Exercise 1.3.1
(Solution on p. 76.)
12,542
Exercise 1.3.2
(Solution on p. 76.)
101,074,003
Exercise 1.3.3
(Solution on p. 76.)
1,000,008
1.3.3 Writing Whole Numbers
To express a number in digits that is expressed in words, use the following method: 1. Notice rst that a number expressed as a verbal phrase will have its periods set o by commas.
2. Starting at the beginning of the phrase, write each period of numbers individually.
3. Using commas to separate periods, combine the periods to form one number.
1.3.3.1 Sample Set B
Write each number using digits.
Example 1.9
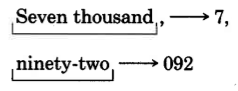
Seven thousand, ninety-two.
Using the comma as a period separator, we have
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

18
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
7,092
Example 1.10
Fifty billion, one million, two hundred thousand, fourteen.
Using the commas as period separators, we have
50,001,200,014
Example 1.11
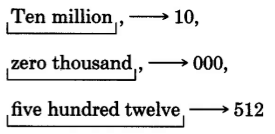
Ten million, ve hundred twelve.
The comma sets o the periods. We notice that there is no thousands period. We’ll have to insert this ourselves.
10,000,512
1.3.3.2 Practice Set B
Express each number using digits.
Exercise 1.3.4
(Solution on p. 77.)
One hundred three thousand, twenty-ve.
Exercise 1.3.5
(Solution on p. 77.)
Six million, forty thousand, seven.
Exercise 1.3.6
(Solution on p. 77.)
Twenty trillion, three billion, eighty million, one hundred nine thousand, four hundred two.
Exercise 1.3.7
(Solution on p. 77.)
Eighty billion, thirty-ve.
1.3.4 Exercises
For the following problems, write all numbers in words.
Exercise 1.3.8
(Solution on p. 77.)
912
Exercise 1.3.9
84
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 1.3.10
(Solution on p. 77.)
1491
Exercise 1.3.11
8601
Exercise 1.3.12
(Solution on p. 77.)
35,223
Exercise 1.3.13
71,006
Exercise 1.3.14
(Solution on p. 77.)
437,105
Exercise 1.3.15
201,040
Exercise 1.3.16
(Solution on p. 77.)
8,001,001
Exercise 1.3.17
16,000,053
Exercise 1.3.18
(Solution on p. 77.)
770,311,101
Exercise 1.3.19
83,000,000,007
Exercise 1.3.20
(Solution on p. 77.)
106,100,001,010
Exercise 1.3.21
3,333,444,777
Exercise 1.3.22
(Solution on p. 77.)
800,000,800,000
Exercise 1.3.23
A particular community college has 12,471 students enrolled.
Exercise 1.3.24
(Solution on p. 77.)
A person who watches 4 hours of television a day spends 1460 hours a year watching T.V.
Exercise 1.3.25
Astronomers believe that the age of the earth is about 4,500,000,000 years.
Exercise 1.3.26
(Solution on p. 77.)
Astronomers believe that the age of the universe is about 20,000,000,000 years.
Exercise 1.3.27
There are 9690 ways to choose four objects from a collection of 20.
Exercise 1.3.28
(Solution on p. 77.)
If a 412 page book has about 52 sentences per page, it will contain about 21,424 sentences.
Exercise 1.3.29
In 1980, in the United States, there was $1,761,000,000,000 invested in life insurance.
Exercise 1.3.30
(Solution on p. 77.)
In 1979, there were 85,000 telephones in Alaska and 2,905,000 telephones in Indiana.
Exercise 1.3.31
In 1975, in the United States, it is estimated that 52,294,000 people drove to work alone.
Exercise 1.3.32
(Solution on p. 77.)
In 1980, there were 217 prisoners under death sentence that were divorced.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
Exercise 1.3.33
In 1979, the amount of money spent in the United States for regular-session college education was $50,721,000,000,000.
Exercise 1.3.34
(Solution on p. 77.)
In 1981, there were 1,956,000 students majoring in business in U.S. colleges.
Exercise 1.3.35
In 1980, the average fee for initial and follow up visits to a medical doctors oce was about $34.
Exercise 1.3.36
(Solution on p. 77.)
In 1980, there were approximately 13,100 smugglers of aliens apprehended by the Immigration border patrol.
Exercise 1.3.37
In 1980, the state of West Virginia pumped 2,000,000 barrels of crude oil, whereas Texas pumped 975,000,000 barrels.
Exercise 1.3.38
(Solution on p. 77.)
The 1981 population of Uganda was 12,630,000 people.
Exercise 1.3.39
In 1981, the average monthly salary oered to a person with a Master’s degree in mathematics was $1,685.
For the following problems, write each number using digits.
Exercise 1.3.40
(Solution on p. 77.)
Six hundred eighty-one
Exercise 1.3.41
Four hundred ninety
Exercise 1.3.42
(Solution on p. 77.)
Seven thousand, two hundred one
Exercise 1.3.43
Nineteen thousand, sixty-ve
Exercise 1.3.44
(Solution on p. 77.)
Five hundred twelve thousand, three
Exercise 1.3.45
Two million, one hundred thirty-three thousand, eight hundred fty-nine
Exercise 1.3.46
(Solution on p. 77.)
Thirty-ve million, seven thousand, one hundred one
Exercise 1.3.47
One hundred million, one thousand
Exercise 1.3.48
(Solution on p. 77.)
Sixteen billion, fty-nine thousand, four
Exercise 1.3.49
Nine hundred twenty billion, four hundred seventeen million, twenty-one thousand Exercise 1.3.50
(Solution on p. 78.)
Twenty-three billion
Exercise 1.3.51
Fifteen trillion, four billion, nineteen thousand, three hundred ve
Exercise 1.3.52
(Solution on p. 78.)
One hundred trillion, one
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
21
1.3.4.1 Exercises for Review
Exercise 1.3.53
(Section 1.2) How many digits are there?
Exercise 1.3.54
(Solution on p. 78.)
(Section 1.2) In the number 6,641, how many tens are there?
Exercise 1.3.55
(Section 1.2) What is the value of 7 in 44,763?
Exercise 1.3.56
(Solution on p. 78.)
(Section 1.2) Is there a smallest whole number? If so, what is it?
Exercise 1.3.57
(Section 1.2) Write a four-digit number with a 9 in the tens position.
1.4 Rounding Whole Numbers4
1.4.1 Section Overview
• Rounding as an Approximation
• The Method of Rounding Numbers
1.4.2 Rounding as an Approximation
A primary use of whole numbers is to keep count of how many objects there are in a collection. Sometimes we’re only interested in the approximate number of objects in the collection rather than the precise number.
For example, there are approximately 20 symbols in the collection below.
The precise number of symbols in the above collection is 18.
Rounding
We often approximate the number of objects in a collection by mentally seeing the collection as occurring in groups of tens, hundreds, thousands, etc. This process of approximation is called rounding. Rounding is very useful in estimation. We will study estimation in Chapter 8.
When we think of a collection as occurring in groups of tens, we say we’re rounding to the nearest ten. When we think of a collection as occurring in groups of hundreds, we say we’re rounding to the nearest hundred.
This idea of rounding continues through thousands, ten thousands, hundred thousands, millions, etc.
The process of rounding whole numbers is illustrated in the following examples.
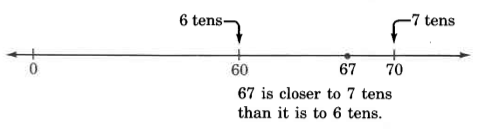
Example 1.12
Round 67 to the nearest ten.
4This content is available online at <http://cnx.org/content/m34780/1.3/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
22
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
On the number line, 67 is more than halfway from 60 to 70. The digit immediately to the right of the tens digit, the round-o digit, is the indicator for this.
Thus, 67, rounded to the near-
est ten, is 70.
Example 1.13
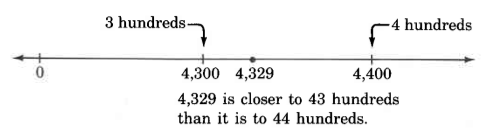
Round 4,329 to the nearest hundred.
On the number line, 4,329 is less than halfway from 4,300 to 4,400. The digit to the immediate right of the hundreds digit, the round-o digit, is the indicator.
Thus, 4,329, rounded to the
nearest hundred is 4,300.
Example 1.14
Round 16,500 to the nearest thousand.
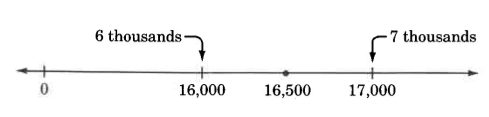
On the number line, 16,500 is exactly halfway from 16,000 to 17,000.
By convention, when the number to be rounded is exactly halfway between two numbers, it is rounded to the higher number.
Thus, 16,500, rounded to the nearest thousand, is 17,000.
Example 1.15
A person whose salary is $41,450 per year might tell a friend that she makes $41,000 per year. She has rounded 41,450 to the nearest thousand. The number 41,450 is closer to 41,000 than it is to 42,000.
1.4.3 The Method of Rounding Whole Numbers
From the observations made in the preceding examples, we can use the following method to round a whole number to a particular position.
1. Mark the position of the round-o digit.
2. Note the digit to the immediate right of the round-o digit.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
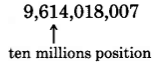

23
a. If it is less than 5, replace it and all the digits to its right with zeros. Leave the round-o digit unchanged.
b. If it is 5 or larger, replace it and all the digits to its right with zeros. Increase the round-o digit by 1.
1.4.3.1 Sample Set A
Use the method of rounding whole numbers to solve the following problems.
Example 1.16
Round 3,426 to the nearest ten.
1. We are rounding to the tens position. Mark the digit in the tens position 2. Observe the digit immediately to the right of the tens position. It is 6. Since 6 is greater than 5, we round up by replacing 6 with 0 and adding 1 to the digit in the tens position (the round-o position): 2 + 1 = 3 .
3,430
Thus, 3,426 rounded to the nearest ten is 3,430.
Example 1.17
Round 9,614,018,007 to the nearest ten million.
1. We are rounding to the nearest ten million.
2. Observe the digit immediately to the right of the ten millions position. It is 4. Since 4 is less than 5, we round down by replacing 4 and all the digits to its right with zeros.
9,610,000,000
Thus, 9,614,018,007 rounded to the nearest ten million is 9,610,000,000.
Example 1.18
Round 148,422 to the nearest million.
1. Since we are rounding to the nearest million, we’ll have to imagine a digit in the millions position. We’ll write 148,422 as 0,148,422.
2. The digit immediately to the right is 1. Since 1 is less than 5, we’ll round down by replacing it and all the digits to its right with zeros.
0,000,000
This number is 0.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
24
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
Thus, 148,422 rounded to the nearest million is 0.
Example 1.19
Round 397,000 to the nearest ten thousand.
1. We are rounding to the nearest ten thousand.
2. The digit immediately to the right of the ten thousand position is 7. Since 7 is greater than 5, we round up by replacing 7 and all the digits to its right with zeros and adding 1 to the digit in the ten thousands position. But 9 + 1 = 10 and we must carry the 1 to the next (the hundred thousands) position.
400,000
Thus, 397,000 rounded to the nearest ten thousand is 400,000.
1.4.3.2 Practice Set A
Use the method of rounding whole numbers to solve each problem.
Exercise 1.4.1
(Solution on p. 78.)
Round 3387 to the nearest hundred.
Exercise 1.4.2
(Solution on p. 78.)
Round 26,515 to the nearest thousand.
Exercise 1.4.3
(Solution on p. 78.)
Round 30,852,900 to the nearest million.
Exercise 1.4.4
(Solution on p. 78.)
Round 39 to the nearest hundred.
Exercise 1.4.5
(Solution on p. 78.)
Round 59,600 to the nearest thousand.
1.4.4 Exercises
For the following problems, complete the table by rounding each number to the indicated positions.
Exercise 1.4.6
(Solution on p. 78.)
1,642
hundred thousand ten thousand million
Table 1.1
Exercise 1.4.7
5,221
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
hundred thousand ten thousand million
Table 1.2
Exercise 1.4.8
(Solution on p. 78.)
91,803
Hundred thousand ten thousand million
Table 1.3
Exercise 1.4.9
106,007
hundred thousand ten thousand million
Table 1.4
Exercise 1.4.10
(Solution on p. 78.)
208
hundred thousand ten thousand million
Table 1.5
Exercise 1.4.11
199
hundred thousand ten thousand million
Table 1.6
Exercise 1.4.12
(Solution on p. 78.)
863
hundred thousand ten thousand million
Table 1.7
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
Exercise 1.4.13
794
hundred thousand ten thousand million
Table 1.8
Exercise 1.4.14
(Solution on p. 79.)
925
hundred thousand ten thousand million
Table 1.9
Exercise 1.4.15
909
hundred thousand ten thousand million
Table 1.10
Exercise 1.4.16
(Solution on p. 79.)
981
hundred thousand ten thousand million
Table 1.11
Exercise 1.4.17
965
hundred thousand ten thousand million
Table 1.12
Exercise 1.4.18
(Solution on p. 79.)
551,061,285
hundred thousand ten thousand million
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Table 1.13
Exercise 1.4.19
23,047,991,521
hundred thousand ten thousand million
Table 1.14
Exercise 1.4.20
(Solution on p. 79.)
106,999,413,206
Hundred thousand ten thousand million
Table 1.15
Exercise 1.4.21
5,000,000
hundred thousand ten thousand million
Table 1.16
Exercise 1.4.22
(Solution on p. 79.)
8,006,001
hundred thousand ten thousand million
Table 1.17
Exercise 1.4.23
94,312
hundred thousand ten thousand million
Table 1.18
Exercise 1.4.24
(Solution on p. 79.)
33,486
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
hundred thousand ten thousand million
Table 1.19
Exercise 1.4.25
560,669
hundred thousand ten thousand million
Table 1.20
Exercise 1.4.26
(Solution on p. 80.)
388,551
hundred thousand ten thousand million
Table 1.21
Exercise 1.4.27
4,752
hundred thousand ten thousand million
Table 1.22
Exercise 1.4.28
(Solution on p. 80.)
8,209
hundred thousand ten thousand million
Table 1.23
Exercise 1.4.29
In 1950, there were 5,796 cases of diphtheria reported in the United States. Round to the nearest hundred.
Exercise 1.4.30
(Solution on p. 80.)
In 1979, 19,309,000 people in the United States received federal food stamps. Round to the nearest ten thousand.
Exercise 1.4.31
In 1980, there were 1,105,000 people between 30 and 34 years old enrolled in school. Round to the nearest million.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 1.4.32
(Solution on p. 80.)
In 1980, there were 29,100,000 reports of aggravated assaults in the United States. Round to the nearest million.
For the following problems, round the numbers to the position you think is most reasonable for the situation.
Exercise 1.4.33
In 1980, for a city of one million or more, the average annual salary of police and reghters was $16,096.
Exercise 1.4.34
(Solution on p. 80.)
The average percentage of possible sunshine in San Francisco, California, in June is 73%.
Exercise 1.4.35
In 1980, in the state of Connecticut, $3,777,000,000 in defense contract payroll was awarded.
Exercise 1.4.36
(Solution on p. 80.)
In 1980, the federal government paid $5,463,000,000 to Viet Nam veterans and dependants.
Exercise 1.4.37
In 1980, there were 3,377,000 salespeople employed in the United States.
Exercise 1.4.38
(Solution on p. 80.)
In 1948, in New Hampshire, 231,000 popular votes were cast for the president.
Exercise 1.4.39
In 1970, the world production of cigarettes was 2,688,000,000,000.
Exercise 1.4.40
(Solution on p. 80.)
In 1979, the total number of motor vehicle registrations in Florida was 5,395,000.
Exercise 1.4.41
In 1980, there were 1,302,000 registered nurses the United States.
1.4.4.1 Exercises for Review
Exercise 1.4.42
(Solution on p. 80.)
(Section 1.2) There is a term that describes the visual displaying of a number. What is the term?
Exercise 1.4.43
(Section 1.2) What is the value of 5 in 26,518,206?
Exercise 1.4.44
(Solution on p. 80.)
(Section 1.3) Write 42,109 as you would read it.
Exercise 1.4.45
(Section 1.3) Write “six hundred twelve” using digits.
Exercise 1.4.46
(Solution on p. 80.)
(Section 1.3) Write “four billion eight” using digits.
1.5 Addition of Whole Numbers5
1.5.1 Section Overview
• Addition
• Addition Visualized on the Number Line
• The Addition Process
5This content is available online at <http://cnx.org/content/m34786/1.5/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

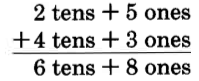
30
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
• Addition Involving Carrying
• Calculators
1.5.2 Addition
Suppose we have two collections of objects that we combine together to form a third collection. For example, We are combining a collection of four objects with a collection of three objects to obtain a collection of seven objects.
Addition
The process of combining two or more objects (real or intuitive) to form a third, the total, is called addition.
In addition, the numbers being added are called addends or terms, and the total is called the sum. The plus symbol (+) is used to indicate addition, and the equal symbol (=) is used to represent the word
“equal.” For example, 4 + 3 = 7 means “four added to three equals seven.”
1.5.3 Addition Visualized on the Number Line
Addition is easily visualized on the number line. Let’s visualize the addition of 4 and 3 using the number line.
To nd 4 + 3,
1. Start at 0.
2. Move to the right 4 units. We are now located at 4.
3. From 4, move to the right 3 units. We are now located at 7.
Thus, 4 + 3 = 7.
1.5.4 The Addition Process
We’ll study the process of addition by considering the sum of 25 and 43.
25
means
+43
We write this as 68.
We can suggest the following procedure for adding whole numbers using this example.
Example 1.20: The Process of Adding Whole Numbers
To add whole numbers,
The process:
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
1. Write the numbers vertically, placing corresponding positions in the same column.
25
+43
2. Add the digits in each column. Start at the right (in the ones position) and move to the left, placing the sum at the bottom.
25
+43
68
Caution: Confusion and incorrect sums can occur when the numbers are not aligned in columns properly. Avoid writing such additions as
25
+43
25
+43
1.5.4.1 Sample Set A
Example 1.21
Add 276 and 103.
276
6 + 3 = 9 .
+103
7 + 0 = 7 .
379
2 + 1 = 3 .
Example 1.22
Add 1459 and 130
9 + 0 = 9 .
1459
5 + 3 = 8 .
+130
4 + 1 = 5 .
1589
1 + 0 = 1 .
In each of these examples, each individual sum does not exceed 9. We will examine individual sums that exceed 9 in the next section.
1.5.4.2 Practice Set A
Perform each addition. Show the expanded form in problems 1 and 2.
Exercise 1.5.1
(Solution on p. 80.)
Add 63 and 25.
Exercise 1.5.2
(Solution on p. 80.)
Add 4,026 and 1,501.
Exercise 1.5.3
(Solution on p. 80.)
Add 231,045 and 36,121.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
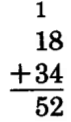
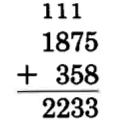
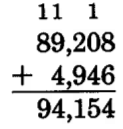
32
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
1.5.5 Addition Involving Carrying
It often happens in addition that the sum of the digits in a column will exceed 9. This happens when we add 18 and 34. We show this in expanded form as follows.
Notice that when we add the 8 ones to the 4 ones we get 12 ones. We then convert the 12 ones to 1 ten and 2 ones. In vertical addition, we show this conversion by carrying the ten to the tens column. We write a 1
at the top of the tens column to indicate the carry. This same example is shown in a shorter form as follows: 8 + 4 = 12 Write 2, carry 1 ten to the top of the next column to the left.
1.5.5.1 Sample Set B
Perform the following additions. Use the process of carrying when needed.
Example 1.23
Add 1875 and 358.
5 + 8 = 13
Write 3, carry 1 ten.
1 + 7 + 5 = 13
Write 3, carry 1 hundred.
1 + 8 + 3 = 12
Write 2, carry 1 thousand.
1 + 1 = 2
The sum is 2233.
Example 1.24
Add 89,208 and 4,946.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>


33
8 + 6 = 14
Write 4, carry 1 ten.
1 + 0 + 4 = 5
Write the 5 (nothing to carry).
2 + 9 = 11
Write 1, carry one thousand.
1 + 9 + 4 = 14
Write 4, carry one ten thousand.
1 + 8 = 9
The sum is 94,154.
Example 1.25
Add 38 and 95.
8 + 5 = 13
Write 3, carry 1 ten.
1 + 3 + 9 = 13
Write 3, carry 1 hundred.
1 + 0 = 1
As you proceed with the addition, it is a good idea to keep in mind what is actually happening.
The sum is 133.
Example 1.26
Find the sum 2648, 1359, and 861.
8 + 9 + 1 = 18
Write 8, carry 1 ten.
1 + 4 + 5 + 6 = 16
Write 6, carry 1 hundred.
1 + 6 + 3 + 8 = 18
Write 8, carry 1 thousand.
1 + 2 + 1 = 4
The sum is 4,868.
Numbers other than 1 can be carried as illustrated in Example 1.27.
Example 1.27
Find the sum of the following numbers.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
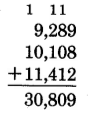
34
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
6 + 5 + 1 + 7 = 19
Write 9, carry the 1.
1 + 1 + 0 + 5 + 1 = 8
Write 8.
0 + 9 + 9 + 8 = 26
Write 6, carry the 2.
2 + 8 + 9 + 8 + 6 = 33
Write 3, carry the 3.
3 + 7 + 3 + 5 = 18
Write 8, carry the 1.
1 + 8 = 9
Write 9.
The sum is 983,689.
Example 1.28
The number of students enrolled at Riemann College in the years 1984, 1985, 1986, and 1987 was 10,406, 9,289, 10,108, and 11,412, respectively. What was the total number of students enrolled at Riemann College in the years 1985, 1986, and 1987?
We can determine the total number of students enrolled by adding 9,289, 10,108, and 11,412, the number of students enrolled in the years 1985, 1986, and 1987.
The total number of students enrolled at Riemann College in the years 1985, 1986, and 1987 was 30,809.
1.5.5.2 Practice Set B
Perform each addition. For the next three problems, show the expanded form.
Exercise 1.5.4
(Solution on p. 80.)
Add 58 and 29.
Exercise 1.5.5
(Solution on p. 81.)
Add 476 and 85.
Exercise 1.5.6
(Solution on p. 81.)
Add 27 and 88.
Exercise 1.5.7
(Solution on p. 81.)
Add 67,898 and 85,627.
For the next three problems, nd the sums.
Exercise 1.5.8
(Solution on p. 81.)
57
26
84
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 1.5.9
(Solution on p. 81.)
847
825
796
Exercise 1.5.10
(Solution on p. 81.)
16, 945
8, 472
387, 721
21, 059
629
1.5.6 Calculators
Calculators provide a very simple and quick way to nd sums of whole numbers. For the two problems in Sample Set C, assume the use of a calculator that does not require the use of an ENTER key (such as many Hewlett-Packard calculators).
1.5.6.1 Sample Set C
Use a calculator to nd each sum.
Example 1.29
34 + 21
Display Reads
Type 34 34
Press +
34
Type 21 21
Press =
55
Table 1.24
The sum is 55.
Example 1.30
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
106 + 85 + 322 + 406 Display Reads
Type 106
106
The calculator keeps a running subtotal
Press +
106
Type 85
85
Press =
191
← 106 + 85
Type 322
322
Press +
513
← 191 + 322
Type 406
406
Press =
919
← 513 + 406
Table 1.25
The sum is 919.
1.5.6.2 Practice Set C
Use a calculator to nd the following sums.
Exercise 1.5.11
(Solution on p. 81.)
62 + 81 + 12
Exercise 1.5.12
(Solution on p. 81.)
9, 261 + 8, 543 + 884 + 1, 062
Exercise 1.5.13
(Solution on p. 81.)
10, 221 + 9, 016 + 11, 445
1.5.7 Exercises
For the following problems, perform the additions. If you can, check each sum with a calculator.
Exercise 1.5.14
(Solution on p. 81.)
14 + 5
Exercise 1.5.15
12 + 7
Exercise 1.5.16
(Solution on p. 81.)
46 + 2
Exercise 1.5.17
83 + 16
Exercise 1.5.18
(Solution on p. 81.)
77 + 21
Exercise 1.5.19
321
+ 42
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 1.5.20
(Solution on p. 82.)
916
+ 62
Exercise 1.5.21
104
+561
Exercise 1.5.22
(Solution on p. 82.)
265
+103
Exercise 1.5.23
552 + 237
Exercise 1.5.24
(Solution on p. 82.)
8, 521 + 4, 256
Exercise 1.5.25
16, 408
+ 3, 101
Exercise 1.5.26
(Solution on p. 82.)
16, 515
+42, 223
Exercise 1.5.27
616, 702 + 101, 161
Exercise 1.5.28
(Solution on p. 82.)
43, 156, 219 + 2, 013, 520
Exercise 1.5.29
17 + 6
Exercise 1.5.30
(Solution on p. 82.)
25 + 8
Exercise 1.5.31
84
+ 7
Exercise 1.5.32
(Solution on p. 82.)
75
+ 6
Exercise 1.5.33
36 + 48
Exercise 1.5.34
(Solution on p. 82.)
74 + 17
Exercise 1.5.35
486 + 58
Exercise 1.5.36
(Solution on p. 82.)
743 + 66
Exercise 1.5.37
381 + 88
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
Exercise 1.5.38
(Solution on p. 82.)
687
+175
Exercise 1.5.39
931
+853
Exercise 1.5.40
(Solution on p. 82.)
1, 428 + 893
Exercise 1.5.41
12, 898 + 11, 925
Exercise 1.5.42
(Solution on p. 82.)
631, 464
+509, 740
Exercise 1.5.43
805, 996
+ 98, 516
Exercise 1.5.44
(Solution on p. 82.)
38, 428, 106
+522, 936, 005
Exercise 1.5.45
5, 288, 423, 100 + 16, 934, 785, 995
Exercise 1.5.46
(Solution on p. 82.)
98, 876, 678, 521, 402 + 843, 425, 685, 685, 658
Exercise 1.5.47
41 + 61 + 85 + 62
Exercise 1.5.48
(Solution on p. 82.)
21 + 85 + 104 + 9 + 15
Exercise 1.5.49
116
27
110
110
+
8
Exercise 1.5.50
(Solution on p. 82.)
75, 206
4, 152
+16, 007
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 1.5.51
8, 226
143
92, 015
8
487, 553
5, 218
Exercise 1.5.52
(Solution on p. 82.)
50, 006
1, 005
100, 300
20, 008
1, 000, 009
800, 800
Exercise 1.5.53
616
42, 018
1, 687
225
8, 623, 418
12, 506, 508
19
2, 121
195, 643
For the following problems, perform the additions and round to the nearest hundred.
Exercise 1.5.54
(Solution on p. 82.)
1, 468
2, 183
Exercise 1.5.55
928, 725
15, 685
Exercise 1.5.56
(Solution on p. 82.)
82, 006
3, 019, 528
Exercise 1.5.57
18, 621
5, 059
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
Exercise 1.5.58
(Solution on p. 82.)
92
48
Exercise 1.5.59
16
37
Exercise 1.5.60
(Solution on p. 82.)
21
16
Exercise 1.5.61
11, 172
22, 749
12, 248
Exercise 1.5.62
(Solution on p. 82.)
240
280
210
310
Exercise 1.5.63
9, 573
101, 279
122, 581
For the next ve problems, replace the letter m with the whole number that will make the addition true.
Exercise 1.5.64
(Solution on p. 82.)
62
+
m
67
Exercise 1.5.65
106
+
m
113
Exercise 1.5.66
(Solution on p. 82.)
432
+
m
451
Exercise 1.5.67
803
+
m
830
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
41
Exercise 1.5.68
(Solution on p. 82.)
1, 893
+
m
1, 981
Exercise 1.5.69
The number of nursing and related care facilities in the United States in 1971 was 22,004. In 1978, the number was 18,722. What was the total number of facilities for both 1971 and 1978?
Exercise 1.5.70
(Solution on p. 83.)
The number of persons on food stamps in 1975, 1979, and 1980 was 19,179,000, 19,309,000, and 22,023,000, respectively. What was the total number of people on food stamps for the years 1975, 1979, and 1980?
Exercise 1.5.71
The enrollment in public and nonpublic schools in the years 1965, 1970, 1975, and 1984 was 54,394,000, 59,899,000, 61,063,000, and 55,122,000, respectively. What was the total enrollment for those years?
Exercise 1.5.72
(Solution on p. 83.)
The area of New England is 3,618,770 square miles. The area of the Mountain states is 863,563
square miles. The area of the South Atlantic is 278,926 square miles. The area of the Pacic states is 921,392 square miles. What is the total area of these regions?
Exercise 1.5.73
In 1960, the IRS received 1,188,000 corporate income tax returns. In 1965, 1,490,000 returns were received. In 1970, 1,747,000 returns were received. In 1972 1977, 1,890,000; 1,981,000; 2,043,000; 2,100,000; 2,159,000; and 2,329,000 returns were received, respectively. What was the total number of corporate tax returns received by the IRS during the years 1960, 1965, 1970, 1972 1977?
Exercise 1.5.74
(Solution on p. 83.)
Find the total number of scientists employed in 1974.
Exercise 1.5.75
Find the total number of sales for space vehicle systems for the years 1965-1980.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

42
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
Exercise 1.5.76
(Solution on p. 83.)
Find the total baseball attendance for the years 1960-1980.
Exercise 1.5.77
Find the number of prosecutions of federal ocials for 1970-1980.
For the following problems, try to add the numbers mentally.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 1.5.78
(Solution on p. 83.)
5
5
3
7
Exercise 1.5.79
8
2
6
4
Exercise 1.5.80
(Solution on p. 83.)
9
1
8
5
2
Exercise 1.5.81
5
2
5
8
3
7
Exercise 1.5.82
(Solution on p. 83.)
6
4
3
1
6
7
9
4
Exercise 1.5.83
20
30
Exercise 1.5.84
(Solution on p. 83.)
15
35
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
Exercise 1.5.85
16
14
Exercise 1.5.86
(Solution on p. 83.)
23
27
Exercise 1.5.87
82
18
Exercise 1.5.88
(Solution on p. 83.)
36
14
1.5.7.1 Exercises for Review
Exercise 1.5.89
(Section 1.2) Each period of numbers has its own name. From right to left, what is the name of the fourth period?
Exercise 1.5.90
(Solution on p. 83.)
(Section 1.2) In the number 610,467, how many thousands are there?
Exercise 1.5.91
(Section 1.3) Write 8,840 as you would read it.
Exercise 1.5.92
(Solution on p. 83.)
(Section 1.4) Round 6,842 to the nearest hundred.
Exercise 1.5.93
(Section 1.4) Round 431,046 to the nearest million.
1.6 Subtraction of Whole Numbers6
1.6.1 Section Overview
• Subtraction
• Subtraction as the Opposite of Addition
• The Subtraction Process
• Subtraction Involving Borrowing
• Borrowing From Zero
• Calculators
6This content is available online at <http://cnx.org/content/m34784/1.5/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
45
1.6.2 Subtraction
Subtraction
Subtraction is the process of determining the remainder when part of the total is removed.
Suppose the sum of two whole numbers is 11, and from 11 we remove 4. Using the number line to help our visualization, we see that if we are located at 11 and move 4 units to the left, and thus remove 4 units, we will be located at 7. Thus, 7 units remain when we remove 4 units from 11 units.
The Minus Symbol
The minus symbol (-) is used to indicate subtraction. For example, 11 − 4 indicates that 4 is to be subtracted from 11.
Minuend
The number immediately in front of or the minus symbol is called the minuend, and it represents the original number of units.
Subtrahend
The number immediately following or below the minus symbol is called the subtrahend, and it represents the number of units to be removed.
Dierence
The result of the subtraction is called the dierence of the two numbers. For example, in 11 − 4 = 7, 11 is the minuend, 4 is the subtrahend, and 7 is the dierence.
1.6.3 Subtraction as the Opposite of Addition
Subtraction can be thought of as the opposite of addition. We show this in the problems in Sample Set A.
1.6.3.1 Sample Set A
Example 1.31
8 − 5 = 3 since 3 + 5 = 8.
Example 1.32
9 − 3 = 6 since 6 + 3 = 9.
1.6.3.2 Practice Set A
Complete the following statements.
Exercise 1.6.1
(Solution on p. 83.)
7 − 5 =
since
+5 = 7.
Exercise 1.6.2
(Solution on p. 83.)
9 − 1 =
since
+1 = 9.
Exercise 1.6.3
(Solution on p. 83.)
17 − 8 =
since
+8 = 17.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
46
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
1.6.4 The Subtraction Process
We’ll study the process of the subtraction of two whole numbers by considering the dierence between 48
and 35.
which we write as 13.
Example 1.33: The Process of Subtracting Whole Numbers
To subtract two whole numbers,
The process
1. Write the numbers vertically, placing corresponding positions in the same column.
48
−35
2. Subtract the digits in each column. Start at the right, in the ones position, and move to the left, placing the dierence at the bottom.
48
−35
13
1.6.4.1 Sample Set B
Perform the following subtractions.
Example 1.34
275
−142
133
5 – 2 = 3 .
7 – 4 = 3 .
2 – 1 = 1 .
Example 1.35
46, 042
− 1, 031
45, 011
2 – 1 = 1 .
4 – 3 = 1 .
0 – 0 = 0 .
6 – 1 = 5 .
4 – 0 = 4 .
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
47
Example 1.36
Find the dierence between 977 and 235.
Write the numbers vertically, placing the larger number on top. Line up the columns properly.
977
−235
742
The dierence between 977 and 235 is 742.
Example 1.37
In Keys County in 1987, there were 809 cable television installations. In Flags County in 1987, there were 1,159 cable television installations. How many more cable television installations were there in Flags County than in Keys County in 1987?
We need to determine the dierence between 1,159 and 809.
There were 350 more cable television installations in Flags County than in Keys County in 1987.
1.6.4.2 Practice Set B
Perform the following subtractions.
Exercise 1.6.4
(Solution on p. 83.)
534
−203
Exercise 1.6.5
(Solution on p. 83.)
857
− 43
Exercise 1.6.6
(Solution on p. 83.)
95, 628
−34, 510
Exercise 1.6.7
(Solution on p. 83.)
11, 005
− 1, 005
Exercise 1.6.8
(Solution on p. 83.)
Find the dierence between 88,526 and 26,412.
In each of these problems, each bottom digit is less than the corresponding top digit. This may not always be the case. We will examine the case where the bottom digit is greater than the corresponding top digit in the next section.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

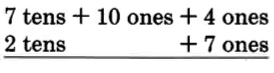
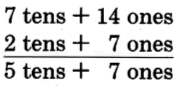
48
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
1.6.5 Subtraction Involving Borrowing
Minuend and Subtrahend
It often happens in the subtraction of two whole numbers that a digit in the minuend (top number) will be less than the digit in the same position in the subtrahend (bottom number). This happens when we subtract 27 from 84.
84
−27
We do not have a name for 4 − 7. We need to rename 84 in order to continue. We’ll do so as follows: Our new name for 84 is 7 tens + 14 ones.
= 57
Notice that we converted 8 tens to 7 tens + 1 ten, and then we converted the 1 ten to 10 ones. We then had 14 ones and were able to perform the subtraction.
Borrowing
The process of borrowing (converting) is illustrated in the problems of Sample Set C.
1.6.5.1 Sample Set C
Example 1.38
1. Borrow 1 ten from the 8 tens. This leaves 7 tens.
2. Convert the 1 ten to 10 ones.
3. Add 10 ones to 4 ones to get 14 ones.
Example 1.39
1. Borrow 1 hundred from the 6 hundreds. This leaves 5 hundreds.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
49
2. Convert the 1 hundred to 10 tens.
3. Add 10 tens to 7 tens to get 17 tens.
1.6.5.2 Practice Set C
Perform the following subtractions. Show the expanded form for the rst three problems.
Exercise 1.6.9
(Solution on p. 83.)
53
−35
Exercise 1.6.10
(Solution on p. 84.)
76
−28
Exercise 1.6.11
(Solution on p. 84.)
872
−565
Exercise 1.6.12
(Solution on p. 84.)
441
−356
Exercise 1.6.13
(Solution on p. 84.)
775
− 66
Exercise 1.6.14
(Solution on p. 84.)
5, 663
−2, 559
Borrowing More Than Once
Sometimes it is necessary to borrow more than once. This is shown in the problems in Section 1.6.5.3
(Sample Set D).
1.6.5.3 Sample Set D
Perform the Subtractions. Borrowing more than once if necessary
Example 1.40
1. Borrow 1 ten from the 4 tens. This leaves 3 tens.
2. Convert the 1 ten to 10 ones.
3. Add 10 ones to 1 one to get 11 ones. We can now perform 11 − 8.
4. Borrow 1 hundred from the 6 hundreds. This leaves 5 hundreds.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

50
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
5. Convert the 1 hundred to 10 tens.
6. Add 10 tens to 3 tens to get 13 tens.
7. Now 13 − 5 = 8.
8. 5 − 3 = 2.
Example 1.41
1. Borrow 1 ten from the 3 tens. This leaves 2 tens.
2. Convert the 1 ten to 10 ones.
3. Add 10 ones to 4 ones to get 14 ones. We can now perform 14 − 5.
4. Borrow 1 hundred from the 5 hundreds. This leaves 4 hundreds.
5. Convert the 1 hundred to 10 tens.
6. Add 10 tens to 2 tens to get 12 tens. We can now perform 12 − 8 = 4.
7. Finally, 4 − 0 = 4.
Example 1.42
71529
– 6952
After borrowing, we have
1.6.5.4 Practice Set D
Perform the following subtractions.
Exercise 1.6.15
(Solution on p. 84.)
526
−358
Exercise 1.6.16
(Solution on p. 84.)
63, 419
− 7, 779
Exercise 1.6.17
(Solution on p. 84.)
4, 312
−3, 123
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

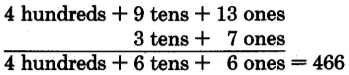
51
1.6.6 Borrowing from Zero
It often happens in a subtraction problem that we have to borrow from one or more zeros. This occurs in problems such as
503
1. − 37
and
5000
2. − 37
We’ll examine each case.
Example 1.43: Borrowing from a single zero.
503
Consider the problem − 37
Since we do not have a name for 3 − 7, we must borrow from 0.
Since there are no tens to borrow, we must borrow 1 hundred. One hundred = 10 tens.
We can now borrow 1 ten from 10 tens (leaving 9 tens). One ten = 10 ones and 10 ones + 3 ones
= 13 ones.
Now we can suggest the following method for borrowing from a single zero.
Borrowing from a Single Zero
To borrow from a single zero,
1. Decrease the digit to the immediate left of zero by one.
2. Draw a line through the zero and make it a 10.
3. Proceed to subtract as usual.
1.6.6.1 Sample Set E
Example 1.44
Perform this subtraction.
503
− 37
The number 503 contains a single zero
Available for free at Connexions <http://cnx.org/content/col10615/1.4>



52
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
1. The number to the immediate left of 0 is 5. Decrease 5 by 1.
5 − 1 = 4
2. Draw a line through the zero and make it a 10.
3. Borrow from the 10 and proceed.
1 ten + 10 ones
10 ones + 3 ones = 13 ones
1.6.6.2 Practice Set E
Perform each subtraction.
Exercise 1.6.18
(Solution on p. 84.)
906
− 18
Exercise 1.6.19
(Solution on p. 84.)
5102
− 559
Exercise 1.6.20
(Solution on p. 85.)
9055
− 386
Example 1.45: Borrowing from a group of zeros
5000
Consider the problem − 37
In this case, we have a group of zeros.
Since we cannot borrow any tens or hundreds, we must borrow 1 thousand. One thousand = 10
hundreds.
We can now borrow 1 hundred from 10 hundreds. One hundred = 10 tens.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
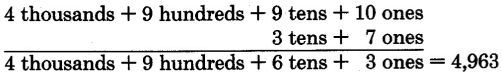


53
We can now borrow 1 ten from 10 tens. One ten = 10 ones.
From observations made in this procedure we can suggest the following method for borrowing from a group of zeros.
Borrowing from a Group of zeros
To borrow from a group of zeros,
1. Decrease the digit to the immediate left of the group of zeros by one.
2. Draw a line through each zero in the group and make it a 9, except the rightmost zero, make it 10.
3. Proceed to subtract as usual.
1.6.6.3 Sample Set F
Perform each subtraction.
Example 1.46
40, 000
−
125
The number 40,000 contains a group of zeros.
1. The number to the immediate left of the group is 4. Decrease 4 by 1.
4 − 1 = 3
2. Make each 0, except the rightmost one, 9. Make the rightmost 0 a 10.
3. Subtract as usual.
Example 1.47
8, 000, 006
−
41, 107
The number 8,000,006 contains a group of zeros.
1. The number to the immediate left of the group is 8. Decrease 8 by 1. 8 − 1 = 7
2. Make each zero, except the rightmost one, 9. Make the rightmost 0 a 10.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

54
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
3. To perform the subtraction, we’ll need to borrow from the ten.
1 ten = 10 ones
10 ones + 6 ones = 16 ones
1.6.6.4 Practice Set F
Perform each subtraction.
Exercise 1.6.21
(Solution on p. 85.)
21, 007
− 4, 873
Exercise 1.6.22
(Solution on p. 85.)
10, 004
− 5, 165
Exercise 1.6.23
(Solution on p. 85.)
16, 000, 000
−
201, 060
1.6.7 Calculators
In practice, calculators are used to nd the dierence between two whole numbers.
1.6.7.1 Sample Set G
Find the dierence between 1006 and 284.
Display Reads
Type 1006 1006
Press −
1006
Type 284
284
Press =
722
Table 1.26
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
The dierence between 1006 and 284 is 722.
(What happens if you type 284 rst and then 1006? We’ll study such numbers in Chapter 10.) 1.6.7.2 Practice Set G
Exercise 1.6.24
(Solution on p. 85.)
Use a calculator to nd the dierence between 7338 and 2809.
Exercise 1.6.25
(Solution on p. 85.)
Use a calculator to nd the dierence between 31,060,001 and 8,591,774.
1.6.8 Exercises
For the following problems, perform the subtractions. You may check each dierence with a calculator.
Exercise 1.6.26
(Solution on p. 85.)
15
− 8
Exercise 1.6.27
19
− 8
Exercise 1.6.28
(Solution on p. 85.)
11
− 5
Exercise 1.6.29
14
− 6
Exercise 1.6.30
(Solution on p. 85.)
12
− 9
Exercise 1.6.31
56
−12
Exercise 1.6.32
(Solution on p. 85.)
74
−33
Exercise 1.6.33
80
−61
Exercise 1.6.34
(Solution on p. 85.)
350
−141
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
Exercise 1.6.35
800
−650
Exercise 1.6.36
(Solution on p. 85.)
35, 002
−14, 001
Exercise 1.6.37
5, 000, 566
−2, 441, 326
Exercise 1.6.38
(Solution on p. 85.)
400, 605
−121, 352
Exercise 1.6.39
46, 400
− 2, 012
Exercise 1.6.40
(Solution on p. 85.)
77, 893
−
421
Exercise 1.6.41
42
−18
Exercise 1.6.42
(Solution on p. 85.)
51
−27
Exercise 1.6.43
622
− 88
Exercise 1.6.44
(Solution on p. 85.)
261
− 73
Exercise 1.6.45
242
−158
Exercise 1.6.46
(Solution on p. 85.)
3, 422
−1, 045
Exercise 1.6.47
5, 565
−3, 985
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 1.6.48
(Solution on p. 85.)
42, 041
−15, 355
Exercise 1.6.49
304, 056
− 20, 008
Exercise 1.6.50
(Solution on p. 85.)
64, 000, 002
−
856, 743
Exercise 1.6.51
4, 109
− 856
Exercise 1.6.52
(Solution on p. 85.)
10, 113
− 2, 079
Exercise 1.6.53
605
− 77
Exercise 1.6.54
(Solution on p. 85.)
59
−26
Exercise 1.6.55
36, 107
− 8, 314
Exercise 1.6.56
(Solution on p. 85.)
92, 526, 441, 820
−59, 914, 805, 253
Exercise 1.6.57
1, 605
− 881
Exercise 1.6.58
(Solution on p. 85.)
30, 000
−26, 062
Exercise 1.6.59
600
−216
Exercise 1.6.60
(Solution on p. 85.)
9, 000, 003
−
726, 048
For the following problems, perform each subtraction.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
Exercise 1.6.61
Subtract 63 from 92.
Hint:
The word “from” means “beginning at.” Thus, 63 from 92 means beginning at 92, or 92 − 63.
Exercise 1.6.62
(Solution on p. 85.)
Subtract 35 from 86.
Exercise 1.6.63
Subtract 382 from 541.
Exercise 1.6.64
(Solution on p. 86.)
Subtract 1,841 from 5,246.
Exercise 1.6.65
Subtract 26,082 from 35,040.
Exercise 1.6.66
(Solution on p. 86.)
Find the dierence between 47 and 21.
Exercise 1.6.67
Find the dierence between 1,005 and 314.
Exercise 1.6.68
(Solution on p. 86.)
Find the dierence between 72,085 and 16.
Exercise 1.6.69
Find the dierence between 7,214 and 2,049.
Exercise 1.6.70
(Solution on p. 86.)
Find the dierence between 56,108 and 52,911.
Exercise 1.6.71
How much bigger is 92 than 47?
Exercise 1.6.72
(Solution on p. 86.)
How much bigger is 114 than 85?
Exercise 1.6.73
How much bigger is 3,006 than 1,918?
Exercise 1.6.74
(Solution on p. 86.)
How much bigger is 11,201 than 816?
Exercise 1.6.75
How much bigger is 3,080,020 than 1,814,161?
Exercise 1.6.76
(Solution on p. 86.)
In Wichita, Kansas, the sun shines about 74% of the time in July and about 59% of the time in November. How much more of the time (in percent) does the sun shine in July than in November?
Exercise 1.6.77
The lowest temperature on record in Concord, New Hampshire in May is 21 ◦F, and in July it is 35 ◦F. What is the dierence in these lowest temperatures?
Exercise 1.6.78
(Solution on p. 86.)
In 1980, there were 83,000 people arrested for prostitution and commercialized vice and 11,330,000
people arrested for driving while intoxicated. How many more people were arrested for drunk driving than for prostitution?
Exercise 1.6.79
In 1980, a person with a bachelor’s degree in accounting received a monthly salary oer of $1,293, and a person with a marketing degree a monthly salary oer of $1,145. How much more was oered to the person with an accounting degree than the person with a marketing degree?
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
59
Exercise 1.6.80
(Solution on p. 86.)
In 1970, there were about 793 people per square mile living in Puerto Rico, and 357 people per square mile living in Guam. How many more people per square mile were there in Puerto Rico than Guam?
Exercise 1.6.81
The 1980 population of Singapore was 2,414,000 and the 1980 population of Sri Lanka was 14,850,000. How many more people lived in Sri Lanka than in Singapore in 1980?
Exercise 1.6.82
(Solution on p. 86.)
In 1977, there were 7,234,000 hospitals in the United States and 64,421,000 in Mainland China.
How many more hospitals were there in Mainland China than in the United States in 1977?
Exercise 1.6.83
In 1978, there were 3,095,000 telephones in use in Poland and 4,292,000 in Switzerland. How many more telephones were in use in Switzerland than in Poland in 1978?
For the following problems, use the corresponding graphs to solve the problems.
Exercise 1.6.84
(Solution on p. 86.)
How many more life scientists were there in 1974 than mathematicians? (this image) Exercise 1.6.85
How many more social, psychological, mathematical, and environmental scientists were there than life, physical, and computer scientists? (this image)
Exercise 1.6.86
(Solution on p. 86.)
How many more prosecutions were there in 1978 than in 1974? (this image) Exercise 1.6.87
How many more prosecutions were there in 1976-1980 than in 1970-1975? (this image) Available for free at Connexions <http://cnx.org/content/col10615/1.4>
60
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
Exercise 1.6.88
(Solution on p. 86.)
How many more dry holes were drilled in 1960 than in 1975? (this image) Exercise 1.6.89
How many more dry holes were drilled in 1960, 1965, and 1970 than in 1975, 1978 and 1979? (this image)
For the following problems, replace the [U+2610] with the whole number that will make the subtraction true.
Exercise 1.6.90
(Solution on p. 86.)
14
−
3
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 1.6.91
21
−
14
Exercise 1.6.92
(Solution on p. 86.)
35
−
25
Exercise 1.6.93
16
−
9
Exercise 1.6.94
(Solution on p. 86.)
28
−
16
For the following problems, nd the solutions.
Exercise 1.6.95
Subtract 42 from the sum of 16 and 56.
Exercise 1.6.96
(Solution on p. 86.)
Subtract 105 from the sum of 92 and 89.
Exercise 1.6.97
Subtract 1,127 from the sum of 2,161 and 387.
Exercise 1.6.98
(Solution on p. 86.)
Subtract 37 from the dierence between 263 and 175.
Exercise 1.6.99
Subtract 1,109 from the dierence between 3,046 and 920.
Exercise 1.6.100
(Solution on p. 86.)
Add the dierence between 63 and 47 to the difference between 55 and 11.
Exercise 1.6.101
Add the dierence between 815 and 298 to the dierence between 2,204 and 1,016.
Exercise 1.6.102
(Solution on p. 86.)
Subtract the dierence between 78 and 43 from the sum of 111 and 89.
Exercise 1.6.103
Subtract the dierence between 18 and 7 from the sum of the dierences between 42 and 13, and 81 and 16.
Exercise 1.6.104
(Solution on p. 86.)
Find the dierence between the dierences of 343 and 96, and 521 and 488.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
62
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
1.6.8.1 Exercises for Review
Exercise 1.6.105
(Section 1.2) In the number 21,206, how many hundreds are there?
Exercise 1.6.106
(Solution on p. 86.)
(Section 1.2) Write a three-digit number that has a zero in the ones position.
Exercise 1.6.107
(Section 1.2) How many three-digit whole numbers are there?
Exercise 1.6.108
(Solution on p. 86.)
(Section 1.4) Round 26,524,016 to the nearest million.
Exercise 1.6.109
(Section 1.5) Find the sum of 846 + 221 + 116.
1.7 Properties of Addition7
1.7.1 Section Overview
• The Commutative Property of Addition
• The Associative Property of Addition
• The Additive Identity
We now consider three simple but very important properties of addition.
1.7.2 The Commutative Property of Addition
Commutative Property of Addition
If two whole numbers are added in any order, the sum will not change.
1.7.2.1 Sample Set A
Example 1.48
Add the whole numbers
8 + 5 = 13
5 + 8 = 13
The numbers 8 and 5 can be added in any order. Regardless of the order they are added, the sum is 13.
7This content is available online at <http://cnx.org/content/m34802/1.5/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
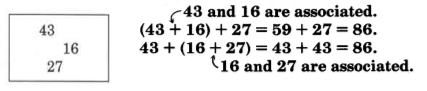

63
1.7.2.2 Practice Set A
Exercise 1.7.1
(Solution on p. 86.)
Use the commutative property of addition to nd the sum of 12 and 41 in two dierent ways.
Exercise 1.7.2
(Solution on p. 86.)
Add the whole numbers
1.7.3 The Associative Property of Addition
Associative Property of Addition
If three whole numbers are to be added, the sum will be the same if the rst two are added rst, then that sum is added to the third, or, the second two are added rst, and that sum is added to the rst.
Using Parentheses
It is a common mathematical practice to use parentheses to show which pair of numbers we wish to combine rst.
1.7.3.1 Sample Set B
Example 1.49
Add the whole numbers.
1.7.3.2 Practice Set B
Exercise 1.7.3
(Solution on p. 87.)
Use the associative property of addition to add the following whole numbers two dierent ways.
Exercise 1.7.4
(Solution on p. 87.)
Available for free at Connexions <http://cnx.org/content/col10615/1.4>



64
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
1.7.4 The Additive Identity
0 Is the Additive Identity
The whole number 0 is called the additive identity, since when it is added to any whole number, the sum is identical to that whole number.
1.7.4.1 Sample Set C
Example 1.50
Add the whole numbers.
29 + 0 = 29
0 + 29 = 29
Zero added to 29 does not change the identity of 29.
1.7.4.2 Practice Set C
Add the following whole numbers.
Exercise 1.7.5
(Solution on p. 87.)
Exercise 1.7.6
(Solution on p. 87.)
Suppose we let the letter x represent a choice for some whole number. For the rst two problems, nd the sums. For the third problem, nd the sum provided we now know that x represents the whole number 17.
Exercise 1.7.7
(Solution on p. 87.)
Exercise 1.7.8
(Solution on p. 87.)
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
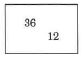

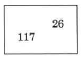



65
Exercise 1.7.9
(Solution on p. 87.)
1.7.5 Exercises
For the following problems, add the numbers in two ways.
Exercise 1.7.10
(Solution on p. 87.)
Exercise 1.7.11
Exercise 1.7.12
(Solution on p. 87.)
Exercise 1.7.13
Exercise 1.7.14
(Solution on p. 87.)
Exercise 1.7.15
Exercise 1.7.16
(Solution on p. 87.)
Available for free at Connexions <http://cnx.org/content/col10615/1.4>







66
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
Exercise 1.7.17
Exercise 1.7.18
(Solution on p. 87.)
Exercise 1.7.19
Exercise 1.7.20
(Solution on p. 87.)
Exercise 1.7.21
Exercise 1.7.22
(Solution on p. 87.)
Exercise 1.7.23
Exercise 1.7.24
(Solution on p. 87.)
For the following problems, show that the pairs of quantities yield the same sum.
Exercise 1.7.25
(11 + 27) + 9 and 11 + (27 + 9)
Exercise 1.7.26
(Solution on p. 87.)
(80 + 52) + 6 and 80 + (52 + 6)
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 1.7.27
(114 + 226) + 108 and 114 + (226 + 108)
Exercise 1.7.28
(Solution on p. 87.)
(731 + 256) + 171 and 731 + (256 + 171)
Exercise 1.7.29
The fact that (a rst number + a second number) + third number = a rst number + (a second number + a third number) is an example of the
property of addition.
Exercise 1.7.30
(Solution on p. 87.)
The fact that 0 + any number = that particular number is an example of the property of addition.
Exercise 1.7.31
The fact that a rst number + a second number = a second number + a rst number is an example of the
property of addition.
Exercise 1.7.32
(Solution on p. 87.)
Use the numbers 15 and 8 to illustrate the commutative property of addition.
Exercise 1.7.33
Use the numbers 6, 5, and 11 to illustrate the associative property of addition.
Exercise 1.7.34
(Solution on p. 87.)
The number zero is called the additive identity. Why is the term identity so appropriate?
1.7.5.1 Exercises for Review
Exercise 1.7.35
(Section 1.2) How many hundreds in 46,581?
Exercise 1.7.36
(Solution on p. 87.)
(Section 1.3) Write 2,218 as you would read it.
Exercise 1.7.37
(Section 1.4) Round 506,207 to the nearest thousand.
Exercise 1.7.38
(Solution on p. 87.)
482
(Section 1.5) Find the sum of + 68
Exercise 1.7.39
3, 318
(Section 1.6) Find the dierence: − 429
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

68
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
1.8 Summary of Key Concepts8
1.8.1 Summary of Key Concepts
Number / Numeral (Section 1.2)
A number is a concept. It exists only in the mind. A numeral is a symbol that represents a number. It is customary not to distinguish between the two (but we should remain aware of the dierence).
Hindu-Arabic Numeration System (Section 1.2)
In our society, we use the Hindu-Arabic numeration system. It was invented by the Hindus shortly before the third century and popularized by the Arabs about a thousand years later.
Digits (Section 1.2)
The numbers 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 are called digits.
Base Ten Positional System (Section 1.2)
The Hindu-Arabic numeration system is a positional number system with base ten. Each position has value that is ten times the value of the position to its right.
Commas / Periods (Section 1.2)
Commas are used to separate digits into groups of three. Each group of three is called a period. Each period has a name. From right to left, they are ones, thousands, millions, billions, etc.
Whole Numbers (Section 1.2)
A whole number is any number that is formed using only the digits (0, 1, 2, 3, 4, 5, 6, 7, 8, 9).
Number Line (Section 1.2)
The number line allows us to visually display the whole numbers.
Graphing (Section 1.2)
Graphing a whole number is a term used for visually displaying the whole number. The graph of 4 appears below.
Reading Whole Numbers (Section 1.3)
To express a whole number as a verbal phrase:
1. Begin at the right and, working right to left, separate the number into distinct periods by inserting commas every three digits.
2. Begin at the left, and read each period individually.
Writing Whole Numbers (Section 1.3)
To rename a number that is expressed in words to a number expressed in digits: 8This content is available online at <http://cnx.org/content/m34798/1.3/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
69
1. Notice that a number expressed as a verbal phrase will have its periods set o by commas.
2. Start at the beginning of the sentence, and write each period of numbers individually.
3. Use commas to separate periods, and combine the periods to form one number.
Rounding (Section 1.4)
Rounding is the process of approximating the number of a group of objects by mentally “seeing” the collection as occurring in groups of tens, hundreds, thousands, etc.
Addition (Section 1.5)
Addition is the process of combining two or more objects (real or intuitive) to form a new, third object, the total, or sum.
Addends / Sum (Section 1.5)
In addition, the numbers being added are called addends and the result, or total, the sum.
Subtraction (Section 1.6)
Subtraction is the process of determining the remainder when part of the total is removed.
Minuend / Subtrahend Dierence (Section 1.6)
Commutative Property of Addition (Section 1.7)
If two whole numbers are added in either of two orders, the sum will not change.
3 + 5 = 5 + 3
Associative Property of Addition (Section 1.7)
If three whole numbers are to be added, the sum will be the same if the rst two are added and that sum is then added to the third, or if the second two are added and the rst is added to that sum.
(3 + 5) + 2 = 3 + (5 + 2)
Parentheses in Addition (Section 1.7)
Parentheses in addition indicate which numbers are to be added rst.
Additive Identity (Section 1.7)
The whole number 0 is called the additive identity since, when it is added to any particular whole number, the sum is identical to that whole number.
0 + 7 = 7
7 + 0 = 7
1.9 Exercise Supplement9
1.9.1 Exercise Supplement
For problems 1-35, nd the sums and dierences.
Exercise 1.9.1
(Solution on p. 87.)
908
+ 29
9This content is available online at <http://cnx.org/content/m34800/1.5/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
Exercise 1.9.2
529
+161
Exercise 1.9.3
(Solution on p. 87.)
549
+ 16
Exercise 1.9.4
726
+892
Exercise 1.9.5
(Solution on p. 87.)
390
+169
Exercise 1.9.6
166
+660
Exercise 1.9.7
(Solution on p. 88.)
391
+951
Exercise 1.9.8
48
+36
Exercise 1.9.9
(Solution on p. 88.)
1, 103
+ 898
Exercise 1.9.10
1, 642
+ 899
Exercise 1.9.11
(Solution on p. 88.)
807
+1, 156
Exercise 1.9.12
80, 349
+ 2, 679
Exercise 1.9.13
(Solution on p. 88.)
70, 070
+ 9, 386
Exercise 1.9.14
90, 874
+ 2, 945
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 1.9.15
(Solution on p. 88.)
45, 292
+51, 661
Exercise 1.9.16
1, 617
+54, 923
Exercise 1.9.17
(Solution on p. 88.)
702, 607
+ 89, 217
Exercise 1.9.18
6, 670, 006
+
2, 495
Exercise 1.9.19
(Solution on p. 88.)
267
+8, 034
Exercise 1.9.20
7, 007
+11, 938
Exercise 1.9.21
(Solution on p. 88.)
131, 294
+
9, 087
Exercise 1.9.22
5, 292
+
161
Exercise 1.9.23
(Solution on p. 88.)
17, 260
+58, 964
Exercise 1.9.24
7, 006
−5, 382
Exercise 1.9.25
(Solution on p. 88.)
7, 973
−3, 018
Exercise 1.9.26
16, 608
− 1, 660
Exercise 1.9.27
(Solution on p. 88.)
209, 527
−
23, 916
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
Exercise 1.9.28
584
−226
Exercise 1.9.29
(Solution on p. 88.)
3, 313
−1, 075
Exercise 1.9.30
458
−122
Exercise 1.9.31
(Solution on p. 88.)
1, 007
+ 331
Exercise 1.9.32
16, 082
+ 2, 013
Exercise 1.9.33
(Solution on p. 88.)
926
− 48
Exercise 1.9.34
736
+5, 869
Exercise 1.9.35
(Solution on p. 88.)
676, 504
− 58, 277
For problems 36-39, add the numbers.
Exercise 1.9.36
769
795
298
746
Exercise 1.9.37
(Solution on p. 88.)
554
184
883
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 1.9.38
30, 188
79, 731
16, 600
66, 085
39, 169
95, 170
Exercise 1.9.39
(Solution on p. 88.)
2, 129
6, 190
17, 044
30, 447
292
41
428, 458
For problems 40-50, combine the numbers as indicated.
Exercise 1.9.40
2, 957 + 9, 006
Exercise 1.9.41
(Solution on p. 88.)
19, 040 + 813
Exercise 1.9.42
350, 212 + 14, 533
Exercise 1.9.43
(Solution on p. 88.)
970 + 702 + 22 + 8
Exercise 1.9.44
3, 704 + 2, 344 + 429 + 10, 374 + 74
Exercise 1.9.45
(Solution on p. 88.)
874 + 845 + 295 − 900
Exercise 1.9.46
904 + 910 − 881
Exercise 1.9.47
(Solution on p. 88.)
521 + 453 − 334 + 600
Exercise 1.9.48
892 − 820 − 9
Exercise 1.9.49
(Solution on p. 88.)
159 + 4, 085 − 918 − 608
Exercise 1.9.50
2, 562 + 8, 754 − 393 − 385 − 910
For problems 51-63, add and subtract as indicated.
Exercise 1.9.51
(Solution on p. 88.)
Subtract 671 from 8,027.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
74
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
Exercise 1.9.52
Subtract 387 from 6,342.
Exercise 1.9.53
(Solution on p. 88.)
Subtract 2,926 from 6,341.
Exercise 1.9.54
Subtract 4,355 from the sum of 74 and 7,319.
Exercise 1.9.55
(Solution on p. 88.)
Subtract 325 from the sum of 7,188 and 4,964.
Exercise 1.9.56
Subtract 496 from the dierence of 60,321 and 99.
Exercise 1.9.57
(Solution on p. 89.)
Subtract 20,663 from the dierence of 523,150 and 95,225.
Exercise 1.9.58
Add the dierence of 843 and 139 to the dierence of 4,450 and 839.
Exercise 1.9.59
(Solution on p. 89.)
Add the dierence of 997,468 and 292,513 to the dierence of 22,140 and 8,617.
Exercise 1.9.60
Subtract the dierence of 8,412 and 576 from the sum of 22,140 and 8,617.
Exercise 1.9.61
(Solution on p. 89.)
Add the sum of 2,273, 3,304, 847, and 16 to the dierence of 4,365 and 864.
Exercise 1.9.62
Add the sum of 19,161, 201, 166,127, and 44 to the dierence of the sums of 161, 2,455, and 85, and 21, 26, 48, and 187.
Exercise 1.9.63
(Solution on p. 89.)
Is the sum of 626 and 1,242 the same as the sum of 1,242 and 626? Justify your claim.
1.10 Prociency Exam10
1.10.1 Prociency Exam
Exercise 1.10.1
(Solution on p. 89.)
(Section 1.2) What is the largest digit?
Exercise 1.10.2
(Solution on p. 89.)
(Section 1.2) In the Hindu-Arabic number system, each period has three values assigned to it.
These values are the same for each period. From right to left, what are they?
Exercise 1.10.3
(Solution on p. 89.)
(Section 1.2) In the number 42,826, how many hundreds are there?
Exercise 1.10.4
(Solution on p. 89.)
(Section 1.2) Is there a largest whole number? If so, what is it?
Exercise 1.10.5
(Solution on p. 89.)
(Section 1.2) Graph the following whole numbers on the number line: 2, 3, 5.
10This content is available online at <http://cnx.org/content/m34805/1.4/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Exercise 1.10.6
(Solution on p. 89.)
(Section 1.3) Write the number 63,425 as you would read it aloud.
Exercise 1.10.7
(Solution on p. 89.)
(Section 1.3) Write the number eighteen million, three hundred fty-nine thousand, seventy-two.
Exercise 1.10.8
(Solution on p. 89.)
(Section 1.4) Round 427 to the nearest hundred.
Exercise 1.10.9
(Solution on p. 89.)
(Section 1.4) Round 18,995 to the nearest ten.
Exercise 1.10.10
(Solution on p. 89.)
(Section 1.4) Round to the most reasonable digit: During a semester, a mathematics instructor uses 487 pieces of chalk.
For problems 11-17, nd the sums and dierences.
Exercise 1.10.11
(Solution on p. 89.)
627
(Section 1.5) + 48
Exercise 1.10.12
(Solution on p. 89.)
(Section 1.5) 3106 + 921
Exercise 1.10.13
(Solution on p. 89.)
152
(Section 1.5) + 36
Exercise 1.10.14
(Solution on p. 89.)
5, 189
6, 189
(Section 1.5)
4, 122
+8, 001
Exercise 1.10.15
(Solution on p. 89.)
(Section 1.5) 21 + 16 + 42 + 11
Exercise 1.10.16
(Solution on p. 89.)
(Section 1.6) 520 − 216
Exercise 1.10.17
(Solution on p. 89.)
80, 001
(Section 1.6) − 9,878
Exercise 1.10.18
(Solution on p. 89.)
(Section 1.6) Subtract 425 from 816.
Exercise 1.10.19
(Solution on p. 89.)
(Section 1.6) Subtract 712 from the sum of 507 and 387.
Exercise 1.10.20
(Solution on p. 89.)
(Section 1.7) Is the sum of 219 and 412 the same as the sum of 412 and 219? If so, what makes it so?
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

76
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
Solutions to Exercises in Chapter 1
Solution to Exercise 1.2.1 (p. 10)
Yes. Letters are symbols. Taken as a collection (a written word), they represent a number.
Solution to Exercise 1.2.2 (p. 12)
ve thousand
Solution to Exercise 1.2.3 (p. 12)
four hundred billion
Solution to Exercise 1.2.4 (p. 12)
zero tens, or zero
Solution to Exercise 1.2.5 (p. 13)
Solution to Exercise 1.2.6 (p. 13)
4, 5, 6, 113, 978
Solution to Exercise 1.2.7 (p. 14)
concept
Solution to Exercise 1.2.9 (p. 14)
Yes, since it is a symbol that represents a number.
Solution to Exercise 1.2.11 (p. 14)
positional; 10
Solution to Exercise 1.2.13 (p. 14)
ones, tens, hundreds
Solution to Exercise 1.2.15 (p. 14)
4
Solution to Exercise 1.2.17 (p. 14)
0
Solution to Exercise 1.2.19 (p. 14)
0
Solution to Exercise 1.2.21 (p. 14)
ten thousand
Solution to Exercise 1.2.23 (p. 14)
6 ten millions = 60 million
Solution to Exercise 1.2.25 (p. 14)
1,340 (answers may vary)
Solution to Exercise 1.2.27 (p. 15)
900
Solution to Exercise 1.2.29 (p. 15)
yes; zero
Solution to Exercise 1.2.31 (p. 15)
graphing
Solution to Exercise 1.2.33 (p. 15)
Solution to Exercise 1.2.35 (p. 15)
61, 99, 100, 102
Solution to Exercise 1.3.1 (p. 17)
Twelve thousand, ve hundred forty-two
Solution to Exercise 1.3.2 (p. 17)
One hundred one million, seventy-four thousand, three
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 1.3.3 (p. 17)
One million, eight
Solution to Exercise 1.3.4 (p. 18)
103,025
Solution to Exercise 1.3.5 (p. 18)
6,040,007
Solution to Exercise 1.3.6 (p. 18)
20,003,080,109,402
Solution to Exercise 1.3.7 (p. 18)
80,000,000,035
Solution to Exercise 1.3.8 (p. 18)
nine hundred twelve
Solution to Exercise 1.3.10 (p. 19)
one thousand, four hundred ninety-one
Solution to Exercise 1.3.12 (p. 19)
thirty-ve thousand, two hundred twenty-three
Solution to Exercise 1.3.14 (p. 19)
four hundred thirty-seven thousand, one hundred ve
Solution to Exercise 1.3.16 (p. 19)
eight million, one thousand, one
Solution to Exercise 1.3.18 (p. 19)
seven hundred seventy million, three hundred eleven thousand, one hundred one Solution to Exercise 1.3.20 (p. 19)
one hundred six billion, one hundred million, one thousand ten
Solution to Exercise 1.3.22 (p. 19)
eight hundred billion, eight hundred thousand
Solution to Exercise 1.3.24 (p. 19)
four; one thousand, four hundred sixty
Solution to Exercise 1.3.26 (p. 19)
twenty billion
Solution to Exercise 1.3.28 (p. 19)
four hundred twelve; fty-two; twenty-one thousand, four hundred twenty-four Solution to Exercise 1.3.30 (p. 19)
one thousand, nine hundred seventy-nine; eighty-ve thousand; two million, nine hundred ve thousand Solution to Exercise 1.3.32 (p. 19)
one thousand, nine hundred eighty; two hundred seventeen
Solution to Exercise 1.3.34 (p. 20)
one thousand, nine hundred eighty one; one million, nine hundred fty-six thousand Solution to Exercise 1.3.36 (p. 20)
one thousand, nine hundred eighty; thirteen thousand, one hundred
Solution to Exercise 1.3.38 (p. 20)
twelve million, six hundred thirty thousand
Solution to Exercise 1.3.40 (p. 20)
681
Solution to Exercise 1.3.42 (p. 20)
7,201
Solution to Exercise 1.3.44 (p. 20)
512,003
Solution to Exercise 1.3.46 (p. 20)
35,007,101
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
Solution to Exercise 1.3.48 (p. 20)
16,000,059,004
Solution to Exercise 1.3.50 (p. 20)
23,000,000,000
Solution to Exercise 1.3.52 (p. 20)
100,000,000,000,001
Solution to Exercise 1.3.54 (p. 21)
4
Solution to Exercise 1.3.56 (p. 21)
yes, zero
Solution to Exercise 1.4.1 (p. 24)
3400
Solution to Exercise 1.4.2 (p. 24)
27,000
Solution to Exercise 1.4.3 (p. 24)
31,000,000
Solution to Exercise 1.4.4 (p. 24)
0
Solution to Exercise 1.4.5 (p. 24)
60,000
Solution to Exercise 1.4.6 (p. 24)
hundred thousand ten thousand million
1,600
2000
0
0
Table 1.27
Solution to Exercise 1.4.8 (p. 25)
Hundred thousand ten thousand million
91,800
92,000
90,000
0
Table 1.28
Solution to Exercise 1.4.10 (p. 25)
hundred thousand ten thousand million
200
0
0
0
Table 1.29
Solution to Exercise 1.4.12 (p. 25)
hundred thousand ten thousand million
900
1,000
0
0
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Table 1.30
Solution to Exercise 1.4.14 (p. 26)
hundred thousand ten thousand million
900
1,000
0
0
Table 1.31
Solution to Exercise 1.4.16 (p. 26)
hundred thousand ten thousand million
1,000
1,000
0
0
Table 1.32
Solution to Exercise 1.4.18 (p. 26)
hundred
thousand
ten thousand million
551,061,300 551,061,000 551,060,000
551,000,000
Table 1.33
Solution to Exercise 1.4.20 (p. 27)
hundred
thousand
ten thousand
million
106,999,413,200 106,999,413,000 106,999,410,000 106,999,000,000
Table 1.34
Solution to Exercise 1.4.22 (p. 27)
Hundred
Thousand ten thousand Million
8,006,000 8,006,000
8,010,000
8,000,000
Table 1.35
Solution to Exercise 1.4.24 (p. 27)
hundred thousand ten thousand million
33,500
33,000
30,000
0
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

80
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
Table 1.36
Solution to Exercise 1.4.26 (p. 28)
hundred thousand ten thousand million
388,600
389,000
390,000
0
Table 1.37
Solution to Exercise 1.4.28 (p. 28)
hundred thousand ten thousand million
8,200
8,000
10,000
0
Table 1.38
Solution to Exercise 1.4.30 (p. 28)
19,310,000
Solution to Exercise 1.4.32 (p. 29)
29,000,000
Solution to Exercise 1.4.34 (p. 29)
70% or 75%
Solution to Exercise 1.4.36 (p. 29)
$5,500,000,000
Solution to Exercise 1.4.38 (p. 29)
230,000
Solution to Exercise 1.4.40 (p. 29)
5,400,000
Solution to Exercise 1.4.42 (p. 29)
graphing
Solution to Exercise 1.4.44 (p. 29)
Forty-two thousand, one hundred nine
Solution to Exercise 1.4.46 (p. 29)
4,000,000,008
Solution to Exercise 1.5.1 (p. 31)
88
Solution to Exercise 1.5.2 (p. 31)
5,527
Solution to Exercise 1.5.3 (p. 31)
267,166
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
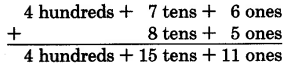
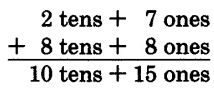
81
Solution to Exercise 1.5.4 (p. 34)
87
= 7 tens + 1 ten + 7 ones
= 8 tens + 7 ones
= 87
Solution to Exercise 1.5.5 (p. 34)
561
= 4 hundreds + 15 tens + 1 ten + 1 one
= 4 hundreds + 16 tens + 1 one
= 4 hundreds + 1 hundred + 6 tens + 1 one
= 5 hundreds + 6 tens + 1 one
= 561
Solution to Exercise 1.5.6 (p. 34)
115
= 10 tens + 1 ten + 5 ones
= 11 tens + 5 ones
= 1 hundred + 1 ten + 5 ones
= 115
Solution to Exercise 1.5.7 (p. 34)
153,525
Solution to Exercise 1.5.8 (p. 34)
167
Solution to Exercise 1.5.9 (p. 35)
2,468
Solution to Exercise 1.5.10 (p. 35)
434,826
Solution to Exercise 1.5.11 (p. 36)
155
Solution to Exercise 1.5.12 (p. 36)
19,750
Solution to Exercise 1.5.13 (p. 36)
30,682
Solution to Exercise 1.5.14 (p. 36)
19
Solution to Exercise 1.5.16 (p. 36)
48
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
Solution to Exercise 1.5.18 (p. 36)
98
Solution to Exercise 1.5.20 (p. 36)
978
Solution to Exercise 1.5.22 (p. 37)
368
Solution to Exercise 1.5.24 (p. 37)
12,777
Solution to Exercise 1.5.26 (p. 37)
58,738
Solution to Exercise 1.5.28 (p. 37)
45,169,739
Solution to Exercise 1.5.30 (p. 37)
33
Solution to Exercise 1.5.32 (p. 37)
81
Solution to Exercise 1.5.34 (p. 37)
91
Solution to Exercise 1.5.36 (p. 37)
809
Solution to Exercise 1.5.38 (p. 38)
862
Solution to Exercise 1.5.40 (p. 38)
2,321
Solution to Exercise 1.5.42 (p. 38)
1,141,204
Solution to Exercise 1.5.44 (p. 38)
561,364,111
Solution to Exercise 1.5.46 (p. 38)
942,302,364,207,060
Solution to Exercise 1.5.48 (p. 38)
234
Solution to Exercise 1.5.50 (p. 38)
95,365
Solution to Exercise 1.5.52 (p. 39)
1,972,128
Solution to Exercise 1.5.54 (p. 39)
3,700
Solution to Exercise 1.5.56 (p. 39)
3,101,500
Solution to Exercise 1.5.58 (p. 39)
100
Solution to Exercise 1.5.60 (p. 40)
0Solution to Exercise 1.5.62 (p. 40)
1,000
Solution to Exercise 1.5.64 (p. 40)
5Solution to Exercise 1.5.66 (p. 40)
19
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 1.5.68 (p. 40)
88
Solution to Exercise 1.5.70 (p. 41)
60,511,000
Solution to Exercise 1.5.72 (p. 41)
5,682,651 square miles
Solution to Exercise 1.5.74 (p. 41)
1,190,000
Solution to Exercise 1.5.76 (p. 42)
271,564,000
Solution to Exercise 1.5.78 (p. 43)
20
Solution to Exercise 1.5.80 (p. 43)
25
Solution to Exercise 1.5.82 (p. 43)
40
Solution to Exercise 1.5.84 (p. 43)
50
Solution to Exercise 1.5.86 (p. 44)
50
Solution to Exercise 1.5.88 (p. 44)
50
Solution to Exercise 1.5.90 (p. 44)
0Solution to Exercise 1.5.92 (p. 44)
6,800
Solution to Exercise 1.6.1 (p. 45)
7 − 5 = 2 since 2 + 5 = 7
Solution to Exercise 1.6.2 (p. 45)
9 − 1 = 8 since 8 + 1 = 9
Solution to Exercise 1.6.3 (p. 45)
17 − 8 = 9 since 9 + 8 = 17
Solution to Exercise 1.6.4 (p. 47)
331
Solution to Exercise 1.6.5 (p. 47)
814
Solution to Exercise 1.6.6 (p. 47)
61,118
Solution to Exercise 1.6.7 (p. 47)
10,000
Solution to Exercise 1.6.8 (p. 47)
62,114
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
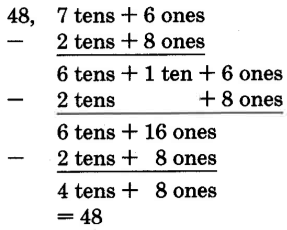
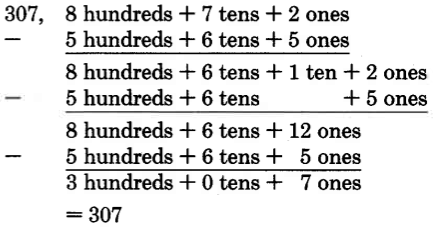
84
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
Solution to Exercise 1.6.9 (p. 49)
Solution to Exercise 1.6.10 (p. 49)
Solution to Exercise 1.6.11 (p. 49)
Solution to Exercise 1.6.12 (p. 49)
85
Solution to Exercise 1.6.13 (p. 49)
709
Solution to Exercise 1.6.14 (p. 49)
3,104
Solution to Exercise 1.6.15 (p. 50)
168
Solution to Exercise 1.6.16 (p. 50)
55,640
Solution to Exercise 1.6.17 (p. 50)
1,189
Solution to Exercise 1.6.18 (p. 52)
888
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 1.6.19 (p. 52)
4,543
Solution to Exercise 1.6.20 (p. 52)
8,669
Solution to Exercise 1.6.21 (p. 54)
16,134
Solution to Exercise 1.6.22 (p. 54)
4,839
Solution to Exercise 1.6.23 (p. 54)
15,789,940
Solution to Exercise 1.6.24 (p. 55)
4,529
Solution to Exercise 1.6.25 (p. 55)
22,468,227
Solution to Exercise 1.6.26 (p. 55)
7
Solution to Exercise 1.6.28 (p. 55)
6
Solution to Exercise 1.6.30 (p. 55)
3
Solution to Exercise 1.6.32 (p. 55)
41
Solution to Exercise 1.6.34 (p. 55)
209
Solution to Exercise 1.6.36 (p. 56)
21,001
Solution to Exercise 1.6.38 (p. 56)
279,253
Solution to Exercise 1.6.40 (p. 56)
77,472
Solution to Exercise 1.6.42 (p. 56)
24
Solution to Exercise 1.6.44 (p. 56)
188
Solution to Exercise 1.6.46 (p. 56)
2,377
Solution to Exercise 1.6.48 (p. 56)
26,686
Solution to Exercise 1.6.50 (p. 57)
63,143,259
Solution to Exercise 1.6.52 (p. 57)
8,034
Solution to Exercise 1.6.54 (p. 57)
33
Solution to Exercise 1.6.56 (p. 57)
32,611,636,567
Solution to Exercise 1.6.58 (p. 57)
3,938
Solution to Exercise 1.6.60 (p. 57)
8,273,955
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
Solution to Exercise 1.6.62 (p. 58)
51
Solution to Exercise 1.6.64 (p. 58)
3,405
Solution to Exercise 1.6.66 (p. 58)
26
Solution to Exercise 1.6.68 (p. 58)
72,069
Solution to Exercise 1.6.70 (p. 58)
3,197
Solution to Exercise 1.6.72 (p. 58)
29
Solution to Exercise 1.6.74 (p. 58)
10,385
Solution to Exercise 1.6.76 (p. 58)
15%
Solution to Exercise 1.6.78 (p. 58)
11,247,000
Solution to Exercise 1.6.80 (p. 59)
436
Solution to Exercise 1.6.82 (p. 59)
57,187,000
Solution to Exercise 1.6.84 (p. 59)
165,000
Solution to Exercise 1.6.86 (p. 59)
74
Solution to Exercise 1.6.88 (p. 60)
4,547
Solution to Exercise 1.6.90 (p. 60)
11
Solution to Exercise 1.6.92 (p. 61)
10
Solution to Exercise 1.6.94 (p. 61)
12
Solution to Exercise 1.6.96 (p. 61)
76
Solution to Exercise 1.6.98 (p. 61)
51
Solution to Exercise 1.6.100 (p. 61)
60
Solution to Exercise 1.6.102 (p. 61)
165
Solution to Exercise 1.6.104 (p. 61)
214
Solution to Exercise 1.6.106 (p. 62)
330 (answers may vary)
Solution to Exercise 1.6.108 (p. 62)
27,000,000
Solution to Exercise 1.7.1 (p. 63)
12 + 41 = 53 and 41 + 12 = 53
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Solution to Exercise 1.7.2 (p. 63)
837 + 1, 958 = 2, 795 and 1, 958 + 837 = 2, 795
Solution to Exercise 1.7.3 (p. 63)
(17 + 32) + 25 = 49 + 25 = 74 and 17 + (32 + 25) = 17 + 57 = 74
Solution to Exercise 1.7.4 (p. 63)
(1, 629 + 806) + 429 = 2, 435 + 429 = 2, 864
1, 629 + (806 + 429) = 1, 629 + 1, 235 = 2, 864
Solution to Exercise 1.7.5 (p. 64)
8
Solution to Exercise 1.7.6 (p. 64)
5Solution to Exercise 1.7.7 (p. 64)
xSolution to Exercise 1.7.8 (p. 64)
xSolution to Exercise 1.7.9 (p. 65)
17
Solution to Exercise 1.7.10 (p. 65)
37
Solution to Exercise 1.7.12 (p. 65)
45
Solution to Exercise 1.7.14 (p. 65)
568
Solution to Exercise 1.7.16 (p. 65)
122,323
Solution to Exercise 1.7.18 (p. 66)
45
Solution to Exercise 1.7.20 (p. 66)
100
Solution to Exercise 1.7.22 (p. 66)
556
Solution to Exercise 1.7.24 (p. 66)
43,461
Solution to Exercise 1.7.26 (p. 66)
132 + 6 =80 + 58 = 138
Solution to Exercise 1.7.28 (p. 67)
987 + 171 =731 + 427 = 1, 158
Solution to Exercise 1.7.30 (p. 67)
Identity
Solution to Exercise 1.7.32 (p. 67)
15 + 8 = 8 + 15 = 23
Solution to Exercise 1.7.34 (p. 67)
. . .because its partner in addition remains identically the same after that addition Solution to Exercise 1.7.36 (p. 67)
Two thousand, two hundred eighteen.
Solution to Exercise 1.7.38 (p. 67)
550
Solution to Exercise 1.9.1 (p. 69)
937
Solution to Exercise 1.9.3 (p. 70)
565
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
Solution to Exercise 1.9.5 (p. 70)
559
Solution to Exercise 1.9.7 (p. 70)
1,342
Solution to Exercise 1.9.9 (p. 70)
2,001
Solution to Exercise 1.9.11 (p. 70)
1,963
Solution to Exercise 1.9.13 (p. 70)
79,456
Solution to Exercise 1.9.15 (p. 70)
96,953
Solution to Exercise 1.9.17 (p. 71)
791,824
Solution to Exercise 1.9.19 (p. 71)
8,301
Solution to Exercise 1.9.21 (p. 71)
140,381
Solution to Exercise 1.9.23 (p. 71)
76,224
Solution to Exercise 1.9.25 (p. 71)
4,955
Solution to Exercise 1.9.27 (p. 71)
185,611
Solution to Exercise 1.9.29 (p. 72)
2,238
Solution to Exercise 1.9.31 (p. 72)
1,338
Solution to Exercise 1.9.33 (p. 72)
878
Solution to Exercise 1.9.35 (p. 72)
618,227
Solution to Exercise 1.9.37 (p. 72)
1,621
Solution to Exercise 1.9.39 (p. 73)
484,601
Solution to Exercise 1.9.41 (p. 73)
19,853
Solution to Exercise 1.9.43 (p. 73)
1,702
Solution to Exercise 1.9.45 (p. 73)
1,114
Solution to Exercise 1.9.47 (p. 73)
1,300
Solution to Exercise 1.9.49 (p. 73)
2,718
Solution to Exercise 1.9.51 (p. 73)
7,356
Solution to Exercise 1.9.53 (p. 74)
3,415
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
89
Solution to Exercise 1.9.55 (p. 74)
11,827
Solution to Exercise 1.9.57 (p. 74)
407,262
Solution to Exercise 1.9.59 (p. 74)
718,478
Solution to Exercise 1.9.61 (p. 74)
9,941
Solution to Exercise 1.9.63 (p. 74)
626 + 1, 242 = 1, 242 + 626 = 1, 868
Solution to Exercise 1.10.1 (p. 74)
9Solution to Exercise 1.10.2 (p. 74)
ones, tens, hundreds
Solution to Exercise 1.10.3 (p. 74)
8Solution to Exercise 1.10.4 (p. 74)
no
Solution to Exercise 1.10.5 (p. 74)
Solution to Exercise 1.10.6 (p. 75)
Sixty-three thousand, four hundred twenty-ve
Solution to Exercise 1.10.7 (p. 75)
18,359,072
Solution to Exercise 1.10.8 (p. 75)
400
Solution to Exercise 1.10.9 (p. 75)
19,000
Solution to Exercise 1.10.10 (p. 75)
500
Solution to Exercise 1.10.11 (p. 75)
675
Solution to Exercise 1.10.12 (p. 75)
4,027
Solution to Exercise 1.10.13 (p. 75)
188
Solution to Exercise 1.10.14 (p. 75)
23,501
Solution to Exercise 1.10.15 (p. 75)
90
Solution to Exercise 1.10.16 (p. 75)
304
Solution to Exercise 1.10.17 (p. 75)
70,123
Solution to Exercise 1.10.18 (p. 75)
391
Solution to Exercise 1.10.19 (p. 75)
182
Solution to Exercise 1.10.20 (p. 75)
Yes, commutative property of addition
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
CHAPTER 1. ADDITION AND SUBTRACTION OF WHOLE NUMBERS
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
Multiplication and Division of Whole
Numbers
2.1 Objectives1
After completing this chapter, you should
Multiplication of Whole Numbers (Section 2.2)
• understand the process of multiplication
• be able to multiply whole numbers
• be able to simplify multiplications with numbers ending in zero
• be able to use a calculator to multiply one whole number by another
Concepts of Division of Whole Numbers (Section 2.3)
• understand the process of division
• understand division of a nonzero number into zero
• understand why division by zero is undened
• be able to use a calculator to divide one whole number by another
Division of Whole Numbers (Section 2.4)
• be able to divide a whole number by a single or multiple digit divisor
• be able to interpret a calculator statement that a division results in a remainder Some Interesting Facts about Division (Section 2.5)
• be able to recognize a whole number that is divisible by 2, 3, 4, 5, 6, 8, 9, or 10
Properties of Multiplication (Section 2.6)
• understand and appreciate the commutative and associative properties of multiplication
• understand why 1 is the multiplicative identity
1This content is available online at <http://cnx.org/content/m18888/1.4/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4> 91
CHAPTER 2. MULTIPLICATION AND DIVISION OF WHOLE NUMBERS
2.2 Multiplication of Whole Numbers2
2.2.1 Section Overview
• Multiplication
• The Multiplication Process With a Single Digit Multiplier
• The Multiplication Process With a Multiple Digit Multiplier
• Multiplication With Numbers Ending in Zero
• Calculators
2.2.2 Multiplication
Multiplication is a description of repeated addition.
In the addition of
5 + 5 + 5
the number 5 is repeated 3 times. Therefore, we say we have three times ve and describe it by writing 3 × 5
Thus,
3 × 5 = 5 + 5 + 5
Multiplicand
In a multiplication, the repeated addend (number being added) is called the multiplicand. In 3 × 5, the 5
is the multiplicand.
Multiplier
Also, in a multiplication, the number that records the number of times the multiplicand is used is called the multiplier. In 3 × 5, the 3 is the multiplier.
2.2.2.1 Sample Set A
Express each repeated addition as a multiplication. In each case, specify the multiplier and the multiplicand.
Example 2.1
7 + 7 + 7 + 7 + 7 + 7
6 × 7.
Multiplier is 6.
Multiplicand is 7.
Example 2.2
18 + 18 + 18
3 × 18.
Multiplier is 3.
Multiplicand is 18.
2This content is available online at <http://cnx.org/content/m34863/1.2/>.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
93
2.2.2.2 Practice Set A
Express each repeated addition as a multiplication. In each case, specify the multiplier and the multiplicand.
Exercise 2.2.1
(Solution on p. 142.)
12 + 12 + 12 + 12
. Multiplier is
. Multiplicand is
.
Exercise 2.2.2
(Solution on p. 142.)
36 + 36 + 36 + 36 + 36 + 36 + 36 + 36
. Multiplier is
. Multiplicand is
.
Exercise 2.2.3
(Solution on p. 142.)
0 + 0 + 0 + 0 + 0
. Multiplier is
. Multiplicand is
.
Exercise 2.2.4
(Solution on p. 142.)
1847 + 1847 + … + 1847
|
{z
}
12, 000 times
. Multiplier is
. Multiplicand is
.
Factors
In a multiplication, the numbers being multiplied are also called factors.
Products
The result of a multiplication is called the product. In 3 × 5 = 15, the 3 and 5 are not only called the multiplier and multiplicand, but they are also called factors. The product is 15.
Indicators of Multiplication ×,·,( )
The multiplication symbol (×) is not the only symbol used to indicate multiplication. Other symbols include the dot ( · ) and pairs of parentheses ( ). The expressions
3 × 5,
3 · 5,
3 (5),
(3) 5,
(3) (5)
all represent the same product.
2.2.3 The Multiplication Process With a Single Digit Multiplier
Since multiplication is repeated addition, we should not be surprised to notice that carrying can occur.
Carrying occurs when we nd the product of 38 and 7:
First, we compute 7 × 8 = 56. Write the 6 in the ones column. Carry the 5. Then take 7 × 3 = 21. Add to 21 the 5 that was carried: 21 + 5 = 26. The product is 266.
Available for free at Connexions <http://cnx.org/content/col10615/1.4>
94
CHAPTER 2. MULTIPLICATION AND DIVISION OF WHOLE NUMBERS
2.2.3.1 Sample Set B
Find the following products.
Example 2.3
3 × 4 = 12
Write the 2, carry the 1.
3 × 6 = 18
Add to 18 the 1 that was carried: 18 + 1 = 19.
The product is 192.
Example 2.4
5 × 6 = 30
Write the 0, carry the 3.
5 × 2 = 10
Add to 10 the 3 that was carried: 10 + 3 = 13. Write the 3, carry the 1.
5 × 5 = 25
Add to 25 the 1 that was carried: 25 + 1 = 6.
The product is 2,630.
Example 2.5
9 × 4 = 36
Write the 6, carry the 3.
9 × 0 = 0
Add to the 0 the 3 that was carried: 0 + 3 = 3. Write the 3.
9 × 8 = 72
Write the 2, carry the 7.
Add to the 9 the 7 that was carried: 9 + 7 = 16.
9 × 1 = 9
Since there are no more multiplications to perform,write both the 1 and 6.
The product is 16,236.
2.2.3.2 Practice Set B
Find the following products.
Exercise 2.2.5
(Solution on p. 142.)
37
× 5
Available for free at Connexions <http://cnx.org/content/col10615/1.4>

95
Exercise 2.2.6
(Solution on p. 142.)
78
× 8
Exercise 2.2.7
(Solution on p. 142.)
536
×
7
Exercise 2.2.8
(Solution on p. 142.)
40, 019
×
8
Exercise 2.2.9
(Solution on p. 142.)
301, 599
×
3
2.2.4 The Multiplication Process With a Multiple Digit Multiplier
In a multiplication in which the multiplier is composed of two or more digits, the multiplication must take place in parts. The process is as follows:
Part 1: First Partial Product Multiply the multiplicand by the ones digit of the multiplier. This product is called the rst partial product.
Part 2: Second Partial Product Multiply the multiplicand by the tens digit of the multiplier. This product is called the second partial product. Since the tens digit is used as a factor, the second partial product is written below the rst partial product so that its rightmost digit appears in the tens column.
Part 3: If necessary, continue this way nding partial products. Write each one below the previous one so that the rightmost digit appears in the column directly below the digit that was used as a factor.
Part 4: Total Product Add the partial products to obtain the total product.
note: It may be necessary to carry when nding each partial product.
2.2.4.1 Sample Set C
Example 2.6
Multiply 326 by 48.
Part 1: