Chapter 5. Free Fall
Learning Objectives
By the end of this chapter, you will be able to:
- Identify the types of free fall motion.
- Describe the physical quantities related to free fall motion, such as maximum height, time to reach the maximum height, etc.
- Use kinematic equations to solve problems of free fall motion.
Introduction
An object falling freely from a certain height is undergoing free fall motion. If first we assume that air resistance is negligible, the only force acting on the object is the force of gravity, meaning that the object will accelerate towards the surface of the Earth with an acceleration due to gravity: [latex]g = 9.8 \, \text{m/s}^2[/latex]
If air resistance is now taken into consideration, then the object will be subjected to two forces:
- Gravity
- Air resistance
Initially, the force of gravity will be greater than that exerted by air resistance (Figure 5.1 a).
Air resistance increases during the fall (it is directly proportional to the square of the speed), so as the speed of the falling object increases, at some point air resistance might become equal to the force of gravity.
When this happens, the object will continue falling at a constant velocity, called the terminal velocity (Figure 5.1 b).
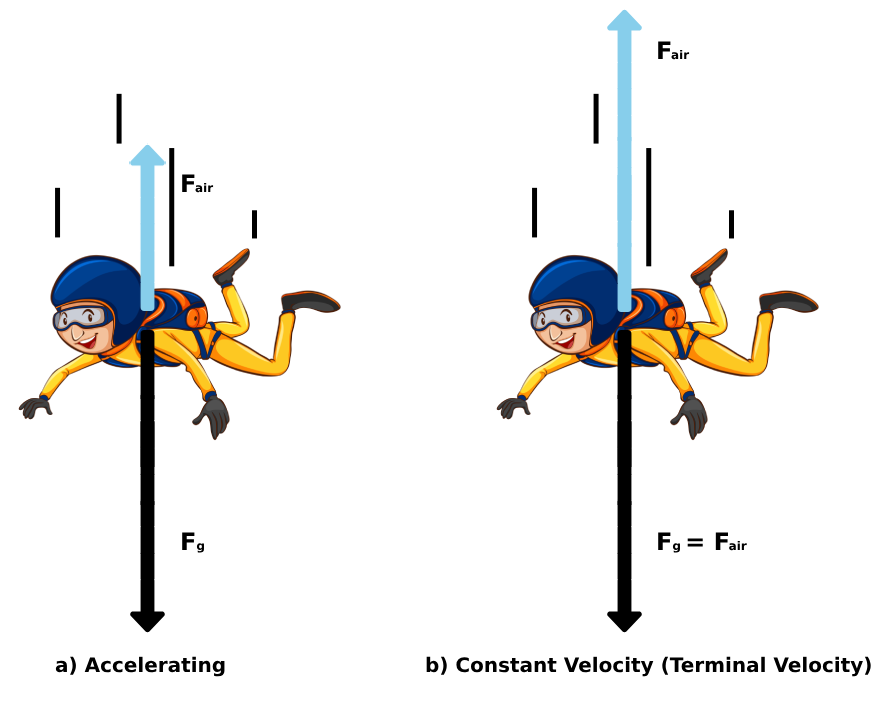
Concepts
There are several real-life situations that are considered free-falling motions:
- Throwing an object upwards: the object reaches a maximum height, then comes back to either the same level from which it started or to a different level (for instance, it falls onto another object, it is caught before reaching the initial level on its way back, etc.).
- Throwing an object downwards.
- Dropping an object from a height.
Regardless of the situation, free-fall motion is described by the same formulas as accelerated motion. That is because:
- On its way upward, an object will decelerate with an acceleration equal to [latex]g = 9.8 \, \text{m/s}^2[/latex] (the acceleration due to gravity) until it reaches the maximum height. At the maximum height, the instantaneous velocity is zero.
- On its way downward, an object will accelerate with an acceleration equal to [latex]g = 9.8 \, \text{m/s}^2[/latex] (the acceleration due to gravity).
It follows that all the equations used for accelerated motion apply to the free-fall motion with the note that acceleration is always [latex]g = 9.8 \, \text{m/s}^2[/latex] near the surface of the Earth. On another planet, the value of acceleration due to gravity will change.
Example
On the surface of the Moon, the acceleration due to gravity is approximately 6 times less than that on Earth.
Throwing an object upwards with an initial velocity [latex]v_i[/latex]
Notations and analysis of the motion
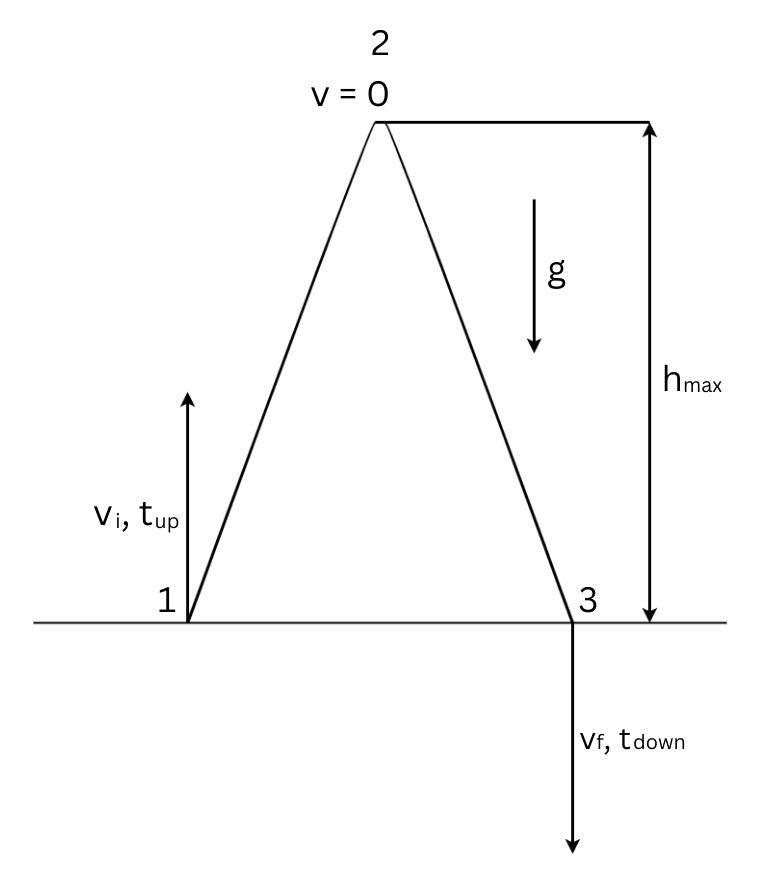
Notations:
[latex]v_{i, f}[/latex] represent the object’s initial velocity and final velocity respectively;
Analysis of the motion
From point 1 to point 2 (see Figure 5.2):
To calculate the maximum height, we use the following equation:
[latex]v_f^2 = v_i^2 + 2aS[/latex]
which becomes:
[latex]v_{f}^2 = v_{i}^2 - 2gh_{\text{max}}[/latex] (1)
The acceleration is negative because the object loses speed when going upward (decelerated motion).
From equation (1), the maximum height becomes:
[latex]h_{\text{max}} = \frac{v_{i}^2}{2g}[/latex] (2)
From point 2 to point 3 (see Figure 5.2):
On its way down, the object will come back down from the maximum height, where the velocity is zero, to the same level where it started.
We can express the maximum height using the same formula above:
[latex]v_f^2 = v_i^2 + 2aS[/latex]
which becomes:
[latex]v_{f}^2 = v_{i}^2 + 2gh_{\text{max}}[/latex] (3)
In this case [latex]v_i = 0[/latex], and the acceleration is positive, which means:
[latex]h_{\text{max}} = \frac{v_f^2}{2g}[/latex] (4)
Since expressions (2) and (4) represent the same quantity, they are equal.
Conclusion: The initial velocity (at the time of the throw) is equal to final velocity (at the time the object reaches the same level on its way down).
Using this concept, it can be shown that the time to reach the maximum height is equal to the time to come back from the maximum height to the same level.
So, the following equations can be used in solving problems of free fall:
[latex]v_i = v_f[/latex] (5)
[latex]t_{\text{up}} = t_{\text{down}}[/latex] (6)
An important note! The equations above are true ONLY for situations in which the object returns to the same level from which it started.
Solved examples
Example 1. An object is thrown upwards with a velocity of [latex]25 \, \text{m/s}[/latex]
- Find the maximum height reached by the object.
- Find the time to reach the maximum height.
- Find the time the object was in flight.
Given:
[latex]v_i = 25 \, \text{m/s}[/latex]
[latex]v_f = 0 \, \text{m/s}[/latex]
[latex]g = 9.8 \, \text{m/s}^2[/latex]
Find:
[latex]\text{a) } h_{\text{max}} = ?[/latex]
[latex]\text{b) } t_{\text{up}} = ?[/latex]
[latex]\text{c) } t_{\text{total}} = ?[/latex]
Solution:
-
Decide which equation works to solve the question by examining what information is given and what needs to be found.
[latex]v_f^2 = v_i^2 - 2gs[/latex]
Rearrange the equation to express the wanted quantity:
[latex]h_{\text{max}} = \frac{v_i^2}{2a}[/latex]
Substitute the values for the known quantities in the last equation:
[latex]h_{\text{max}} = \frac{v_i^2}{2a} = 31.9 \, \text{m} \approx 32 \, \text{m}[/latex]
Answer:
[latex]h_{\text{max}} = 32 \, \text{m}[/latex]
-
Choose the equation:
[latex]v_f = v_i - gt[/latex]
Rearrange the equation:
[latex]t_{\text{up}} = \frac{v_i}{g}[/latex]
[latex]t_{\text{up}} = \frac{v_i}{g} = 2.55 \, \text{s} \approx 2.6 \, \text{s}[/latex]
Answer:
[latex]t_{\text{up}} \approx 2.6 \, \text{s}[/latex]
-
Since the object returns to the same level from which it started:
[latex]t_{\text{up}} = t_{\text{down}}[/latex]
[latex]t_{\text{total}} = 2 \times t_{\text{up}} = 5.2 \, \text{s}[/latex]
Answer:
[latex]t_{\text{total}} = 5.2 \, \text{s}[/latex]
Chapter equations
[latex]g = \frac{\Delta v}{t} = \frac{v_f - v_i}{t}[/latex] (1)
[latex]h = \frac{v_i + v_f}{2} \times t[/latex] (2)
[latex]h = v_i t + \frac{1}{2} a t^2[/latex] (3)
[latex]v_{f}^2 = v_{i}^2 + 2gh_{\text{max}}[/latex] (4)
[latex]v_i = v_f[/latex] (5)
[latex]t_{\text{up}} = t_{\text{down}}[/latex] (6)
Try It!
- A basketball player throws a ball upward from [latex]1.95 \, \text{m}[/latex] above the floor; the ball is caught by another player on its way back down, at [latex]1.50 \, \text{m}[/latex] above the floor. Which of the following statements are true:
- The time the ball travels upward is greater than the time it travels downward.
- The time the ball travels upward is equal to the time it travels downward.
- The time the ball travels upward is less than the time it travels downward.
- A child drops a toy from a bridge into the water below. This is a free-fall motion described by the following (choose the correct statement):
- The final velocity is zero.
- The initial velocity is zero.
- The motion is a decelerated motion (negative [latex]g[/latex]).
- This is a uniform motion.
- A student throws a book upward from floor level. The book’s round trip takes [latex]8.0 \, \text{s}[/latex] Which of the following statements are true:
- The initial throwing velocity cannot be calculated (there is not enough information).
- The time the book took to reach the maximum height is not known.
- The time the book took to reach the floor (on its way down) is [latex]4.0 \, \text{s}[/latex].
Practice
- A ball is being thrown upwards with a velocity of [latex]15 \, \text{m/s}[/latex]. Find:
- the maximum height the ball can reach;
- the time needed for the ball to reach the maximum height;
- the time the ball was in flight assuming it is coming back to the same level.
Answer:
- [latex]11.5 \, \text{m}[/latex]
- [latex]1.53 \, \text{s}[/latex]
- [latex]3.06 \, \text{s}[/latex]
- A person throws a ball up in the air from the top of a [latex]25 \, \text{m}[/latex] high building. Knowing that the ball goes up in the air for [latex]12 \, \text{m}[/latex] (from the throwing point), find:
- the velocity of the ball at the moment it was thrown;
- the velocity of the ball when it reaches the ground;
- the time it takes the ball to reach the ground.
Answer:
- [latex]15.3 \, \text{m/s}[/latex]
- [latex]26.9 \, \text{m/s}[/latex]
- [latex]4.3 \, \text{s}[/latex]
- A book is being dropped from the top of a [latex]3.5 \, \text{m}[/latex] high flight of stairs. Find:
- the velocity of the book when it reaches the ground;
- the time needed for the book to reach the ground.
Answer:
- [latex]8.28 \, \text{m/s}[/latex]
- [latex]0.845 \, \text{s}[/latex]
- A child throws a rock from a bridge with a velocity of [latex]5.6 \, \text{m/s}[/latex]. Given that it takes the rock [latex]6.0 \, \text{s}[/latex] to reach the water underneath the bridge, how far down is the surface of the water?
Answer:[latex]210 \, \text{m}[/latex]
Challenge Question
An elephant taking a bath in a river is sucking water into its trunk. Suddenly, the passage of water is blocked by a rock. The elephant then turns its trunk upward and blows the water out.
Click and drag the scroll bar beneath the image below to solve the three associated questions.
An elephant blowing water and a rock upwards by Juan Pablo Amorocho in OER Lab Centennial College
- If he blows the water vertically upward with a velocity of [latex]14.5 \, \text{m/s}[/latex] how long will it take for the rock to reach its maximum height?
Answer:[latex]1.48 \, \text{s}[/latex] - What will be the maximum height reached by the rock?
Answer:[latex]10.7 \, \text{m}[/latex] - If the top of the elephant’s trunk in its upward position is [latex]4.7 \, \text{m}[/latex] above the water level, find the speed of the rock when it reaches the surface of the water.
Answer:[latex]17.4 \, \text{m/s}[/latex]
Image Attributions
- Figure 5.1: A simple sketch of a man sky diving by brgfx on Freepik

