Chapter 2. Vectors and Scalars. Vector Components
Learning Objectives
By the end of this chapter, you will be able to:
- Distinguish between vector and scalar quantities;
- Apply right angle trigonometry to find components of a vector.
Introduction
Vectors are physical quantities that can be completely described by a number (their magnitude), direction, and a unit.
Examples of vectors:
- Velocity
- Force
- Acceleration
- Displacement
For instance, we express velocity as [latex]60 \, \text{km/h}[/latex] due north. So, velocity is a vector because it has magnitude and direction (north). Another example of a vector is displacement. For instance, we can express a displacement as 30 km due south. Again, we see that displacement has both magnitude and direction.
Scalars are physical quantities that have a magnitude, but no direction. For instance, we can express the kinetic energy of a car travelling 30 m/s north and that of a car travelling 30 m/s south. We see that the kinetic energy will be the same regardless of the direction of travel. That means that energy is a scalar quantity.
Other examples of scalar quantities are:
- Speed
- Distance
- Work
- Power
Concepts
To find the components of a vector, we use the following diagram:
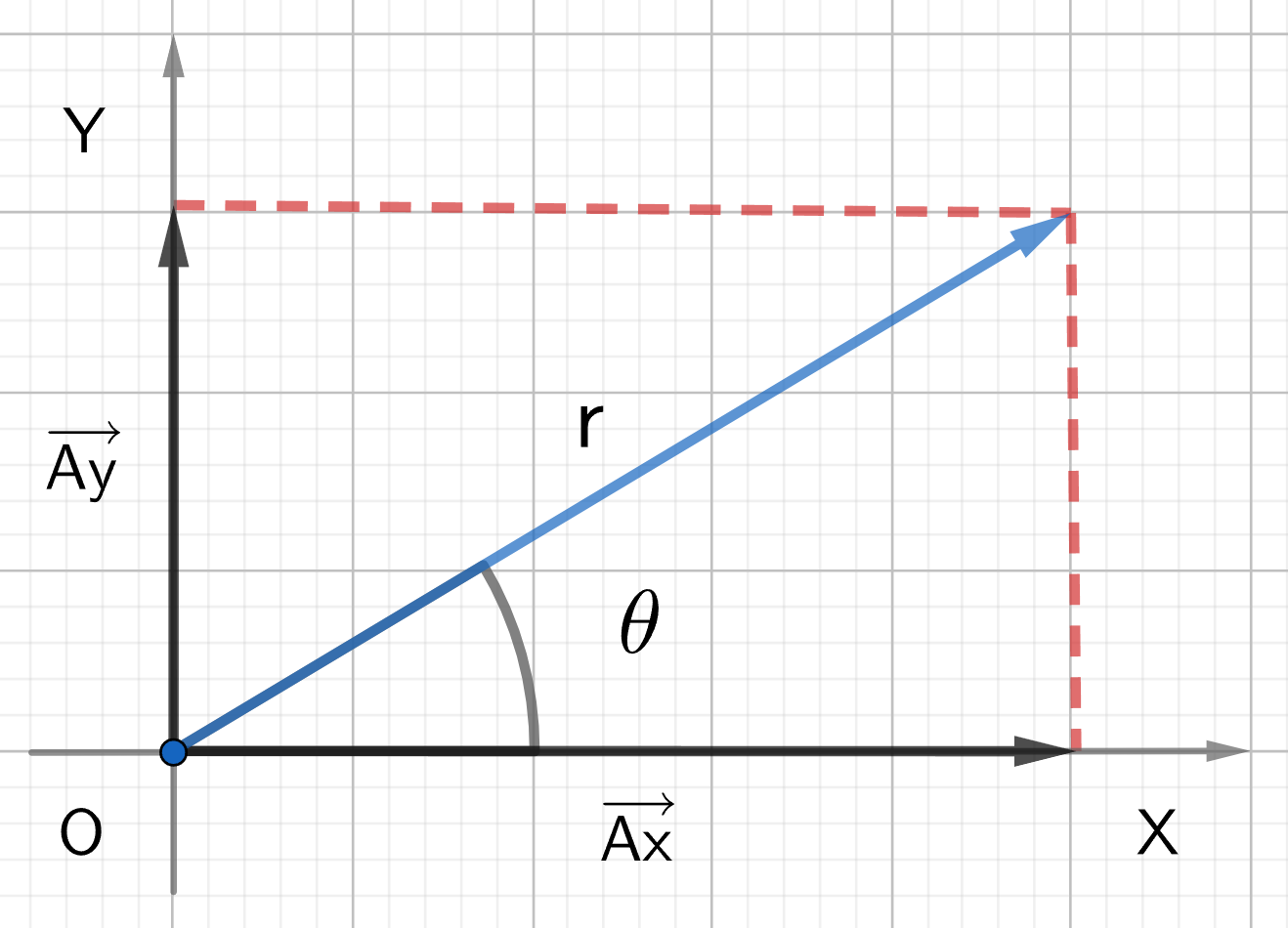
To find the x-component:
- Draw a perpendicular line from the tip of the vector to the x-axis.
- Connect the origin of the axes to the drop point.
To find the y-component:
- Draw a perpendicular to the y-axis.
- Connect the origin of the axes to the drop point.
The components can be calculated by using the trigonometric functions in the right-angle triangle from the diagram above:
Solved examples
Example 1. A car moves at 45 m/s, 40° north of east. Find the x and y components of the velocity vector.
Diagram:
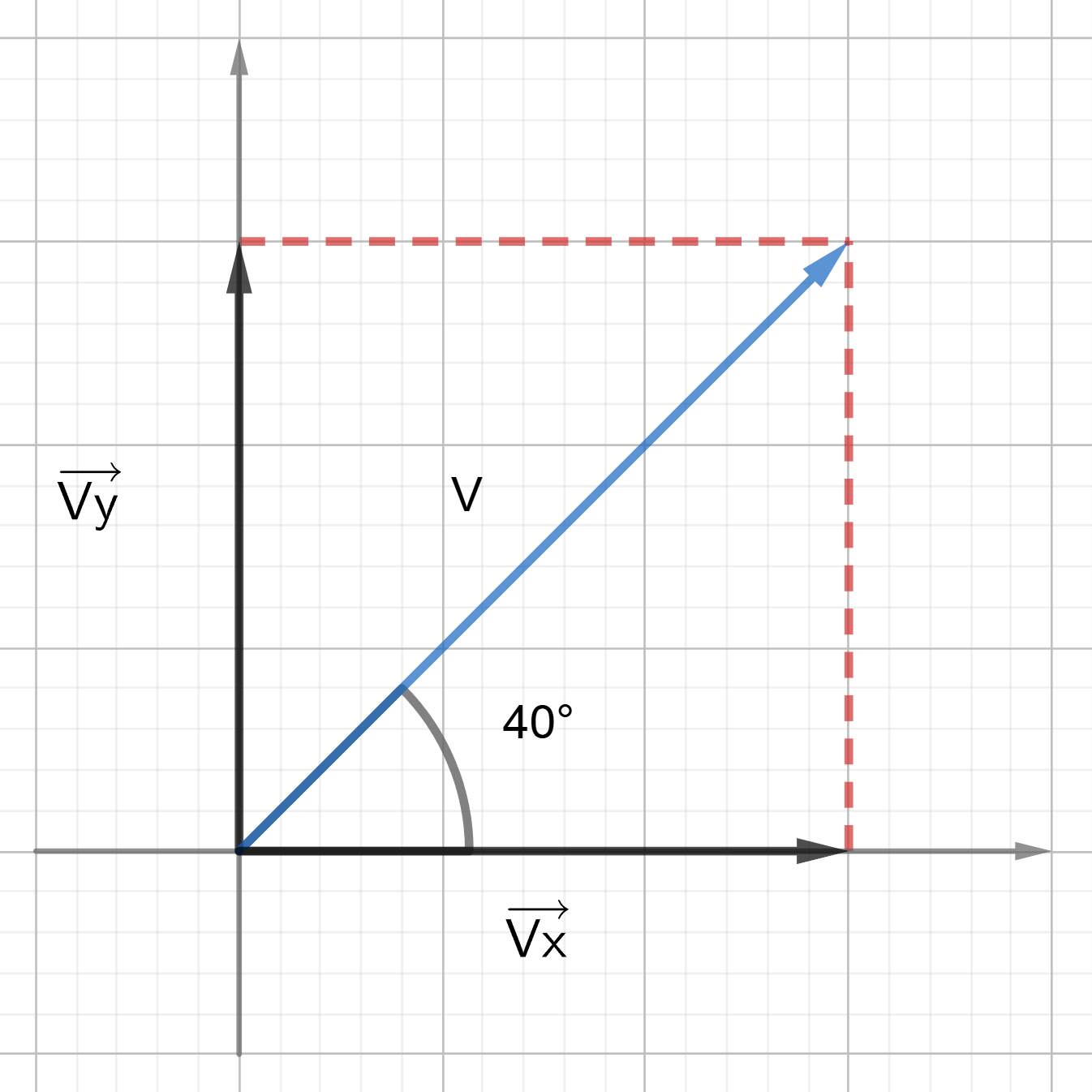
Solution:
[latex]v_x = v \times \cos \theta = 45 \times \cos 40^\circ = 34.47 \, \frac{m}{s} \simeq 34 \, \frac{m}{s}[/latex]
[latex]v_y = v \times \sin \theta = 45 \times \sin 40^\circ = 28.93 \, \frac{m}{s} \simeq 29 \, \frac{m}{s}[/latex]
Example 2. A crate is subjected to a 125 N force directed 30° west of south. Find the components of the force.
Diagram:
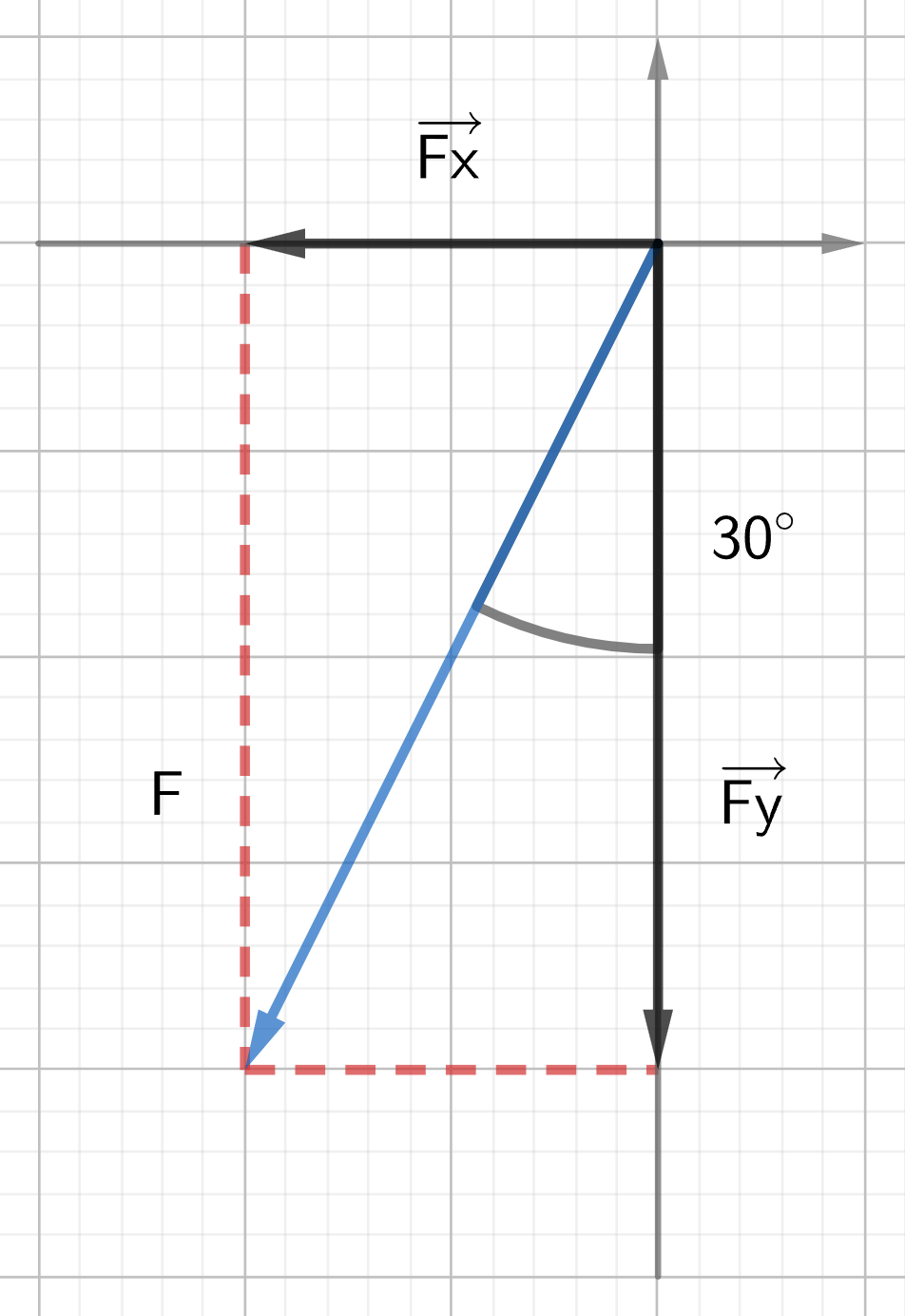
Solution:
Since the given angle is an angle with the y-axis, we first need to calculate the angle with the x-axis (the reference angle).
[latex]\alpha = 90^\circ - 30^\circ = 60^\circ[/latex]
The components are:
[latex]F_x = -F \times \cos \alpha = -125 \times \cos 60^\circ = -62.5 \, N[/latex]
[latex]F_y = -F \times \sin \alpha = 125 \times \sin 60^\circ = -108.25 \, N \simeq -108 \, N[/latex]
Note: When using the reference angle to calculate the components, the sign has to be adjusted depending on the quadrant in which the vector is positioned. In the example above, the vector is in the third quadrant, meaning both the x component and y component are negative.
Chapter equations
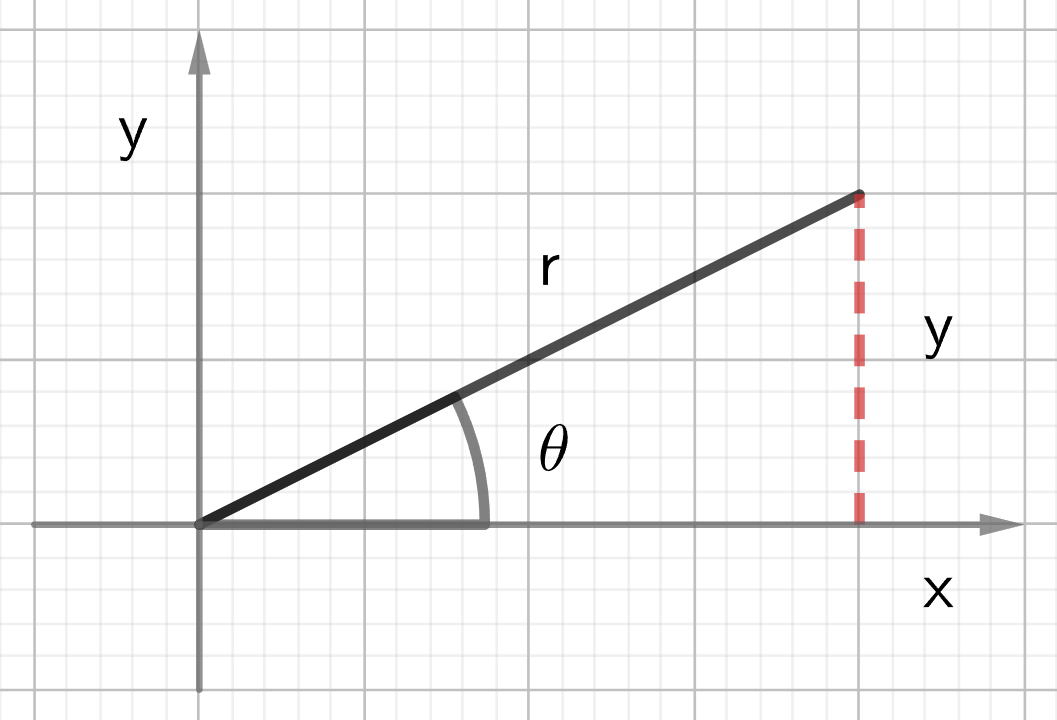
Based on the right-angle triangle in the diagram above:
[latex]x = r \cos \theta[/latex]
[latex]y = r \sin \theta[/latex]
𝛼– the reference angle is, by definition, the shortest angular distance from the terminal side of the angle to the x-axis.
[latex]r^2 = x^2 + y^2[/latex]
The relationship between the angle in standard position and the reference angle is:
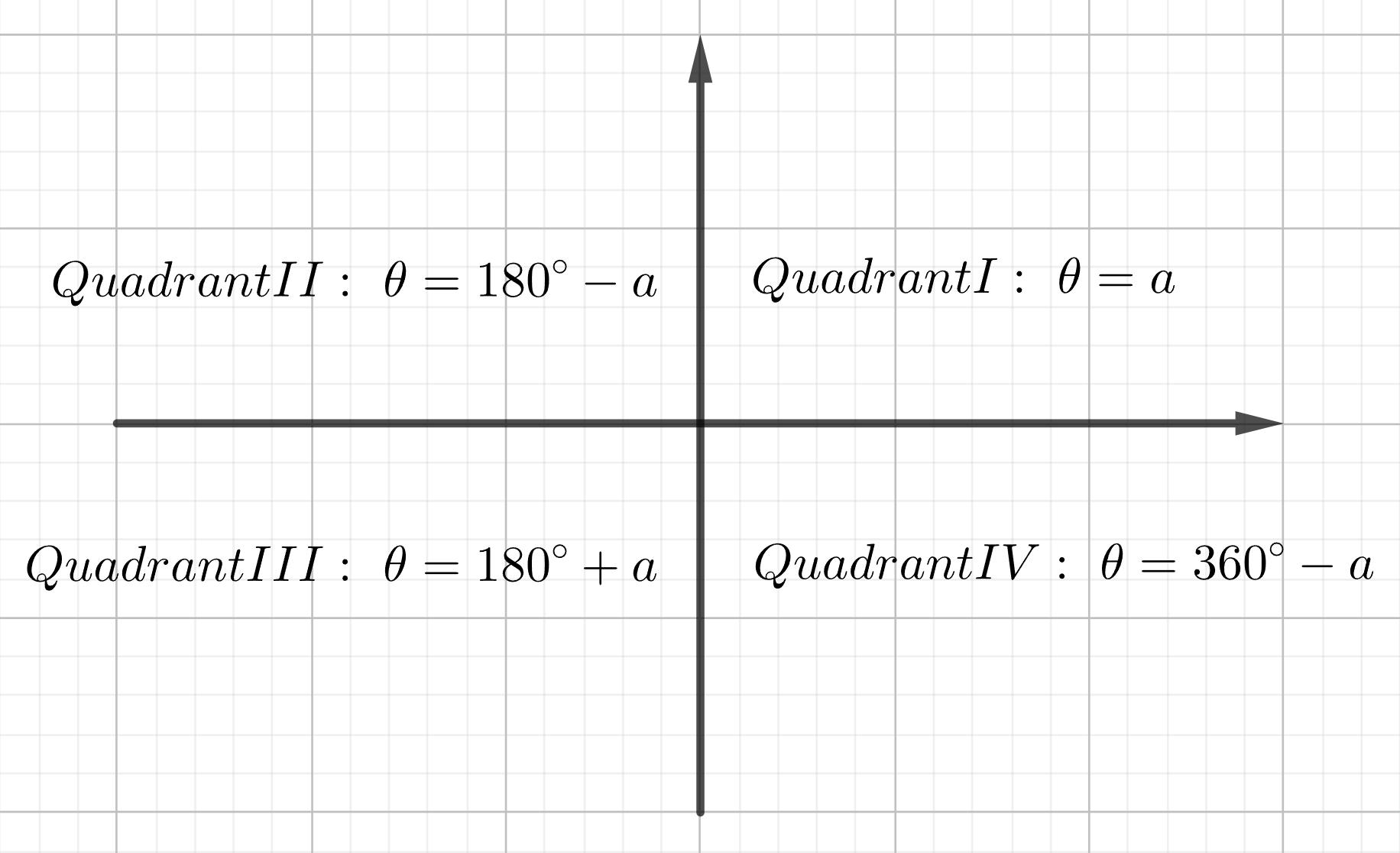
Try it!
- A vector v is given. The horizontal component of v is vx, while the vertical component of v is vy. Vector v makes an angle with the horizontal of 𝛼. Which equation helps us determine vx?
- A vector v is given. The horizontal component of v is vx, while the vertical component of v is vy. Vector v makes an angle with the horizontal of 𝛼. Which equation helps us determine vy?
- Under which circumstances can we use the Pythagorean theorem to find the resultant of two vectors?
Practice
- Find the x and y components of a force vector F = 35 N, positioned 56° north of west.
Answer:–19.6 N, 29.0 N - Find the x and y components of a velocity vector v = 20 m/s, positioned 25° south of east.
Answer:18.1 m/s, –8.5 m/s - Sketch and find the displacement vector in standard position given the x-component is +32.2 cm and the y-component is –22.2 cm.
Answer:39.1 cm, 325.4° - Sketch and find the displacement vector in standard position given the x-component is –45 cm and the y-component is –75 cm.
Answer:87.5 cm, 239°
Challenge Question
Image Attributions
- Figure 2.1 – 2.5: Created with Geogebra and licensed under CC-BY-NC-SA 3.0.

