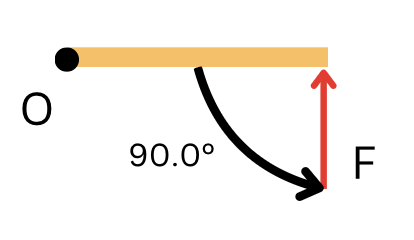
"

9.3. Practice Sets: Torque, Rotational Equilibrium

Chapter equations

[latex]\tau = F \times r \times \sin\theta[/latex]

[latex]\overrightarrow{\tau}_{\text{net}} = {\sum} \overrightarrow{\tau}[/latex]

[latex]\tau_{\text{net}} = {\sum} \tau[/latex] – called the first condition of equilibrium (linear equilibrium)

[latex]{\sum} \tau_{\text{CW}} = {\sum} \tau_{\text{CCW}}[/latex] – called the second condition of equilibrium (rotational equilibrium)

Try It!

  1. Which one is the correct statement? The torque created by a force gets bigger when:
    1. The applied force gets greater
    2. The distance from the force to the pivot point gets bigger
    3. The angle between the force and the pivot point gets closer to 90 degrees
    4. All of the above
  2. Which one is the correct statement?
    1. The net torque acting on a bar is positive. That means the bar will rotate CCW.
    2. The net torque acting on a bar is positive. That means the bar will rotate CW.
    3. Not enough information to establish which way the bar will rotate.
  3. Calculate the torque for the following situations, knowing that the length of the rod is [latex]3.4 \text{ m}[/latex] and the magnitude of the force is [latex]50 \text{ N}[/latex]:
    1. A 3.4 m rod is pivoted at the left end; a 50 N force is applied vertically upward at the right end, forming 90° angle.
    2. A rod is pivoted at the left end; a 50 N force is applied at 2.0 m from the right end at a 60° angle to the horizontal rod.
    3. A 3.4 m rod is pivoted at the left end with a 50 N force applied horizontally inward at the far right end.

Practice

  1. For the system in the figure below, calculate the net torque with respect to:
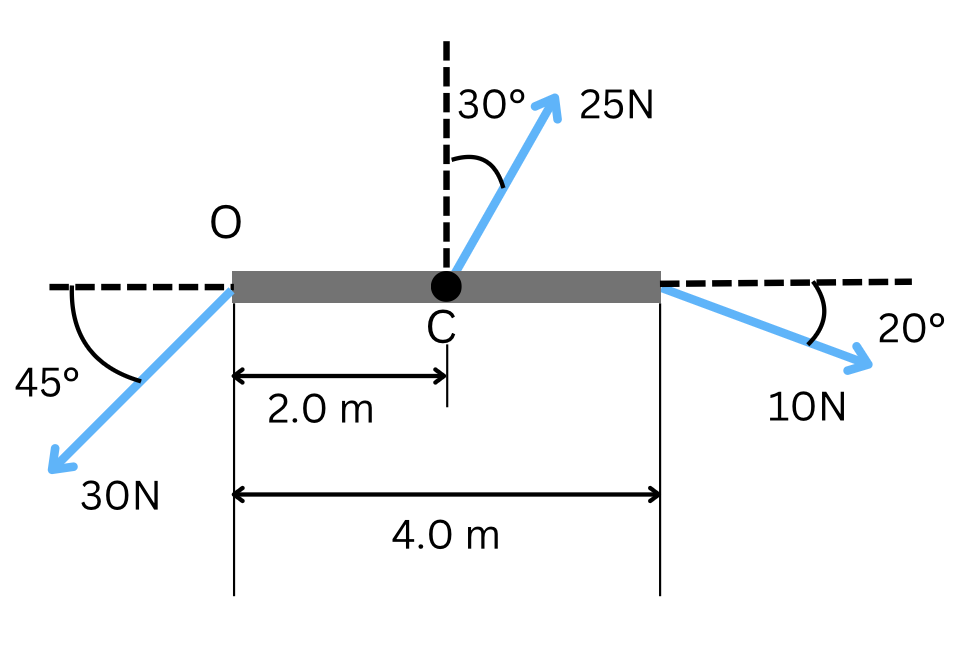
    A beam is acted on by three angled forces: 30 N at 45°, 25 N at 30°, and 10 N at 20°, with torque calculated about point O.
    1. Point O
      Answer:

      [latex]29.6\,\text{Nm}[/latex]
    2. Point C
      Answer:

      [latex]35.6\,\text{Nm}[/latex]
  2. A beam of [latex]7 \text{ kg}[/latex] and a length of [latex]1.5 \text{ m}[/latex] has 2 loads attached to it: one of [latex]2.0 \text{ kg}[/latex] at the left end of the beam and one of [latex]1.7 \text{ kg}[/latex] at [latex]1.2 \text{ m}[/latex] from the left end. The beam is suspended by a cable so that it maintains a horizontal position. Find the position of the cable (from the left end) so that the beam is in equilibrium (horizontal position).
    Answer:

    [latex]0.68\,\text{m}[/latex]
  3. A diver, who’s mass is [latex]55.0 \text{ kg}[/latex], is standing at the end of a [latex]7.0 \text{ m}[/latex] diving board, which has a mass of [latex]42.0 \text{ kg}[/latex]. What force must the bracket and fulcrum exert on the diving board? Show the direction of all forces on the diagram.
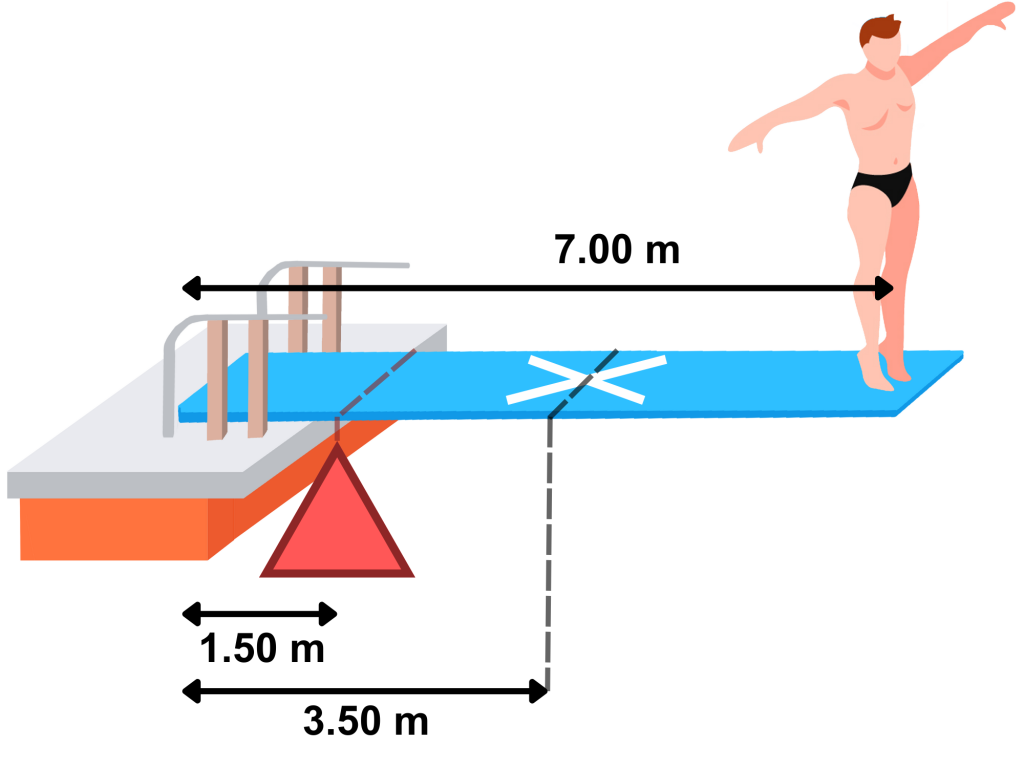
    A diver stands on a 7.0 m diving board supported by a bracket and a fulcrum; distances and forces are labeled clearly.

    Answer:

    [latex]F_f = 3475.7\,\text{N} - \text{up}, \quad F_b = 2525.1\,\text{N} - \text{down}[/latex]
  4. A meterstick has one weight hanging at its [latex]25 \text{ cm}[/latex] mark and another weight hanging at the [latex]68 \text{ cm}[/latex] mark. A person is trying to balance the meterstick on her hand. Where should she place her hand (at which mark) so that the meterstick is balanced? The mass of the first weight is [latex]0.023 \text{ kg}[/latex] and the mass of the second weight is [latex]0.045 \text{ kg}[/latex].
    Answer:

    [latex]0.53456\,\text{m}[/latex]

Challenge Question(s)

Given the diagram below, the tension in the cable is [latex]\text{T } = 12 \text{ N}[/latex], and the mass of the beam is [latex]3.5 \text{ kg}[/latex]. The system is in equilibrium.

Find:

  1. The mass of the box hanging on the right side of the beam.
  2. The upwards force that the fulcrum exerts on the beam.

Enter your answers by clicking on the blue circles in the diagram below.

Test Version of the Challenge Question(s)
  • Given the diagram above, the tension in the cable is [latex]\text{T } = 12 \text{ N}[/latex], and the mass of the beam is [latex]3.5 \text{ kg}[/latex]. The system is in equilibrium.
    a) Find the mass of the box hanging on the right side of the beam
    Answer: [latex]5.2\,\text{kg}[/latex]
  • Given the diagram above, the tension in the cable is [latex]\text{T } = 12 \text{ N}[/latex], and the mass of the beam is [latex]3.5 \text{ kg}[/latex]. The system is in equilibrium.
    b) Find the upwards force that the fulcrum exerts on the beam
    Answer: [latex]97\,\text{N}[/latex]

Image Attributions

License

Icon for the Creative Commons Attribution-NonCommercial 4.0 International License

College Physics – Fundamentals and Applications Copyright © by Daniela Stanescu, Centennial College is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License, except where otherwise noted.

Share This Book