"

9.1. Concepts: Torque; Rotational Equilibrium

Introduction

When a force acts on an object at a certain distance from a pivot or rotation point (or rotation axis), it is said that the force creates a torque. The torque will cause the object to either start rotating or accelerate/decelerate its original rotational motion.

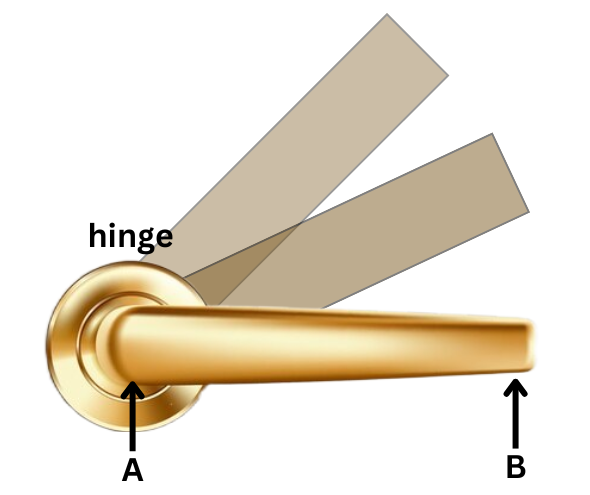
For instance, a force that we apply to the doorknob to open the door will create a torque that will determine the door to rotate with respect to its hinges, thus, to open (Figure 9.1 a).

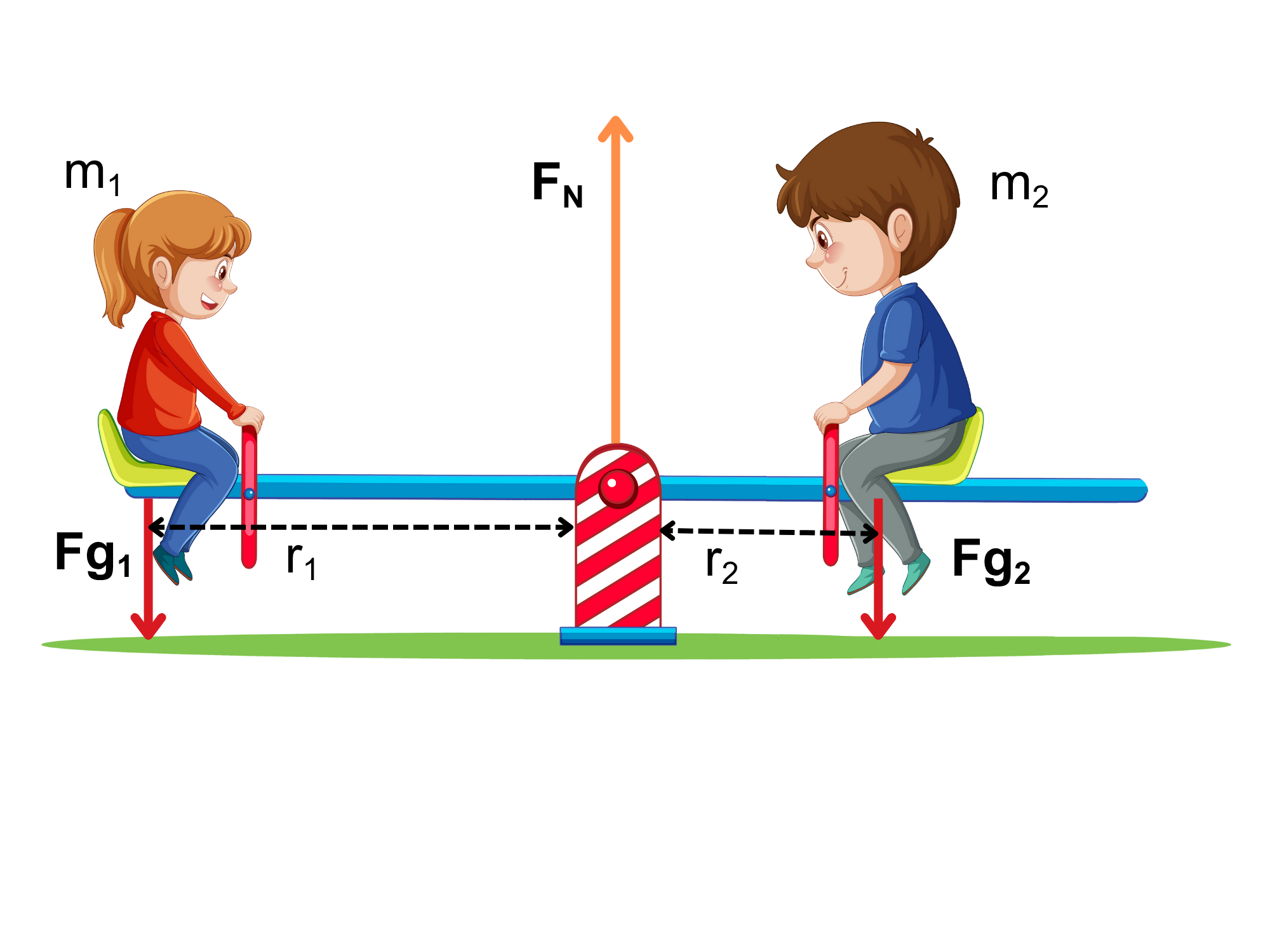
The weight of a child sitting on a seesaw will create a torque forcing the seesaw to rotate with respect to the pivot point. If a second child finds a certain position on the other side of the pivot point, rotational equilibrium can be achieved (Figure 9.1 b).

A gold door handle rotates around its hinge, with labeled arrows A and B showing torque direction and applied force.
A girl and boy sit on opposite ends of a seesaw in balance, with forces and distances from the pivot labeled for torque analysis.
Figure 9.1. a) A force applied in point B rotates the door to open; b) Balanced net torque (equilibrium situation).

Concepts

Consider a wrench used to tighten or loosen a bolt.

A force F is applied at an angle θ to a wrench, with vectors showing the force direction and distance from the rotation point.
Figure 9.2. Loosening a bolt using a wrench by applying a force F at a distance r from the pivot point

The force producing the torque is applied at a distance r from the point of rotation (the bolt). This distance, r, is called the arm of the force or the position vector; this is also a vector.

The components of the applied forces are:

[latex]F_x = F \times \cos\theta[/latex]  (1)

[latex]F_y = F \times \sin\theta[/latex]  (2)

We notice that [latex]F_x[/latex] will not produce any rotation since it is parallel to the arm of the force; hence the torque will be created by the y component of the force, [latex]F_y[/latex].

Torque is a vector quantity, so it is described by a magnitude and a direction.

The magnitude of the torque can be calculated as:

[latex]{\tau} = F \times r \times \sin\theta \text{ (3)}[/latex]

In Formula 3:

[latex]F[/latex] – represents the force applied to the object in [latex]\text{[N]}[/latex]

[latex]r[/latex] – represents the arm of the force in [latex]\text{[m]}[/latex]

[latex]\theta[/latex] – represents the angle between the force and the arm of the force

The unit for torque is [latex]\text{Nm}[/latex].

Torque depends on three factors (as it can be seen from formula 3):

  • The magnitude of the force (the bigger the force, the bigger the torque).
  • The arm of the force (the bigger the arm, the bigger the torque).
  • The angle between the force and the arm of the vector. The closer the angle gets to 90 degrees, the bigger the torque. When the angle is exactly 90 degrees, the torque becomes:

[latex]\tau = F \times r \times \sin 90^\circ = F \times r[/latex]

In this situation the torque is at its maximum value for a given force and arm of the force

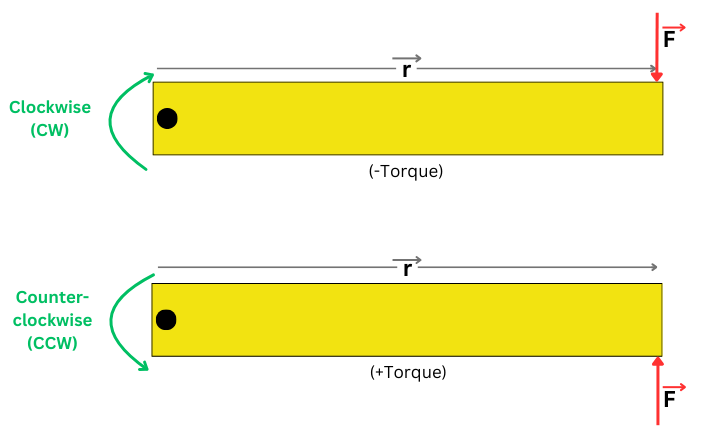
The direction of torque, by convention is:

  1. If the force tends to rotate the object clockwise (CW), the torque is considered negative.
  2. If the force tends to rotate the object counterclockwise (CCW), the torque is considered positive.
Two torque diagrams showing that clockwise torque from a downward force is negative and counterclockwise is positive.
Figure 9.3. Direction of torque

Net torque

When more than one force acts on an object producing torque, a net torque can be calculated. Similarly to the net force, the net torque is the vector sum of all torques acting on the object.

[latex]\overrightarrow{\tau}_{\text{net}} = \sum \overrightarrow{\tau}[/latex]  (4)

Image Attributions

License

Icon for the Creative Commons Attribution-NonCommercial 4.0 International License

College Physics – Fundamentals and Applications Copyright © by Daniela Stanescu, Centennial College is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License, except where otherwise noted.

Share This Book