"

7.1. Concepts: Force of Friction and Normal Force; Free Body Diagrams

Introduction

Friction is a common force in nature. It is a force that is created whenever two surfaces in contact move or try to move across each other. Friction is also a contact force (it appears when there is contact between two surfaces).

When we apply a pushing or pulling force on an object sitting on the floor, a force of friction will appear; the direction of this force will oppose the tendency of the object’s motion.

Concepts

There are two possible outcomes:

  1. The force is not big enough to overcome friction—the object will not move. Friction will be called static friction.
  2. The force is big enough to overcome friction—the object will start moving. Friction will be called kinetic friction.
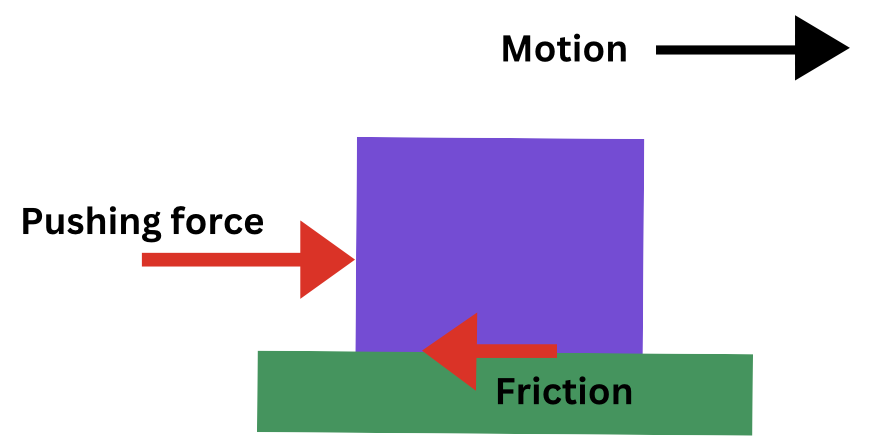
A block on a green surface being pushed to the right, with a rightward pushing force, leftward friction, and rightward motion.
Figure 7.1. Force of friction

The force of friction has the following properties:

  1. Friction is a contact force.
  2. Friction always opposes the motion of the object.
  3. Friction is dependent on the type and smoothness of the material of both surfaces in contact.
  4. Friction is dependent on the amount of contact force pushing the two surfaces together (called normal force).

The type and smoothness of the surfaces are described by the coefficient of friction. The coefficient of friction is defined as the ratio between the force of friction and the normal force:

[latex]\mu = \frac{{F_f}}{{F_N}}[/latex]

Since it is the ratio between two forces, coefficient of friction is unitless. Refer to Appendix 1 for values of coefficient of friction.

Coefficient of Static Friction

Static friction occurs when two surfaces try to move past each other. It can be thought of as the friction that prevents an object from sliding on a surface. For instance, a person pushing a box on the floor when the box is not moving, is an example of static friction.

Using the coefficient of static friction, the force of friction can be calculated as:

[latex]F_f = \mu_s F_N[/latex]

Coefficient of Kinetic Friction

Kinetic friction occurs when two surfaces move past each other. It can be thought as the force that makes it harder for an object to slide on a surface. For instance, a crate moving while pulled on a level floor is an example of kinetic friction.

Using the coefficient of kinetic friction, the force of friction can be calculated as:

[latex]F_f = \mu_k F_N[/latex]

Analyzing the motion with friction

Example 1: Horizontal contact surface

Assume a brick is being pulled with a force F across a horizontal floor. A force of friction will develop acting in the opposite direction of the motion.

The first step in analyzing the motion is to create a free body diagram (FBD) appropriate for the situation.

A free body diagram is a graphical representation of the object and of all external forces acting on it.

To create a free body diagram and to analyze the motion of the object, follow these steps:

  1. Remove the object from its surroundings.
  2. Assign a frame of reference (x and y axes).
  3. Draw all external forces acting on the object.
  4. Resolve forces on the x and y axis.

An example of a FBD is represented below; in this situation, a box is being pulled on the floor by a force F that makes an angle θ with the horizontal.

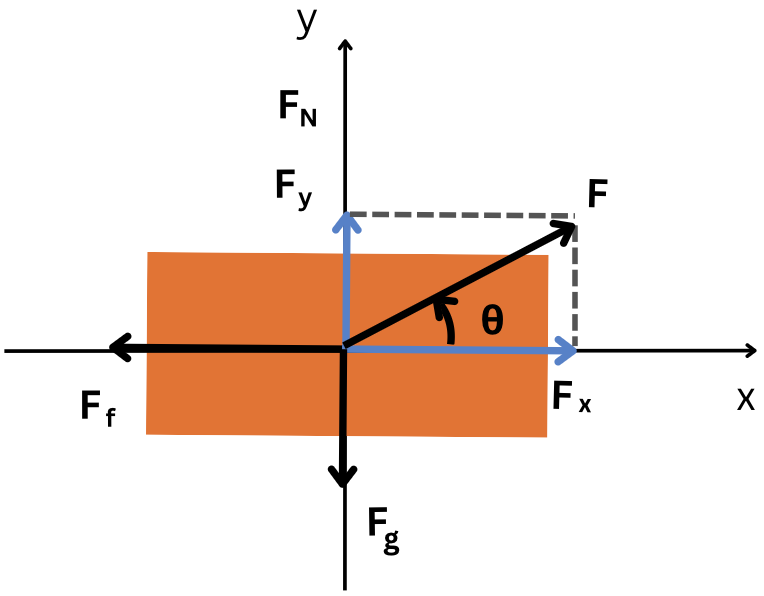
Free-body diagram of a block on a horizontal surface with applied force F at an angle, and force components Fx and Fy.
Figure 7.2. FBD for an object pulled on a horizontal floor

In Figure 7.2:

[latex]F[/latex] – represents the pulling force. The force is not on the x or y axis, so it needs to be resolved on the axes (components, [latex]F_x[/latex] and [latex]F_y[/latex], need to be drawn on the FBD and calculated)

[latex]F_f[/latex] – represents the force of friction (opposite to the motion)

[latex]F_g[/latex] – represents the force of gravity (always directed towards the ground)

[latex]F_N[/latex] – normal force (the reaction to the force of gravity). The normal force is always perpendicular to the contact surface.

Example 2: Vertical contact surface

An object is being pushed against a vertical wall (Figure 7.3).

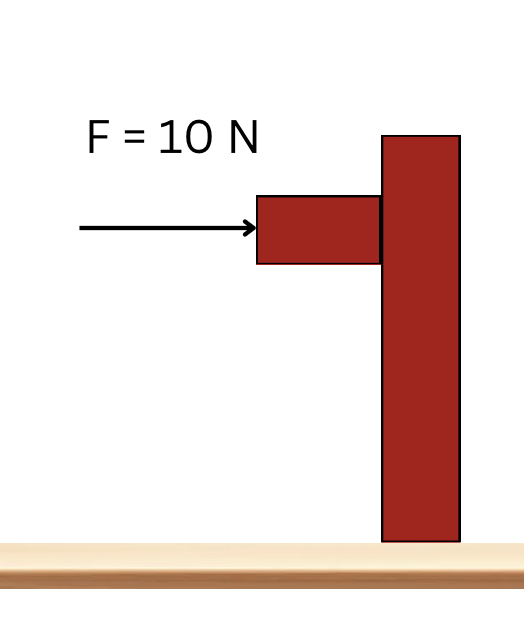
A horizontal 10 N force pushes the top of a two-block object against a vertical wall.
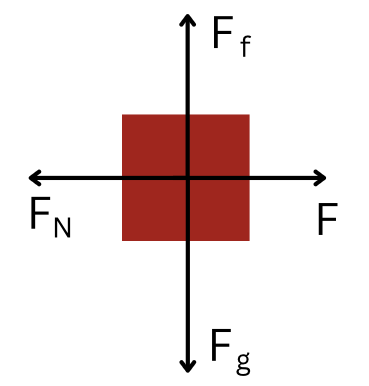
Free-body diagram showing an object pressed against a vertical wall with four labeled forces: F, FN, Fg, and Ff.
Figure 7.3. FBD for an object pressed against a vertical wall

In Figure 7.3:

[latex]F = 10 \text{ N}[/latex] – represents the pushing force.

[latex]F_f[/latex] – represents the force of friction (opposite to the motion). The object has a normal tendency to slide down; force of friction will oppose this tendency of motion, therefore being directed upwards.

[latex]F_g[/latex] – represents the force of gravity (always directed towards the ground).

[latex]F_N[/latex] – normal force (the reaction to the pushing force). The person pushes with a force F on the wall; the wall reacts with a force equal in magnitude and opposite in direction – normal force. The normal force is always perpendicular to the contact surface.

Example 3: Inclined contact surface

A brick sits on an inclined plane that makes an angle [latex]\theta[/latex] with the horizontal.

The FBD to analyze the motion in this case is:

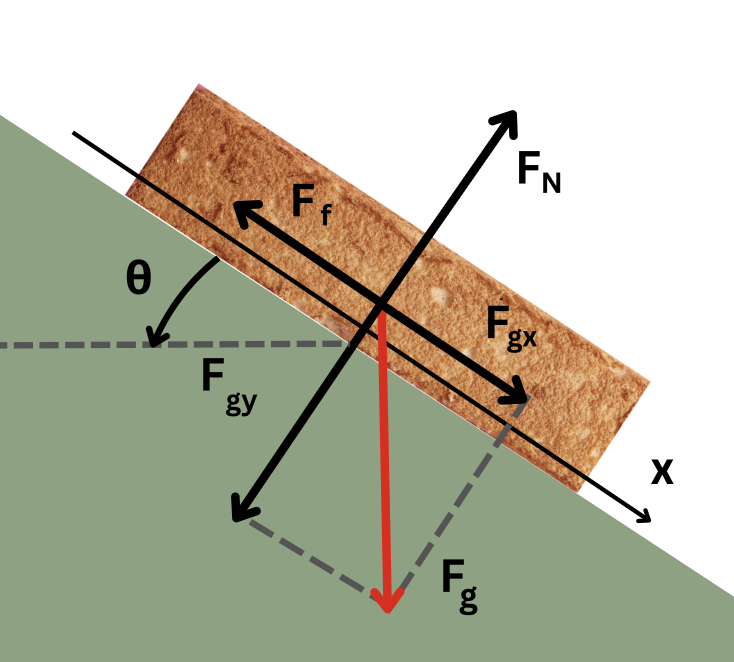
Free-body diagram of a brick on an inclined plane, showing gravity, friction, normal force, and gravity components Fgx and Fgy.
Figure 7.4. FBD for an object at rest on a ramp that makes an angle θ with the horizontal

In Figure 7.4:

[latex]F_g[/latex] – represents the force due to gravity (resolved on the x and y axes to [latex]F_{gx}[/latex] and [latex]F_{gy}[/latex])

[latex]F_f[/latex] – represents the force of friction (opposes the natural tendency of the object sliding down the incline due to the x component of gravity)

[latex]F_N[/latex] – represents normal force (always perpendicular to the contact surface – here the ramp)

Image Attributions

License

Icon for the Creative Commons Attribution-NonCommercial 4.0 International License

College Physics – Fundamentals and Applications Copyright © by Daniela Stanescu, Centennial College is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License, except where otherwise noted.

Share This Book