6.1. Concepts: Introduction to Forces; Newton’s Laws
Introduction
What is force? Any force can be defined as a pull or a push. A force can change the state of motion of an object. It may change the shape of an object. We encounter forces in nature, such as: friction, weight, normal force, etc.
The SI unit of force is the newton (N).
Example
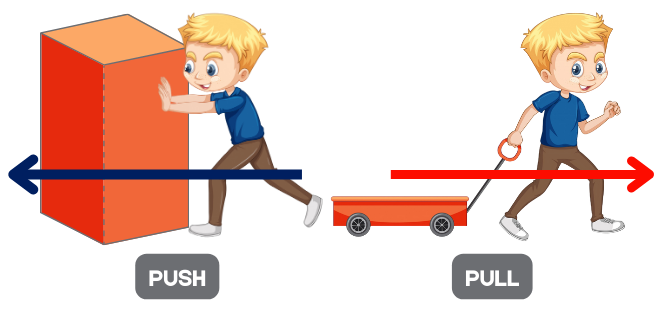
The two children in the figure below are both applying a force to a brick. The child on the left is pushing with a force F and the child on the right is pulling with the same force F. The result of applying that push or pull can be any of the following (depending on the magnitude of the force, the type and roughness of the surfaces, the previous state of motion of the object, etc.):
- The brick was at rest and remains at rest.
- The brick was at rest, and it starts moving.
- The brick was in uniform motion and it either accelerates or decelerates when the force is applied.
All these situations will be discussed in Chapter 6 and Chapter 7.
Concepts
In many real-life situations, multiple forces are applied on an object. In these situations, we need to consider the effect of all forces acting on the object in order to analyze their combined effect.
The combined effect of all external forces acting on an object is described by the net force. The net force represents the vector sum of all forces acting on a particular object:
[latex]\vec F_{\text{net}} = \sum \normalsize \vec F[/latex]
This means the net force will be calculated by the vector addition of forces (as we have seen in Chapter 3).
Example
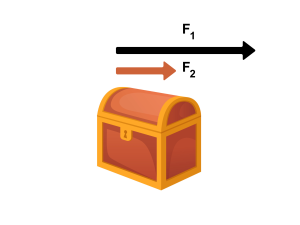
In the figure below, consider the treasure chest, which is pushed/pulled as follows. The net force is indicated for each situation.
[latex]F_1[/latex]= 50 N
[latex]F_2[/latex]= 20 N
[latex]F_{net} = F_1 + F_2[/latex] = 70 N (to the right)
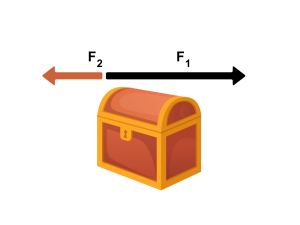
[latex]F_1[/latex]= 50 N
[latex]F_2[/latex]= 20 N
[latex]F_{net} = F_1 - F_2[/latex] = 30 N (to the right)
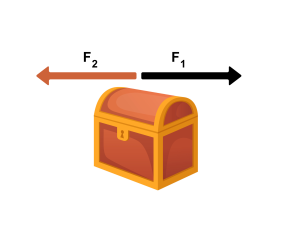
[latex]F_1[/latex]= 35 N
[latex]F_2[/latex]= 35 N
[latex]F_{net}[/latex]= 0 N
When [latex]F_{net}[/latex]= 0 N, we have an equilibrium situation.
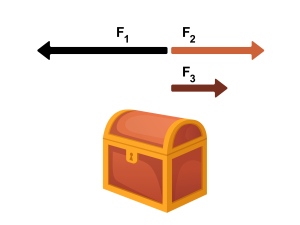
[latex]F_1[/latex]= 50 N
[latex]F_2[/latex]= 30 N
[latex]F_3[/latex]= 17 N
[latex]F_{net}[/latex] = -3 N, (to the left)
Newton’s Laws
Newton’s First Law
Every object at rest or in a state of uniform motion tends to remain in that state of motion unless acted upon an unbalanced net force.
When an object is subjected to a net force equal to zero, the object is said to be in equilibrium. There are two situations of equilibrium (according to Newton’s first law):
- The object is at rest [latex]( v = 0 )[/latex]
- The object is moving at a constant speed [latex]( v = constant; a = 0 )[/latex]
Example
A puck sitting on the ice is an example of an object at rest tending to remain at rest if no unbalanced net force acts on it. If we hit the puck, we upset the balanced net force acting on it; if the hitting force overcomes the friction with the ice, then the puck will change its state of motion. That is because the net force will not be balanced anymore (will not be zero any more).
Newton’s Second Law
The acceleration of an object is produced by a net force and is directly proportional to the magnitude of the net force, and inversely proportional to the mass of the object.
In formula 1:
[latex]a[/latex] – represents the acceleration of the object in [latex][\text{m/s}^2][/latex]
[latex]F_{net}[/latex] – represents the force in [N]
[latex]m[/latex] – represents the mass of the object in [kg]
Example
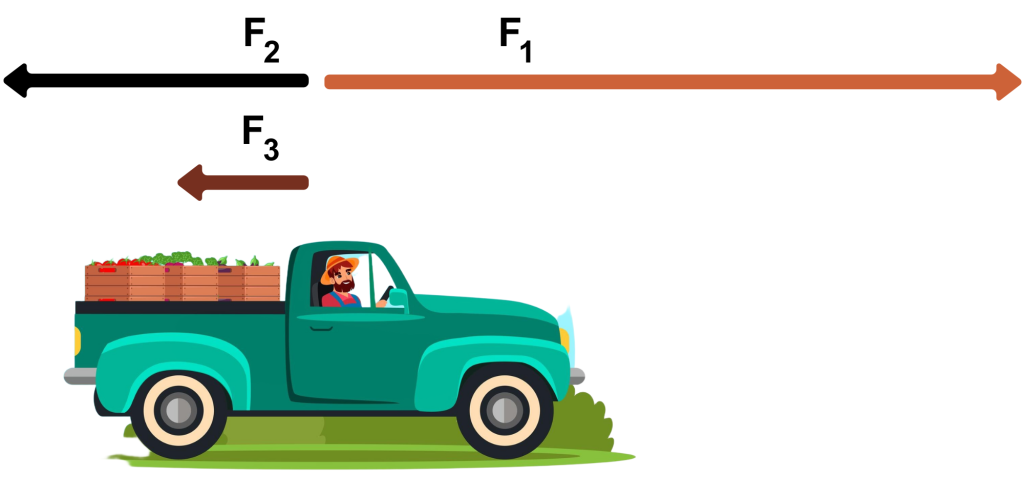
A 1700 kg truck is subjected to the forces shown in the diagram below, where [latex]F_1[/latex]= 1000 N, and [latex]F_3[/latex]= 200 N.
- If the acceleration of the truck is zero, how big is [latex]F_2[/latex]?
Applying Newton’s second law:
[latex]a = \frac{F_{\text{net}}}{m}[/latex], when [latex]a[/latex] = 0, [latex]F_{net}[/latex] = 0.
Since [latex]F_{net}[/latex] = [latex]F_1[/latex] – [latex]F_2[/latex] – [latex]F_3[/latex] = 0,
[latex]F_2[/latex] = 800 N. - If [latex]F_2[/latex] is now 300 N, what is the new acceleration of the truck?
Applying Newton’s second law:
[latex]a = \frac{F_{\text{net}}}{m}[/latex], where [latex]F_{net}[/latex] = 1000 – 300 – 200 = 500 N.
[latex]a = \frac{F_{\text{net}}}{m} = \frac{500}{1700} = \text{0.29 m/s}^2[/latex]
Weight
When we apply Newton’s second law to weight:
[latex]W = m[/latex] x [latex]a[/latex] (2)
but [latex]a = g[/latex] (acceleration due to gravity)
Therefore:
[latex]W = m[/latex] x [latex]g[/latex] (3)
Weight is also called the force due to gravity, and another form for formula (3) is:
[latex]F_g = m[/latex] x [latex]g[/latex] (4)
Newton’s Third Law
For every action there is an equal and opposite reaction.
One simple example of Newton’s third law is a book sitting on a table (Figure 6.4). The book pushes down on the table with the force of gravity (the book’s weight) while the table pushes back upwards with a force that we call normal force (a reaction force).
Image Attributions
- Figure 6.1 adapted from:
- A boy pushing an object designed by Freepik.
- A boy pulling a wagon designed by Freepik.
- Figure 6.2 adapted from:
- Wooden Chest Box designed by Freepik.
- Figure 6.3 adapted from:
- Farmer Driving a Vegetable Truck designed by Freepik.
- Figure 6.4 adapted from:
- A Wooden Table designed by Freepik.
- An Open Book designed by Freepik.
