"

5.1. Concepts: Free Fall

Introduction

An object falling freely from a certain height is undergoing free fall motion. If first we assume that air resistance is negligible, the only force acting on the object is the force of gravity, meaning that the object will accelerate towards the surface of the Earth with an acceleration due to gravity: [latex]g = 9.8 \, \text{m/s}^2[/latex].

If air resistance is now taken into consideration, then the object will be subjected to two forces:

  • Gravity
  • Air resistance

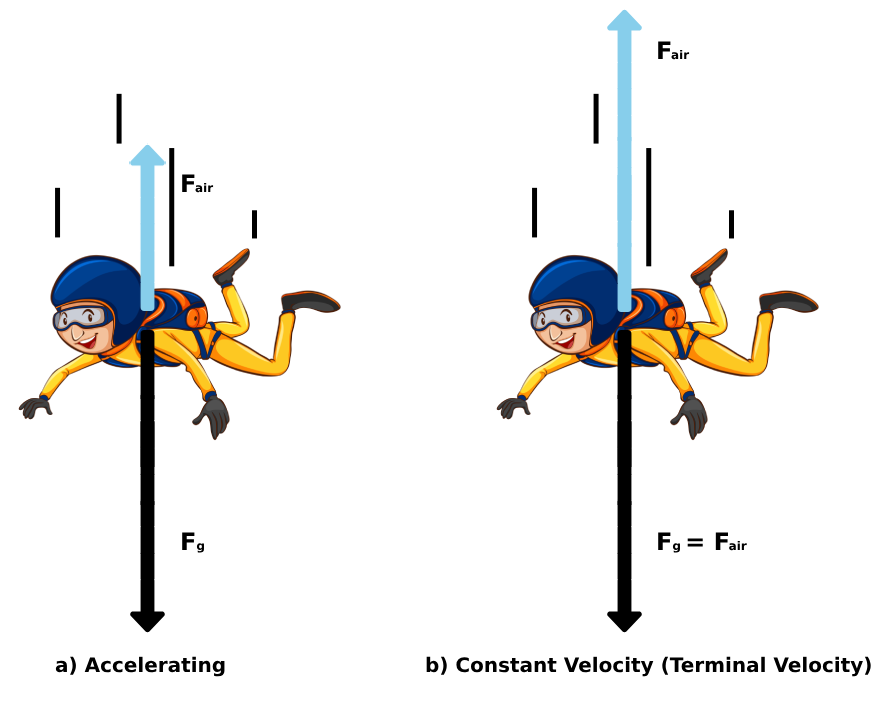
Initially, the force of gravity will be greater than that exerted by air resistance (Figure 5.1 a).

Air resistance increases during the fall (it is directly proportional to the square of the speed), so as the speed of the falling object increases, at some point air resistance might become equal to the force of gravity.

When this happens, the object will continue falling at a constant velocity, called the terminal velocity (Figure 5.1 b).

Two skydivers: one on the left is accelerating with larger gravity (Fg) than air resistance (Fair), while the right shows terminal velocity with equal forces.
Figure 5.1 Free fall motion with air resistance

Concepts

There are several real-life situations that are considered free-falling motions:
  1. Throwing an object upwards: the object reaches a maximum height, then comes back to either the same level from which it started or to a different level (for instance, it falls onto another object, it is caught before reaching the initial level on its way back, etc.).
  2. Throwing an object downwards.
  3. Dropping an object from a height.
Regardless of the situation, free-fall motion is described by the same formulas as accelerated motion. That is because:
  1. On its way upward, an object will decelerate with an acceleration equal to [latex]g = 9.8 \, \text{m/s}^2[/latex] (the acceleration due to gravity) until it reaches the maximum height. At the maximum height, the instantaneous velocity is zero.
  2. On its way downward, an object will accelerate with an acceleration equal to [latex]g = 9.8 \, \text{m/s}^2[/latex] (the acceleration due to gravity).
It follows that all the equations used for accelerated motion apply to the free-fall motion with the note that acceleration is always [latex]{g = 9.8 \, \text{m/s}^2}[/latex] near the surface of the Earth. On another planet, the value of acceleration due to gravity will change.

Example

On the surface of the Moon, the acceleration due to gravity is approximately 6 times less than that on Earth. Throwing an object upwards with velocity [latex]v_i[/latex].

Notations and analysis of the motion

A physics diagram showing a projectile motion trajectory, with points labeled 1 (start), 2 (peak), and 3 (end). Variables include initial velocity (vi), max height (hmax), gravity (g), and final velocity (vf).
Figure 5.2 Free-fall motion notations

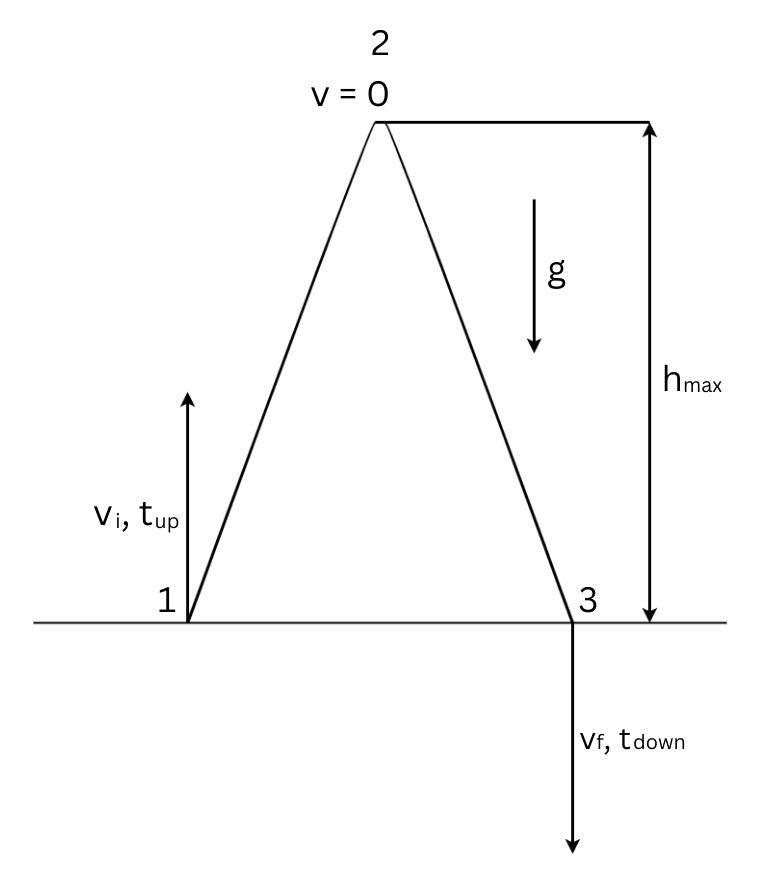
Notations

[latex]\large v_{i, f}[/latex] – represent the object’s initial velocity and final velocity respectively.

[latex]\large v[/latex] – represents the velocity at the maximum height (equal to zero).

[latex]\large h_{max}[/latex] – represents the maximum height reached by the object.

[latex]\large t_{up, down}[/latex] – represent the time needed to reach the maximum height and the time to come back down from the maximum height respectively.

[latex]\large g[/latex] – represents acceleration due to gravity.

Analysis of the motion

From point 1 to point 2 (see Figure 5.2):
To calculate the maximum height, we use the following equation:

[latex]v_{\large f}^2 = v_{\large i}^2 + 2aS[/latex]

which becomes:

[latex]v_{\large f}^2 = v_{\large i}^2 - 2gh_{\text{max}}[/latex]   (1)

The acceleration is negative because the object loses speed when going upward (decelerated motion).

From equation (1), the maximum height becomes:

[latex]h_{\large \text{max}} = \frac{\large v_{\large i}^2}{2g}[/latex]   (2)

From point 2 to point 3 (see Figure 5.2):

On its way down, the object will come back down from the maximum height, where the velocity is zero, to the same level where it started.

We can express the maximum height using the same formula above:

[latex]v_{\large f}^2 = v_{\large i}^2 + 2aS[/latex]

which becomes:

[latex]v_{\large f}^2 = v_{\large i}^2 + 2gh_{\large \text{max}}[/latex]   (3)

In this case [latex]v_{\large i} = 0[/latex], and the acceleration is positive, which means:

[latex]h_{\large \text{max}} = \frac{\large v_f^2}{2g}[/latex]   (4)

Since expressions (2) and (4) represent the same quantity, they are equal.

Conclusion

The initial velocity (at the time of the throw) is equal to final velocity (at the time the object reaches the same level on its way down).

Using this concept, it can be shown that the time to reach the maximum height is equal to the time to come back from the maximum height to the same level.

So, the following equations can be used in solving problems of free fall:

[latex]\large v_i = v_f[/latex]   (5)
[latex]\large t_{\text{up}} = t_{\text{down}}[/latex]   (6)

An important note!

The equations above are true ONLY for situations in which the object returns to the same level from which it started.

Image Attributions

License

Icon for the Creative Commons Attribution-NonCommercial 4.0 International License

College Physics – Fundamentals and Applications Copyright © by Daniela Stanescu, Centennial College is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License, except where otherwise noted.

Share This Book