4.1. Concepts: Linear Motion
Introduction
Linear motion is a change in position from one point to another in a straight line in one dimension.
Examples of linear motion are driving on a straight highway, walking on a straight path in a park, and so on.
If the speed at which the object travels does not change in time (i.e., remains constant), then the motion is called uniform linear motion. If the speed changes over time (either increasing or decreasing) then the motion is called accelerated linear motion.
Concepts
- 4.1 Displacement
- 4.2 Velocity
- 4.3 Acceleration
4.1.1 Displacement
Displacement is the vector equivalent of distance, and it can be represented as the line that connects the starting point to the end point of the motion.
Example
Suppose a bee flies from the forest (point A) to the hive (point B) following the dotted orange path. Measuring the length of this path will indicate the distance travelled by the bee. The displacement, though, will be the vector that connects point A to point B; this displacement will have a magnitude equal to the length of the vector [latex]\overrightarrow{AB}[/latex] and the direction indicated by the arrow of the vector.
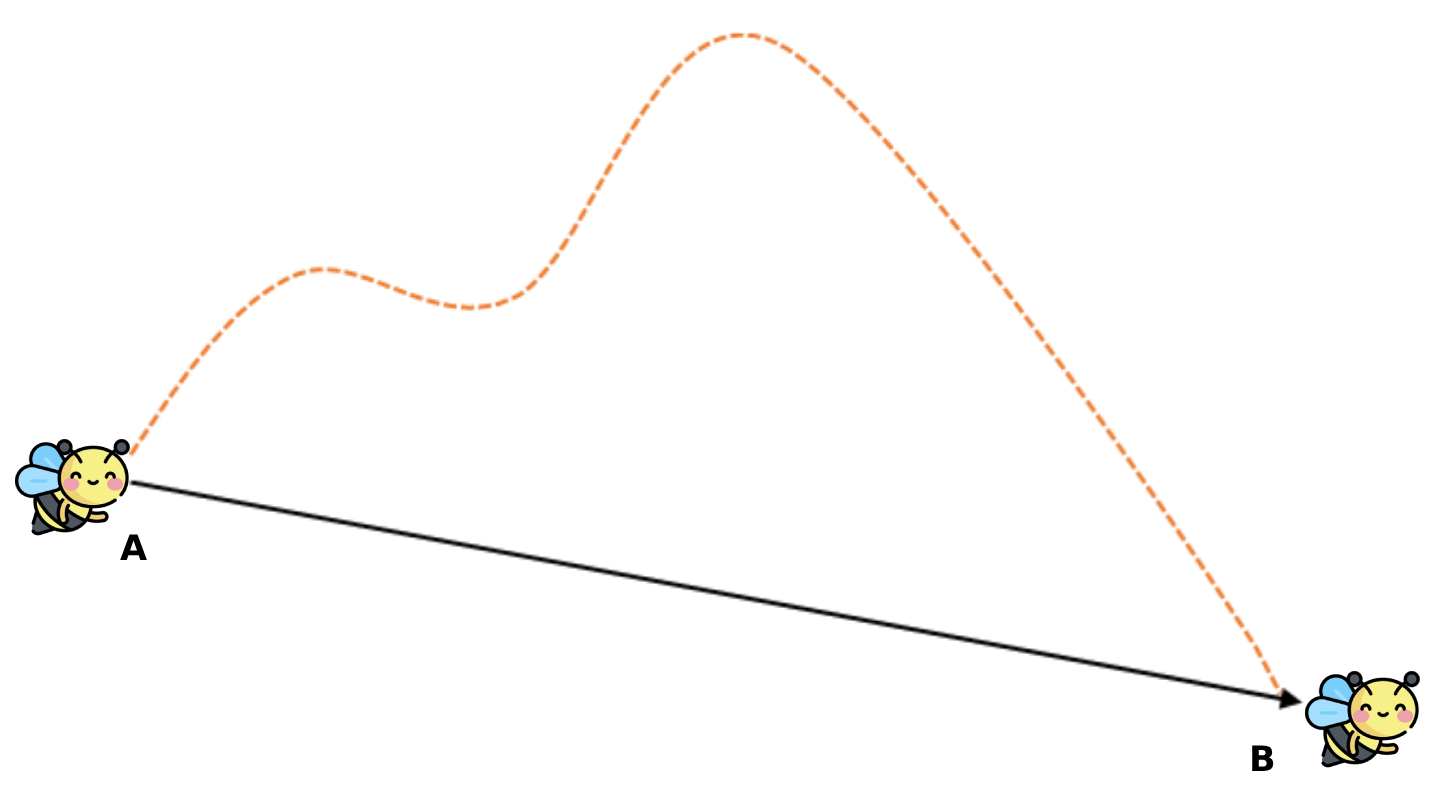
In the SI system, displacement is measured in meters (m). Prefixes are used to represent smaller or greater displacements, such as centimetres, kilometres, etc.
4.2 Velocity
Velocity is a vector quantity that represents the distance travelled in a certain amount of time (i.e., it describes how fast objects move). Velocity is the vector equivalent of speed.
The average speed can be calculated as:
[latex]v_{\text{average}} = \frac{s}{t}[/latex]
where:
[latex]s[/latex] - represents the distance in [latex][\text{m}][/latex] and [latex]t[/latex] represents the time in [latex][\text{s}][/latex]
It follows that speed will be measured in [latex][\text{m/s}][/latex].
There are two types of linear motion (decided by the qualities of speed or velocity):
- If the velocity stays constant during the motion (i.e., does not change in magnitude or direction), the motion is called uniform linear motion: [latex]\boldsymbol{\mathcal{v}} = \text{constant}[/latex].
- If the velocity changes in magnitude during the motion (either increases or decreases), the motion is called accelerated linear motion: [latex]\boldsymbol{\mathcal{v}} \neq \text{constant}[/latex].
In the second case, there is another quantity that will describe the motion: the acceleration.
4.3 Acceleration
Acceleration is a vector quantity that represents the rate of change for the velocity in an accelerated linear motion.
The acceleration can be calculated as:
[latex]a = \frac{\Delta v}{t} = \frac{v_{f} - v_{i}} {t}[/latex] (1)
where:
[latex]{\Delta v}[/latex] - represents the change in velocity in [latex][\text{m/s}][/latex]
[latex]t[/latex] - represents the time in [latex][\text{s}][/latex]
[latex]v_f[/latex] - represents the final velocity in [latex][\text{m/s}][/latex]
[latex]v_i[/latex] - represents the initial velocity in [latex][\text{m/s}][/latex]
[latex]a[/latex] - represents the acceleration in [latex][\text{m/s}^2][/latex]
In the formula above, the change in velocity is calculated by subtracting the initial velocity from the final velocity.
Acceleration can be positive or negative. In the figures below, if the car is increasing its velocity, the acceleration is positive; if the car is decreasing its velocity, the acceleration will be negative.
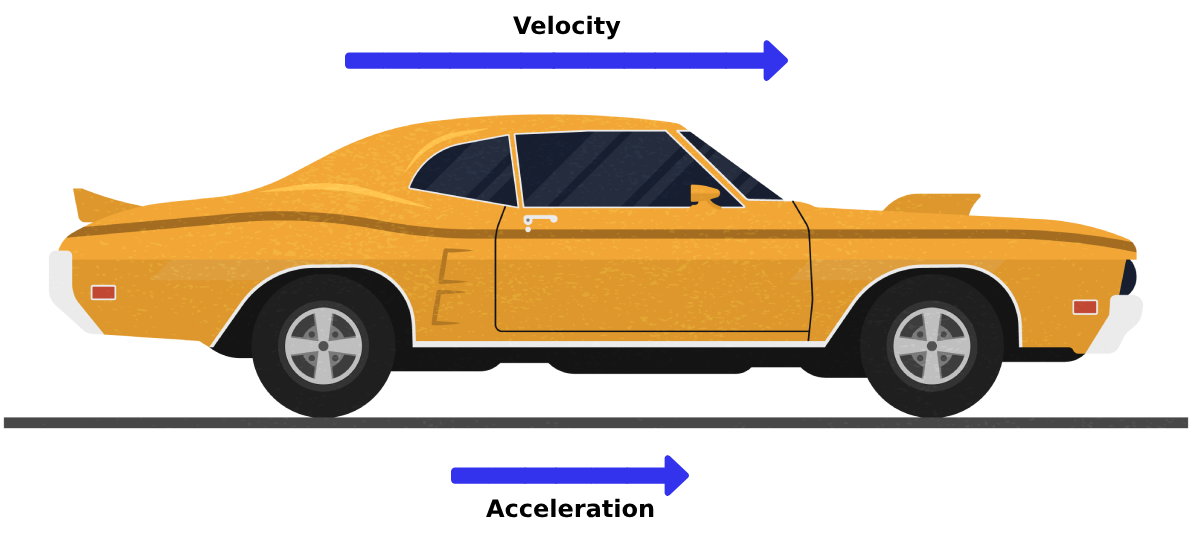
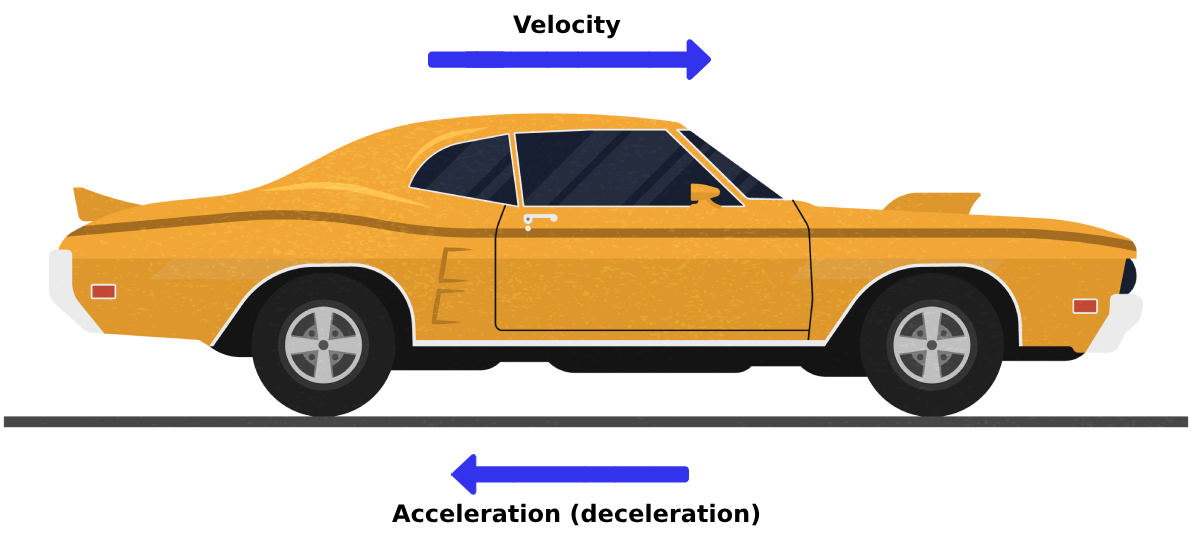
Identifying the initial and the final velocity in linear motion questions
Example 1. A car accelerates from [latex]10 \, \text{m/s}[/latex] to [latex]20 \, \text{m/s}[/latex] in [latex]10 \, \mathrm{s}[/latex].
[latex]v_i[/latex] = [latex]10 \, \mathrm{m/s}[/latex]
[latex]v_f[/latex] = [latex]20 \, \mathrm{m/s}[/latex]
Example 2. A train accelerates from rest to [latex]50 \, \mathrm{km/h}[/latex] in 5 minutes.
[latex]v_i[/latex] = [latex]0 \, \mathrm{km/h}[/latex]
[latex]v_f[/latex] = [latex]50 \, \mathrm{km/h}[/latex]
Example 3. A runner going at [latex]2.0 \, \mathrm{m/s}[/latex] slows to a stop in [latex]4 \, \mathrm{s}[/latex].
[latex]v_i[/latex] = [latex]2.0 \, \mathrm{m/s}[/latex]
[latex]v_f[/latex] = [latex]0 \, \mathrm{m/s}[/latex]
Using the initial and final velocity in an accelerated linear motion, we can express the displacement:
[latex]S = \frac{v_{i} + v_{f}}{2} \times t[/latex] (2)
Combining formulas (1) and (2), we can derive two more formulas for the accelerated linear motion:
[latex]S = v_{i} t + \frac{1}{2} a t{^2}[/latex] (3)
[latex]v_{f}{^2} = v_{i}{^2} + 2aS[/latex] (4)
Image Attributions
- Figure 4.1 adapted from:
- Figure 4.2 and 4.3 adapted from:
- Hand drawn muscle car illustration designed by Freepik

