12.2. Solved Examples: Transmitting rotational motion through gears
Example 1.
Consider the system of gears below. Find the speed of gear 6 (in rpm).
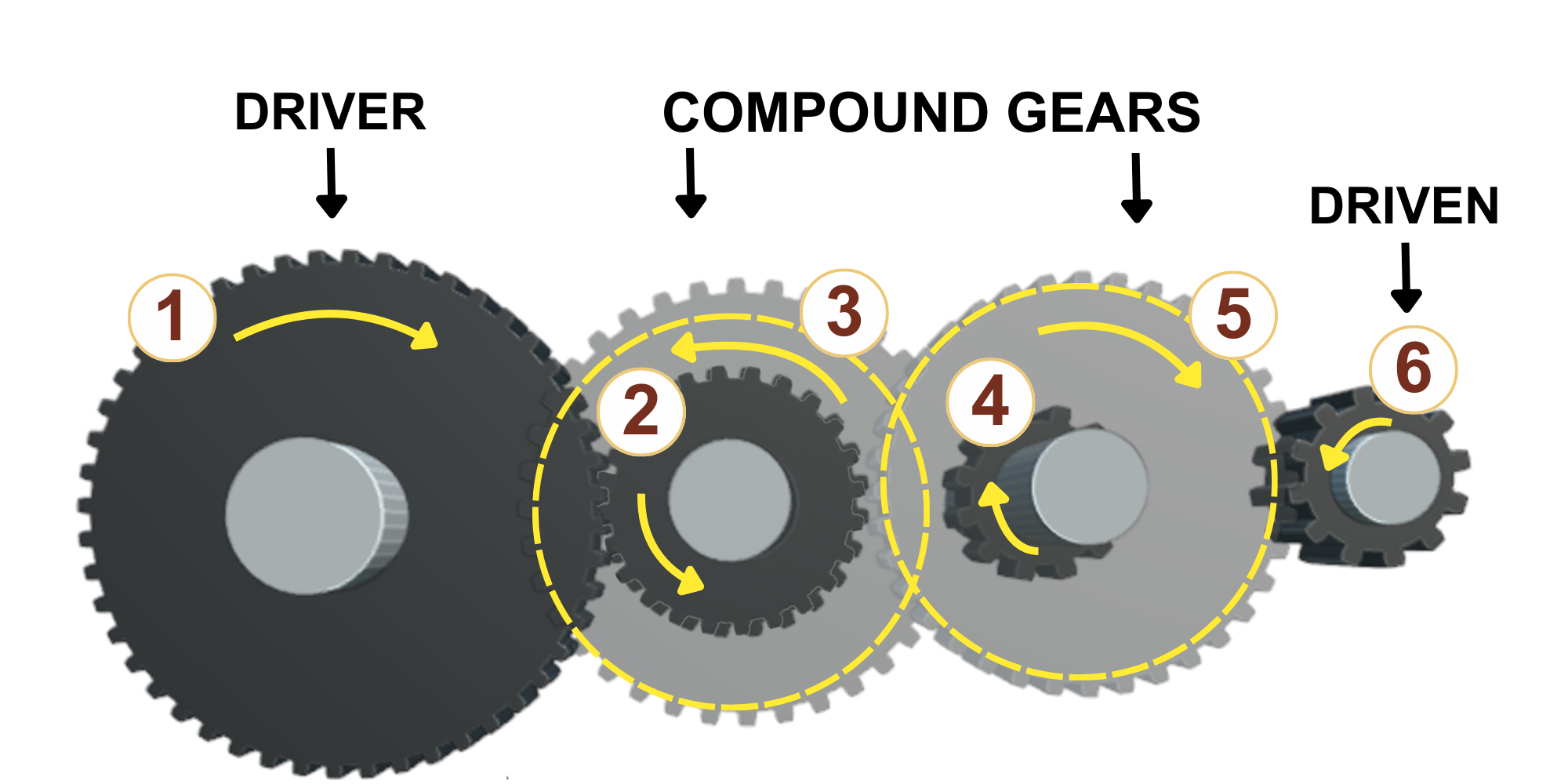

| Gear 1 | Gear 2 | Gear 3 | Gear 4 | Gear 5 | Gear 6 | |
|---|---|---|---|---|---|---|
| Number of teeth | 41 | 23 | 37 | 19 | 29 | 17 |
| Rotational Speed [rpm] | 85 rpm | ? |
Solution:
To apply equation (7) in solving the system, we need to decide which gears are drivers and which are driven.
Drivers: 1, 3, 5
Driven: 2, 4, 6
The equation becomes:
[latex]N \times T_1 \times T_3 \times T_5 = n \times t_2 \times t_4 \times t_6[/latex]
Rearranging for n, we get:
[latex]n = {\frac{n \times T_1 \times T_3 \times T_5}{t_2 \times t_4 \times t_6}} = {\frac{85 \times 41 \times 37 \times 29}{23 \times 19 \times 17}} = 503.35 \text{ rpm}[/latex]
Example 2.
Consider the system below, for which gear A has 45 teeth and rotates at 200 rpm, gear B has 51 teeth, and gear C rotates at 150 rpm. Find the number of teeth for gear C.
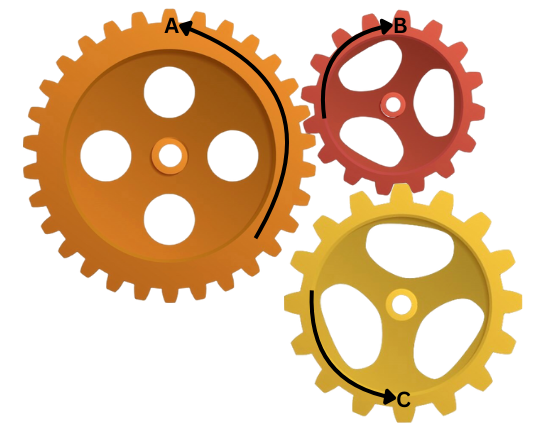
Solution:
To apply equation (7) in solving the system, we need to decide which gears are drivers and which are driven.
Drivers: A, B
Driven: B, C
Note: In this situation gear B has both driver and driven functions.
The equation becomes:
[latex]N \times T_A \times T_B = n \times t_B \times t_C[/latex]
Rearranging for [latex]t_c[/latex], we get:
[latex]t_C = {\frac{n \times T_A}{n}} = 60 \text{ teeth}[/latex]
Image Attributions
- Example 1 adapted from:
- Gears V2.0 by Helindu courtesy of Sketchfab, CC BY 4.0
- Example 2 adapted from:
- Colored cogwheels background designed by Freepik

