1.1. Concepts: Units and Unit Conversions; Systems of Measurement
Introduction
In industrial settings and in real life, we are exposed to a lot of information regarding the size of various physical quantities. This size can present itself in the form of a length, area, speed, etc. To be able to interpret and make sense out of these quantities we need to use a standardized system of units. These units help us describe and compare physical quantities in a meaningful way.
The magnitude (size) of a physical quantity does not tell the whole story if it is not accompanied by a unit. For example, if we say that a crate is subjected to a horizontal pulling force of 120, we do not know the amount of force, since the information could mean: [latex]120 \text{ N}[/latex], [latex]120 \text{ lbs}[/latex], [latex]120 \text{ MN}[/latex], [latex]120 \text{ kN}[/latex], etc. Unless followed by a unit, the magnitude is not helpful in any calculations, conclusions, or interpretations.
Concepts
1. Systems of measurements
The main systems of measurement used in North America are the SI system and the imperial system (British or American system). SI (International System of Measurement) is the latest form of the metric system. It is a convenient system because conversions between metric units can be done simply by moving the decimal place of a number. This is because the metric prefixes are powers of 10. For instance, there are [latex]1000 \text{ (or } 10^3\text{) m in 1 km}[/latex], [latex]0.000001 \text{ m (or } 10^{-6} \text{ m) in } 1 \,\mu\text{m}[/latex], etc.
Prefixes help with expressing very large or very small quantities, without having to introduce new units. For instance, in the construction industry we would use metres or centimetres to express lengths, but in the road building industry we would use kilometres to express the same physical quantity – length.
Figure 1.1 shows some examples of prefixes and conversions from one unit of length to another. For instance, to convert from km to m we multiply by 1000, whereas converting from m to km would require dividing by 1000.
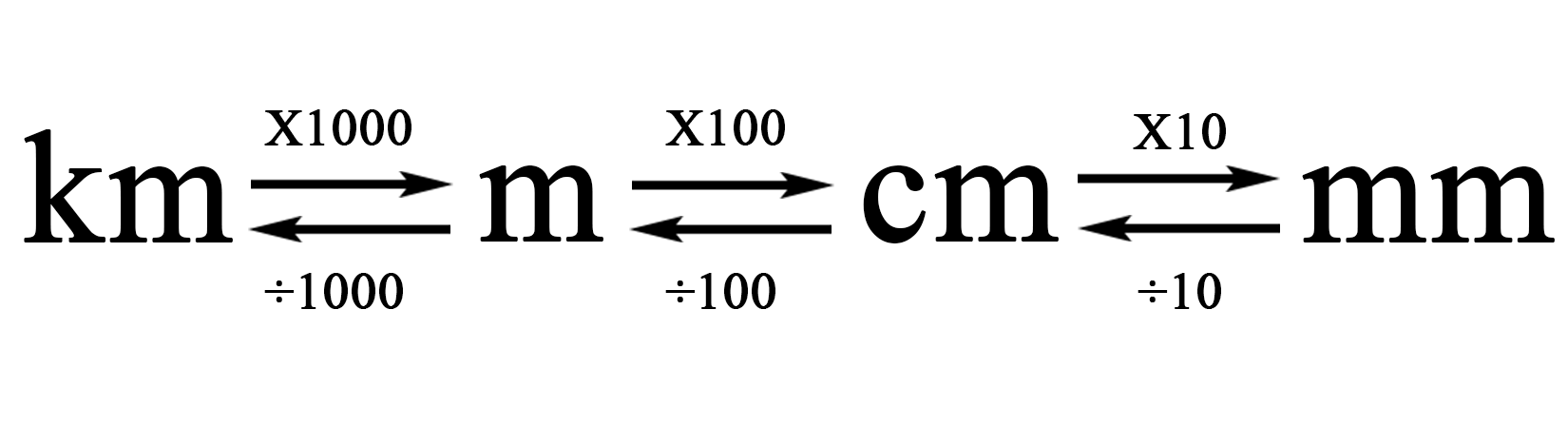
In the imperial system, the relationships are less simple. For instance, there are 12 inches in a foot, 3 feet in a yard, 1,760 yards in a mile, and so on.
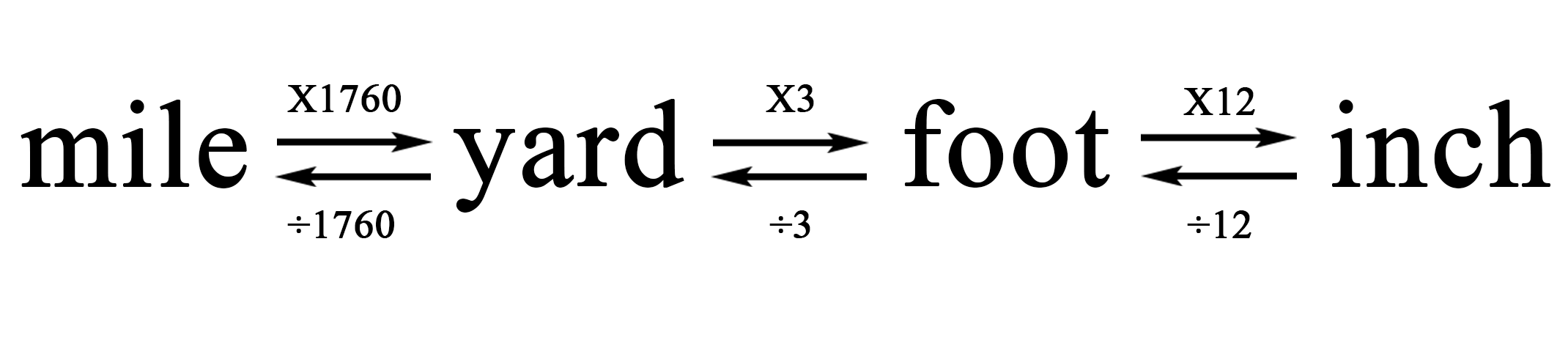
The SI system contains three main elements:
- Base units
- Derived units
- Prefixes
The table below represents the seven basic units of the SI system.
| Quantity | Unit Name | Unit Symbol |
|---|---|---|
| Length | Metre | m |
| Mass | Kilogram | kg |
| Time | Second | s |
| Electric current | Ampere | A |
| Temperature | Kelvin | K |
| Amount of substance | Mole | mol |
| Luminous intensity | Candela | cd |
Derived units are units created from a combination of two or more basic units.
The table below shows some examples of derived units.
| Quantity | Unit Name | Unit Symbol |
|---|---|---|
| Force | Newton = kg × metre / second² | N, kg·m/s2 |
| Torque | Newton × metre | N·m |
| Work | Joule = Newton × metre | J |
| Velocity | Metre / second | m/s |
| Acceleration | Metre / second² | m/s2 |
SI prefixes are shown in the table below.
| Prefix | Symbol | Value | Example Name | Example Symbol | Example Value |
|---|---|---|---|---|---|
| exa | E | 1018 | Exametre | Em | 1018m |
| peta | P | 1015 | Petasecond | Ps | 1015s |
| tera | T | 1012 | Terawatt | TW | 1012W |
| giga | G | 109 | Gigahertz | GHz | 109Hz |
| mega | M | 106 | MegaNewton | MN | 106N |
| kilo | k | 103 | Kilometre | km | 103m |
| hector | h | 102 | Hectolitre | hL | 102L |
| deka | da | 101 | Dekagram | dag | 101g |
| 100(=1) | |||||
| deci | d | 10-1 | Decilitre | dL | 10-1L |
| centi | c | 10-2 | centimetre | cm | 10-2m |
| milli | m | 10-3 | Millimetre | mm | 10-3m |
| micro | µ | 10-6 | Micrometre | µm | 10-6m |
| nano | n | 10-9 | Nanogram | ng | 10-9g |
| pico | p | 10-12 | Picosecond | ps | 10-12s |
| femto | f | 10-15 | Femtometre | fm | 10-15m |
| atto | a | 10-18 | Attosecond | as | 10-18s |
2. Unit conversions
Every physics formula comes with attached matching units. Using different units than those indicated for any specific formula will result in an incorrect answer. A lot of times measurements done in a real-life setting or information collected from studies, research projects, etc., will provide us with measurements of physical quantities that do not correspond to those required in the formulas. This creates the need to convert units to those that match a specific type of calculation. Another need for converting units arises when it is necessary to use consistent units of measurement in situations where some quantities are expressed in SI units and others in Imperial units. A conversion factor is a ratio or a fraction equal to 1. You can multiply any number by 1 without changing the original value. When you multiply a number by a conversion factor, you are simply multiplying it by one. The conversion factor will contain either:
- The new (desired) units in the numerator and the old units in the denominator:
[latex]{\text{OLD UNITS}} \times \frac{\text{NEW UNITS (DESIRED UNITS)}}{\text{OLD UNITS}} \rightarrow {\text{NEW UNITS (DESIRED UNITS)}}[/latex]
or
- The new (desired) units in the denominator and the old units in the numerator:
[latex]{\textstyle \frac{1}{\text{OLD UNITS}}} \times {\textstyle \frac{\text{OLD UNITS}}{\text{NEW UNITS (DESIRED UNITS)}}} \rightarrow {\textstyle \frac{1}{\text{NEW UNITS (DESIRED UNITS)}}}[/latex]
The conversion factor is constructed so that the old units will cancel out and the resulting quantity will be expressed in the new (desired) units. Sometimes we will need more than one conversion factor to obtain the desired units.
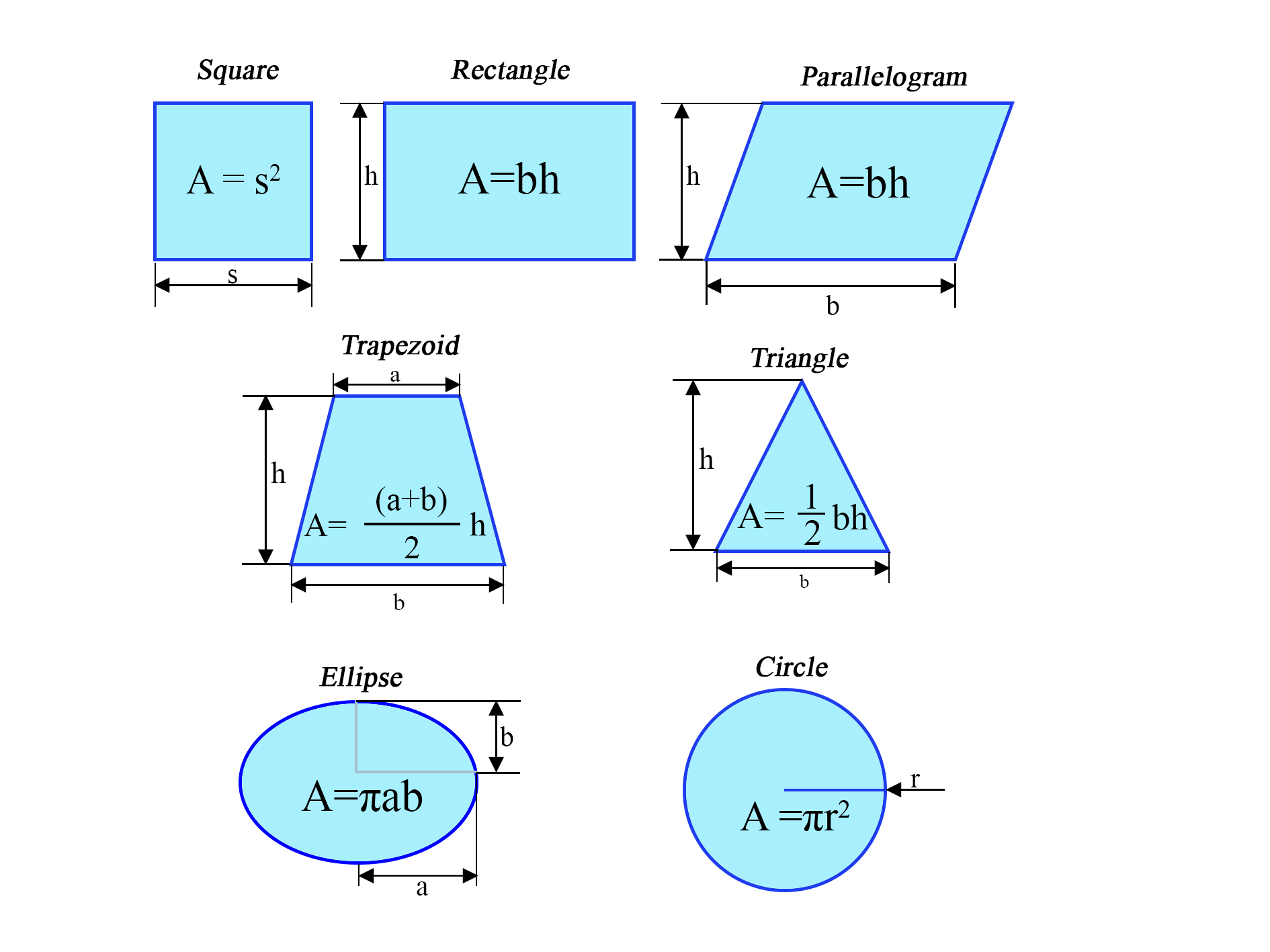
3. Area and volume
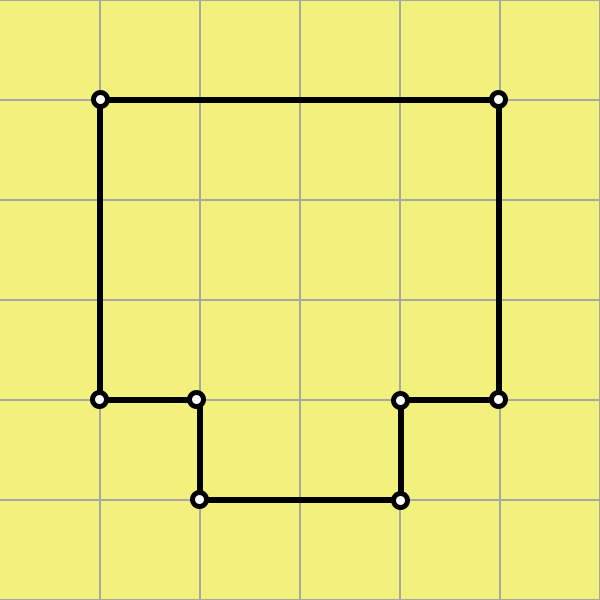
The area of a plane figure is measured in square units. It can be thought as the number of squares required to cover it completely. For instance, if an individual square in the figure below represents [latex]1 \text{ cm}^2[/latex], then the area of the figure below is [latex]14 \text{ cm}^2[/latex].
This can be converted to smaller or bigger units as necessary (such as [latex]\text{mm}^2[/latex] or [latex]\text{m}^2[/latex], etc.). It can also be converted to imperial units such as [latex]\text{ft}^2[/latex] or [latex]\text{in}^2[/latex], depending on the circumstances in which we use the area.
Areas for common shapes are shown below:
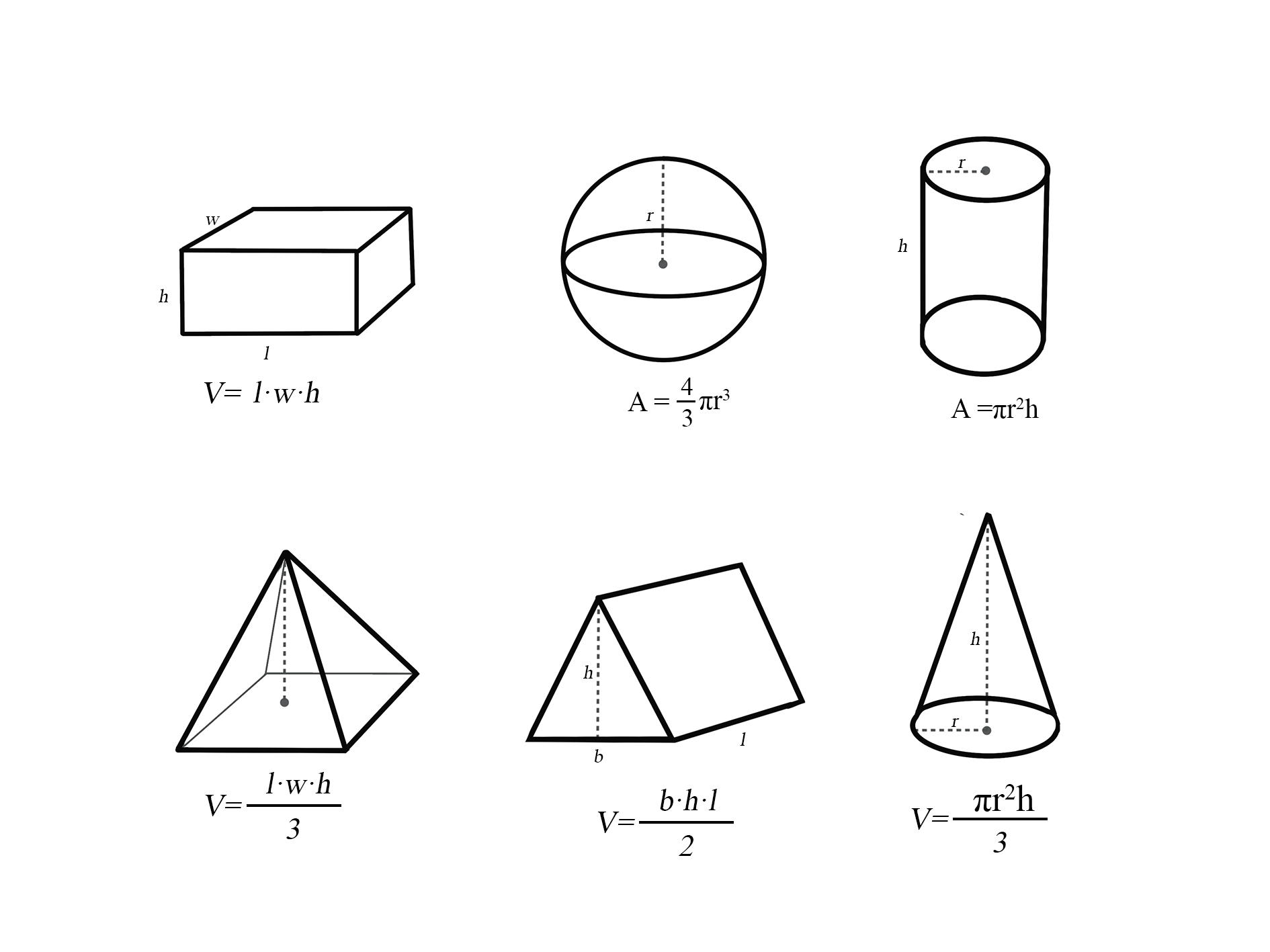
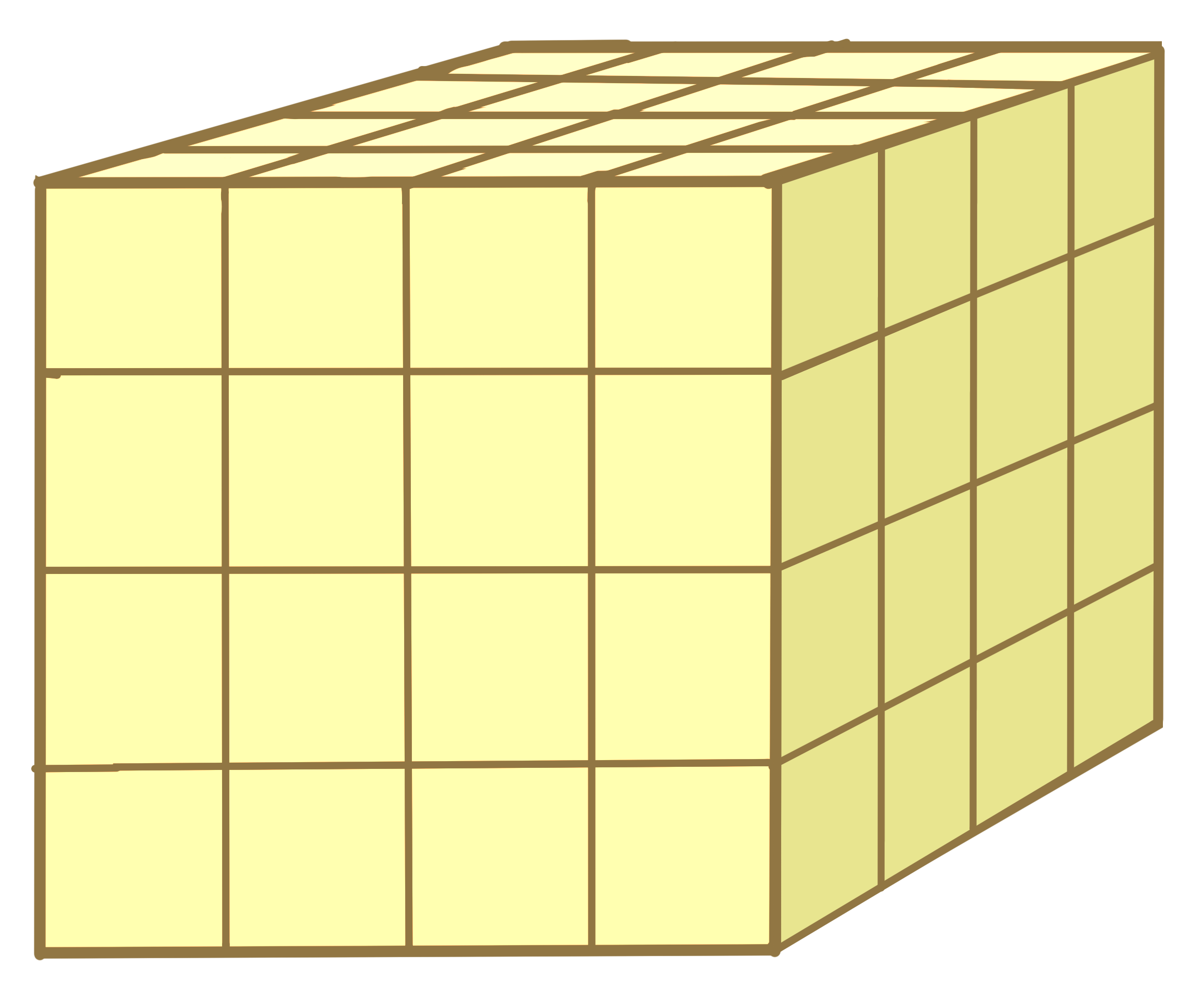
The volume of a figure is measured in cubic units. It can be thought as the number of cubes needed to fill the shape.
For instance, the volume of the rectangular prism below can be found by counting the number of cubes whose sides are each [latex]1 \text{ cm}[/latex] long that are needed to fill up the prism. There are 64 cubes whose sides are [latex]1 \text{ cm}[/latex] long, so the volume of the prism in figure 1.5 is [latex]64 \text{ cm}^3[/latex].
Volume formulas for common shapes are shown below: