Chapter 4. Linear Motional

Learning Objectives

By the end of this chapter, you will be able to:

  1. Define displacement, velocity, and acceleration for a linear motion.
  2. Distinguish between speed and velocity, distance and displacement.
  3. Use kinematic equations to solve linear motion questions.

Introduction

Linear motion is a change in position from one point to another in a  straight line in one dimension.

Examples of linear motion are driving on a straight highway, walking on a straight path in a park, and so on.

If the speed at which the object travels does not change in time (i.e., remains constant), then the motion is called uniform linear motion. If the speed changes over time (either increasing or decreasing) then the motion is called accelerated linear motion.

Concepts

4.1 Displacement
4.2 Velocity
4.3 Acceleration

4.1 Displacement 

Displacement is the vector equivalent of distance, and it can be represented as the line that connects the starting point to the end point of the motion.

Example

Suppose a bee flies from the forest (point A) to the hive (point B) following the dotted orange path. Measuring the length of this path will indicate the distance travelled by the bee. The displacement, though, will be the vector that connects point A to point B; this displacement will have a magnitude equal to the length of the vector [latex]\overrightarrow{AB}[/latex] and the direction indicated by the arrow of the vector.
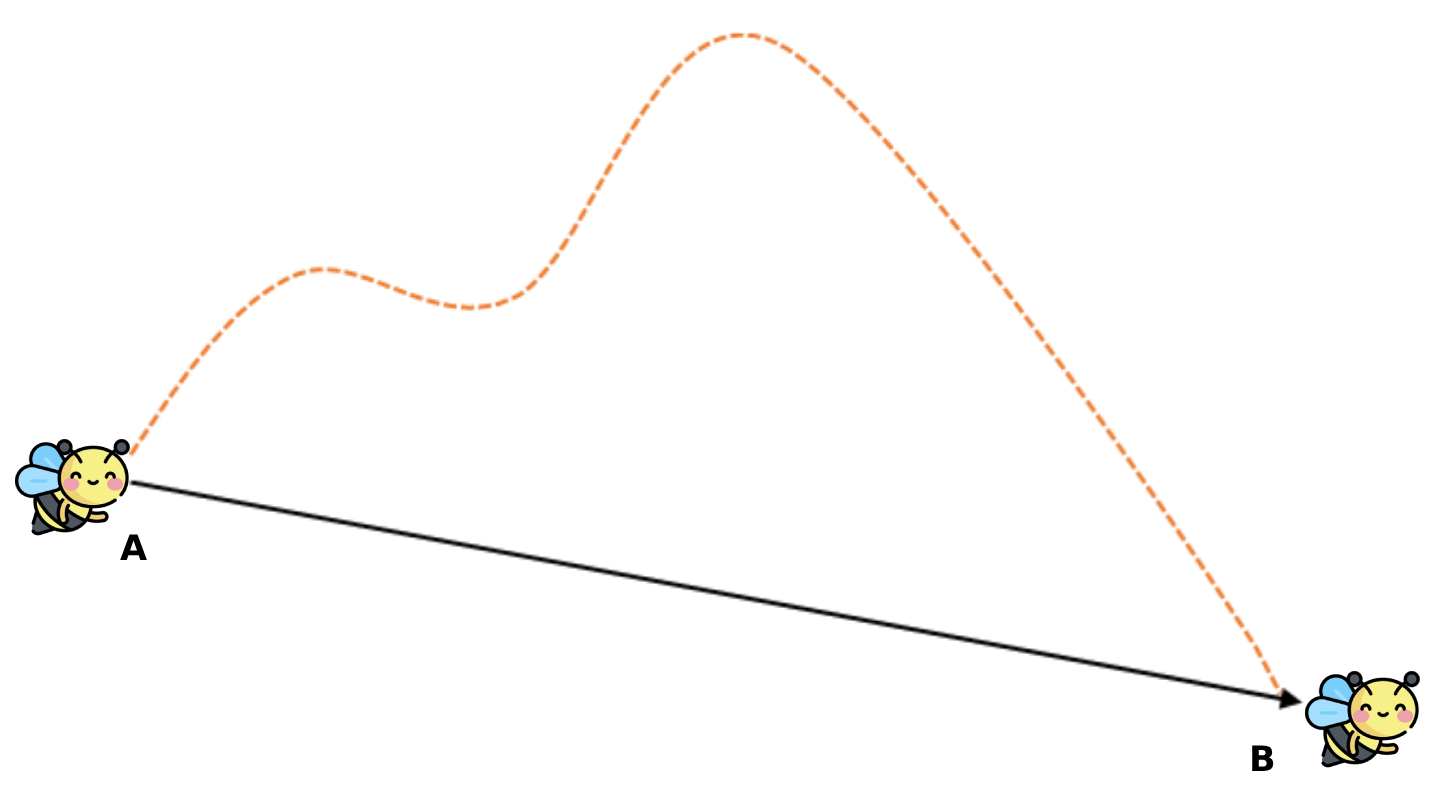
Two bees are positioned at points A and B, connected by a straight black arrow and a wavy orange dashed line, representing direct and indirect paths between the points.
Figure 4.1 Displacement versus distance

In the SI system, displacement is measured in meters (m). Prefixes are used to represent smaller or greater displacements, such as centimetres, kilometres, etc.

4.2 Velocity

Velocity is a vector quantity that represents the distance travelled in a certain amount of time (i.e., it describes how fast objects move). Velocity is the vector equivalent of speed.

The average speed can be calculated as:

[latex]\large v_{\text{average}} = \frac{s}{t}[/latex]

where:

[latex]s[/latex] represents the distance in [m]; and

[latex]t[/latex] represents the time in [s].

It follows that speed will be measured in [m/s].

There are two types of linear motion (decided by the qualities of speed or velocity):

  1. If the velocity stays constant during the motion (i.e., does not change in magnitude or direction), the motion is called uniform linear motion: [latex]\boldsymbol{\mathcal{v}} = \text{constant}[/latex].
  2. If the velocity changes in magnitude during the motion (either increases or decreases), the motion is called accelerated linear motion: [latex]\boldsymbol{\mathcal{v}} \neq \text{constant}[/latex].

In the second case, there is another quantity that will describe the motion: the acceleration.

4.3 Acceleration

Acceleration is a vector quantity that represents the rate of change for the velocity in an accelerated linear motion.

The acceleration can be calculated as:

[latex]\large a = \frac{\Delta v}{t} = \frac{v_f - v_i}{t}[/latex]   (1)

where:

[latex]{\Delta v}[/latex] represents the change in velocity in [m/s];

[latex]t[/latex] represents the time in [s]

[latex]v_f[/latex] represents the final velocity in [m/s]

[latex]v_i[/latex] represents the initial velocity in [m/s]

[latex]a[/latex] represents the acceleration in [m/s2].

In the formula above, the change in velocity is calculated by subtracting the initial velocity from the final velocity.

Acceleration can be positive or negative. In the figures below, if the car is increasing its velocity, the acceleration is positive; if the car is decreasing its velocity, the acceleration will be negative.

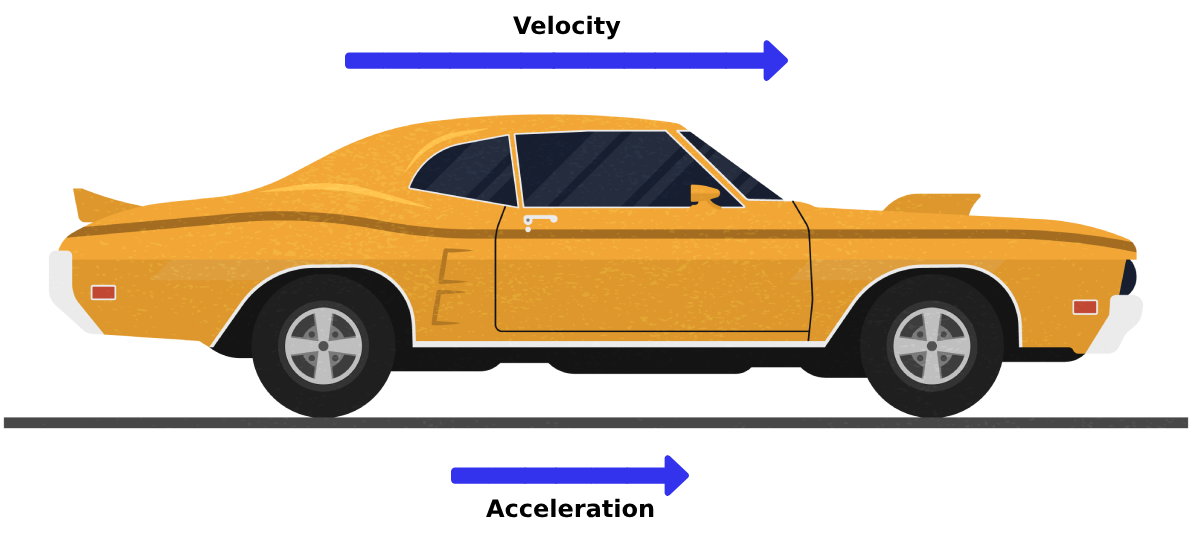
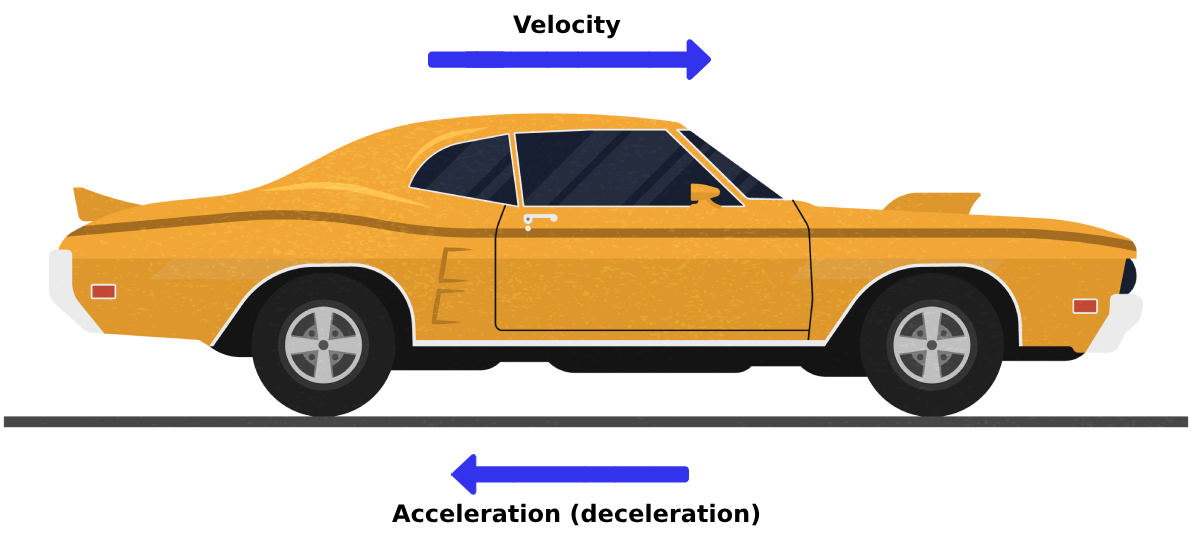
The image shows a yellow car with two blue arrows: one labeled "Velocity" and another labeled "Acceleration," both pointing to the right, indicating that the car is moving and accelerating in the same direction.
Figure 4.2 Speeding up (increasing velocity)

 

The image shows a yellow car with two blue arrows: one labeled "Velocity" and another labeled "Acceleration," both pointing to the right, indicating that the car is moving and accelerating in the same direction.
Figure 4.3 Slowing down (decreasing velocity)

 

Identifying the initial and the final velocity in linear motion questions 

Example 1. A car accelerates from [latex]10 \, \text{m/s}[/latex] to [latex]20 \, \text{m/s}[/latex] in [latex]10 \, \mathrm{s}[/latex]. 

[latex]v_i[/latex] = [latex]10 \, \mathrm{m/s}[/latex]

[latex]v_f[/latex] = [latex]20 \, \mathrm{m/s}[/latex]

Example 2. A train accelerates from rest to [latex]50 \, \mathrm{km/h}[/latex] in 5 minutes. 

[latex]v_i[/latex] = [latex]0 \, \mathrm{km/h}[/latex]

[latex]v_f[/latex] = [latex]50 \, \mathrm{km/h}[/latex]

Example 3. A runner going at [latex]2.0 \, \mathrm{m/s}[/latex] slows to a stop in [latex]4 \, \mathrm{s}[/latex]. 

[latex]v_i[/latex] = [latex]2.0 \, \mathrm{m/s}[/latex]

[latex]v_f[/latex] = [latex]0 \, \mathrm{m/s}[/latex]

Using the initial and final velocity in an accelerated linear motion, we can express the displacement:  

[latex]S = \frac{v_i + v_f}{2} \times t[/latex]   (2)

Combining formulas (1) and (2), we can derive two more formulas for the accelerated linear motion: 

[latex]S = v_i t + \frac{1}{2} a t^2[/latex]   (3)

[latex]v_f^2 = v_i^2 + 2aS[/latex]   (4)

Solved Examples

Example 1     

A car starts from rest and accelerates at a rate of [latex]2.1\mathrm{m/s^2}[/latex] for [latex]10\, \text{s}[/latex]. Find the final velocity of the car.

Given:
[latex]v_i[/latex] = [latex]0\mathrm{m/s}[/latex]
[latex]a[/latex] = [latex]2.1\mathrm{m/s^2}[/latex]
[latex]t[/latex] = [latex]20\, \text{s}[/latex]
Find:
[latex]v_f[/latex] = [latex]?[/latex]

Solution:

    1. Decide which equation works for the question by examining what information is given and what needs to be found.

      [latex]a = \frac{v_f - v_i}{t}[/latex]

    2. Rearrange the equation to express the wanted quantity:

      [latex]v_f = v_i + at[/latex]

    3. Substitute the values for the known quantities in the last equation:

      [latex]v_f = 0 + 2.1 \times 10 = 21 \, \text{m/s}[/latex]

Answer:

[latex]v_f = 21 \text{m/s}[/latex]

Example 2 

A truck travelling at 25 m/s slows down to 10 m/s in 100 m. Find the truck’s acceleration.

Given:
[latex]v_i[/latex] = [latex]25\mathrm{m/s}[/latex]
[latex]v_f[/latex] = [latex]10\mathrm{m/s}[/latex]
[latex]s[/latex] = [latex]25m[/latex]
Find:
[latex]a[/latex] = [latex]?[/latex]

Solution:

  1. Decide which equation works for the question by examining what information is given and what needs to be found.

    [latex]v_f^2 = v_i^2 + 2aS[/latex]

  2. Rearrange the equation to express the wanted quantity:

    [latex]a = \frac{v_f^2 - v_i^2}{2S}[/latex]

  3. Substitute the values for the known quantities in the last equation:

    [latex]a = \frac{10^2 - 25^2}{2 \times 100} = -2.6 \, \text{m/s}^2[/latex]

Answer:

[latex]a = -2.6 \, \text{m/s}^2[/latex]

Chapter Equations

 

[latex]a = \frac{\Delta v}{t} = \frac{v_f - v_i}{t}[/latex]   (1)

[latex]S = \frac{v_i + v_f}{2} \times t[/latex]   (2)

[latex]S = v_i t + \frac{1}{2} a t^2[/latex]   (3)

[latex]v_f^2 = v_i^2 + 2aS[/latex]   (4)

Try It!

Choose the appropriate formula from the chapter equations above for a one-step solution to the following:

  1. A cheetah reached a speed of [latex]35 \, \mathrm{m/s}[/latex] after covering a distance of [latex]125 \, \mathrm{m}[/latex] in [latex]9.0 \, \mathrm{s}[/latex]. What was the cheetah’s initial velocity?
  2. A streetcar starts from rest and travels [latex]58 \, \mathrm{m}[/latex] accelerating at a rate of [latex]0.65 \, \mathrm{m/s^2}[/latex]. How long did it take to cover the [latex]58 \, \mathrm{m}[/latex]?
  3. A train is decelerating at a rate of [latex]1.5 \, \mathrm{m/s^2}[/latex] to a stop. If the velocity at the time it was starting to decelerate was [latex]30 \, \mathrm{m/s}[/latex], find the stopping distance.

Practice

    1. A penguin slides down a glacier starting from rest and accelerates at a rate of [latex]7.6 \, \text{m/s}^2[/latex]. If it reaches the bottom of the hill travelling [latex]15 \, \text{m/s}[/latex], how long does it take to get to the bottom?

      Answer:

      [latex]1.97\, \text{s}[/latex]

       

    2. A car slows from [latex]45 \, \text{m/s}[/latex] to [latex]30 \, \text{m/s}[/latex] in [latex]6.2 \, \text{s}[/latex]. How far does it travel in that time?

      Answer:

      [latex]232.5 \, \text{m}[/latex]

       

    3. A cyclist speeds up from his [latex]8.45 \, \text{m/s}[/latex] pace. As he accelerates, he travels [latex]325 \, \text{m}[/latex] in [latex]30 \, \text{s}[/latex]. What is his final velocity?

      Answer:

      [latex]13.2 \, \text{m/s}[/latex]

       

    4. If a car was going at a speed of [latex]35 \, \text{m/s}[/latex] when it starts to decelerate at a rate of [latex]4.64 \, \text{m/s}^2[/latex] to a complete stop, how long did it take for the car to stop?
      ​
      Answer:

      [latex]7.5 \, \text{s}[/latex]

       

    5. A train decelerates at a rate of [latex]3.5 \, \text{m/s}^2[/latex] to a stop in [latex]150 \, \text{m}[/latex]. What was the train’s speed when it started to decelerate?

      Answer:

      [latex]32.4 \, \text{m/s}[/latex]

       

 

Challenge Questions

Question 1. A drag-racing car accelerates from rest at a rate of [latex]11.0 \, \text{m/s}^2[/latex] for a distance of [latex]120 \, \text{m}[/latex]. The car coasts for [latex]0.75 \, \text{s}[/latex]; then the driver brakes and opens the parachute to decelerate until the end of the track. If the total length of the track is [latex]200 \, \text{m}[/latex], what is the minimum deceleration rate to stop before reaching the end of the track?

Answer:

[latex]-11.8 \, \text{m/s}^2[/latex]

 

Question 2. A driver is going at a constant speed of [latex]28.0 \, \text{m/s}[/latex]. She sees a moose jump onto the road [latex]56.0 \, \text{m}[/latex] in front of her. The driver brakes and decelerates at [latex]7.5 \, \text{m/s}^2[/latex], stopping in front of the moose. What is the driver’s reaction time? (In other words, how long did it take the driver to react to the event prior to decelerating?)

Answer:

[latex]0.13 \, \text{s}[/latex]

 

Image Attributions

License

Icon for the Creative Commons Attribution-NonCommercial 4.0 International License

College Physics – Fundamentals and Applications Copyright © by Daniela Stanesca, Centennial College is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License, except where otherwise noted.

Share This Book