1.2. Solved Examples: Units and Unit Conversions; Systems of Measurement
Example 1. Converting between two sets of SI units
Convert [latex]45 \text{ km/h}[/latex] to [latex]\text{ m/s}[/latex].
Solution:
We need to create two conversion factors: one to change kilometres to metres, and one to change hours to seconds.
[latex]{45 \, \text{km/h}} \times \frac{1000 \, \text{m}}{1 \, \text{km}} \times \frac{1 \, \text{h}}{3600 \, \text{s}} = {12.5 \, \text{m/s}}[/latex]
Answer:
[latex]{12.5 \, \text{m/s}}[/latex]
Example 2. Converting between an SI unit and an Imperial unit
Convert [latex]0.57 \text{ ft}[/latex] to metres, knowing that [latex]1 \text{ inch}[/latex] = [latex]2.54 \text{ cm}[/latex] and [latex]1 \text{ ft}[/latex] = [latex]12 \text{ inch}[/latex].
Solution:
We need to create three conversion factors: one to change the unit of measurement from feet to inches, the second to change the unit of measurement from inches to centimetres, and the last to change the unit of measurement from centimetres to metres.
[latex]{0.57 \, \text{ft}} \times \frac{12 \, \text{in}}{1 \, \text{ft}} \times \frac{2.54 \, \text{cm}}{1 \, \text{in}} \times \frac{1 \, \text{m}}{100 \, \text{cm}} = {0.17 \, \text{m}}[/latex]
Answer:
[latex]{0.17 \, \text{m}}[/latex]
Example 3. Calculating areas and converting between area units
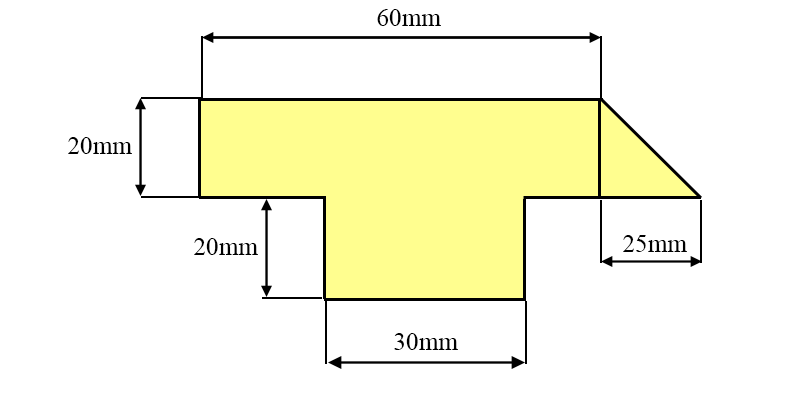
- Calculate the cross-sectional area of the figure below.
- Convert from [latex]\text{mm}^2[/latex] to [latex]\text{m}^2[/latex].
Answer:
- [latex]20 \times 60 + 20 \times 30 + \frac{25 \times 20}{2} = 2050 \text{ mm}^{2}[/latex]
- [latex]2050 \text{ mm}^{2} \times 10^{-6} = 2.050 \times 10^{-3} \text{ m}^{2}[/latex]
Example 4. Calculating volume
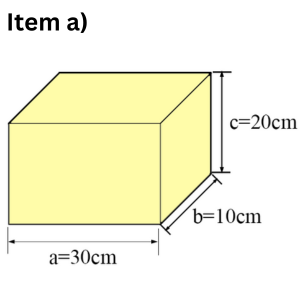
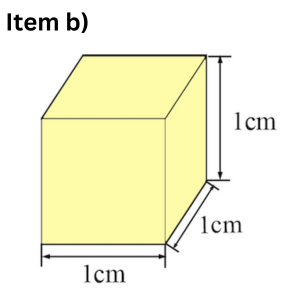
Find the volume of the rectangular prism shown below.
Answer:
It will take [latex]6000[/latex] small cubes to fill out that rectangular prism, so that the volume of the prism is[latex]\text{ V } = 6000 \, \text{cm}^{3}[/latex].
Example 5. Calculating volumes and converting between volume units
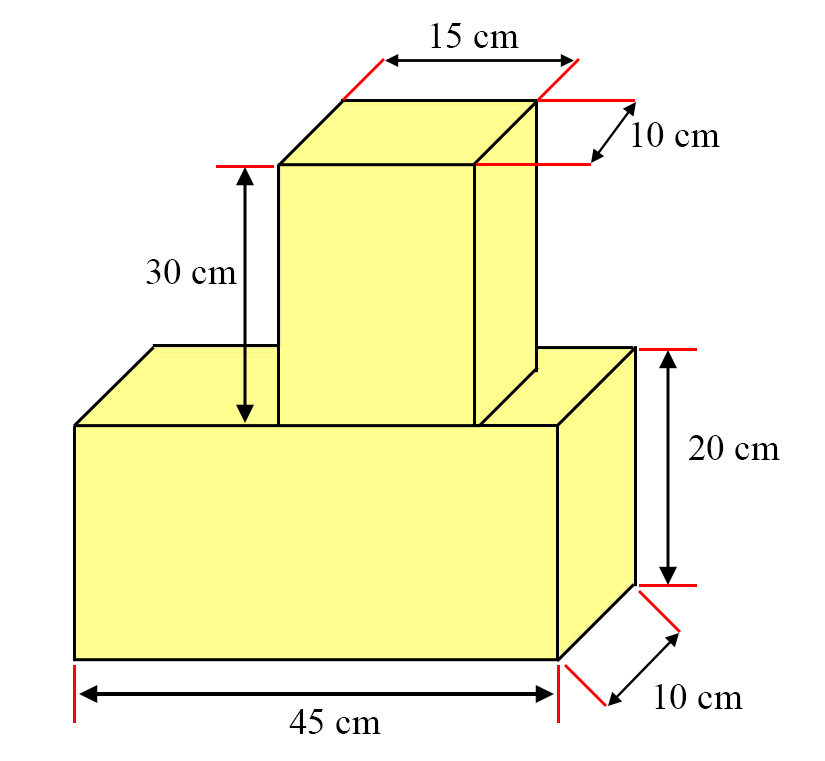
- Calculate the volume of the shape above in [latex]\text{m}^3[/latex].
- Convert the volume to [latex]\text{in}^3[/latex].
Answer:
- [latex]{30 \times 15 \times 10 + 45 \times 10 \times 20 = 13{,}500 \text{ cm}^{3} = 0.0135 \text{ m}^{3}}[/latex]
- [latex]13{,}500 \text{ cm}^{3} \times \frac{1 \text{ in}^{3}}{(2.54)^{3} \text{ cm}^{3}} = 823.82 \text{ in}^{3}[/latex]
Try it!
Choose the correct solution:
When we convert from a bigger unit (such as a kilometre) to a smaller unit (such as a metre), we multiply by a power of 10 that has a:
- positive exponent
- negative exponent
When converting between units of volume, what is the correct approach:
- [latex]2 \text{ m}^{3}[/latex] converted to [latex]\text{in}^{3}[/latex] will be converted as:
[latex]{2 \text{ m}^{3}} \times \frac{10^{6} \, \text{cm}^{3}}{1 \, \text{m}^{3}} \times \frac{1 \, \text{in}^{3}}{(2.54)^{3} \, \text{cm}^{3}} = {1.22 \times 10^{5} \, \text{in}^{3}}[/latex] - [latex]2 \text{ m}^{3}[/latex] converted to [latex]\text{in}^{3}[/latex] will be converted as:
[latex]{2 \, \text{m}^{3}} \times \frac{10^{6} \, \text{cm}^{3}}{1 \, \text{m}^{3}} \times \frac{1 \, \text{in}^{3}}{2.54 \, \text{cm}^{3}} = {7.87 \times 10^{5} \, \text{in}^{3}}[/latex]

