3.2. Solved Examples: Vector Addition
Solved example
Three forces act on a point: 3 N at 0°, 4 N at 90°, and 5 N at 217°. What is the net force? Round off intermediate answers to whole numbers.
|
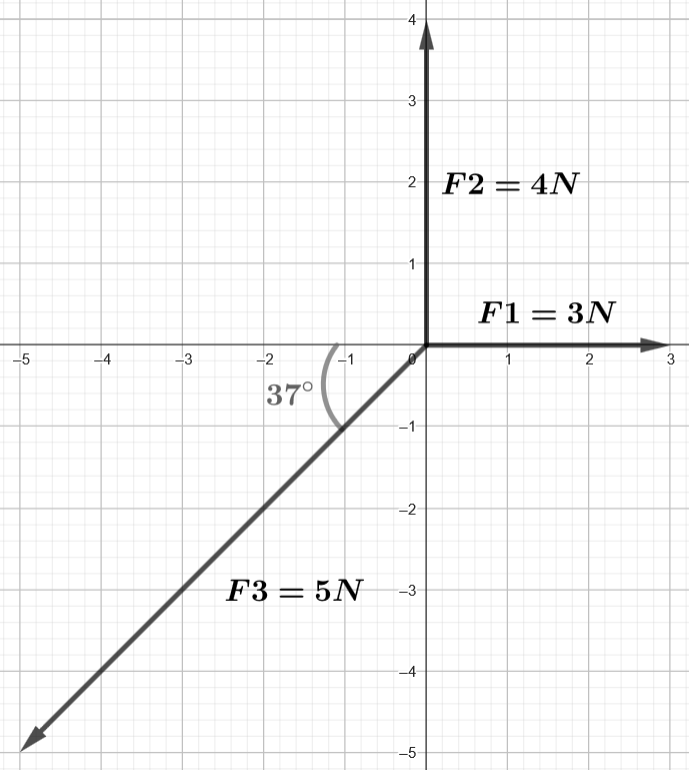
[latex]x_{components}[/latex]
|
[latex]y_{components}[/latex] | |
|---|---|---|
| [latex]\overrightarrow{F1}[/latex] | 3 | 0 |
| [latex]\overrightarrow{F2}[/latex] | 0 | 4 |
| [latex]\overrightarrow{F3}[/latex] | [latex]5 * \cos(217°) = -4[/latex] | [latex]5 * \sin(217°) = -3[/latex] |
| [latex]\overrightarrow{R}[/latex] | -1 | 1 |
Step 1. Calculate both x and y components of all vectors that are to be added, and organize the information in a table (as shown above).
Step 2. Add all x components and then all corresponding y components, and write the results in the last row. The results represent the x component and the y component of the resultant, R.
Step 3. Calculate the magnitude of the resultant by using the Pythagorean theorem:
[latex]R=\sqrt{x^2+y^2}=\sqrt{2}=1.41N[/latex]
Step 4. Decide what quadrant the resultant lies into, by analyzing the signs of the components. Since the x component is negative and the y component is positive, the resultant will be positioned in the second quadrant.
Step 5. Calculate the reference angle related to the resultant by using the inverse tangent:
[latex]\alpha=\tan^{-1}(\frac{\left|y\right|}{\left|x\right|})=\tan^{-1}(\frac{1}{1})=45°[/latex]
Step 6. Calculate the angle in standard position related to the resultant by using the corresponding formula for the quadrant of the resultant.
Recall:
Quadrant 1: [latex]\theta=\alpha[/latex]
Quadrant 2: [latex]\theta=180°-\alpha[/latex]
Quadrant 3: [latex]\theta=180°+\alpha[/latex]
Quadrant 4: [latex]\theta=360°-\alpha[/latex]
Quadrant 2: [latex]\theta=180°-\alpha =180°-45°=135°[/latex]
Answer: [latex]R=1.41N,\theta=135°[/latex]
Image Attributions
-
- Figure 3.4: Created with Geogebra and licensed under CC-BY-NC-SA 3.0.
